Dependable Wireless System with Shortened Code Using Distance Information between Integrated Terminals

Abstract

Since wireless systems allow for easier access to communication paths than wired systems, it is necessary to improve their dependability against cyberterrorists. To make wireless systems more dependable, additional measures at the lower layer are required, in addition to those at the upper layers. Our proposal uses an integrated terminal-like cellular phone which has multiple radio access technologies (RATs) such as cellular, wireless local area network (LAN), Bluetooth, and an ultra-wide band (UWB). We propose to communicate information encoded by shortened code using multiple RATs. Redundancy by RATs and their error correction capability can simultaneously improve wiretap resistance and attack resistance. A codeword of shortened code is obtained by removing a part of a codeword of popular code. A decoder can improve the error correction capability if the removed part is known. By using shortened codes, the dependability can be further enhanced because the error correction capability between the legitimate receiver and the cyberterrorist can make a difference. To do this, it is necessary to securely share the removed part between the sender and receiver. Our proposal is to securely measure the distance between the sender and receiver using UWB and use it as the removed part. It was confirmed that the secrecy capacity is improved.

1. Introduction

Since fifth-generation mobile communication systems (5G) can provide high performance such as high data rate or capacity, ultra-low latency, and massive connectivity, 5G is expected to be applied to various applications [1]. Although sixth-generation mobile communication systems are being researched for extreme high performance over 5G, one of the most important concepts is network dependability. If a wireless sensor network (WSN) is not able to report critical alerts due to a network failure such as the crash of a node and battery exhaustion, it has been pointed out that it may cause severe failures with dangerous consequences. Examples of such critical applications are health monitoring, ambient intelligent systems, and environmental monitoring. Therefore, when using WSNs in critical applications, it is important to verify their reliability properties based on heuristic strategies such as “what-if analysis” and “robustness checking” at design time [2]. In addition to trustworthiness, dependability of WSN is also related to attributes like safety and security [3]. Therefore, the proper management of these attributes could avoid economic losses and danger to people or to the system [4,5]. Taking this into account, since WSNs provide easier access to communication channels than wired networks, measures should be taken not only for the crash of a node and battery exhaustion, but also for human-induced wiretapping such as packet sniffing and attacks such as jamming.

Although countermeasures against wiretapping and attacks have been studied individually, countermeasures against cyberterrorists who can wiretap and attack simultaneously are necessary. Typically, countermeasures against wiretapping and attacks are implemented with cryptography [6] and authentication [7] at higher layers. To make a wireless system more dependable, it is necessary to take additional measures at lower layers.

We propose that a terminal with multiple radio access technologies (RATs), such as a cellular phone, defined as an integrated terminal, communicates using multiple RATs. If multiple RATs are used for communication, even if one RAT is attacked by a cyberterrorist, the receiver can recover the original information by using the information received from the sender via the other RATs. However, if the sender transmits the same information using multiple RATs, the cyberterrorist can obtain the original information with only one RAT wiretapping. Therefore, we propose the forward error correction (FEC) coding of information. There are still issues. If there are not enough RATs available, countermeasures against wiretapping and attacks cannot be realized simultaneously.

If there are two RATs available, the sender encodes in a way that the cyberterrorist cannot obtain the original information even if one RAT is wiretapped. If the cyberterrorist attacks one RAT instead of wiretapping, the receiver cannot obtain the original information. We use shortened code as an FEC code. Shortened code is obtained by adding a simple modification to a known code [8]. We propose to use distance information between the sender and the receiver as the shortened information used for the encoding and decoding of shortened code.

The mutual information is used as an evaluation index of the attack resistance. It is a measure of the mutual dependence between the two variables [9]. It is the index suitable for evaluating how much information can be shared between the sender and the receiver under an attack. The secrecy capacity is used as an evaluation index of the wiretapping resistance. It is defined as the maximum transmission rate between the sender and the receiver with no information available to the cyberterrorist [10].

The remainder of this paper is organized as follows. Section 2 presents related work. In Section 3, the system configuration of the proposed dependable wireless system is described. Performance evaluations are provided in Section 4. Conclusions and suggestions for future research are presented in Section 5.

2. Related Works

Cryptography is commonly used as a countermeasure against wiretapping, and authentication is commonly used as a countermeasure against attacks. Cryptography is classified into common key cryptography and public key cryptography [6]. The common key cryptography performs encryption and decryption using the common key in the sender and the receiver. Therefore, it is necessary for the sender and the receiver to share the key which is known to no one else [6]. On the other hand, public key cryptography involves the receiver publishing the public key, the sender encrypts information using the public key, and the receiver decrypts it using the private key paired with the public key. Although public key encryption does not require key sharing, many studies have been conducted to discover public keys securely and efficiently [11,12,13].

Authentication includes password authentication, biometric authentication, and one-time password authentication [7]. Password authentication uses passwords that are registered on the authentication server. Only users who know the password can be authenticated. Biometric authentication uses biometric information as the password. It has a lower risk of forgery, theft, and forgetting than a password. One-time password authentication is effective as a countermeasure against forgery and theft because the password is changed every time.

These are countermeasures for the upper layer, but countermeasures for the lower layer—that we are targeting—are also being studied.

As countermeasures against wiretapping at the lower layer, there are key generation methods using biometric and physical information. Examples of physical information are channel state information, received signal strength indicators, distance, angle of arrival, and so on [14,15]. Biometric information is specific to each user, and physical information is specific to the location of the user. Using user-specific information, keys can be created securely. For this reason, attempts to use biometric information for authentication have been made for a long time, and it has been used practically for unlocking cellular phones. Distance or location information measured by an ultra-wide band (UWB) is applied for keyless entry authentication to prevent relay attacks for unlocking automobiles [16], and it is expected to be put into practical use soon. These key generation methods can also be used for our proposed shortened information. We select the distance information considering the accuracy and feasibility of cellular phones.

Shamir’s secret sharing has been applied to multiple communication channels [17]. Shamir’s secret sharing is an algorithm in cryptography [18]. Information is divided into multiple parts of distributed information using polynomials and shared. To reconstruct the original information, a certain number of parts are required. Shamir’s secret sharing is not efficient in communication, and many studies have been conducted to solve this problem [19,20,21]. In [17], when encrypted information is transmitted using multiple channels, the encryption key for the information is encrypted by using Shamir’s secret sharing and transmitted through multiple channels, thereby achieving highly reliable communication. We used the concept of secret sharing, but our proposal uses shortened code to transmit more efficiently and to increase attack resistance simultaneously.

As countermeasures against attacks at the lower layer, improvements are made to the signal-to-noise ratio (SNR) by a smart antenna composed of multiple antennas [22]. Beamforming is realized by adjusting the phase and amplitude of each antenna. The sender can increase the SNR of the receiver by directing the beam toward the receiver. The sender can decrease the SNR of the cyberterrorist by directing the null to the cyberterrorist. This study differentiates the reception performance of the receiver and the cyberterrorist by the directivity of the antenna, but our proposal differentiates between them by the error correction capability.

Packet duplication is a technique to improve reliability by transmitting the same packet over multiple redundant parallel links [23]. Although it is the same as using multiple redundant parallel links, our proposal can increase attack resistance to a greater degree than this study because it sends encoded information.

Frequency hopping is a technique used in Bluetooth. By periodically changing the frequency used for communication, attack resistance is increased. In [24], an adaptive frequency hopping method which changes to a new frequency only when the packet drop rate of the channel beyond a given threshold is proposed. The adaptive frequency hopping can increase the network reliability by 10–20%. We have always used multiple RATs, but we would like to consider selecting the RATs by scheduling.

The novelty of our proposal is to communicate information encoded by shortened code using multiple RATs. Redundancy by RATs and error correction capability can simultaneously improve wiretap resistance and attack resistance. By using shortened codes, the dependability can be further enhanced because the error correction capability between the receiver and the cyberterrorist can make a difference. To do this, the distance between the sender and the receiver is shared securely using UWB.

3. Dependable Wireless System

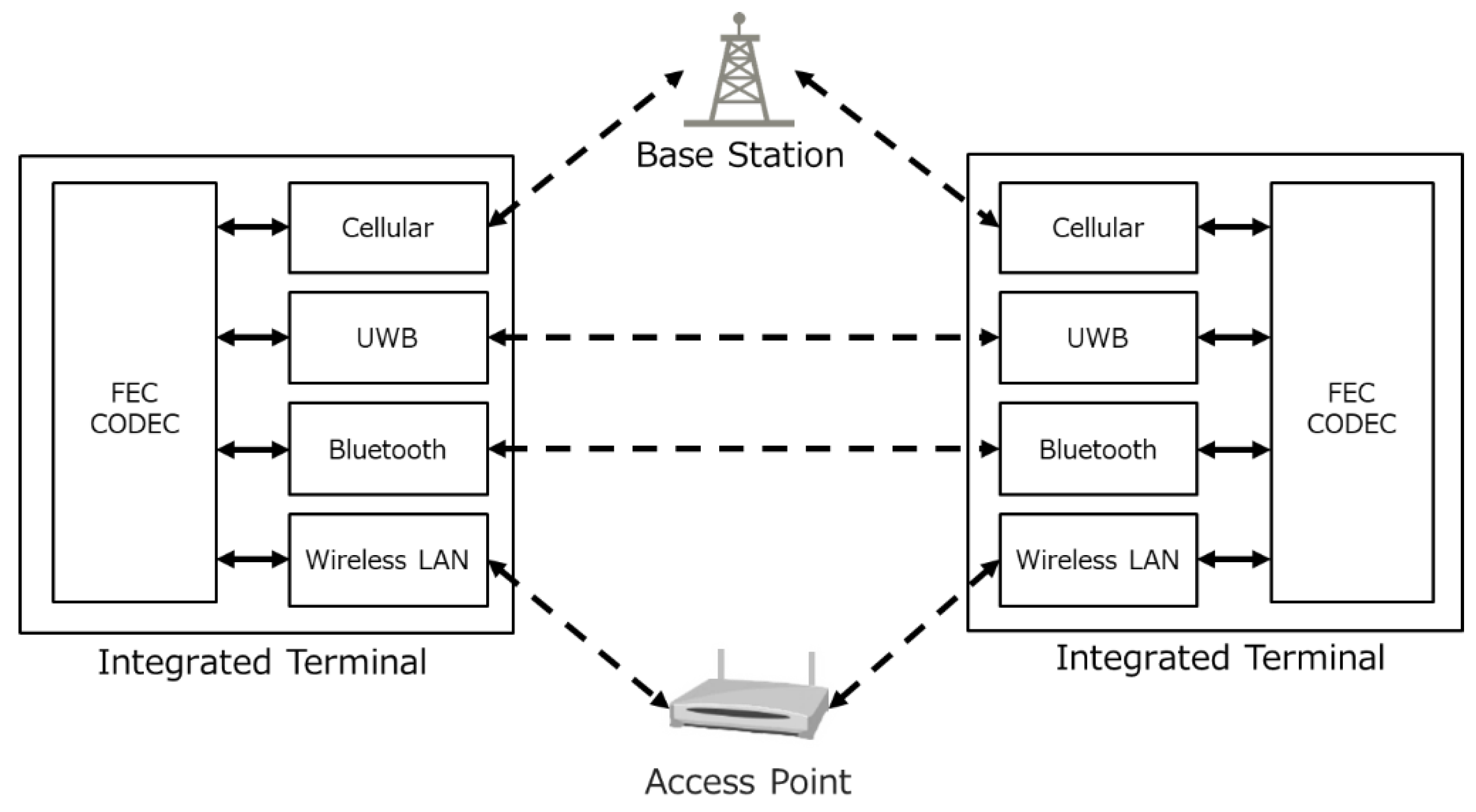
3.1. System Configuration

Figure 1 shows the proposed dependable wireless system. The terminal is an integrated terminal with multiple RATs such as cellular, UWB, Bluetooth, wireless local area network (LAN), and so on. Integrated terminals are commonplace because many cellular phones have cellular, Bluetooth, wireless LAN, and the iPhone 11 and 12 already have UWB chips, U1 chips, and many future cellular phones will have UWB chips. UWB is a technology which enables both communication and ranging [25]. Integrated terminals are equipped with an FEC coder–decoder (CODEC), and the encoded information is divided and communicated using multiple RATs simultaneously. Even if some RATs are attacked, the transmitted information can be recovered using encoded information received by other RATs. Even if some RATs are wiretapped, the transmitted information cannot be recovered using less encoded information. Thus, the proposed system is a realistic system that can be implemented with cellular phones to improve the information-theoretic security capability against wiretapping and attacks.

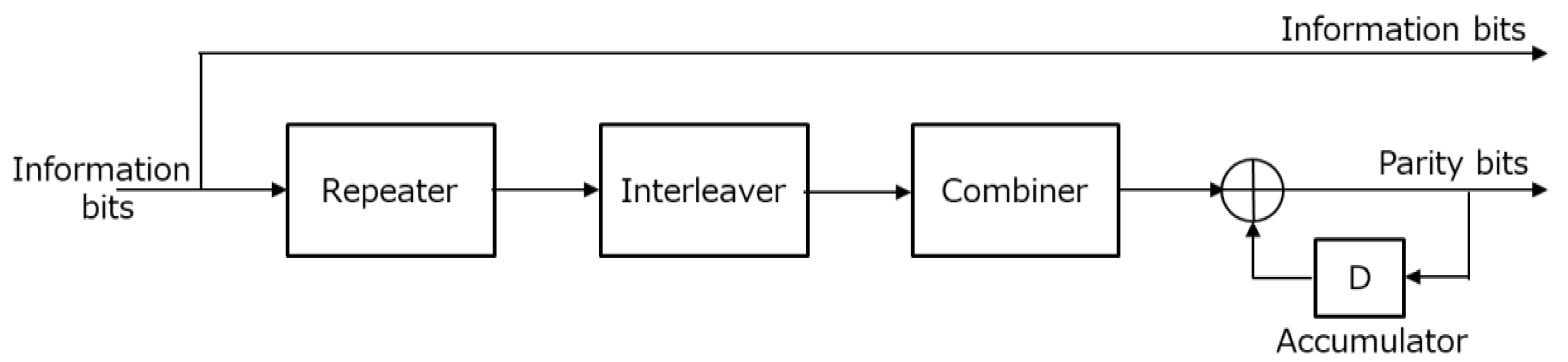
3.2. Shortened Code

The definitions of terms and symbols used in Section 3.2 are listed in

Table 1. Definitions of terms and symbols.

Term/Symbol	Definition
Shortened information	Information to be removed after encoding
Unencoded bits	Bit sequence containing the shortened information and information
Column weight	Number of 1’s in column of information bits of the parity check matrix
Row weight	Number of 1’s in row of information bits of the parity check matrix
$k$	Unencoded bit length
$n$	Codeword length
$m$	Shortened information length
$t$	Number of bits that can be decoded by decoder of ($n$, $k$) code
$s$	Number of bits that can be decoded by decoder of ($n-m$, $k-m$) shortened code without the shortened information
$E$	Efficiency of ($n$, $k$) code
$E_y$	Efficiency of ($n-m$, $k-m$) shortened code when decoder uses the shortened information
$E_z$	Efficiency of ($n-m$, $k-m$) shortened code when decoder does not use the shortened information
$q$	Column weight
$r$	Row weight

.

We propose to adopt shortened code [8] as the FEC code. Figure 2 shows the encoding procedure of ($n-m$, $k-m$) shortened code. The unencoded bits are encoded with ($n$, $k$) code, where $k$ is the unencoded bit length, $n$ is the codeword length. The unencoded bits consists of $m$ ($m >$ 1) bits shortened information and $k-m$ bits information. The codeword of shortened code is obtained by removing $m$ bits shortened information from the codeword of ($n$, $k$) code. ($n-m$, $k-m$) shortened code uses only a limited number of codewords in ($n$, $k$) code, and the minimum distance of ($n-m$, $k-m$) shortened code is not smaller than the minimum distance of ($n$, $k$) code.

If ($n$, $k$) code can correct $t$ bit errors, the efficiency is defined as $E$.

$$E=\frac{t}{n}$$

(1)

($n-m$, $k-m$) shortened code can correct $t$ bit errors, if the decoder uses the shortened information. The efficiency $E_y$ is expressed by the following equation.

$$E_y=\frac{t}{n-m}$$

(2)

From Equations (1) and (2), the relationship between $E$ and $E_y$ is as follows.

$$E<E_y$$

(3)

This indicates that the error correction capability is improved by shortening, and the same error rate can be obtained at a lower SNR than before shortening under an additive white Gaussian noise (AWGN) channel. If the decoder does not use the shortened information, only $s$ ($s\le t$) bit errors can be corrected by the decoder. The efficiency $E_z$ is expressed by the following equation.

$$E_z=\frac{s}{n-m}$$

(4)

Since the decoder does not use the shortened information, it is easy to imagine that $s$ decreases rapidly as $m$ increases. The relation between $E_z$ and $E$ is as follows.

$$E_z\le E$$

(5)

If the sender and the receiver share the shortened information, and the sender and the cyberterrorist do not share the shortened information, by changing the shortened information length, it is possible to provide a gap in the required SNR for the receiver and the cyberterrorist. To realize this, the shortened information must be shared securely between the sender and the receiver. Then, countermeasures against wiretapping and attacks can be realized simultaneously.

We adopted shortened repeat-accumulate (RA) code as the shortened code from the viewpoint that the construction of the encoder is simple, but it is also applicable to the Turbo code, low-density parity check (LDPC) code, and Polar code used in 5G. RA code is a code which was proposed in 1998 by Divsalar et al. [26]. Figure 3 shows the structure of systematic RA code encoder. Define $q$ as the number of copies of a bit in the repeater and $r$ as the number of additions of bits in the combiner. The parameters $q$ and $r$ are important factors that determine the characteristics of the code. The parity check matrix of systematic RA code is shown in Figure 4. The number of 1’s in the column of information bits is called the column weight, and its number is equal to $q$. The number of 1’s in the row of information bits is called the row weight, and its number is equal to $r$. When designing RA codes, the number and position of 1′s are important parameters which affect the characteristics. As seen from the parity check matrix, it can also be considered as a low-density generator matrix (LDGM) code [27] which is a kind of LDPC code [28]. Therefore, RA code can be decoded by an algorithm such as message passing as in LDPC code, and its characteristics are close to the Shannon limit.

3.3. Sharing Method of Shortened Information

To provide high error correction capability to the receiver and low error correction capability to the cyberterrorist, the sender and the receiver need to share the shortened information securely. We propose to use distance information between integrated terminals as the shortened information. Distance information is measured by UWB which performs ranging and positioning with high resolution in the order of centimeters because it communicates over a wide band using pulses with short time intervals in the order of nanoseconds [29]. Therefore, it can be treated as confidential information that can be only known between integrated terminals in a practical wireless system.

In June 2020, IEEE 802.15.4z, a standard of UWB with an enhanced reliability ranging method, was approved [30]. IEEE 802.15.4z specifies three ranging methods: single-sided two-way ranging (SS-TWR), double-sided two-way ranging (DS-TWR), and time difference of arrival (TDOA). Here, DS-TWR, in which distance information can be shared between the terminals, will be described using Figure 5.

First, a message frame is sent from terminal A to terminal B. Terminal B then sends a message frame to terminal A. Terminal A measures the round-trip time, $R_a$, and if the reply time of terminal B, $D_b$, is known, Equation (6) can be used to calculate the propagation time ${\widehat{T}}_f$. The distance between terminal A and terminal B is obtained by multiplying ${\widehat{T}}_f$ by the speed of light. This is SS-TWR.

$${\widehat{T}}_f=\frac{1}{2}\left(R_a-D_b\right)$$

(6)

The disadvantage of SS-TWR is that when the reply time becomes large, the measurement accuracy degrades due to the influence of the clock error between terminals A and B. Therefore, a message frame is further sent from terminal A to terminal B, and the effect of the clock error between terminals A and B is minimized by calculating using Equation (7). This is DS-TWR.

$${\widehat{T}}_f=\frac{R_a{R}_b-D_a{D}_b}{R_a+D_a+R_b+D_b}$$

(7)

4. Performance Evaluation and Discussion

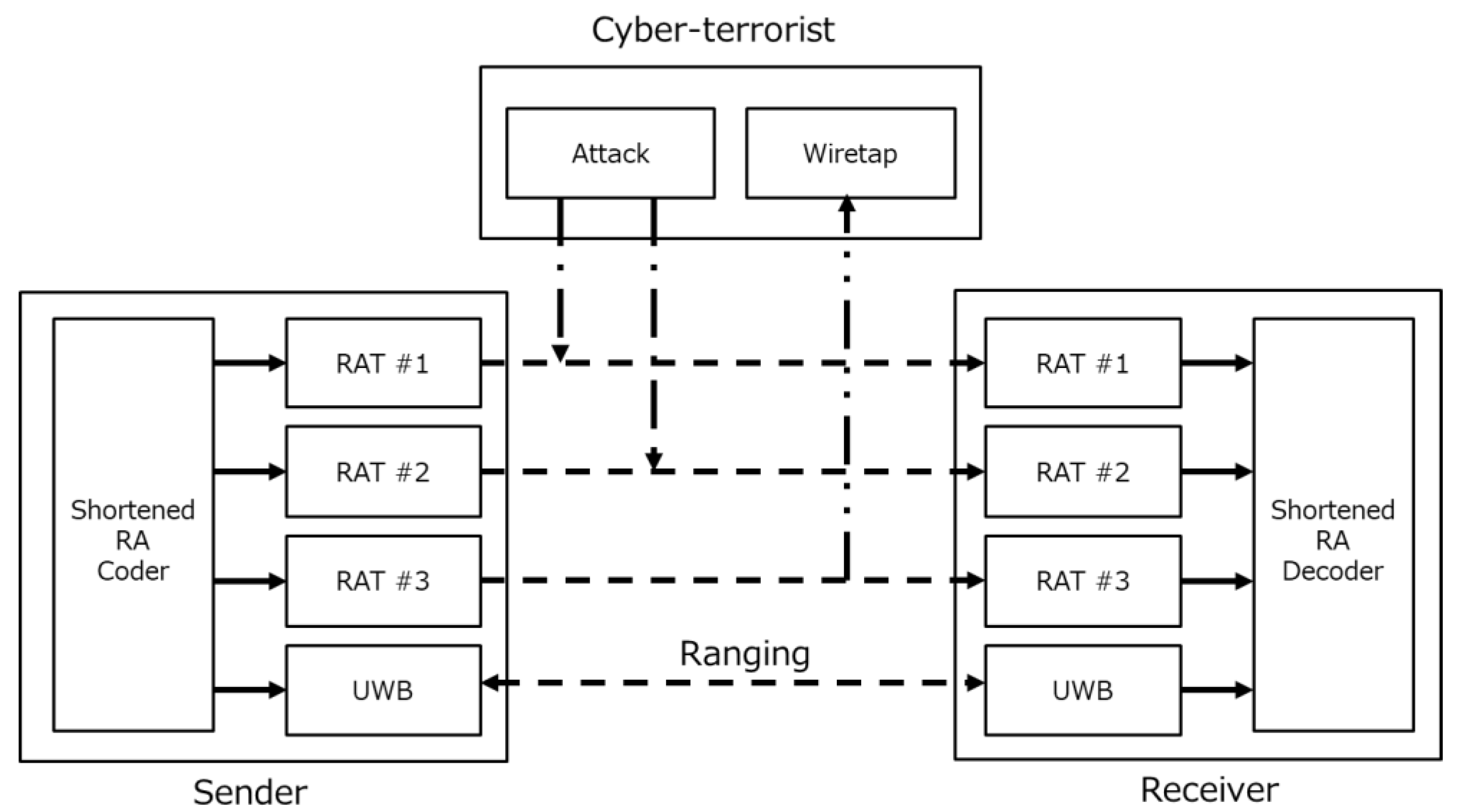
4.1. Secrecy Capacity

The definitions of terms and symbols used in Section 4.1 are listed in

Table 2. Definitions of terms and symbols.

Term/Symbol	Definition
Sender	Terminal sending information to the receiver
Receiver	Terminal receiving information from the sender
Cyberterrorist	Terminal that can be wiretapped and attacked simultaneously
$C_y$	Channel capacity of the receiver under attack
$C_z$	Channel capacity due to wiretapping by the cyberterrorist
$C$	Secrecy capacity
$X$	Random sequence sent by the sender $X=\left\{x_1=0, x_2=1\right\}$
$Y$	Received sequence by the receiver under attack $Y=\left\{y_1=0, y_2=1\right\}$
$Z$	Wiretapped sequence by the cyberterrorist $Z=\left\{z_1=0, z_2=1\right\}$
$D$	Errors not corrected by decoder
$H\left(X\right)$	Entropy of $X$
$H\left(Y\right)$	Entropy of $Y$
$H\left(Z\right)$	Entropy of $Z$
$P\left(x_i\right)$	Probability of $x_i$
$P\left(y_i\right)$	Probability of $y_i$
$P\left(z_i\right)$	Probability of $z_i$
$I\left(X;Y\right)$	Mutual information between $X$ and $Y$
$I\left(X;Z\right)$	Mutual information between $X$ and $Z$
$P_{ey}$	Probability of different bits of $X$ and $Y$
$P_{ez}$	Probability of different bits of $X$ and $Z$

.

The sender and the receiver are communicating, and their communications are tapped by a cyberterrorist. The maximum transmission rate between the sender and the receiver when the cyberterrorist cannot receive any information is called the secrecy capacity. Wyner showed that for discrete memoryless channels, the secrecy capacity is the difference between the channel capacity of the receiver and the cyberterrorist [10,31]. This result has been generalized to Gaussian channels by Leung [32]. We use the secrecy capacity as an evaluation index of the wiretapping resistance. If $C_y$ is the channel capacity of the receiver under attack and $C_z$ is the channel capacity due to wiretapping by the cyberterrorist, the secrecy capacity, $C$ can be calculated by the following Equation [31].

$$C=C_y-C_z$$

(8)

Information transmitted by the sender is represented by $X=\left\{x_1=0, x_2=1\right\}$, information received by the receiver under attack is represented by $Y=\left\{y_1=0, y_2=1\right\}$, and information obtained by the cyberterrorist through wiretapping is represented by $Z=\left\{z_1=0, z_2=1\right\}$. The entropies of $X, Y$ and $Z$ are represented by $H\left(X\right)$, $H\left(Y\right)$, and $H\left(Z\right)$, respectively. The entropy $H\left(X\right)$ is given by the probability $P\left(x_i\right)$ of $x_i$ as Equation (9).

$$H\left(X\right)=-{\displaystyle \sum }_{i=1}^{2}P\left(x_i\right){\log }_2\left(P\left(x_i\right)\right)$$

(9)

$H\left(Y\right)$ and $H\left(Z\right)$ can be calculated in the same way as Equation (9). The amount of information shared by the receiver with the sender can be calculated by the mutual information $I\left(X;Y\right)$ as follows.

$$I\left(X;Y\right)=H\left(Y\right)-H\left(Y|X\right)$$

(10)

In this paper, $Y$ corresponds to the received information corrected by the shortened RA code. If $D$ is the error that could not be corrected, $Y$ can be expressed as Equation (11).

$$Y=X+D$$

(11)

If $X$ and $D$ are independent, Equation (10) can be transformed into Equation (12).

$$I\left(X;Y\right)=H\left(Y\right)-H\left(X+D|X\right)=H\left(Y\right)-H\left(D\right)$$

(12)

If $P\left(x_1\right)=P\left(x_2\right)=1/2$, $P\left(y_1\right)=P\left(y_2\right)=1/2$, and $D$ is a random error with an error rate $P_{ey}$, the mutual information $I\left(X;Y\right)$ is given by Equation (13) which is equal to the channel capacity.

$$I\left(X;Y\right)=1+P_{ey}{\log }_2\left(P_{ey}\right)+\left(1-P_{ey}\right){\log }_2\left(1-P_{ey}\right)=C_y$$

(13)

Similarly, $Z$ corresponds to the received information corrected by the shortened RA code, $P\left(z_1\right)=P\left(z_2\right)=1/2$, and the error is a random error with an error rate of $P_{ez}$, the mutual information between the sender and the cyberterrorist is expressed by Equation (14).

$$I\left(X;Z\right)=1+P_{ez}{\log }_2\left(P_{ez}\right)+\left(1-P_{ez}\right){\log }_2\left(1-P_{ez}\right)=C_z$$

(14)

If the information from the sender is completely received, $P_{ey}$ = 0. By substituting $P_{ey}$ = 0 into Equation (13) the mutual information $I\left(X;Y\right)$ becomes 1. If the information from the sender cannot be received at all and $X$ and $Y$ are independent with $P\left(x_1\right)=P\left(x_2\right)=1/2$ and $P\left(y_1\right)=P\left(y_2\right)=1/2$, $P_{ey}$ = 0.5. By substituting $P_{ey}$ = 0.5 into Equation (13) the mutual information $I\left(X;Y\right)$ becomes 0. $I\left(X;Z\right)$ can be calculated in the same way as $I\left(X;Y\right)$. From Equations (13) and (14), it can be proven that when the information from the sender can be completely received, the mutual information becomes 1, and when the information cannot be received at all, the mutual information becomes 0. We measured the bit error ratio (BER) by simulation under the above assumption.

4.2. Simulation Conditions

Figure 6 shows the evaluated simulation model with one sender, one receiver and one cyberterrorist. The sender and the receiver can use up to three RATs for communication. In the evaluation, it is assumed that the distance between the sender and the receiver is accurately measured using UWB. Assuming that the distance is always changing, distance information with the length of shortened information is generated by the uniform random number for each codeword using the function of MATLAB. The sender and the receiver use the same value of distance information. Assuming that the cyberterrorist cannot get any distance information at all, a random value independent of distance information is used for the cyberterrorist. Details of shortened RA code parameters are described in Section 4.3. The encoder and decoder of the RA code use the function of the Communications Toolbox of MATLAB. A total of 5 million codewords were simulated. Codewords of shortened RA code are defined as $c\left(0\right), c\left(1\right),c\left(2\right),\cdots , c\left(n-m-1\right)$. Assuming communication using two RATs with almost the same capability, such as 2.4 GHz band and 5 GHz band of wireless LAN, $c\left(0\right), c\left(2\right), c\left(4\right),\cdots , c\left(n-m-2\right)$ are assigned to the first RAT and $c\left(1\right), c\left(3\right),c\left(5\right),\cdots , c\left(n-m-1\right)$ are assigned to the second RAT. When three RATs are used for communication, codewords are allocated sequentially from the beginning as in the case of two RATs. Since the codewords are distributed equally to each RAT in this manner, the wiretapping resistance and the attack resistance of each RAT are equal. The communication model will be described. If RAT communication is completely lost due to the attack, the received codeword is a random value. So, the codewords received via the attacked RAT are generated by the uniform random number of MATLAB for each decoding process. The unattacked RAT has no communication errors. So, the codewords received via the unattacked RAT for the decoder are the same codewords assigned by the RAT. The cyberterrorist shall be able to wiretap and attack simultaneously. In other words, when two RATs are used for communication, one RAT can be wiretapped while the other RAT can be attacked simultaneously. We confirm the information-theoretic effect by evaluating the mutual information between the sender and the receiver when some RATs are attacked and the mutual information between the sender and the cyberterrorist when some RATs are wiretapped. Then, we confirm the information-theoretic security capability against wiretapping and attacks by using the secrecy capacity.

4.3. Performance of Shortened RA Code

Table 3. Parameters of shortened RA code.

Parameter	Detail
Unencoded bit length ($k$)	600
Codeword length ($n$)	1200
Shortened information length ($m$)	0~500
Column weight ($q$)	3
Decoding algorithm	LogMAP
Maximum number of repetitions	100

shows the parameters of the shortened RA code used in this evaluation. As the RA code used for the shortened RA code, a code with 600 bits of unencoded bit length $k$, 1200 bits of codeword length $n$, and 3 of column weight $q$ was designed. The interleaver after the repeater is a random interleaver, and the row weight $r$ is uniquely determined by the random interleaver. The shortened information length $m$ using distance information is varied from 0 to 500. The LogMAP algorithm was used as a decoding algorithm, and the maximum number of repetitions was set to 100.

Figure 7 and Figure 8 show the BER of the designed shortened RA code under the AWGN channel. Figure 7 shows the BER characteristics of the receiver for which the shortened information is known. The BER characteristics are improved as the shortened information length is increased. When the shortened information length is 300, it corresponds to the coding rate R = (600 − 300)/(1200 − 300) = 1/3. Theoretically, as compared with the coding rate R = 1/2 before shortening, $10{\log }_{10}\left(3/2\right)$ = 1.76 (dB) characteristic improvement can be expected, but almost the same improvement has been obtained. Figure 8 shows the BER characteristic of the cyberterrorist for which the shortened information is unknown. Here, it is assumed that the cyberterrorist knows about shortened code other than the shortened information, e.g., the parity check matrix. The BER characteristics degrade as the length of the shortened information is increased. When the shortened information length is 100 bits, the required SNR difference between the receiver and the cyberterrorist at BER = ${10}^{-4}$ is 0.9 dB, while when the shortened information length is 400 bits, it is expanded to 6.2 dB. From this, it was confirmed that providing the receiver with a high correction capability and the cyberterrorist with a low correction capability can be achieved by using the designed shortened RA code.

4.4. Performance of UWB Ranging

Dacawave’s MDEK1001 Development Kit was used to evaluate the accuracy of ranging using UWB. The measurement results of 36 nodes when the anchor nodes were placed at the positions of (0.0 (m), 0.0 (m)), (2.4 m, 0.0 m), (0.0 m, 2.4 m), and (2.4 m, 2.4 m) are shown in Figure 9. In Figure 9, the circle marks represent the installation position, and the cross marks represent the measurement position. The error is within 20 cm. Therefore, it is considered that distance information can be shared between terminals by handling the distance information with the unit of at least 20 cm.

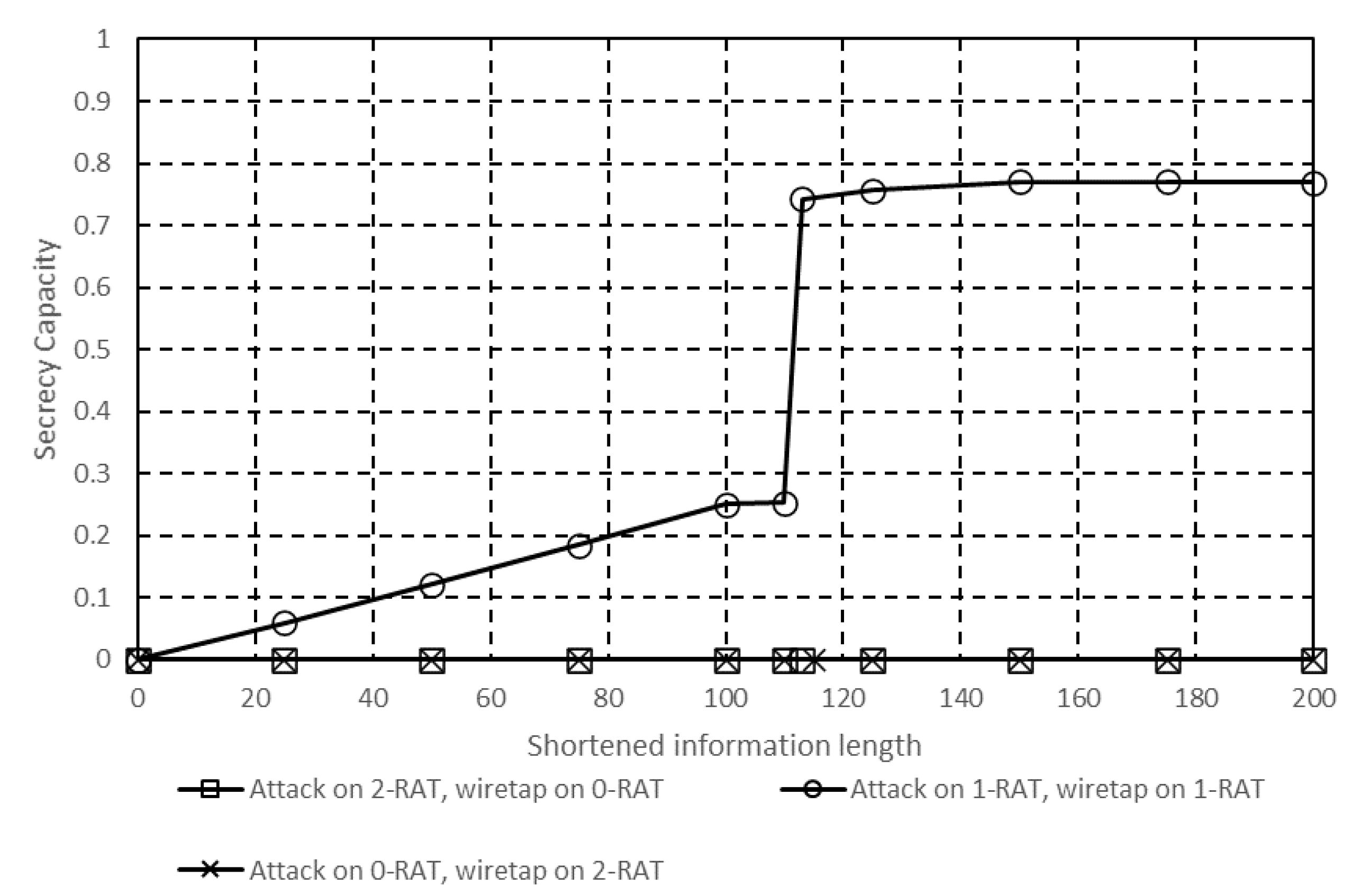
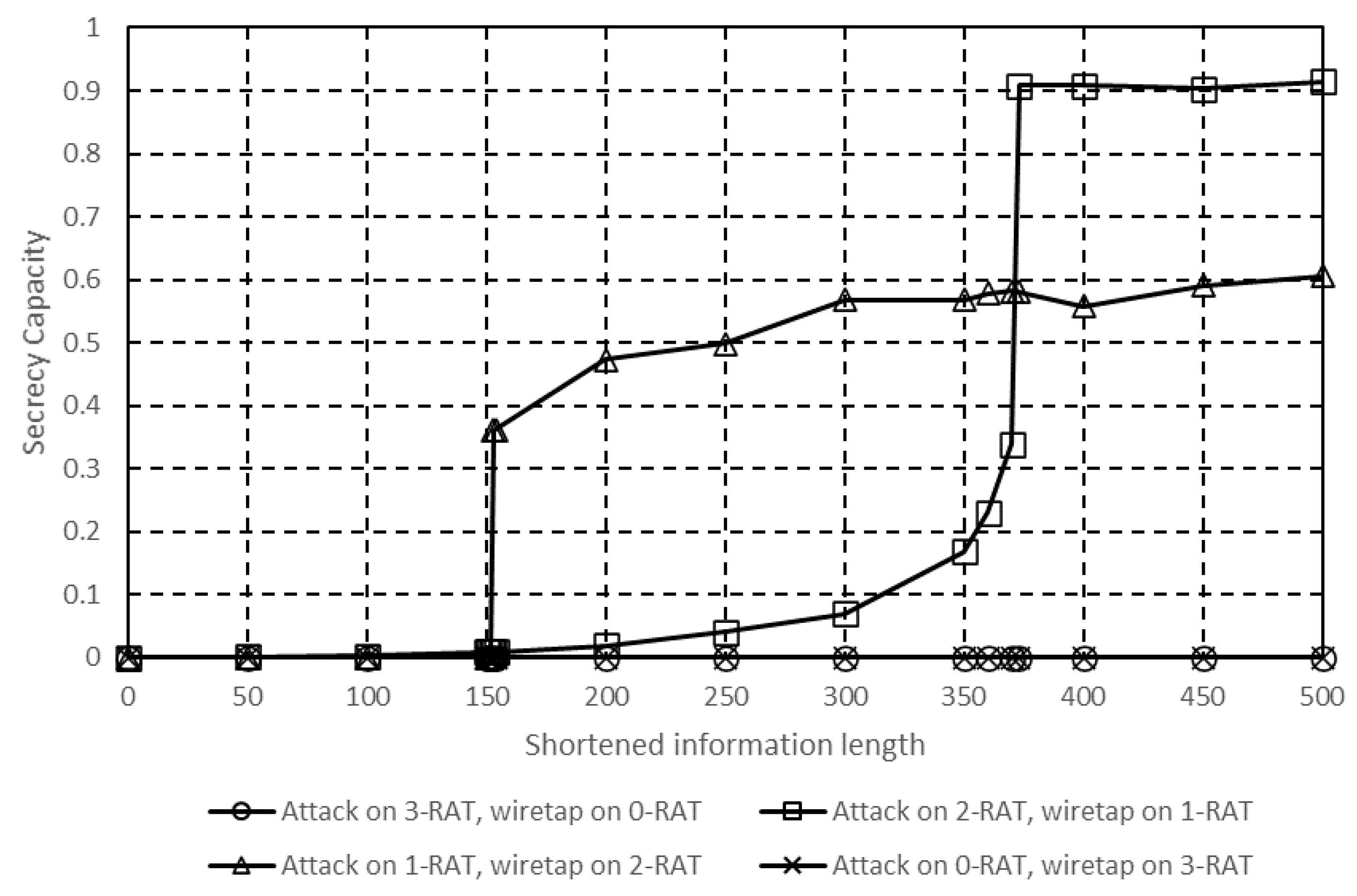
4.5. Performance Using Two RATs for Communication

Figure 10 shows the characteristics of the mutual information with respect to the shortened information length when the sender and the receiver communicate using two RATs. The square marks indicate the mutual information between the sender and the receiver when one RAT cannot be used for communication due to an attack, and the cross marks indicate the mutual information between the sender and the cyberterrorist when one RAT is wiretapped. When the receiver cannot use one RAT for communication, communication is not possible without shortening. The mutual information of the receiver is slightly increased until the shortened information length is 112, but when the shortened information length is set to 113 bits, the mutual information suddenly becomes one and communication becomes possible. On the other hand, the mutual information of the cyberterrorist continues to decrease with no improvement even if the shortened information length is increased.

Figure 11 shows the characteristics of the secrecy capacity. The square marks, the circle marks and the cross marks indicate the secrecy capacity of the cyberterrorist attacking on two RATs, attacking on one RAT and wiretapping on one RAT, and wiretapping on two RATs, respectively. When the cyberterrorist attacks or wiretaps on two RATs, the secrecy capacity does not improve and is always zero. However, if the cyberterrorist attacks and wiretaps on another RAT simultaneously, the secrecy capacity can be improved by increasing the shortened information length, such that if the shortened information length exceeds 113, the value is 0.7 or greater. As a result, it is confirmed that information-theoretic security is improved even when the sender and the receiver communicate using two RATs.

Therefore, when the designed shortened RA code is used, by setting the shortened information length to 113 bits or more, it is possible to achieve both countermeasures against wiretapping and attacks. To increase the resistance of distance measurement error, the shortened information length may be set large. However, when the shortened information length is increased, the transmission efficiency decreases. Therefore, the shortened information length should be determined by the relationship between the ranging error and the transmission efficiency. The decision algorithm of the shortened information length should be the focus of further study.

4.6. Performance Using Three RATs for Communication

Figure 12 shows the characteristics of the mutual information with respect to the shortened information length when the sender and the receiver communicate using three RATs. The circle marks and the square marks indicate the mutual information between the sender and receiver when two and one RAT(s) cannot be used for communication due to an attack, respectively. The triangle marks and the cross marks indicate the mutual information between the sender and the cyberterrorist when two and one RAT(s) are/is wiretapped, respectively. By communicating using three RATs, even if one RAT is attacked, communication is possible without shortening. In addition, information cannot be wiretapped simply by wiretapping on one RAT. Simultaneous use of multiple RATs is an effective approach to achieve both countermeasures against wiretapping and attacks. When the cyberterrorist attacks two RATs, the mutual information increases slightly up to the shortened information length of about 300 bits, but increases exponentially beyond that, and the mutual information becomes one when the shortened information length is 373 bits or more. On the other hand, when two RATs are wiretapped, the mutual information is one up to the shortened information length of 152 bits, but rapidly decreases as the shortened information length becomes 153 bits or more.

Figure 13 shows the characteristics of the secrecy capacity. The circle marks, the square marks, the triangle marks, and the cross marks indicate the secrecy capacity of the cyberterrorist attacking on three RATs, attacking on two RATs and wiretapping on one RAT, attacking on one RAT and wiretapping on two RATs, and wiretapping on three RATs, respectively. When the cyberterrorist attacks or wiretaps on three RATs, the secrecy capacity does not improve and is zero. If the cyberterrorist attacks on one RAT and wiretaps on two RATs simultaneously, the secrecy capacity increases to approximately 0.6 by increasing the shortened information length. If the cyberterrorist attacks on two RATs and wiretaps on one RAT simultaneously, the secrecy capacity gradually increases by increasing the shortened information length, and when the shortened information length exceeds 373 bits, the secrecy capacity becomes about 0.9. As a result, it is confirmed that information-theoretic security is further improved even when the sender and the receiver communicate using three RATs. Since the degree of freedom of countermeasures increases as the number of RATs used for communication increases, various countermeasures can be implemented depending on the assumed cyberterrorist by changing the shortened information length. However, since it is ineffective if all the RATs are wiretapped or attacked, it is desirable to implement countermeasures at the upper layers as well.

5. Conclusions

This paper proposes a dependable wireless system with shortened code using distance information between integrated terminals. The proposed wireless system has three features to enhance resistance from cyberterrorists. First, integrated terminals with multiple RATs and CODEC communicate encoded information using multiple RATs. Even if some RATs are attacked, the transmitted information can be recovered using encoded information received by other RATs. Even if some RATs are wiretapped, the transmitted information cannot be recovered using less encoded information. Second, the shortened code is adopted as an error correction code. If the receiver knows the shortened information and the cyberterrorist does not know it, it is possible to provide a high correction capability to the receiver and low correction capability to the cyberterrorist. Finally, the distance information between integrated terminals can be measured securely and accurately using UWB. This can improve the capability to protect against wiretapping and attacks in a practical system.

It was confirmed that when two RATs were used for communication, by increasing the shortened information length, the secrecy capacity defined by the maximum transmission rate between the sender and the receiver when the cyberterrorist cannot receive any information could be over 0.7, and that it could be further increased by using three RATs. Although the proposed scheme has a limited capability to protect against wiretapping and attacks, the information-theoretic security capability can be improved. Since the degree of freedom of countermeasures increases as the number of RATs used for communication increases, various countermeasures can be implemented depending on the assumed cyberterrorist by changing the shortened information length.

The following points are mentioned as topics for future work.

• Though the shortened information length is the parameter which decides the wiretapping resistance and attack resistance, it is necessary to investigate optimization of the shortened information length and quantization technique, because it is also related to error resistance of distance information.
• It is necessary to examine the effect of the shortened information predicted by the cyberterrorist and the countermeasures and to analyze the performance limit and drawback.
• The evaluation assumes that RAT communication is completely lost due to the attack, but it is necessary to evaluate the actual attack pattern and the impact of attack resistance on each RAT.
• It is necessary to analyze performance degradation due to measured distance error or accuracy.
• It is necessary to examine the application to other codes, because large gain can be obtained by using powerful codes.
• Evaluation of dependability properties based on heuristic strategies such as “what-if analysis” and “robustness checking” are described in [2].
• Finally, an evaluation using a real system is necessary.