Multiscale 3D CFD Modeling of CO2 Methanation over Ni/Al2O3 in a Lab-Scale Sabatier Fixed-Bed Reactor
Abstract
1. Introduction
2. Materials and Methods
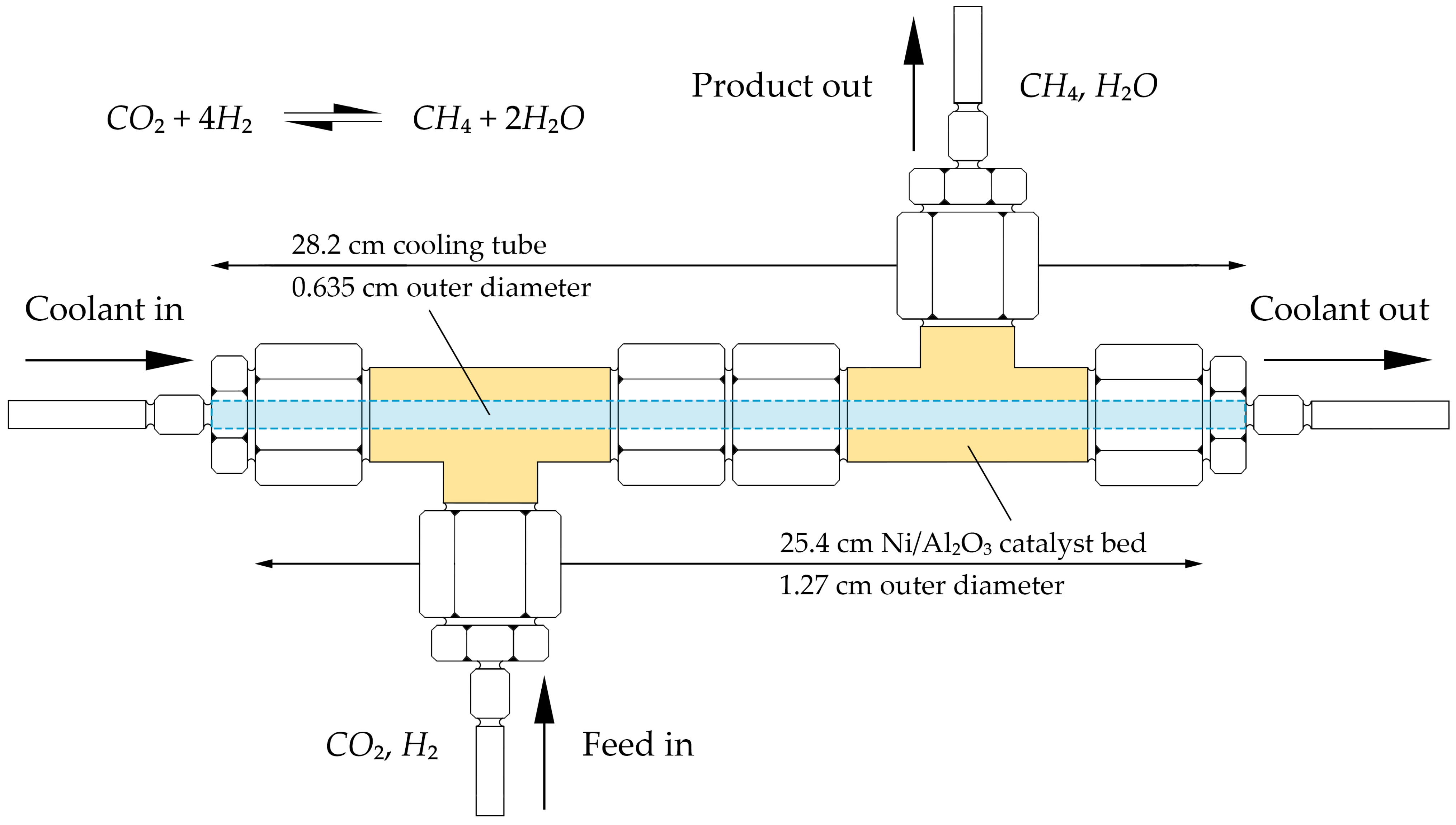
2.1. Process Description
2.2. Kinetic Model Description
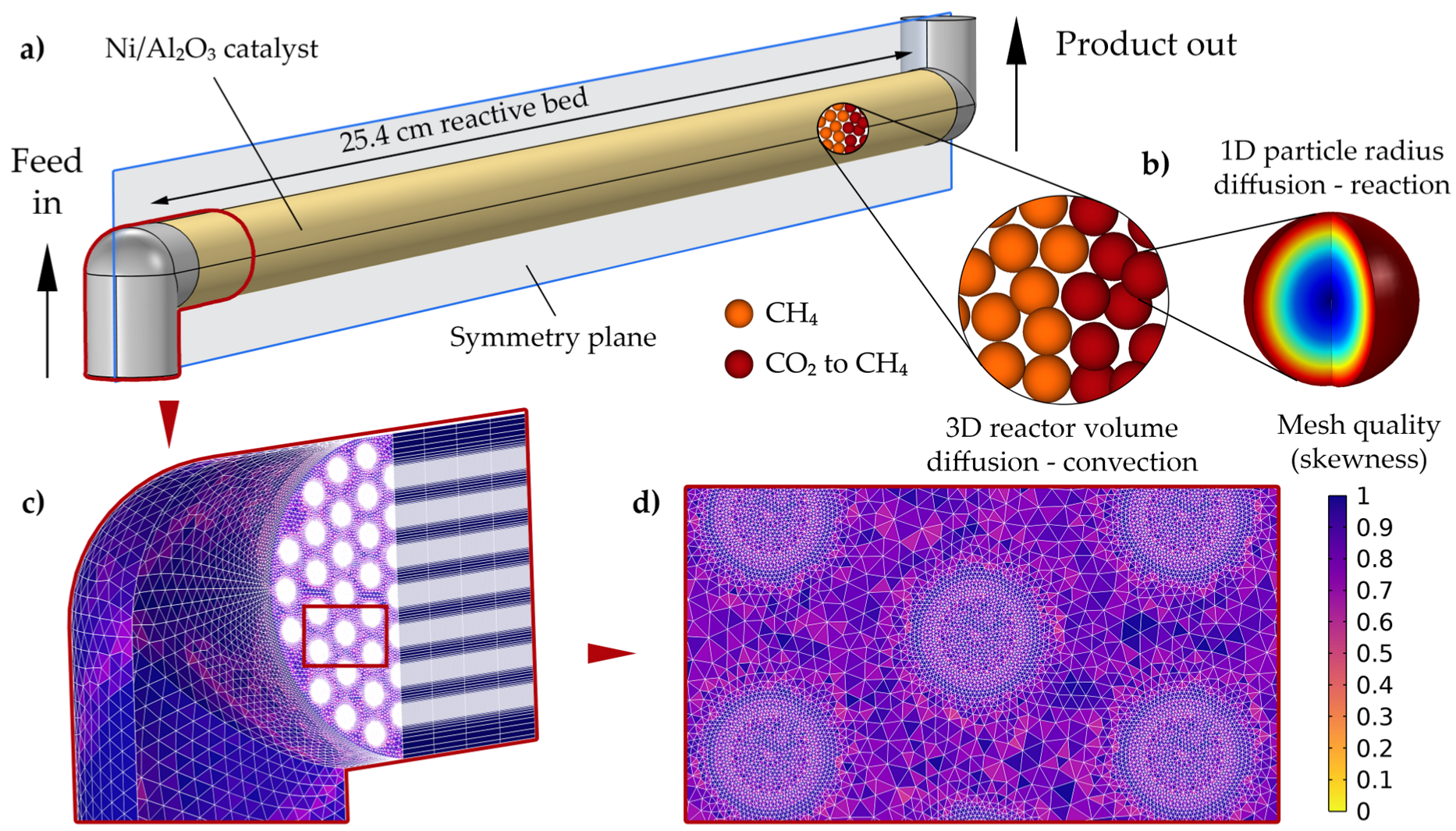
2.3. 3D CFD Multiscale Sabatier Reactor Model Development
2.3.1. Model Parameters, Operating Conditions, and Assumptions
- Stationary solid catalyst particles were spherical with identical radii.
- Fick’s law was considered for diffusion estimation.
- Methanation reaction occurs within the catalyst particles.
- Isothermal operating conditions were considered.
2.3.2. Model Equations
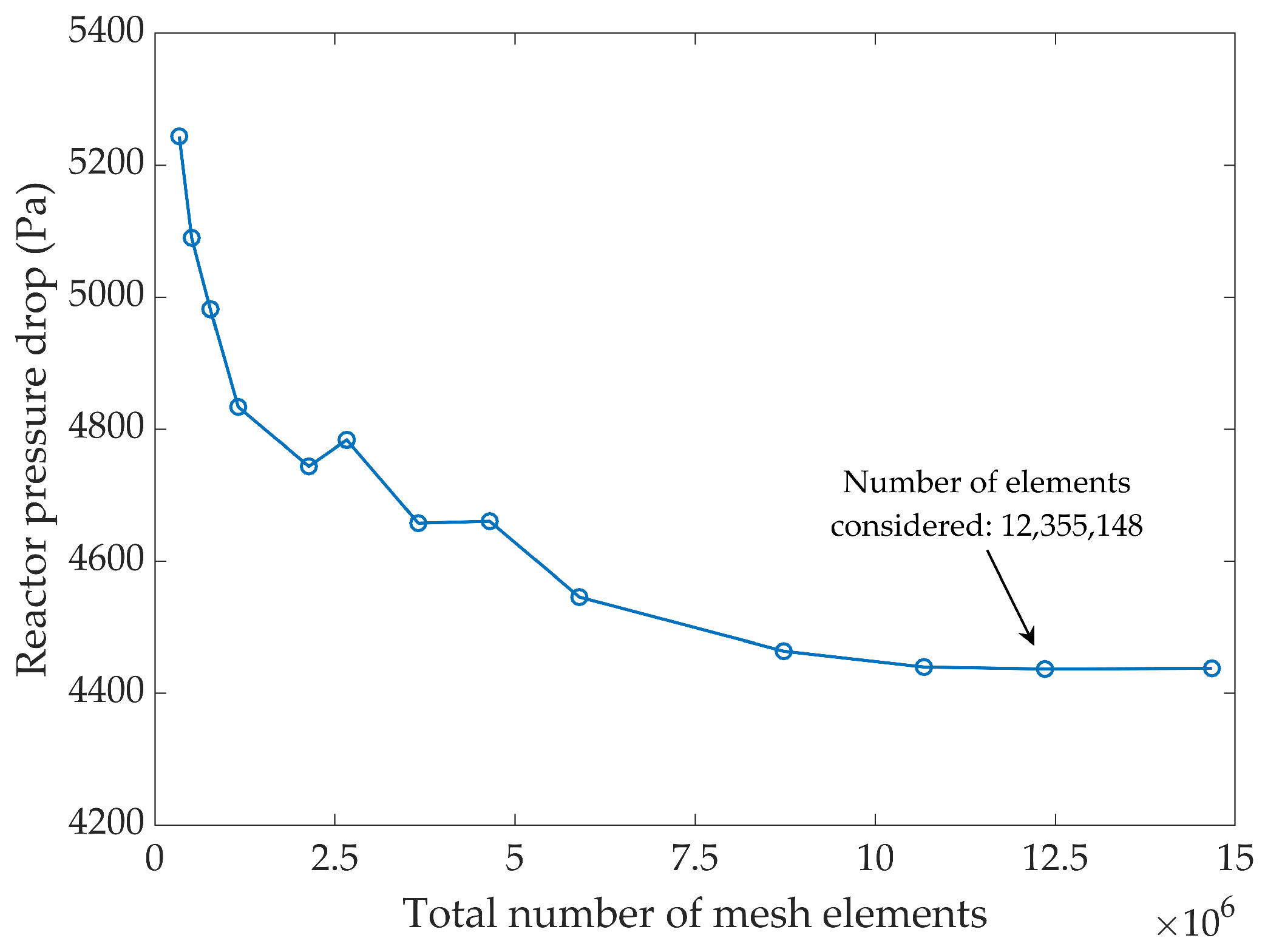
2.4. Sensitivity Analysis Methodology
3. Results and Discussion
3.1. Model Validation
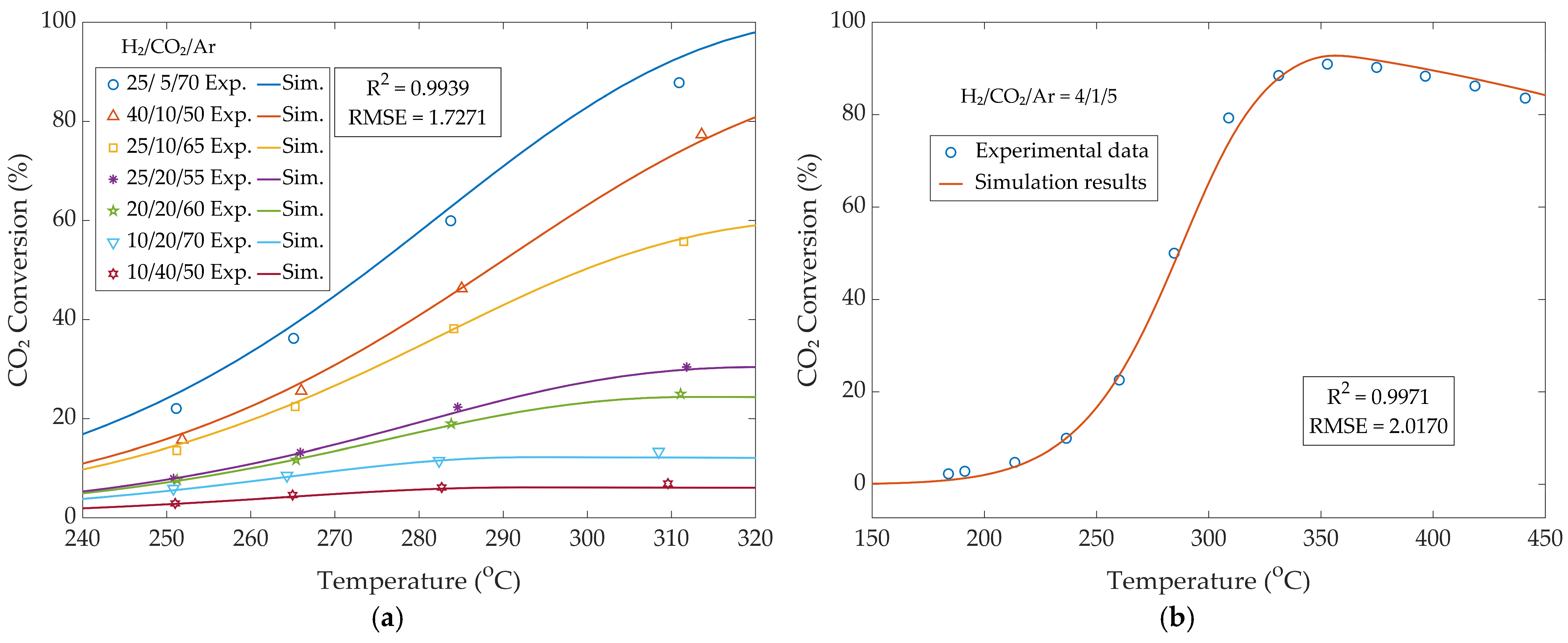
3.1.1. Kinetic Model Validation
3.1.2. Reactor Model Validation—Conversion and Yield
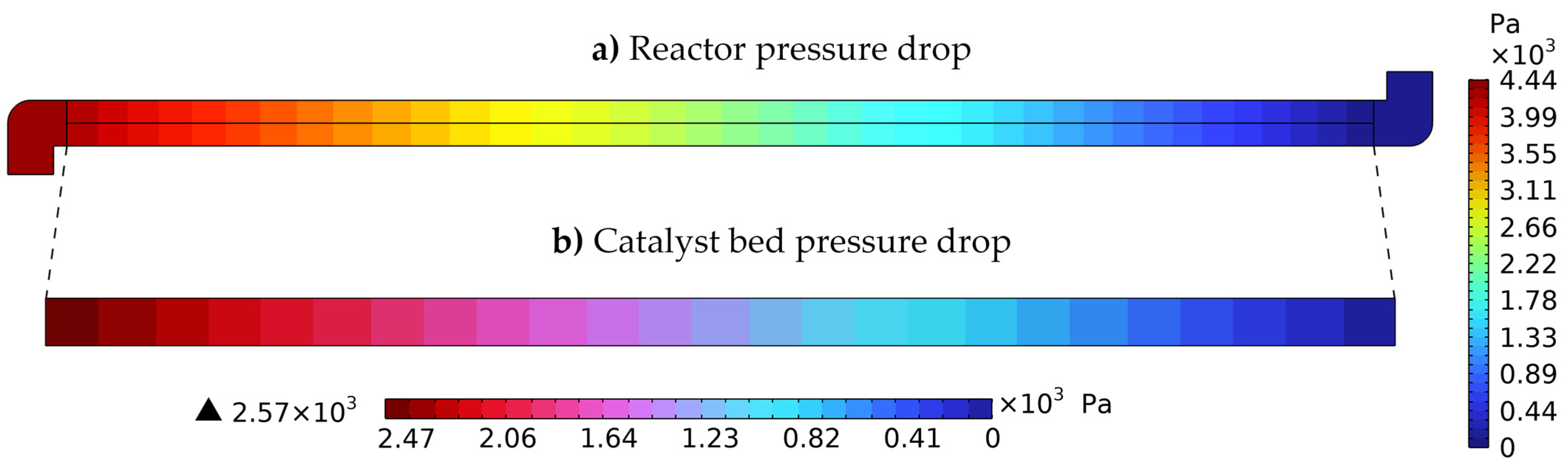
3.1.3. Hydrodynamic Model Validation—Pressure Distribution
3.2. Multiscale 3D CFD Sabatier Reactor Model Predictions
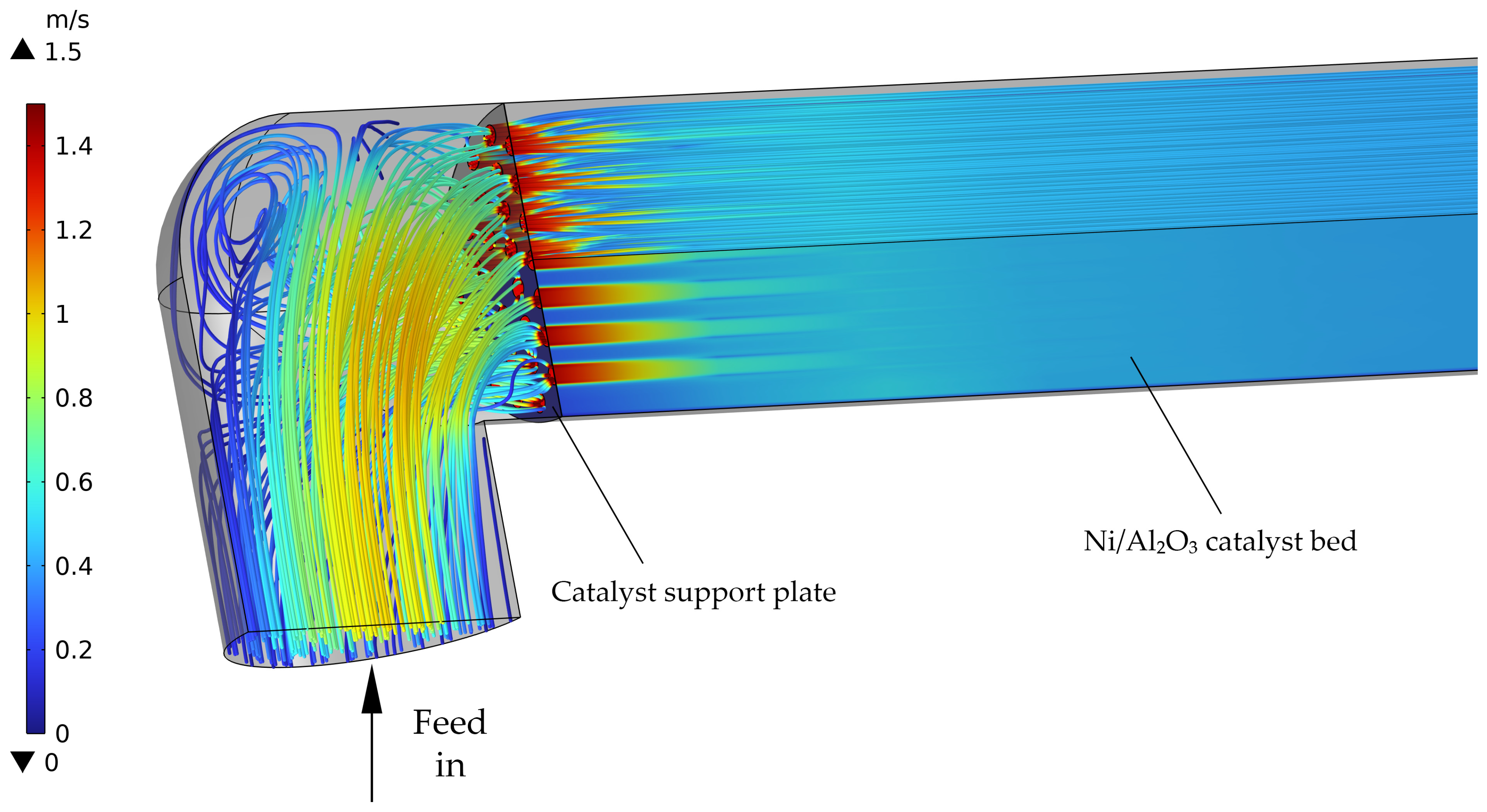
3.2.1. Simulated Velocity Profiles
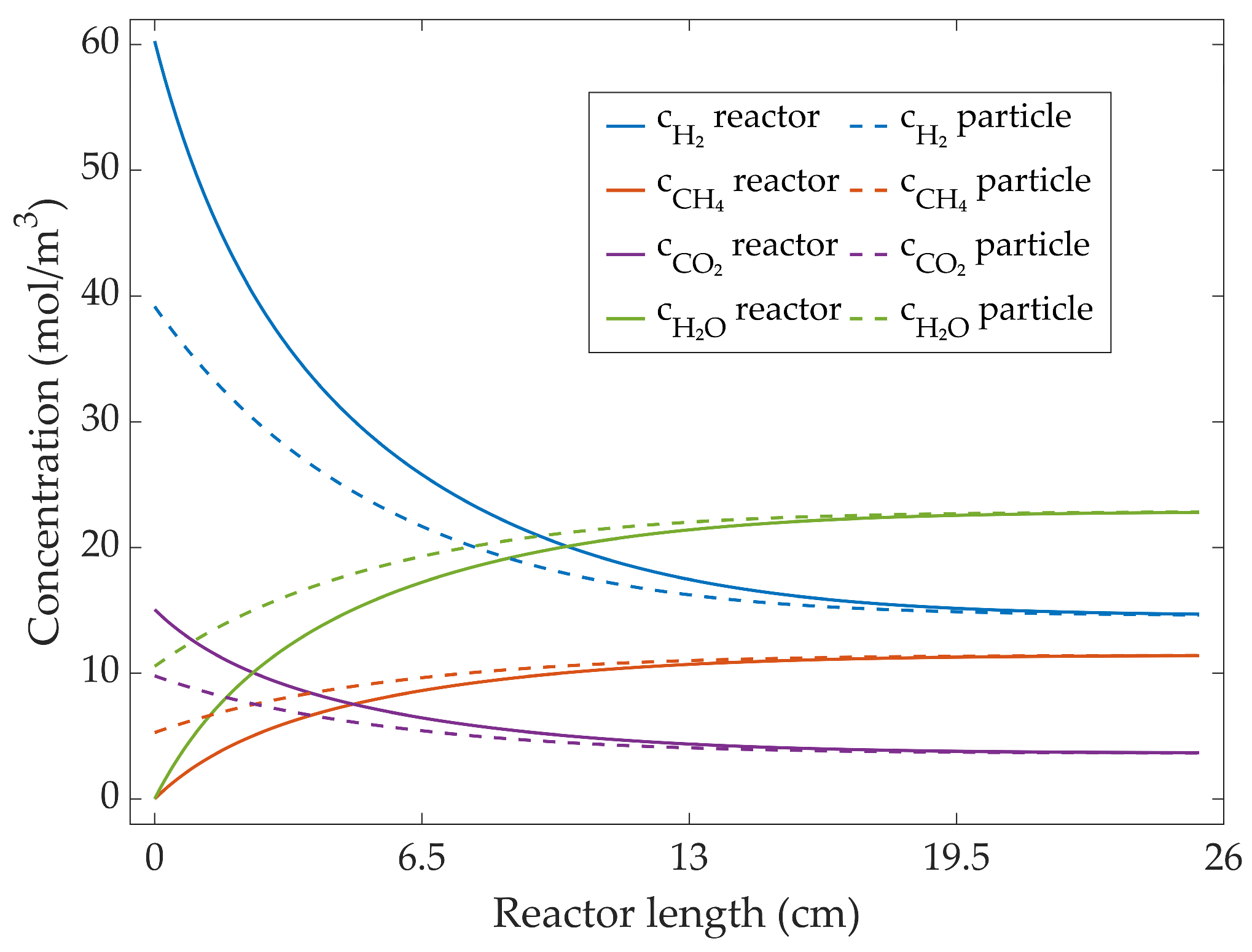
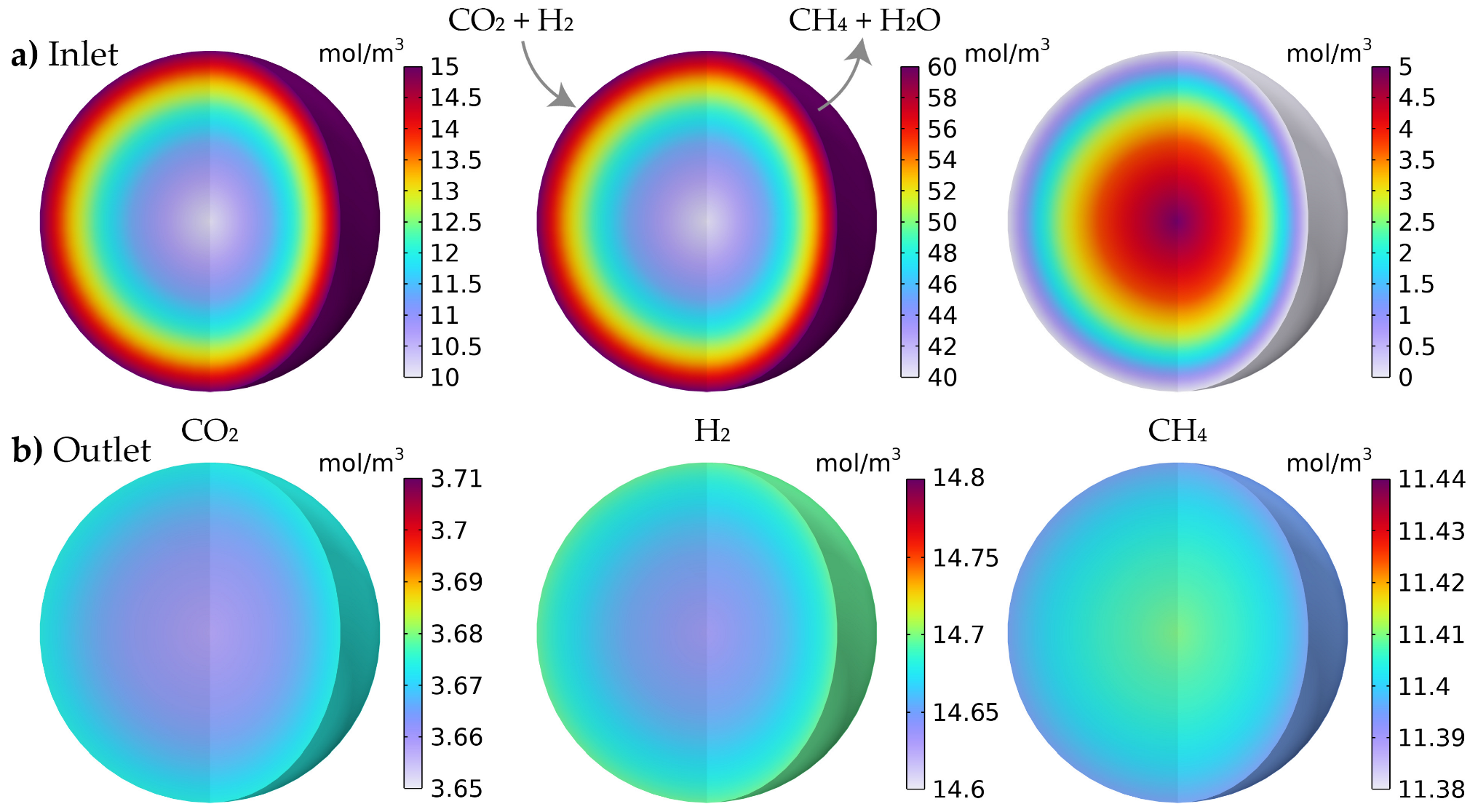
3.2.2. Simulated Concentration Profiles
3.3. Sensitivity Studies Performed
3.3.1. Temperature and Pressure Variation
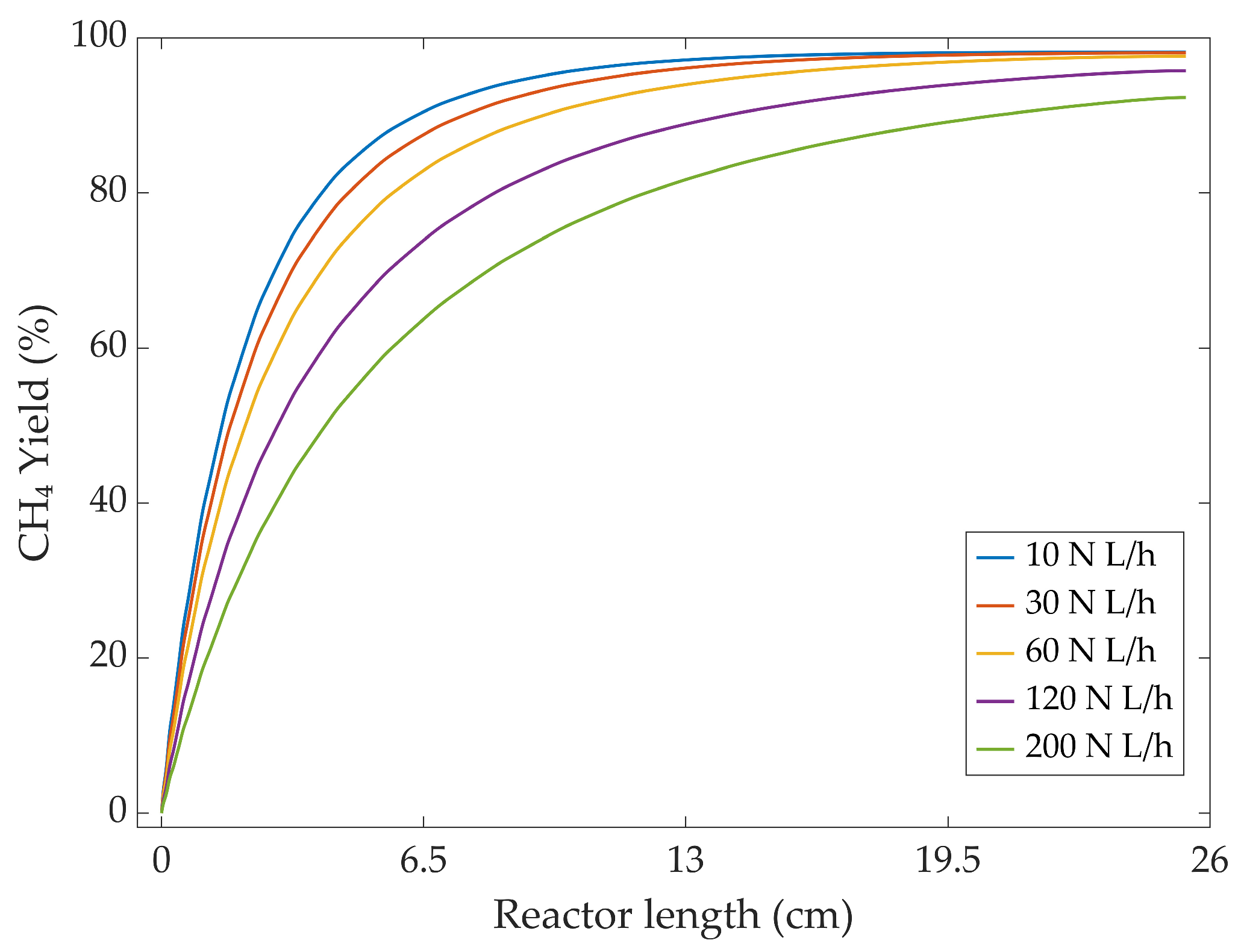
3.3.2. Flow Rate Variation
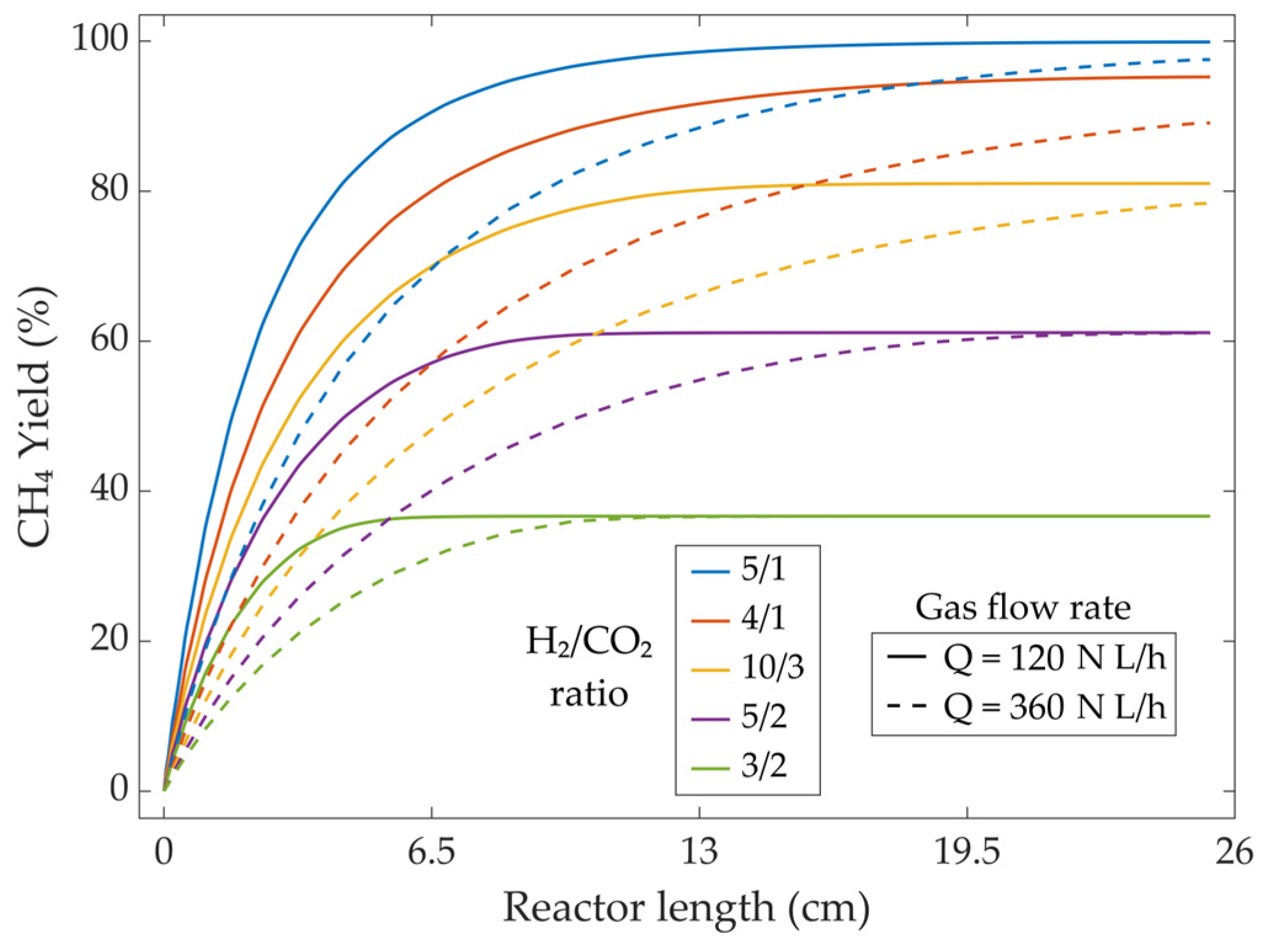
3.3.3. Inlet Gas Composition Variation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | Bulk-phase concentration (mol/m3) |
| cp | Intraparticle concentration (mol/m3) |
| DL | Axial dispersion diffusion coefficient (m2/s) |
| Dp | Intraparticle diffusion coefficient (m2/s) |
| Dp,eff | Effective intraparticle diffusion coefficient (m2/s) |
| Ea | Activation energy (kJ/mol) |
| hD | Mass transfer coefficient (m/s) |
| ΔH | Reaction enthalpy (kJ/mol) |
| i | Species index (-) |
| I | Identity tensor (-) |
| Jp | Molar flux from the free fluid into a pellet (mol/(m2·s)) |
| k | Rate coefficient (mol/(bar·s·gcat)) |
| K | Adsorption constant (bar−0.5) |
| Ke | Equilibrium constant (-) |
| P | Pressure (bar) |
| r | Radial coordinate (-) |
| rp | Catalyst particle radius (m) |
| R | Interparticle reaction rate in the bed (mol/(m3·s)) |
| Rp | Reaction rate (mol/(m3·s)) |
| Sb | Specific surface of the bed (m2/m3) |
| T | Temperature (K) |
| Tref | Reference temperature (K) |
| u | Velocity (m/s) |
| Greek symbols | |
| εb | Bed porosity (i.e., void) (-) |
| εp | Particle porosity (i.e., void) (-) |
| ε,∆P | Successive-refinement relative change (%) |
| κ | Permeability (m2) |
| μ | Dynamic viscosity (Pa·s) |
| ρ | Density (kg/m3) |
| Abbreviations | |
| CCU | Carbon capture and utilization |
| CFD | Computational fluid dynamics |
| GHG | Greenhouse gas |
| LHHW | Langmuir–Hinshelwood–Hougen–Watson |
| PtG | Power-to-gas |
| RWGS | Reverse water–gas shift |
| SNG | Synthetic natural gas |
References
- IPCC. Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2023. [Google Scholar]
- NASA Carbon Dioxide|Vital Signs—Climate Change. Available online: https://climate.nasa.gov/vital-signs/carbon-dioxide/ (accessed on 25 May 2025).
- International Energy Agency (IEA). CO2 Emissions in 2023; IEA: Paris, France, 2024. [Google Scholar]
- IEA. Renewables 2024; IEA: Paris, France, 2024. [Google Scholar]
- Ren, J.; Lou, H.; Xu, N.; Zeng, F.; Pei, G.; Wang, Z. Methanation of CO/CO2 for Power to Methane Process: Fundamentals, Status, and Perspectives. J. Energy Chem. 2023, 80, 182–206. [Google Scholar] [CrossRef]
- Rönsch, S.; Schneider, J.; Matthischke, S.; Schlüter, M.; Götz, M.; Lefebvre, J.; Prabhakaran, P.; Bajohr, S. Review on Methanation—From Fundamentals to Current Projects. Fuel 2016, 166, 276–296. [Google Scholar] [CrossRef]
- Gao, R.; Zhang, C.; Jun, K.W.; Kim, S.K.; Park, H.G.; Zhao, T.; Wang, L.; Wan, H.; Guan, G. Green Liquid Fuel and Synthetic Natural Gas Production via CO2 Hydrogenation Combined with Reverse Water-Gas-Shift and Co-Based Fischer-Tropsch Synthesis. J. CO2 Util. 2021, 51, 101619. [Google Scholar] [CrossRef]
- Guilera, J.; Ramon Morante, J.; Andreu, T. Economic Viability of SNG Production from Power and CO2. Energy Convers. Manag. 2018, 162, 218–224. [Google Scholar] [CrossRef]
- Kirchbacher, F.; Biegger, P.; Miltner, M.; Lehner, M.; Harasek, M. A New Methanation and Membrane Based Power-to-Gas Process for the Direct Integration of Raw Biogas—Feasability and Comparison. Energy 2018, 146, 34–46. [Google Scholar] [CrossRef]
- Patrizio, P.; Chinese, D. The Impact of Regional Factors and New Bio-Methane Incentive Schemes on the Structure, Profitability and CO2 Balance of Biogas Plants in Italy. Renew. Energy 2016, 99, 573–583. [Google Scholar] [CrossRef]
- Gao, J.; Wang, Y.; Ping, Y.; Hu, D.; Xu, G.; Gu, F.; Su, F. A Thermodynamic Analysis of Methanation Reactions of Carbon Oxides for the Production of Synthetic Natural Gas. RSC Adv. 2012, 2, 2358–2368. [Google Scholar] [CrossRef]
- Lee, W.J.; Li, C.; Prajitno, H.; Yoo, J.; Patel, J.; Yang, Y.; Lim, S. Recent Trend in Thermal Catalytic Low Temperature CO2 Methanation: A Critical Review. Catal. Today 2021, 368, 2–19. [Google Scholar] [CrossRef]
- Shen, C.; Liu, M.; He, S.; Zhao, H.; Liu, C. Advances in the Studies of the Supported Ruthenium Catalysts for CO2 Methanation. Chin. J. Catal. 2024, 63, 1–15. [Google Scholar] [CrossRef]
- Ridzuan, N.D.M.; Shaharun, M.S.; Anawar, M.A.; Ud-Din, I. Ni-Based Catalyst for Carbon Dioxide Methanation: A Review on Performance and Progress. Catalysts 2022, 12, 469. [Google Scholar] [CrossRef]
- Medina, O.E.; Amell, A.A.; López, D.; Santamaría, A. Comprehensive Review of Nickel-Based Catalysts Advancements for CO2 Methanation. Renew. Sustain. Energy Rev. 2025, 207, 114926. [Google Scholar] [CrossRef]
- Gaikwad, R.; Villadsen, S.N.B.; Rasmussen, J.P.; Grumsen, F.B.; Nielsen, L.P.; Gildert, G.; Møller, P.; Fosbøl, P.L. Container-Sized CO2 to Methane: Design, Construction and Catalytic Tests Using Raw Biogas to Biomethane. Catalysts 2020, 10, 1428. [Google Scholar] [CrossRef]
- Stangeland, K.; Kalai, D.; Li, H.; Yu, Z. CO2 Methanation: The Effect of Catalysts and Reaction Conditions. Energy Procedia 2017, 105, 2022–2027. [Google Scholar]
- Sun, D.; Simakov, D.S.A. Thermal Management of a Sabatier Reactor for CO2 Conversion into CH4: Simulation-Based Analysis. J. CO2 Util. 2017, 21, 368–382. [Google Scholar] [CrossRef]
- Brooks, K.P.; Hu, J.; Zhu, H.; Kee, R.J. Methanation of Carbon Dioxide by Hydrogen Reduction Using the Sabatier Process in Microchannel Reactors. Chem. Eng. Sci. 2007, 62, 1161–1170. [Google Scholar] [CrossRef]
- Sudiro, M.; Bertucco, A.; Groppi, G.; Tronconi, E. Simulation of a Structured Catalytic Reactor for Exothermic Methanation Reactions Producing Synthetic Natural Gas. Comput. Aided Chem. Eng. 2010, 28, 691–696. [Google Scholar] [CrossRef]
- Hervy, M.; Maistrello, J.; Brito, L.; Rizand, M.; Basset, E.; Kara, Y.; Maheut, M. Power-to-Gas: CO2 Methanation in a Catalytic Fluidized Bed Reactor at Demonstration Scale, Experimental Results and Simulation. J. CO2 Util. 2021, 50, 101610. [Google Scholar] [CrossRef]
- Lefebvre, J.; Götz, M.; Bajohr, S.; Reimert, R.; Kolb, T. Improvement of Three-Phase Methanation Reactor Performance for Steady-State and Transient Operation. Fuel Process. Technol. 2015, 132, 83–90. [Google Scholar] [CrossRef]
- Currie, R.; Mottaghi-Tabar, S.; Zhuang, Y.; Simakov, D.S.A. Design of an Air-Cooled Sabatier Reactor for Thermocatalytic Hydrogenation of CO2: Experimental Proof-of-Concept and Model-Based Feasibility Analysis. Ind. Eng. Chem. Res. 2019, 58, 12964–12980. [Google Scholar] [CrossRef]
- Dannesboe, C.; Hansen, J.B.; Johannsen, I. Catalytic Methanation of CO2 in Biogas: Experimental Results from a Reactor at Full Scale. React. Chem. Eng. 2019, 5, 183–189. [Google Scholar] [CrossRef]
- Herrmann, F.; Grünewald, M.; Meijer, T.; Gardemann, U.; Feierabend, L.; Riese, J. Operating Window and Flexibility of a Lab-Scale Methanation Plant. Chem. Eng. Sci. 2022, 254, 117632. [Google Scholar] [CrossRef]
- Tommasi, M.; Degerli, S.N.; Ramis, G.; Rossetti, I. Advancements in CO2 Methanation: A Comprehensive Review of Catalysis, Reactor Design and Process Optimization. Chem. Eng. Res. Des. 2024, 201, 457–482. [Google Scholar] [CrossRef]
- Koschany, F.; Schlereth, D.; Hinrichsen, O. On the Kinetics of the Methanation of Carbon Dioxide on Coprecipitated NiAl(O)x. Appl. Catal. B 2016, 181, 504–516. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Columns. Chem. Eng. Prog. 1952, 48, 89–94. Available online: https://www.scirp.org/reference/referencespapers?referenceid=2324749 (accessed on 21 July 2025).
- Shirsath, A.B.; Schulte, M.L.; Kreitz, B.; Tischer, S.; Grunwaldt, J.D.; Deutschmann, O. Spatially-Resolved Investigation of CO2 Methanation over Ni/γ-Al2O3 and Ni3.2Fe/γ-Al2O3 Catalysts in a Packed-Bed Reactor. Chem. Eng. J. 2023, 469, 143847. [Google Scholar] [CrossRef]
- Gamal, A.; Jlassi, K.; Ahmad, Y.H.; Tang, M.; Al-Qaradawi, S.Y.; Chehimi, M.M.; Ozoemena, K.I.; Abdullah, A.M. Carbon-Supported Catalysts for Carbon Dioxide Methanation: A Review. J. CO2 Util. 2024, 85, 102881. [Google Scholar] [CrossRef]
- Wang, W.; Duong-Viet, C.; Ba, H.; Baaziz, W.; Tuci, G.; Caporali, S.; Nguyen-Dinh, L.; Ersen, O.; Giambastiani, G.; Pham-Huu, C. Nickel Nanoparticles Decorated Nitrogen-Doped Carbon Nanotubes (Ni/N-CNT); A Robust Catalyst for the Efficient and Selective CO2 Methanation. ACS Appl. Energy Mater. 2019, 2, 1111–1120. [Google Scholar] [CrossRef]
- Miguel, C.V.; Soria, M.A.; Mendes, A.; Madeira, L.M. Direct CO2 Hydrogenation to Methane or Methanol from Post-Combustion Exhaust Streams—A Thermodynamic Study. J. Nat. Gas Sci. Eng. 2015, 22, 1–8. [Google Scholar] [CrossRef]


| Parameter | Value | Unit |
|---|---|---|
| k0,555K | 3.46 × 10−4 ± 4.1 × 10−5 | mol/(bar∙s∙gcat) |
| Ea | 77.5 ± 6.9 | kJ/mol |
| KOH,555K | 0.5 ± 0.05 | bar(−0.5) |
| ∆HOH | 22.4 ± 6.4 | kJ/mol |
| KH2,555K | 0.44 ± 0.08 | bar(−0.5) |
| ∆HH2 | −6.2 ± 10 | kJ/mol |
| Kmix,555K | 0.88 ± 0.1 | bar(−0.5) |
| ∆Hmix | −10 ± 5.7 | kJ/mol |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Reactor length | 27.7 cm | Particle porosity | 0.4 |
| Bed length | 25.4 cm | Bed porosity | 0.5 |
| Reactor diameter | 0.89 cm | Gas hourly space velocity | 5000 mL/(g∙h) |
| Particle diameter | 0.85 mm | Reactor temperature | 452 °C |
| Ni/Al2O3 catalyst mass | 62.5 g | Reactor pressure | 10 bar |
| Ni/Al2O3 catalyst density | 2352 kg/m3 | Ratio H2/CO2 | 4/1 |
| Inflow Gas Temperature (°C) | Operating Pressure (bar) | Flow Rate (N L/h) | H2/CO2 Ratio |
|---|---|---|---|
| 260 | 1 | 10 | 5/1 |
| 280 | 3 | 30 | 4/1 |
| 300 | 10 | 60 | 10/3 |
| 320 | – | 120 | 5/2 |
| 400 | – | 200 | 3/2 |
| 450 | – | 360 | – |
| Simulated ΔP (Pa) | Analytical ΔP (Pa) [28] | Relative Error (%) |
|---|---|---|
| 2568.8 | 2568.7 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bozonc, A.-C.; Sandu, V.-C.; Buzila, A.-M.; Cormos, A.-M. Multiscale 3D CFD Modeling of CO2 Methanation over Ni/Al2O3 in a Lab-Scale Sabatier Fixed-Bed Reactor. Fuels 2025, 6, 79. https://doi.org/10.3390/fuels6040079
Bozonc A-C, Sandu V-C, Buzila A-M, Cormos A-M. Multiscale 3D CFD Modeling of CO2 Methanation over Ni/Al2O3 in a Lab-Scale Sabatier Fixed-Bed Reactor. Fuels. 2025; 6(4):79. https://doi.org/10.3390/fuels6040079
Chicago/Turabian StyleBozonc, Alexandru-Constantin, Vlad-Cristian Sandu, Alexia-Maria Buzila, and Ana-Maria Cormos. 2025. "Multiscale 3D CFD Modeling of CO2 Methanation over Ni/Al2O3 in a Lab-Scale Sabatier Fixed-Bed Reactor" Fuels 6, no. 4: 79. https://doi.org/10.3390/fuels6040079
APA StyleBozonc, A.-C., Sandu, V.-C., Buzila, A.-M., & Cormos, A.-M. (2025). Multiscale 3D CFD Modeling of CO2 Methanation over Ni/Al2O3 in a Lab-Scale Sabatier Fixed-Bed Reactor. Fuels, 6(4), 79. https://doi.org/10.3390/fuels6040079






