A Geothermal-Driven Zero-Emission Poly-Generation Energy System for Power and Green Hydrogen Production: Exergetic Analysis, Impact of Operating Conditions, and Optimization
Abstract
1. Introduction
| Authors/Year | Cogeneration | Energy Sources | Working Fluids | Net Power and Hydrogen Production |
|---|---|---|---|---|
| Yilmaz et al. [21] (2024) | Geothermal cycle + ORC + PEME + OD (SiM) (Green hydrogen, freshwater, and heat) | Geothermal | Organic fluid + water | 2046 kW; 0.002367 kg/s |
| Sabbaghi and Sefid [22] (2024) | ORC + PEME (SiM) (Electricity and green hydrogen) | Geothermal | Carbon dioxide | 3.99 lit/s |
| Hajabdollahi et al. [23] (2023) | Reverse osmosis desalination + ORC + PEME (SiM) (Electricity, heating, hydrogen, and freshwater) | Geothermal | Organic fluid | 1556.2 kW; 0.42 m3/day |
| Wenqiang Li et al. [24] (2024) | Double-flash cycle + PEME + PTC (SiM) (Electricity and hydrogen) | Geothermal | Water | 25.48 kg/h |
| Arslan et al. [25] (2024) | Geothermal Power Plant (AFJES) + PEME (SiM) (Electricity and hydrogen) | Geothermal | Water | 4132 kW; 150 kg/s |
| Kun Li et al. [26] (2022) | Flash-binary geothermal cycle + ERC + (KC + ERC) + PEME (SiM) (Electricity, hydrogen, cooling, and freshwater) | Geothermal | Water + Ammonia–water | 782 kW; 0.181 kg/h |
| Almutairi et al. [27] (2021) | Flash-binary geothermal cycle + ORC + PEME (SiM) (Electricity and hydrogen) | Geothermal | Organic fluid + Water | 128.16 kW; 0.39626 kg/h |
| Gao et al. [28] (2024) | Steam-methanol reforming + KC + Flash-binary geothermal cycle (SiM) (Electricity, hydrogen, and freshwater) | Geothermal–Solar | Ammonia–water | 215.9 kW; 0.0224 kg/s |
| Shubo Zhang et al. [18] (2023) | Parabolic trough solar collectors (PTSC) + KC + PEME + ARC (SiM) (Electricity, hydrogen, and hot water) | Geothermal, biomass, Solar | Ammonia–water | 3.71 MW; 11.42 kg/h |
| Laleh et al. [19] (2023) | Brayton cycle + ORC + RC (CoM) (Electricity and hydrogen) | Biomass | LNG, Organic fluid, Water | 10 MW; 0.66 kg/s |
| Wang et al. [29] (2022) | RC + PEME + Solid oxide electrolyzer (SOE) + Multi-effect desalination (MED) (SiM) (Electricity, hydrogen, and freshwater) | Biomass | Water | 1735 kW; 9880 kg/h |
| Karthikeyan et al. [30] (2024) | Heat pump + ORC + PEME (SiM) (Electricity, hydrogen, and heat) | Biomass–Solar | Organic fluid | 815 kW; 3 kg/h |
| Sharifishourabi et al. [31] (2025) | KC + Alkaline electrolyzer + Refrigeration cycle (SiM) (Electricity, hydrogen, cooling and heat) | Biomass–Wind | Ammonia–water | 5.38 kg/h |
| Forootan et al. [32] (2024) | ORC + PEME + Brayton cycle + Multi-effect distillation (SiM) (Electricity, oxygen, hydrogen, hot water and freshwater) | Solar | Organic fluid | 133 MW; 201.6 kg/h |
| Bamisile et al. [33] (2020) | 2 RC + PEME + SE-ARC + DE-ARC + PTC (SiM) (Electricity, hydrogen, hot water, and freshwater) | Solar | Water | 1027 kW; 0.9785 kg/h |
| Lykas et al. [34] (2023) | ORC + PEME (SiM) (Electricity and hydrogen) | Solar | Organic fluid | 24 kW; 0.205 kg/h |
| Mansir [11] (2024) | Brayton cycle + PVT + KC + PEME (SiM) (Electricity and hydrogen) | Solar | Carbon dioxide +NH3H2O | 33,585 kW; 16.90 kg/day |
| Colakoglu and Durmayaz [12] (2022) | Solar-tower + Brayton cycle + RC + KC (SiM) (Electricity and hydrogen) | Solar | Organic fluid +NH3H2O | 1478 kW; 22.48 kg/h |
| Sharifishourabi et al. [20] (2024) | RC + PEME + ORC + PTC + KC (CoM) (Electricity and hydrogen) | Solar | Organic fluid +NH3H2O | 1957 kW; 1 kg/h |
| Effatpanah et al. [13] (2023) | advanced alkaline electrolyzer (AAE) system + ORC + ARC + CPV/T system (SiM) (Electricity, hydrogen, and cooling) | Solar–Wind | LiBr-H2O and organic fluid | 315 kW; 1.012 kg/s |
| Gargari et al. [35] (2018) | Gas Turbine-Modular Helium Reactor (GT-MHR) and a biogas steam reforming (BSR) (SiM) (Electricity and hydrogen) | Biogas | Methane and carbon dioxide | 260.13 MW; 0.217 kg/s |
2. Geothermal Potential in the DRC
- 90 °C corresponds to 1019.21 m.
- 100 °C corresponds to 1231.54 m
- 195 °C corresponds to 3333.66 m.
3. System Description
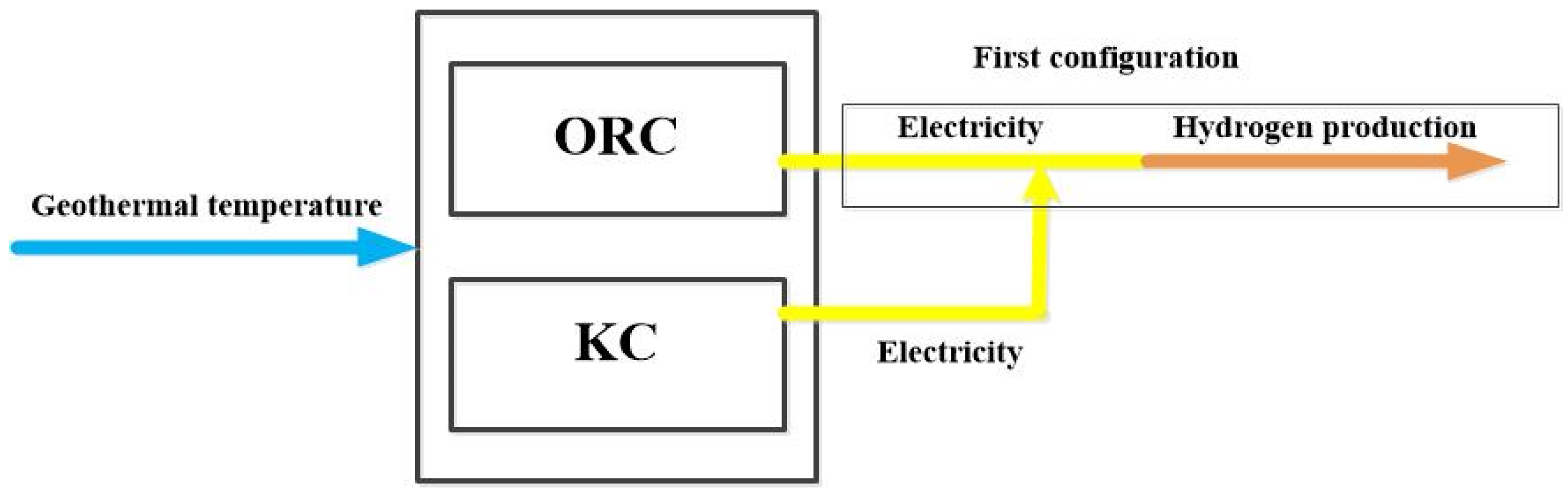
3.1. Configurations Under Study
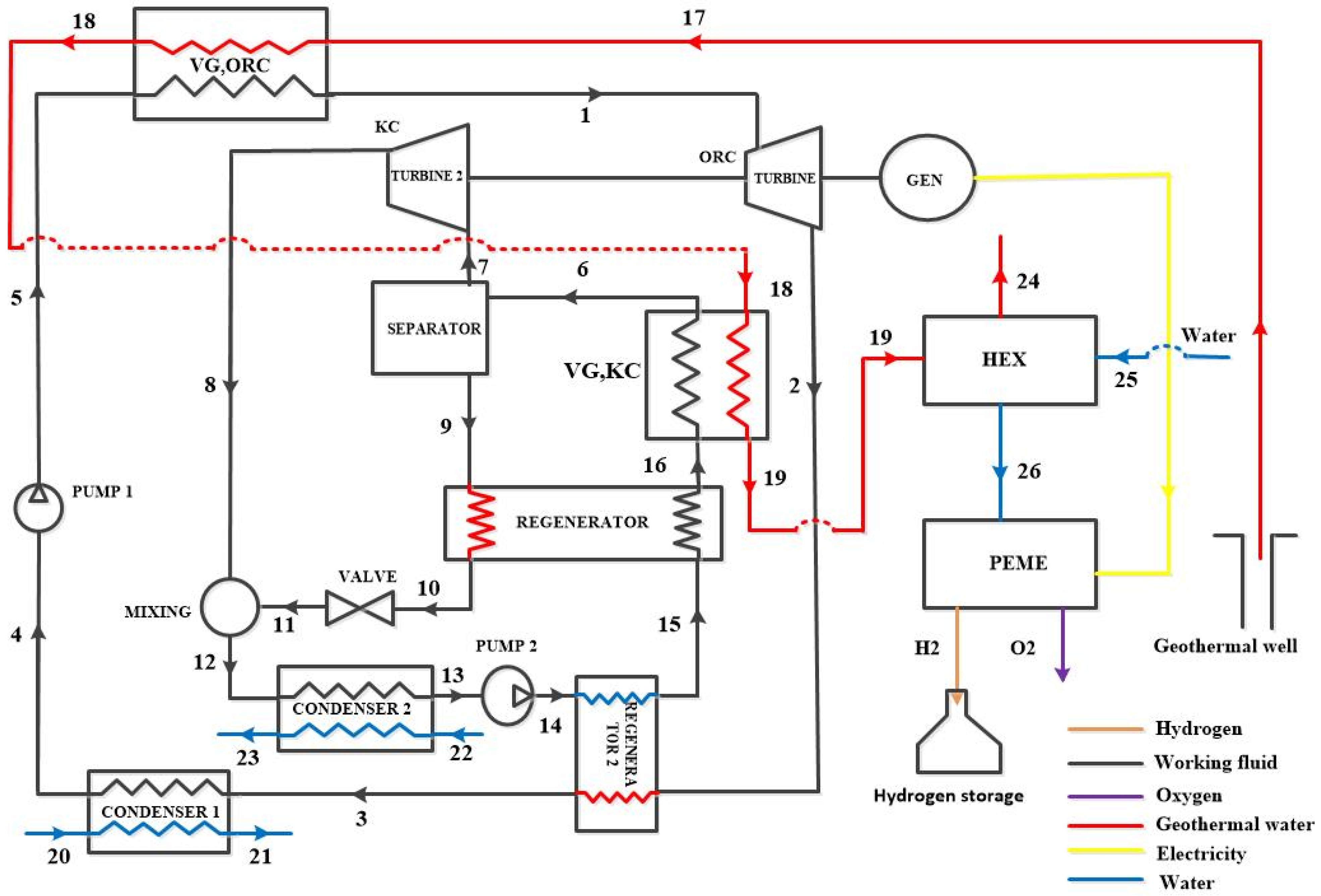
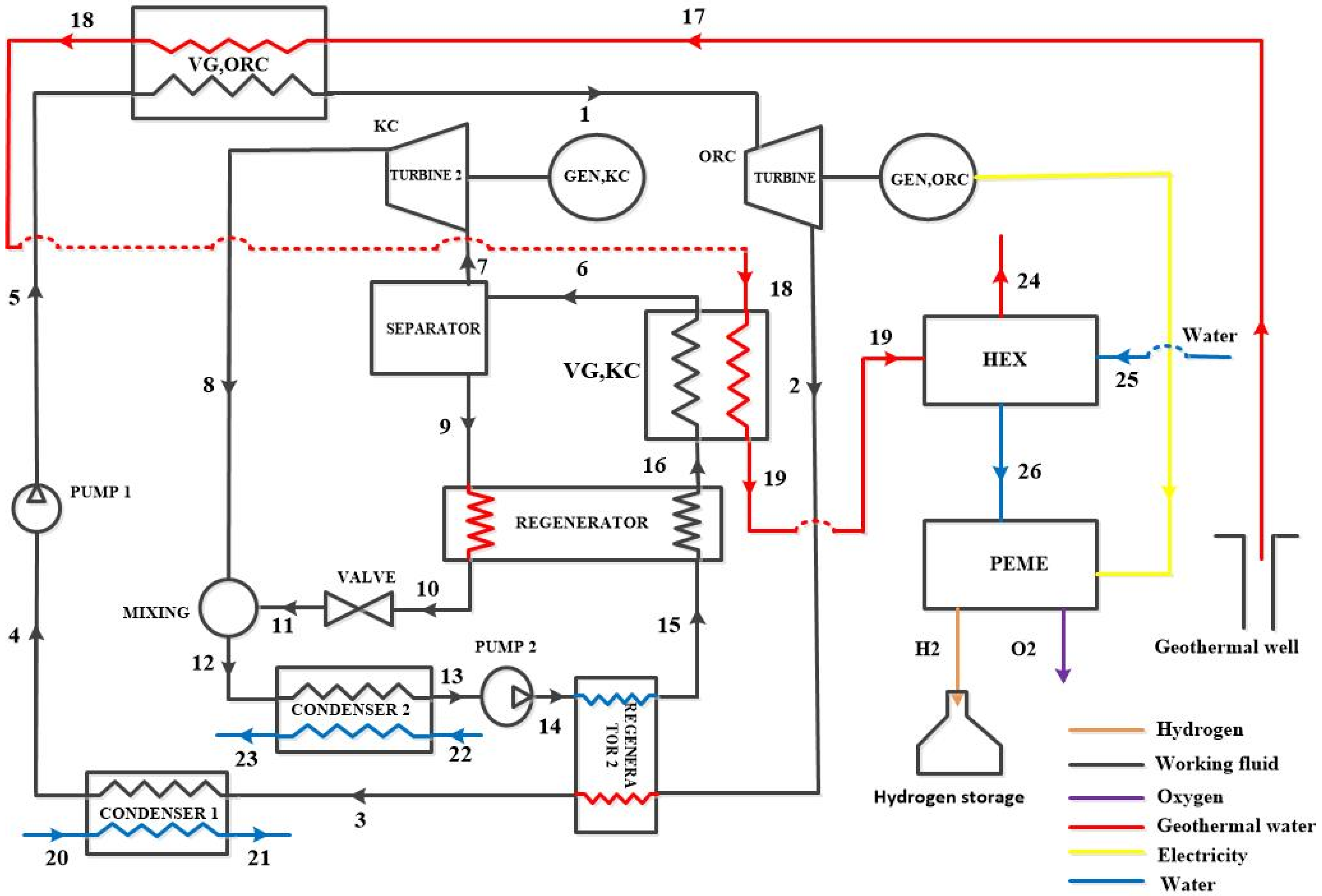
3.2. Working Fluid Selection
4. Modeling System
4.1. Assumptions
- The model operates under steady-state conditions;
- Pressure drops in all piping are neglected;
- The vapor at the turbine inlet is considered to be in a state of dry saturation;
- It is assumed that the fluid leaving the condensers is saturated;
- Flow through throttle valves are isenthalpic.
4.2. Proton Exchange Membrane Electrolyzer (PEME)
4.3. Organic Rankine Cycle (ORC) and Kalina Cycle (KC) Modeling
4.3.1. Energy Modeling
4.3.2. Exergy Modeling
4.4. Economic Modeling
5. Optimization
6. Results and Discussion
6.1. Validation Model
6.2. Thermodynamic Results
6.2.1. Overall Thermodynamic Evaluation Results
6.2.2. Effect of Operating Conditions on Thermodynamic Quantities and Exergetic Analysis
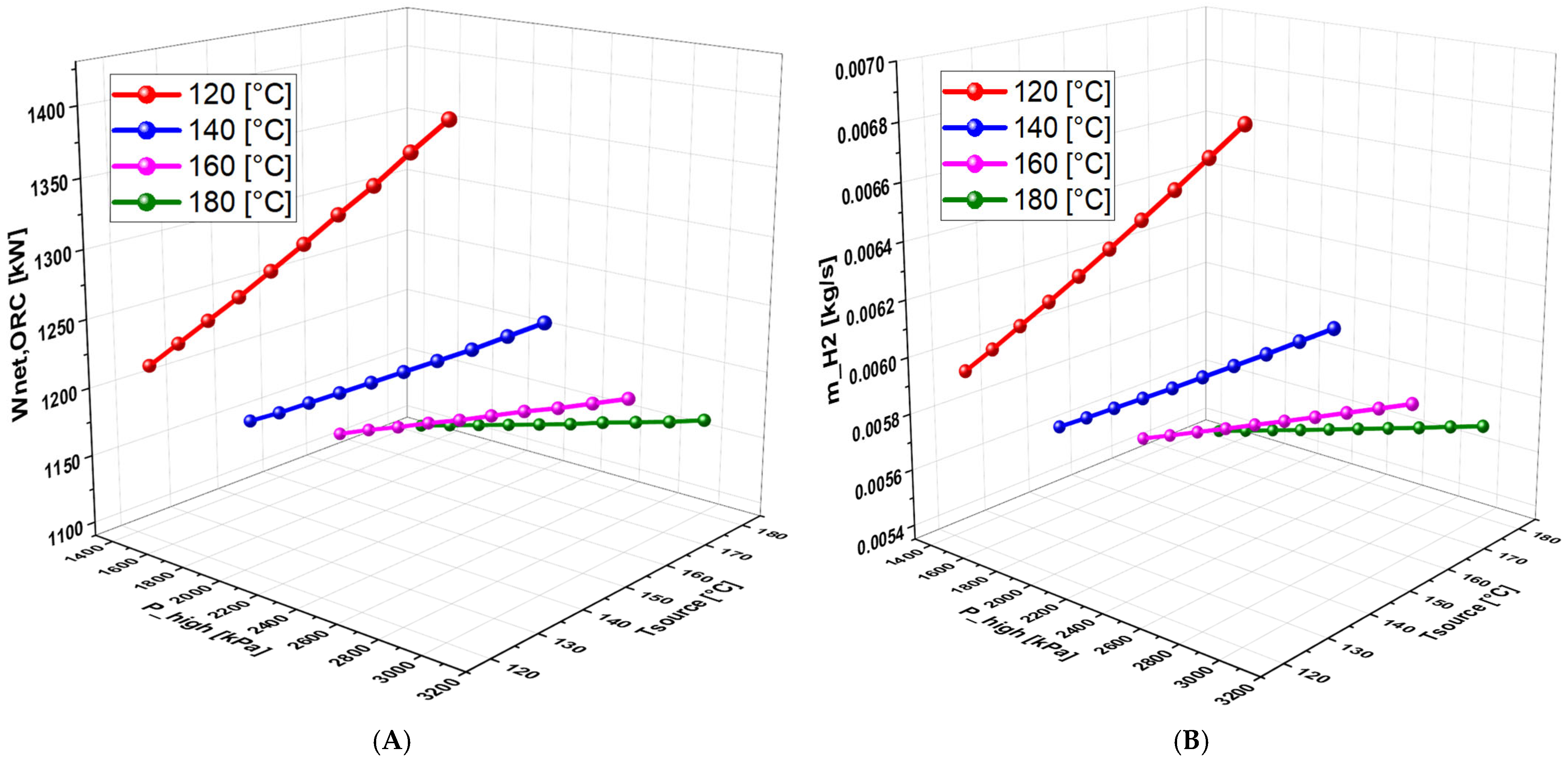
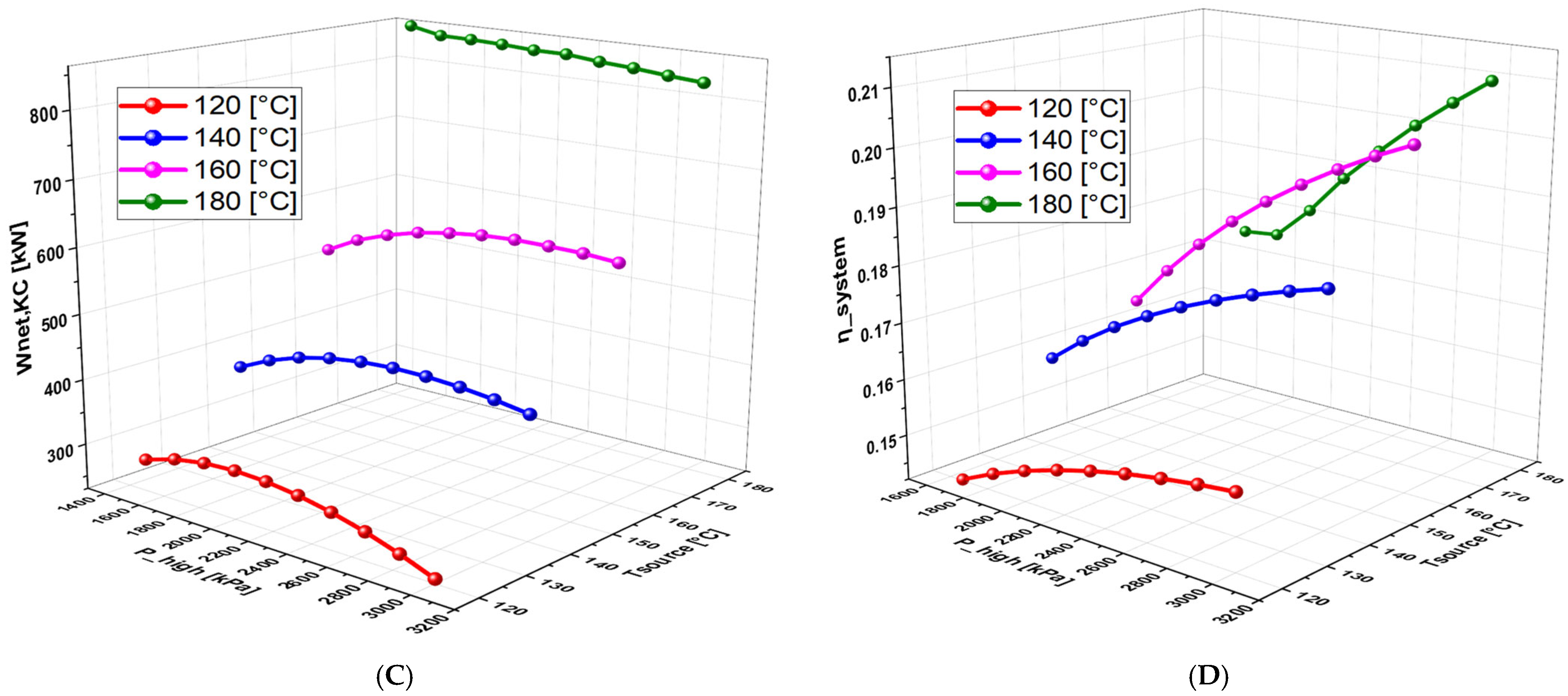
6.2.3. Effect of Geothermal Temperature on the System Performance
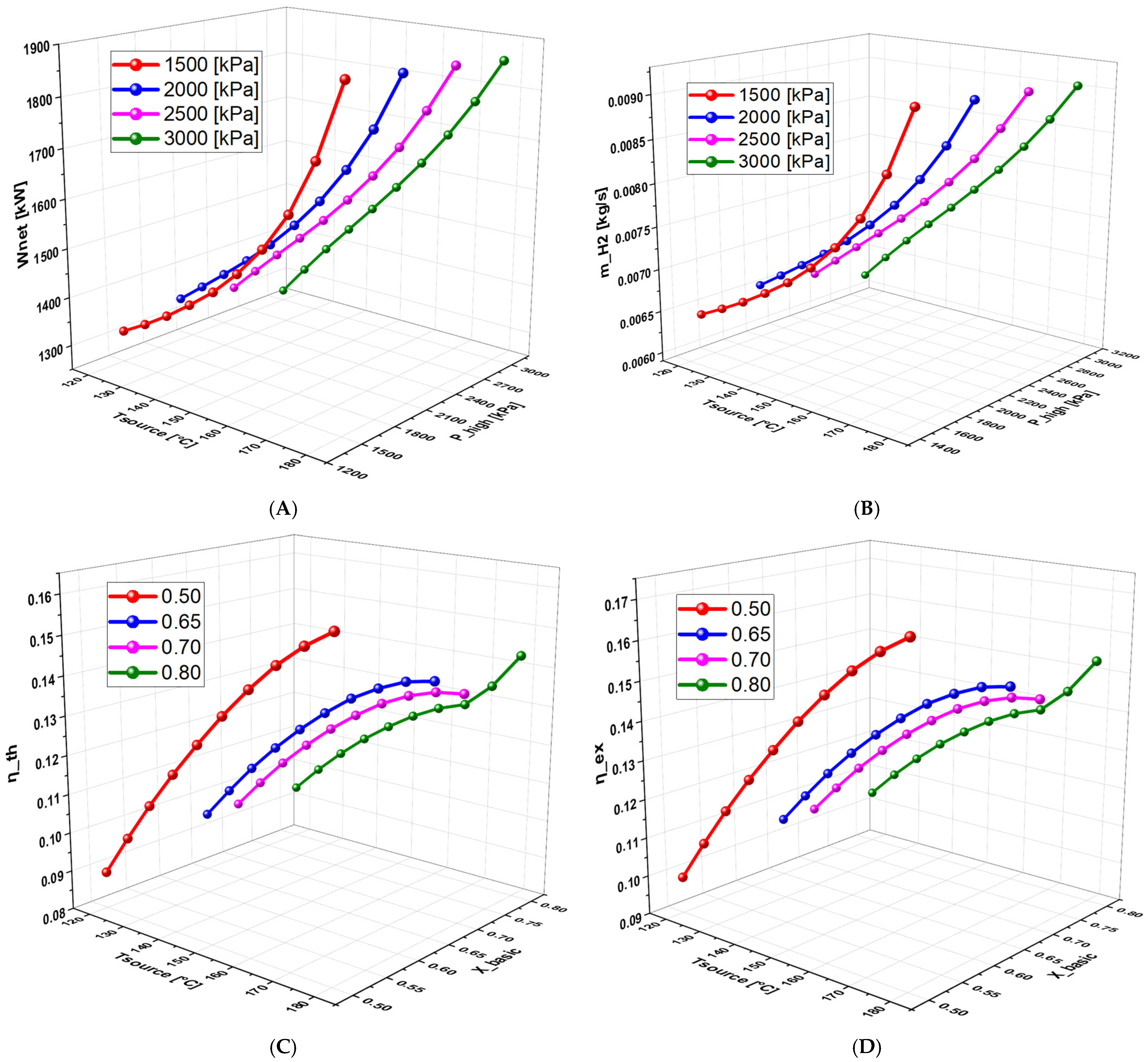
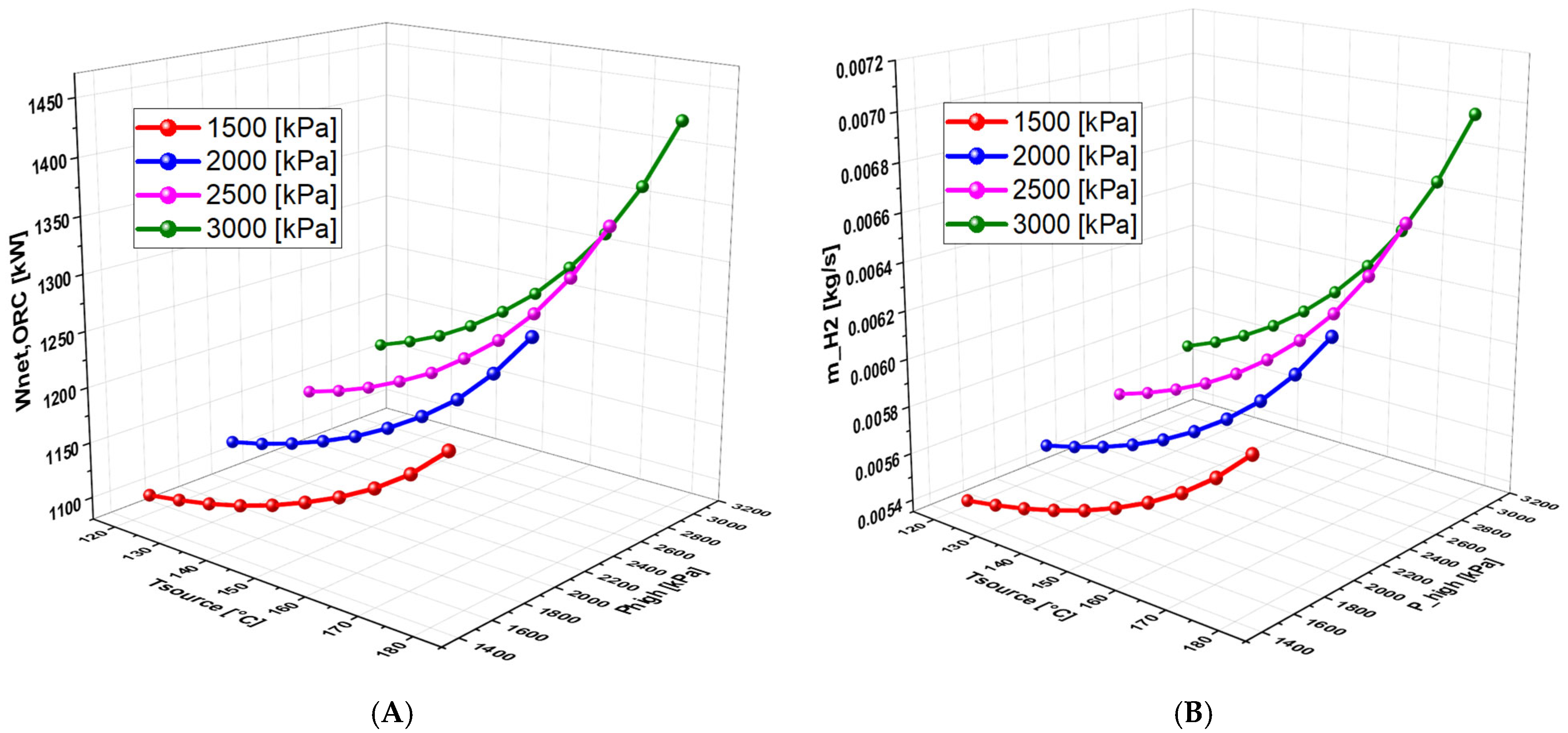
6.2.4. Effect of High Pressure on System Performance
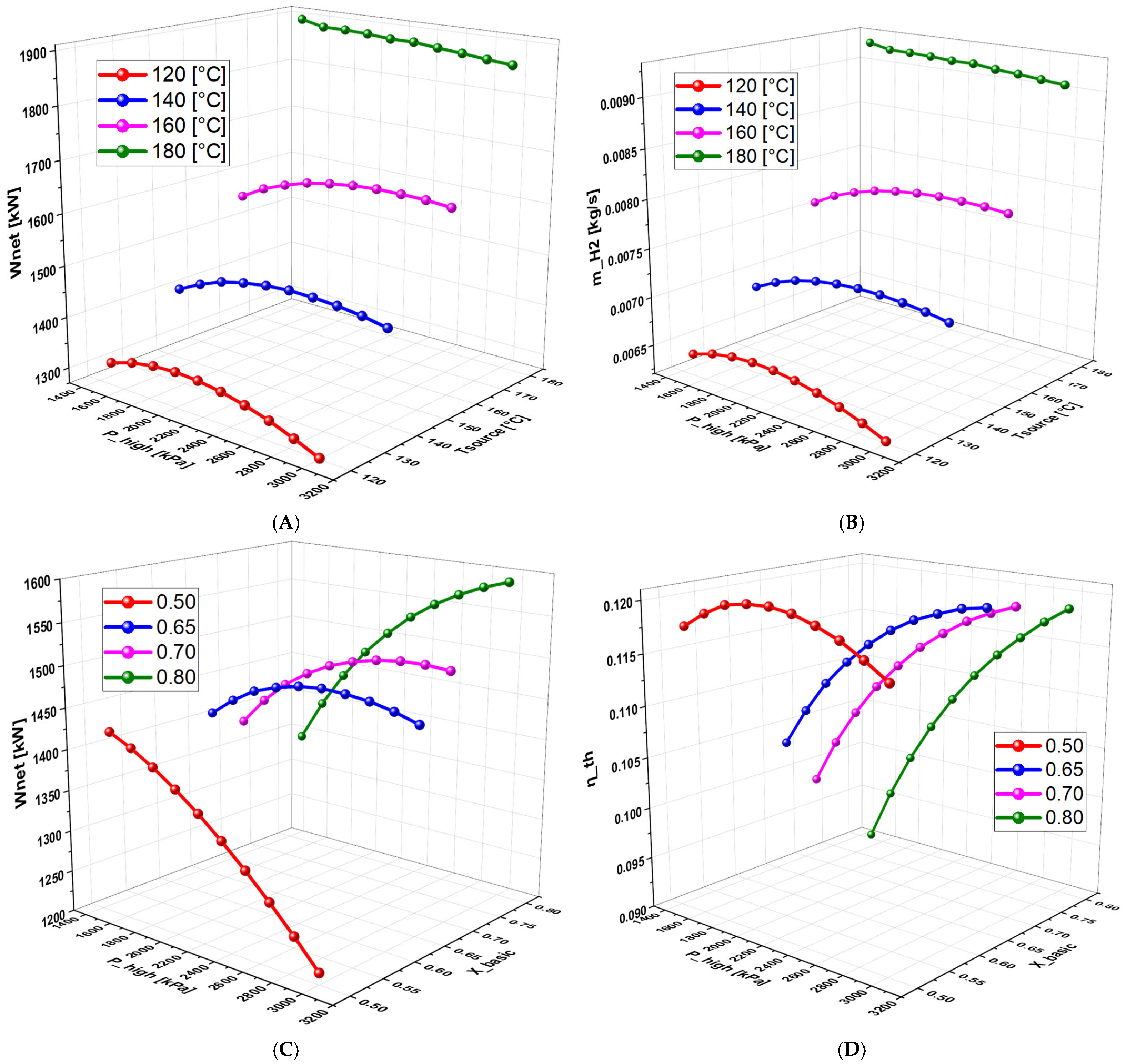
6.2.5. Effect of Basic Concentration on the System Performance
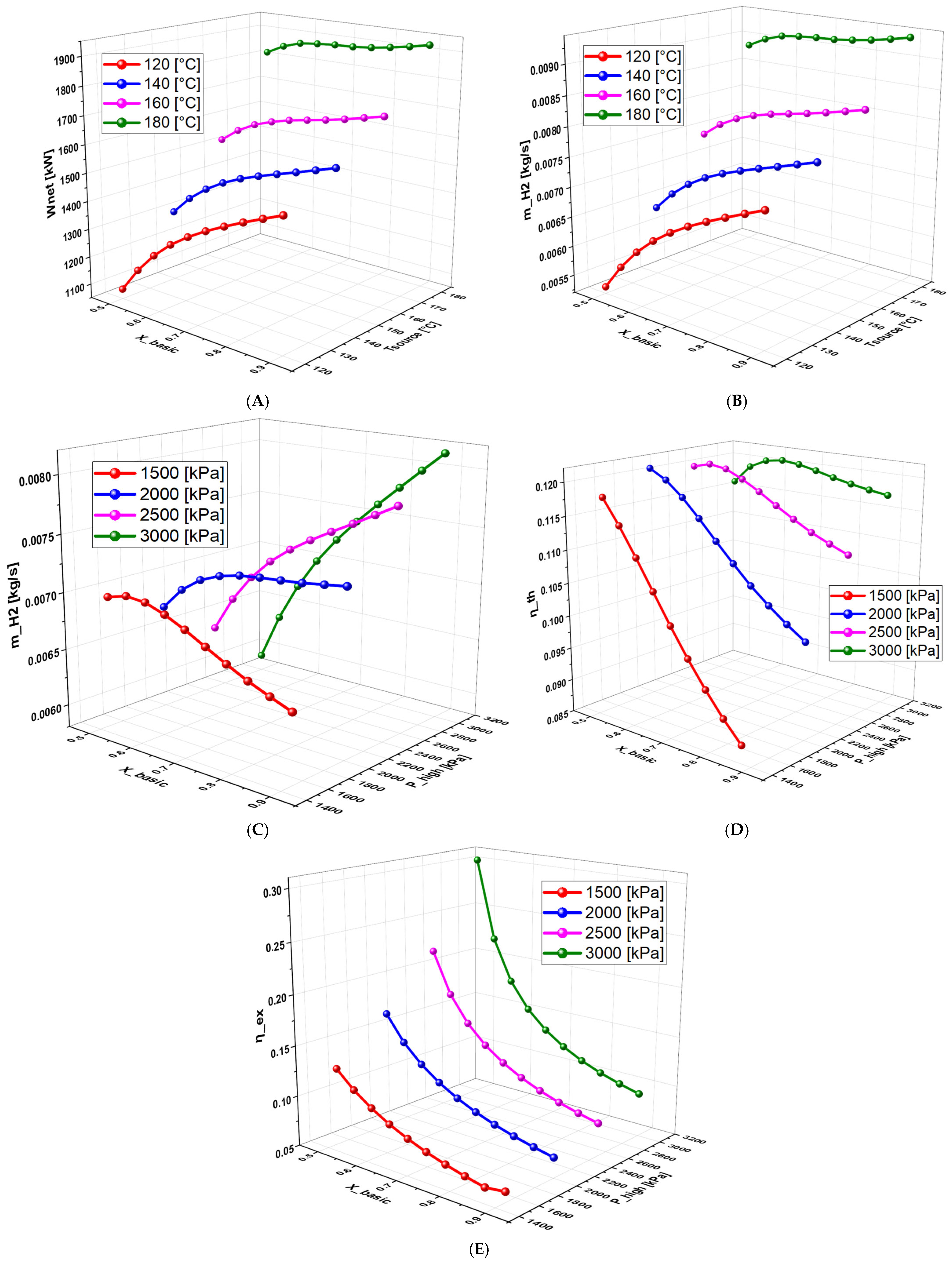
6.2.6. Effect of Terminal Temperature Difference (TTD) on the System Performance
6.3. Optimization Results
6.4. Effect of the Separation of Turbines on the System Performance
6.4.1. Effect of Geothermal Temperature on the System Performance (With Separate Turbines)
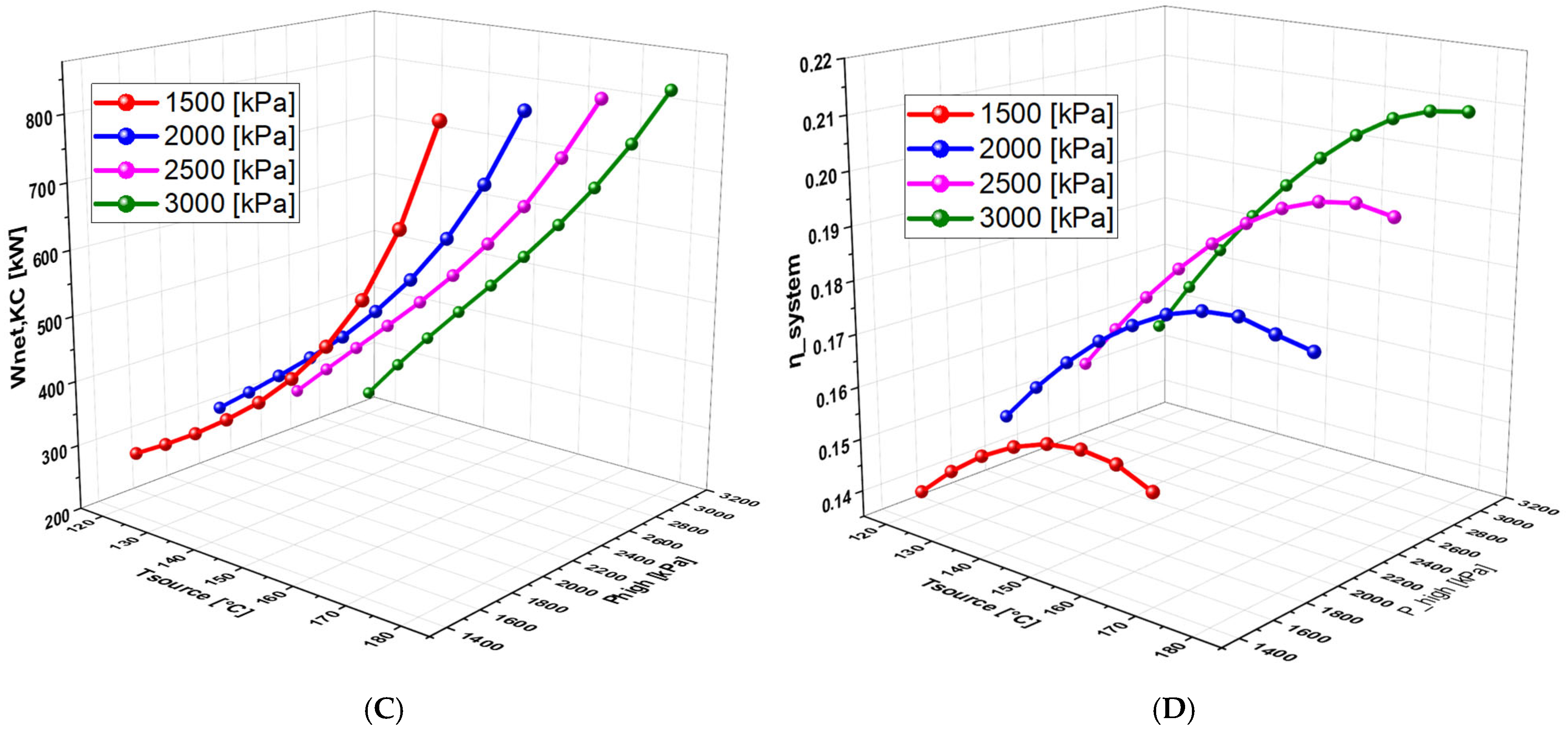
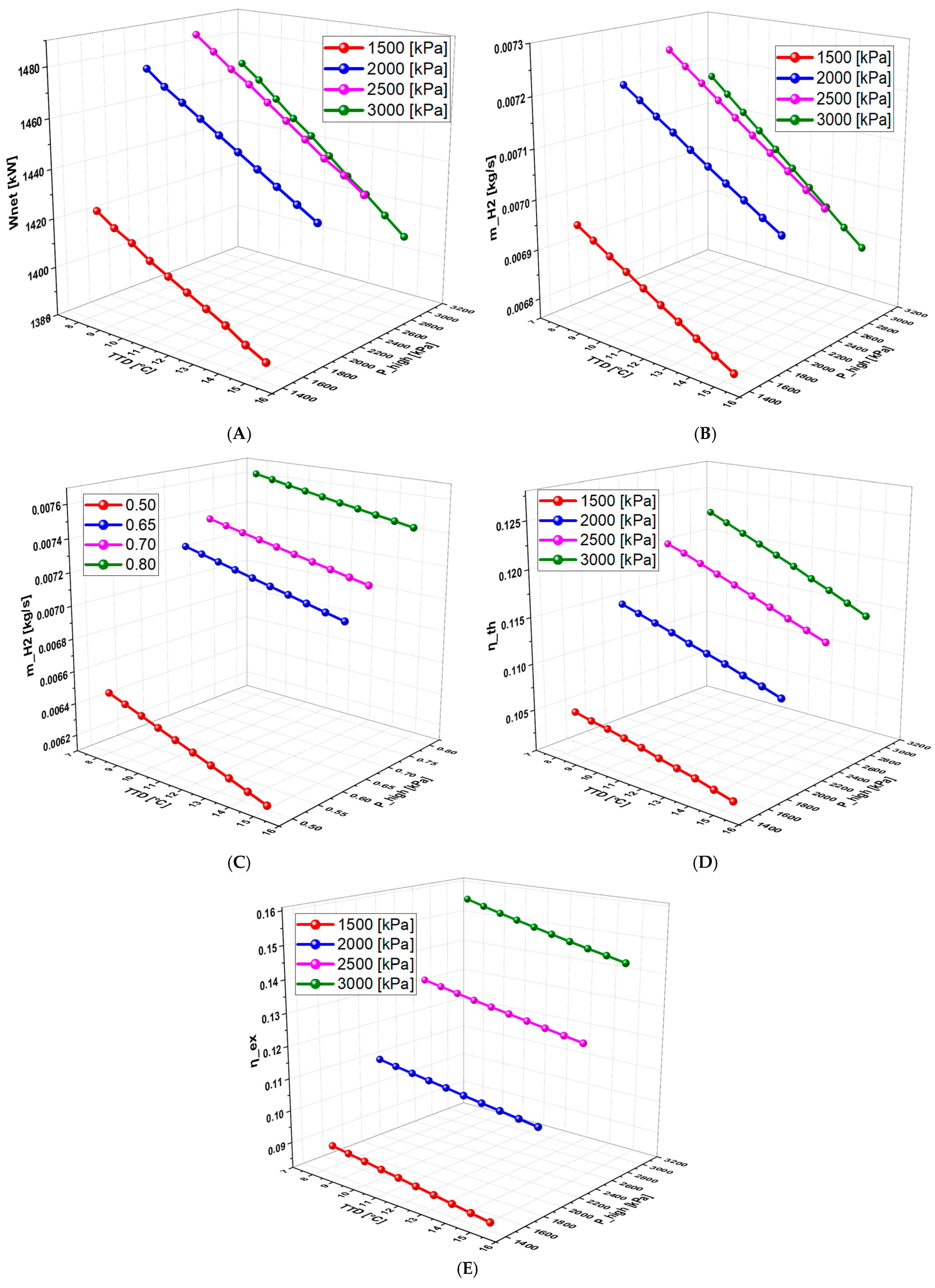
6.4.2. Effect of High Pressure on the System Performance (With separate turbines)
6.4.3. Effect of TTD on the System Performance (With Separate Turbines)

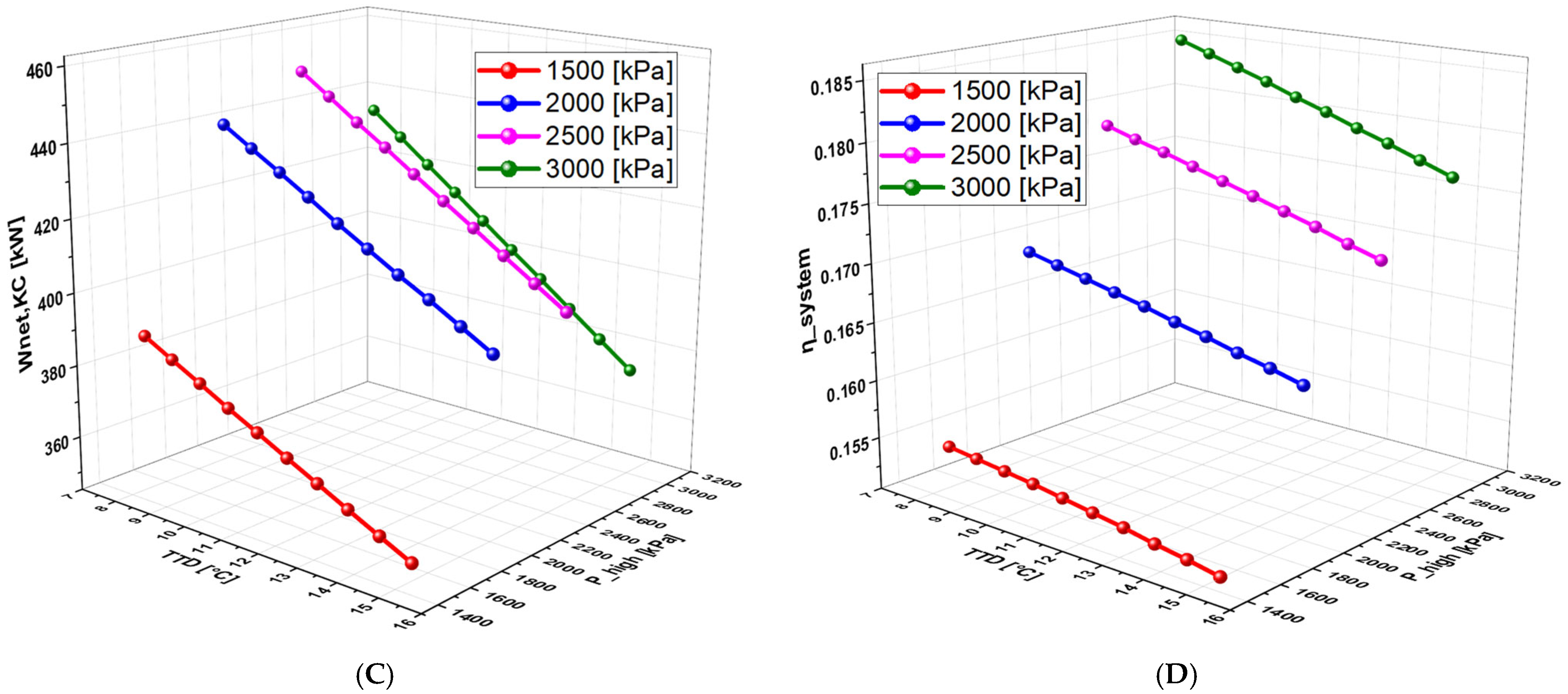
7. Conclusions
- Under the same operating conditions, the combination of an ammonia–water mixture and MD2M allowed to accomplish the best performance in comparison to the other combinations, with a net power of 1470 kW and hydrogen production rate of 0.007178 kg/s (620.17 kg/day).
- Optimization results show that among the different combinations analyzed, the combination of ammonia–water + R152a offers the best performance, with a net power of 2004 kW and hydrogen production rate of 0.009742 kg/s (841.708 kg/day). It is followed by the ammonia–water + MD2M combination.
- The combination of ammonia–water + R152a further provides a significant improvement in the system performance, with an increase of 7.16% in net power and an improvement of 7.08% in hydrogen production.
- Adjusting the reference temperature to a maximum of 180 °C leads to an increase in energy efficiency from 12% to 15% and a decrease in the total exergy destruction from 14,831 kW to 14,581 kW.
- Optimization results also indicate that the optimum ammonia concentration for the proposed system is between 0.50 and 0.51 for different combinations.
- A detailed study of the evolution of the system performance as a function of the main parameters investigated over various ranges of variation reveals that the geothermal temperature is the parameter with the most significant impact on the overall operation of the system.
- An economic study allows to determine the total investment and payback time of $3,342,000 and 5.37 years, respectively.
- The levelized cost of hydrogen (LCOH) for the proposed system is estimated at 3.007 USD/kg H2, aligning well with values reported in the literature.
- In the case of the combined turbine configuration, hydrogen production rate reaches 0.007178 kg/s (i.e., 620.17 kg/day) for a net power output of 1470 kW. In comparison, the separate turbine configuration yields a hydrogen production rate of 0.006044 kg/s (i.e., 522.20 kg/day) with a net power output of 1235 kW. This corresponds to a reduction of 18.76% in hydrogen production compared to the combined configuration.
- Comparing the performance of the proposed cycle combinations with the existing one without accounting for the economic part indicates that this cycle performs better and is simply flexible as the amount of electricity to be allocated for the hydrogen production can vary between 1235 and 1470 kW.

Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| EES | Engineering Equation Solver |
| F | Faraday constant |
| GA | Genetic algorithm |
| GEN | Generator |
| h | Enthalpy (kJ/kg) |
| HEX | Exchanger |
| J | Current density |
| KC | Kalina cycle |
| LHV | Lower heating value |
| Mass flow rate (kg/s) | |
| Hydrogen production rate (kg/s), (kg/day) | |
| ORC | Organic Rankine cycle |
| P | Pressure (kPa) |
| PEM | Proton exchange membrane |
| PEME | Proton exchange membrane electrolyzer |
| Heat flow (kW) | |
| reg | Regenerator |
| s | Entropy (kJ/kg K) |
| T0 | Ambient temperature (°C) |
| T | Temperature (°C) |
| TTD | Terminal temperature difference (°C) |
| VG | Vapor generator |
| VG | Overpotential (V) |
| V_O | Reversible potential (V) |
| V_act,a | Cathode overpotential (V) |
| V_act,c | Anode overpotential (V) |
| V_ohm | Ohmic overpotential (V) |
| W | Power (KW) |
| Wnet | Power net (KW) |
| Greek letters | |
| η | Efficiency (%) |
| ε | Effectiveness |
| Subscripts | |
| cond | Condenser |
| ex | Exergy |
| gen | Generator |
| in | Inlet |
| out | Outlet |
| th | Thermal |
Appendix A
| State | T [°C] | P [kPa] | h [kJ/kg] | s [kJ/kg K] | x [%] | [kg/s] |
|---|---|---|---|---|---|---|
| 1 | 130 | 2500 | 740.3 | 2.519 | 16.53 | |
| 2 | 70.73 | 404.5 | 672.6 | 2.554 | 16.53 | |
| 3 | 32.41 | 404.5 | 599.7 | 2.329 | 16.53 | |
| 4 | 30 | 404.5 | 271.8 | 1.248 | 16.53 | |
| 5 | 31.65 | 2500 | 276.9 | 1.252 | 16.53 | |
| 6 | 128.9 | 2500 | 965.4 | 3.168 | 0.65 | 5 |
| 7 | 128.9 | 2500 | 1589 | 4.783 | 0.9284 | 2.459 |
| 8 | 85.46 | 671.1 | 1407 | 5.14 | 0.9284 | 2.459 |
| 9 | 128.9 | 2500 | 362.1 | 1.605 | 0.3806 | 2.541 |
| 10 | 50.31 | 2500 | 1.092 | 0.6077 | 0.3806 | 2.541 |
| 11 | 50.64 | 671.1 | 1.092 | 0.6143 | 0.3806 | 2.541 |
| 12 | 69.43 | 671.1 | 692.7 | 2.714 | 0.65 | 5 |
| 13 | 30 | 671.1 | −76.39 | 0.3147 | 0.65 | 5 |
| 14 | 30.4 | 2500 | −73.18 | 0.3174 | 0.65 | 5 |
| 15 | 46.18 | 2500 | −0.3076 | 0.5514 | 0.65 | 5 |
| 16 | 88.93 | 2500 | 360.7 | 1.587 | 0.65 | 5 |
| 17 | 140 | 400 | 589.2 | 1.739 | 0 | 100 |
| 18 | 138.9 | 400 | 584.6 | 1.728 | 0 | 100 |
| 19 | 110.8 | 400 | 465 | 1.427 | 0 | 100 |
| 20 | 20 | 101.3 | 84.01 | 0.2965 | 64.52 | |
| 21 | 40 | 101.3 | 167.6 | 0.5724 | 64.52 | |
| 22 | 20 | 101.3 | 84.01 | 0.2965 | 45.78 | |
| 23 | 40 | 101.3 | 167.6 | 0.5724 | 45.78 | |
| 24 | 86.16 | 400 | 361.2 | 1.148 | 100 | |
| 25 | 25 | 101.3 | 104.9 | 0.3672 | 0.064 | |
| 26 | 80 | 101.3 | 335.1 | 1.076 | 0.064 | |
| 27 | 80 | 101.3 | 4723 | 55.81 | 0.007155 | |
| 28 | 80 | 101.3 | 50.8 | 0.1564 | 0.05684 |
| State | T [°C] | P [kPa] | h [kJ/kg] | s [kJ/kgK] | x [%] | [kg/s] |
|---|---|---|---|---|---|---|
| 1 | 130 | 2500 | 568.6 | 1.6 | 14.98 | |
| 2 | 60.93 | 353.8 | 494.6 | 1.64 | 14.98 | |
| 3 | 31.92 | 353.8 | 442.3 | 1.476 | 14.98 | |
| 4 | 30 | 353.8 | 84.13 | 0.2946 | 14.98 | |
| 5 | 30.88 | 2500 | 89.02 | 0.2986 | 14.98 | |
| 6 | 128.9 | 2500 | 964.9 | 3.166 | 0.65 | 5 |
| 7 | 128.9 | 2500 | 1589 | 4.782 | 0.9285 | 2.458 |
| 8 | 85.43 | 671.1 | 1407 | 5.139 | 0.9285 | 2.458 |
| 9 | 128.9 | 2500 | 361.9 | 1.604 | 0.3808 | 2.542 |
| 10 | 46.1 | 2500 | −17.4 | 0.5502 | 0.3808 | 2.542 |
| 11 | 46.44 | 671.1 | −17.4 | 0.5569 | 0.3808 | 2.542 |
| 12 | 68.68 | 671.1 | 682.8 | 2.686 | 0.65 | 5 |
| 13 | 30 | 671.1 | −76.39 | 0.3147 | 0.65 | 5 |
| 14 | 30.4 | 2500 | −73.18 | 0.3174 | 0.65 | 5 |
| 15 | 41.74 | 2500 | −20.87 | 0.4865 | 0.65 | 5 |
| 16 | 88.82 | 2500 | 358.4 | 1.58 | 0.65 | 5 |
| 17 | 140 | 400 | 589.2 | 1.739 | 0 | 100 |
| 18 | 138.9 | 400 | 584.4 | 1.728 | 0 | 100 |
| 19 | 110.7 | 400 | 464.5 | 1.426 | 0 | 100 |
| 20 | 20 | 101.3 | 84.01 | 0.2965 | 63.86 | |
| 21 | 40 | 101.3 | 167.6 | 0.5724 | 63.86 | |
| 22 | 20 | 101.3 | 84.01 | 0.2965 | 45.19 | |
| 23 | 40 | 101.3 | 167.6 | 0.5724 | 45.19 | |
| 24 | 86.13 | 400 | 310.7 | 1.148 | 100 | |
| 25 | 25 | 101.3 | 104.9 | 0.3672 | 0.064 | |
| 26 | 80 | 101.3 | 335.1 | 1.076 | 0.064 | |
| 27 | 80 | 101.3 | 4723 | 55.81 | 0.007153 | |
| 28 | 80 | 101.3 | 50.8 | 0.1564 | 0.05684 |
| State | T [°C] | P [kPa] | h [kJ/kg] | s [kJ/kgK] | x [%] | [kg/s] |
|---|---|---|---|---|---|---|
| 1 | 130 | 2500 | 446.8 | 1.7 | 38.26 | |
| 2 | 72.21 | 320.4 | 417.6 | 1.715 | 38.26 | |
| 3 | 32.49 | 320.4 | 381.3 | 1.604 | 38.26 | |
| 4 | 30 | 320.4 | 236.6 | 1.127 | 38.26 | |
| 5 | 31.44 | 2500 | 238.8 | 1.128 | 38.26 | |
| 6 | 129.5 | 2500 | 973.6 | 3.188 | 0.65 | 5 |
| 7 | 129.5 | 2500 | 1592 | 4.791 | 0.9267 | 2.479 |
| 8 | 86.02 | 671.1 | 1410 | 5.148 | 0.9267 | 2.479 |
| 9 | 129.5 | 2500 | 365.3 | 1.612 | 0.378 | 2.521 |
| 10 | 42.84 | 2500 | −30.92 | 0.5064 | 0.378 | 2.521 |
| 11 | 43.19 | 671.1 | −30.92 | 0.5132 | 0.378 | 2.521 |
| 12 | 68.74 | 671.1 | 683.6 | 2.688 | 0.65 | 5 |
| 13 | 30 | 671.1 | −76.39 | 0.3147 | 0.65 | 5 |
| 14 | 30.4 | 2500 | −73.18 | 0.3174 | 0.65 | 5 |
| 15 | 38.28 | 2500 | −36.9 | 0.4353 | 0.65 | 5 |
| 16 | 88.86 | 2500 | 359.4 | 1.583 | 0.65 | 5 |
| 17 | 140 | 400 | 589.2 | 1.739 | 0 | 100 |
| 18 | 139.5 | 400 | 587.1 | 1.734 | 0 | 100 |
| 19 | 110.9 | 400 | 465.6 | 1.429 | 0 | 100 |
| 20 | 20 | 101.3 | 84.01 | 0.2965 | 65.89 | |
| 21 | 40 | 101.3 | 167.6 | 0.5724 | 65.89 | |
| 22 | 20 | 101.3 | 84.01 | 0.2965 | 45.24 | |
| 23 | 40 | 101.3 | 167.6 | 0.5724 | 45.24 | |
| 24 | 86.19 | 400 | 361.3 | 1.148 | 100 | |
| 25 | 25 | 101.3 | 104.9 | 0.3672 | 0.064 | |
| 26 | 80 | 101.3 | 335.1 | 1.076 | 0.064 | |
| 27 | 80 | 101.3 | 4723 | 55.81 | 0.007176 | |
| 28 | 80 | 101.3 | 50.8 | 0.1564 | 0.05684 |
| State | T [°C] | P [kPa] | h [kJ/kg] | s [kJ/kgK] | x [%] | [kg/s] |
|---|---|---|---|---|---|---|
| 1 | 130 | 2500 | 344.8 | 1.424 | 79.69 | |
| 2 | 74.59 | 109.7 | 329.7 | 1.433 | 79.69 | |
| 3 | 31.92 | 109.7 | 401.3 | 1.669 | 79.69 | |
| 4 | 30 | 109.7 | 231.4 | 1.109 | 79.69 | |
| 5 | 31.38 | 2500 | 233.6 | 1.11 | 79.69 | |
| 6 | 129.7 | 2500 | 976.7 | 3.196 | 0.65 | 5 |
| 7 | 129.7 | 2500 | 1594 | 4.794 | 0.926 | 2.486 |
| 8 | 86.22 | 671.1 | 1412 | 5.151 | 0.926 | 2.486 |
| 9 | 129.7 | 2500 | 366.6 | 1.615 | 0.377 | 2.514 |
| 10 | 20.51 | 2500 | −128.1 | 0.1869 | 0.377 | 2.514 |
| 11 | 20.92 | 671.1 | −128.1 | 0.194 | 0.377 | 2.514 |
| 12 | 65.23 | 671.1 | 637.5 | 2.553 | 0.65 | 5 |
| 13 | 30 | 671.1 | −76.39 | 0.3147 | 0.65 | 5 |
| 14 | 30.4 | 2500 | −73.18 | 0.3174 | 0.65 | 5 |
| 15 | 14.76 | 2500 | −144.8 | 0.07511 | 0.65 | 5 |
| 16 | 88.42 | 2500 | 349.9 | 1.557 | 0.65 | 5 |
| 17 | 140 | 400 | 589.2 | 1.739 | 0 | 100 |
| 18 | 139.7 | 400 | 588.1 | 1.736 | 0 | 100 |
| 19 | 110.6 | 400 | 464.1 | 1.425 | 0 | 100 |
| 20 | 20 | 101.3 | 84.01 | 0.2965 | 161.2 | |
| 21 | 40 | 101.3 | 167.6 | 0.5724 | 161.2 | |
| 22 | 20 | 101.3 | 84.01 | 0.2965 | 42.49 | |
| 23 | 40 | 101.3 | 167.6 | 0.5724 | 42.49 | |
| 24 | 86.12 | 400 | 361 | 1.147 | 100 | |
| 25 | 25 | 101.3 | 104.9 | 0.3672 | 0.064 | |
| 26 | 80 | 101.3 | 335.1 | 1.076 | 0.064 | |
| 27 | 80 | 101.3 | 4723 | 55.81 | 0.007178 | |
| 28 | 80 | 101.3 | 50.8 | 0.1564 | 0.05684 |
| State | T [°C] | P [kPa] | h [kJ/kg] | s [kJ/kgK] | x [%] | [kg/s] |
|---|---|---|---|---|---|---|
| 1 | 130 | 2500 | 627.1 | 2.237 | 25.11 | |
| 2 | 74.59 | 690.7 | 583.2 | 2.259 | 25.11 | |
| 3 | 32.61 | 690.7 | 529.1 | 2.093 | 25.11 | |
| 4 | 30 | 690.7 | 253.1 | 1.183 | 25.11 | |
| 5 | 31.38 | 2500 | 255.8 | 1.185 | 25.11 | |
| 6 | 129.1 | 2500 | 968.4 | 3.175 | 0.65 | 5 |
| 7 | 129.1 | 2500 | 1590 | 4.786 | 0.9278 | 2.466 |
| 8 | 85.66 | 671.1 | 1408 | 5.143 | 0.9278 | 2.466 |
| 9 | 129.1 | 2500 | 363.3 | 1.607 | 0.3797 | 2.534 |
| 10 | 46.49 | 2500 | −15.42 | 0.5559 | 0.3797 | 2.534 |
| 11 | 46.83 | 671.1 | −15.42 | 0.5626 | 0.3797 | 2.534 |
| 12 | 68.98 | 671.1 | 686.8 | 2.698 | 0.65 | 5 |
| 13 | 30 | 671.1 | −76.39 | 0.3147 | 0.65 | 5 |
| 14 | 30.4 | 2500 | −73.18 | 0.3174 | 0.65 | 5 |
| 15 | 42.14 | 2500 | −19.06 | 0.4923 | 0.65 | 5 |
| 16 | 88.88 | 2500 | 359.6 | 1.584 | 0.65 | 5 |
| 17 | 140 | 400 | 589.2 | 1.739 | 0 | 100 |
| 18 | 139.1 | 400 | 585.5 | 1.73 | 0 | 100 |
| 19 | 110.8 | 400 | 465.1 | 1.428 | 0 | 100 |
| 20 | 20 | 101.3 | 84.01 | 0.2965 | 82.51 | |
| 21 | 40 | 101.3 | 167.6 | 0.5724 | 82.51 | |
| 22 | 20 | 101.3 | 84.01 | 0.2965 | 45.43 | |
| 23 | 40 | 101.3 | 167.6 | 0.5724 | 45.43 | |
| 24 | 86.16 | 400 | 361.2 | 1.148 | 100 | |
| 25 | 25 | 101.3 | 104.9 | 0.3672 | 0.064 | |
| 26 | 80 | 101.3 | 335.1 | 1.076 | 0.064 | |
| 27 | 80 | 101.3 | 4723 | 55.81 | 0.007162 | |
| 28 | 80 | 101.3 | 50.8 | 0.1564 | 0.05684 |
References
- Singla, M.K.; Nijhawan, P.; Oberoi, A.S. Hydrogen fuel and fuel cell technology for cleaner future: A review. Environ. Sci. Pollut. Res. 2021, 28, 15607–15626. [Google Scholar] [CrossRef] [PubMed]
- Kannah, R.Y.; Kavitha, S.; Preethi; Karthikeyan, O.P.; Kumar, G.; Dai-Viet, N.V.; Banu, J.R. Techno-economic assessment of various hydrogen production methods—A review. Bioresour. Technol. 2021, 319, 124175. [Google Scholar] [CrossRef]
- Dash, S.K.; Chakraborty, S.; Elangovan, D. A Brief Review of Hydrogen Production Methods and Their Challenges. Energies 2023, 16, 1141. [Google Scholar] [CrossRef]
- Wen, X.; Dressler, L.; Dreizler, A.; Sadiki, A.; Janicka, J.; Hasse, C. Flamelet LES of turbulent premixed/stratified flames with H 2 addition. Combust. Flame 2021, 230, 111428. [Google Scholar] [CrossRef]
- Zainal, B.S.; Ker, P.J.; Mohamed, H.; Ong, H.C.; Fattah, I.M.R.; Rahman, S.M.A.; Nghiem, L.D.; Mahlia, T.M.I. Recent advancement and assessment of green hydrogen production technologies. Renew. Sustain. Energy Rev. 2024, 189, 113941. [Google Scholar] [CrossRef]
- Aravindan, M.; Kumar, G.P. Optimizing novel green hydrogen production from solar and municipal solid waste: A thermo-economic investigation with environmental comparison between integrated low temperature power cycles. Process Saf. Environ. Prot. 2024, 186, 421–447. [Google Scholar] [CrossRef]
- Baral, S.; Šebo, J. Techno-economic assessment of green hydrogen production integrated with hybrid and organic Rankine cycle (ORC) systems. Heliyon 2024, 10, e25742. [Google Scholar] [CrossRef]
- Hassan, Q.; Sameen, A.Z.; Salman, H.M.; Jaszczur, M. Large-scale green hydrogen production via alkaline water electrolysis using solar and wind energy. Int. J. Hydrogen Energy 2023, 48, 34299–34315. [Google Scholar] [CrossRef]
- Karthikeyan, B.; Kumar, G.P. Thermoeconomic and optimization approaches for integrating cooling, power, and green hydrogen production in dairy plants with a novel solar-biomass cascade ORC system. Energy Convers. Manag. 2023, 295, 117645. [Google Scholar] [CrossRef]
- Elrhoul, D.; Naveiro, M.; Gómez, M.R.; Adams, T.A. Thermo-economic analysis of green hydrogen production onboard LNG carriers through solid oxide electrolysis powered by organic Rankine cycles. Appl. Energy 2025, 380, 124996. [Google Scholar] [CrossRef]
- Alirahmi, S.M.; Assareh, E.; Pourghassab, N.N.; Delpisheh, M.; Barelli, L.; Baldinelli, A. Green hydrogen & electricity production via geothermal-driven multi-generation system: Thermodynamic modeling and optimization. Fuel 2022, 308, 122049. [Google Scholar] [CrossRef]
- Hai, T.; El-Shafay, A.S.; Alizadeh, A.; Chauhan, B.S.; Almojil, S.F.; Almohana, A.I.; Alali, A.F. Combination of a geothermal-driven double-flash cycle and a Kalina cycle to devise a polygeneration system: Environmental assessment and optimization. Appl. Therm. Eng. 2023, 228, 120437. [Google Scholar] [CrossRef]
- Madhesh, K.; Devesh, D.R.; Vivin, T.; Raj, M.P.; Phelan, P.E.; Kumar, V.V.; Kumar, G.P. Analysis and multi-objective evolutionary optimization of Solar-Biogas hybrid system operated cascade Kalina organic Rankine cycle for sustainable cooling and green hydrogen production. Energy Convers. Manag. 2024, 301, 117999. [Google Scholar] [CrossRef]
- Saoud, A.; Boukhchana, Y.; Bruno, J.C.; Fellah, A. Thermodynamic investigation of an innovative solar-driven trigeneration plant based on an integrated ORC-single effect-double lift absorption chiller. Therm. Sci. Eng. Prog. 2024, 50, 102596. [Google Scholar] [CrossRef]
- Sharifishourabi, M.; Dincer, I.; Mohany, A. A novel trigeneration energy system with two modes of operation for thermal energy storage and hydrogen production. Energy 2024, 304, 132121. [Google Scholar] [CrossRef]
- Yilmaz, F.; Ozturk, M.; Selbas, R. A parametric examination of the energetic, exergetic, and environmental performances of the geothermal energy-based multigeneration plant for sustainable products. Int. J. Hydrogen Energy 2024, 143, 947–957. [Google Scholar] [CrossRef]
- Sabbaghi, M.A.; Sefid, M. Thermo-economic analysis of a combined flash-binary geothermal cycle with a transcritical CO2 cycle to produce green hydrogen. Int. J. Exergy 2024, 43, 110–122. [Google Scholar] [CrossRef]
- Hajabdollahi, H.; Saleh, A.; Dehaj, M.S. A multi-generation system based on geothermal driven: Energy, exergy, economic and exergoenvironmental (4E) analysis for combined power, freshwater, hydrogen, oxygen, and heating production. Environ. Dev. Sustain. 2023, 26, 26415–26447. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Abed, A.M.; Ayed, H.; Khadimallah, M.A.; Deifalla, A.; Lee, V.F. Enhancing green hydrogen production via improvement of an integrated double flash geothermal cycle; Multi-criteria optimization and exergo-environmental evaluation. Case Stud. Therm. Eng. 2024, 59, 104538. [Google Scholar] [CrossRef]
- Arslan, M.; Yilmaz, C. Development of models for green hydrogen production of Turkey geothermal Resources: A case study demonstration of thermodynamics and thermoeconomics analyses. Fuel 2024, 359, 130430. [Google Scholar] [CrossRef]
- Li, K.; Ding, Y.-Z.; Ai, C.; Sun, H.; Xu, Y.-P.; Nedaei, N. Multi-objective optimization and multi-aspect analysis of an innovative geothermal-based multi-generation energy system for power, cooling, hydrogen, and freshwater production. Energy 2022, 245, 123198. [Google Scholar] [CrossRef]
- Almutairi, K.; Dehshiri, S.S.H.; Mostafaeipour, A.; Issakhov, A.; Techato, K.; Dhanraj, J.A. Performance optimization of a new flash-binary geothermal cycle for power/hydrogen production with zeotropic fluid. J. Therm. Anal. Calorim. 2021, 145, 1633–1650. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, Y.; Li, X.; Zhou, X.; Kilburn, Z.J. Thermodynamic and thermoeconomic analysis and optimization of a renewable-based hybrid system for power, hydrogen, and freshwater production. Energy 2024, 295, 131002. [Google Scholar] [CrossRef]
- Zhang, S.; Jian, W.; Zhou, J.; Li, J.; Yan, G. A new solar, natural gas, and biomass-driven polygeneration cycle to produce electrical power and hydrogen fuel; thermoeconomic and prediction approaches. Fuel 2023, 334, 126825. [Google Scholar] [CrossRef]
- Laleh, S.S.; Gharamaleki, F.P.; Alavi, S.F.; Soltani, S.; Mahmoudi, S.M.S.; Rosen, M.A. A novel sustainable biomass-fueled cogeneration cycle integrated with carbon dioxide capture utilizing LNG regasification and green hydrogen production via PEM electrolysis: Thermodynamic assessment. J. Clean. Prod. 2023, 421, 138529. [Google Scholar] [CrossRef]
- Wang, S.; Lin, H.; Abed, A.M.; Sharma, A.; Fooladi, H. Exergoeconomic assessment of a biomass-based hydrogen, electricity and freshwater production cycle combined with an electrolyzer, steam turbine and a thermal desalination process. Int. J. Hydrogen Energy 2022, 47, 33699–33718. [Google Scholar] [CrossRef]
- Karthikeyan, B.; Kumar, G.P.; Narayanan, R.; Saravanan, R.; Coronas, A. Thermo-economic optimization of hybrid solar-biomass driven organic rankine cycle integrated heat pump and PEM electrolyser for combined power, heating, and green hydrogen applications. Energy 2024, 299, 131436. [Google Scholar] [CrossRef]
- Sharifishourabi, M.; Dincer, I.; Mohany, A. Development of a novel biomass-wind energy system for clean hydrogen production along with other useful products for a residential community. Energy Built Environ. 2025. [Google Scholar] [CrossRef]
- Forootan, M.M.; Ahmadi, A. Machine learning-based optimization and 4E analysis of renewable-based polygeneration system by integration of GT-SRC-ORC-SOFC-PEME-MED-RO using multi-objective grey wolf optimization algorithm and neural networks. Renew. Sustain. Energy Rev. 2024, 200, 114616. [Google Scholar] [CrossRef]
- Bamisile, O.; Huang, Q.; Hu, W.; Dagbasi, M.; Kemena, A.D. Performance analysis of a novel solar PTC integrated system for multi-generation with hydrogen production. Int. J. Hydrogen Energy 2020, 45, 190–206. [Google Scholar] [CrossRef]
- Lykas, P.; Georgousis, N.; Kitsopoulou, A.; Korres, D.N.; Bellos, E.; Tzivanidis, C. A Detailed Parametric Analysis of a Solar-Powered Cogeneration System for Electricity and Hydrogen Production. Appl. Sci. 2022, 13, 433. [Google Scholar] [CrossRef]
- Mansir, I.B. Thermodynamic investigation of novel hybrid plant with hydrogen as a green energy carrier. Int. J. Hydrogen Energy 2024, 51, 1171–1180. [Google Scholar] [CrossRef]
- Colakoglu, M.; Durmayaz, A. Energy, exergy and economic analyses and multiobjective optimization of a novel solar multi-generation system for production of green hydrogen and other utilities. Int. J. Hydrogen Energy 2022, 47, 19446–19462. [Google Scholar] [CrossRef]
- Effatpanah, S.K.; Rahbari, H.R.; Ahmadi, M.H.; Farzaneh, A. Green hydrogen production and utilization in a novel SOFC/GT-based zero-carbon cogeneration system: A thermodynamic evaluation. Renew. Energy 2023, 219, 119493. [Google Scholar] [CrossRef]
- Gargari, S.G.; Rahimi, M.; Ghaebi, H. Thermodynamic analysis of a novel power-hydrogen cogeneration system. Energy Convers. Manag. 2018, 171, 1093–1105. [Google Scholar] [CrossRef]
- Makuku, L. Inventory of geothermal sources in the DRC and their development plan for the electrification of locals areas. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 2nd International Geothermal Conference, Petropavlovsk-Kamchatsky, Russian, 4–7 September 2018; IOP Publishing: Bristol, UK, 2019; Volume 249, p. 012016. [Google Scholar] [CrossRef]
- Mukandala, P.S.; Mahinda, C.K. Geothermal Development in the Democratic Republic of the Congo-a Country Update. In Proceedings of the 8th African Rift Geothermal Conference, Nairobi, Kenya, 2–8 November 2020. [Google Scholar] [CrossRef]
- Mbuto, M.; Albert, Y.-Y.; Albert, K. Etude Differentielle Des Sites Geothermiques De Kankule A Katana Au Sud-Kivu I. Rev. Littérature 2020, 12, 2278–4861. [Google Scholar]
- Mergner, H.; Weimer, T. Performance of ammonia–water based cycles for power generation from low enthalpy heat sources. Energy 2015, 88, 93–100. [Google Scholar] [CrossRef]
- Ayou, D.S.; Coronas, A. New Developments and Progress in Absorption Chillers for Solar Cooling Applications. Appl. Sci. 2020, 10, 4073. [Google Scholar] [CrossRef]
- Hannon, C.L.; Gerstmann, J.; Mansfeld, F.B.; Sun, Z.N. Development of Improved Corrosion Inhibitors for Ammonia–Water Absorption Heat Pumps. In Advanced Energy Systems; American Society of Mechanical Engineers: Orlando, FL, USA, 2000; pp. 35–46. [Google Scholar] [CrossRef]
- Jiang, W.; Li, S.; Yang, L.; Du, K. Experimental investigation on performance of ammonia absorption refrigeration system with TiO2 nanofluid. Int. J. Refrig. 2019, 98, 80–88. [Google Scholar] [CrossRef]
- Yang, J.; Wang, S.; Xu, D.; Guo, Y.; Yang, C.; Li, Y. Effect of ammonium chloride on corrosion behavior of Ni-based alloys and stainless steel in supercritical water gasification process. Int. J. Hydrogen Energy 2017, 42, 19788–19797. [Google Scholar] [CrossRef]
- Chaboki, Y.A.; Khoshgard, A.; Salehi, G.; Fazelpour, F. Thermoeconomic analysis of a new waste heat recovery system for large marine diesel engine and comparison with two other configurations. Energy Sources Part A Recovery Util. Environ. Eff. 2024, 46, 10159–10184. [Google Scholar] [CrossRef]
- Öksel, C.; Koç, A. Modeling of a Combined Kalina and Organic Rankine Cycle System for Waste Heat Recovery from Biogas Engine. Sustainability 2022, 14, 7135. [Google Scholar] [CrossRef]
- Rostamzadeh, H.; Ghaebi, H.; Vosoughi, S.; Jannatkhah, J. Thermodynamic and thermoeconomic analysis and optimization of a novel dual-loop power/refrigeration cycle. Appl. Therm. Eng. 2018, 138, 1–17. [Google Scholar] [CrossRef]
- Bamisile, O.; Huang, Q.; Dagbasi, M.; Adebayo, V.; Okonkwo, E.C.; Ayambire, P.; Al-Ansari, T.; Ratlamwala, T.A.H. Thermo-environ study of a concentrated photovoltaic thermal system integrated with Kalina cycle for multigeneration and hydrogen production. Int. J. Hydrogen Energy 2020, 45, 26716–26732. [Google Scholar] [CrossRef]
- Bahrami, H.-R.; Rosen, M.A. Exergoeconomic evaluation and multi-objective optimization of a novel geothermal-driven zero-emission system for cooling, electricity, and hydrogen production: Capable of working with low-temperature resources. Geotherm. Energy 2024, 12, 12. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C. Energy and exergy analysis of hydrogen production by a proton exchange membrane (PEM) electrolyzer plant. Energy Convers. Manag. 2008, 49, 2748–2756. [Google Scholar] [CrossRef]
- Taheripour, M.; Kahani, M.; Ahmadi, M.H. A hybrid poly-generation system for power and hydrogen production by thermal recovery from waste streams in a steel plant: Techno-economic analysis. Energy Rep. 2024, 11, 2921–2934. [Google Scholar] [CrossRef]
- Nami, H.; Akrami, E.; Ranjbar, F. Hydrogen production using the waste heat of Benchmark pressurized Molten carbonate fuel cell system via combination of organic Rankine cycle and proton exchange membrane (PEM) electrolysis. Appl. Therm. Eng. 2017, 114, 631–638. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Dehghani, M.J. Enhancing energo-exergo-economic performance of Kalina cycle for low- to high-grade waste heat recovery: Design and optimization through deep learning methods. Appl. Therm. Eng. 2021, 195, 117221. [Google Scholar] [CrossRef]
- Sadiki, A.; Ries, F. Entropy Generation Analysis in Turbulent Reacting Flows and Near Wall: A Review. Entropy 2022, 24, 1099. [Google Scholar] [CrossRef]
- Shankar, R.; Rivera, W. Investigation of new cooling cogeneration cycle using NH3H2O mixture. Int. J. Refrig. 2020, 114, 88–97. [Google Scholar] [CrossRef]
- Srinivas, T.; Ganesh, N.S.; Shankar, R. Flexible Kalina Cycle Systems; Apple Academic Press: Palm Bay, FL, USA, 2019. [Google Scholar] [CrossRef]
- Mosaffa, A.H.; Mokarram, N.H.; Farshi, L.G. Thermoeconomic analysis of a new combination of ammonia/water power generation cycle with GT-MHR cycle and LNG cryogenic exergy. Appl. Therm. Eng. 2017, 124, 1343–1353. [Google Scholar] [CrossRef]
- Alelyani, S.M.; Fette, N.W.; Stechel, E.B.; Doron, P.; Phelan, P.E. Techno-economic analysis of combined ammonia–water absorption refrigeration and desalination. Energy Convers. Manag. 2017, 143, 493–504. [Google Scholar] [CrossRef]
- Dehghani, M.J.; Yoo, C.K. Modeling and extensive analysis of the energy and economics of cooling, heat, and power trigeneration (CCHP) from textile wastewater for industrial low-grade heat recovery. Energy Convers. Manag. 2020, 205, 112451. [Google Scholar] [CrossRef]
- Köse, Ö.; Koç, Y.; Yağlı, H. Energy, exergy, economy and environmental (4E) analysis and optimization of single, dual and triple configurations of the power systems: Rankine Cycle/Kalina Cycle, driven by a gas turbine. Energy Convers. Manag. 2021, 227, 113604. [Google Scholar] [CrossRef]
- Cao, Y.; Haghghi, M.A.; Shamsaiee, M.; Athari, H.; Ghaemi, M.; Rosen, M.A. Evaluation and optimization of a novel geothermal-driven hydrogen production system using an electrolyser fed by a two-stage organic Rankine cycle with different working fluids. J. Energy Storage 2020, 32, 101766. [Google Scholar] [CrossRef]
- Emadi, M.A.; Mahmoudimehr, J. Modeling and thermo-economic optimization of a new multi-generation system with geothermal heat source and LNG heat sink. Energy Convers. Manag. 2019, 189, 153–166. [Google Scholar] [CrossRef]
- AShirazi; Taylor, R.A.; Morrison, G.L.; White, S.D. A comprehensive, multi-objective optimization of solar-powered absorption chiller systems for air-conditioning applications. Energy Convers. Manag. 2017, 132, 281–306. [Google Scholar] [CrossRef]
- Ghaebi, H.; Parikhani, T.; Rostamzadeh, H.; Farhang, B. Thermodynamic and thermoeconomic analysis and optimization of a novel combined cooling and power (CCP) cycle by integrating of ejector refrigeration and Kalina cycles. Energy 2017, 139, 262–276. [Google Scholar] [CrossRef]
- Sharifi, S.; Heravi, F.N.; Shirmohammadi, R.; Ghasempour, R.; Petrakopoulou, F.; Romeo, L.M. Comprehensive thermodynamic and operational optimization of a solar-assisted LiBr/water absorption refrigeration system. Energy Rep. 2020, 6, 2309–2323. [Google Scholar] [CrossRef]
- Ghaebi, H.; Parikhani, T.; Rostamzadeh, H.; Farhang, B. Proposal and assessment of a novel geothermal combined cooling and power cycle based on Kalina and ejector refrigeration cycles. Appl. Therm. Eng. 2018, 130, 767–781. [Google Scholar] [CrossRef]
- Gogoi, T.K.; Hazarika, P. Comparative assessment of four novel solar based triple effect absorption refrigeration systems integrated with organic Rankine and Kalina cycles. Energy Convers. Manag. 2020, 226, 113561. [Google Scholar] [CrossRef]
- Ghaebi, H.; Namin, A.S.; Rostamzadeh, H. Exergoeconomic optimization of a novel cascade Kalina/Kalina cycle using geothermal heat source and LNG cold energy recovery. J. Clean. Prod. 2018, 189, 279–296. [Google Scholar] [CrossRef]
- Ghaebi, H.; Farhang, B.; Parikhani, T.; Rostamzadeh, H. Energy, exergy and exergoeconomic analysis of a cogeneration system for power and hydrogen production purpose based on TRR method and using low grade geothermal source. Geothermics 2018, 71, 132–145. [Google Scholar] [CrossRef]
- Akrami, E.; Chitsaz, A.; Ghamari, P.; Mahmoudi, S.M.S. Energy and exergy evaluation of a tri-generation system driven by the geothermal energy. J. Mech. Sci. Technol. 2017, 31, 401–408. [Google Scholar] [CrossRef]
- Soleymani, E.; Gargari, S.G.; Ghaebi, H. Thermodynamic and thermoeconomic analysis of a novel power and hydrogen cogeneration cycle based on solid SOFC. Renew. Energy 2021, 177, 495–518. [Google Scholar] [CrossRef]
- Kasuyoka, K. Techno-Economic Analysis of Geothermal Hydrogen Power Generation for Load Management in Kenya. 2023. Available online: https://hdl.handle.net/10371/196544 (accessed on 5 July 2025).
- Hamlehdar, M.; Beardsmore, G.; Narsilio, G.A. Hydrogen production from low-temperature geothermal energy—A review of opportunities, challenges, and mitigating solutions. Int. J. Hydrogen Energy 2024, 77, 742–768. [Google Scholar] [CrossRef]
| Reference | Sites | Temperatures [°C] | Depth [m] |
|---|---|---|---|
| Kankule [38] | Kankule 1 | 90–203 | 1019.21–3514.15 |
| Upemba-Moero-Tanganyika [37] | Tanganyika | 40–50 | |
| Upemba | 70–100 | ||
| Kivu-Edouard [37] | Kivu-Edouard | 20–100 | |
| Rwenzori [37] | Soixante sites | 20–100 | |
| Virunga [37] | Mayi-ya-Moto | 96 | |
| Kahuzi Biega Ruzizi [37] | Nyangezi | 40 | |
| Uvira | 44 |
| Working Fluids | Molar Mass [kg/kmol] | [°C] | [Bar] | ODP | GWP [100/yr] | ASHRAE * |
|---|---|---|---|---|---|---|
| R236fa | 152.04 | 124.85 | 32 | 0 | 6300 | - |
| MD2M | 310.7 | 326.3 | 11.44 | 0 | 1 | A1 |
| ISOBUTANE | 58.13 | 134.66 | 36.29 | 0 | 20 | A3 |
| R152a | 66.05 | 113.30 | 45.2 | 0 | 12.4 | A2 |
| ISOBUTENE | 56.13 | 144.7 | 40 | - | 3 | - |
| Parameters | Value | Unit |
|---|---|---|
| Reference temperature, T0 | 25 | °C |
| Reference pressure, P0 | 101.3 | kPa |
| Geothermal inlet temperature, T_source | 140 | °C |
| Geothermal water mass flow rate, m_geo | 100 | kg/s |
| Terminal temperature difference, TTD | 10 | °C |
| Basic ammonia mass fraction, Xbasic | 65 | % |
| Regenerators effectiveness 1 and 2, εReg | 95 | % |
| High pressure, P_high | 2500 | kPa |
| Turbines isentropic efficiency, ηTur | 87 | % |
| Pumps isentropic efficiency, ηPump | 75 | % |
| Temperature of condenser 1 | 30 | °C |
| Exchanger, Hex | 80 | % |
| Basic mixture mass flow rate, m_basic | 5 | kg/s |
| Anode activation energy, Eacta | 76 | (kJ/kg) |
| Cathode activation energy, Eactc | 18 | (kJ/kg) |
| Anode pre-exponential factor, Jre,a | 1.7 × 105 | (A/m2) |
| Cathode pre-exponential factor, Jref,c | 4.6 × 103 | (A/m2) |
| Faraday constant, F | 96,486 | (C/mol) |
| Components | First Low Equations | Second Low Equations |
|---|---|---|
| Vapor generator, KC | ||
| Vapor generator, ORC | ||
| Separator | ||
| Turbine, ORC | ||
| Turbine, KC | ||
| Pump 1 | ||
| Pump 2 | ||
| Regenerator | ||
| Regenerator 2 | ||
| Valve 1 | ||
| Mixer 1 | ||
| Condenser 1 | ||
| Condenser 2 | ||
| HEX |
| Components | Purchasing Cost | CEPCI |
|---|---|---|
| Turbine | ||
| Pump | ||
| CI2000, CI2012 and CI2024 are equal to 394.1, 584.6, and 795.4, respectively [53,58] | ||
| Parameters | Values |
|---|---|
| Individuals number in the population | 32 |
| Number of generations | 64 |
| Maximum mutation rate | 0.25 |
| Minimum mutation rate | 0.0005 |
| Initial mutation rate | 0.25 |
| Crossover probability | 0.85 |
| Decision Variable | Range |
|---|---|
| TTD (°C) | 8–15 |
| 0.50–0.90 | |
| (kPa) | 1500–3000 |
| (°C) | 120–180 |
| State | Temperature [°C] | Pressure [kPa] | Enthalpy [kJ/kg] | Entropy [kJ/kgK] | ||||
|---|---|---|---|---|---|---|---|---|
| Reference | Study | Reference | Study | Reference | Study | Reference | Study | |
| 1 | 145 | 145 | 1129.81 | 1130 | 531.84 | 531.8 | 1.943 | 1.943 |
| 2 | 98.9 | 98.71 | 177.79 | 177.2 | 494.03 | 494 | 1.954 | 1.954 |
| 3 | 47.50 | 47.48 | 177.79 | 177.3 | 443.38 | 443.4 | 1.808 | 1.808 |
| 4 | 30 | 30 | 177.79 | 177.4 | 239.10 | 239.1 | 1.135 | 1.135 |
| 5 | 30.40 | 30.4 | 1129.81 | 1130 | 239.90 | 239.9 | 1.136 | 1.136 |
| 6 | 69.54 | 67.13 | 1129.81 | 1130 | 290.94 | 290.5 | 1.303 | 1.293 |
| Wnet [kW] | 3810 | 3947 | ||||||
| Thermal efficiency | 0.1508 | 0.1536 | ||||||
| Pressure [kPa] | Temperature [K] | Ammonia Concentration | |||||||
|---|---|---|---|---|---|---|---|---|---|
| N° | Present Work | Reference | Relative Error [%] | Present Work | Reference | Relative Error [%] | Present Work | Reference | Relative Error [%] |
| 1 | 4919 | 4919 | 0 | 433.2 | 433.15 | 0.012 | 0.6299 | 0.6299 | 0 |
| 2 | 4919 | 4919 | 0 | 433.2 | 433.15 | 0.012 | 0.9094 | 0.9094 | 0 |
| 3 | 4919 | 4919 | 0 | 433.2 | 433.15 | 0.012 | 0.4269 | 0.4269 | 0 |
| 4 | 4919 | 4919 | 0 | 319 | 319.07 | −0.002 | 0.4269 | 0.4269 | 0 |
| 5 | 823.2 | 823 | 0.024 | 319.8 | 319.81 | −0.003 | 0.4269 | 0.4269 | 0 |
| 6 | 823.2 | 823 | 0.024 | 352.3 | 356.54 | −1.189 | 0.9094 | 0.9094 | 0 |
| 7 | 823.2 | 823 | 0.024 | 342.2 | 342.16 | 0.012 | 0.6299 | 0.6299 | 0 |
| 8 | 823.2 | 823 | 0.024 | 312.1 | 312.1 | 0 | 0.6299 | 0.6299 | 0 |
| 9 | 4919 | 4919 | 0 | 313 | 313.06 | −0.019 | 0.6299 | 0.6299 | 0 |
| 10 | 4919 | 4919 | 0 | 378.7 | 378.69 | 0.003 | 0.6299 | 0.6299 | 0 |
| Present work | Reference | Relative error [%] | |||||||
| Thermal efficiency | 0.1353 | 0.1352 | 0.07396 | ||||||
| Parameters | Present Work | Reference |
|---|---|---|
| Current density [A/m2] | 5000 | 5000 |
| Water primary temperature [°C] | 25 | 25 |
| Electrolyzer temperature [°C] | 80 | 80 |
| Net power [kW] | 29,421 | 29,421 |
| Hydrogen production [kg/s] | 0.0940 | 0.0940 |
| Working Fluids | Wnet [kW] | [kg/s] | ||
|---|---|---|---|---|
| NH3H2O–MD2M | 1470 | 0.007178 | 0.1184 | 0.1258 |
| NH3H2O–R236fa | 1469 | 0.007176 | 0.1332 | 0.1269 |
| NH3H2O–R152a | 1467 | 0.007162 | 0.1186 | 0.1261 |
| NH3H2O–ISOBUTANE | 1465 | 0.007155 | 0.1371 | 0.1258 |
| NH3H2O–ISOBUTENE | 1465 | 0.007153 | 0.1434 | 0.1253 |
| Outputs | Values |
|---|---|
| Net power, Wnet | 1470 [kW] |
| Hydrogen production, | 0.007178 [kg/s] |
| Energy efficiency, | 0.1184 |
| Exergy efficiency, | 0.1258 |
| PEME efficiency, | 0.5831 |
| System efficiency, | 0.1875 |
| TIC | ($) 3,342,000 |
| DPT | 5.37 (yr) |
| LCOH | 3.007 $/kg H2 |
| (a) | ||||
|---|---|---|---|---|
| Working Fluids | Wnet [kW] | [kg/s] | ||
| NH3H2O–MD2M | 1774 | 0.008639 | 0.166 | 0.2438 |
| NH3H2O–R236fa | 1744 | 0.008498 | 0.1555 | 0.248 |
| NH3H2O–R152a | 2004 | 0.009742 | 0.1491 | 0.252 |
| NH3H2O–ISOBUTANE | 1754 | 0.008543 | 0.1625 | 0.2468 |
| NH3H2O–ISOBUTENE | 1729 | 0.008425 | 0.1714 | 0.2537 |
| (b) | ||||
| Terms | Pre-Optimization | Post-Optimization | ||
| Temperature source [°C] | 180 | 180 | ||
| Terminal temperature difference [°C] | 10 | 8.968 | ||
| High pression [kPa] | 2500 | 3000 | ||
| Ammonia concentration (X_basic) | 0.65 | 0.8966 | ||
| Net power, Wnet [kW] | 1870 | 2004 | ||
| Hydrogen production, [kg/s] | 0.009098 | 0.009742 | ||
| Energy efficiency, | 0.1232 | 0.1491 | ||
| Exergy efficiency, | 0.2007 | 0.252 | ||
| System efficiency, | 0.1954 | 0.2358 | ||
| TIC [$] | 3,994,000 | 4,120,000 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muya, G.T.; Fellah, A.; Yaquan, S.; Boukhchana, Y.; Molima, S.; Kanyama, M.; Sadiki, A. A Geothermal-Driven Zero-Emission Poly-Generation Energy System for Power and Green Hydrogen Production: Exergetic Analysis, Impact of Operating Conditions, and Optimization. Fuels 2025, 6, 65. https://doi.org/10.3390/fuels6030065
Muya GT, Fellah A, Yaquan S, Boukhchana Y, Molima S, Kanyama M, Sadiki A. A Geothermal-Driven Zero-Emission Poly-Generation Energy System for Power and Green Hydrogen Production: Exergetic Analysis, Impact of Operating Conditions, and Optimization. Fuels. 2025; 6(3):65. https://doi.org/10.3390/fuels6030065
Chicago/Turabian StyleMuya, Guy Trudon, Ali Fellah, Sun Yaquan, Yasmina Boukhchana, Samuel Molima, Matthieu Kanyama, and Amsini Sadiki. 2025. "A Geothermal-Driven Zero-Emission Poly-Generation Energy System for Power and Green Hydrogen Production: Exergetic Analysis, Impact of Operating Conditions, and Optimization" Fuels 6, no. 3: 65. https://doi.org/10.3390/fuels6030065
APA StyleMuya, G. T., Fellah, A., Yaquan, S., Boukhchana, Y., Molima, S., Kanyama, M., & Sadiki, A. (2025). A Geothermal-Driven Zero-Emission Poly-Generation Energy System for Power and Green Hydrogen Production: Exergetic Analysis, Impact of Operating Conditions, and Optimization. Fuels, 6(3), 65. https://doi.org/10.3390/fuels6030065







