Comparison of the Methods for Predicting the Critical Temperature and Critical Pressure of Petroleum Fractions and Individual Hydrocarbons
Abstract
:1. Introduction
2. Materials and Methods
- 24 n-alkanes;
- 24 alkenes;
- 41 iso-alkanes;
- 16 iso-alkenes;
- 17 cyclo-alkanes;
- 5 cyclo-alkenes;
- 32 mono-aromatic compounds;
- 6 bicyclic hydrocarbons;
- 7 di-aromatic compounds;
- 3 tri-aromatic compounds;
- 1 tricyclic compound.
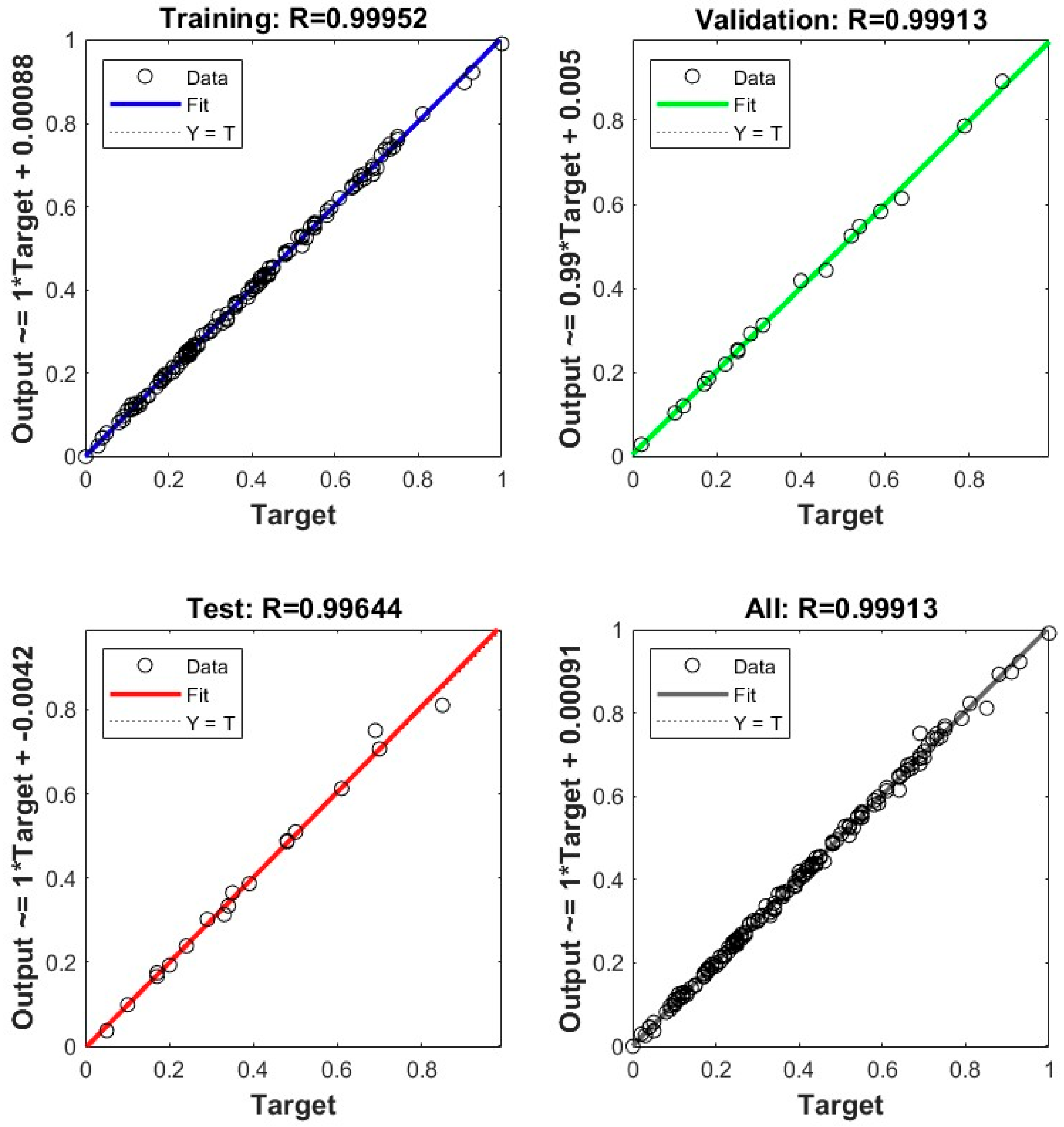
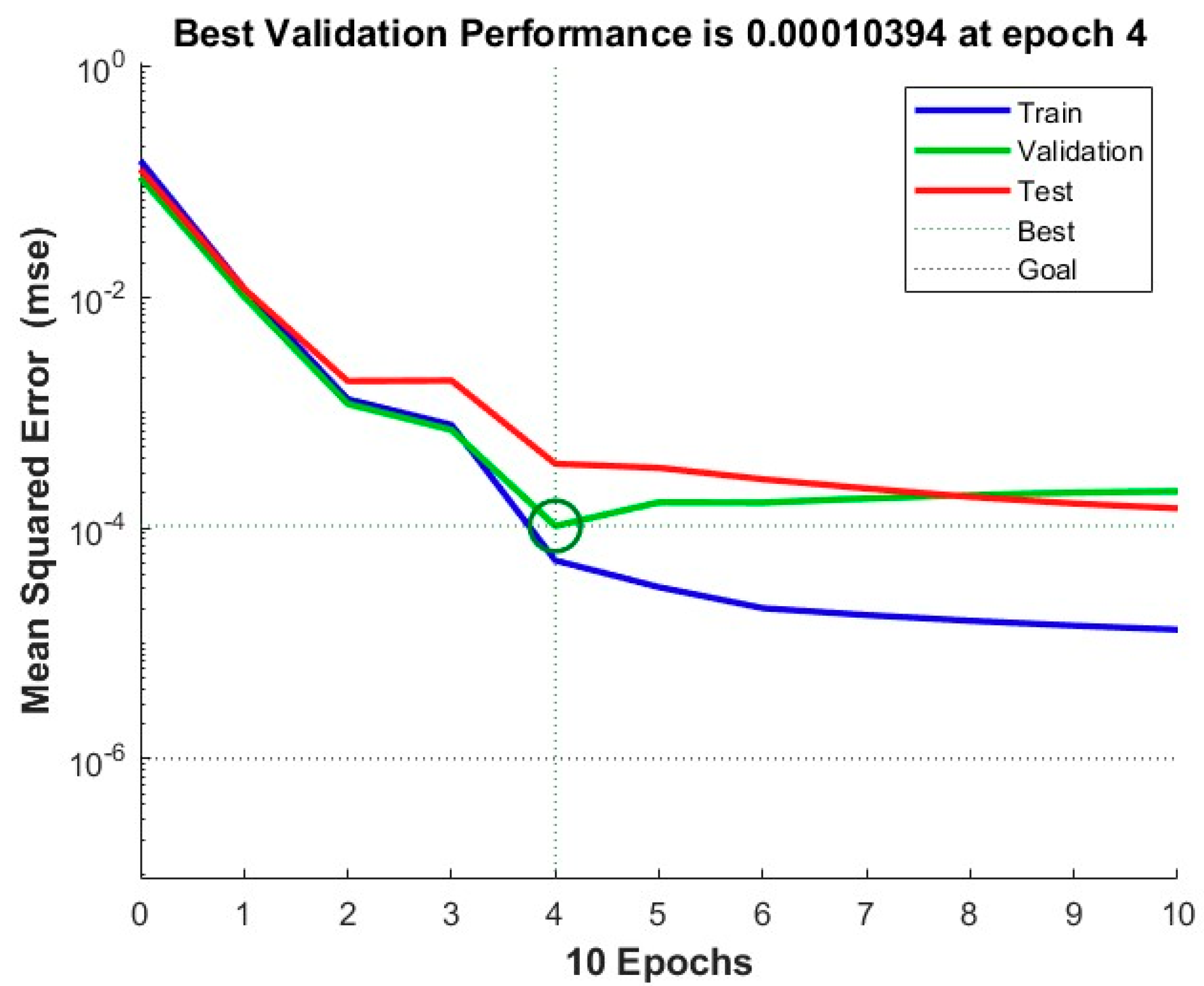
3. Results
- Critical Temperature Correlation (17): R2 = 0.9955.
- Critical Pressure Correlation (18): R2 = 0.9832.
4. Discussion
- Straight-run naphtha predominantly consists of n-alkanes and iso-alkanes, with up to 10% aromatic compounds.
- Isomerate and alkylate are mostly iso-alkanes with small amounts of n-alkanes.
- FCC-Gasoline contains 20–40% olefins and 20–35% aromatics, with the rest being n-alkanes and iso-alkanes.
- Reformate comprises 60–70% aromatics and 0–2% olefins, with the remainder as normal alkanes, iso-alkanes, and cyclo-alkanes.
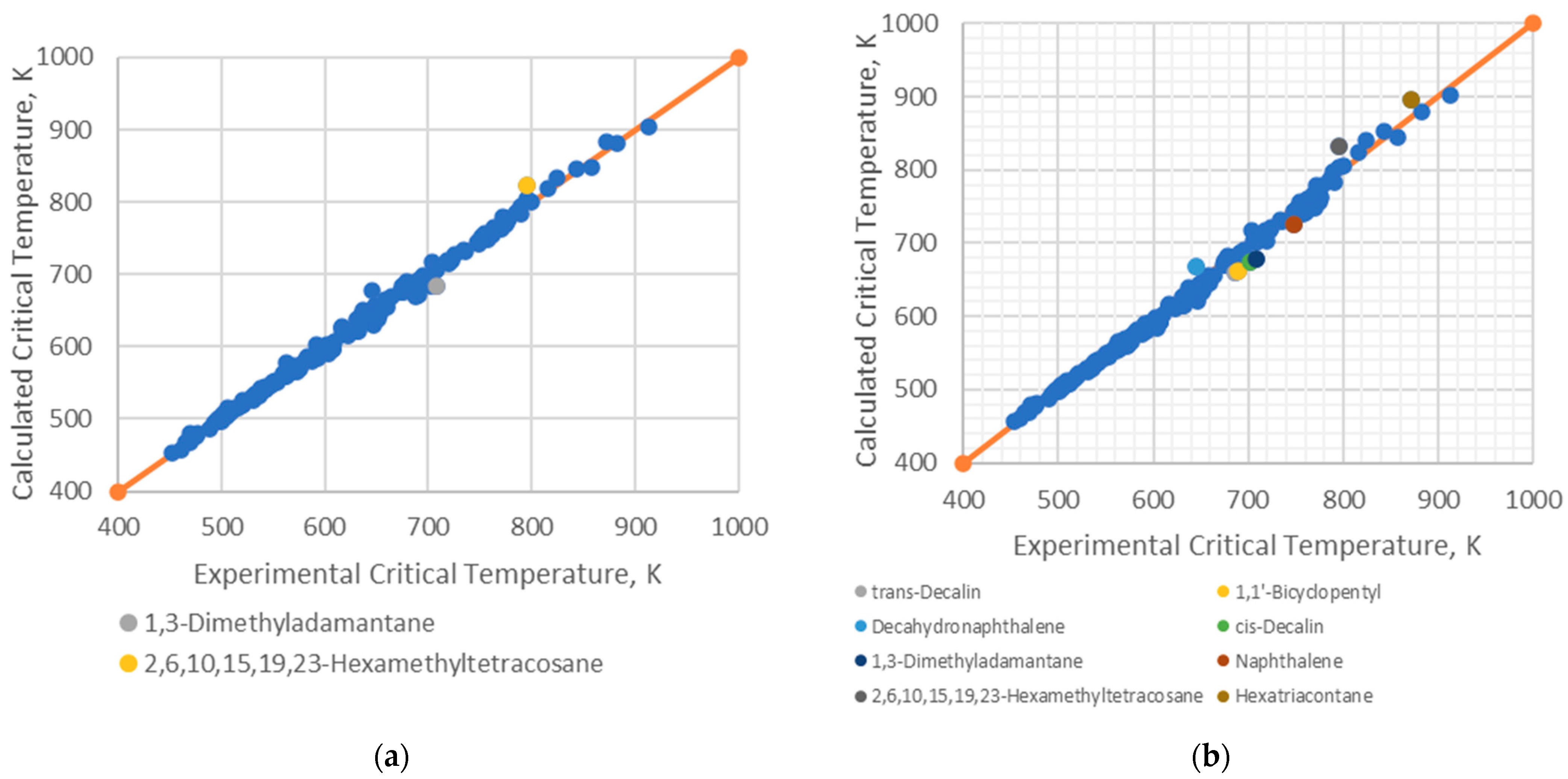
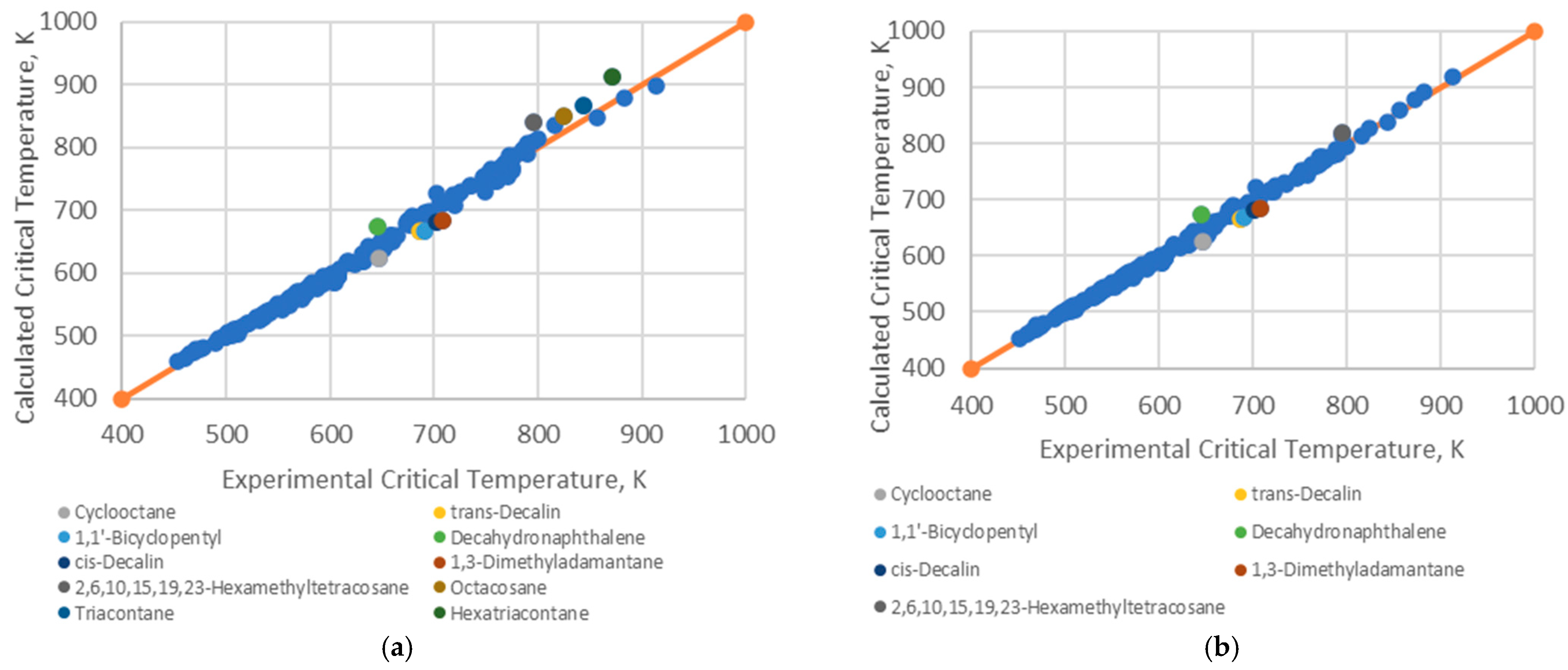
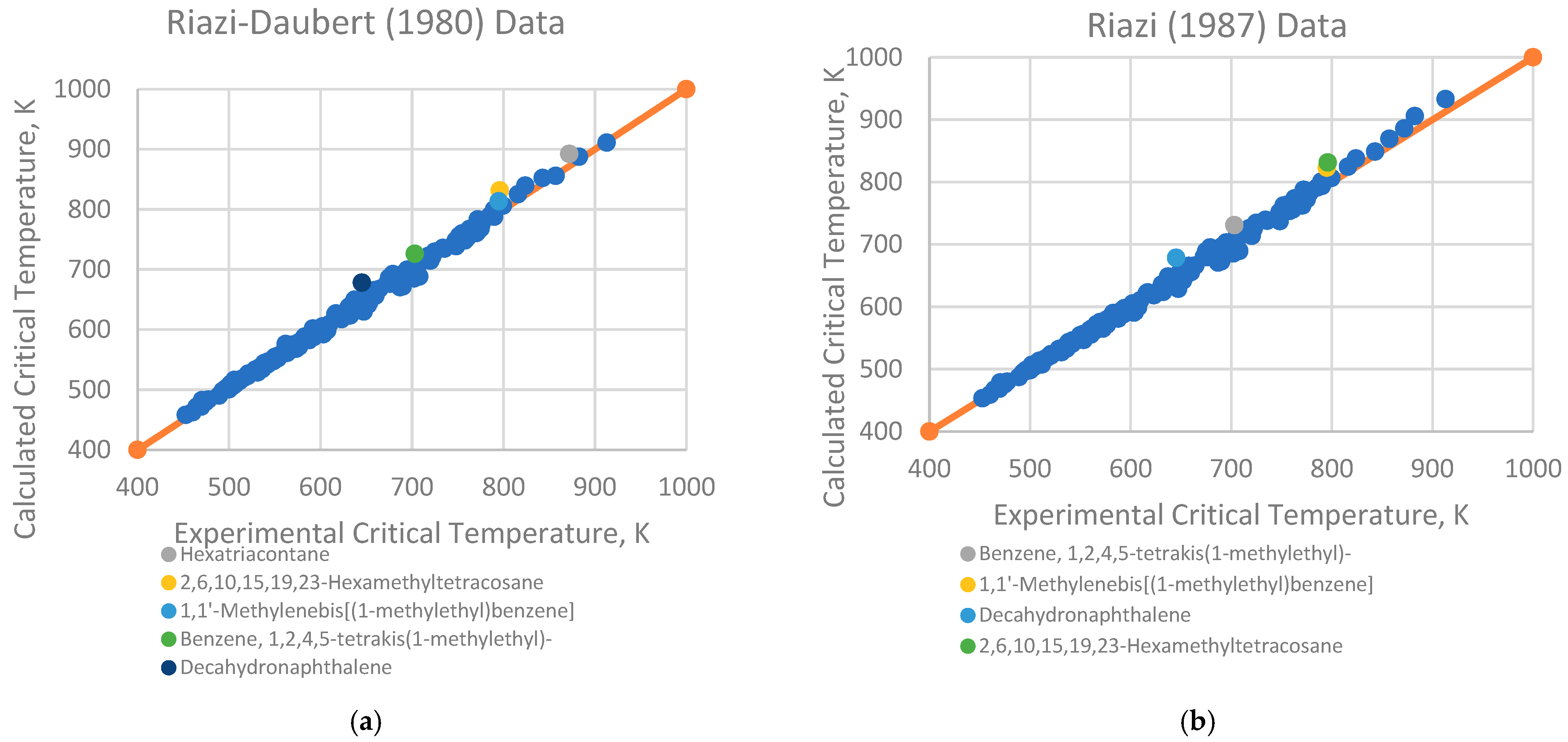
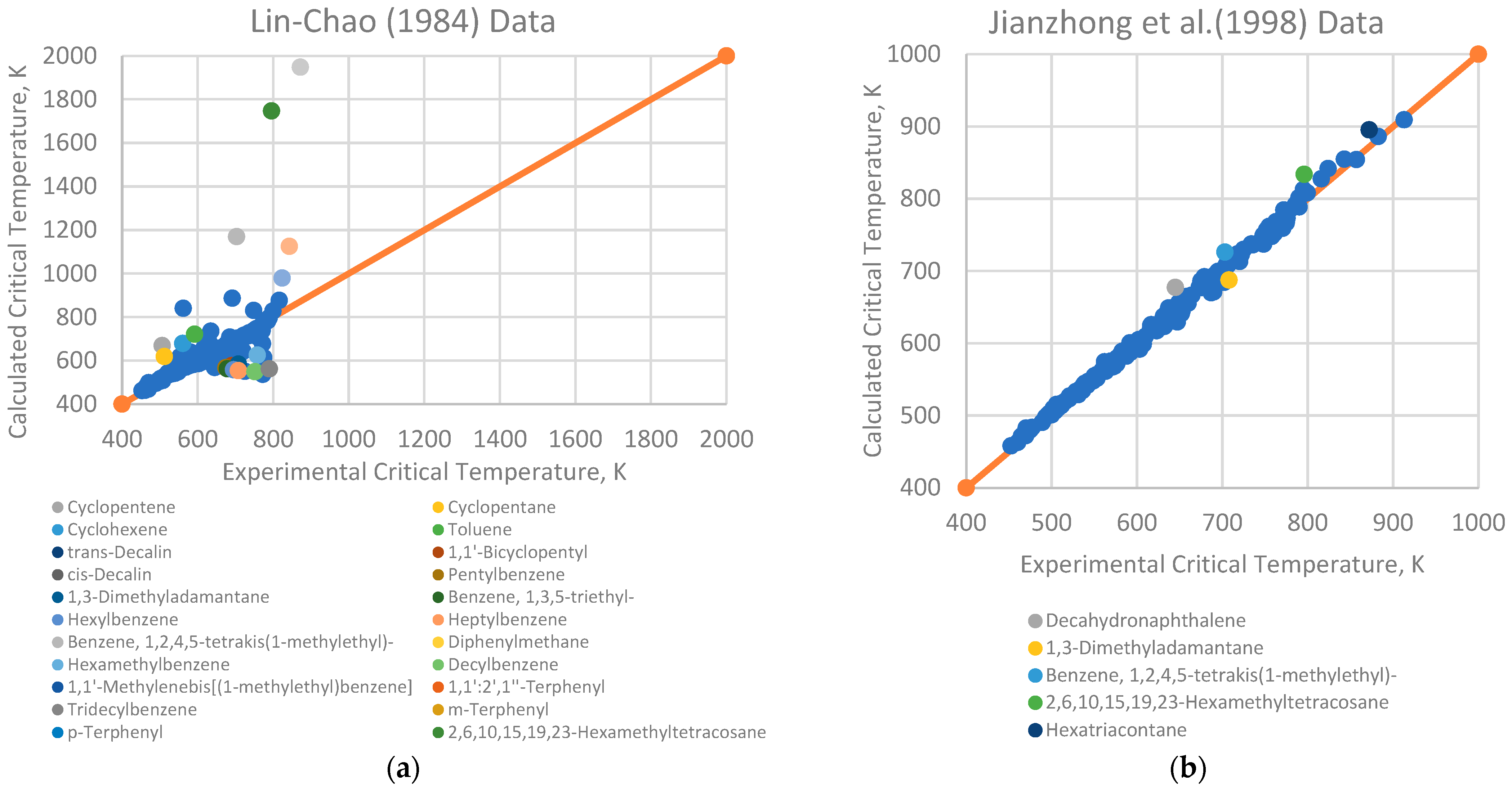
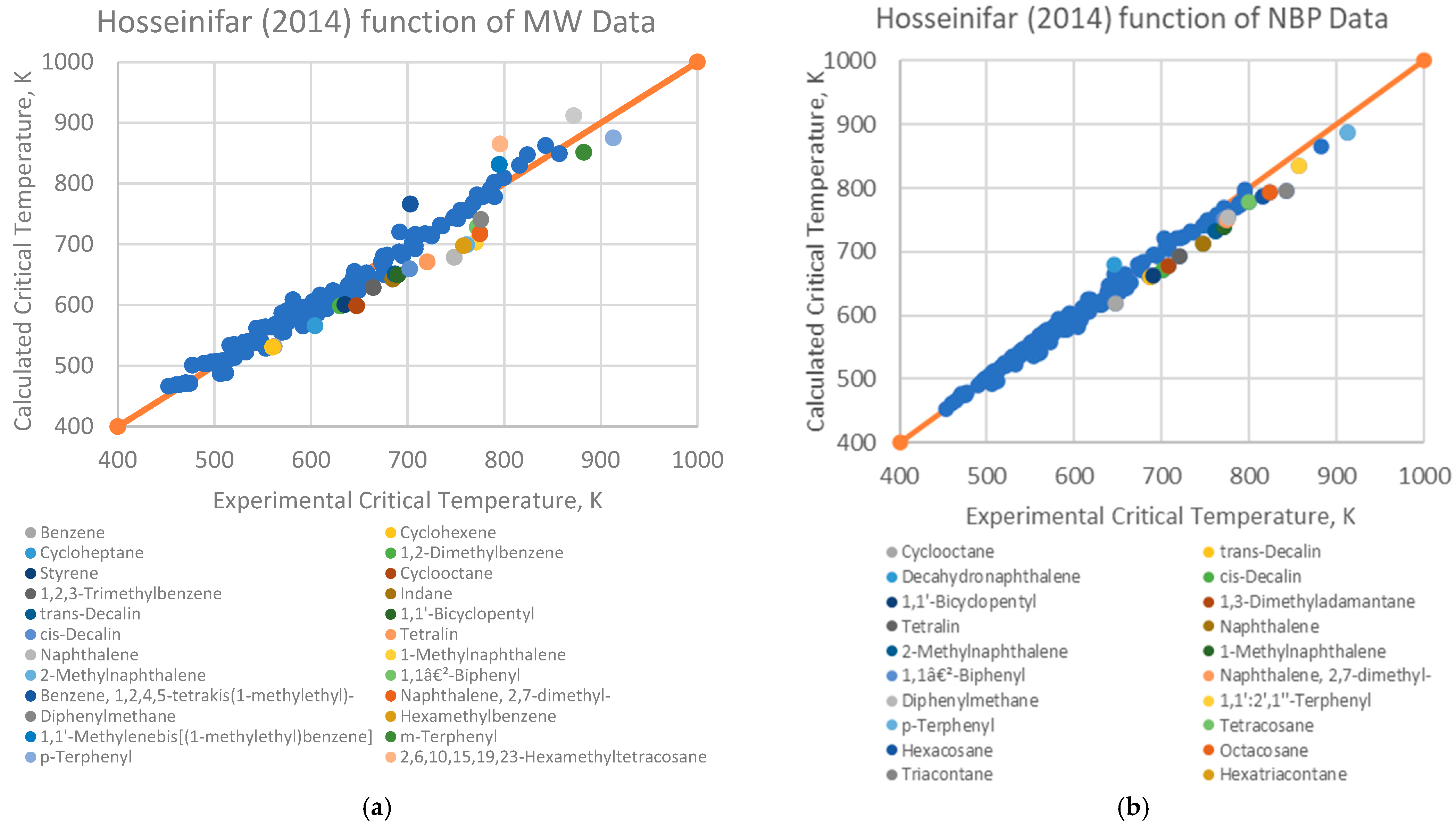
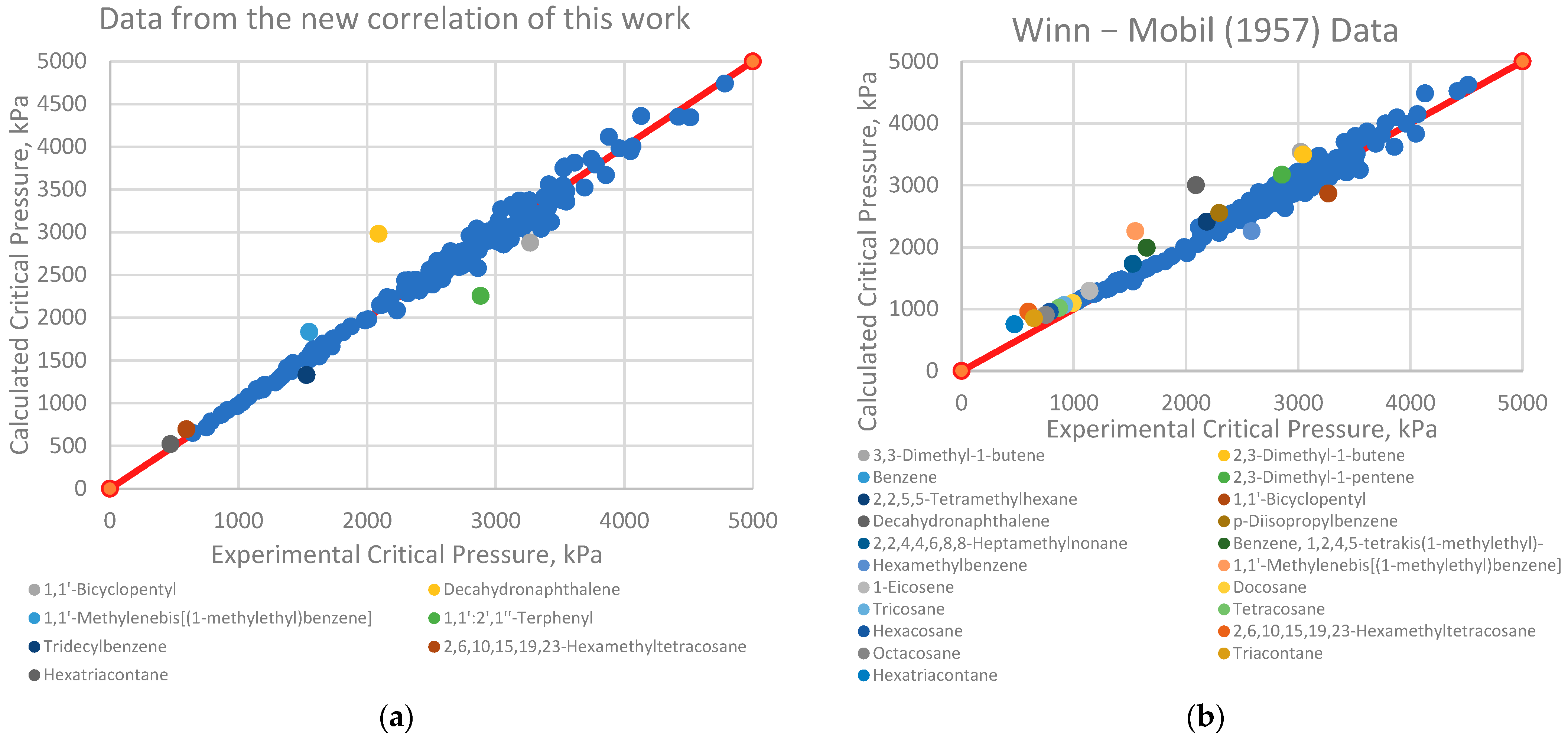
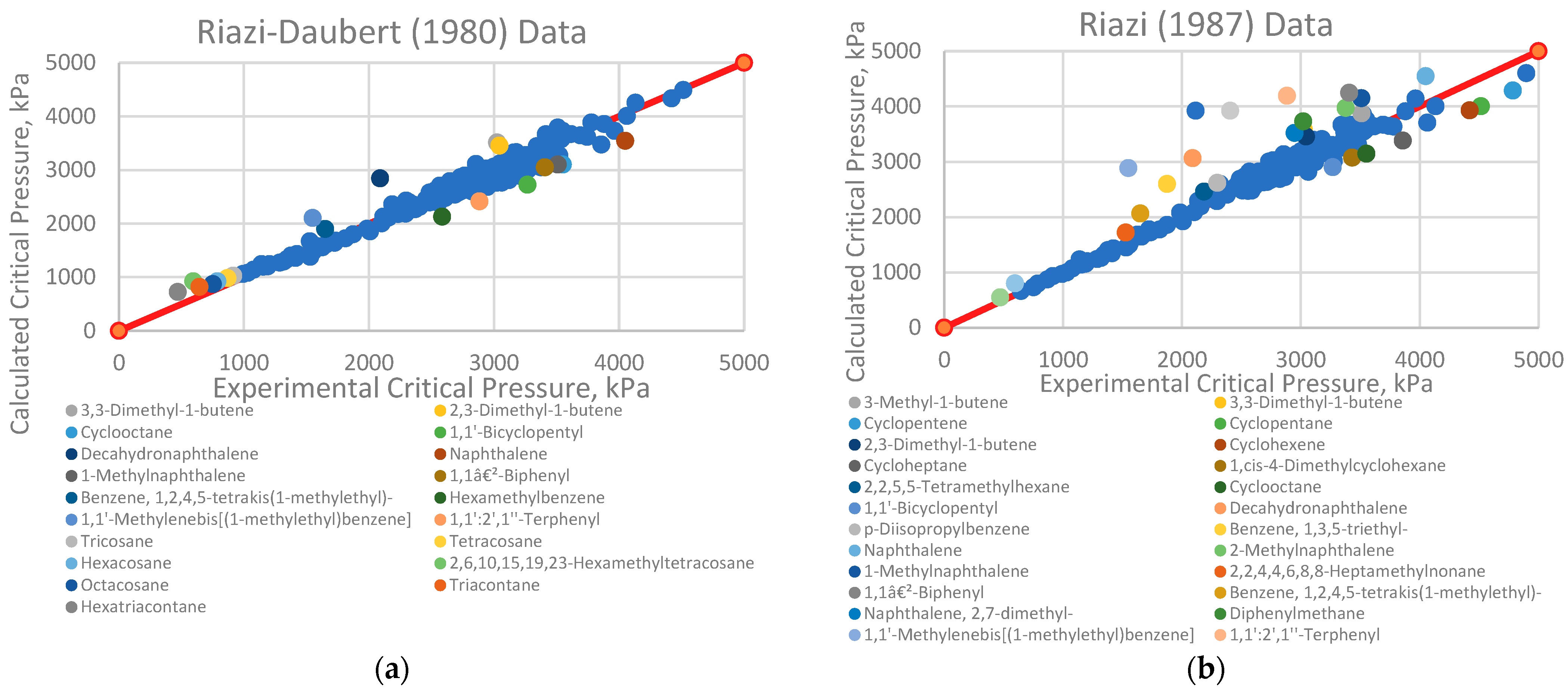
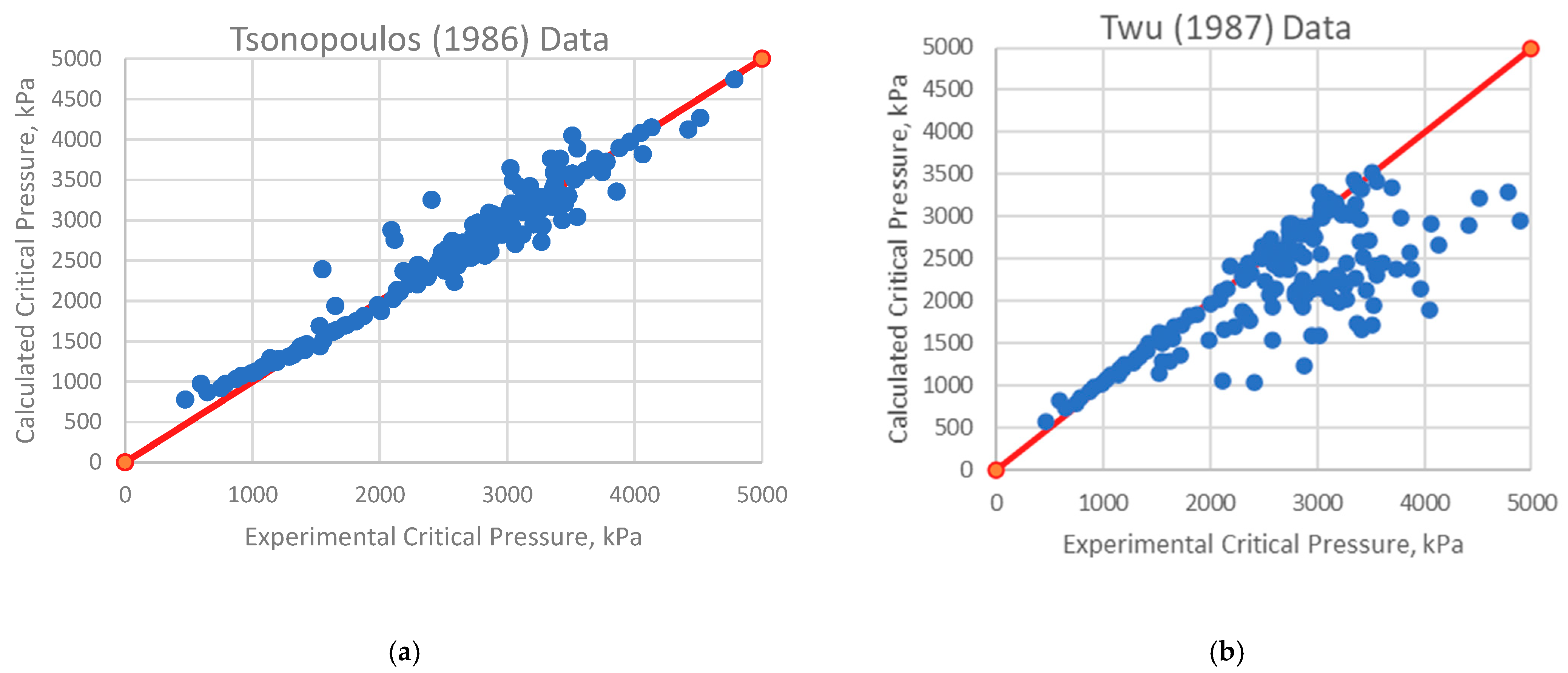
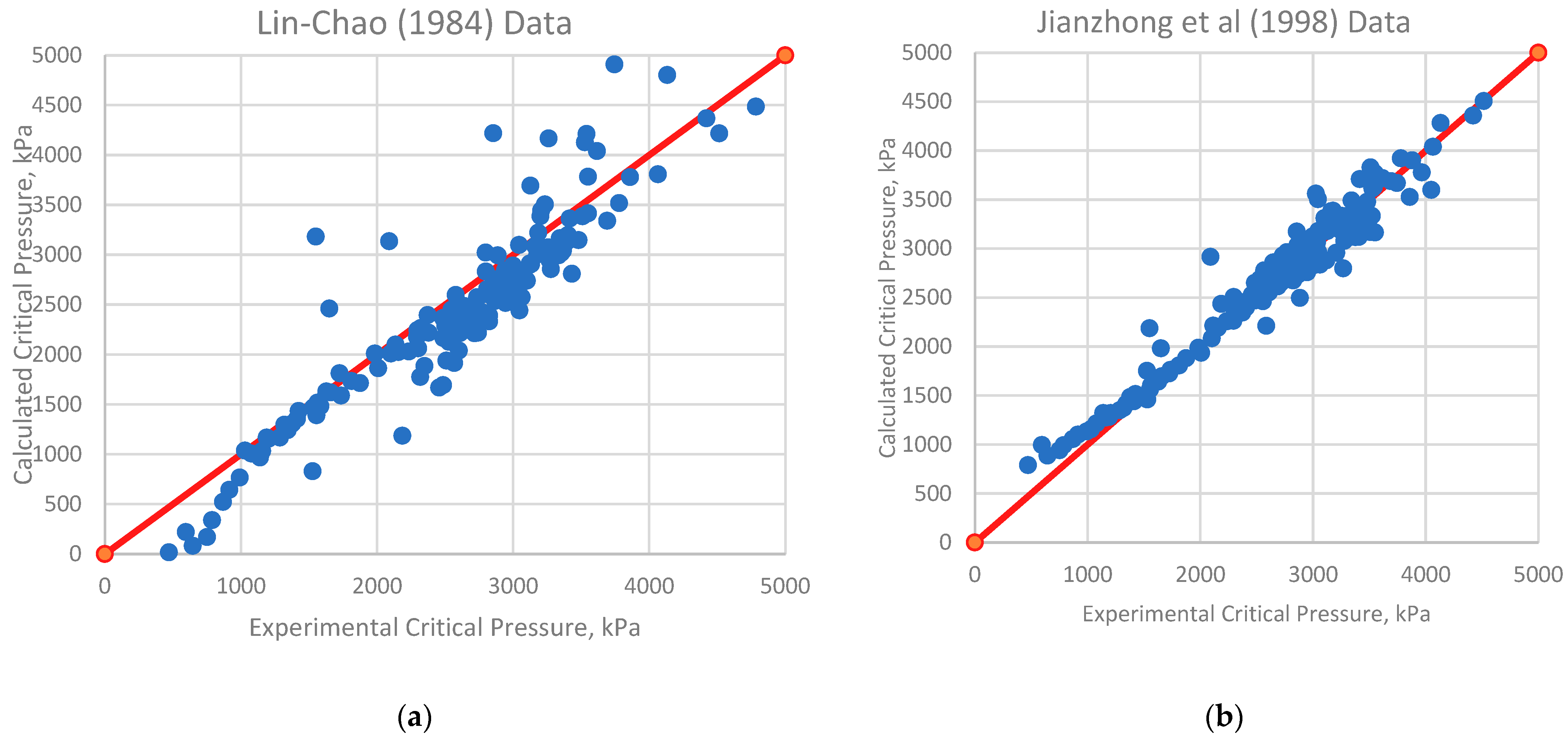
4.1. Analysis of Deviations
- Branched alkenes, such as 3,3-dimethyl-1-butene and 2,3-dimethyl-1-butene.
- Cyclo-alkanes/alkenes, including cyclohexene, cycloheptane, and cyclooctane.
- Poly-substituted benzene derivatives, for example, indane, p-diisopropylbenzene, and 1,3,5-triethylbenzene.
- Poly-aromatics, such as naphthalene and 1-methylnaphthalene.
- Polycyclic compounds, including 1,1’-bicyclopentyl, decahydronaphthalene, tetralin, and triacontane.
- Heavy alkanes, like tricosane, tetracosane, hexacosane, and hexatriacontane.
4.2. Implications for Correlation Performance
4.3. Future Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| %AAD | average absolute relative deviation: % |
| ANN | artificial neural network |
| API | API gravity, °API |
| API-TDB | American Petroleum Institute—Technical Data Book |
| E | error |
| function of the normal boiling point and specific gravity used in the calculation of critical pressure | |
| function of the normal boiling point and specific gravity used in the calculation of critical temperature | |
| function of the normal boiling point and specific gravity used in the calculation of critical volume | |
| FCC | fluid catalytic cracking |
| MABP | mean average boiling point |
| MW | molecular weight |
| N | number of experimental points |
| NBP | normal boiling point of a hydrocarbon, K |
| Pc | critical pressure |
| RSE | relative standard error |
| SG | specific gravity |
| SEi | standard error |
| SRE | sum of relative errors |
| SRK | Soave–Redlich–Kwong |
| SSE | sum of square errors |
| Tc | critical temperature |
| Tb | normal boiling point |
| Vc | critical volume |
| Greek letters | |
| reduced normal boiling point; | |
| ξexp | experimental value of the critical temperature or critical pressure |
| ξcalc | calculated value of the critical temperature or critical pressure |
References
- Ambrose, D. Correlation and Estimation of Vapour-Liquid Critical Properties. I. Critical Temperatures of Organic Compounds; NPL Rep. Chem. 92; National Physical Laboratory: Teddington, UK, 1978. [Google Scholar]
- Lydersen, A.L. Estimation of Critical Properties of Organic Compounds; Eng Exp Sta Report 3; University of Wisconsin: Madison, WI, USA, 1955. [Google Scholar]
- Nannoolal, Y.; Rarey, J.; Ramjugernath, D. Estimation of Pure Component Properties. Part 2. Estimation of Critical Property Data by Group Contribution. Fluid Phase Equilibria 2007, 252, 1–27. [Google Scholar] [CrossRef]
- Korsten, H. Critical Properties of Hydrocarbon Systems. Chem. Eng. Technol. 1998, 21, 229–244. [Google Scholar] [CrossRef]
- Hajipour, S.; Satyro, M.A. Uncertainty Analysis Applied to Thermodynamic Models and Process Design—1. Pure Components. Fluid Phase Equilibria 2011, 307, 78–94. [Google Scholar] [CrossRef]
- Kumar, A.; Okuno, R. Critical Parameters Optimized for Accurate Phase Behavior Modeling for Heavy N-Alkanes up to C100 Using the Peng–Robinson Equation of State. Fluid Phase Equilibria 2012, 335, 46–59. [Google Scholar] [CrossRef]
- Riazi, M.R. Characterization and Properties of Petroleum Fractions, 1st ed.; ASTM International: West Conshohocken, PA, USA, 2005; pp. 60–66. [Google Scholar]
- Riazi, M.R.; Daubert, T.E. Simplify Property Predictions. Hydrocarb. Process. 1980, 59, 115–116. [Google Scholar]
- The American Petroleum Institute and EPCON International. API Technical Data Book, 10th ed.; EPCON International™: Houston, TX, USA, 2016. [Google Scholar]
- Kesler, M.G.; Lee, B.I. Improve Prediction of Enthalpy of Fractions. Hydrocarb. Process. 1976, 55, 153–158. [Google Scholar]
- Cavett, R.H. Physical Data for Distillation Calculations, Vapor-Liquid Equilibria. In Proceedings of the 27th Midyear Meeting, API Division of Refining, San Francisco, CA, USA, 15 May 1962. [Google Scholar]
- Twu, C.H. An Internally Consistent Correlation for Predicting the Critical Properties and Molecular Weights of Petroleum and Coal-Tar Liquids. Fluid Phase Equilibria 1984, 16, 137–150. [Google Scholar] [CrossRef]
- Winn, F.W. Physical Properties by Nomogram. Petroleum Refiners. 1957, 36, 157–159. [Google Scholar]
- Tsonopoulos, C.; Heidman, J.L.; Hwang, S.C. Thermodynamic and Transport Properties of Coal Liquids (Exxon Monographs Series), 1st ed.; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Hosseinifar, P.; Jamshidi, S. Development of a New Generalized Correlation to Characterize Physical Properties of Pure Components and Petroleum Fractions. Fluid Phase Equilibria 2014, 363, 189–198. [Google Scholar] [CrossRef]
- Lin, H.-M.; Chao, K.-C. Correlation of Critical Properties and Acentric Factor of Hydrocarbons and Derivatives. AIChE J. 1984, 30, 981–983. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, B.; Zhao, S.; Wang, R.; Yang, G. Simplified Prediction of Critical Properties of Nonpolar Compounds, Petroleum, and Coal Liquid Fractions. Ind. Eng. Chem. Res. 1998, 37, 2059–2060. [Google Scholar]
- Atanassov, K.; Mavrov, D.; Atanassova, V. Intercriteria Decision Making: A New Approach for Multicriteria Decision Making, Based on Index Matrices and Intuitionistic Fuzzy Sets. In Issues in Intuitionistic Fuzzy Sets and Generalized Nets, 11; Atanassov, K., Kacprzyk, J., Krawczak, M., Szmidt, E., Eds.; Warsaw School of Information Technology: Warsaw, Poland, 2014; pp. 1–8. [Google Scholar]
- Atanassov, K.; Atanassova, V.; Gluhchev, G. Intercriteria Analysis: Ideas and Problems. Notes Intuitionistic Fuzzy Sets 2015, 21, 81–88. [Google Scholar]
- Mavrov, D. Software for InterCriteria Analysis: Implementation of the Main Algorithm. Notes Intuitionistic Fuzzy Sets 2015, 21, 77–86. [Google Scholar]
- Mavrov, D. Software for Intercriteria Analysis: Working with the Results. Annu. Inform. Sect. Union Sci. Bulg. 2015, 8, 37–44. [Google Scholar]
- Ikonomov, N.; Vassilev, P.; Roeva, O. ICrAData—Software for InterCriteria Analysis. Int. J. Bioautom. 2018, 22, 1–10. [Google Scholar] [CrossRef]
- Atanassov, K.; Atanassova, V.; Chountas, P.; Mitkova, M.; Sotirova, E.; Sotirov, S.; Stratiev, D. Intercriteria analysis over normalized data. In Proceedings of the 2016 IEEE 8th International Conference on Intelligent Systems (IS), Sofia, Bulgaria, 4–6 September 2016; pp. 564–566. [Google Scholar]
- Atanassov, K. On Intuitionistic Fuzzy Sets Theory; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Stratiev, D.; Sotirov, S.; Sotirova, E.; Nenov, S.; Dinkov, R.; Shishkova, I.; Kolev, I.V.; Yordanov, D.; Vasilev, S.; Atanassov, K.; et al. Prediction of Molecular Weight of Petroleum Fluids by Empirical Correlations and Artificial Neuron Networks. Processes 2023, 11, 426. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium Constants from a Modified Redlich-Kwong Equation of State. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Lee, B.I.; Kesler, M.G. A Generalized Thermodynamic Correlation Based on Three-parameter Corresponding States. AIChE J. 1975, 21, 510–527. [Google Scholar] [CrossRef]
- le Goff, P.Y.; Kostka, W.; Ross, J. Catalytic Reforming. In Springer Handbook of Petroleum Technology (Springer Handbooks), 2nd ed.; Hsu, C.S., Robinson, P.R., Eds.; Springer: Cham, Switzerland, 2017; pp. 589–615. [Google Scholar]





| Source (Year of Publication) | Correlation | Range of Applicability | Equation |
|---|---|---|---|
| Winn–Mobil (1957) [13] | Based on Winn’s nomogram 80 F < MABP < 1200 F 80 < MW < 600 | (1) | |
| Cavett (1962) [11] | Tb is in degrees Fahrenheit | (2) | |
| Lee–Kesler (1976) [10] | 70 < MW < 700 C5 ÷ C50 | (3) | |
| Riazi–Daubert (1980) [8] | 70 < MW < 700 | (4) | |
| Riazi (1987) [7] | 70 < MW < 700 >C20 | (5) | |
| Tsonopoulos (1986) [14] | Coal liquid fractions high in aromatic hydrocarbons | (6) | |
| Twu (1987) [12] | (7) | ||
| Lin–Chao (1984) [16] | Tc and Tb are in Kelvin; Pc is in MPa | (8) | |
| Jianzhong et al. (1998) [17] | Tc and Tb are in Kelvin; Pc is in MPa | (9) | |
| Hosseinifar (2014) [15] | Critical properties based on MW: a = −9.45549; b = 6.98465; c = −1.31059; d = 6.34728; e = 0.54432 f = 0.09807; g = 2.55998 a = 0.06878; b = −1.03534; c = 0.37339; d = 18.73579; e = 3.34733 f = −2.03812; g = −2.6534 Critical properties based on Tb: a = −0.0419; b = −1.47872; c = 2.73355; d = 2.45861; e = −0.35125 f = 2.09619; g = 0.50569 a = −41.24678; b = 2.55879; c = −1.02425; d = 7.29072; e = 0.66689 f = −0.28966; g = 9.70427 | (10) |
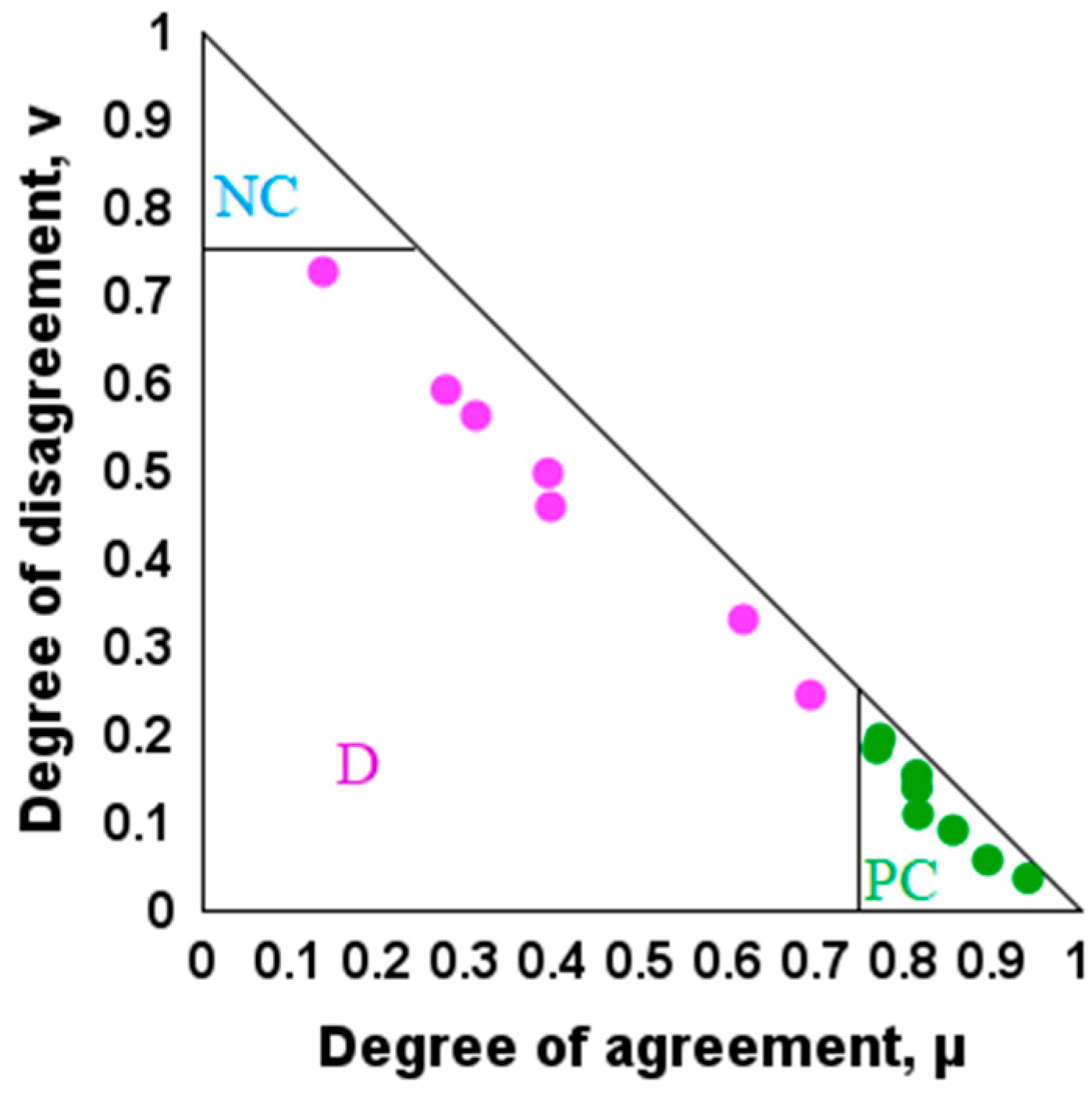
| μ | Tb (K) | SG | MW | H/C Ratio | Omega | Tc (K) |
|---|---|---|---|---|---|---|
| Tb (K) | 1.00 | 0.77 | 0.89 | 0.31 | 0.81 | 0.94 |
| SG | 0.77 | 1.00 | 0.69 | 0.14 | 0.62 | 0.81 |
| MW | 0.89 | 0.69 | 1.00 | 0.39 | 0.82 | 0.86 |
| H/C ratio | 0.31 | 0.14 | 0.39 | 1.00 | 0.40 | 0.28 |
| Omega | 0.81 | 0.62 | 0.82 | 0.40 | 1.00 | 0.77 |
| Tc (K) | 0.94 | 0.81 | 0.86 | 0.28 | 0.77 | 1.00 |
| υ | Tb (K) | SG | MW | H/C Ratio | Omega | Tc (K) |
|---|---|---|---|---|---|---|
| Tb (K) | 0.00 | 0.19 | 0.06 | 0.56 | 0.14 | 0.04 |
| SG | 0.19 | 0.00 | 0.24 | 0.73 | 0.33 | 0.15 |
| MW | 0.06 | 0.24 | 0.00 | 0.50 | 0.11 | 0.09 |
| H/C ratio | 0.56 | 0.73 | 0.50 | 0.00 | 0.46 | 0.59 |
| Omega | 0.14 | 0.33 | 0.11 | 0.46 | 0.00 | 0.18 |
| Tc (K) | 0.04 | 0.15 | 0.09 | 0.59 | 0.18 | 0.00 |
| μ | Tb (K) | SG | MW | H/C Ratio | Omega | Pc (kPa) |
|---|---|---|---|---|---|---|
| Tb (K) | 1.00 | 0.77 | 0.89 | 0.31 | 0.81 | 0.24 |
| SG | 0.77 | 1.00 | 0.69 | 0.14 | 0.62 | 0.45 |
| MW | 0.89 | 0.69 | 1.00 | 0.39 | 0.82 | 0.17 |
| H/C ratio | 0.31 | 0.14 | 0.39 | 1.00 | 0.40 | 0.35 |
| Omega | 0.81 | 0.62 | 0.82 | 0.40 | 1.00 | 0.14 |
| Pc (kPa) | 0.25 | 0.45 | 0.17 | 0.35 | 0.14 | 1.00 |
| υ | Tb (K) | SG | MW | H/C ratio | Omega | Pc (kPa) |
|---|---|---|---|---|---|---|
| Tb (K) | 0.00 | 0.19 | 0.06 | 0.56 | 0.14 | 0.73 |
| SG | 0.19 | 0.00 | 0.24 | 0.73 | 0.33 | 0.52 |
| MW | 0.06 | 0.24 | 0.00 | 0.50 | 0.11 | 0.77 |
| H/C ratio | 0.56 | 0.73 | 0.50 | 0.00 | 0.46 | 0.52 |
| Omega | 0.14 | 0.33 | 0.11 | 0.46 | 0.00 | 0.81 |
| Pc (kPa) | 0.75 | 0.52 | 0.77 | 0.52 | 0.81 | 0.00 |
| Correlation | Standard Error | Relative Standard Error | Sum of Squared Errors | %AAD | SRE |
|---|---|---|---|---|---|
| New empirical correlation (this work) | 6.94 | 1.1 | 0.0195 | 0.74% | −4.62 |
| ANN model | 4.1 | 0.66 | 0.006 | 0.39% | 190.258 |
| Winn–Mobil (1957) [13] | 9.74 | 1.6 | 0.0359 | 0.86% | −762.003 |
| Cavett (1962) [11] | 9.99 | 1.6 | 0.0358 | 0.99% | −234.396 |
| Lee–Kesler (1976) [10] | 7.35 | 1.2 | 0.0215 | 0.74% | −405.665 |
| Riazi–Daubert (1980) [8] | 7.69 | 1.2 | 0.02341 | 0.75% | 0.64 |
| Riazi (1987) [7] | 8.205 | 1.3 | 0.0240 | 0.77% | 412.145 |
| Tsonopoulos (1986) [14] | 9.53 | 1.5 | 0.0312 | 0.88% | 46.36 |
| Twu (1987) [12] | 7.55 | 1.2 | 0.0212 | 0.73% | 311.856 |
| Lin–Chao (1984) [16] | 196.38 | 31.4 | 10.063 | 10.84% | −2896.87 |
| Jianzhong et al. (1998) [17] | 7.95 | 1.3 | 0.0243 | 0.77% | 392.453 |
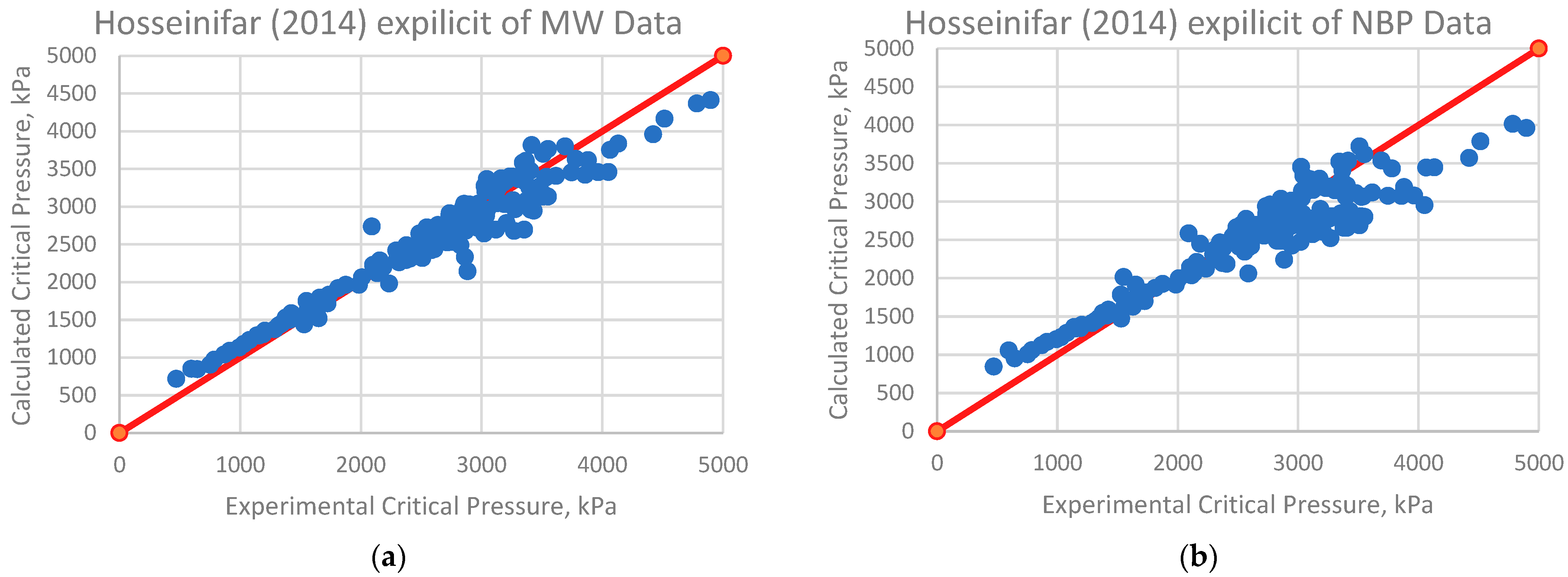
| Hosseinifar (2014) from MW [15] | 20.84 | 3.3 | 0.1599 | 2.13% | −1016.19 |
| Hosseinifar (2014) from NBP [15] | 16.65 | 2.7 | 0.0845 | 1.47% | −673.57 |
| Correlation | Standard Error | Relative Standard Error | Sum of Squared Errors | %AAD | SRE |
|---|---|---|---|---|---|
| New empirical correlation (this work) | 138.016 | 6.8 | 0.5317 | 3.39% | 0.25 |
| ANN model | 91.7 | 3.44 | 0.170 | 2.12% | −1.14 |
| Winn–Mobil (1957) | 182.536 | 6.8 | 1.879 | 5.66% | 6.62 |
| Cavett (1962) | 183.363 | 7.3 | 1.611 | 5.02% | 6.51 |
| Lee–Kesler (1976) | 160.420 | 6.0 | 1.007 | 4.48% | 2.04 |
| Riazi–Daubert (1980) | 180.936 | 6.8 | 1.524 | 5.50% | 0.64 |
| Riazi (1987) | 358.963 | 13.5 | 4.095 | 7.39% | 8.06 |
| Tsonopoulos (1986) | 210.334 | 7.9 | 2.342 | 6.81% | 4.15 |
| Twu (1987) | 689.905 | 25.9 | 7.904 | 14.79% | −21.50 |
| Lin–Chao (1984) | 104,181.9 | 3907.6 | 328,939.3 | 798.89% | 730.10 |
| Jianzhong et al. (1998) | 182.262 | 6.8 | 2.18 | 6.08% | 6.11 |
| Hosseinifar (2014) from MW | 224.501 | 8.4 | 1.7616 | 7.16% | 1.39 |
| Hosseinifar (2014) from NBP | 338.231 | 12.7 | 3.865 | 9.91% | −1.12 |
| Correlation | Standard Error | Relative Standard Error | Sum of Squared Errors | %AAD | SRE |
|---|---|---|---|---|---|
| SRK equation with original critical properties | 2.33 | 2.30 | 0.092 | 1.21% | 0.60 |
| Lee–Kesler equation with original critical properties (for comparison) | 1.164 | 1.15 | 0.0229 | 0.61% | −0.21 |
| New empirical correlation (this work) | 8.705 | 8.59 | 1.284 | 6.46% | 0.74 |
| ANN model | 6.93 | 6.84 | 0.814 | 4.25% | −2.54 |
| Winn–Mobil (1957) [13] | 16.482 | 16.27 | 4.604 | 8.13% | 21.30 |
| Cavett (1962) [11] | 14.037 | 13.85 | 3.339 | 9.65% | 11.00 |
| Lee–Kesler (1976) [10] | 11.144 | 10.99 | 2.105 | 7.22% | 10.07 |
| Riazi–Daubert (1980) [8] | 9.473 | 9.35 | 1.521 | 6.83% | −6.34 |
| Riazi (1987) [7] | 9.532 | 9.41 | 1.54 | 7.06% | −6.01 |
| Tsonopoulos (1986) [14] | 9.611 | 9.49 | 1.565 | 7.16% | 4.22 |
| Twu (1987) [12] | 31.689 | 31.27 | 17.019 | 20.45% | −35.59 |
| Lin–Chao (1984) [16] | 10,065.9 | 9934.3 | 1,687,593.0 | 2483.99% | 2373.21 |
| Jianzhong et al. (1998) [17] | 9.165 | 9.05 | 1.4236 | 7.16% | −1.27 |
| Hosseinifar (2014) from MW [15] | 36.318 | 35.84 | 22.35 | 22.54% | 25.06 |
| Hosseinifar (2014) from NBP [15] | 31.080 | 30.67 | 16.371 | 15.91% | 13.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sotirova, E.; Vasilev, S.; Stratiev, D.; Shishkova, I.; Sotirov, S.; Nikolova, R.; Veli, A.; Bureva, V.; Atanassov, K.; Georgieva, V.; et al. Comparison of the Methods for Predicting the Critical Temperature and Critical Pressure of Petroleum Fractions and Individual Hydrocarbons. Fuels 2025, 6, 36. https://doi.org/10.3390/fuels6020036
Sotirova E, Vasilev S, Stratiev D, Shishkova I, Sotirov S, Nikolova R, Veli A, Bureva V, Atanassov K, Georgieva V, et al. Comparison of the Methods for Predicting the Critical Temperature and Critical Pressure of Petroleum Fractions and Individual Hydrocarbons. Fuels. 2025; 6(2):36. https://doi.org/10.3390/fuels6020036
Chicago/Turabian StyleSotirova, Evdokia, Svetlin Vasilev, Dicho Stratiev, Ivelina Shishkova, Sotir Sotirov, Radoslava Nikolova, Anife Veli, Veselina Bureva, Krassimir Atanassov, Vanya Georgieva, and et al. 2025. "Comparison of the Methods for Predicting the Critical Temperature and Critical Pressure of Petroleum Fractions and Individual Hydrocarbons" Fuels 6, no. 2: 36. https://doi.org/10.3390/fuels6020036
APA StyleSotirova, E., Vasilev, S., Stratiev, D., Shishkova, I., Sotirov, S., Nikolova, R., Veli, A., Bureva, V., Atanassov, K., Georgieva, V., Stratiev, D., & Nenov, S. (2025). Comparison of the Methods for Predicting the Critical Temperature and Critical Pressure of Petroleum Fractions and Individual Hydrocarbons. Fuels, 6(2), 36. https://doi.org/10.3390/fuels6020036










