Modeling of Magnetoconductivity (MC) Behavior in Dilute p-Si/SiGe/Si
Abstract
1. Introduction
2. Construction of a Theoretical Model for MC
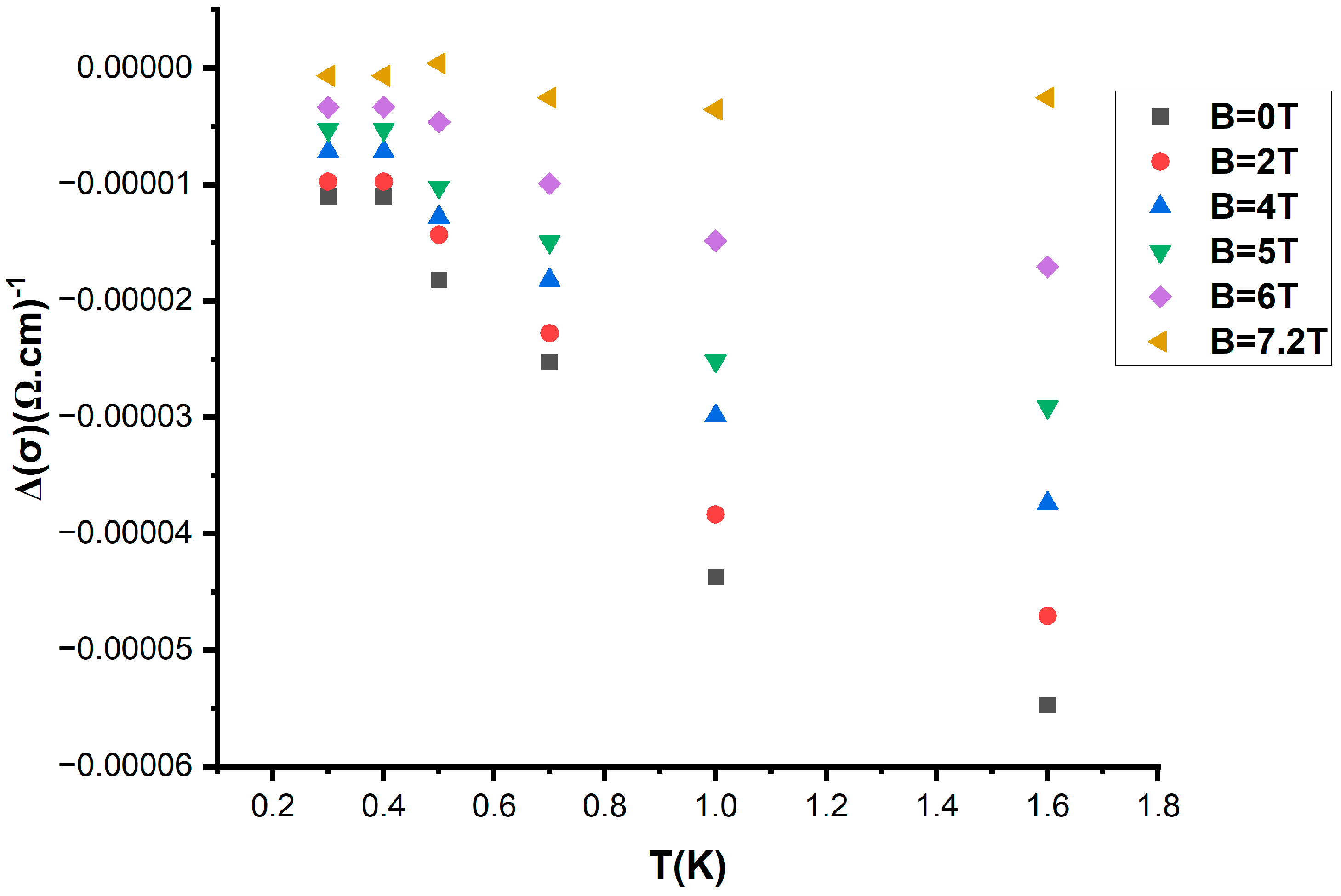
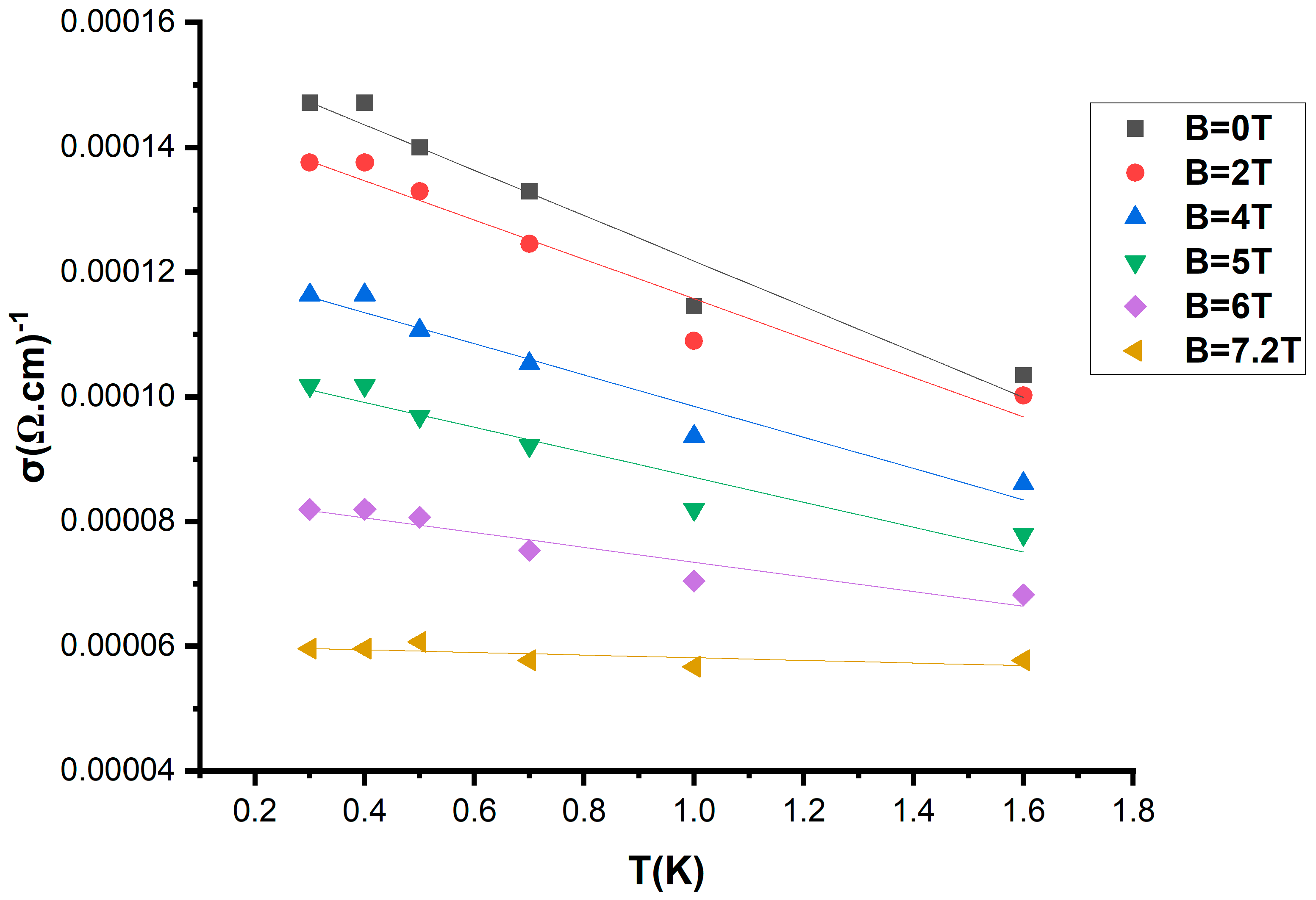
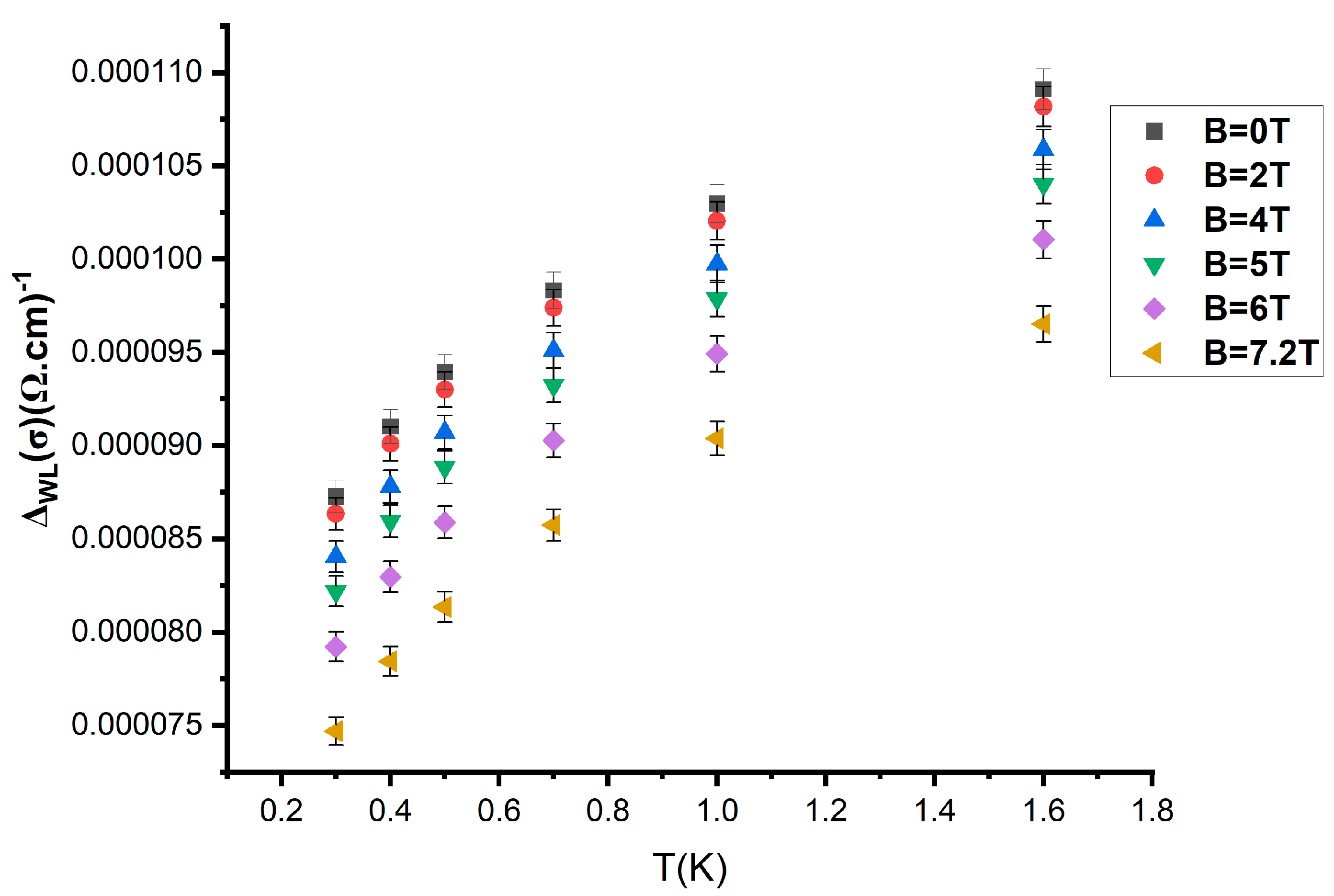
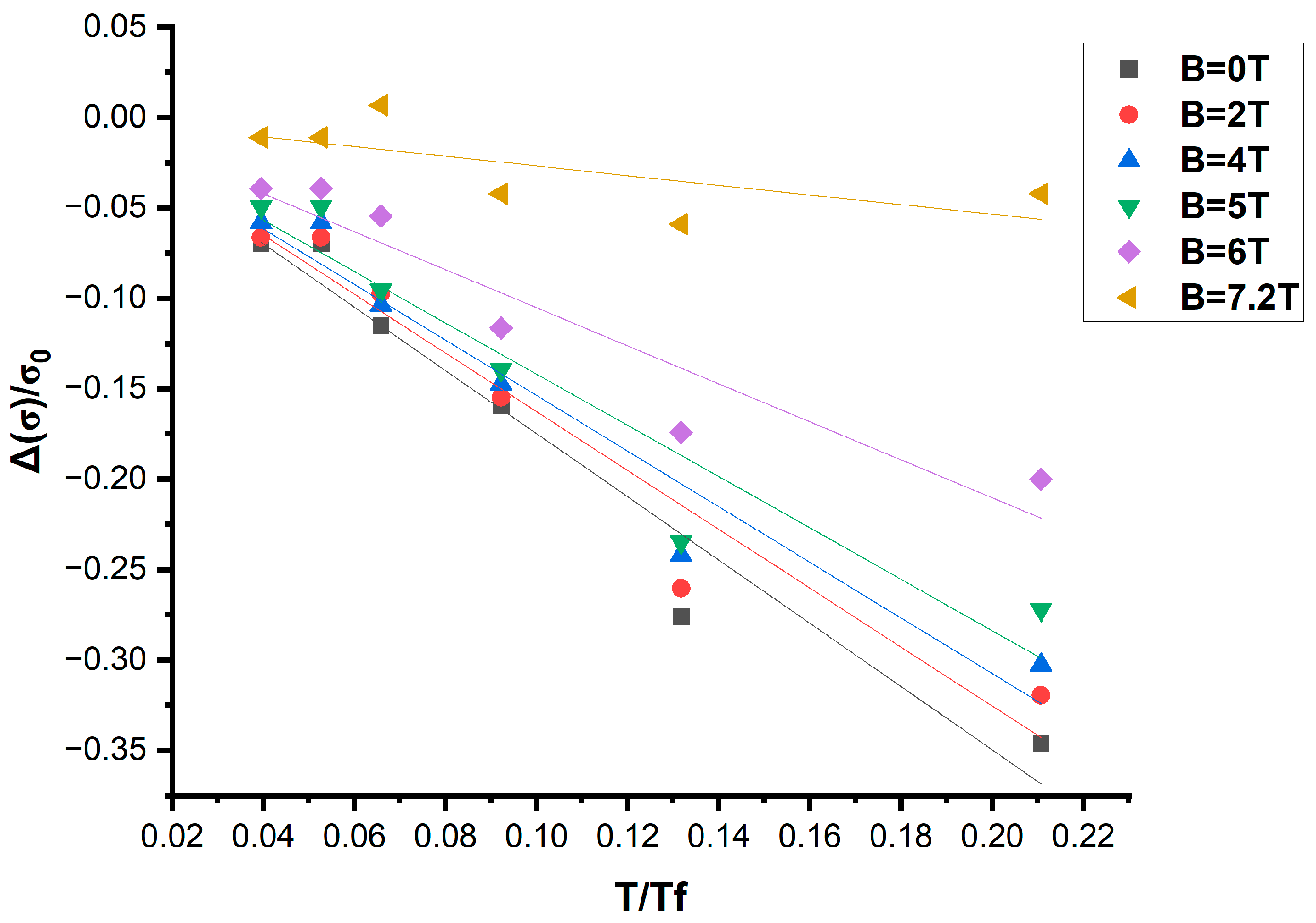
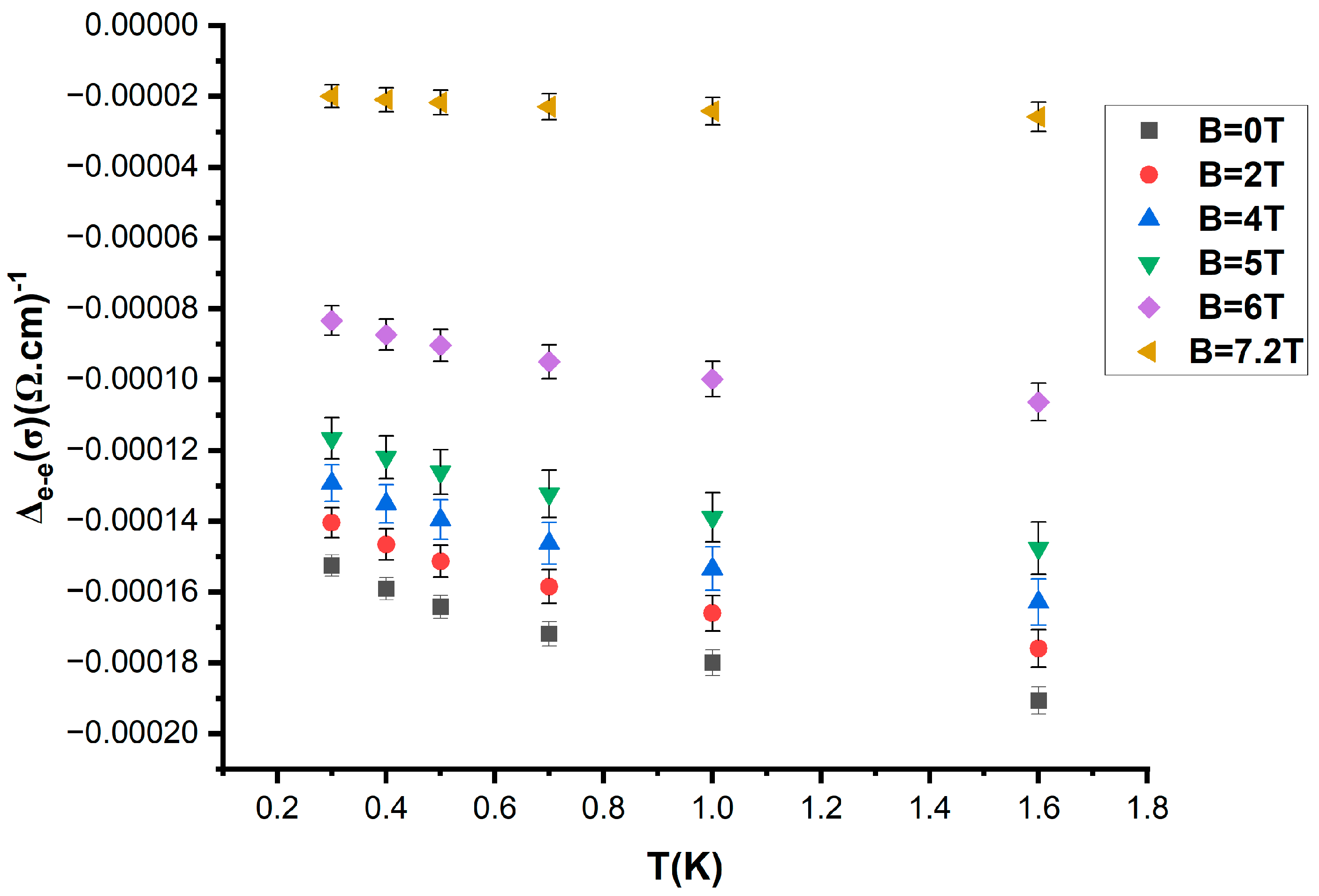
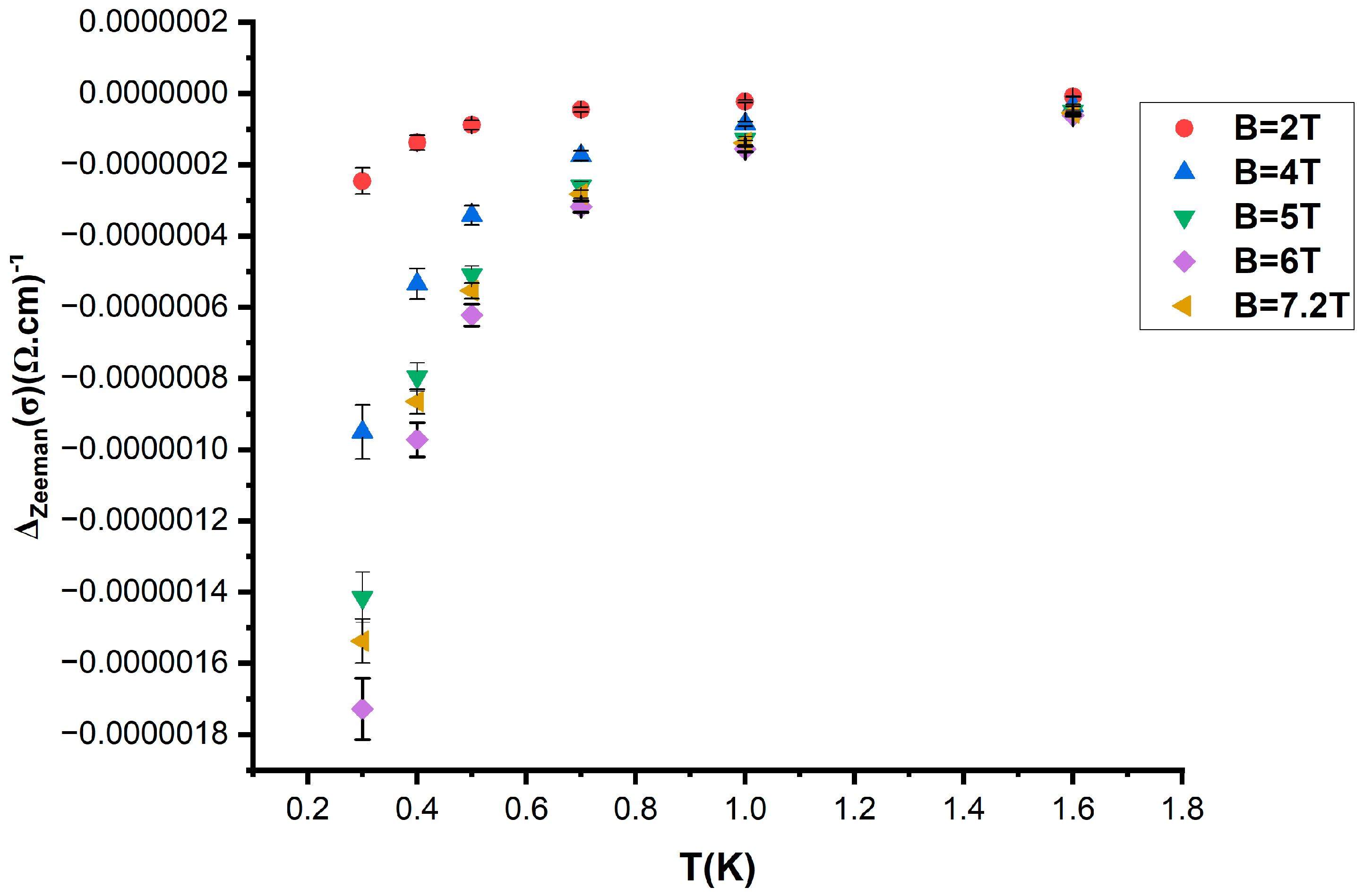
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Babar, Z.U.D.; Raza, A.; Cassinese, A.; Iannotti, V. Two Dimensional Heterostructures for Optoelectronics: Current Status and Future Perspective. Molecules 2023, 28, 2275. [Google Scholar] [CrossRef] [PubMed]
- Yoon, M. The Extraction of the Density of States of Atomic-Layer-Deposited ZnO Transistors by Analyzing Gate-Dependent Field-Effect Mobility. Electron. Mater. 2024, 5, 239–248. [Google Scholar] [CrossRef]
- Hasan, M.N.; Li, C.; Lai, J.; Seo, J.-H. Theoretical Prediction of Heterogeneous Integration of Dissimilar Semiconductor with Various Ultra-Thin Oxides and 2D Materials. Electron. Mater. 2021, 2, 495–503. [Google Scholar] [CrossRef]
- Chiang, T.-K. A Unified Semiconductor-Device-Physics-Based Ballistic Model for the Threshold Voltage of Modern Multiple-Gate Metal-Oxide-Semiconductor Field-Effect-Transistors. Electron. Mater. 2024, 5, 321–330. [Google Scholar] [CrossRef]
- Darwish, M.; Pohl, L. Insulator Metal Transition-Based Selector in Crossbar Memory Arrays. Electron. Mater. 2024, 5, 17–29. [Google Scholar] [CrossRef]
- Dlimi, S.; Limouny, L.; El kaaouachi, A. Crossover between ballistic and diffusive regime in 2D SiGe quantum well. Appl. Surf. Sci. Adv. 2021, 3, 100045. [Google Scholar] [CrossRef]
- Limouny, L.; El kaaouachi, A.; Abdia, R.; Narjis, A.; Biskupski, G.; Hemine, J.; Sybous, A.; Dlimi, S. Study of electrical resistivity in 2D Si-MOSFETS at very low temperature. AIP Conf. Proc. 2012, 1435, 385. [Google Scholar]
- Dlimi, S.; El kaaouachi, A.; Narjis, A.; Limouny, L.; Sybous, A.; Errai, M.; Daoudi, E. Evidence for the correlated hopping mechanism in p-GaAs near the 2D MIT AT B=0T. J. Optoelectron. Adv. Mater. 2013, 15, 1222. [Google Scholar]
- Elmourabit, F.; Dlimi, S.; El Moutaouakil, A.; Ouissaaden, F.I.; Khoukh, A.; Limouny, L.; Elkhatat, H.; El kaaouachi, A. Nature of the Metal Insulator Transition in High-Mobility 2D_Si-MOSFETs. Nanomaterials 2023, 13, 2047. [Google Scholar] [CrossRef]
- Huth, M.; Klingenberger, D.; Grimm, C.; Porrati, F.; Sachser, R. Conductance regimes of W-based granular metals prepared by electron beam induced deposition. New J. Phys. 2009, 11, 033032. [Google Scholar] [CrossRef]
- Lenko, D.; Schlögl, S.; Bichler, S.; Lemesch, G.; Ramsauer, F.; Ladstätter, W.; Rosc, J.; Kern, W. New approaches towards the investigation on defects and failure mechanisms of insulating composites used in high voltage applications. Compos. Part B Eng. 2014, 58, 83–90. [Google Scholar] [CrossRef]
- Qu, L.; Vörös, M.; Zimanyi, G.T. Metal-Insulator Transition in Nanoparticle Solids: Insights from Kinetic Monte Carlo Simulations. Sci. Rep. 2017, 7, 7071. [Google Scholar] [CrossRef] [PubMed]
- Toyozwa, Y. Theory of Localized Spins and Negative Magnetoresistance in the Metallic Impurity Conduction. J. Phys. Soc. Jap. 1962, 14, 986. [Google Scholar] [CrossRef]
- Nguyen, V.L.; Spivak, B.Z.; Shklovskii, B.I. Tunnel hopping in disordered systems. Sov. Phys. JETP 1985, 62, 1021. [Google Scholar]
- Schirmacher, W. Quantum-interference magnetoconductivity in the variable-range-hopping regime. Phys. Rev. B 1990, 41, 2461. [Google Scholar] [CrossRef]
- Holstein, T. Hall Effect in Impurity Conduction. Phys. Rev. B 1961, 108, 222. [Google Scholar] [CrossRef]
- Drichko, L.; Smirnov, I.Y.; Suslov, A.V.; Mironov, O.A.; Leadley, D.R. Large magnetoresistance of a dilute p-Si/SiGe/Si quantum well in a parallel magnetic field. Phys. Rev. B 2009, 79, 205310. [Google Scholar] [CrossRef]
- Drichko, I.L.; Dyakonov, A.M.; Smirnov, I.Y.; Suslov, A.V.; Galperin, Y.M.; Vinokur, V.; Myronov, M.; Mironov, O.A.; Leadley, D.R. Magnetotransport in low-density p-Si/Si Ge heterostructures: From metal through hopping insulator to Wigner glass. Phys. Rev. B 2008, 77, 085327. [Google Scholar] [CrossRef]
- Altshuler, B.L.; Aronov, A.; Khmelnitski, D.E. Effects of electron-electron collisions with small energy transfers on quantum localization. J. Phys. C Solid. State Phys. 1982, 15, 7367. [Google Scholar] [CrossRef]
- Altshuler, B.L.; Aronov, A.; Khmelnitski, D.E. Suppression of localization effects by the high frequency field and the nyquist noise. Solid. State. Commun. 1981, 39, 619. [Google Scholar] [CrossRef]
- Shashkin, A.A.; Dolgopolov, V.T.; Huang, S.-H.; Liu, C.W.; Zhu, A.Y.X.; Kravchenko, S.V. Metallic state in a strongly interacting spinless two-valley electron system in two dimensions. Phys. Rev. B 2020, 101, 045302. [Google Scholar]
- Shlimak, I.; Butenko, A.; Golosov, D.I.; Friedland, K.-J.; Kravchenko, S.V. Influence of spin polarization on resistivity of a two-dimensional electron gas in Si MOSFET at metallic densities. Europhys. Lett. 2012, 97, 37002. [Google Scholar] [CrossRef]
- Kopelevich, Y.; Pantoja, J.C.M.; da Silva, R.R.; Moehlecke, S. Universal magnetic-field-driven metal-insulator-metal transformations in graphite and bismuth. Phys. Rev. B 2006, 73, 165128. [Google Scholar] [CrossRef]
- Senz, V.; Ihn, T.; Heinzel, T.; Ensslin, K.; Dehlinger, G.; Grùtzmacher, D.; Gennser, U. Analysis of the Metallic Phase of Two-Dimensional Holes in SiGe in Terms of Temperature Dependent Screening. Phys. Rev. Lett. 2000, 85, 4357. [Google Scholar] [CrossRef] [PubMed]
- Lei, Z.; Cheah, E.; Rubi, K.; Bal, M.E.; Adam, C.; Schott, R.; Zeitler, U.; Wegscheider, W.; Ihn, T.; Ensslin, K. High-quality two-dimensional electron gas in undoped InSb quantum wells. Phys. Rev. Res. 2022, 4, 013039. [Google Scholar] [CrossRef]
- Kawabata, J. Theory of negative magnetoresistance in three-dimensional systems. Solid. State. Commun. 1980, 34, 431. [Google Scholar] [CrossRef]
- Dlimi, S.; El Kaaouachi, A.; Limouny, L. Magnetoconductivity in a Disordered and Interacting 2D p-SiGe Quantum Well. J. Korean. Phys. Soc. 2020, 77, 1218. [Google Scholar] [CrossRef]
- Lee, P.A.; Ramakrishnan, T.V. Magnetoresistance of weakly disordered electrons. Phys. Rev. B 1982, 26, 4009. [Google Scholar] [CrossRef]
- Altshuler, B.L.; Aronov, A.; Larkin, A.I.; Khmelnitski, D.E. Negative magnetoresistance in semiconductors in the hopping conduction region. Sov. Phys. JETP 1981, 54, 411. [Google Scholar]
- Mounir, E.; Mabchour, H.; Hammou, B.A.; El Oujdi, A.; Dlimi, S.; El kaaouachi, A. Magnetoconductivity behaviour due to electron–electron interactions, weak localization and Zeeman effects in 2-D-layered WS2. Bull. Mater. Sci. 2024, 47, 161. [Google Scholar] [CrossRef]
- Sarma, S.D.; Hwang, E.H. Parallel Magnetic Field Induced Giant Magnetoresistance in Low Density Quasi-Two-Dimensional Layers. Phys. Rev. Lett. 2000, 84, 5596. [Google Scholar]
- Basnet, R.; Upreti, D.; McCarthy, T.T.; Ju, Z.; McMinn, A.M.; Sharma, M.M.; Zhang, Y.-H.; Hu, J. Magneto-transport study on Sn-rich Sn1−xGex thin films enabled by CdTe buffer layer. J. Vac. Sci. Technol. B 2024, 42, 042210. [Google Scholar] [CrossRef]
- Sharma, M.M.; Rani, P.; Awana, V.P.S. Probing the topological surface states in superconducting Sn4Au single crystal: A magneto transport study. J. Phys. Condens. Matter. 2022, 34, 415701. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.; Sharma, M.M.; Awana, V.P.S. Weak antilocalization and ferromagnetism in magnetic Weyl semimetal Co3Sn2S2. Appl. Phys. Lett. 2023, 133, 023901. [Google Scholar] [CrossRef]
- Liu, H.-L.; Luo, Z.-Y.; Guo, J.-J.; Wang, X.-G.; Nie, Y.-Z.; Xia, Q.-L.; Guo, G.-H. Magnetoresistance and magnetic field-induced phase transition in two-dimensional antiferromagnet Fe1/3NbS2. AIP Adv. 2024, 14, 055220. [Google Scholar] [CrossRef]
- Papp, G.; Peeters, F.M. Giant magnetoresistance in a two-dimensional electron gas modulated by magnetic barriers. J. Phys. Condens. Matter 2004, 16, 8275. [Google Scholar] [CrossRef]
- Dorozhkin, S.I.; Emeleus, C.J.; Whall, T.E.; Landwehr, G. Tuning of the quantum-Hall-effect-state–insulator transition by tilting of magnetic field. Phys. Rev. B 1995, 52, R11638. [Google Scholar] [CrossRef]
- Yoshimi, R.; Tsukazaki, A.; Kozuka, Y.; Falson, J.; Takahashi, K.; Checkelsky, J.; Nagaosa, N.; Kawasaki, M.; Tokura, Y. Quantum Hall effect on top and bottom surface states of topological insulator (Bi1−xSbx)2Te3 films. Nat. Commun. 2015, 6, 6627. [Google Scholar] [CrossRef]
- Lu, T.M.; Tracy, L.A.; Laroche, D.; Huang, S.-H.; Chuang, Y.; Su, Y.-H.; Li, J.-Y.; Liu, C.W. Density-controlled quantum Hall ferromagnetic transition in a two-dimensional hole system. Sci. Rep. 2017, 7, 2468. [Google Scholar] [CrossRef]
- Abrisokov, A. Quantum linear magnetoresistance. Europhys. Lett. 2000, 49, 789. [Google Scholar]
- Gopinadhan, K.; Shin, Y.J.; Jalil, R.; Venkatesan, T.; Geim, A.; Neto, A.H.C.; Yang, H. Extremely large magnetoresistance in few-layer graphene/boron–nitride heterostructures. Nat. Commun. 2015, 6, 8337. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mabchour, H.; Essakali, Y.; El Hassan, M.; Elouaham, S.; Nassiri, B.; Dlimi, S.; El Kaaouachi, A. Modeling of Magnetoconductivity (MC) Behavior in Dilute p-Si/SiGe/Si. Electron. Mater. 2025, 6, 5. https://doi.org/10.3390/electronicmat6020005
Mabchour H, Essakali Y, El Hassan M, Elouaham S, Nassiri B, Dlimi S, El Kaaouachi A. Modeling of Magnetoconductivity (MC) Behavior in Dilute p-Si/SiGe/Si. Electronic Materials. 2025; 6(2):5. https://doi.org/10.3390/electronicmat6020005
Chicago/Turabian StyleMabchour, Hamza, Yassine Essakali, Mounir El Hassan, Samir Elouaham, Boujemaa Nassiri, Said Dlimi, and Abdelhamid El Kaaouachi. 2025. "Modeling of Magnetoconductivity (MC) Behavior in Dilute p-Si/SiGe/Si" Electronic Materials 6, no. 2: 5. https://doi.org/10.3390/electronicmat6020005
APA StyleMabchour, H., Essakali, Y., El Hassan, M., Elouaham, S., Nassiri, B., Dlimi, S., & El Kaaouachi, A. (2025). Modeling of Magnetoconductivity (MC) Behavior in Dilute p-Si/SiGe/Si. Electronic Materials, 6(2), 5. https://doi.org/10.3390/electronicmat6020005






