Research on Automatic Recognition and Dimensional Quantification of Surface Cracks in Tunnels Based on Deep Learning

Abstract

Cracks serve as a critical indicator of tunnel structural degradation. Manual inspections are difficult to meet engineering requirements due to their time-consuming and labor-intensive nature, high subjectivity, and significant error rates, while traditional image processing methods exhibit poor performance under complex backgrounds and irregular crack morphologies. To address these limitations, this study developed a high-quality dataset of tunnel crack images and proposed an improved lightweight semantic segmentation network, LiteSqueezeSeg, to enable precise crack identification and quantification. The model was systematically trained and optimized using a dataset comprising 10,000 high-resolution images. Experimental results demonstrate that the proposed model achieves an overall accuracy of 95.15% in crack detection. Validation on real-world tunnel surface images indicates that the method effectively suppresses background noise interference and enables high-precision quantification of crack length, average width, and maximum width, with all relative errors maintained within 5%. Furthermore, an integrated intelligent detection system was developed based on the MATLAB (R2023b) platform, facilitating automated crack feature extraction and standardized defect grading. This system supports routine tunnel maintenance and safety assessment, substantially enhancing both inspection efficiency and evaluation accuracy. Through synergistic innovations in lightweight network architecture, accurate quantitative analysis, and standardized assessment protocols, this research establishes a comprehensive technical framework for tunnel crack detection and structural health evaluation, offering an efficient and reliable intelligent solution for tunnel condition monitoring.

1. Introduction

Concrete structure has become the preferred form for the main structural components of numerous infrastructure projects such as tunnels, bridges, and dams due to its excellent mechanical properties and durability [1,2,3]. However, it is affected by multiple factors such as the complex external environment and inadequate maintenance management measures during the operation period after a tunnel is put into operation, resulting in the generation and expansion of cracks on the inner surface of the tunnel. These cracks will weaken the overall bearing capacity and water resistance of the tunnel structure, accelerate the corrosion of internal reinforcing bars and the deterioration of the structure, and seriously threaten the long-term operational safety of the tunnel [4]. Advance identification and evaluation of cracks on the tunnel inner surface, coupled with the formulation of corresponding preventive maintenance strategies, can enhance structural durability, extend service life, and ensure long-term operational safety of the tunnel [5]. Based on quantitative crack detection indicators (such as length and width), and combined with relevant specifications to classify risk levels, key data support can be provided for tunnel operation and management.

Traditional manual inspection of cracks relies on individual experience judgment and subjective perception, which has limitations such as low detection efficiency, long inspection cycle, and human subjectivity [6]. With the development of the computer vision theory system and the continuous innovation of deep learning network architectures, the maturity of automated crack detection technology in the tunnel field has significantly improved [7]. In this context, the application of machine vision to automated tunnel crack detection has exhibited a rapidly growing trend. Currently, deep learning-based crack detection methods can be broadly categorized into three types: classification algorithms designed specifically to determine the presence or absence of cracks, object detection algorithms that simultaneously address crack recognition and localization, and segmentation algorithms capable of achieving pixel-level differentiation between cracks and background [8].

In the field of image classification, Lecun et al. [9] proposed the LeNet-5 model, initially for handwritten character recognition and classification. Its innovative “convolution-pooling-full connection” architecture not only broke through detection accuracy but also laid the foundation for the CNN paradigm, providing a core framework for the development of CNN in the field of computer vision. Szegedy et al. [10] proposed the classic deep convolutional neural network model GoogleNet, and the designed Inception deep convolutional network module helped the model achieve a 6.66% error rate in image classification tasks. Hoang [11] constructed a network model integrating multiple support vector machines (SVM) and combined with the optimistic algorithm of artificial bee colony, achieving a classification accuracy of 96%. Que et al. [12] improved the G-set network, introducing global average pooling layer and batch normalization layer, adjusting the Softmax classifier, optimizing the learning rate, activation function and convolution kernel size, and the experimental recognition accuracy was 0.9630, F1 score 0.9623. Among these studies, some methods have strong crack detection capabilities but low accuracy. While certain methods achieve high classification accuracy, they suffer from inadequate precision in crack classification criteria.

In the field of object detection, the YOLO (You Only Look Once) series models, with their unique design concepts and outstanding performance, have become a research hotspot in the field of object detection. Redmon et al. [13] proposed the YOLOv1 model, which can directly predict bounding boxes and category probabilities from the complete image, with fast detection speed and high performance. The following year, Redmon et al. [14] designed the Darknet-19 architecture, optimizing the loss function to reduce the difficulty of model learning, improve the effect of feature learning and stability; YOLOv2 model performed well in evaluations on datasets such as PASCAL VOC and COCO. YOLOv3 has adopted the Darknet-53 backbone network with 53 convolutional layers, which has a significant increase compared to YOLOv2’s 19 layers [15]. Alipour [16] identified that material property changes would notably diminish the crack detection accuracy of custom models, leading to the proposition of joint training, sequential training, and ensemble learning to build a cross-material robust model, where the experimental training accuracy of all three methods attained 97%. Adel et al. [17] used the U-Net network to detect the distribution of concrete crack pits. The dataset was expanded from 1600 images to 6400 images by flipping and rotating and the model accuracy reached 99.65%. Yilmaz [18] utilized YOLOv5, YOLOv8, and YOLOv11 models for the segmentation and quantification of mortar cracks, achieving a mean Intersection over Union (mIoU) of 81.2%, an accuracy of 95%, and an error rate of 4.1% in crack width measurement.

Pixel-level semantic segmentation classifies and labels the crack areas pixel by pixel, providing accurate geometric information for structural assessment and supporting detailed analysis [19]. Hsieh et al. [20] reviewed machine learning-based crack detection methods, evaluated 8 segmentation models, found that specific network structures can improve performance, and pointed out that solving the false-positive problem is the key to optimization. Zhang et al. [21] proposed a crack visual detection system based on a context-aware deep semantic segmentation network: by adaptively sliding windows to locate image blocks, pixel labels are assigned through the SegNet encoder–decoder, and then integrated using the CAOPF scheme, enabling the detection of cracks in different environments. Wang et al. [22] proposed a new pixel-level crack segmentation model called SegCrack, which uses a hierarchical-structured Transformer encoder to output multi-scale features; this model achieves an F1 score of 96.05% and an mIoU of 92.63%. Chen et al. [23] designed a fully convolutional neural network, enhancing the representation of crack features through multi-level extraction and class feature optimization. Ma et al. [24] proposed the CRTransU-Net underwater concrete crack real-time segmentation model, which can solve the problem of foreground-background imbalance, achieving a segmentation performance superior to U-Net and other models, and the quantitative results of crack geometric dimensions have a high degree of consistency. Kang et al. [25] proposed an integrated method for automatic crack detection, location, and quantification, integrating Faster R-CNN to detect crack areas; experiments show that the average detection accuracy reaches 95%. Hang et al. [26] improved the pixel-level detection accuracy by using vertical and horizontal compression attention modules and efficient channel attention upsampling. Currently, numerous studies exist on pixel-level semantic segmentation for crack images. While some achieve ideal detection accuracy, model recognition efficiency remains improvable. Furthermore, the majority of studies concentrate merely on segmentation and recognition, while related research and application schemes need further advancement in efficiently transforming segmentation results into quantitative references for structural safety assessment and underpinning subsequent engineering decisions.

In the field of quantitative analysis of the length and width of concrete cracks, KO et al. [27] developed an open-source automatic detection software (ABECIS) specifically for external cracks in buildings. The software has a median error of 8.2% in the total estimated length of detected cracks. The research team also pointed out that in the future, the research direction will be further expanded to the prediction of crack width, depth, and other dimensional parameters. Patzelt et al. [28] achieved quantitative analysis of cracks with a maximum area of 40 cm² through a series of technical processes including image preprocessing, machine learning algorithm design, and Python 3.14.2 script development. This method can automatically estimate the area, length, and width of cracks in a single workflow. Yuan et al. [29] proposed a deep learning crack detection method called R-FPANet, which can automatically segment and quantify the shape of cracks at the pixel scale. The core improvement lies in the introduction of channel attention modules and position attention modules, which strengthen the dependency and correlation between features. Experimental results show that this method can quantitatively analyze core geometric parameters such as crack area, length, average width, and maximum width at the pixel level, with an average intersection-over-union (mIoU) of 83.07%. Feng et al. [30] optimized and improved the CDDS network by leveraging the core architecture of SegNet to accurately extract fracture size parameters. Crack length is quantified as the cumulative count of skeleton pixels, while crack area is determined by the total number of pixels in the crack prediction mask. The average crack width is subsequently derived from the computed area. The network achieved a recall rate, precision rate, and F1 score of 80.45%, 80.31%, and 79.16%, respectively. Maslan et al. [31] conducted automatic detection, size measurement, and position positioning research on transverse cracks in concrete runway plates based on the YOLOv2 model. The average accuracy (AP) of crack detection reached 0.89, meeting the requirements for practical deployment in engineering, and the method can further achieve position positioning of cracks within the concrete plate and the calculation of length, width parameters. Existing studies still have significant limitations in the quantitative dimension and scene adaptability of cracks. In response to problems such as dim lighting, illumination light obstruction, and complex crack distribution patterns in tunnel scenarios, the precise quantitative analysis of concrete cracks in complex tunnel environments remains a current research hotspot.

To achieve rapid and accurate identification of cracks on the inner surface of tunnel concrete, this study proposes an LiteSqueezeSeg network, which is an enhanced version of the open-source semantic segmentation model SqueezeNet. The core innovation lies in focusing on the “Lightweight Semantic Segmentation” as the core objective. Miao et al. [32] previously conducted a comparative study between the LiteSqueezeSeg method and other lightweight models (e.g., MobileNet, GoogleNet), demonstrating that LiteSqueezeSeg has only half the number of parameters as GoogleNet and outperforms MobileNet in all three core evaluation metrics: accuracy, intersection over union (IoU), and F1-score. The proposed network is applied to the precise detection and quantitative measurement of concrete surface crack widths. Furthermore, the segmentation results are integrated with established industry standards to provide a scientific basis for monitoring and assessing tunnel structural conditions.

2. Crack Recognition

Deep learning technology builds a deep neural network model with multiple layers of nonlinear transformations to utilize massive data for automatic feature learning, enabling end-to-end automated processing of complex tasks. In the field of crack recognition, since cracks typically manifest as local, slender, and complex-edge-targets, convolutional neural networks, with their unique local receptive fields, weight sharing, and pooling operations, can efficiently extract spatial hierarchical features (such as edges, textures, shapes, etc.) from images, effectively improving the accuracy of small target recognition and the robustness of target extraction in complex backgrounds. Therefore, this study selects the convolutional neural network algorithm to conduct research on deep learning recognition of cracks. The open-source semantic segmentation model SqueezeSeg was improved specifically to enable it to effectively extract the local spatial features of cracks in the research.

2.1. Dataset Preparation

The labeled image serves as the foundation for pixel-level semantic segmentation. The Image Labeler tool was employed to perform pixel-level and region-level annotation on a total of 10,000 images in JPG format. Among these, 6000 images were sourced from the Surface Crack Detection public dataset, while the remaining 4000 were generated by augmenting approximately 500 tunnel inner surface images through geometric transformations, including rotation, flipping, and cropping. Targeted image processing techniques are adopted to preprocess the original images: the uneven lighting issue is corrected via a brightness equalization algorithm, surface impurity interference is eliminated using image denoising and stain segmentation technologies, and visual features of crack regions are enhanced by combining operations such as contrast enhancement and sharpening. Through the aforementioned preprocessing pipeline, the consistency of images and the distinguishability of target regions are effectively improved. The corresponding annotation labels are stored in PNG format. 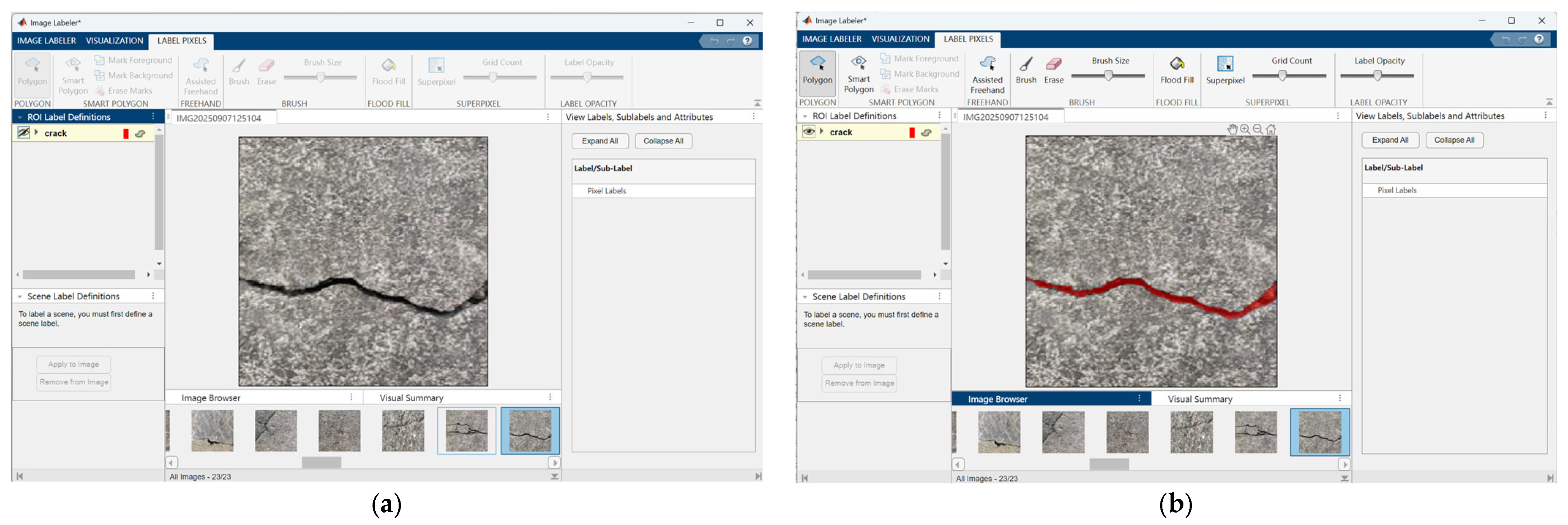Figure 1 illustrates the image labeling process, presenting both the original and annotated images. Specifically, Figure 1a displays an original textured image containing cracks; although the cracks are partially distinguishable within the complex background, they are not explicitly delineated. In contrast, Figure 1b shows the annotated version produced using the pixel-level labeling tool, in which the crack regions are clearly highlighted in red. This enhanced visualization improves the prominence of the target cracks, thereby facilitating subsequent analysis and research efforts.

The cracks in the dataset are divided into three typical crack types on the tunnel inner surface: longitudinal cracks (accounting for 48% of the labeled samples), circumferential cracks (35%), and network cracks (17%).

To enhance the reliability of the results, we divided 4000 enhanced samples, of which 3200 were used for model training and 800 were used as an independent validation set specifically for verifying the generalization ability of the LiteSqueezeSeg model for unseen tunnel crack data.

2.2. LiteSqueezeSeg Network Model

Image semantic segmentation is a computer vision task that involves assigning precise category labels to every pixel within an image. In the context of crack detection in tunnel structures, achieving pixel-level accuracy necessitates that the model exhibits fine-grained discriminative capabilities at the boundaries between cracks and background regions. The LiteSqueezeSeg architecture employed in this study is a lightweight and efficient convolutional neural network (CNN). Compared to conventional large-scale semantic segmentation models such as Deeplabv3+ and Inceptionresnetv2, it has significantly fewer parameters, yet maintains competitive performance in crack segmentation tasks. This architecture effectively captures critical crack features—including texture and shape—enabling accurate differentiation between crack and non-crack pixels, thereby supporting reliable pixel-level detection in tunnel structural inspections.

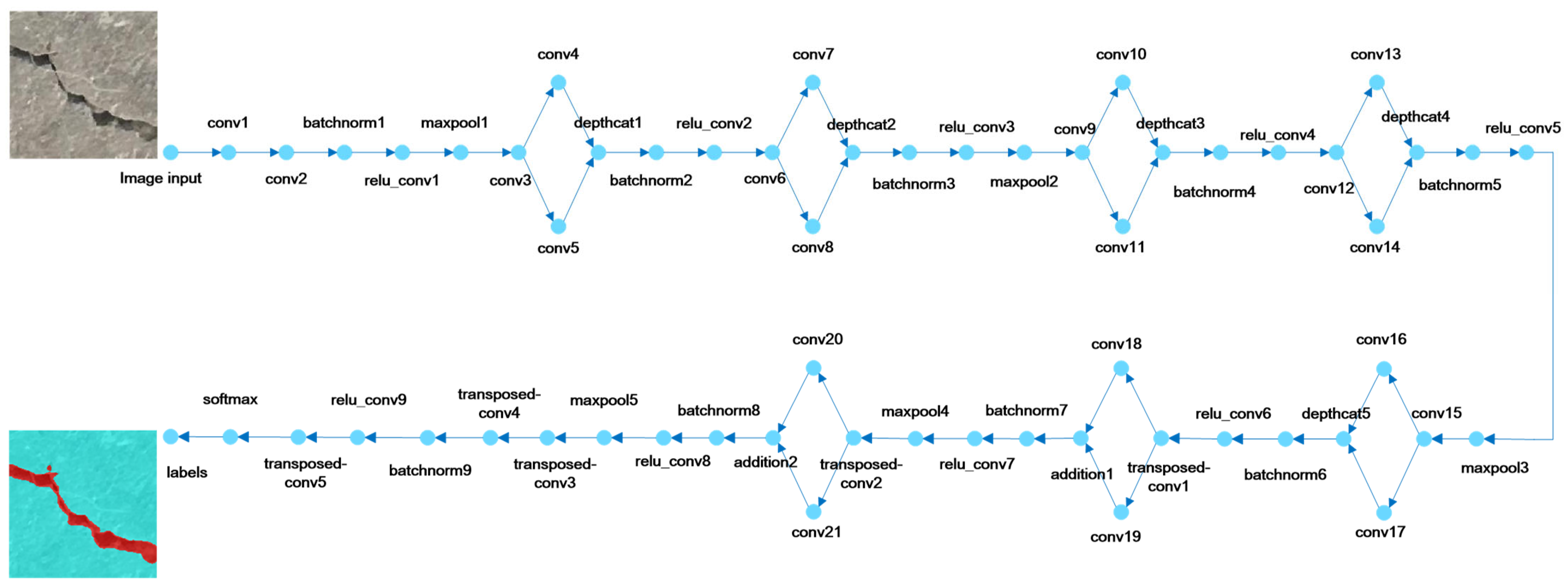
The network structure is illustrated in Figure 2 and can be broadly divided into three stages: feature extraction, feature restoration, and classification. LiteSqueezeSeg is an enhanced deep neural network derived from SqueezeSeg, an open-source lightweight semantic segmentation model. Designed for crack recognition, it achieves high effectiveness with low computational overhead, making it suitable for deployment across diverse operational environments and applicable to crack identification, quantification, and segmentation tasks. In contrast, the original SqueezeNet architecture primarily consists of sequentially connected Fire Modules, where the encoder progressively reduces spatial resolution while increasing channel depth. Its decoder is relatively simplistic, typically employing transposed convolutions for direct upsampling; however, since the final output layer directly predicts the class map, certain architectural modifications are required to enable effective pixel-wise classification in deep network designs.

Building upon these foundations, LiteSqueezeSeg retains the parallel branching design of the Fire Module but adopts a more flexible configuration. On the one hand, it integrates an encoder–decoder framework with skip connections (inspired by U-Net), where the decoder performs multi-stage progressive upsampling; after each upsampling step, the generated feature map is element-wise fused with the corresponding feature map (matching spatial resolution) from the encoder pathway. On the other hand, LiteSqueezeSeg omits the rigid 1 × 1 squeezing step of the original SqueezeSeg while preserving SqueezeNet’s parallel branch structure—a targeted adjustment to the Fire Module that maximizes feature retention (avoiding spatial detail loss) without compromising lightweight performance or increasing computational complexity. This design integrates SqueezeNet’s efficient parallel convolutional branches with U-Net’s encoder–decoder architecture and element-wise addition fusion skip connections, achieving a balance between efficient computation and fine-grained segmentation, and thus overcoming the limitations of SqueezeSeg’s pure encoder design and U-Net’s high computational cost.

With the rapid advancement of deep learning technologies, crack detection approaches based on deep neural networks have increasingly demonstrated notable advantages. In particular, the LiteSqueezeSeg architecture has shown promising potential in the domain of crack detection. Given the critical role of crack morphology and width characteristics in structural health assessment, this study leverages the MATLAB Deep Learning Toolbox and the Deep Network Designer to develop a semantic segmentation model tailored for crack detection tasks using LiteSqueezeSeg. The proposed model not only effectively determines the presence of cracks in images but, more importantly, enables precise pixel-level localization and segmentation of crack regions. Experimental results indicate that the developed semantic segmentation network successfully reconstructs crack target areas, delivering high-quality pixel-level outputs that facilitate accurate measurement of crack geometric parameters—such as width and length—and support comprehensive structural health evaluation. In comparison with conventional crack detection methods, the proposed approach achieves comparable or superior detection accuracy while significantly enhancing model generalization and practical applicability. In terms of software configuration, this experiment was conducted using MATLAB on a Windows 11 operating system, with Deep Learning Designer serving as the primary deep learning framework. The LiteSqueezeSeg model employed in this study is an enhanced deep neural network architecture derived from the lightweight semantic segmentation model SqueezeSeg, capable of achieving high accuracy in crack recognition while maintaining low computational complexity.

2.3. Crack Recognition Effect Based on LiteSqueezeSeg Network Model

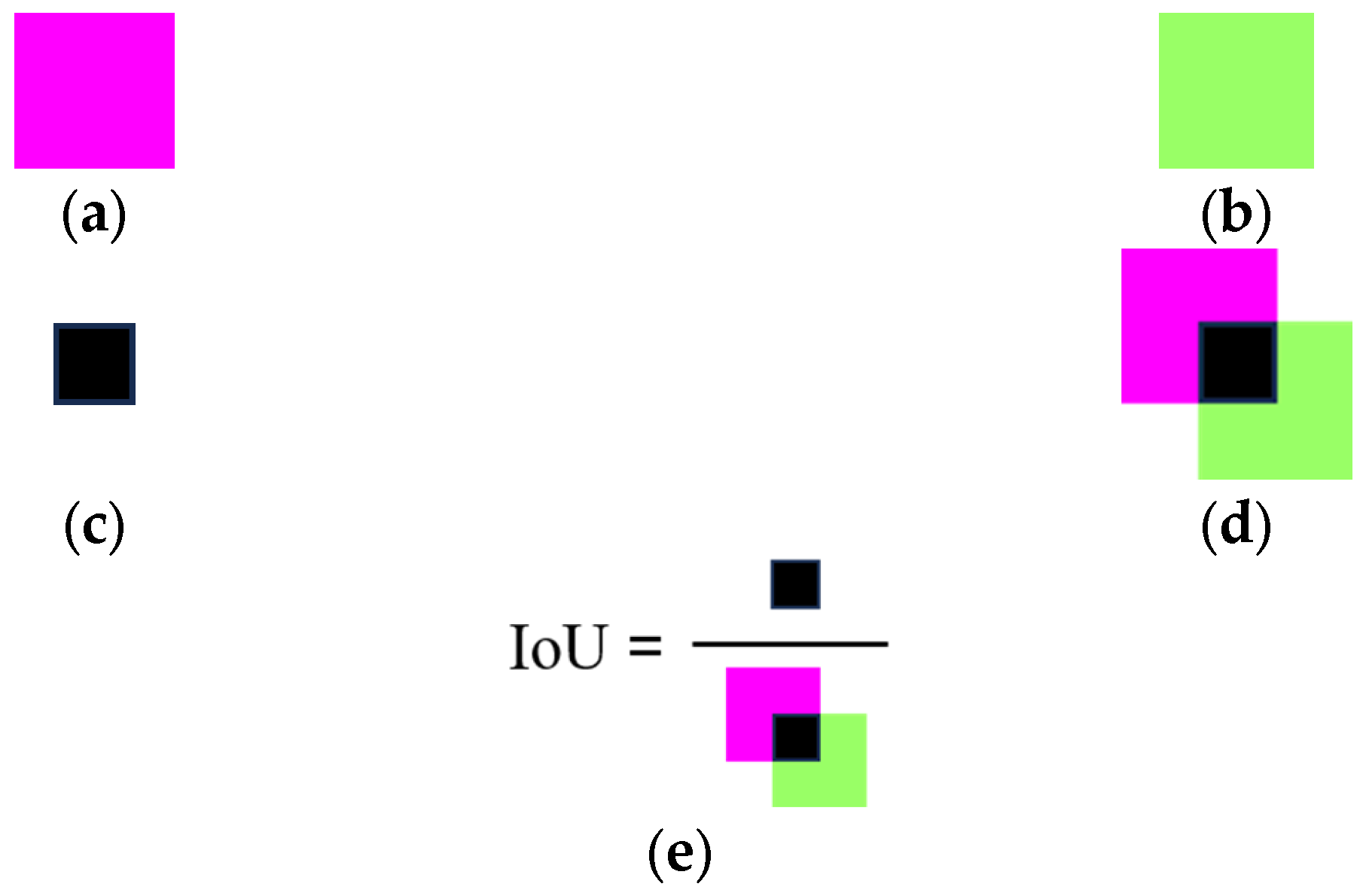
In the task of detection, the Intersection over Union (IoU) is adopted as the evaluation metric. This metric quantifies the degree of overlap between the predicted output and the ground truth, as defined in this study [33]. Specifically, IoU is calculated as the ratio of the intersection area of the crack prediction and the ground truth to their union area in terms of pixels. Figure 3 illustrates the conceptual definition of IoU: Figure 3a depicts the pixels identified by the model (pink region); Figure 3b represents the manually annotated pixels (green region); Figure 3c highlights the overlapping pixels between the model-predicted and manually labeled regions (black region); and Figure 3d displays the union of the two regions (comprising both pink and green areas). The formula presented in Figure 3e formalizes IoU as the ratio of the intersecting pixel area to the total union pixel area. In this study, IoU serves as a quantitative measure of the spatial agreement between predicted crack segments and corresponding ground truth annotations. The IoU value ranges from 0 to 1, with values closer to 1 indicating a higher degree of prediction accuracy.

Table 1. Recognition effect of LiteSqueezeSeg on typical images.

Actual Crack	Identified Crack	Truth Value	Union of Identified and True Values	IoU
				0.80
				0.76
				0.73
				0.72
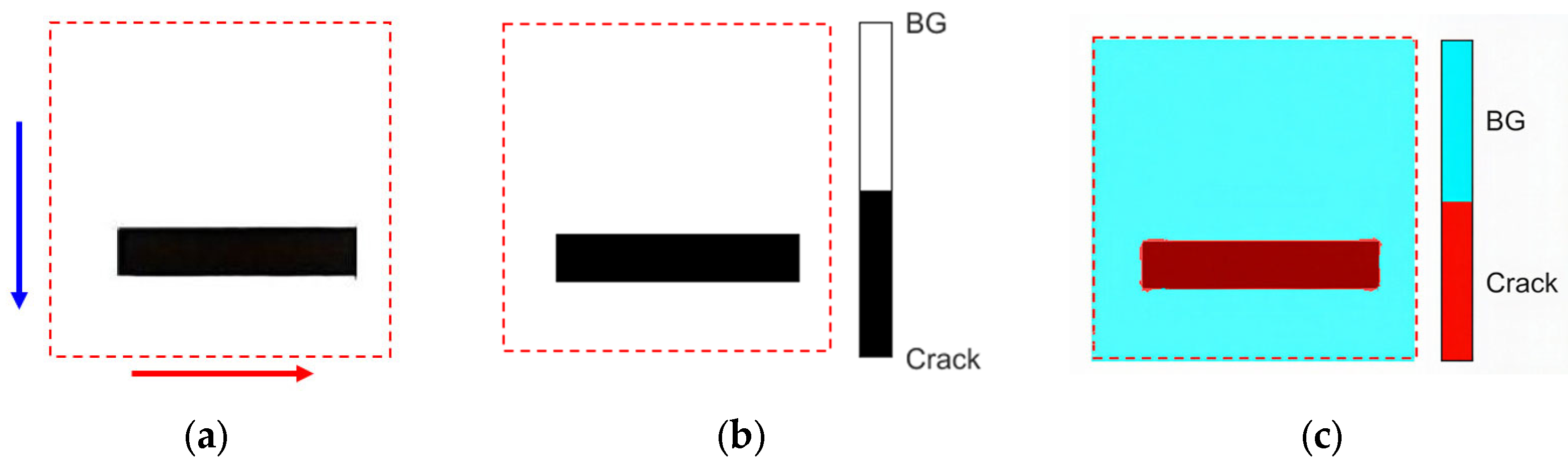
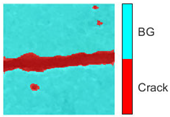
				0.75
				0.84

presents the crack segmentation performance of the LiteSqueezeSeg model on representative images. The first column displays the original scene images containing cracks. The second column illustrates the model’s predicted segmentation, where cyan denotes the background (BG) and red indicates detected cracks (Crack). The third column shows manually annotated crack labels in black. The fourth column provides a visual comparison by overlaying the model’s predictions with the ground truth labels: magenta pixels represent false positives (crack predictions not matching the labels), green pixels indicate false negatives (labeled cracks not captured by the model), and black pixels denote true positives (overlapping regions between predictions and labels), thereby enabling an intuitive assessment of prediction accuracy. The fifth column quantifies the segmentation performance using the IoU metric, which measures the degree of overlap between predicted and actual crack regions. Higher IoU values correspond to greater segmentation accuracy. The reported IoU scores range from 0.72 to 0.84, reflecting the model’s robust and consistent performance in crack detection.

2.4. Performance Analysis Based on the LiteSqueezeSeg Network Model

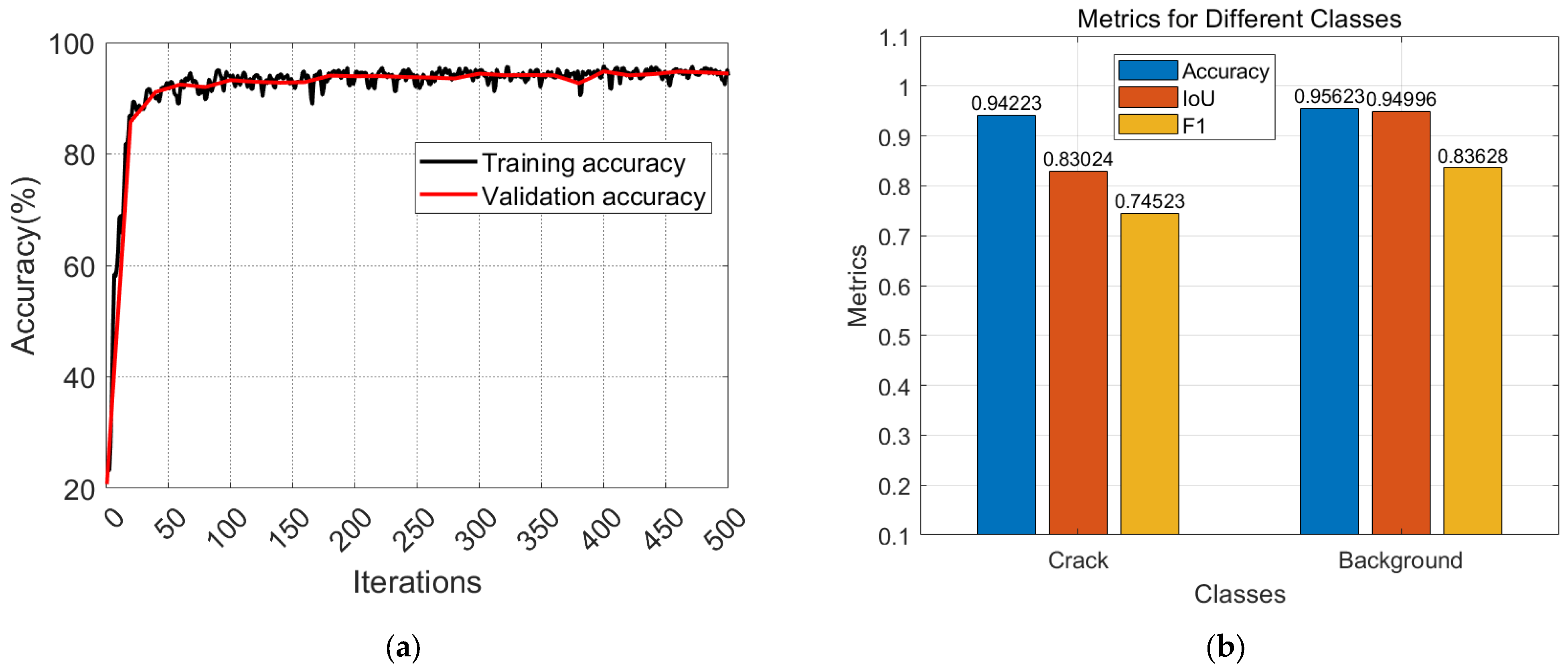
Figure 4 presents the training history and performance evaluation results of the LiteSqueezeSeg model. Specifically, Figure 4a shows the training and validation histories with the training accuracy converging to approximately 95.15%. For the concrete structure crack identification task, Precision, Recall, and F1-score are the commonly used evaluation metrics [34].

Accuracy refers to the proportion of correctly predicted positive and negative instances relative to the total number of instances, as defined by Equation (1):

$$Accuracy={\displaystyle \frac{TP+TN}{TP+FP+FN+TN}}$$

(1)

where TP denotes the number of true positives, representing cracks correctly identified; TN denotes the number of true negatives, representing non-cracks correctly identified; FP denotes the number of false positives, indicating non-cracks incorrectly classified as cracks; and FN denotes the number of false negatives, referring to cracks that were missed during detection.

The accuracy rate is the proportion of the targets that are predicted as cracks among all the targets that are predicted as cracks, reflecting the model’s error detection ability. It mainly measures the degree of correct classification of the crack detection model for the tunnel entrance wall cracks. The calculation formula for the accuracy rate is Equation (2):

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(2)

The recall rate is the proportion of the number of cracks that were correctly predicted among all the detected samples, reflecting the model’s ability to accurately detect cracks. The formula for calculating the recall rate is Equation (3):

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(3)

The F1 score is a comprehensive evaluation metric, which is the harmonic mean used to balance the accuracy and recall rates of crack detection. Generally, when the F1 score is higher, it indicates that the model performance is better. The calculation formula for the F1 score is as shown in Equation (4):

$$F_1=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}$$

(4)

Figure 4b presents the quantitative evaluation results of crack and background regions in the test dataset across three core metrics: Precision, IoU, and F1 score, which serve as the primary criteria for benchmarking the segmentation performance of the model. Overall, the model exhibits significantly superior performance on the background class compared to the crack class across all three-evaluation metrics.

This phenomenon stems from two underlying aspects: on one hand, it is associated with the characteristics of crack pixels—their extremely low proportion and random distribution in the entire image; on the other hand, it is closely related to the morphological characteristics of cracks. Cracks typically feature narrow gaps and rough edges, which tend to be confused with noise and textures in the image. This substantially increases the risk of misclassifying such interferences as cracks, ultimately resulting in the model’s suboptimal performance across all evaluation metrics for the crack segmentation task.

The training results of the LiteSqueezeSeg model proposed in this study indicate that concrete cracks usually present as small-area distribution characteristics in images, and their spatial distribution is random. This characteristic leads to the model’s difficulty in correctly classifying minor interfering information such as voids and surface roughness points as crack targets during the segmentation process, thereby affecting the segmentation accuracy.

Table 2. Description of weights.

Type	Pixel Count	Image Pixel	Frequency	Weight
Crack	5.6949 × 107	5.1529 × 108	0.1105	4.5236
Background	4.5828 × 108	5.1529 × 108	0.8895	0.5621

presents the pixel count, total image pixel count, proportional frequency, and corresponding weight values for two categories, namely Crack and Background.

To mitigate the above class imbalance and misclassification issues, the model incorporates a class weight mechanism with the weight calculation Equation (5):

$$W=1/(2\times f_i)$$

(5)

where W represents the weight of either the crack or the background class; The “2” in the denominator is because this is a binary classification task (only two classes: crack and background); f_i denotes frequence, i presents crack or background.

The weights are used to adjust the proportion of contributions of different classes in the loss function, with the core goal of increasing the proportion of the loss from low-frequency classes (e.g., cracks) in the total loss.

An exhaustive comparative analysis against contemporary state-of-the-art models is performed to highlight the superiority of our proposed architecture in lightweight design and high accuracy. The comparison parameters are shown in

Table 3. Model performance comparison.

Architecture	Para (Million)	Acc	IoU	F1	Latency (ms)
Ours	3.4	95.15%	0.8302	0.7452	16.33
Mobilenetv2	6.7	94.71%	0.7422	0.6983	32.99
Resnet18	20.6	94.38%	0.7481	0.7032	18.44
U-Net	31.0	96.11%	0.8452	0.7466	39.86
Inceptionresnetv2	71.1	96.20%	0.8536	0.7792	111.22

:

The model achieves a remarkable balance between efficiency and performance: with only 3.4 million parameters (49% fewer than Mobilenetv2, 84% fewer than Resnet18, 89% fewer than U-Net, and 95% fewer than Inceptionresnetv2) and a latency of 16.33 ms (50% faster than Mobilenetv2, 11% faster than Resnet18, 59% faster than U-Net, and 85% faster than Inceptionresnetv2), it exhibits unparalleled lightweight characteristics. Meanwhile, our model maintains a high accuracy of 95.15%—surpassing Mobilenetv2 (94.71%) and Resnet18 (94.38%), and approaching the performance of U-Net (96.11%) and Inceptionresnetv2 (96.20%). Additionally, our model outperforms most counterparts in IoU and F1-score further demonstrating its superiority in comprehensive task performance. In summary, this model stands out as a lightweight yet high-performance solution, outcompeting existing architectures in efficiency while delivering competitive accuracy.

To verify the practical effectiveness of the proposed model in the real-world task of identifying cracks in tunnels,

Table 4. Comparison of recognition effects of different models.

Original Image	Mobilenetv2	Inceptionresnetv2	Ours

presents the image semantic segmentation results of MobileNetv2, Inceptionresnetv2, and LiteSqueezeSeg in complex tunnel scenarios (where the original images contain typical interference factors such as stains and texture disturb-ances). The experimental visualization results show that in such challenging environ-ments, the denoising ability and crack target recognition accuracy of our model are significantly better than those of MobileNetv2. Although its crack recognition accuracy is slightly lower than that of Inceptionresnetv2, LiteSqueezeSeg has a clear advantage in terms of parameter quantity, making it more suitable for deployment in tunnel scenarios.

Experimental results show that this mechanism effectively balances the training weights of crack and background classes, achieving a more balanced accuracy rate (ACC) for both classes, significantly reducing the risk of misclassification caused by minor interference and improving the reliability of the model’s recognition of crack targets.

3. Crack Quantification and Algorithm Validation

3.1. Algorithm Accuracy Verification

Figure 5 presents the original and preprocessed crack scale images. Camera imaging is susceptible to interference from external environmental factors and operational conditions, which are the primary causes of image blurriness and reflection artifacts. Figure 5a shows the original crack scale image captured by a camera. Affected by strong light, obvious specular reflection areas appear on the surface of the scale ruler, leading to uneven light distribution and poor overall image clarity. Relevant details of the cracks are obscured by reflections, and some regions appear visually rough and blurred. Furthermore, excessive reflections or insufficient illumination can both result in overall image darkness and indistinct crack edges. Therefore, image preprocessing is necessary to remove noise and ensure the image is clear and free of reflections. Figure 5b depicts the crack scale image after preprocessing. The light has been effectively adjusted, and the reflection issue has been completely eliminated. The overall image brightness is uniform, and the scales, markings on the ruler, as well as details related to the cracks are clearly distinguishable, presenting excellent visual effects. This provides a clear image foundation for subsequent crack identification and analysis.

Figure 6 presents a schematic diagram of 227 × 227 pixel images. To enhance the performance of the crack recognition model, data augmentation was conducted on the original crack images: specifically, for each original crack image, transformations including rotation, horizontal flipping, and vertical flipping were implemented. Through these diverse transformations, multiple new samples were generated from a single original image. After this process, the number of crack samples was expanded to approximately 200, which provides a richer and more diversified dataset for the subsequent training of the crack recognition model and contributes to improving the model’s recognition accuracy and generalization ability.

When performing positional shift transformation on the standard crack comparison scale in the crack comparison scale images, an accurate 1-pixel displacement was achieved. Fine-tuning was performed using the arrow keys, and each operation was strictly controlled to ensure that the scale moved by only 1 pixel in the horizontal or vertical direction. During the process, the displacement accuracy was verified multiple times to ensure that the standard crack scale completed the positional shift transformation accurately as required, thereby meeting the accuracy requirements for subsequent analysis or processing of the crack scale.

Among them, Figure 6a–l shows the image samples after software cropping, with a unified pixel size of 227 × 227. This batch of standardized images is mainly used to construct an accuracy verification dataset for the crack recognition model, providing standardized data support for the subsequent quantitative evaluation of the model’s recognition accuracy, positioning accuracy, and anti-interference ability, and ensuring the reliability and comparability of the model performance verification results.

Figure 7 is a schematic diagram of the model’s prediction results, illustrating the process from the input of the original image to the output of the prediction result. Figure 7a is the original image, with a size of 227 × 227 pixels. The black strips in the image represent the scale of the crack comparison chart with a width of 0.9 mm, which is used to simulate the cracks. Figure 7b is the labeled image: it is the annotation result of the cracks (Crack) and the background (BG) in the original image. Figure 7c represents the verification result overlay: the cracked area predicted by the model (the red part) is superimposed and displayed on the original image. The red color in the right column chart represents the predicted cracked area, and the cyan color represents the background area. Comparison with labeled images enables intuitive assessment of the model’s crack recognition accuracy, as well as verification of its ability to effectively differentiate cracks from the background. This serves as a foundation for subsequent model performance analysis and optimization.

Figure 8 shows the crack distribution characteristics in the image: Figure 8a corresponds to an image with a size of 227 × 227 pixels, presenting the crack width distribution along the columns from left to right. The average width of the cracks is 2.08 mm and the maximum width is 2.13 mm, which clearly and reflects the width characteristics and variation law of the cracks from left to right; Figure 8b presents the crack length distribution along the rows from top to bottom, with an average length of 9.94 mm and a maximum length of 10.02 mm (Note: The original text incorrectly stated “maximum width” here, which has been corrected to “maximum length”), and it also clearly and reflects the characteristics and variation law of the cracks in the length direction. The distribution results of the two figures together accurately present the spatial distribution characteristics of crack initiation, variation, and termination, providing support for understanding the crack development characteristics from the spatial dimension.

Figure 9 presents the width prediction results for 5 randomly selected crack samples. As indicated by the data distribution in the figure, the average predicted width of each crack output by the model generally shows a trend of being higher than the corresponding actual width. Additionally, there are significant individual differences in the deviation magnitude among different crack samples, reflecting the heterogeneity of model prediction deviations affected by the inherent characteristics of the cracks themselves.

Table 3 further quantitatively characterizes this prediction deviation through the relative error of the average width, and the data shows that the average relative width errors of cracks 1 to 5 are 2.22%, 3.00%, 4.50%, 1.67%, and 2.80%, respectively.

Through an integrated analysis of the visual characteristics of crack distributions presented in Figure 9 and the quantitative prediction accuracy data summarized in

Table 5. Relative error of average width.

	Crack 1	Crack 2	Crack 3	Crack 4	Crack 5
Relative error (%)	2.22	3.00	4.50	1.67	2.80

, the following observations can be made: First, the predicted crack widths for all tested samples consistently exceed the actual measured values. This statistically consistent trend reveals a systematic deviation between predicted and observed values, indicating a clear pattern of overestimation in the model’s crack width predictions. Second, the relative error across all validation samples remains within the predefined 5% threshold, which is fully compliant with the acceptable error margins established in structural health monitoring practices for evaluating crack detection algorithms. Despite the presence of a systematic bias toward overprediction, a comprehensive assessment based on overall accuracy indicates that the model maintains high reliability and practical utility for engineering applications. Thus, it is well suited to meet the requirements for quantitative crack width assessment in tunnel structural health monitoring.

3.2. Crack Quantitative Analysis

Yu et al. [35] proposed a calibration factor to enable the conversion between pixel scale and physical scale. This factor, defined as the ratio of actual width to pixel width, effectively minimizes scaling errors during the conversion process. Following this approach, the present study employs the pre-determined physical size per pixel, denoted as α, to convert crack measurements from pixel dimensions to their corresponding real-world physical dimensions. By utilizing pre-calibrated parameters, a precise and consistent mapping between pixel-based measurements and physical units is established, thereby providing a reliable foundation for subsequent quantitative crack analysis conducted on a physical scale.

$$W=\alpha w$$

(6)

where W is the actual crack width (mm), α is the actual size of a unit pixel point (mm/pixel), and w is the pixel size of the crack in the input image (pixel).

The core of calibration involves establishing a precise mapping relationship between the pixel coordinates generated by the machine vision system and the corresponding physical dimensions in millimeters within an engineering context. A critical aspect of this process is determining the number of pixels that correspond to a unit of actual length. For instance, in a practical scenario, if a physical length of 10 mm corresponds to 222 pixels in the captured image, the conversion ratio between pixel coordinates and millimeter-scale measurements can be explicitly calculated. To minimize the effects of perspective distortion, it is essential that the calibration target remains parallel to the plane of the mobile phone’s image sensor during image acquisition. As illustrated in Figure 10, when the camera has a focal length of 23 mm, the relationship between the shooting distance and the real-world size represented by a single pixel is clearly depicted.

The straight-line distance between the camera and the crack can be accurately obtained through laser ranging technology. This technology is based on the time difference between the emission and reflection of laser pulses, combined with the physical principle that the speed of light is constant. It can quickly and accurately calculate the spatial interval between the plane of the camera lens and the surface of the crack, providing key distance parameters for the subsequent quantitative analysis of crack size based on images.

Table 6. Crack width, crack identification and prediction of crack width.

Real Crack Image	Predicted Crack	Type	Crack Length (Pixel)	Average Width (Pixel)	Maximum Width (Pixel)
		Real crack Predicted crack	277 280	13 12	38 32
		Real crack Predicted crack	271 270	14 15	38 42
		Real crack Predicted crack	270 269	8 9	37 36
		Real crack Predicted crack	257 279	12 16	41 47

shows the calculation results of crack width, covering the original crack and the predicted crack width. For each image sample, in the study, the original crack was measured and the length, average width, and maximum width of the crack identified through prediction (all in pixels) were measured. The first column shows the original crack image, the second column displays the predicted crack area (where “BG” represents the background and “Crack” marks the predicted crack area), and the fourth to sixth columns detail the quantitative measurement results of various cracks.

The conversion between pixel and physical dimensions is realized based on actual distance parameters obtained via laser ranging. To offset the impacts of image distortion and camera system errors, Zhang’s Camera Calibration Method [36] is introduced to accurately solve the camera’s intrinsic parameters (focal length, principal point coordinates, distortion coefficients) and extrinsic parameters. This method captures images of a chessboard calibration board with multiple poses, constructs a model based on perspective projection constraints, and iteratively optimizes parameters, effectively correcting radial/tangential distortion.

The specific calibration process is as follows: a standard chessboard calibration board (5 mm × 5 mm grid size) is adopted to capture 20 sets of multi-pose calibration images at the tunnel site; after corner detection and subpixel-level extraction (with elimination of abnormal corners caused by noise interference) via the calibration module in the OpenCV open-source library, the camera’s intrinsic/extrinsic matrices and distortion coefficients (k1, k2, p1, p2) are solved; finally, the calibration accuracy is verified by reprojection error, with the average reprojection error after calibration controlled within 0.5 pixels in this study, meeting the accuracy requirements for pixel-physical dimension conversion in tunnel crack detection. After calibration and correction, geometric distortion caused by image aberration is effectively corrected, the impact of camera system errors on dimension conversion is significantly reduced, and high-precision mapping from pixel coordinates to physical dimensions (mm) is achieved by combining object distance parameters obtained via laser ranging.

4. Crack Warning Grading

The construction period of tunnels is long and the investment is large. The service life of the tunnels directly affects the long-term benefits of the infrastructure. Cracks are common diseases in tunnel structures. If not promptly warned and controlled, they will accelerate the erosion of the structure by environmental factors. Grading warning provides tunnel maintenance personnel with the health status of the tunnel at different risk stages, ensuring that they can take targeted intervention measures in time, effectively preventing the expansion of cracks and the deterioration of diseases, delaying the aging speed of the tunnel structure, and ensuring that the tunnel continues to perform core functions such as transportation and water conservancy within the designed service period, and guaranteeing the long-term stable performance of the tunnel.

In the field of tunnel engineering, the cracking and displacement of tunnel linings are important indicators for evaluating the structural safety of the tunnels. According to the Technical Specifications for Prevention of Cracks in Railway Tunnel Linings TB/T 2820.2-1997), the evaluation criteria for crack and displacement of the lining are shown in

Table 7. Crack grade classification in Chinese railway specification.

Grade Classification	A (Critical)	B (Serious)	C (Medium)	D (Slight)
TB/T 2820.2-1997 [37]	10 m ≥ L > 5 m B > 5 mm	L < 5 m 5 mm > b > 3 mm	L < 5 m B < 5 mm	Generally cracked

.

Where Grade C (medium) cracks are defined as those with a length of less than 5 m and a width of less than 3 mm. Such cracks indicate a relatively minor level of structural damage and have negligible effects on the overall integrity of the tunnel structure. As stipulated in the relevant standards, Grade C defects require enhanced monitoring but do not necessitate structural reinforcement.

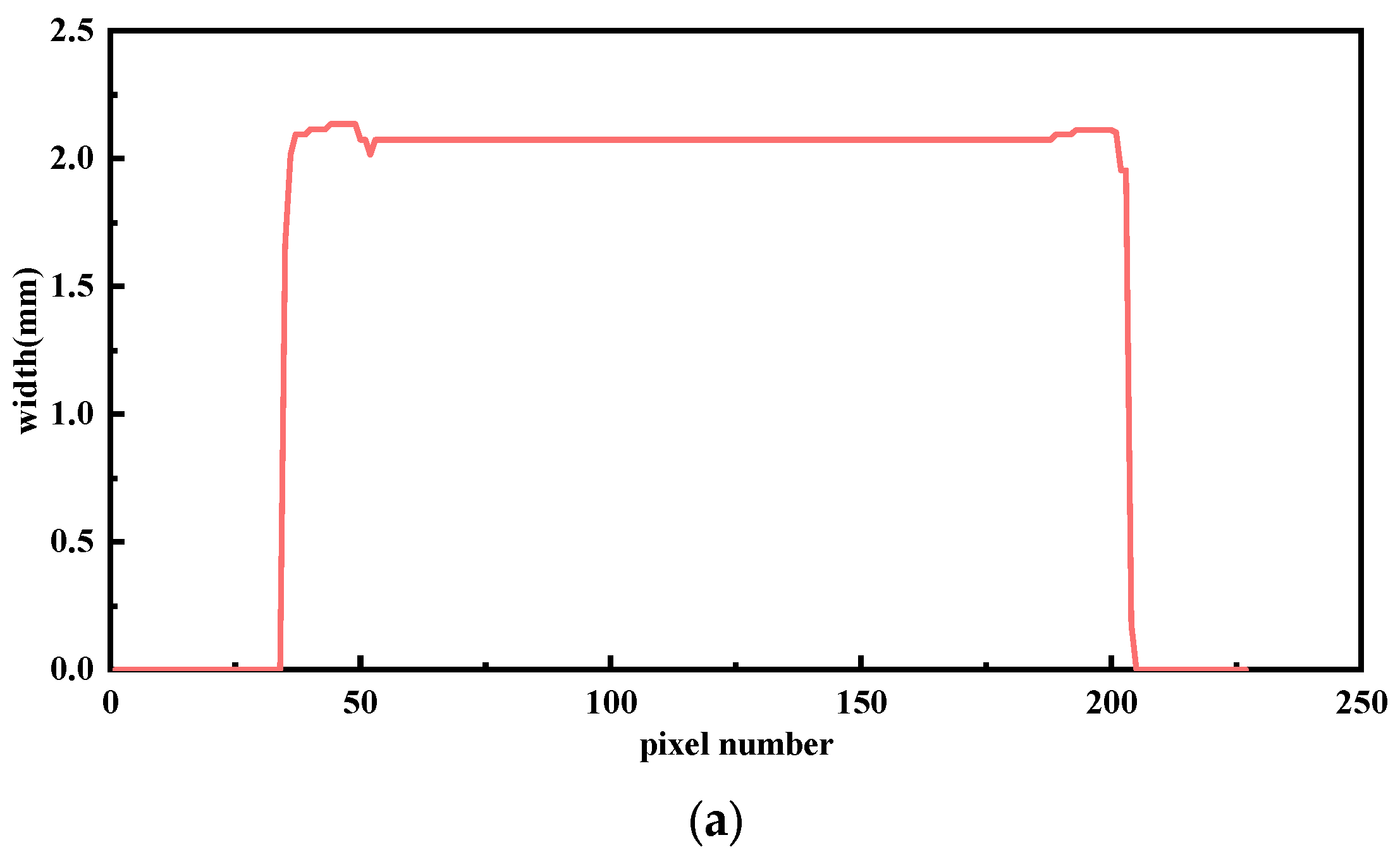
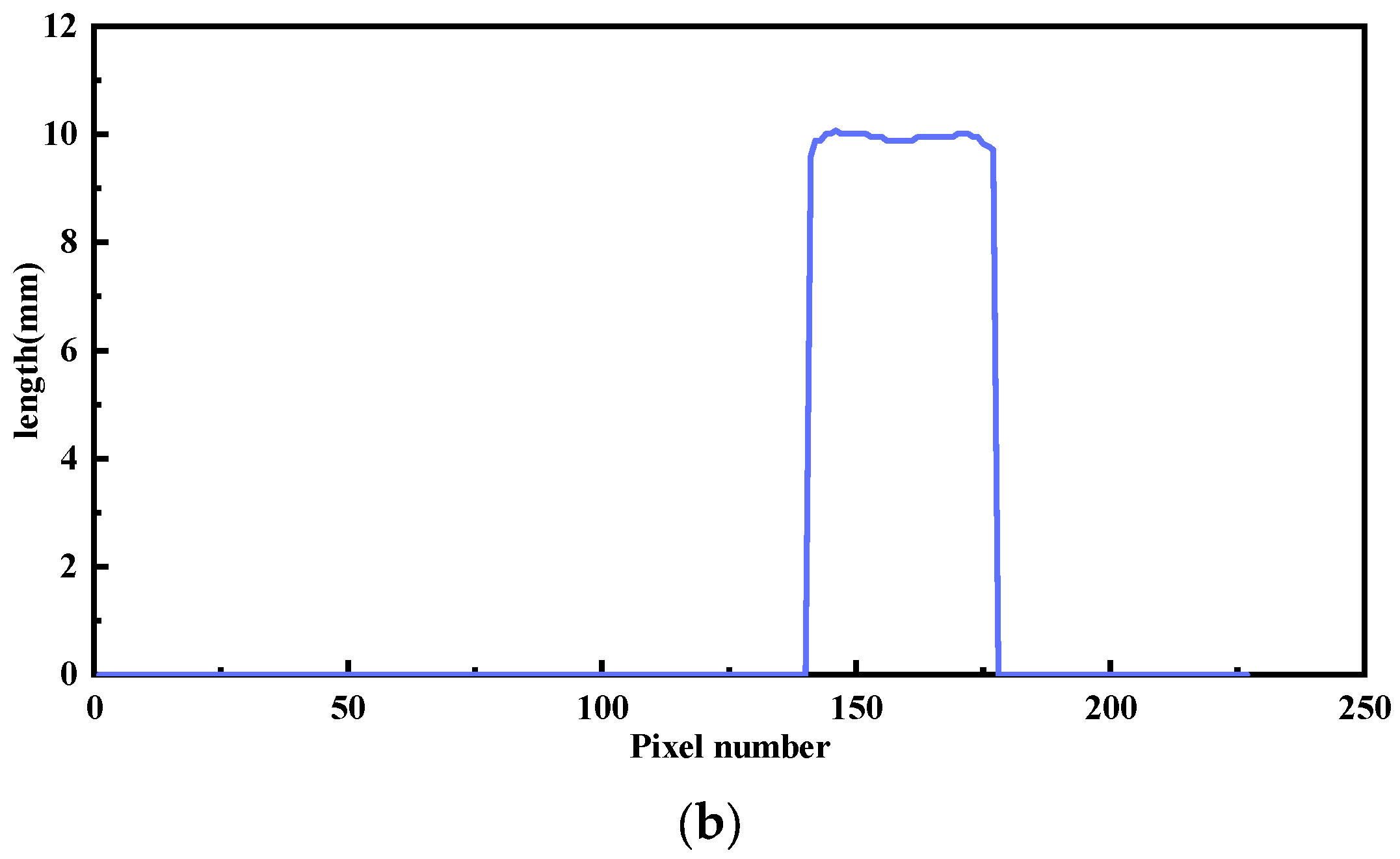
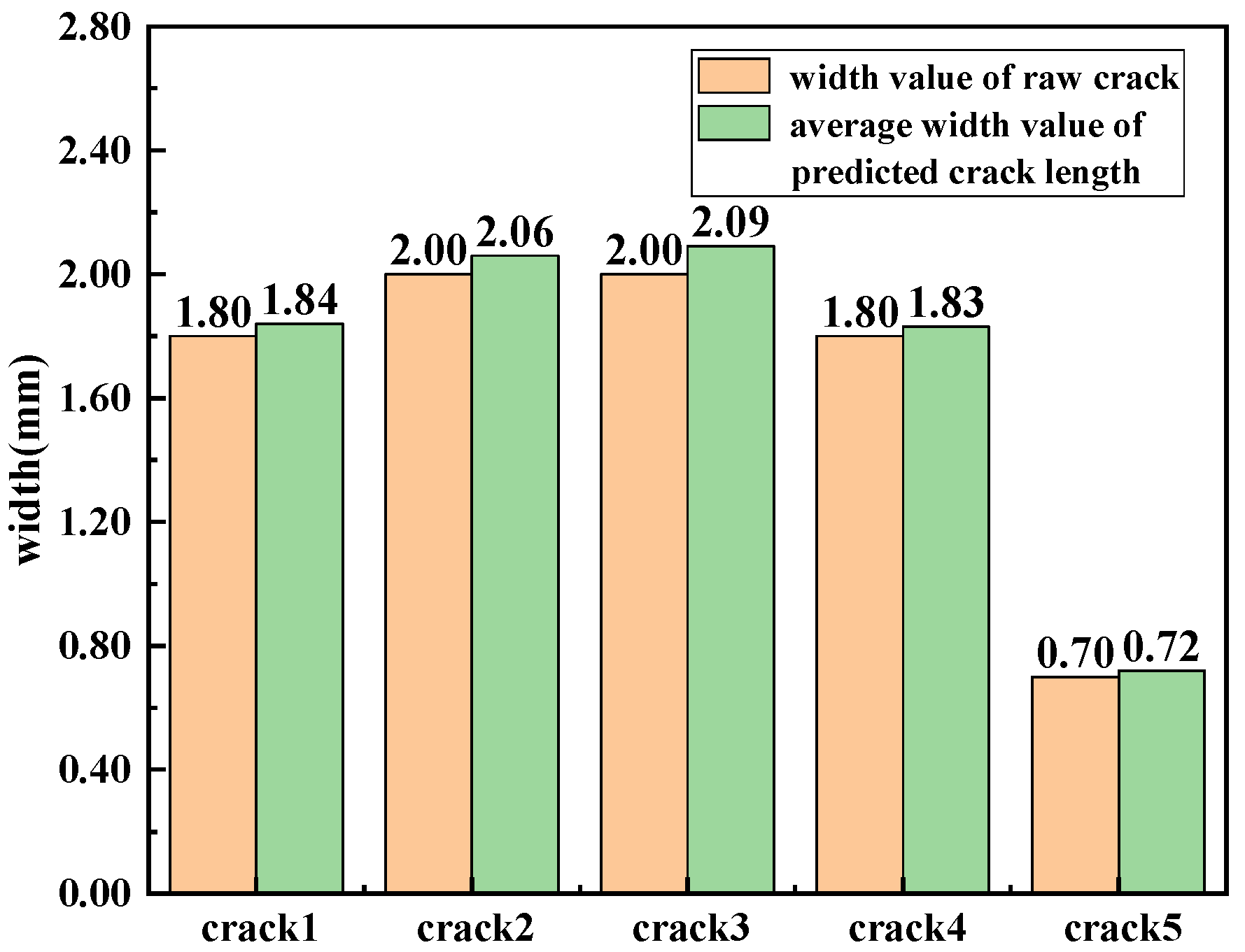
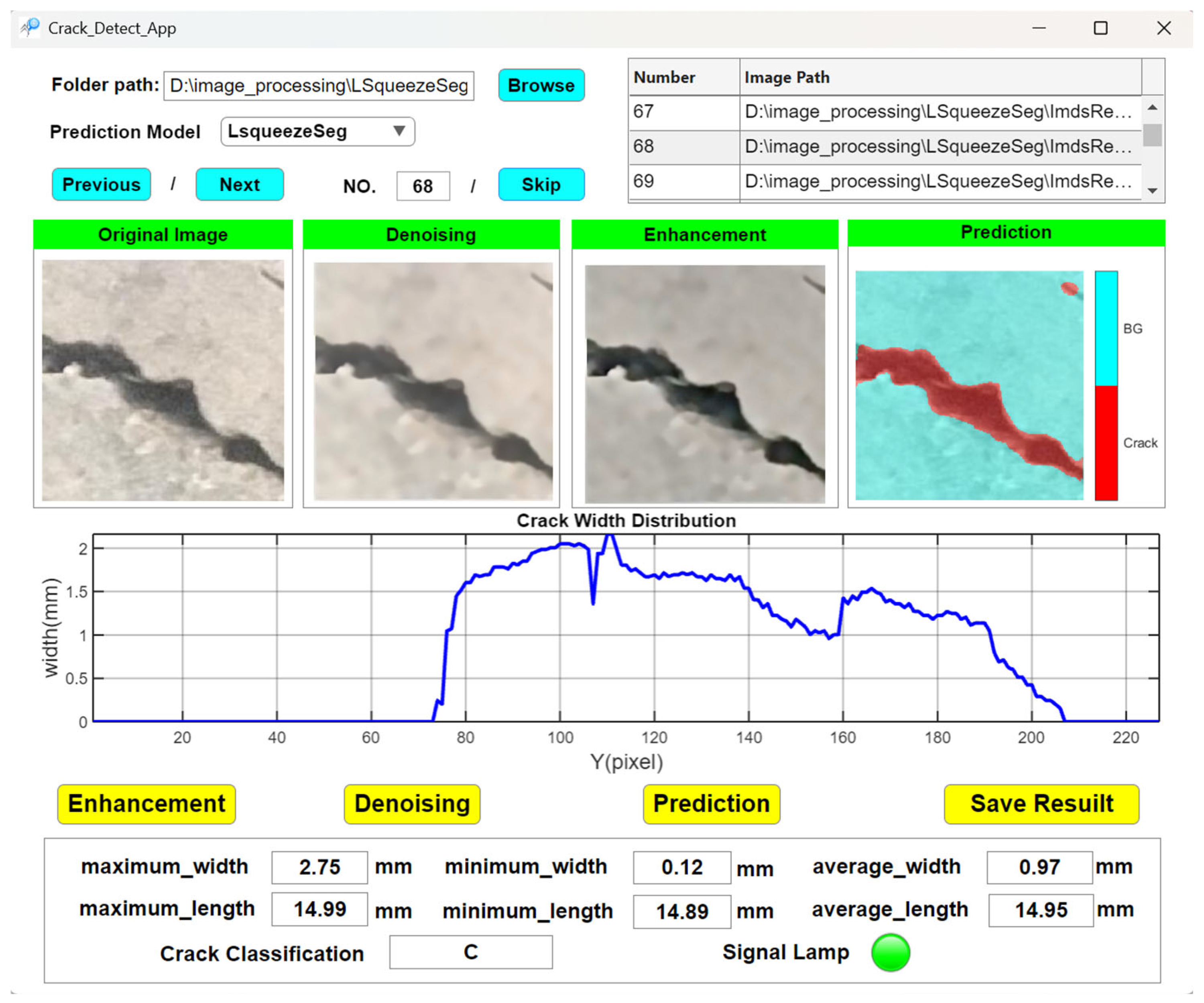
Based on the quantitative identification and analysis of cracks, this study has developed a specialized software system capable of automatically detecting and measuring crack dimensions. The software interface is shown in Figure 11. In tunnel lining inspection, the system can accurately determine key geometric parameters such as crack length and width. According to the crack classification criteria specified in the TB/T 2820.21997 standard, cracks with a width of less than 3 mm are classified as Grade C defects. This result aligns with the defect classification system stipulated in relevant tunnel engineering standards, where Grade C defects have the least adverse impact on the tunnel structure and typically do not require structural reinforcement. Instead, dynamic control can be effectively maintained through enhanced monitoring. This indicates that the software system developed in this study can accurately identify and classify the severity of tunnel lining crack deterioration in accordance with current engineering standards, providing reliable technical support for the efficient and accurate assessment of tunnel lining structural conditions. Therefore, the system holds significant practical value for engineering applications.

The system’s identification and quantification modules work in synergy to support a comprehensive workflow encompassing automatic crack detection, geometric parameter measurement (e.g., maximum, minimum, and average width), and condition grading. Measurement results can be exported in the form of Excel files or image reports, facilitating subsequent condition assessment and informed maintenance decisions in practical engineering applications.

The software integrates identification and quantitative analysis modules, enabling a seamless workflow from automatic crack detection to quantitative measurement of crack parameters and subsequent condition assessment. It serves as an efficient tool for the rapid detection and scientific evaluation of tunnel lining cracks.

5. Discussion

This study focuses on the accurate mapping between pixel and physical dimensions for tunnel crack detection tasks and the optimization of lightweight segmentation models, verifying the effectiveness of the LiteSqueezeSeg model in crack recognition tasks as well as the reliability of the dimension conversion method combining camera calibration with laser ranging. However, there remain research directions that can be further expanded and deepened:

First, future research will expand the sample dataset for in-tunnel scenarios to address the issues of single-scene distribution and uneven sample distribution in the current dataset, thereby enhancing the model’s adaptability to complex in-tunnel environments.

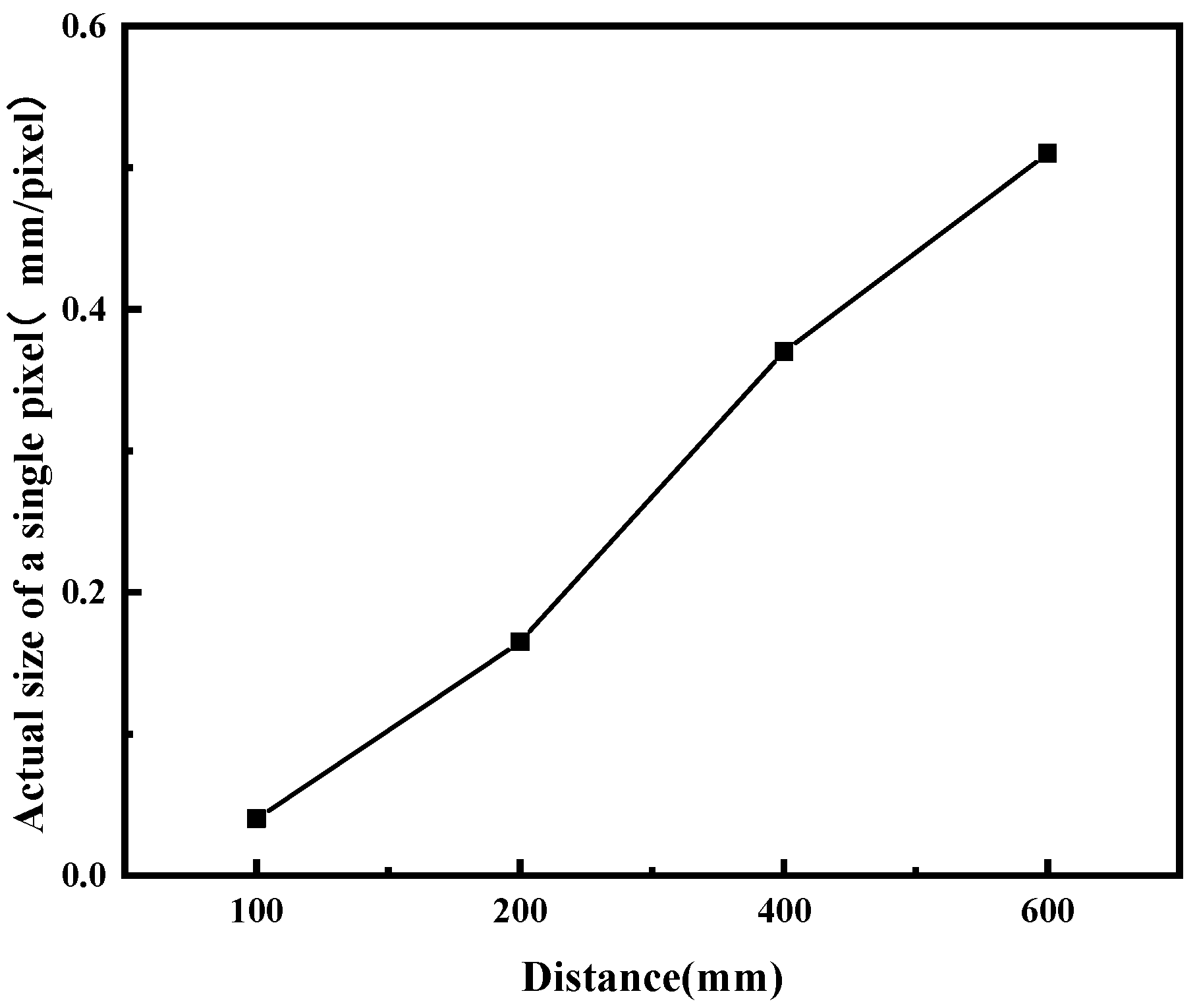
Second, subsequent work will supplement refined annotations of Ground Sampling Distance (GSD) parameters, and integrate engineering parameters such as tunnel cross-sectional dimensions and shooting distance to further improve the quantitative system for pixel-physical dimension conversion.

Furthermore, future research will integrate public tunnel crack datasets with the self-constructed dataset developed in this study to conduct cross-dataset cross-validation. This approach aims to verify the model’s performance stability under different acquisition devices and tunnel environmental operating conditions, as well as to further evaluate its domain generalization capability.

6. Conclusions

This study conducted a systematic investigation into the automatic identification, precise quantification, and disaster-level early warning of internal surface cracks in tunnels. By enhancing a lightweight semantic segmentation network, establishing a comprehensive technical framework, and integrating engineering standards, the research effectively addressed key limitations of existing deep learning models used in traditional detection methods—namely low efficiency, high subjectivity, deployment challenges, and insufficient accuracy. The primary achievements and conclusions are as follows:

(1)

In terms of dataset construction and network optimization, this study combined public datasets and on-site collected images of the tunnel interior, using data augmentation methods such as rotation, flipping, and cropping to construct a custom dataset containing 10,000 high-quality crack images. The precise pixel-level annotation was achieved through the professional annotation tool Image Labeler. Building upon this foundation, a lightweight semantic segmentation model named LiteSqueezeSeg is developed via innovative modifications to the open-source SqueezeSeg network. Experimental findings demonstrate that the proposed model not only maintains high-efficiency inference performance but also attains detection accuracy on par with state-of-the-art deep learning models. Specifically, it achieves an overall accuracy of 95.15%, along with an IoU of 83.02% and an F1-score of 74.52%, thereby realizing an effective trade-off between model performance and computational resource consumption.

(2)

Regarding the measurement of tunnel crack sizes, this study proposed a quantification method based on multi-dimensional information fusion. Through preprocessing algorithms (noise reduction, enhancement) to improve image quality and combining laser ranging technology to achieve precise calibration of “pixel-actual size”. This method successfully overcomes technical challenges brought by the complex tunnel environment (such as reflection, uneven lighting), and experimental verification shows that the relative errors of crack length, average width, and maximum width are all controlled within 5%. Based on this, the system can analyze the horizontal/vertical spatial distribution characteristics of cracks, providing reliable geometric parameter support for tunnel structure health assessment.

(3)

In terms of intelligent application, an integrated and innovative intelligent detection system has been developed. Built on MATLAB’s APP Designer Platform, this system integrates functional modules including digital image processing (preprocessing, edge detection), crack feature extraction, and specification matching. With reference to current specifications, the system can automatically classify disease grades based on crack length (L) and width (b). Actual tests show that the system’s accuracy rate for classifying C-level diseases with a width of less than 3 mm reaches 100%, achieving a transition from traditional experience-based judgment to standardized and automated classification, providing intelligent support tools for tunnel engineering safety management.

This study established a comprehensive technical framework for tunnel crack detection through the synergistic design of a lightweight network to enhance computational efficiency, precise quantification to ensure measurement accuracy, and standardized classification to guide practical applications. The system demonstrates significant engineering value in the domain of infrastructure health monitoring. Future research may focus on integrating attention mechanisms, expanding datasets to encompass more complex scenarios, and optimizing inference speed for edge deployment, thereby further improving the model’s capability in detecting fine cracks and achieving real-time performance.