Generating Bit-Rock Interaction Forces for Drilling Vibration Simulation: An Artificial Neural Network-Based Approach
Abstract
1. Introduction
2. Literature Review
2.1. Modelling Bit-Rock Boundary Conditions and Excitation Forces for Dynamic Simulations
2.2. Rock Properties Simulation Models
2.3. Machine Learning in the Drilling Industry
3. Methodology
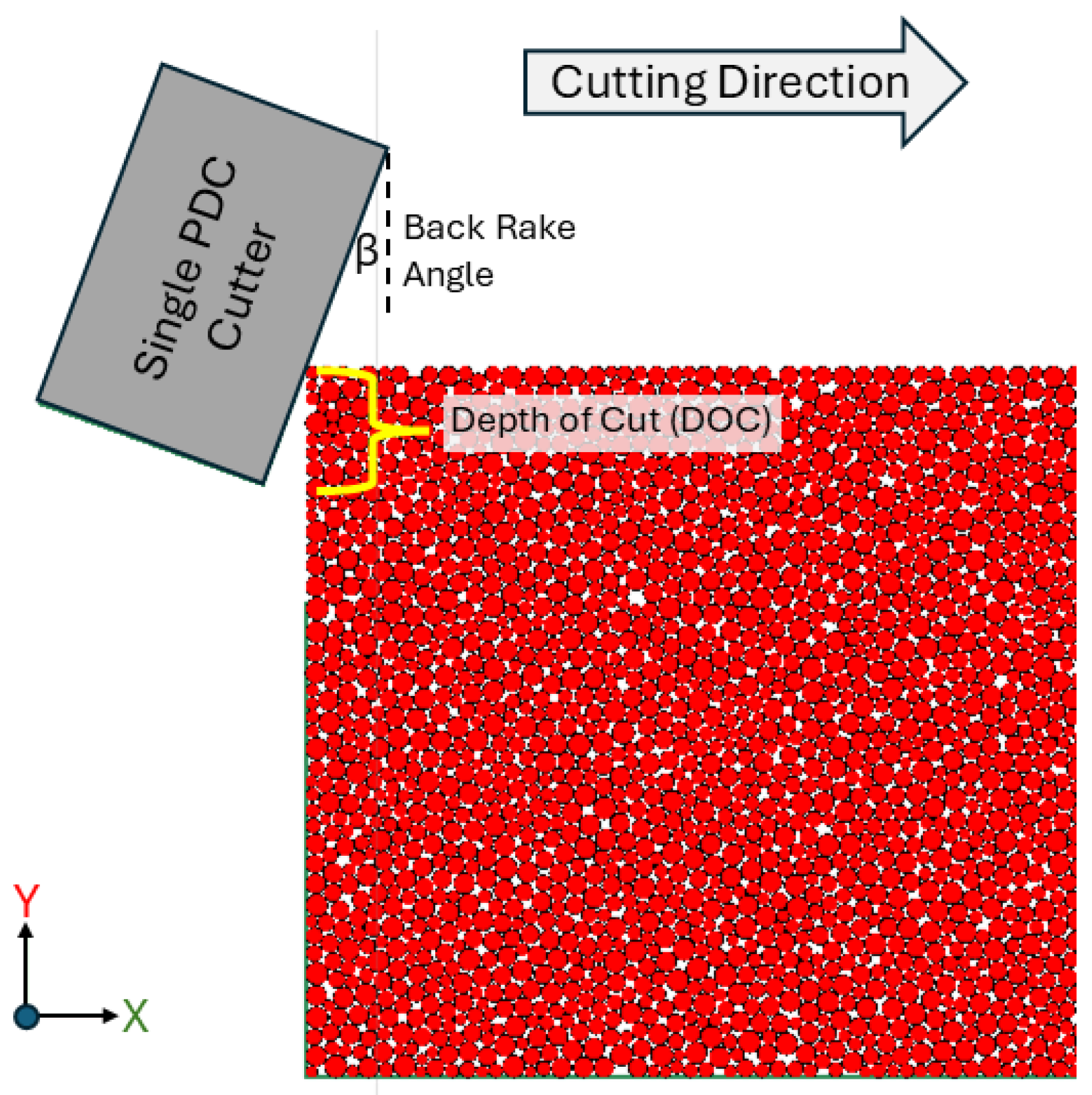
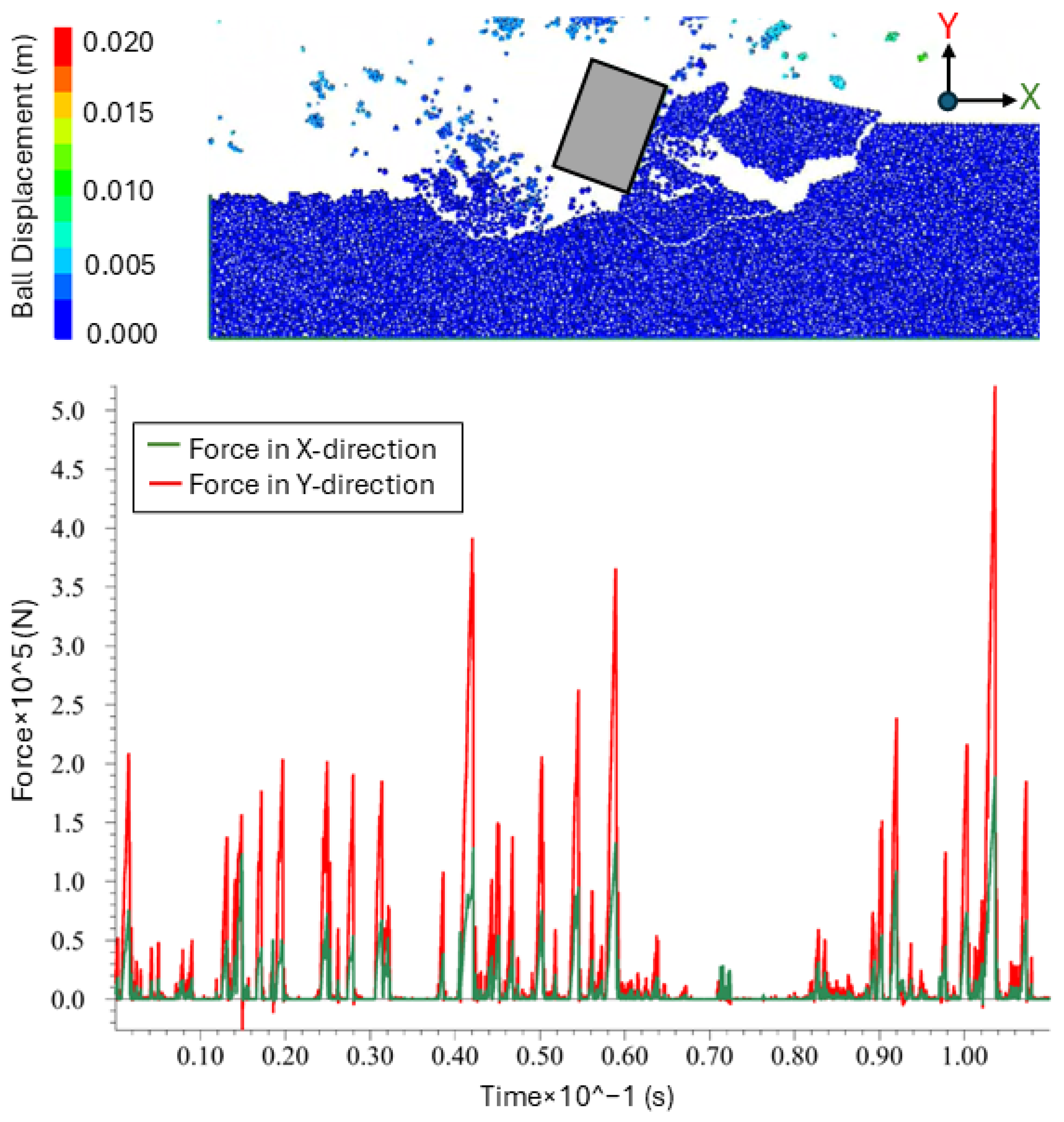
3.1. Development of DEM Model for Rock Fracture Force Variation
- movement of fractured particles out of the modelling plane
- prefracturing of the rock by in-front/nearby cutters
- interactions due to the regrinding of cuttings
3.2. Developing an ANN Model for Rock Fracture Force Calculation
- Amplitude of the highest peak (Maximum amplitude)
- Average amplitude of all peaks
- Number of peaks in the first quadrant (75% to 100%)
- Number of peaks in the second and third quadrant (25% to 75%)
- Number of peaks in the fourth quadrant (0 to 25%)
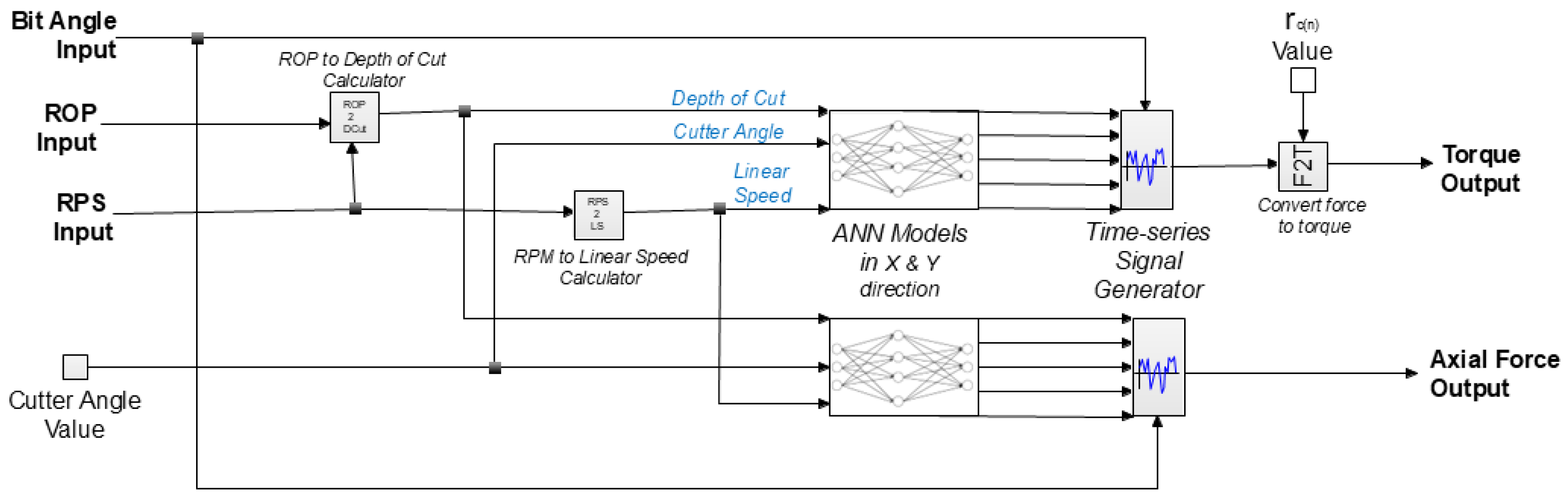
3.3. Generating the Rock Fracture Force Time Series Signal from ANN Results
| for i = 1 to () |
| end |
| for j = 1 to |
| A[j] = (0.75∗) + (0.25∗∗) |
| end |
| for k = 1 to |
| A[ + k] = (0.25∗) + (0.50∗∗) |
| end |
| for l = 1 to |
| A[ + + l] = (0.25∗∗) |
| end |
- x = the independent variable
- = the x value at which the STEP5 function begins
- = the value of the STEP5 function desired at
- = the x value at which the STEP5 function ends
- = the value of the STEP5 function desired at
3.4. Developing a Drill String MBD Simulation Model with Bit-Rock Interaction
3.5. Bit-Rock Interaction Submodel
- Inertia components of the bit
- Axial hydraulic force due to drilling mud jets at the bit
- Bit rotation angle calculation
- Frictional force due to bit-rock contact
- Rock fracture ANN model
- Axial vibrations generated due to rock fracture
- Torsional vibrations generated due to rock fracture
- Stiffness and damping of the rock substrate
- Drilling progression and bit advancement
3.6. Implementing the Bit-Rock Model in a 3D Deviated Well Drill String MBD Model
4. Case Studies
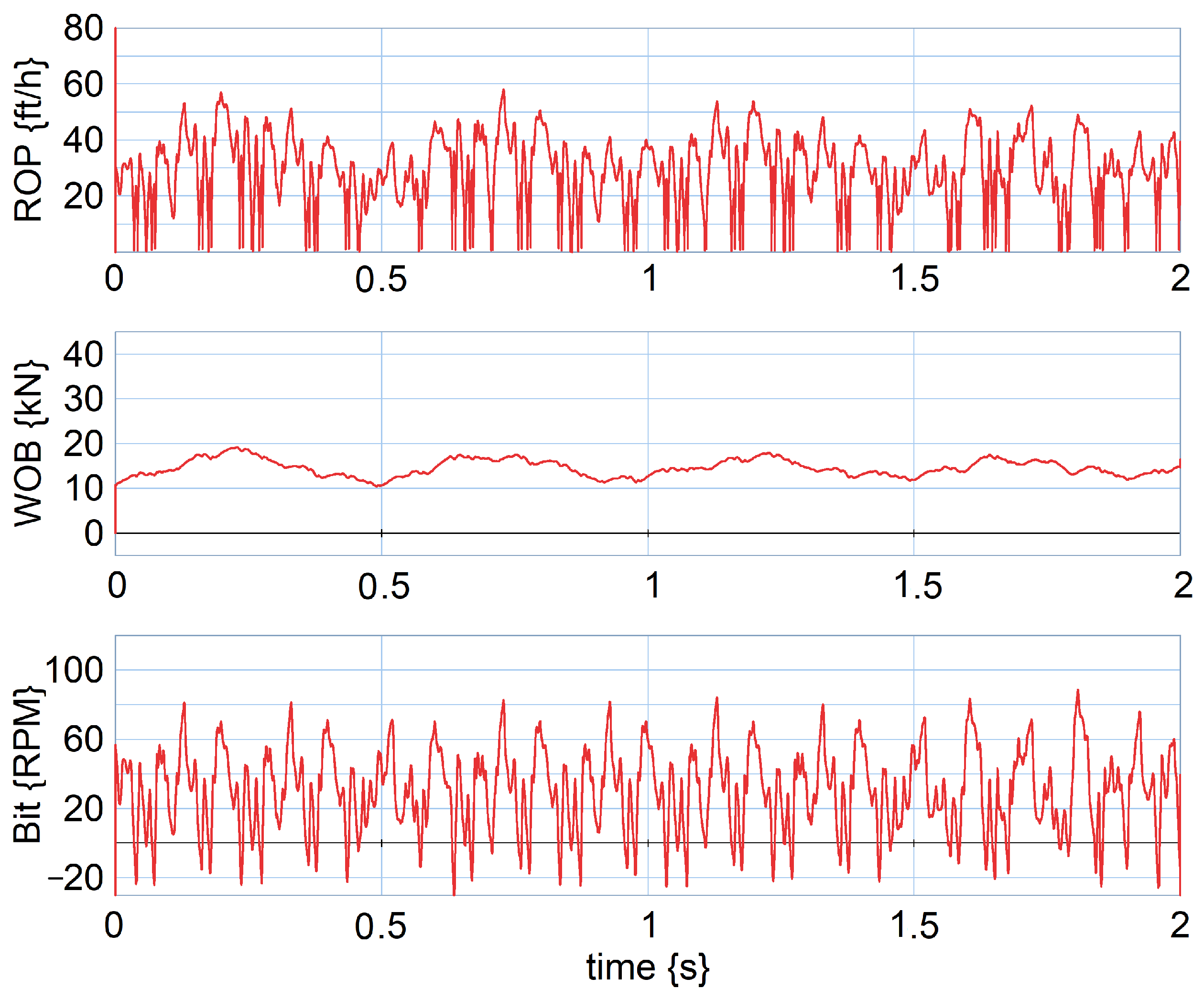
4.1. 2D Drill String Model Under Severe Vibrations
4.2. 3D Deviated Well Drill String MBD Simulation with Bit-Rock Interaction Model
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANFIS | adaptive neuro-fuzzy inference system |
| AI | artifical inteligence |
| ANN | artificial neutral networks |
| BEM | boundary element method |
| BPM | bonded-particle model |
| DEM | discrete element method |
| DFN | discrete fracture networks |
| DOC | depth of cut |
| DT | decision trees |
| FDM | finite difference method |
| FEA | finite element analysis |
| FEM | finite element method |
| FN | functional network |
| HMM | hidden Markov models |
| KNN | K-nearest neighbour |
| PDC | Polycrystalline Diamond Compact |
| PFC | Particle Flow Code |
| LSTM | Long Short-Term Memory |
| ML | machine learning |
| MBD | multibody dynamics |
| NPT | non-productive time |
| RBF | radial basis function |
| ReLU | Rectified Linear Unit |
| ROP | rate of penetration |
| RPM | revolutions per minute |
| RNN | Recurrent neural networks |
| SVM | support vector machines |
| SRM | synthetic rock material |
| UCS | unconfined compressive strength |
| WOB | weight on bit |
References
- Li, M.; Liu, J.; Xia, Y. Risk prediction of gas hydrate formation in the wellbore and subsea gathering system of deep-water turbidite reservoirs: Case analysis from the south China Sea. Reserv. Sci. 2025, 1, 52–72. [Google Scholar] [CrossRef]
- Vanja. How Much Does a Drilling Rig Cost?—SOSS USA. Available online: https://sossusa.com/2024/09/16/how-much-does-a-drilling-rig-cost (accessed on 15 December 2025).
- Li, Q.; Liu, J.; Wang, S.; Guo, Y.; Han, X.; Li, Q.; Cheng, Y.; Dong, Z.; Li, X.; Zhang, X. Numerical insights into factors affecting collapse behavior of horizontal wellbore in clayey silt hydrate-bearing sediments and the accompanying control strategy. Ocean. Eng. 2024, 297, 117029. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Han, Y. A numerical investigation on kick control with the displacement kill method during a well test in a deep-water gas reservoir: A case study. Processes 2024, 12, 2090. [Google Scholar] [CrossRef]
- Jaime, M.C. Numerical Modeling of Rock Cutting and Its Associated Fragmentation Process Using the Finite Element Method. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2011. [Google Scholar]
- Cai, M.; Mao, D.; Li, X.; Peng, H.; Tan, L.; Gui, Y.; Yin, X. Downhole vibration characteristics of 3D curved well under drillstring–bit–rock interaction. Int. J. -Non-Linear Mech. 2023, 154, 104430. [Google Scholar] [CrossRef]
- Richard, T.; Germay, C.; Detournay, E. A simplified model to explore the root cause of stick–slip vibrations in drilling systems with drag bits. J. Sound Vib. 2007, 305, 432–456. [Google Scholar] [CrossRef]
- Aarsnes, U.J.F.; Shor, R.J. Torsional vibrations with bit off bottom: Modeling, characterization and field data validation. J. Pet. Sci. Eng. 2018, 163, 712–721. [Google Scholar] [CrossRef]
- Saldivar, B.; Mondié, S.; Niculescu, S.I.; Mounier, H.; Boussaada, I. A control oriented guided tour in oilwell drilling vibration modeling. Annu. Rev. Control 2016, 42, 100–113. [Google Scholar] [CrossRef]
- Wei, J.; Liu, W.; Gao, D. Modeling of PDC bit-rock interaction behaviors based on the analysis of dynamic rock-cutting process. Geoenergy Sci. Eng. 2024, 239, 212955. [Google Scholar] [CrossRef]
- Mao, L.; He, J.; Zhu, J.; Jia, H.; Gan, L. Dynamic characteristic response of PDC bit vibration coupled with drill string dynamics. Geoenergy Sci. Eng. 2024, 233, 212524. [Google Scholar] [CrossRef]
- Kreisle, L.F.; Vance, J.M. Mathematical analysis of the effect of a shock sub on the longitudinal vibrations of an oilwell drill string. Soc. Pet. Eng. J. 1970, 10, 349–356. [Google Scholar] [CrossRef]
- Macpherson, J.; Jogi, P.; Kingman, J. Application and analysis of simultaneous near bit and surface dynamics measurements. SPE Drill. Complet. 2001, 16, 230–238. [Google Scholar] [CrossRef]
- Dareing, D.; Livesay, B.J. Longitudinal and angular drill-string vibrations with damping. J. Eng. Ind. 1968, 90, 671–679. [Google Scholar] [CrossRef]
- Christoforou, A.; Yigit, A. Dynamic modelling of rotating drillstrings with borehole interactions. J. Sound Vib. 1997, 206, 243–260. [Google Scholar] [CrossRef]
- Sarker, M.; Rideout, D.G.; Butt, S.D. Dynamic model for 3D motions of a horizontal oilwell BHA with wellbore stick-slip whirl interaction. J. Pet. Sci. Eng. 2017, 157, 482–506. [Google Scholar] [CrossRef]
- Jansen, J.D.; Van Den Steen, L. Active damping of self-excited torsional vibrations in oil well drillstrings. J. Sound Vib. 1995, 179, 647–668. [Google Scholar] [CrossRef]
- Kanzari, M. Effects of Drill Mud and Drive Torque Sinusoidal Excitation on Drillstrings Lateral and Torsional StickSlip Vibrations. In Proceedings of the Qatar Foundation Annual Research Conference Proceedings, Doha, Qatar, 19–20 March 2018; HBKU Press: Doha, Qatar, 2018; Volume 2018, p. EEPD868. [Google Scholar]
- Qiu, H.; Yang, J.; Butt, S. Stick-Slip Analysis of a Drill String Subjected to Deterministic Excitation and Stochastic Excitation. Shock Vib. 2016, 2016, 9168747. [Google Scholar] [CrossRef]
- Skaugen, E. The effects of quasi-random drill bit vibrations upon drillstring dynamic behavior. In Proceedings of the SPE Annual Technical Conference and Exhibition? Dallas, TX, USA, 27–30 September 1987; SPE: Richardson, TX, USA, 1987. [Google Scholar]
- Spanos, P.; Chevallier, A.; Politis, N. Nonlinear stochastic drill-string vibrations. J. Vib. Acoust. 2002, 124, 512–518. [Google Scholar] [CrossRef]
- Ritto, T. Numerical Analysis of the Nonlinear Dynamics of a Drill-String with Uncertainty Modeling. Ph.D. Thesis, Université Paris-Est, Paris, France, Pontifícia Universidade Católica, Rio de Janeiro, Brésil, 2010. [Google Scholar]
- Bogdanoff, J.; Goldberg, J. A new analytical approach to drill pipe breakage II. J. Eng. Ind. 1961, 83, 101–106. [Google Scholar] [CrossRef]
- Qiu, H.; Yang, J.; Butt, S.; Zhong, J. Investigation on random vibration of a drillstring. J. Sound Vib. 2017, 406, 74–88. [Google Scholar] [CrossRef]
- He, J.; Li, Y.; Jin, Y.; Wang, A.; Zhang, Y.; Jia, J.; Song, H.; Liang, D. Study on mechanical problems of complex rock mass by composite material micromechanics methods: A literature review. Front. Earth Sci. 2022, 9, 808161. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Starfield, A.M.; Cundall, P. Towards a methodology for rock mechanics modelling. In Proceedings of the International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1988; Volume 25, pp. 99–106. [Google Scholar]
- Agharazi, A. Development of a 3D Equivalent Continuum Model for Deformation Analysis of Systematically Jointed Rock Masses; University of Alberta: Edmonton, AB, Canada, 2013. [Google Scholar]
- Lisjak, A.; Grasselli, G. A review of discrete modeling techniques for fracturing processes in discontinuous rock masses. J. Rock Mech. Geotech. Eng. 2014, 6, 301–314. [Google Scholar] [CrossRef]
- Tezuka, A. Finite element and finite difference methods. In Springer Handbook of Metrology and Testing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1033–1060. [Google Scholar]
- Fang, Z. A Local Degradation Approach to the Numerical Analysis of Brittle Fractures in Heterogeneous Rocks. Ph.D. Thesis, Imperial College London (University of London), London, UK, 2001. [Google Scholar]
- Jing, L.; Hudson, J. Numerical methods in rock mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Logan, D.L. A First Course in the Finite Element Method; Cengage Learning: Boston, MA, USA, 2011; Volume 4. [Google Scholar]
- Chiang, L.E.; Elias, D.A. A 3D FEM methodology for simulating the impact in rock-drilling hammers. Int. J. Rock Mech. Min. Sci. 2008, 45, 701–711. [Google Scholar] [CrossRef]
- Hammah, R.; Yacoub, T.; Corkum, B.; Curran, J. The practical modelling of discontinuous rock masses with finite element analysis. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 1–4 June 2008; ARMA: Arlington, VA, USA, 2012. [Google Scholar]
- Wang, J.K.; Lehnhoff, T. Bit penetration into rock—A finite element study. In Proceedings of the International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1976; Volume 13, pp. 11–16. [Google Scholar]
- Harewood, F.; McHugh, P. Comparison of the implicit and explicit finite element methods using crystal plasticity. Comput. Mater. Sci. 2007, 39, 481–494. [Google Scholar] [CrossRef]
- Goodman, R.E.; Taylor, R.L.; Brekke, T.L. A model for the mechanics of jointed rock. J. Soil Mech. Found. Div. 1968, 94, 637–659. [Google Scholar] [CrossRef]
- Beissel, S.; Johnson, G.; Popelar, C. An element-failure algorithm for dynamic crack propagation in general directions. Eng. Fract. Mech. 1998, 61, 407–425. [Google Scholar] [CrossRef]
- Rabczuk, T. Computational methods for fracture in brittle and quasi-brittle solids: State-of-the-art review and future perspectives. Int. Sch. Res. Not. 2013, 2013, 849231. [Google Scholar] [CrossRef]
- Jaime, M.C.; Zhou, Y.; Lin, J.S.; Gamwo, I.K. Finite element modeling of rock cutting and its fragmentation process. Int. J. Rock Mech. Min. Sci. 2015, 80, 137–146. [Google Scholar] [CrossRef]
- Paluszny, A.; Salimzadeh, S.; Zimmerman, R.W. Finite-element modeling of the growth and interaction of hydraulic fractures in poroelastic rock formations. In Hydraulic Fracture Modeling; Elsevier: Amsterdam, The Netherlands, 2018; pp. 1–19. [Google Scholar]
- Lu, Z.; Wan, L.; Zeng, Q.; Zhang, X.; Gao, K. Numerical simulation of fragment separation during rock cutting using a 3D dynamic finite element analysis code. Adv. Mater. Sci. Eng. 2017, 2017, 3024918. [Google Scholar] [CrossRef]
- Li, G.; Wang, K.; Tang, C.; Ye, J. Non-break modeling and numerical simulation for non-intact rock failure process. Int. J. Rock Mech. Min. Sci. 2024, 176, 105725. [Google Scholar] [CrossRef]
- Costabel, M. Principles of boundary element methods. Comput. Phys. Rep. 1987, 6, 243–274. [Google Scholar] [CrossRef]
- Blandford, G.E.; Ingraffea, A.R.; Liggett, J.A. Two-dimensional stress intensity factor computations using the boundary element method. Int. J. Numer. Methods Eng. 1981, 17, 387–404. [Google Scholar] [CrossRef]
- Chen, C.S.; Pan, E.; Amadei, B. Fracture mechanics analysis of cracked discs of anisotropic rock using the boundary element method. Int. J. Rock Mech. Min. Sci. 1998, 35, 195–218. [Google Scholar] [CrossRef]
- Zeller, S.S.; Pollard, D.D. Boundary conditions for rock fracture analysis using the boundary element method. J. Geophys. Res. Solid Earth 1992, 97, 1991–1997. [Google Scholar] [CrossRef]
- Mi, Y.; Aliabadi, M. Dual boundary element method for three-dimensional fracture mechanics analysis. Eng. Anal. Bound. Elem. 1992, 10, 161–171. [Google Scholar] [CrossRef]
- Cundall, P.A. A computer model for simulating progressive, large-scale movement in blocky rock system. In Proceedings of the International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971; Volume 8, pp. 129–136. [Google Scholar]
- Joodi, B. Application of 3D Discrete Element Method in Geomechanics, with A Focus on Rock Scratch Testing. Ph.D. Thesis, Curtin University, Bentley, Australia, 2018. [Google Scholar]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosystem Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Potyondy, D. A flat-jointed bonded-particle model for rock. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Seattle, DC, USA, 17–20 June 2018. [Google Scholar]
- Tsang, M.; Clark, I.; Karlovšek, J. Automating the Calibration of Flat-Jointed Bonded Particle Model Microproperties for the Rewan Sandstone Case Study. Rock Mech. Rock Eng. 2023, 56, 6459–6480. [Google Scholar] [CrossRef]
- Huang, H. Discrete Element Modeling of Tool-Rock Interaction; University of Minnesota: Minneapolis, MN, USA, 1999. [Google Scholar]
- Yaşıtlı, N.E.; Bayram, F.; Unver, B.; Özçelik, Y. Numerical modelling of circular sawing system using discrete element method. Int. J. Rock Mech. Min. Sci. 2012, 55, 86–96. [Google Scholar] [CrossRef]
- Zhang, H.; Ni, H.; Yang, H.; Fu, L.; Wang, Y.; Liu, S.; Huang, B.; Wang, Z.; Chen, G. Numerical simulation and field test research on vibration reduction of PDC cutting of pebbled sandstone under composite impact load. Processes 2023, 11, 671. [Google Scholar] [CrossRef]
- Zheng, Z.; Tang, H.; Zhang, Q.; Pan, P.; Zhang, X.; Mei, G.; Liu, Z.; Wang, W. True triaxial test and PFC3D-GBM simulation study on mechanical properties and fracture evolution mechanisms of rock under high stresses. Comput. Geotech. 2023, 154, 105136. [Google Scholar] [CrossRef]
- Li, P.; Jiang, S.; Tang, D.; Xu, B. A PFC3D-based numerical simulation of cutting load for lunar rock simulant and experimental validation. Adv. Space Res. 2017, 59, 2583–2599. [Google Scholar] [CrossRef]
- Pierce, M.; Fairhurst, C. Synthetic rock mass applications in mass mining. In Proceedings of the ISRM Congress, Beijing, China, 18–21 October 2011; 12th ISRM Congress: Lisboa, Portugal, 2011. [Google Scholar]
- Chen, Y.; Rao, J.; Zhao, C.; Xue, Y.; Liu, C.; Yin, Q. Strength prediction model of fractured dolomite and analysis of mechanical properties based on PFC3D. Sci. Rep. 2023, 13, 13368. [Google Scholar] [CrossRef]
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Morales, E.F.; Escalante, H.J. A brief introduction to supervised, unsupervised, and reinforcement learning. In Biosignal Processing and Classification Using Computational Learning and Intelligence; Elsevier: Amsterdam, The Netherlands, 2022; pp. 111–129. [Google Scholar]
- Nasteski, V. An overview of the supervised machine learning methods. Horizons. b 2017, 4, 56. [Google Scholar] [CrossRef]
- Patel, A.A. Hands-on Unsupervised Learning Using Python: How to Build Applied Machine Learning Solutions from Unlabeled Data; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Li, Y. Deep reinforcement learning: An overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Mohanraj, T.; Yerchuru, J.; Krishnan, H.; Aravind, R.N.; Yameni, R. Development of tool condition monitoring system in end milling process using wavelet features and Hoelder’s exponent with machine learning algorithms. Measurement 2021, 173, 108671. [Google Scholar] [CrossRef]
- Manasa, J.; Gupta, R.; Narahari, N. Machine learning based predicting house prices using regression techniques. In Proceedings of the 2020 2nd International conference on innovative mechanisms for industry applications (ICIMIA), Bangalore, India, 5–7 March 2020; IEEE: New York, NY, USA, 2020; pp. 624–630. [Google Scholar]
- Vidyullatha, P.; Rao, D.R. Machine learning techniques on multidimensional curve fitting data based on R-square and chi-square methods. Int. J. Electr. Comput. Eng. 2016, 6, 974. [Google Scholar]
- Barillaro, L. Artificial Neural Networks. In Encyclopedia of Bioinformatics and Computational Biology, 2nd ed.; Ranganathan, S., Cannataro, M., Khan, A.M., Eds.; Elsevier: Oxford, UK, 2025; pp. 141–145. [Google Scholar] [CrossRef]
- Szandała, T. Review and comparison of commonly used activation functions for deep neural networks. In Bio-Inspired Neurocomputing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 203–224. [Google Scholar]
- Alnuaimi, A.F.; Albaldawi, T.H. An overview of machine learning classification techniques. In Proceedings of the BIO Web of Conferences, Copenhagen, Denmark, 25–30 August 2024; EDP Sciences: Les Ulis Cedex A, France, 2024; Volume 97, p. 00133. [Google Scholar]
- Saadeldin, R.; Gamal, H.; Elkatatny, S.; Abdulraheem, A. Intelligent model for predicting downhole vibrations using surface drilling data during horizontal drilling. J. Energy Resour. Technol. 2022, 144, 083002. [Google Scholar] [CrossRef]
- Saadeldin, R.; Gamal, H.; Elkatatny, S. Detecting downhole vibrations through drilling horizontal sections: Machine learning study. Sci. Rep. 2023, 13, 6204. [Google Scholar] [CrossRef] [PubMed]
- Okoli, P.; Cruz Vega, J.; Shor, R. Estimating downhole vibration via machine learning techniques using only surface drilling parameters. In Proceedings of the SPE Western Regional Meeting, San Jose, CA, USA, 23–26 April 2019; SPE: Richardson, TX, USA. [Google Scholar]
- Don, M.G.; Rideout, G. A digital twinning methodology for vibration prediction and fatigue life prognosis of vertical oil well Drillstrings. IEEE Access 2023, 11, 62892–62905. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Lu, J.; Li, W.; Xue, Q.; Zhang, C.; Zhang, F. Automated classification of drill string vibrations using machine learning algorithms. Geoenergy Sci. Eng. 2024, 239, 212995. [Google Scholar] [CrossRef]
- Brenjkar, E.; Delijani, E.B. Computational prediction of the drilling rate of penetration (ROP): A comparison of various machine learning approaches and traditional models. J. Pet. Sci. Eng. 2022, 210, 110033. [Google Scholar] [CrossRef]
- Soares, C.; Gray, K. Real-time predictive capabilities of analytical and machine learning rate of penetration (ROP) models. J. Pet. Sci. Eng. 2019, 172, 934–959. [Google Scholar] [CrossRef]
- Alali, A.M.; Abughaban, M.F.; Aman, B.M.; Ravela, S. Hybrid data driven drilling and rate of penetration optimization. J. Pet. Sci. Eng. 2021, 200, 108075. [Google Scholar] [CrossRef]
- Al Dushaishi, M.F.; Abbas, A.K.; Al Saba, M.T.; Wise, J. Drilling Optimization Using Artificial Neural Networks and Empirical Models. ChemEngineering 2025, 9, 37. [Google Scholar] [CrossRef]
- Jing, L. A review of techniques, advances and outstanding issues in numerical mod-elling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Itasca. Rock cutting in PFC. Available online: https://www.itasca.ca/software/pfc (accessed on 12 May 2025).
- Itasca. Rock Cutting in PFC. Available online: https://www.itascainternational.com/software/rock-cutting-in-pfc (accessed on 15 October 2025).
- Potyondy, D. A flat-jointed bonded-particle material for hard rock. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 27 June 2012; ARMA: Arlington, VA, USA, 2012. [Google Scholar]
- Liu, Y.H.; Mehta, S. Hands-On Deep Learning Architectures with Python: Create Deep Neural Networks to Solve Computational Problems Using TensorFlow and Keras; Packt Publishing Ltd.: Birmingham, UK, 2019. [Google Scholar]
- Karnopp, D.C.; Margolis, D.L.; Rosenberg, R.C. System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Yigit, A.S.; Christoforou, A.P. Stick-slip and bit-bounce interaction in oil-well drillstrings. J. Energy Resour. Technol. 2006, 128, 268–274. [Google Scholar] [CrossRef]
- Liyanarachchi, S.; Rideout, G. Improved stiff string torque and drag prediction using a computationally ef-ficient contact algorithm. Math. Comput. Model. Dyn. Syst. 2024, 30, 417–443. [Google Scholar] [CrossRef]
- Rideout, D.; Arvani, F.; Butt, S.; Fallahi, E. Three-Dimensional Multi-Body Bond Graph Model for Vibration Control of Long Shafts-Application to Oilwell Drilling. Proc. Integr. Model. Anal. Appl. Control Autom. 2013, 25–27. [Google Scholar]










| Parameter | Value |
|---|---|
| Ball porosity | 0.1 |
| Ball minimal radius | 0.25 mm |
| Ball maximum radius | 0.5 mm |
| Ball density | 2500 kg/m3 |
| Damping ratio | 0.7 |
| Bond tensile strength | 50 MPa |
| Ball-to-ball Friction | 0.5 |
| Parameter | Value Range | Steps |
|---|---|---|
| Linear speed | 0.50 to 1.00 | 10 |
| Dept of cut | 0.004 to 0.009 | 6 |
| Angle | 12.5 to 20.0 | 4 |
| Parameter | Pipe | Collar |
|---|---|---|
| Number of elements | 100 | 20 |
| Length of an elements | 6 m | 7.5 m |
| Inner diameter (ID) | 85 mm | 65 mm |
| Outer diameter (OD) | 102 mm | 158 mm |
| Material | steel | steel |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Liyanarachchi, S.; Rideout, G. Generating Bit-Rock Interaction Forces for Drilling Vibration Simulation: An Artificial Neural Network-Based Approach. Modelling 2026, 7, 11. https://doi.org/10.3390/modelling7010011
Liyanarachchi S, Rideout G. Generating Bit-Rock Interaction Forces for Drilling Vibration Simulation: An Artificial Neural Network-Based Approach. Modelling. 2026; 7(1):11. https://doi.org/10.3390/modelling7010011
Chicago/Turabian StyleLiyanarachchi, Sampath, and Geoff Rideout. 2026. "Generating Bit-Rock Interaction Forces for Drilling Vibration Simulation: An Artificial Neural Network-Based Approach" Modelling 7, no. 1: 11. https://doi.org/10.3390/modelling7010011
APA StyleLiyanarachchi, S., & Rideout, G. (2026). Generating Bit-Rock Interaction Forces for Drilling Vibration Simulation: An Artificial Neural Network-Based Approach. Modelling, 7(1), 11. https://doi.org/10.3390/modelling7010011






