Growing Top-Down or Bottom-Up Vortices: Effect of Thermal Gradients
Abstract
1. Introduction
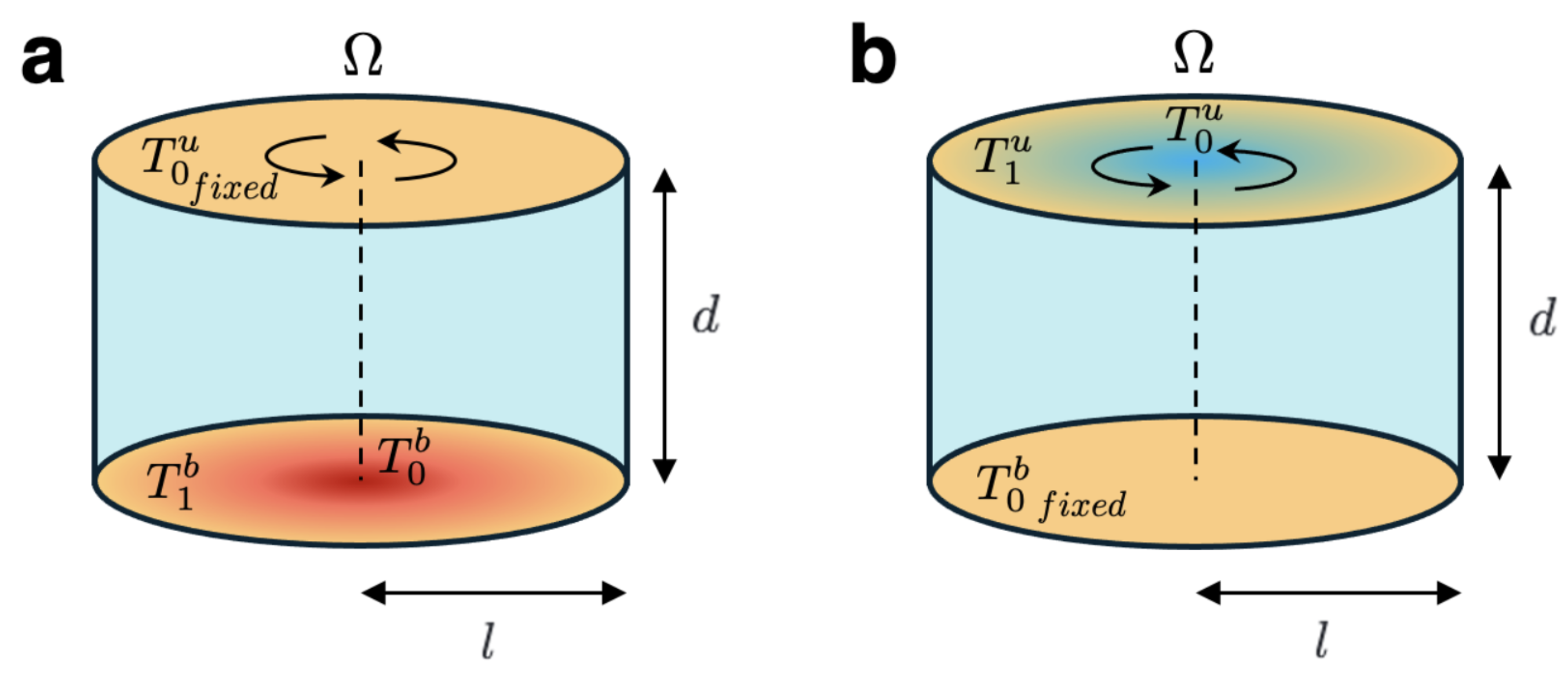
2. Formulation of the Problem
3. Numerical Implementation
- Temperature update: The temperature field is computed using Equation (10).
- Pressure prediction: Applying the divergence operator ∇ to Equation (12) and using Equation (11), a preliminary pressure field is obtained.
- Velocity prediction: A predictor velocity field is calculated from Equation (12) using the predicted pressure .
- Correction step: The final velocity and pressure are obtained by solving the system:
4. Numerical Results
4.1. Non-Destabilizing Axisymmetric Vortex
4.2. Tilted Vortex
4.3. Double Vortex
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lemon, L.R.; Doswell, C.A., III. Severe thunderstorms evolution and mesocylone structure as related to tornadogenesis. Mon. Weather Rev. 1979, 107, 1184–1197. [Google Scholar] [CrossRef]
- Bluestein, H.B. Severe Convective Storms and Tornadoes; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Brown, R.A.; Wood, V.T. The tornadic vortex signature: An update. Wea. Forecast. 2012, 27, 525–530. [Google Scholar] [CrossRef]
- Trapp, R.J.; Davies-Jones, R. Tornadogenesis with and without a dynamic pipe effect. J. Atmos. Sci. 1997, 54, 113–133. [Google Scholar] [CrossRef]
- Trapp, R.J.; Mitchell, E.D.; Tipton, G.A.; Effertz, D.W.; Watson, A.I.; Andra, D.L.; Magsig, M.A. Descending and nondescending tornadic vortex signatures detected by WSR-88Ds. Wea. Forecast. 1999, 14, 625–639. [Google Scholar] [CrossRef]
- Smith, R.K.; Leslie, L.M. A numerical study of tornadogenesis in a rotating thunderstorm. Q. J. R. Meteorol. Soc. 1979, 105, 107–127. [Google Scholar] [CrossRef]
- Wicker, L.J.; Wilhelmson, R.B. Simulation and analysis of tornado development and decay within a three-dimensional supercell thunderstorm. J. Atmos. Sci. 1995, 52, 2675–2703. [Google Scholar] [CrossRef]
- French, M.M.; Bluestein, H.B.; Popstefanija, I.; Baldi, C.A.; Bluth, R.T. Reexamining the vertical development of tornadic vortex signatures in supercells. Mon. Weather Rev. 2013, 141, 4576–4601. [Google Scholar] [CrossRef]
- Bluestein, H.B. A review of ground-based, mobile, W-band Doppler-radar observations of tornadoes and dust devils. Dyn. Atmos. Oceans 2005, 40, 163–188. [Google Scholar] [CrossRef]
- French, M.M.; Bluestein, H.B.; Dowell, D.C.; Wicker, L.J.; Kramar, M.R.; Pazmany, A.L. Mobile, phased-array, Doppler radar observations of tornadoes at X-band. Mon. Weather Rev. 2014, 142, 1010–1036. [Google Scholar] [CrossRef]
- Houser, J.L.; Bluestein, H.B.; Snyder, J.C. Rapid-scan, polarimetric, doppler radar observations of tornadogenesis and tornado dissipation in a tornadic supercell: The El Reno, Oklahoma storm of 24 May 2011. Mon. Weather Rev. 2015, 143, 2685–2710. [Google Scholar] [CrossRef]
- Horn, S.; Aurnou, J.M. Tornado-like Vortices in the Quasi-Cyclostrophic Regime of Coriolis-Centrifugal Convection. J. Turbul. 2021, 22, 197–324. [Google Scholar] [CrossRef]
- Ecke, R.E.; Niemela, J.J. Heat transport in the geostrophic regime of rotating Rayleigh-Bénard convection. Phys. Rev. Lett. 2014, 113, 114301. [Google Scholar] [CrossRef]
- Horn, S.; Shishkina, O. Rotating non-Oberbeck-Boussinesq Rayleigh-Bénard convection in water. Phys. Fluids 2014, 26, 055111. [Google Scholar] [CrossRef]
- Ecke, R.; Shishkina, O. Turbulent Rotating Rayleigh-Bénard Convection. Annu. Rev. Fluid Mech. 2023, 55, 603–638. [Google Scholar] [CrossRef]
- Marques, F.; Mercader, I.; Batiste, O.; Lopez, J. Centrifugal effects in rotating convection: Axisymmetric states and three-dimensional instabilities. J. Fluid Mech. 2007, 580, 303. [Google Scholar] [CrossRef][Green Version]
- Horn, S.; Aurnou, J.M. Regimes of Coriolis-Centrifugal Convection. Phys. Rev. Lett. 2018, 120, 204502. [Google Scholar] [CrossRef]
- Horn, S.; Aurnou, J.M. Rotating convection with centrifugal buoyancy: Numerical predictions for laboratory experiments. Phys. Rev. Fluids 2019, 4, 073501. [Google Scholar] [CrossRef]
- Wordsworth, R.D.; Read, P.L.; Yamazaki, Y.H. Turbulence, waves, and jets in a differentially heated rotating annulus experiment. Phys. Fluids 2008, 20, 126602. [Google Scholar] [CrossRef]
- Vincze, M.; Harlander, U.; von Larcher, T.; Egbers, C. An experimental study of regime transitions in a differentially heated baroclinic annulus with flat and sloping bottom topographies. Nonlinear Process. Geophys. 2014, 21, 237–250. [Google Scholar] [CrossRef]
- Navarro, M.C.; Castaño, D.; Herrero, H. Determining the morphology of tornado-like vortices depending on thermal gradients: A numerical study. Phys. Fluids 2023, 35, 063605. [Google Scholar] [CrossRef]
- Oberbeck, A. Über die Wärmeleitung der Flüssigkeiten bei der Berücksichtigung der Strömungen infolge von Temperaturdiffezen. Ann. Phys. Chem. 1879, 7, 271–292. [Google Scholar] [CrossRef]
- Boussinesq, A. Theorie Analytique de la Chaleur; Gauthier-Villars: Paris, France, 1903. [Google Scholar]
- Rotunno, R.; Bryan, G.H.; Nolan, D.; Dahl, N. Axisymmetric tornado simulations at high Reynolds number. J. Atmos. Sci. 2016, 73, 3843–3854. [Google Scholar] [CrossRef]
- Lewellen, W. Tornado Vortex Theory; Geophys Monograph Series; AGU: Washington, DC, USA, 1993; Volume 79, pp. 19–39. [Google Scholar]
- Castaño, D.; Navarro, M.C.; Herrero, H. Double vortices and single-eyed vortices in a rotating cylinder under thermal gradients. Comput. Math. Appl. 2017, 70, 2238–2257. [Google Scholar] [CrossRef]
- Boronska, K. Three-Dimensional Patterns in Cylindrical Rayleigh-Bénard Convection. Ph.D. Thesis, Paris Sud University, Orsay, France, 2005. [Google Scholar]
- Tuckerman, L. Divergence-free velocity fields in nonperiodic geometries. J. Comput. Phys. 1989, 80, 403–441. [Google Scholar] [CrossRef]
- Rudinger, S.; Knobloch, E. Mode interaction in rotating Rayleigh-Bénard convection. Fluid Dyn. Res. 2003, 33, 477–492. [Google Scholar] [CrossRef]
- Navarro, M.C.; Castaño, D.; Herrero, H. Thermoconvective instabilities to explain the main characteristics of a dust devil-like vortex. Physica D 2015, 308, 109–115. [Google Scholar] [CrossRef]
- Davies-Jones, R.P. Tornado dynamics. In Thunderstorm Morphology and Dynamics, 2nd ed.; Kessler, E., Ed.; University of Oklahoma Press: Norman, OK, USA, 1986; pp. 197–236. [Google Scholar]
- Kieu, C.Q. An investigation into the contraction of the hurricane radius of maximum wind. Meteorol. Atmos. Phys. 2012, 115, 47–56. [Google Scholar] [CrossRef]
- Davies, M. Tornadoes with cold core 500-mb lows. Weather Forecast. 2006, 21, 1051–1062. [Google Scholar] [CrossRef]
- Cooley, J.R. Cold air funnel clouds. Mon. Weather Rev. 1978, 21, 1368–1372. [Google Scholar] [CrossRef]
- Sinclair, P.C. The lower structure of a dust devil. J. Atmos. Sci. 1973, 30, 1599–1619. [Google Scholar] [CrossRef]
- Mattson, J.O.; Nihlén, T.; Yue, W. Observations of dust devils in a semi-arid district of southern Tunisia. Weather 1993, 48, 359–363. [Google Scholar] [CrossRef]
- Wurman, J. The multiple-vortex structure of a tornado. Weather Forecast. 2002, 17, 473–505. [Google Scholar] [CrossRef]
- Emanuel, K.A. Thermodynamic control of hurricane intensity. Nature 1999, 401, 61–100. [Google Scholar] [CrossRef]
- Rotunno, R. The fluid dynamics of tornadoes. Annu. Rev. Fluid. Mech. 2013, 45, 59–84. [Google Scholar] [CrossRef]

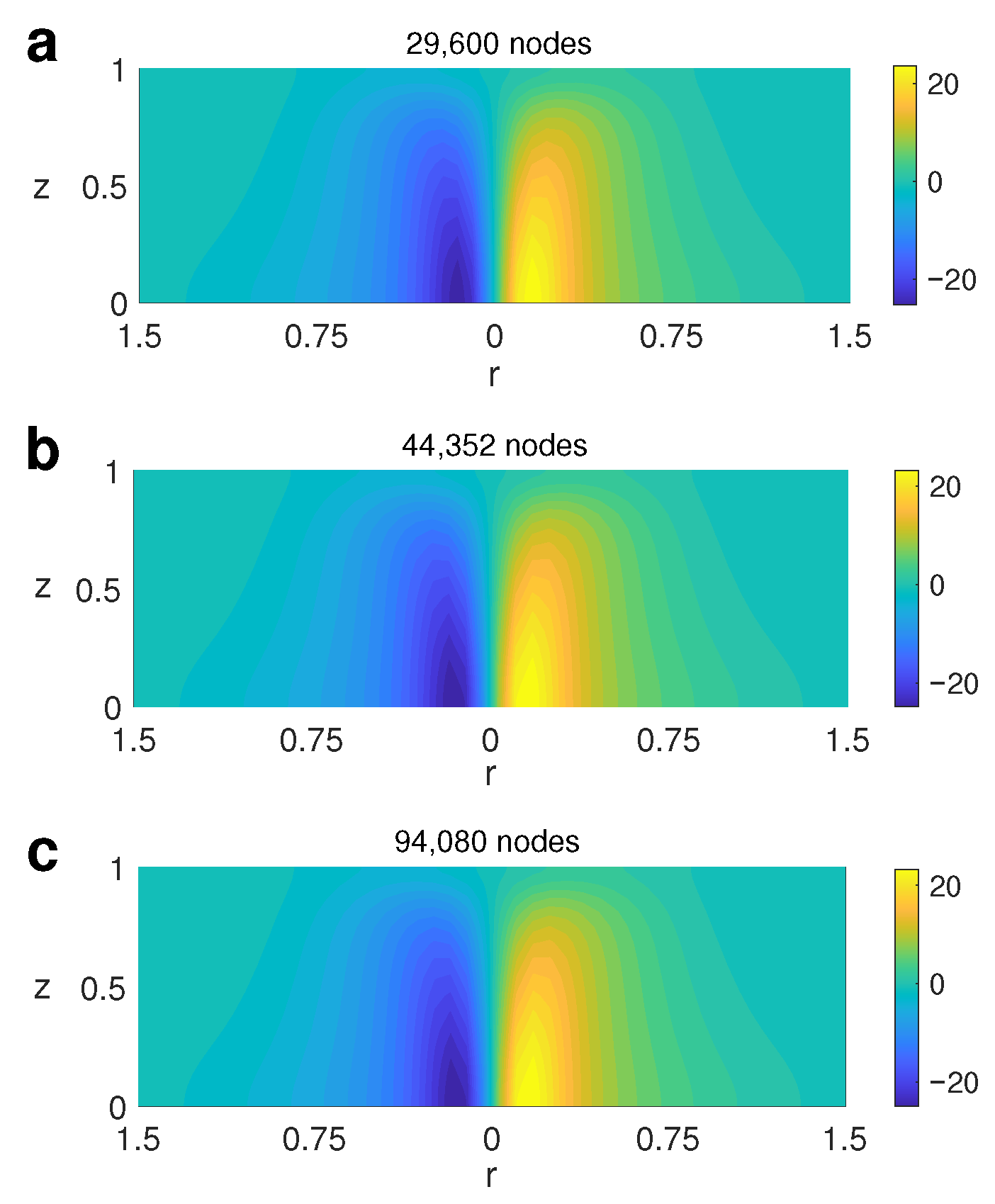







| Nodes | e(max()) | e(max()) | e(max()) |
|---|---|---|---|
| 2604 | 0.0266 | 0.0414 | 0.0127 |
| 2772 | 0.0205 | 0.0239 | 0.0121 |
| 5544 | 0.0200 | 0.0220 | 0.0118 |
| 11,088 | 0.0154 | 0.0219 | 0.0103 |
| 14,800 | 0.0139 | 0.0190 | 0.0091 |
| 22,176 | 0.0124 | 0.0132 | 0.0078 |
| 29,600 | 0.0108 | 0.0103 | 0.0060 |
| 35,424 | 0.0072 | 0.0035 | 0.0027 |
| 44,352 | 0.0037 | 0.0019 | 0.0014 |
| 94,080 | 0.0000 | 0.0000 | 0.0000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, M.C.; Castaño, D.; Herrero, H. Growing Top-Down or Bottom-Up Vortices: Effect of Thermal Gradients. Modelling 2025, 6, 166. https://doi.org/10.3390/modelling6040166
Navarro MC, Castaño D, Herrero H. Growing Top-Down or Bottom-Up Vortices: Effect of Thermal Gradients. Modelling. 2025; 6(4):166. https://doi.org/10.3390/modelling6040166
Chicago/Turabian StyleNavarro, María Cruz, Damián Castaño, and Henar Herrero. 2025. "Growing Top-Down or Bottom-Up Vortices: Effect of Thermal Gradients" Modelling 6, no. 4: 166. https://doi.org/10.3390/modelling6040166
APA StyleNavarro, M. C., Castaño, D., & Herrero, H. (2025). Growing Top-Down or Bottom-Up Vortices: Effect of Thermal Gradients. Modelling, 6(4), 166. https://doi.org/10.3390/modelling6040166








