Comparative Study of Different Modelling Approaches for Progressive Collapse Analysis

Abstract

This paper explores methods of simulating the behaviour of building structures under progressive collapse conditions through alternative models of different levels of structural idealization. Such models have been applied in many previous studies, but there is insufficient information regarding their reliability and their ability to represent actual structural behaviour as the level of idealization is reduced. To address this, the study adopts the alternative load path method through the well-established concept of notional column removal, performed via nonlinear static analyses of models with different levels of structural idealization. The focus is on the interaction between the directly affected structural members and the surrounding structure, which is shown to significantly influence the overall response under progressive collapse. The results demonstrate that this interaction depends on multiple factors and cannot be reliably captured when the surrounding structure is not explicitly modelled. Building on this finding, the study systematically evaluates how reduced models can be enhanced to better represent these interactions and proposes strategies for defining boundary conditions that preserve global structural behaviour. Overall, the study advances understanding of model idealization effects and provides practical guidance for developing efficient reduced models for progressive collapse simulations without compromising essential aspects of structural response.

1. Introduction

Structural robustness has become a key research topic in structural engineering in recent years [1]. This is due to the escalating exposure of structures and infrastructures to various threats, which makes it increasingly important to understand their response to accidental extreme actions and to develop design methods that ensure an acceptable level of structural safety. The latter is considered sufficient when an extreme load does not cause disproportionate damage to the structure [2]. This can be achieved when the structure is sufficiently robust to ensure that local damage does not spread progressively, thus leading to a potentially disproportionate collapse [3,4].

Through intensive research activity over the past decades, the “notional column removal” approach has been established as the most effective method for assessing the response of frame structures to progressive collapse [5,6,7]. This method aims to assess structural redundancy, a fundamental component of the structural robustness of building structures. Redundancy is evaluated based on the ability of the structure to sustain damage to a single load-bearing element, typically through the mobilization of different load-resistance mechanisms and the activation of alternative load paths [8,9], allowing the structure to reach a new stable equilibrium and prevent collapse propagation [10].

The column removal approach has been studied extensively in recent decades [11,12,13,14], and it is found in various forms in most current design codes [15,16,17]. Following column removal, the remaining structural components are expected to act as alternative load paths. Therefore, beams and slabs need to compensate for the column failure by transferring its load to the surrounding structure [18,19]. This imposes large deformations that activate additional load-resistance mechanisms in these elements [20,21]. Figure 1 illustrates the structural behaviour of beams simulated through a double-span mechanism (Figure 1a) that is subject to large vertical displacement at the midspan [13]. In the presence of axial restraint due to the interaction with the surrounding structure, nonlinear geometric effects significantly affect the structural behaviour as they induce the development of axial forces in the beams [22,23]. Of particular importance is the axial tensile force developed at large deformations, which may considerably increase the load-carrying capacity as shown in Figure 1b [4,22].

Both beams and slabs [24,25,26], as well as other load-bearing and non-bearing elements such as infilled walls [27,28,29] and diagonal bracing systems [30,31], may contribute considerably to structural robustness. Beams usually have a predominant role as they provide resistance through different mechanisms [13,21]. Also, for the mobilization of these mechanisms, the beam–column connections must be able to transfer substantial axial forces in addition to increased bending moments and shear forces, whilst undergoing large axial and rotational deformations [32]. For these reasons, extensive research has focused on understanding the response characteristics of the double-span beam mechanism shown in Figure 1. More recent work has explored innovative methods to enhance the structural behaviour, for example, by introducing new design configurations that enable increased strength and rotation capacity in beam–column connections [33,34,35].

As a result of a comprehensive investigation, the structural parameters that govern the progressive collapse response of the double-span beam mechanism are now well-understood. Based on these parameters, it is therefore possible to determine ways in which the beam response will be enhanced in a column removal scenario [4,21,36]. However, sufficient knowledge remains limited regarding the interaction between the beams and the surrounding structure [13,23,32]. Understanding this issue is important both for the proper evaluation of the information obtained from previous studies that were restricted to the double-span beam mechanism (experimental, numerical and analytical studies) and the correct application of the column removal approach through representative simulation models that will consider the effects of interaction with the surrounding structure.

Current research on the interaction between beams and the surrounding structure in progressive collapse scenarios has tended to adopt simplified modelling approaches. For example, many studies reduce the full building to a single floor, a grillage model or the classic double-span beam mechanism, with the surrounding structure represented by idealized boundary conditions or rigid supports [37,38]. In these models, the axial restraint or rotational stiffness imposed by the remaining structure is typically prescribed rather than developing naturally from the system [39]. More advanced numerical studies do attempt full-structure finite element modelling and account for joint deformation and support flexibility [40], but such models remain relatively few. Consequently, while the primary mechanisms (flexure, catenary, arching) are reasonably well-captured, the secondary effects of structural continuity and global redistribution remain less understood and less accurately modelled. Moreover, these simplifications may lead to inaccurate estimation of internal forces and deformations in the directly affected elements once a column is lost. Thus, even though the local beam mechanism is well-understood, the system-level interaction with the surrounding structure remains an important gap in knowledge.

This study aims to investigate this problem by systematically examining the effects of the interaction between beams and the surrounding structure on the progressive collapse response of building frames. By comparing the results of multiple structural simulation models, representing different levels of structural idealization, the study examines the extent to which reduced models can accurately capture system-level behaviour under column loss scenarios. A reinforced concrete frame structure, specifically designed for this study, is analyzed under a carefully selected column removal scenario. The reduced models studied, in addition to the full structure, include three-dimensional multiple-floor and single-floor assemblies, a grillage representation, a two-dimensional plane frame, and an isolated double-span beam system. All models have been numerically studied through nonlinear static analysis that accounts for large deformations, material nonlinearity, and second-order effects, enabling representation of the effects of axial restraint. This approach allows comparisons between different levels of structural idealization and explores the feasibility of defining a representative model with appropriate boundary conditions that can realistically simulate the interaction with the surrounding structure. By assessing how the responses of these models differ from the full structure, the study identifies key parameters that influence progressive collapse resistance, providing guidance for the development of more reliable, efficient, and practical assessment methods.

2. Methodology

This section aims to describe the methodology of the study, providing the necessary information regarding the details and characteristics of the structure under consideration (Section 2.1), the modelling approaches employed to simulate the response against progressive collapse based on a carefully selected column removal scenario (Section 2.2), the material constitutive models and the definition of plastic hinges used to capture nonlinear flexural behaviour in the beams (Section 2.3), and the analysis methods used to draw specific conclusions in accordance with the objectives of the study (Section 2.4).

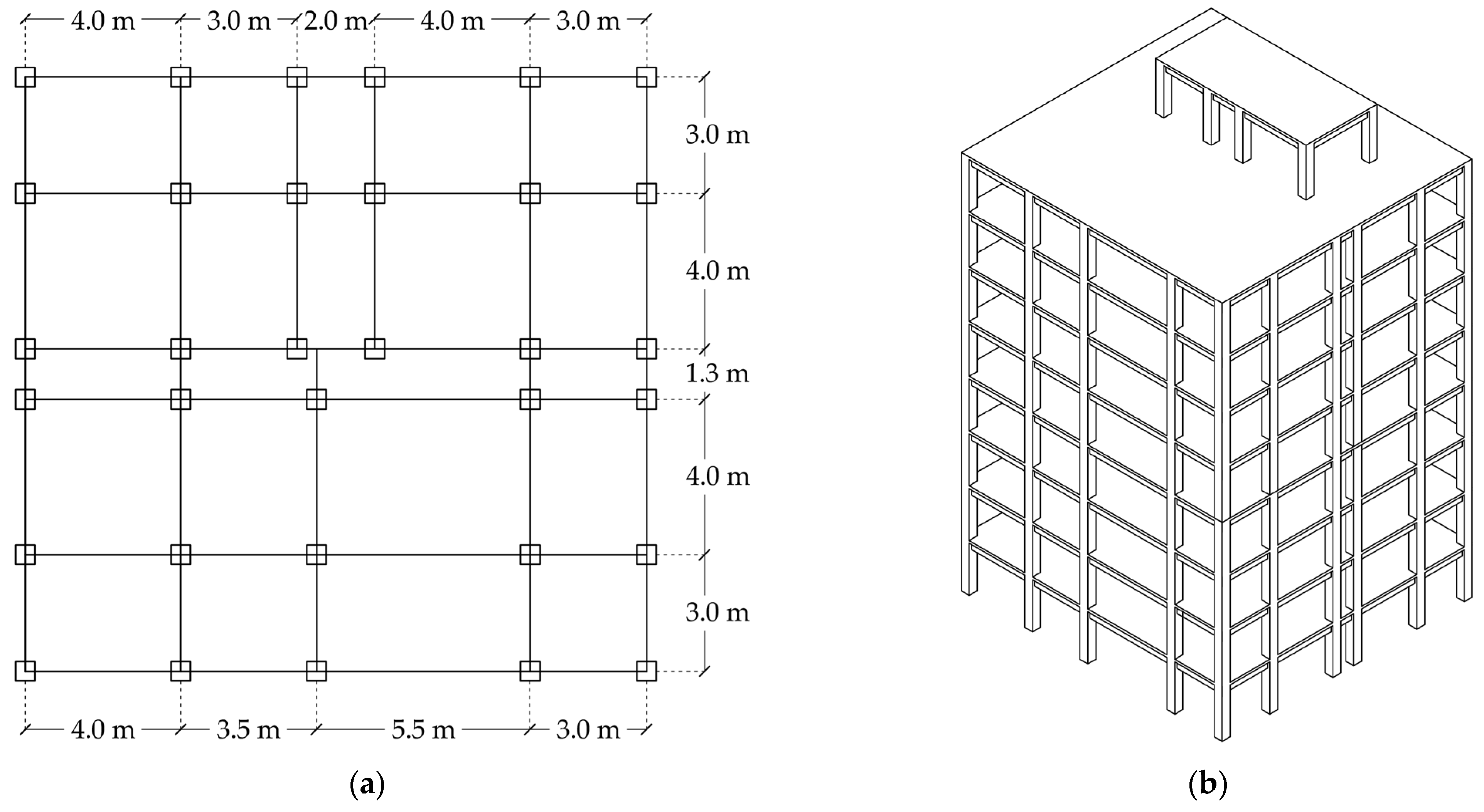
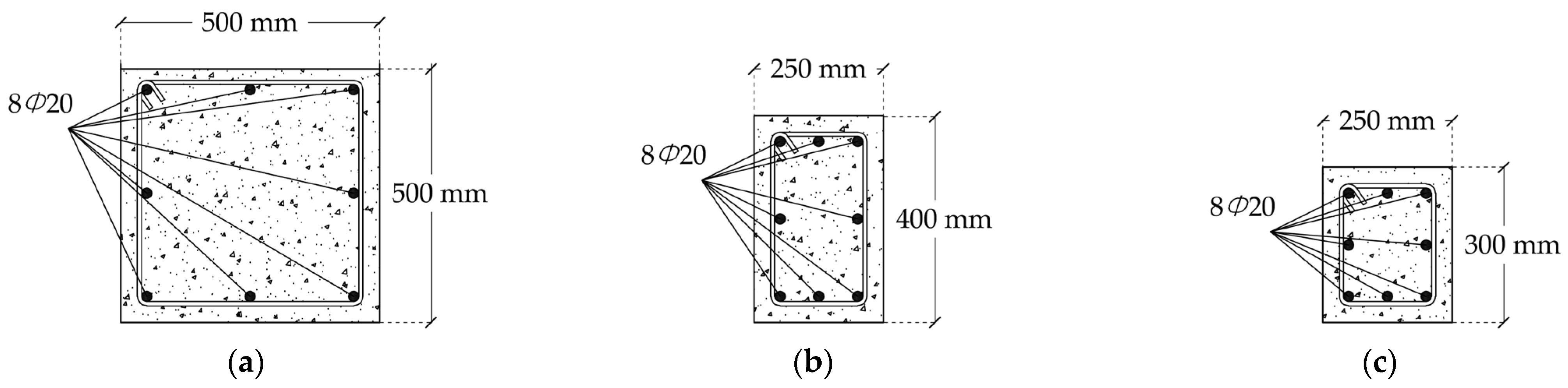
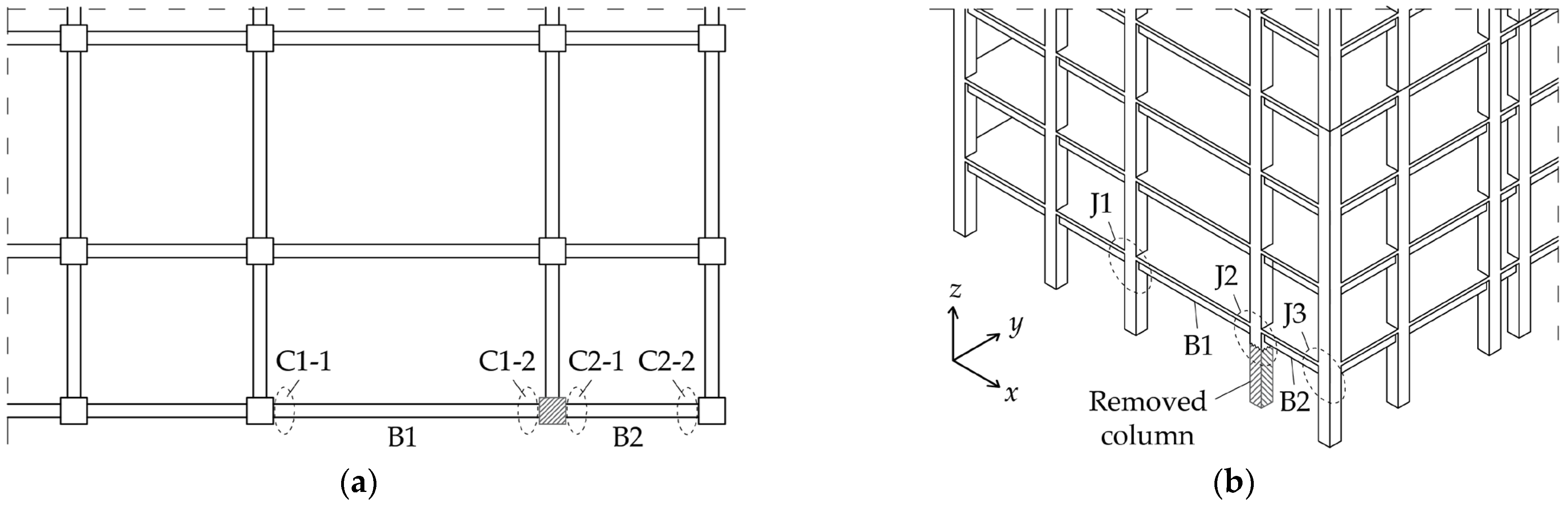
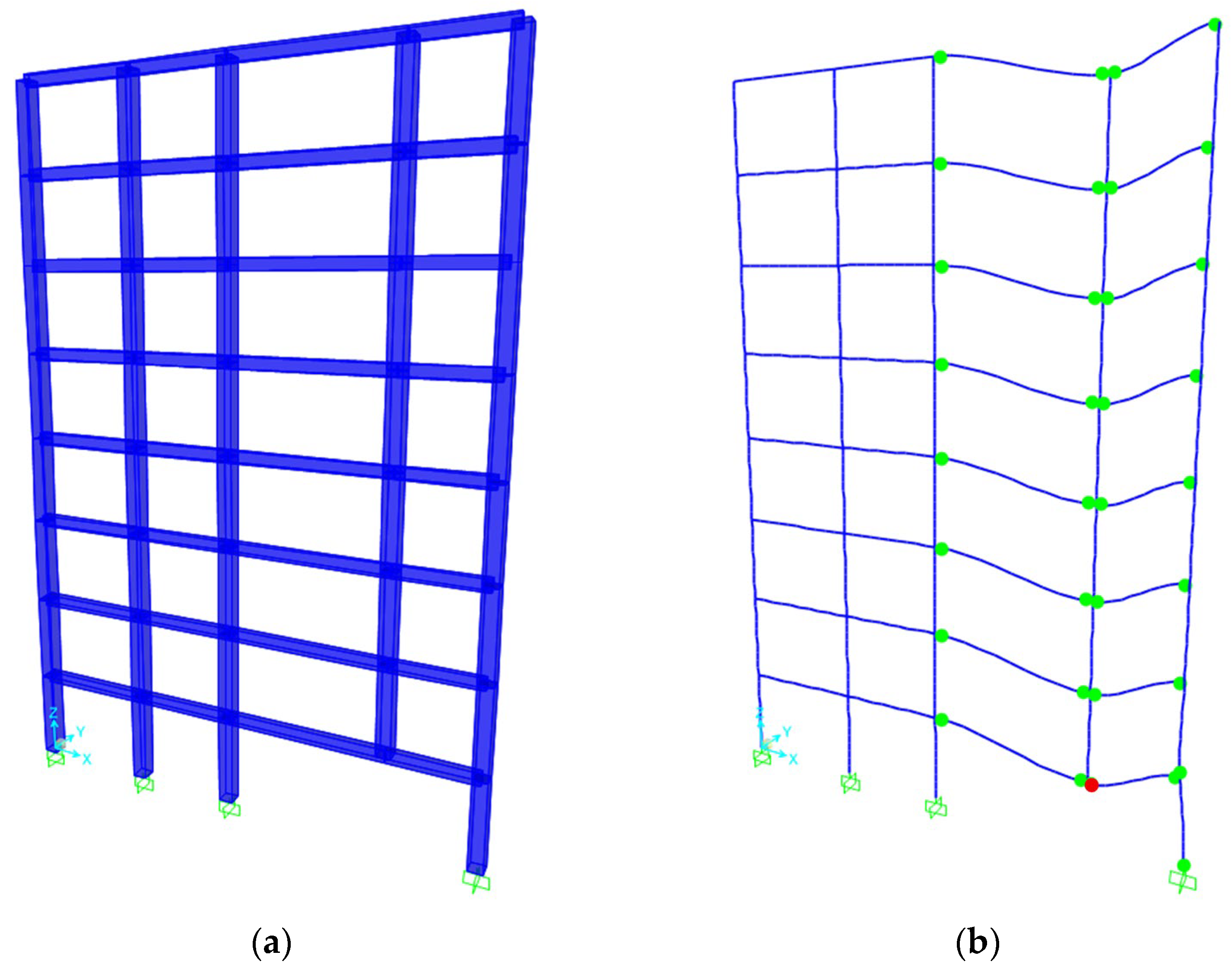
2.1. Prototype Structure

For the purposes of the study, a prototype reinforced concrete multi-storey building is considered. The building consists of eight floors with identical plan layouts as shown in Figure 2. The floor layout is shown in Figure 2a, and the three-dimensional layout of the structure is shown in Figure 2b. The structure type, its layout and the structural details were carefully determined to allow a comprehensive study of the problem under consideration. As shown in Figure 2a, the structure has an almost square plan layout, with a longitudinal dimension of 15 m and a transverse dimension of 15.3 m. Each floor has a height of 3 m; hence, the total height of the eight-storey structure is 24 m, plus an additional 3 m for an extended roof section.

The building structure was designed against conventional design loads, according to the Eurocode ultimate and serviceability limit state design rules. Structural components, i.e., columns, beams and slabs, are made of C35/45 concrete and steel reinforcing with a yield stress of 500 MPa. Based on the design calculations, the dimensions and properties of the cross-sections of columns, external beams and internal beams were determined as shown in Figure 3a–c, respectively.

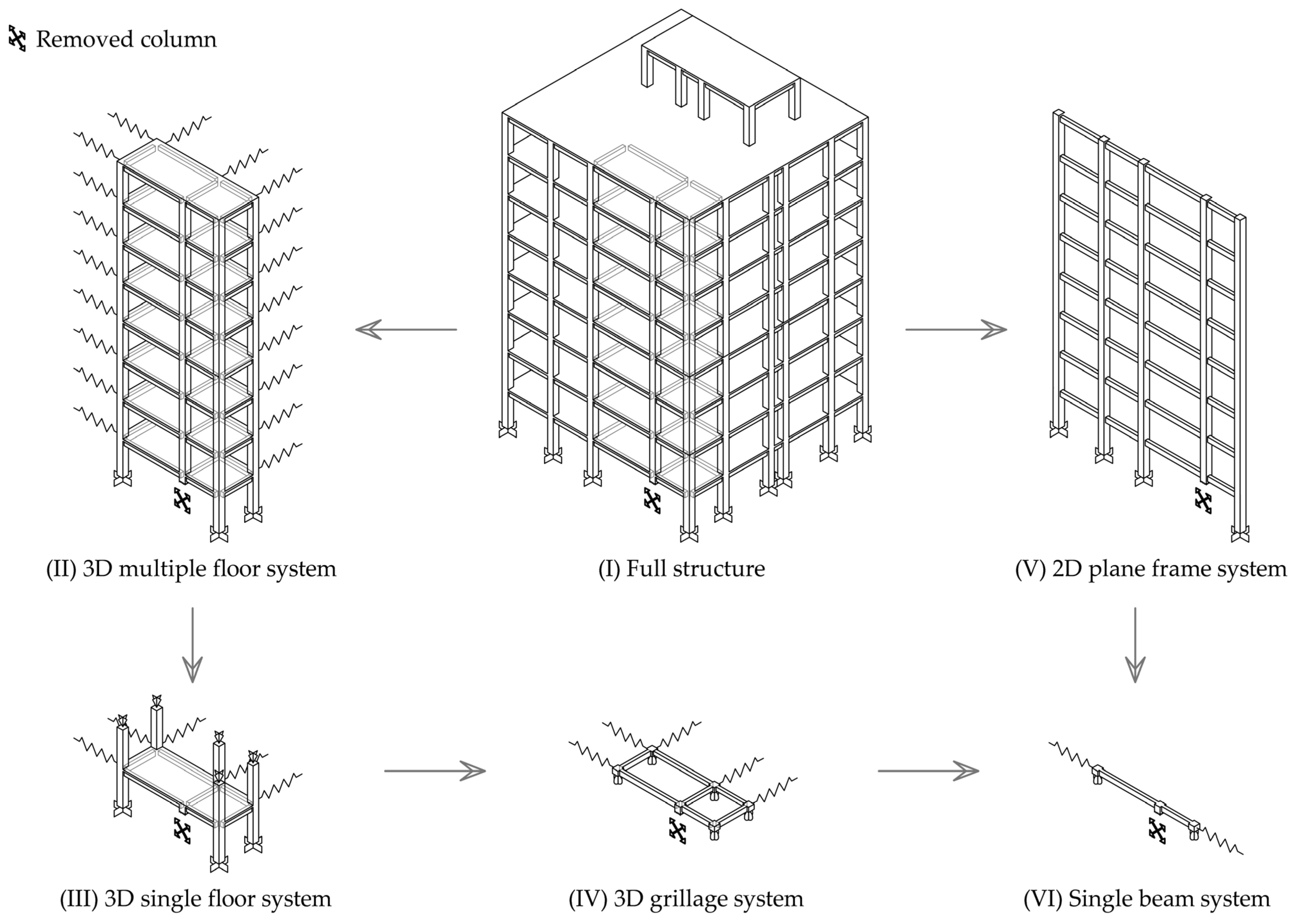
2.2. Modelling Approaches

Previous studies have shown that the structural response to progressive collapse can vary significantly depending on the location of the removed column [8,14,20]. However, it has been found that the parameters that influence behaviour are the geometry of the directly affected structure, the structural properties of its constitutive components, and the degree of axial restraint [37,41]. The latter is likely the most influential parameter, as well as the one that is most difficult to quantify [4,32,42]. Considering this, and in order to avoid extending the study to multiple column removal scenarios—which would be beyond its scope—only the column removal scenario described in Figure 4 is considered.

The study primarily focuses on the response of the directly affected structural components and, in particular, the double-span beam mechanism created by beams B1 and B2. As shown in Figure 4a, the end connections of beam B1 are denoted by C1-1 and C1-2, and the end connections of beam B2 are denoted by C2-1 and C2-2. The lengths of the two beams were chosen to be different (i.e., 5.5 m and 3.0 m, respectively) to examine the influence of this parameter. Beams B1 and B2 intersect at joint J2 (Figure 4b), which is defined as the reference node for measuring vertical displacement following column removal.

The structural response is assessed through different modelling approaches corresponding to varying levels of structural idealization, as shown in Figure 5. In addition to the full-structure model (i.e., Model I), four reduced models are analyzed in which appropriate boundary conditions are applied where required. These involve three 3D substructure models (i.e., Models II-IV) and one 2D plane frame model (i.e., Model V). The double-span beam model (i.e., Model VI) that represents the lowest level of structural idealization is also examined. The contribution of the slabs was excluded from all models in order to focus on the behaviour of the beams and thereby enabling meaningful comparisons.

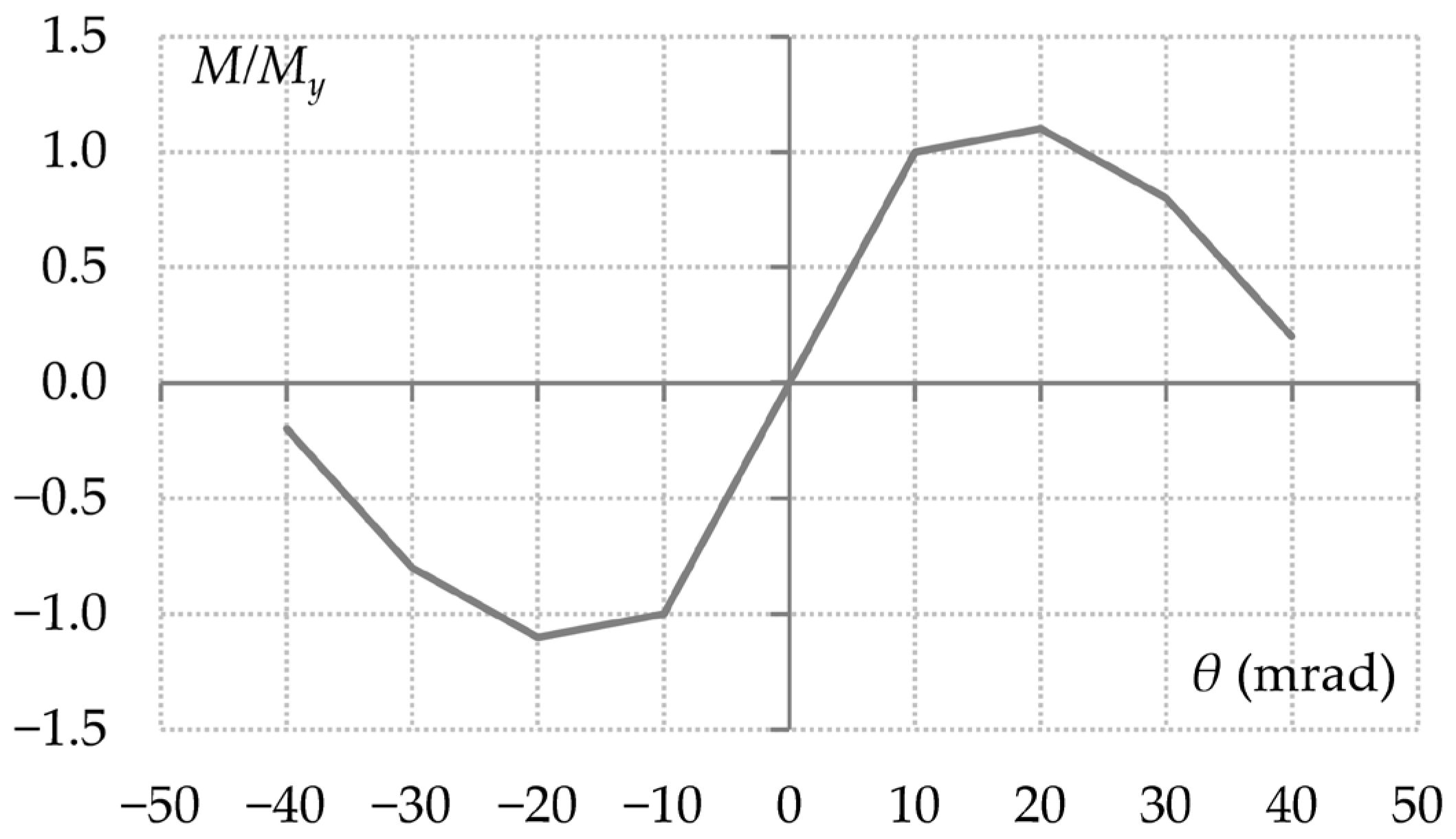
2.3. Material Modelling and Plastic Hinge Definition

The concrete was modelled using the Mander stress–strain relationship [43], assuming a characteristic cylinder strength of 35 MPa. This model captures the gradual softening beyond the peak compressive stress and provides a realistic representation of post-peak ductility. The reinforcing steel was represented by a bi-linear stress–strain model with strain hardening, assuming a yield stress of 500 MPa, a modulus of elasticity of 200 GPa, and a strain-hardening ratio of 1%.

To represent the nonlinear flexural behaviour of reinforced concrete beams under large deformations, plastic hinge zones were introduced at each beam end. The plastic hinge length was taken as 0.5 times the beam depth, consistent with empirical expressions [44] that have been validated through experimental studies [45,46]. Each plastic hinge region was subdivided into five nonlinear hinge elements to simulate distributed plasticity [47]. The central portion of each beam, which primarily experiences elastic bending, was discretized into elements with lengths ranging from 0.31 to 0.64 m. This meshing resolution ensures accurate representation of the elastic curvature and deflection profile while maintaining computational efficiency.

The moment–rotation behaviour of the plastic hinges was defined using the deformation-controlled (ductile) P-M₃ model, calibrated against experimental data [48]. The normalized backbone moment–rotation curve is shown in Figure 6, representing initial yielding, strain hardening, and post-peak softening, with symmetric behaviour due to beam symmetry (Figure 3). The plastic rotation capacity corresponds to experimentally observed ultimate rotations for ductile reinforced concrete beams with adequate transverse reinforcement [45,46].

The interaction between axial load and flexural response was modelled through P-M₃ hinges assigned at both beam ends. The hinge interaction surface was defined using the Concrete (ACI 318-02) formulation, with a strength reduction factor φ = 1.0, such that nominal (unreduced) section capacities were employed to capture the full material strength. The axial load–displacement relationship was modelled as elastic-perfectly plastic, allowing the beam to develop tensile axial forces once yielding occurred [6,36,49]. This definition enables the hinge to capture the reduction in flexural strength under increasing axial tension and the interaction between compression, bending, and large rotations.

The adopted modelling strategy therefore provides a physically grounded and numerically stable framework capable of representing distributed plasticity, stiffness degradation, and axial–flexural interaction. By explicitly incorporating the nonlinear material behaviour of concrete and steel, as well as elastic bending in the beam spans and axial deformation due to tensile axial forces, the model allows for a realistic prediction of the beam response under progressive collapse loading. The subsequent section (Section 2.4) describes the nonlinear static (pushdown) analysis procedure used to simulate these effects.

2.4. Analysis Approach

A nonlinear static (pushdown) analysis [50,51,52], accounting for large displacements and geometric nonlinearity, is performed using the structural analysis software SAP2000 (v.18). The analysis starts from the unloaded configuration corresponding to the removal of the target column, after which gravity loading is gradually applied and increased until the load-carrying capacity of the structure is exhausted.

This procedure enables a step-by-step simulation of the structural response under a notional column loss scenario [13], capturing the redistribution of internal forces, the progressive formation of plastic hinges, and the transition from flexural to axial load-carrying mechanisms. Failure is considered to occur when one or more plastic hinges attain their ultimate rotation capacity, as defined in Section 2.3. The nonlinear static approach provides a complete load–displacement (pushdown) curve and allows direct evaluation of the deformation capacity, residual strength, and collapse mechanism of the structure.

The analysis is displacement-controlled, with incremental steps applied at the location of the removed column to ensure accurate tracing of the structural response. Plastic hinge states, internal moments, and axial forces in the beams are monitored during the analysis. This setup allows detailed insight into the sequence of yielding, hinge development, and the evolution of axial tension in the beams, enabling a thorough understanding of the mechanisms governing progressive collapse and post-yield behaviour.

As noted previously, the study focuses primarily on the response of the directly affected beams B1 and B2 and examines how this response is captured by the different analysis models. The structural response is evaluated based on the following nodal displacements and element joint forces, as defined in Figure 7:

• Vertical displacement of joint J2, denoted by w.
• Horizontal displacements of joints J1 and J3, denoted by Δ₁ and Δ₃, respectively.
• Bending moments at the ends of beam B1 (i.e., M_1-1 and M_1-2) and beam B2 (i.e., M_2-1 and M_2-2).
• Shear forces at the ends of beam B1 (i.e., V_1-1 and V_1-2) and beam B2 (i.e., V_2-1 and V_2-2).
• Axial forces at the ends of beam B1 (i.e., N_1-1 and N_1-2) and beam B2 (i.e., N_2-1 and N_2-2).

Figure 7. Component forces and deformations of the double-span beam system.

Figure 7. Component forces and deformations of the double-span beam system.

The beam gravity loading (q) is obtained by considering the equilibrium of beam B1 or beam B2, as follows:

$$q={\displaystyle \frac{V_1+V_2}{L_i}}$$

(1)

Alternatively, the beam gravity loading is determined using a different equilibrium equation as follows [29]:

$$q=2\left({\displaystyle \frac{V_1{L}_i+M_1+M_2+N_{i}w}{L_i^2}}\right)$$

(2)

Equations (1) and (2) are expected to yield identical results. Moreover, the uniformly distributed gravity loading applied to the two adjacent beams, B1 and B2, should be identical. Finally, the axial forces at the ends of both beams are required to be equal to satisfy the equilibrium of the system.

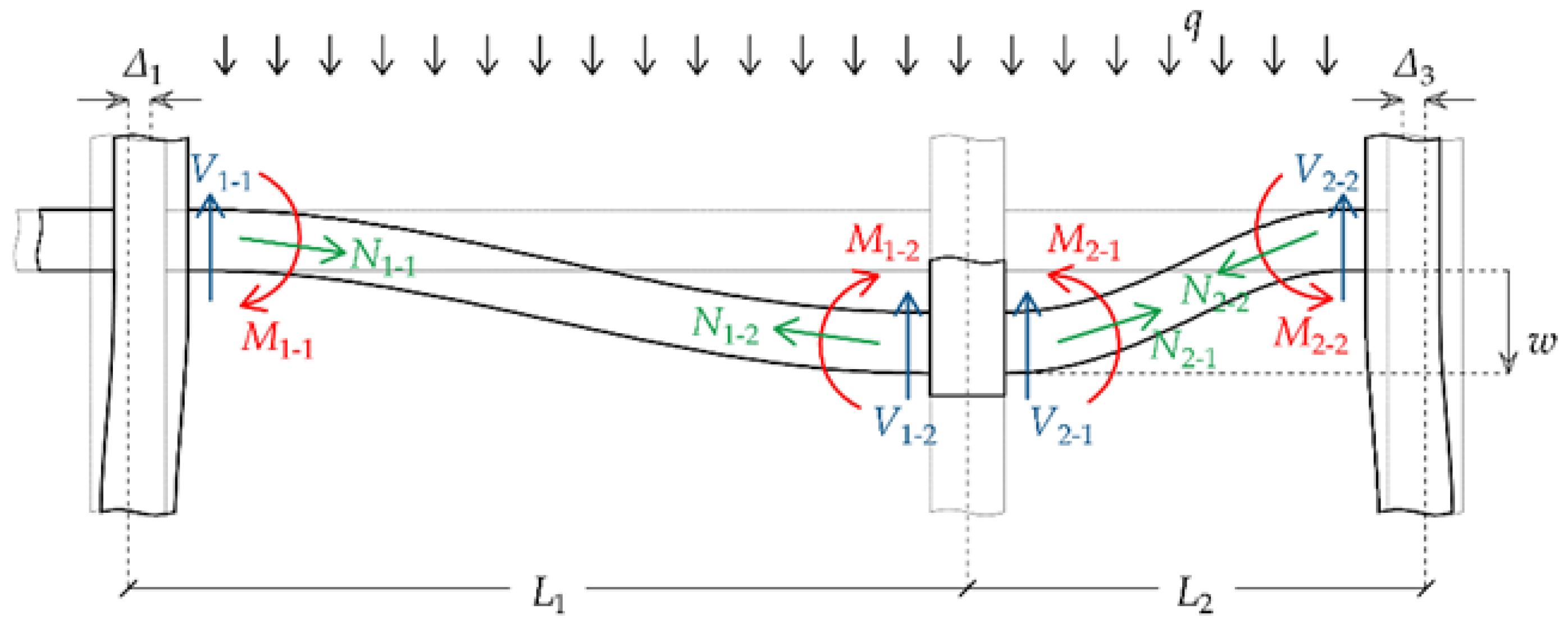
3. Analysis of Full-Structure Model

This section presents the results of the analysis of the full-structure model (i.e., Model I in Figure 5). Initially, a detailed analysis of the behaviour of the directly affected beams B1 and B2 is performed in Section 3.1. Subsequently, Section 3.2 examines the possible influence of the upper floors on the overall response of the structure.

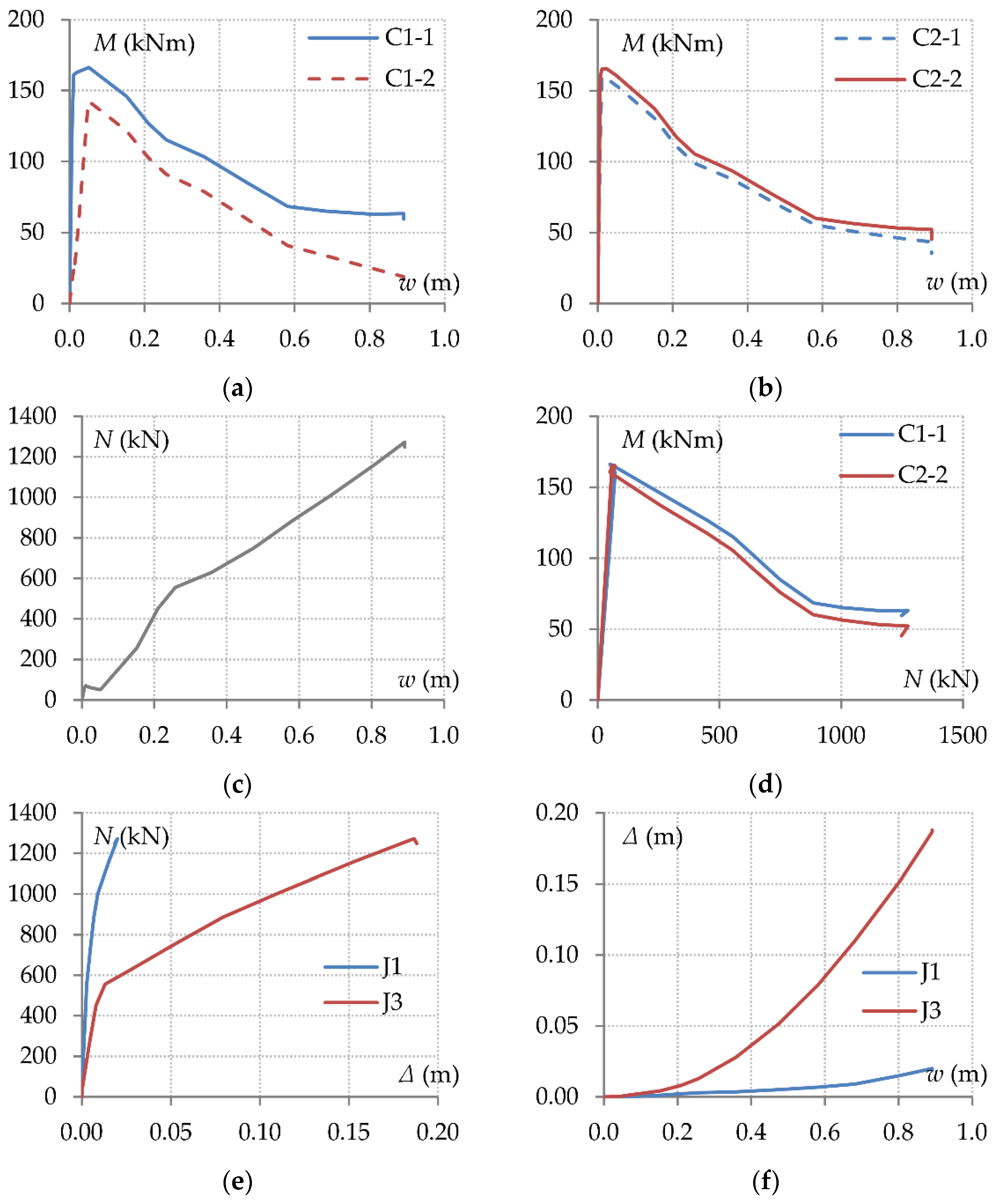
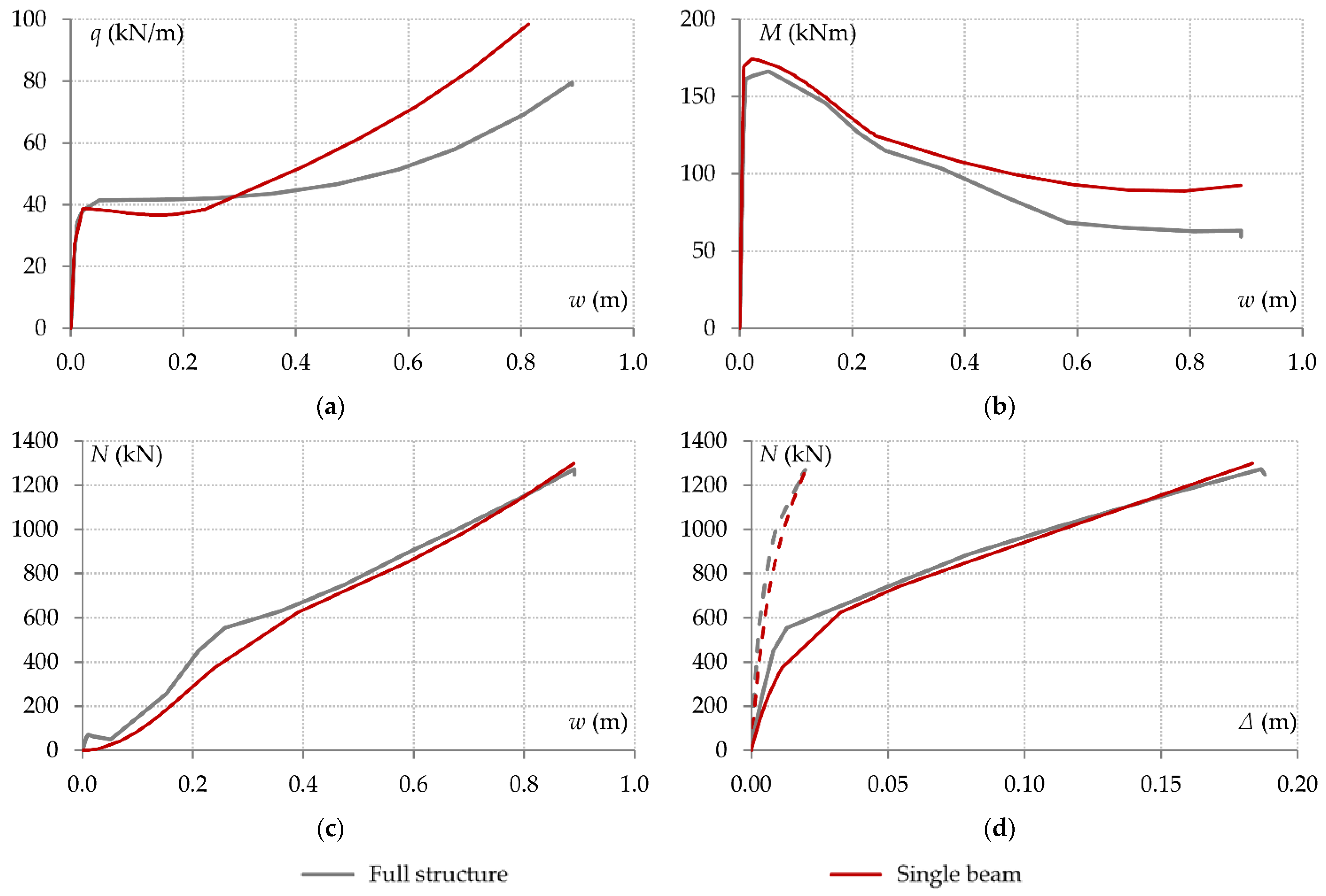
3.1. Response of Beams B1 and B2

The load–deflection response of a single beam is shown in Figure 8. Since the load is considered as uniformly distributed along the beam span, the response is the same for both beam B1 and beam B2, and it is also the same for all the corresponding beams of the upper floors. The curve is representative of the load–deflection response of concrete beams following column removal [14,21,41,53,54]. That is, at low beam deflections, performance is governed by flexural action while compressive arching action effects are insignificant. At higher deflections, structural resistance is enhanced by the effects of tensile catenary action.

It is well-established that the flexural load-carrying capacity of a single beam is governed by the sum of the connection bending moment resistances (under hogging and sagging moments, respectively) and the beam span, as follows [21]:

$$q_y={\displaystyle \frac{2\sum M_{j,Rd}}{L^2}}$$

(3)

For the case of a double-span beam structure with unequal spans L₁ and L₂ and identical hogging and sagging moment resistances (as in symmetric reinforced concrete beams) equal to M, the above equation is modified as follows [55]:

$$q_y={\displaystyle \frac{4M}{L_1{L}_2}}$$

(4)

The flexural strength of the external beams (Figure 3) is 166.2 kNm. Therefore, for the two adjacent beams with spans of 5.5 m and 3.0 m, Equation (4) yields a flexural load-carrying capacity of 40.3 kN/m, which is consistent with the load–deflection curve shown in Figure 8.

In addition, previous numerical and experimental studies [6,7,12,14] have shown that the effects of tensile catenary action in a double-span beam mechanism under sufficient axial restraint become pronounced once the deflection approaches the beam depth. Subsequently, the deflection may increase up to roughly twice the beam depth as substantial axial forces develop along the beam axes. This axial tension progressively increases the load-carrying capacity of the system, enabling it to reach values of approximately twice the flexural load-carrying capacity. Ultimately, failure occurs due to excessive axial deformations in the joint regions, which typically lead to rebar fracture. These benchmarks correspond closely with the characteristics of the load–deflection curve shown in Figure 8, confirming the reliability of the analysis.

The structural response of beams B1 and B2 is analyzed in Figure 9. When the connection moment resistances are exhausted (Figure 9a,b), the beam tensile force increases considerably, as shown in Figure 9c. This causes a reduction in the connection bending moments [54,56] as shown in Figure 9a,b. The connection bending moments of beam B1 are slightly different, since performance is influenced by the flexural deformation of the beam section [4,26]. The flexural stiffness of the shorter beam B2 is substantially higher; thus, the variation in the bending moments of its two end connections is essentially identical. The interaction between the beam axial force and the bending moments of the end connections of the double-span beam is described in Figure 9d.

Figure 9e,f show the variation in the axial displacements of the end joints of the double-span beam with respect to the beam axial force and the beam deflection, respectively. In both cases, the increase in the axial displacements is highly nonlinear. The curves of Figure 9f confirm that performance is governed by geometric nonlinearity, while the curves of Figure 9e demonstrate that the resistance against axial displacement changes due to material nonlinearity. These effects are mainly described by the axial displacement of joint J3. The decrease in the slope of this curve indicates that the axial restraint provided by the free edge decreases due to the formation of plastic hinges in the constitutive components (transverse beams and columns). Due to the higher redundancy of the structure at the left end of beam B1, the rate of decrease in the slope of the blue curve is smaller. Failure of the structure occurs when the plastic hinge in the region of connection C2-1 reaches the maximum rotation limit defined in Figure 6.

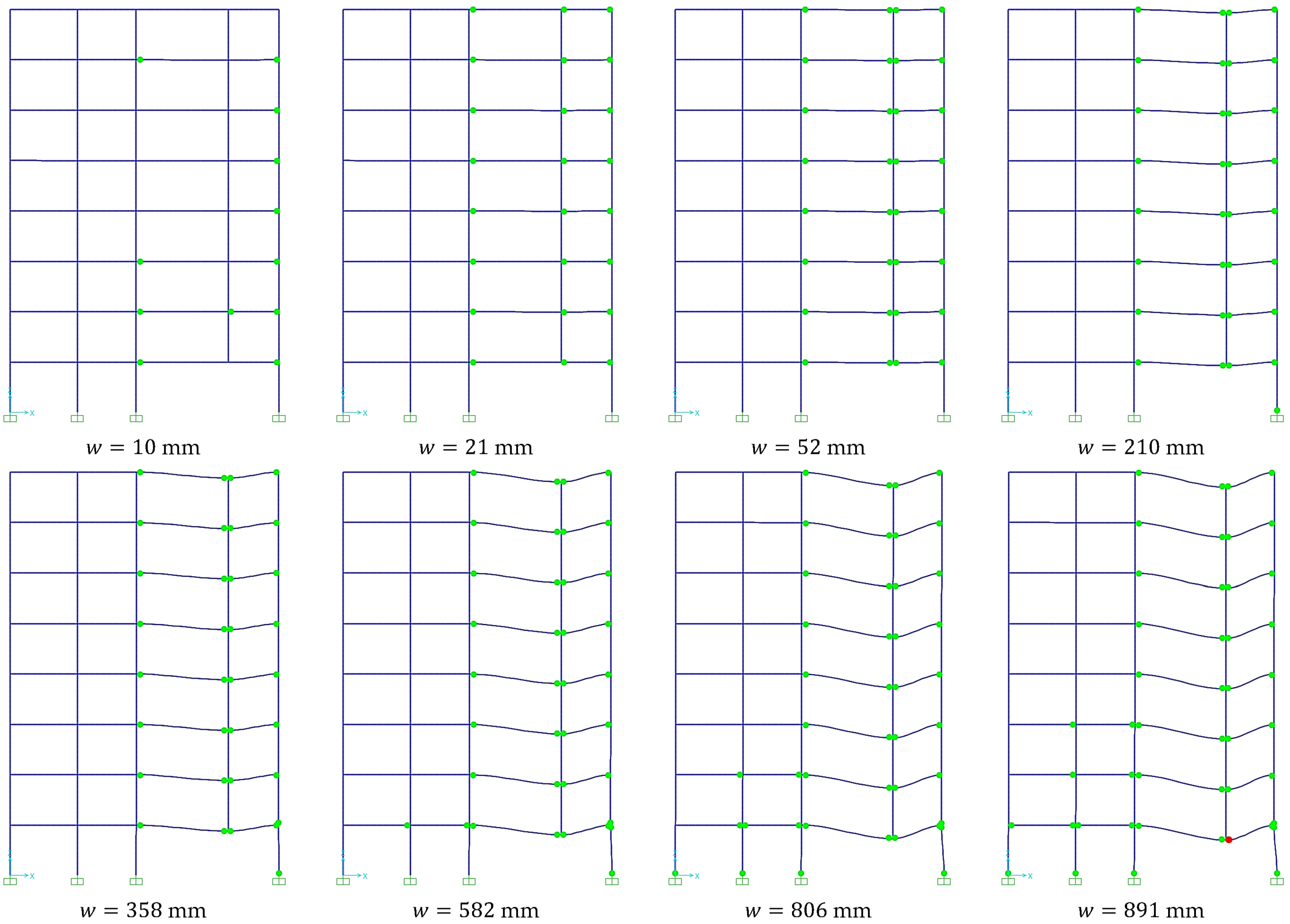
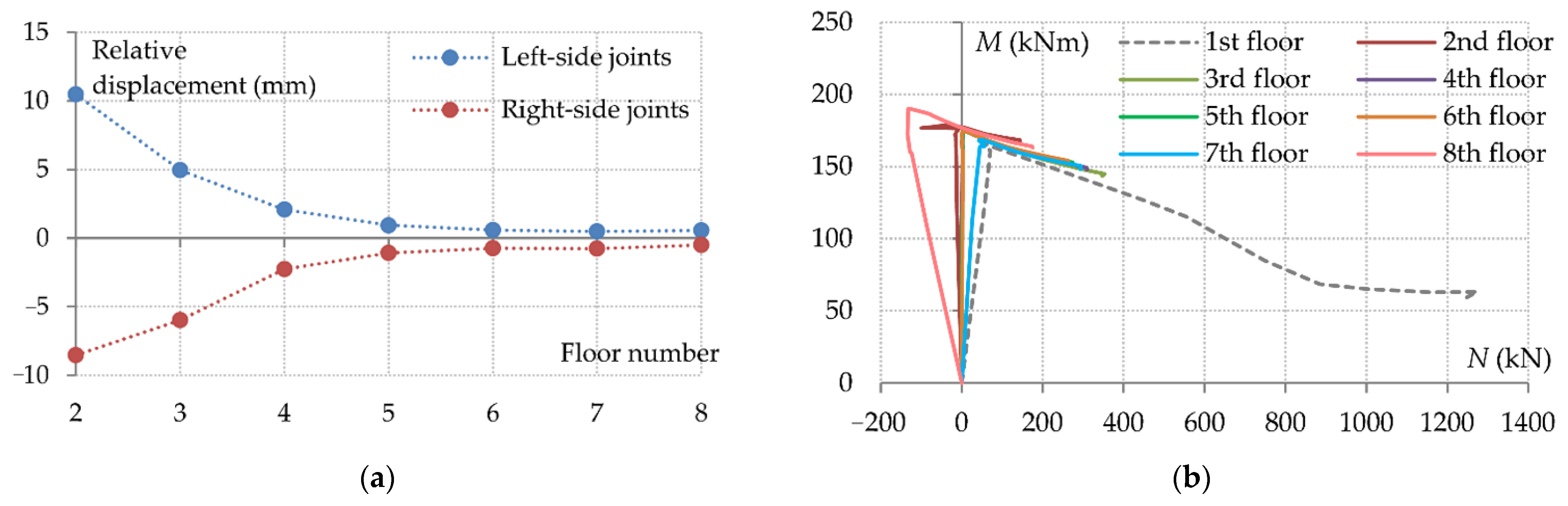
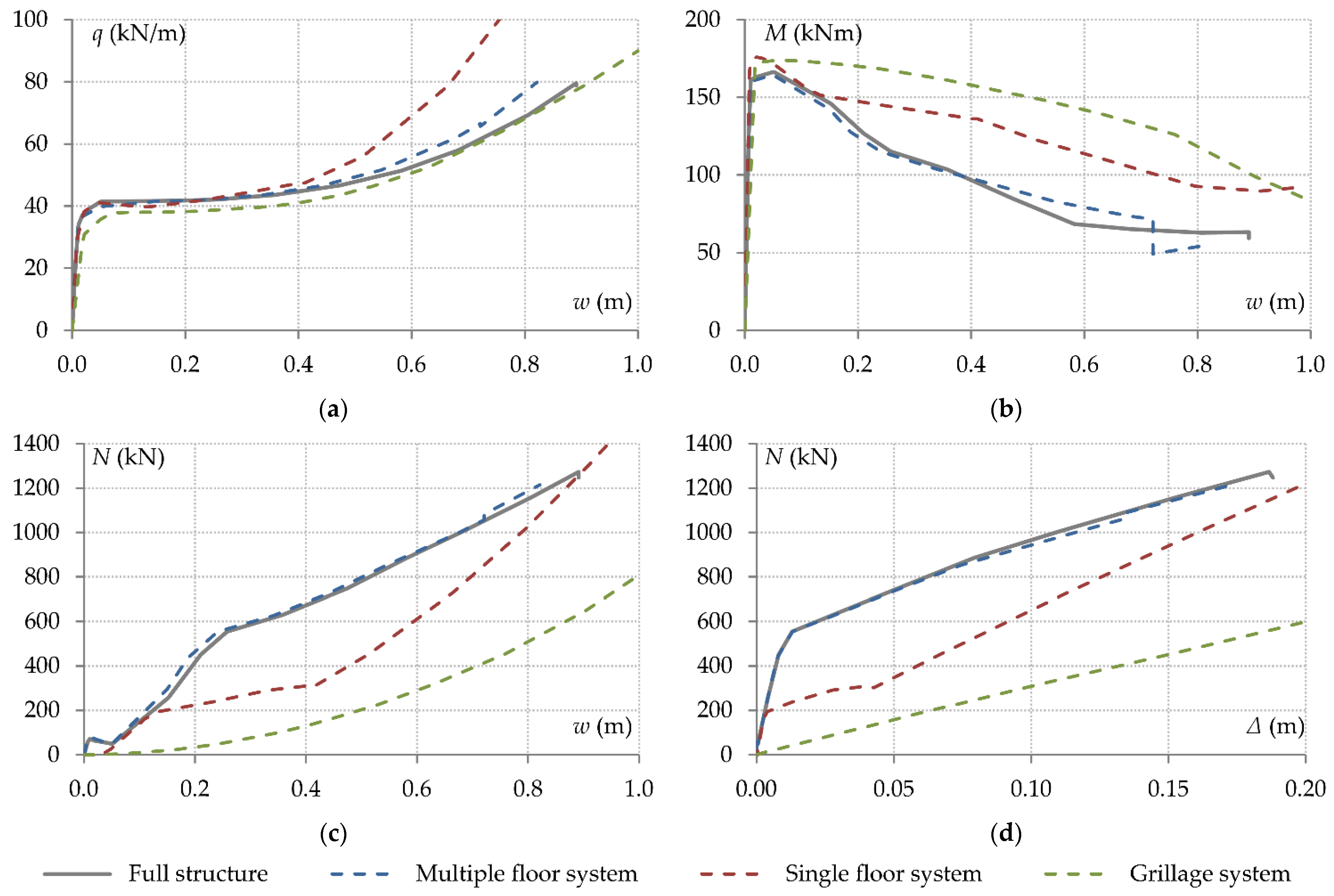
3.2. Contribution of the Upper Floors

Figure 10 describes the sequential formation of plastic hinges, focusing for clarity only on the edge plane frame of the structural system. The green dots indicate the connection regions where the beam flexural resistance has been exhausted (Figure 6). It is observed that plastic hinges have been created at the ends of all directly affected beams from the initial stages of the response. However, the structure continues to maintain and increase its load-carrying capacity, mainly due to the presence of axial tensile force in the beams as well as due to structural redundancy. The red dot indicates the connection region where the plastic hinge has reached its maximum rotation (Figure 6), which is essentially defined as the failure criterion for the structural system. The same figure depicts the sequential deformation of the structural system. In addition to the vertical displacement due to the loss of the column, the horizontal displacements of the nodes at the right edge of the structure, caused by axial forces transferred from the beams to the supports, are clearly visible.

However, it is evident from Figure 10 that the relative horizontal displacements of the upper floors are much smaller than those of the first floor. According to Figure 9e,f, the horizontal displacements of joints J1 and J3 at the ultimate vertical deflection of 891 mm are equal to 18.5 mm and 188 mm, respectively. The horizontal relative displacements of the corresponding joints on the upper floors are given in Figure 11a. The left-side joint displacements decrease following a specific trend. The right-side joint displacements, however, are almost equal and opposite to those of the left side. This indicates that the right-side joints of the upper floors are slightly displaced in the opposite direction relative to joint J3, and that the axial deformations of the beams on the upper floors are relatively small, suggesting that the axial forces in these beams are also small.

The latter is confirmed by the axial force-bending moment (N-M) diagrams of the left-side end connections shown in Figure 11b. The dashed grey curve corresponds to connection C1-1, and it is the same as the blue curve of Figure 9d. The remaining curves describe the N-M interaction of the corresponding connections on the upper floors. During the elastic stage, the tensile forces in the beams on the upper floors are smaller than the tensile force of beam B1, and in some cases (i.e., 2nd and 8th floors) are even compressive. This results in higher bending moment capacities for the connections of these beams [56]. During the plastic stage, these tensile forces increase, but at a much lower rate than that of beam Β1, reaching much smaller maximum values. Similarly, the connection bending moments exhibit a correspondingly reduced rate of decrease.

The fact that the beam axial force and the connection bending moments are both in the numerator of Equation (2) justifies why the beam load–displacement curves of all floors are similar. However, the beams on the upper floors are governed by different resistance mechanisms, transferring the gravity load mainly through flexural action with a small contribution from tensile catenary action at large displacements. The response of beam B1, on the other hand, is mainly governed by tensile catenary action, with flexural action effects having a limited contribution at large displacements.

4. Analysis of Reduced 3D and 2D Models

The objective is to examine whether the response of building structures following column removal can be simulated through lower levels of structural idealization. Reduced 3D models are examined in Section 4.1, in which the level of structural idealization of the structure examined in Section 3 is gradually reduced through appropriate simplifications in the analysis models. A planar 2D model is studied in Section 4.2.

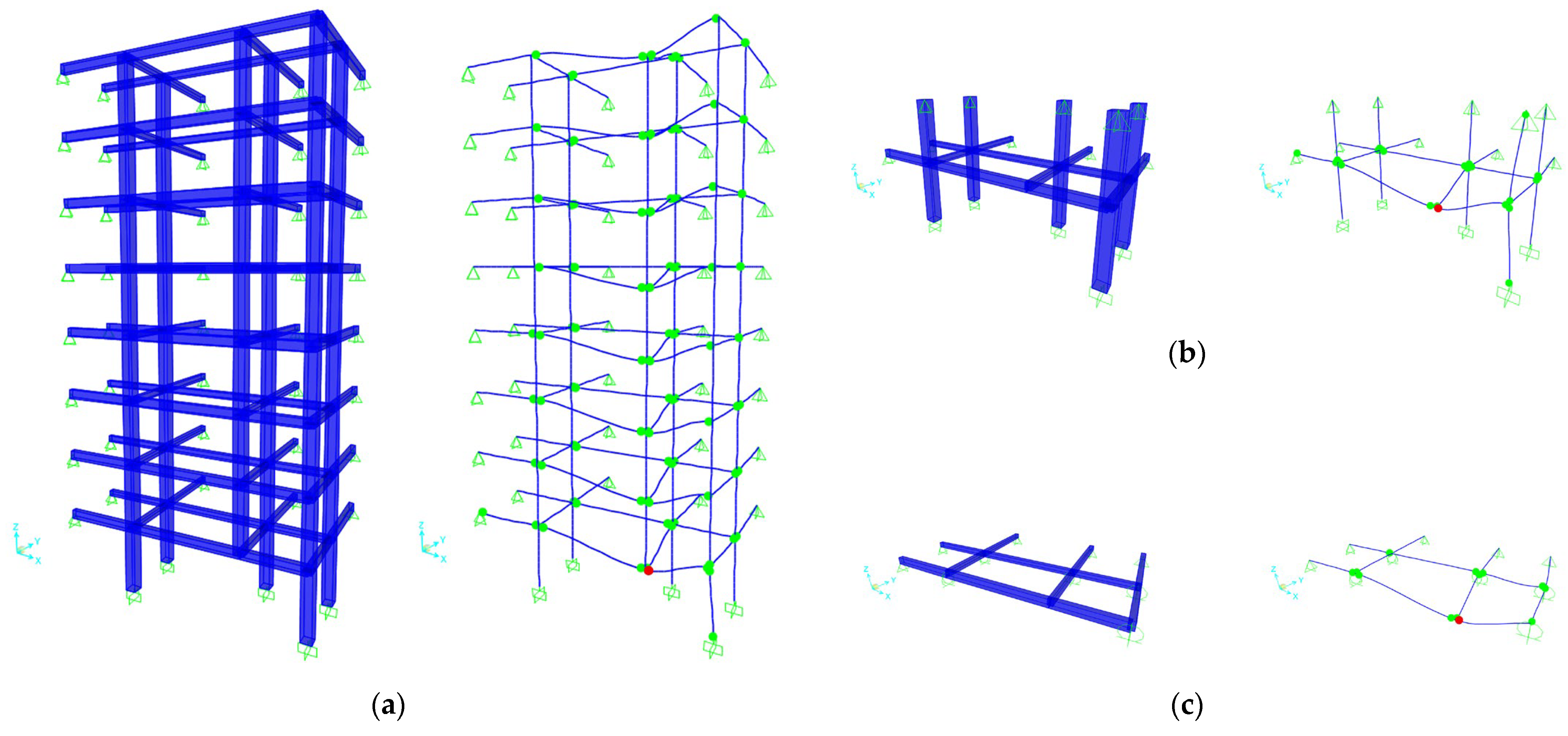
4.1. Three-Dimensional Structural Systems

With respect to Figure 5, the 3D multiple floor system (Model II), the 3D single floor system (Model III), and the 3D grillage system (Model IV) are studied in this section. The analysis models, the deformed shapes of the systems, and the distribution of plastic hinges at the plastic collapse limit state are presented in Figure 12.

The structural responses following column removal are described by the curves in Figure 13, which correspond to the behaviour of the double-span mechanism consisting of beams B1 and B2, and they are compared with the response of the full structure shown in Figure 9.

4.1.1. Multiple Floor System

In the multiple-floor system, only the directly affected multi-storey structural bay and its boundary conditions are considered. The latter parameter is difficult to model accurately, as it must account in a quantitative manner for the degree of axial restraint provided by the surrounding structure. As demonstrated in Section 3, the resistance against axial displacement can vary nonlinearly, which makes its quantification even more challenging. Therefore, the modelling approach should be based on some reasonable assumptions. In many previous studies adopting reduced analysis models, the common assumption made is that the axial stiffness of the supports of a double-span beam is equal to the effective axial stiffness of the adjacent beams [4,26]. This assumption is also adopted and examined in this study. Therefore, all the beams adjacent to the directly affected structural bay are included in the model as shown in Figure 12a. However, the interaction of these beams with the neighbouring structure is ignored; therefore, their end nodes are assumed to be simply supported.

Due to the above simplification, the left-hand side is inevitably stiffer against lateral displacement compared to the full-structure model. However, as shown in Figure 9e,f, this side was already substantially stiffer compared to the other side on the right edge of the structure. Therefore, since the axial displacement of joint J3 is simulated with sufficient accuracy (Figure 13d), the overestimation of the axial restraint on the left-hand side is of minor significance. That is, because the beam axial force and the connection bending moments are predicted with reasonable accuracy with respect to the full-structure model results, as shown in Figure 13c,b, respectively. Since the component forces and deformations are accurate, the load–deflection curve closely matches that of the full-structure model (Figure 13a). These findings indicate that, in the presence of an extensive multi-bay frame structure, the axial restraint is primarily governed by the axial stiffness of the beams and columns in the immediate vicinity of the directly affected area, while components at more remote locations contribute only marginally.

4.1.2. Single Floor System

The single-floor system is modelled by reducing the multiple-floor system examined in Section 4.1.1 to a single-floor sub-assembly with the same boundary conditions along the planar directions, as shown in Figure 12b. The columns of the second floor are also included to simulate boundary conditions, with their top nodes assumed to be simply supported. This is a simplified assumption, as the exact resistance of these nodes against horizontal displacement is particularly difficult to quantify and simulate.

Although the above assumption can be considered conservative, as it might potentially increase the axial restraint of the right-hand side of the structure, the results shown in Figure 13 prove the opposite. Within the elastic stage, the slope of the red curve in Figure 13d coincides with the slopes of the full-structure model and the multiple-floor system model. However, the resistance against axial displacement decreases rapidly due to the formation of plastic hinges, with the reduced structural redundancy of this system playing an important role. When plastic hinges are created at the ends of all members connected to joint J3, the resistance of this joint to horizontal displacement is significantly reduced. However, in the previous models, plastic hinges needed to be formed on many more structural members (i.e., mainly the members of the upper floors) for the same effect to occur.

Due to the lower degree of axial restraint, the beam axial force decreases, as shown in Figure 13c. However, as the horizontal displacement of joint J3 increases, the columns connected to this joint are subject to axial tension due to geometric nonlinearity. This causes an increase in the resistance against axial displacement, as shown in Figure 13d, and a corresponding increase in the beam axial force, as shown in Figure 13c. The high rate of increase in the beam axial force significantly enhances the load-carrying capacity of the system at large deflections, as shown in Figure 13a. This response, however, does not represent the actual structural behaviour. These results demonstrate that the edge lateral stiffness of a multi-storey frame is governed by the combined interaction of beam–column systems across multiple floors and cannot be realistically captured using a simplified single-floor model.

4.1.3. Grillage System

By eliminating the columns from the single-floor model, the system is reduced to a grillage model as depicted in Figure 12c. This model has been adopted in many previous studies [7,8,37,57], mainly because it is the simplest model that may consider three-dimensional effects. Compared to the higher-level models examined above, however, the resistance against lateral displacements of joint J3 provided by the flexural stiffness of the columns is neglected. Essentially, the only component left to provide resistance against lateral displacement is the transverse beam connected to this joint. Since the stiffness of the beams against out-of-plane bending is usually limited, the degree of axial restraint is expected to be relatively small—a trend confirmed by the curve shown in Figure 13d.

Therefore, the axial force developed in the beams of the double-span mechanism is limited, as shown in Figure 13c, and, thus, has less influence on the reduction in the bending moments of the connections as depicted in Figure 13b. The load–deflection curve is very close to the corresponding curve of the full structure, as shown in Figure 13a, but the responses of the two models are governed by different collapse resistance mechanisms. Hence, a reliable simulation of structural behaviour cannot be verified solely based on the load–deflection response; it must also be confirmed that the mechanics of deformation and resistance are appropriately represented. These results highlight that the actual structural mechanics can only be captured when the edge lateral stiffness is accurately represented. In a grillage model, this is not possible because most contributing components are absent, and the equivalent edge lateral stiffness is difficult to quantify and simulate through appropriate spring elements.

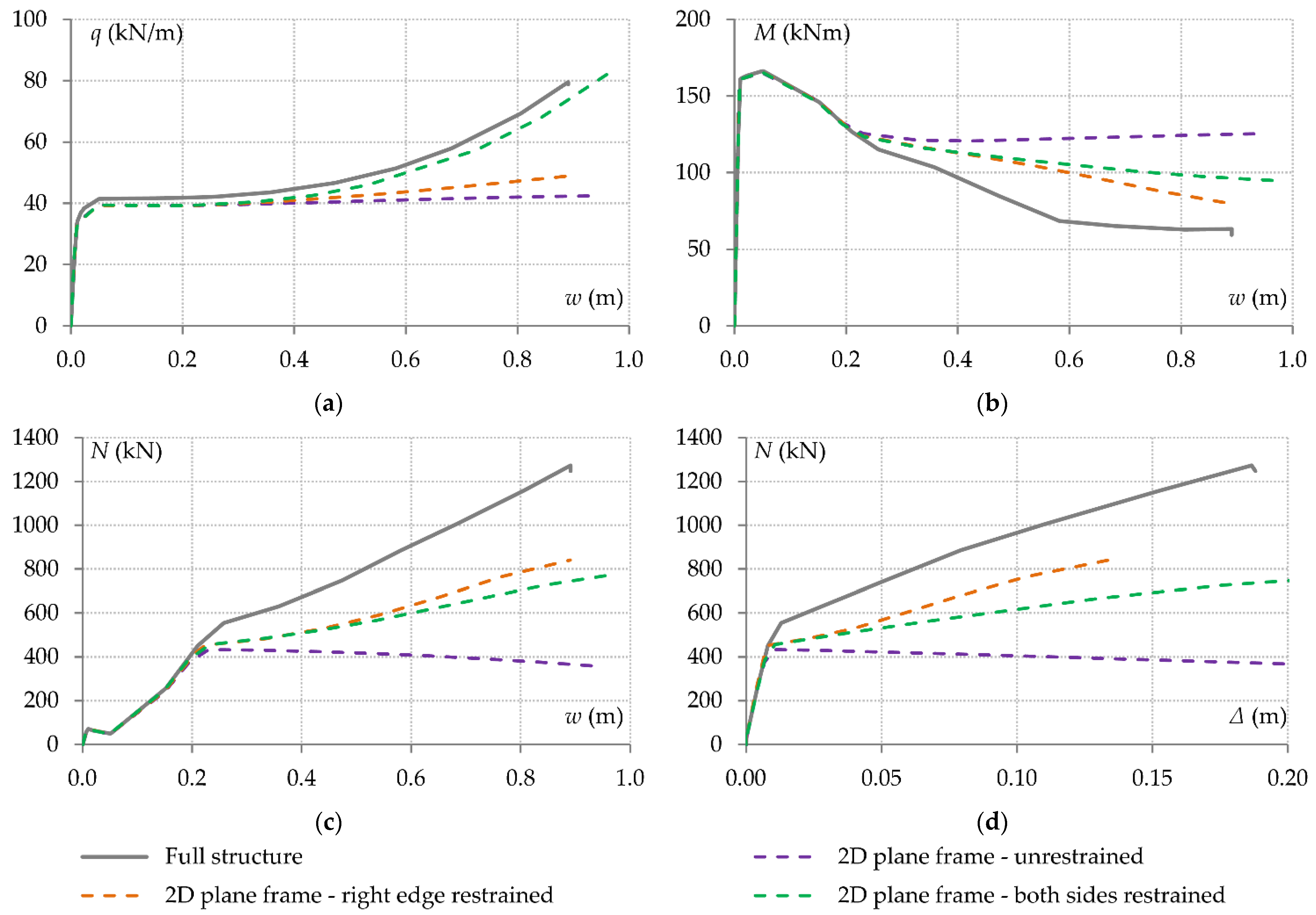
4.2. Multi-Storey Plane Frame

Many experimental and numerical studies have typically focused on two-dimensional simulation models to analyze the behaviour of frame structures under progressive collapse conditions [28,29,51,58]. The objective of this section is to assess whether an isolated multi-storey plane frame model can realistically simulate the actual response of the structure following a notional column removal.

In this case, only the external eight-storey plane frame that includes beams B1 and B2 is considered. The model layout is presented in Figure 14a, which shows that it was obtained by isolating this frame from the structure without applying additional boundary conditions. As a plane frame analysis is applied, the structure cannot undergo out-of-plane deformations. The deformed shape of the system and the distribution of plastic hinges at the plastic collapse limit state are presented in Figure 14b, while the structural behaviour is described by the dashed purple curves of Figure 15. For comparison, the same figure also includes the corresponding results of the full-structure model (solid grey curves), presented in Section 3.

As compared to the response of the full structure, the plane frame model exhibits significantly different behaviour, especially at large deflections. This is mainly due to the absence of tensile catenary effects. As shown in Figure 15d, the degree of axial restraint on the right-hand side (i.e., at the edge of the structure) is the same for the two systems while the response remains elastic. However, a significant decrease occurs in the axial restraint of the plane frame when a plastic hinge is created at the top of the ground floor edge column. Beyond this point, because the bending stiffness of this element is significantly reduced, no additional mechanism remains to resist lateral displacement. For similar reasons, the axial restraint on the left-hand side also decreases—although to a lesser extent—but this is not illustrated in the curves of Figure 15.

The beam tensile force exhibits a gradually decreasing trend, as shown in Figure 15c, with corresponding effects on the bending moments of the connections, which increase (Figure 15b) as the beam deflection increases—in contrast to the reduction observed when significant tensile axial forces develop in the beams. In this case, the system is governed almost entirely by flexural action, and its post-elastic response is characterized by a plateau-type load–deflection curve, as shown in Figure 15a.

The only way to modify the model to more effectively simulate the actual behaviour is to increase the axial stiffness of the supports. However, as also noted in the previous sections, a detailed simulation of the support axial stiffness provided by the surrounding structure is particularly challenging, especially as it depends on a complex interaction of multiple parameters and varies nonlinearly with the progressive formation of plastic hinges in various components. Even if an approximate value of the degree of axial restraint is quantified and simulated using elastic supports to maintain the simplicity of the model, the associated nonlinear effects cannot be captured.

The above simplified solution is examined herein in two steps. First, an approximate value for the degree of axial restraint provided to the right-hand side of the structure is calculated. For joint J3, this value is defined as the post-limit slope of the red curve in Figure 9e, obtained through linear regression. Similarly, the axial restraint provided to all corresponding nodes of the upper floors is calculated based on the respective curves obtained from the analysis of the full structure. On average, it was found that the support axial stiffness is approximately equal to 2030 kN/m. Therefore, in a new model, linear elastic springs with axial stiffness equal to this value are introduced at all nodes on the right-hand side.

As described by the red dashed curves of Figure 15, this modification has an impact on the behaviour, but it still does not satisfactorily approximate the response of the full structure. Similarly, the average value of the axial restraint provided at the joints of the left-hand side (i.e., joint J1 and corresponding joints of upper floors) was found to be equal to approximately 20150 kN/m. By introducing linear elastic springs with axial stiffness equal to this value at all nodes on the left-hand side, the behaviour is modified as described by the green dashed curves of Figure 15. As in the case of the grillage system, the load–deflection curve closely resembles the corresponding curve of the full structure, but it is observed that the component forces are significantly different.

It is concluded that the simulation of the behaviour through a simplified two-dimensional model is limited by insufficient representation of the axial restraint provided by the surrounding structure. The lateral stiffness supplied by the surrounding structure depends on the three-dimensional interaction between the members of the directly affected structural bays and those of the adjacent bays. In particular, the edge lateral stiffness is governed by the flexural stiffness of the directly affected beams and columns, which—as demonstrated in Section 4.1.2 and Section 4.1.3—may vary as plastic hinges develop at the joint regions, making the three-dimensional interaction effects even more significant. These interaction effects, combined with the successive formation of plastic hinges and the resulting progressive reduction in lateral stiffness provided by the surrounding structure to the directly affected beams, are difficult to quantify and cannot be adequately represented using simplified axial and/or rotational springs at the ends of the beams.

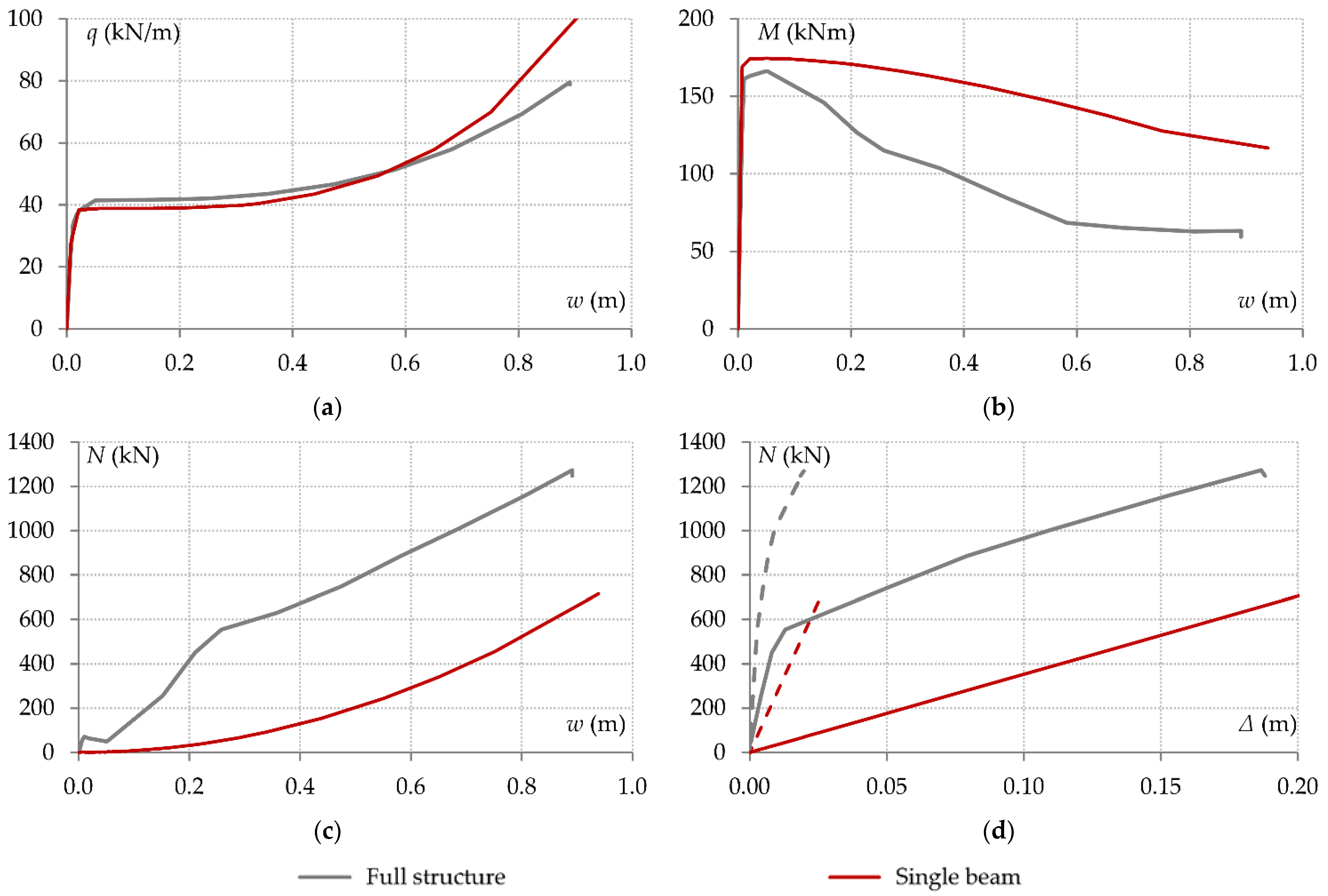
5. Double-Span Beam System

Although several limitations in simulating structural behaviour through lesser levels of structural idealization have already been identified in the previous section, it is worth examining, as a final case, the double-span beam system in isolation. It is easily understood that this system cannot be examined without the consideration of appropriate boundary conditions simulating axial restraint on either side of the double-span beam structure; then, the behaviour will be governed only by flexural action. Therefore, boundary conditions are introduced in the model through two approaches. In Section 5.1, the axial restraint is simulated by linear elastic springs with appropriate axial stiffness. Through a more detailed approach, Section 5.2 examines the variation in the axial stiffness of the supports using bi-linear link elements. The layout of the model and the typical form of the deformed shape at the plastic collapse limit state are shown in Figure 16.

5.1. Simulation of Axial Restraint Through Linear Elastic Springs

Many studies on the progressive collapse of structures focus on the double-span beam mechanism [12,13,14,53]. To enable the mobilization of compressive arching and tensile catenary actions, particular importance is given in these studies to ensure an appropriate degree of axial restraint. In the absence of specific information, an approximation is usually made regarding this parameter, and a degree of axial restraint is determined based on assumptions and simple estimates. In most cases, the axial restraint is approximated through a single value of axial stiffness, representing the resistance of the supports to elastic horizontal displacements.

Based on this consideration, the possibility of accurately approximating the axial restraint of a double-span beam through linear elastic springs is studied herein. There are two issues in this problem. First, as demonstrated in the previous sections, it is unclear whether the axial supports behave elastically. Second, it is not obvious whether the value of the axial stiffness they provide can be easily estimated. Regarding the second issue, as the results of the analysis of the full structure are available (see Section 3), they will be used to determine a representative value of axial stiffness.

The same approach is adopted as in the plane frame of Section 4.2, where the stiffness on either side of the double-span beam is taken as the slope of the post-limit segments of the curves of Figure 9e. Since only the first floor is considered, the values of axial stiffness are larger than the average values used in the plane frame simulation, and specifically, they are equal to 22,200 kN/m and 3550 kN/m, respectively. The results of the analysis are presented in Figure 17, and they are compared with the corresponding results of the full structure. As in some of the cases examined in Section 4, a seemingly representative simulation of the behaviour is obtained through the load–deflection curve in Figure 17a, but this is not supported by the component forces presented in Figure 17b,c.

The difference in the connection bending moments is mainly due to the difference in the beam axial force, which is considerably underestimated because of the assumption made regarding the degree of axial restraint. The results shown in Figure 17d align with that assumption, as the curves corresponding to the double-span beam idealization are parallel to the post-limit parts of the curves corresponding to the full structure. However, the high initial value of the axial stiffness of the supports, which causes a rapid increase in the axial tensile force of the beams at small deflections, is not captured. Thus, it is confirmed that the nonlinear variation in the horizontal displacement of the supports with respect to the increase in the beam axial force has a significant effect on the structural behaviour.

5.2. Simulation of Axial Restraint Through Bi-Linear Links

Provided the characteristics of the nonlinear behaviour of the supports are known, which in practice is rarely the case, a more sophisticated approach can be adopted for simulating performance. Each of the curves in Figure 9e describes an almost bi-linear force–deformation relationship. Therefore, the linear elastic springs of the model of Section 5.1 are replaced herein by bi-linear links with their properties defined according to the detailed curves in Figure 9e, as illustrated in Figure 18. The analysis results are shown in Figure 19 and are again compared with the results of the full-structure model.

Figure 19d confirms that the force–deformation responses of the supports are now represented with sufficient accuracy compared to the full-structure model. For this reason, the variation in the beam axial force is also more accurate, as shown in Figure 19c. Consequently, the variation in the connection bending moments is described more correctly compared to the model of Section 5.1; however, significant deviations are still observed at large deformations according to Figure 19b. These deviations have a significant impact on the load–deflection curve, as shown in Figure 19a.

The significant difference between the bending moments of the connections calculated by the two models indicates that the double-span beam system behaves differently. These results show that the support axial stiffness is not the only boundary condition that significantly affects structural behaviour. Another important factor is the rotational stiffness of the support joints J1 and J3. In addition to the elastic and plastic rotations of the connections, the structural joints undergo additional rigid-body rotations. However, this effect can only be described by the full-structure model; the support joints have been modelled as rigid in terms of rotation in the simplified double-span beam model.

Further modification of the characteristics of the supports to take into account the deformability of the joints is extremely difficult to implement. On the one hand, it is nearly impossible in practice to predict these rotational deformations. On the other hand, the rotations of the joints depend on the redistribution of load to the various members as the stiffness of the elements connected to these joints decreases. The changes in the rotations (Φ) of joints J1 and J3 of the full-structure model with respect to the beam displacement are presented in Figure 20a. It is observed that these curves are neither linear nor monotonic.

The corresponding relationships between the bending moments of the connections included in these joints and the joint rotations are presented in Figure 20b. The curves confirm that these rotations are largely independent of the moments transferred by beams B1 and B2, respectively, instead depending primarily on the interaction with the structural components of the surrounding structure. However, such interaction effects can only be described by the full-structure model, or by reduced models of a sufficient level of structural idealization, such as, for example, the 3D multiple-storey system examined in Section 4.

6. Conclusions

Through this study, the potential of simulating the progressive collapse behaviour of frame structures using different analysis models, representing varying levels of structural idealization, was examined. The characteristics of the studied structure and the method of simulating structural behaviour through a specific notional column removal scenario were carefully determined to allow meaningful conclusions aligned with the study objectives. In addition to the full-structure model, simplified three-dimensional and two-dimensional models were analyzed, as well as the double-span beam model, which represents the lower level of structural idealization for progressive collapse analysis.

The main conclusions of the study are as follows:

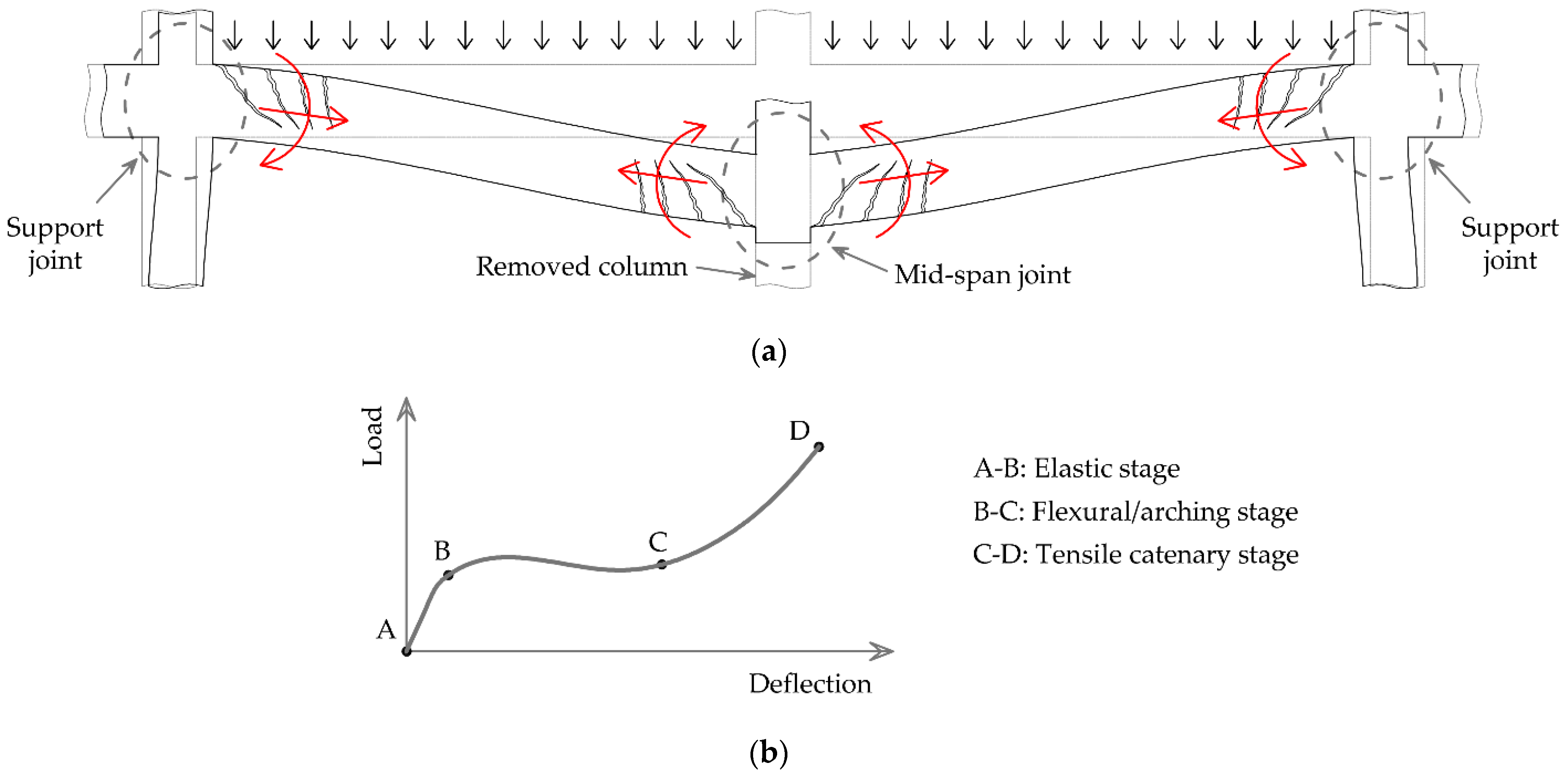
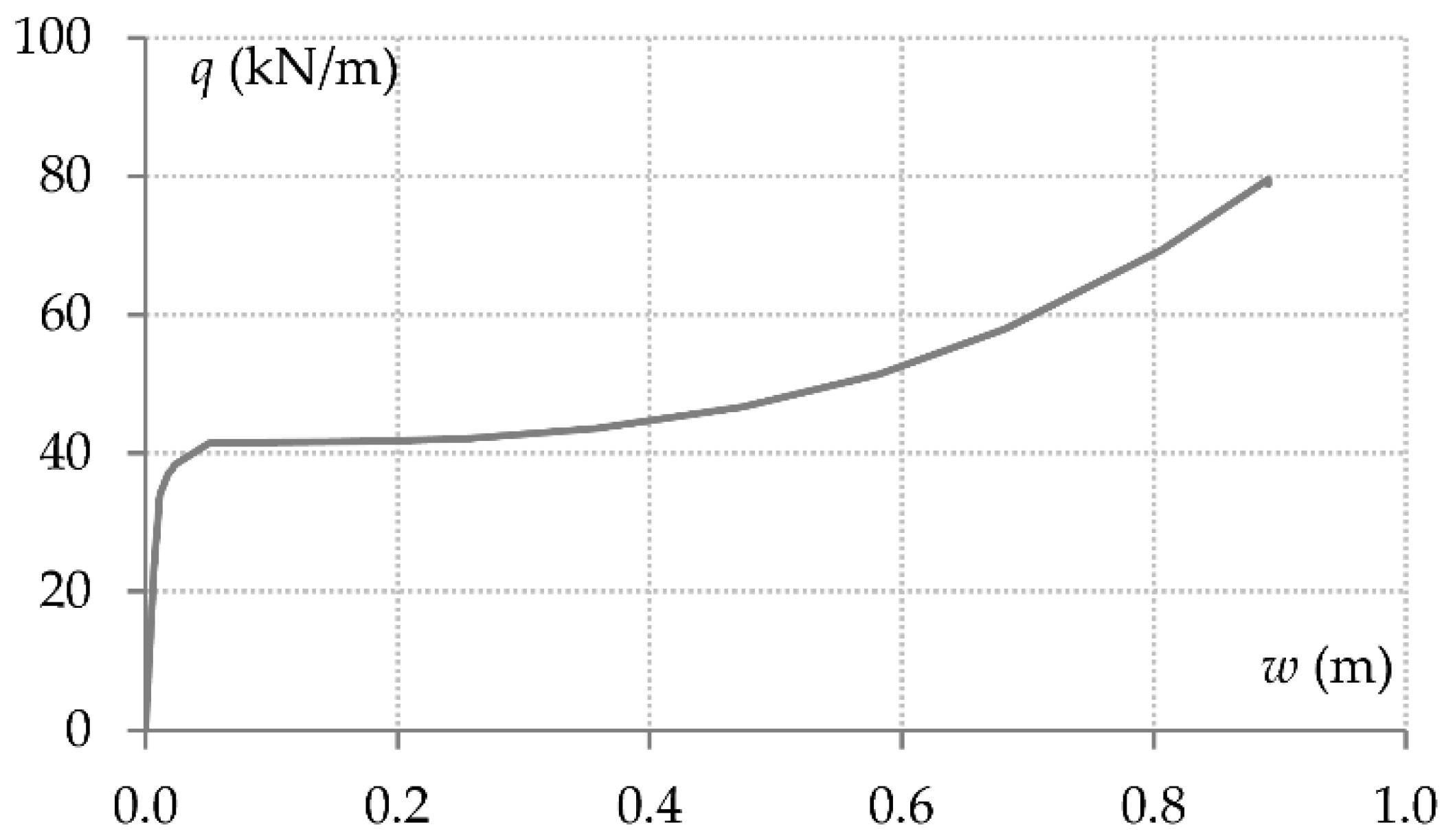
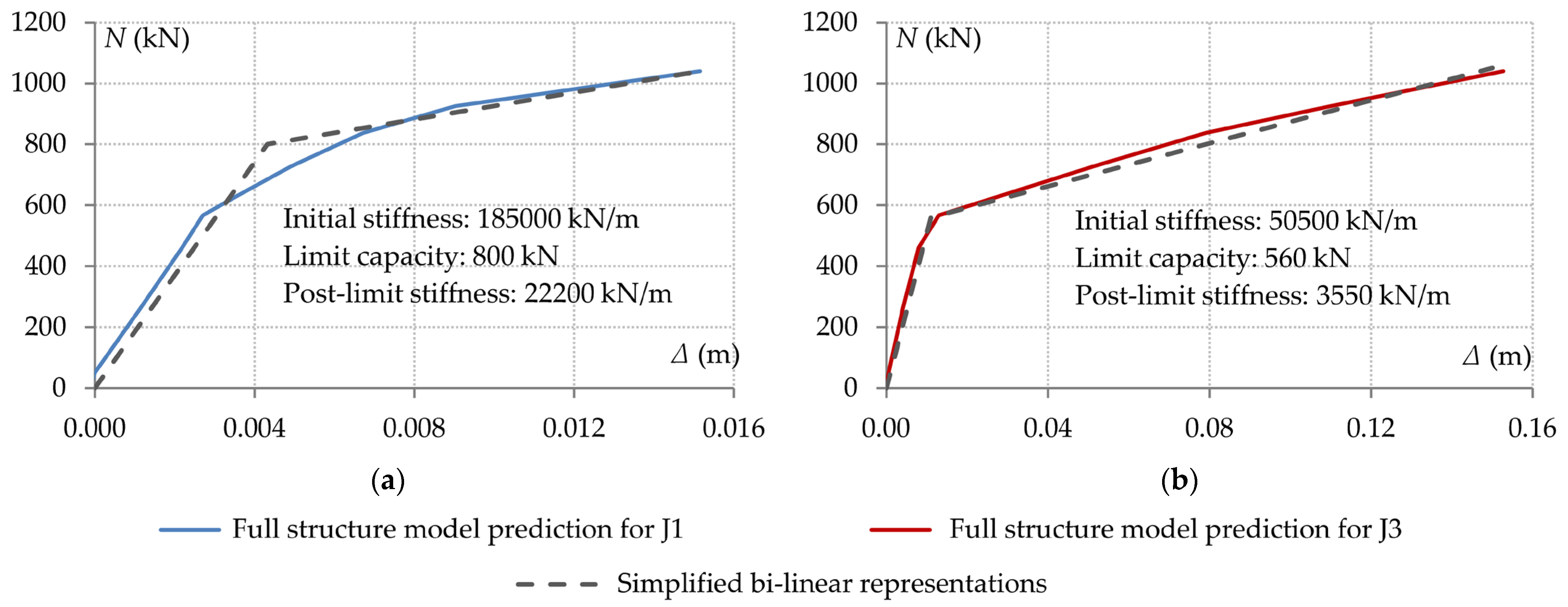
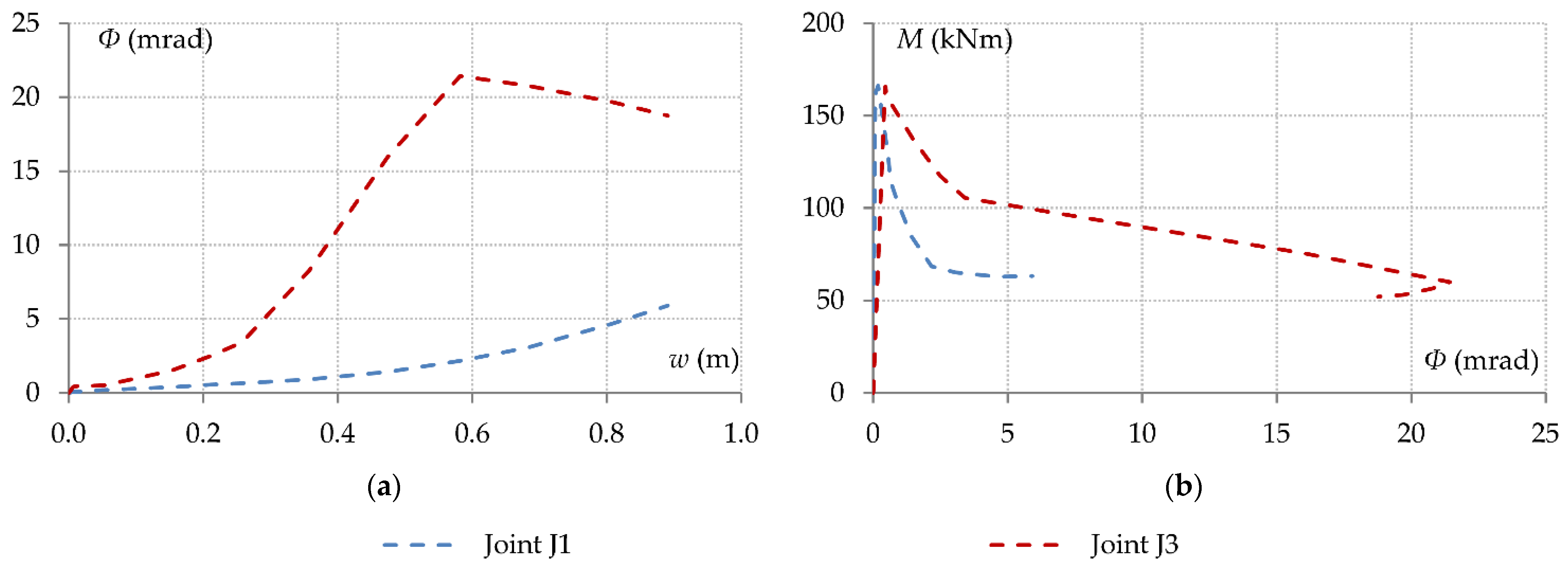
• The axial displacement of the supports of the system that is directly affected by the column loss is significantly influenced by material nonlinearity due to the formation of plastic hinges in adjacent structural elements. As a result, the relationship between the support axial displacements and the axial forces transferred from the end connections is highly nonlinear. The axial restraint is also governed by the redundancy of the structure on either side of the directly affected area, the out-of-plane flexural stiffness of the transverse beams and the in-plane bending stiffness of the surrounding columns.
• In a ground-floor column removal scenario, the ground-floor neighbouring columns are subject to considerably higher bending moments and deformations due to their support boundary restraints, compared with upper-floor columns. Consequently, the axial forces in the upper-floor beams are substantially smaller than those in the first-floor beams. Therefore, the responses of the beams of different floors are governed by very different load-resistance mechanisms.
• A 3D multiple-floor model can describe structural performance with reasonable accuracy. A 3D single-floor model, on the other hand, does not capture the effects of axial restraint adequately. The resistance of the supports to horizontal displacement decreases significantly when the strength of the neighbouring elements is exhausted. However, at large deformation stages, the support axial stiffness increases due to geometric nonlinear effects, which is not representative of the actual structural behaviour. In a grillage model, a reasonable approximation of the load–deflection response was obtained in this study, but it was shown that this resulted from an inaccurate representation of the contributions of different load resistance mechanisms.
• Plane frame models fail to reproduce boundary conditions sufficiently. Key elements of the surrounding structure, such as the transverse beams, are omitted. The representation of axial restraint through linear elastic springs will most likely lead to incorrect results, as the axial deformation of the supports varies nonlinearly. This approximation may also result in incorrect assessment of the contribution of the different load resistance mechanisms, similar to the limitations observed in the grillage model.
• In the double-span beam model, the axial restraint should be simulated with sufficient accuracy. Since the resistance provided by the supports against horizontal displacements varies nonlinearly with respect to the increase in the beam tensile force, linear elastic springs cannot describe the boundary conditions accurately. Instead, by employing suitable links with bi-linear force–deformation characteristics, a more representative approximation is obtained. However, it is found that, although the beam axial force is described accurately, connection bending moments may deviate from actual values. This shows that another parameter that influences the progressive collapse response is the rotational stiffness provided to the support joints from the surrounding structure.

Based on these observations, it is concluded that for reliable progressive collapse analysis, either the full structural model should be considered, or at least a reduced model that explicitly accounts for the axial and rotational stiffness of supports. For lower levels of structural idealization, careful representation of boundary conditions is essential. This remains challenging, as both the axial and rotational stiffness of supports are difficult to quantify and exhibit strongly nonlinear behaviour.

The primary recommendation of this study is that accurate modelling of axial and rotational restraints is critical to capture progressive collapse mechanisms. The main challenge lies in defining these support parameters reliably across different structural configurations. Limitations of the current work include the use of simplified link representations and the absence of detailed material or connection modelling beyond the primary beams and supports. Future research should focus on developing high-fidelity finite element models that capture the full distribution of plastic stresses and strains, investigate the sensitivity of progressive collapse response to support stiffness parameters, and explore practical strategies for simplifying the models without compromising accuracy. Such studies will improve understanding of progressive collapse mechanisms and support the development of more reliable and computationally efficient predictive tools.