Numerical Simulation and Optimization of Novel and Efficient Screw Structures for Spinnable Pitch
Abstract
1. Introduction
2. Mixing Component Structure Design
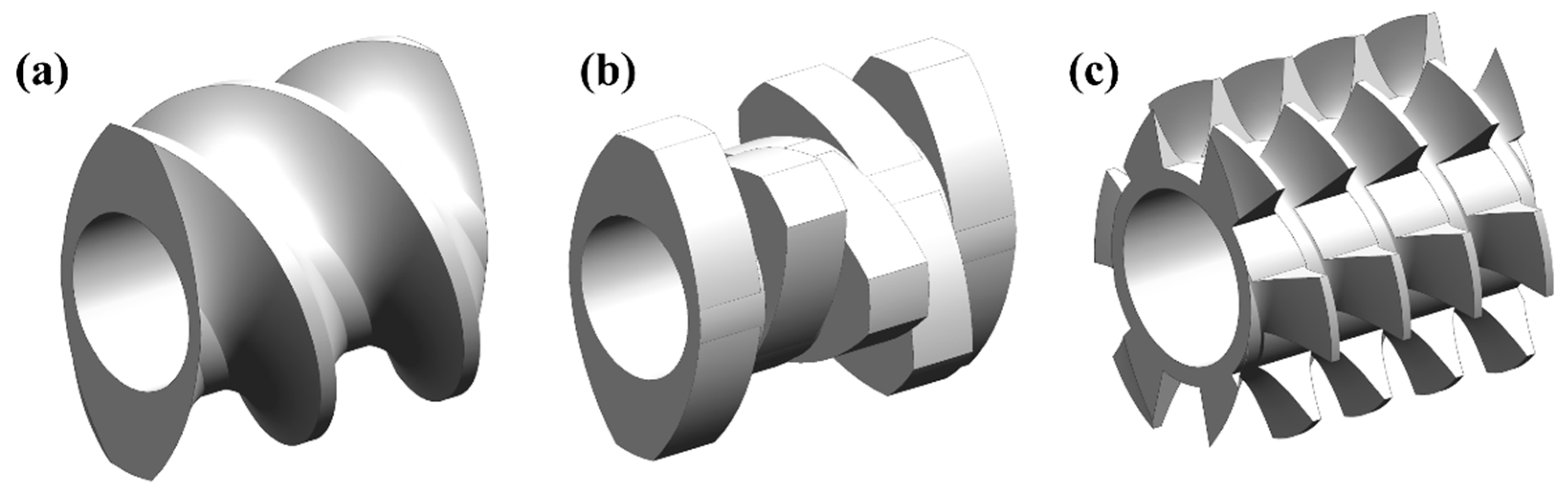
2.1. Design of Novel Mixing Screw Elements
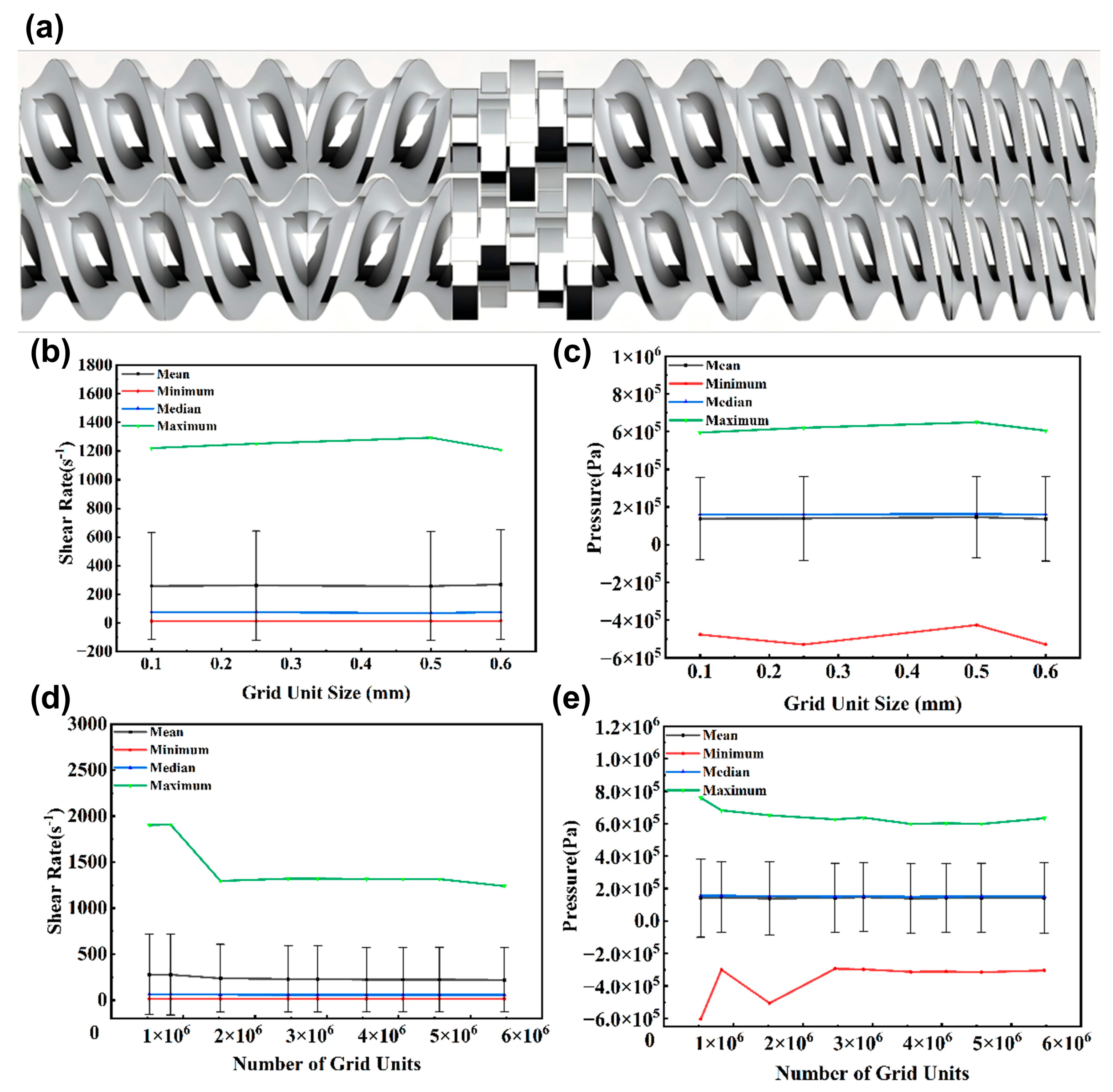
2.2. Grid Independence Verification
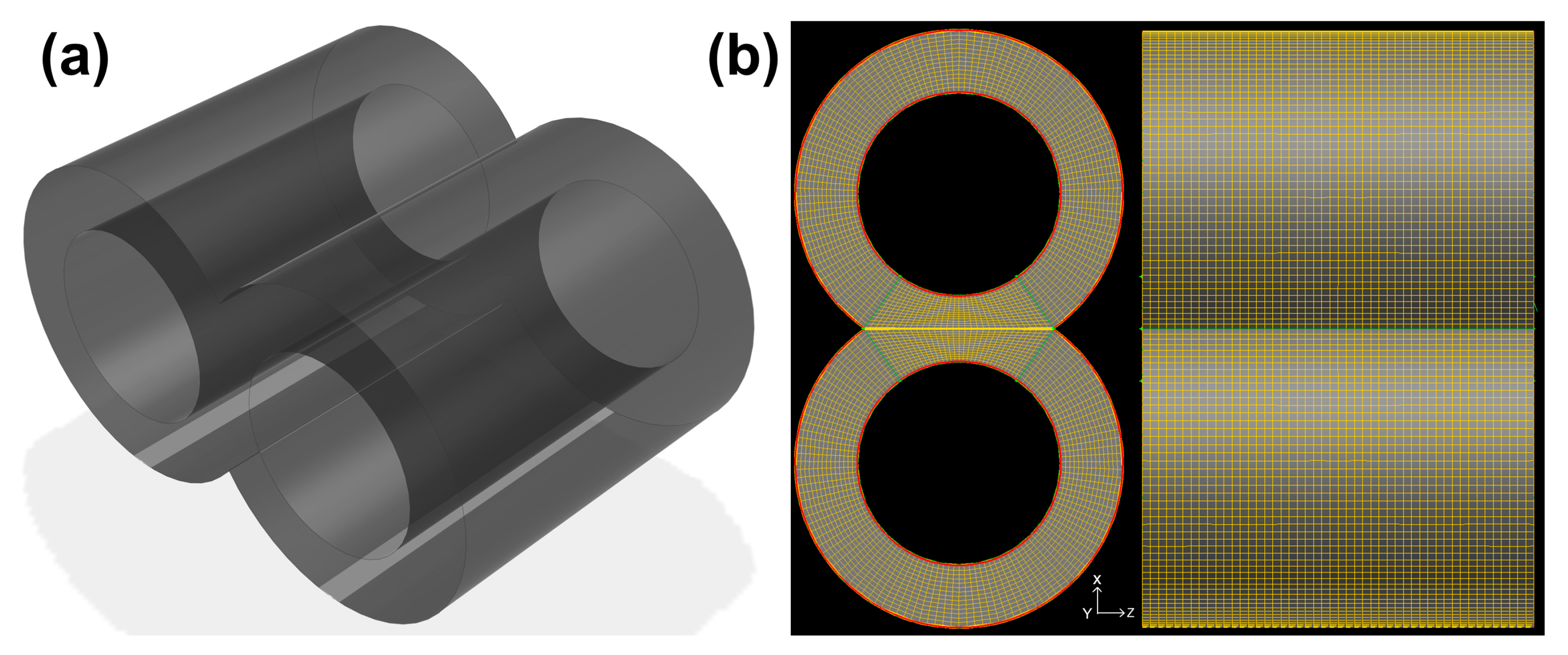
2.3. Mesh Generation and Dynamic Grid Simulation
3. Theoretical Basis of Flow Simulation
3.1. Basic Assumptions and Governing Equations
3.2. Raw Material Rheological Testing and Constitutive Equations
3.3. Boundary Conditions
4. Results and Discussion
4.1. Flow Characteristics Analysis
4.2. Distribution Effect
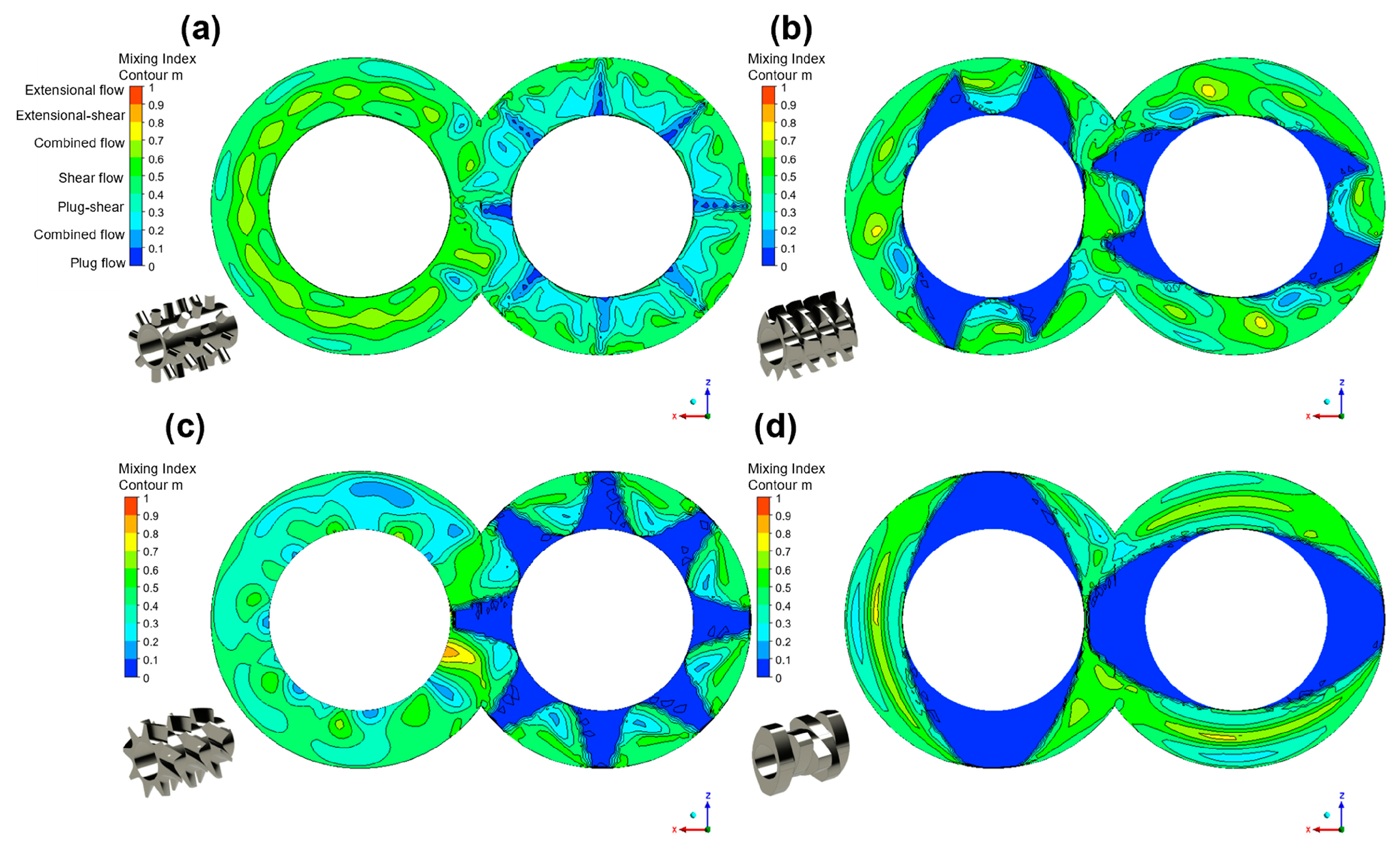
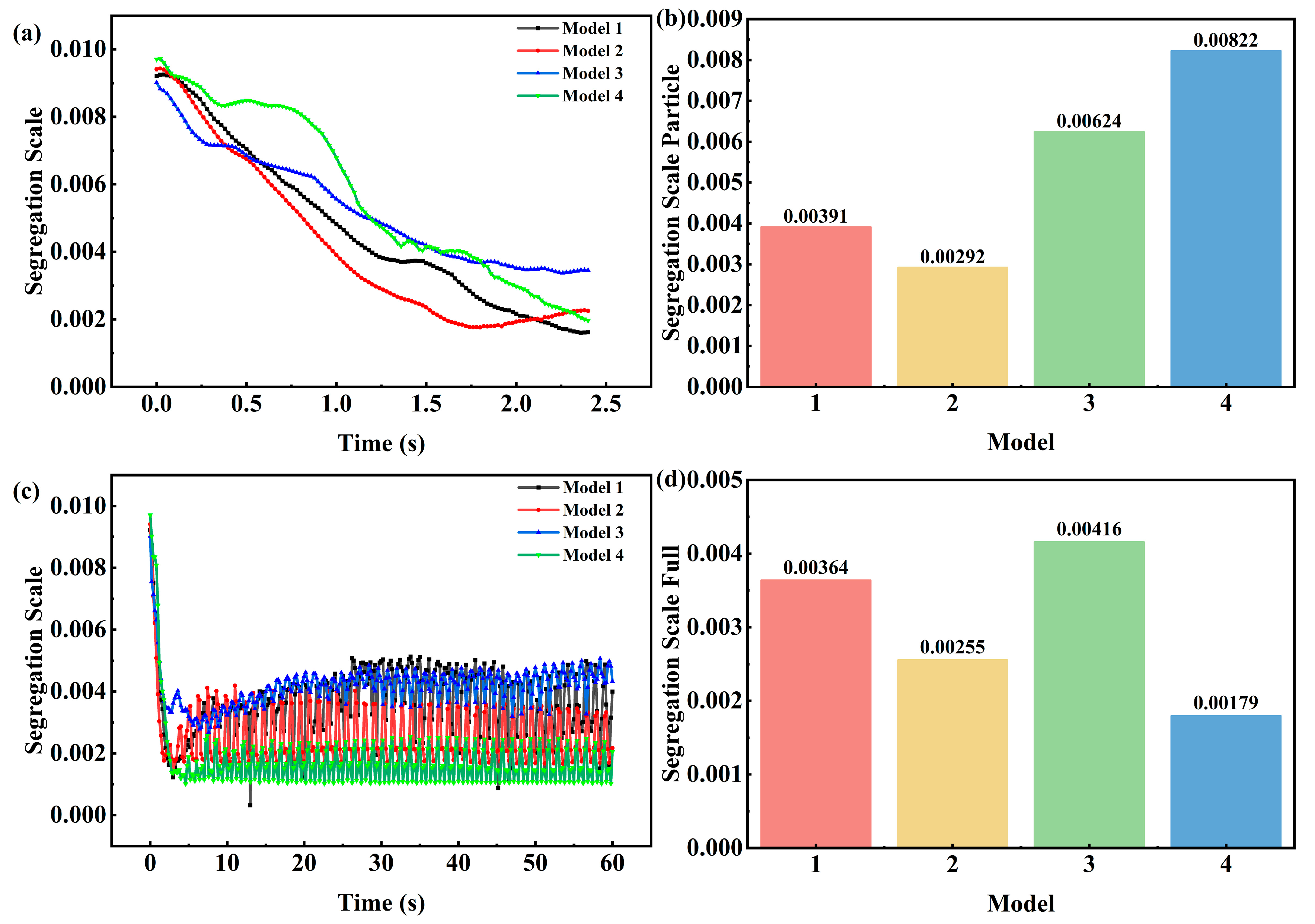
4.3. Mixing Effect
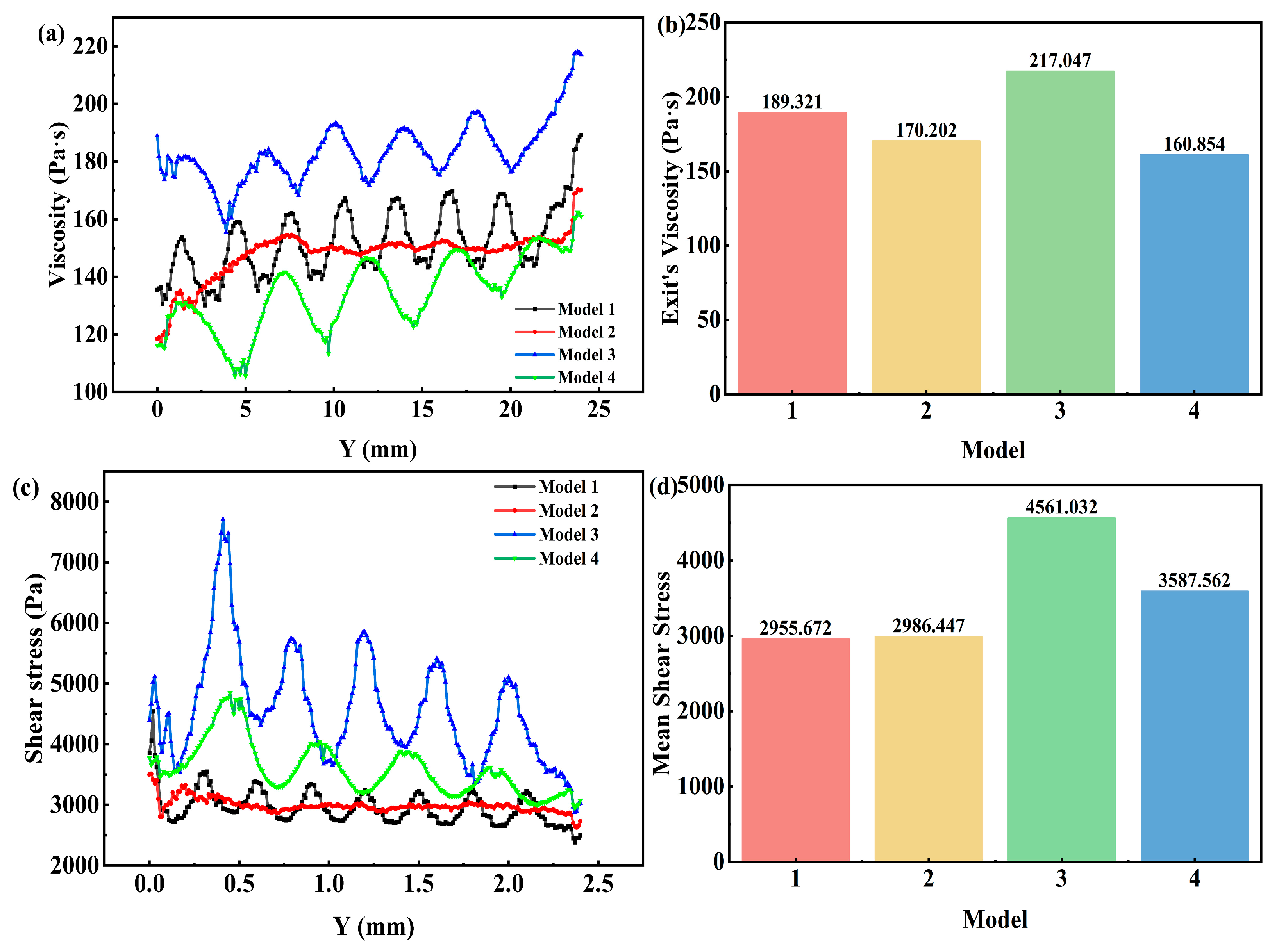
4.4. Shear Effect
4.5. Comprehensive Evaluation of Mixing Effect
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, C.; Yan, J.; Zhang, Z.; Yu, D.; Wang, S.; Jiang, X.; Ai, C.; Leng, Z. Screw extrusion process used in the polymer modified asphalt field: A review. J. Clean. Prod. 2024, 448, 141592. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.A.; Sikora, J. Optimization of Polymer Processing: A Review (Part I—Extrusion). Materials 2022, 15, 384. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A composite model for an intermeshing counter-rotating twin-screw extruder and its experimental verification. Polym. Eng. Sci. 2015, 55, 2838–2848. [Google Scholar] [CrossRef]
- Lin, B.; Thümen, A.; Heim, H.; Scheel, G.; Sundararaj, U. Nylon 66/Clay Nanocomposite Structure Development in a Twin Screw Extruder. Polym. Eng. Sci. 2009, 49, 824–834. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K. Modeling of twin screw extrusion of polymeric materials. Polymers 2022, 14, 274. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Li, J.; Zhang, S.; Li, N.; Li, B.; Zhang, Q.; Ge, L. Excellent microwave absorption of lightweight PAN-based carbon nanofibers prepared by electrospinning. Colloids Surf. A Physicochem. Eng. Asp. 2022, 651, 129670. [Google Scholar] [CrossRef]
- Kang, D.J.; Pal, K.; Bang, D.S.; Kim, J.K. Synergistic Effect on Crystalline Structure of Polyvinylidene Fluoride Nanocomposites with Multiwalled Carbon Nanotube Loading by a Twin Screw Extruder. J. Appl. Polym. Sci. 2011, 121, 226–233. [Google Scholar] [CrossRef]
- Laske, S.; Witschnigg, A.; Selvasankar, R.K.; Holzer, C. Measuring the residence time distribution in a twin screw extruder with the use of NIR-spectroscopy. J. Appl. Polym. Sci. 2014, 131, 39919. [Google Scholar] [CrossRef]
- Naser, M.A.; Moeaz, W.A.; El-Wakad, M.T.; Abdo, M.S. Design a Single Screw Extruder for Polymer-Based Tissue Engineering. Biomed. Eng. Appl. Basis Commun. 2024, 36, 2450015. [Google Scholar] [CrossRef]
- Eitzlmayr, A.; Khinast, J. Co-rotating twin-screw extruders: Detailed analysis of conveying elements based on smoothed particle hydrodynamics. Part 2: Mixing. Chem. Eng. Sci. 2015, 134, 880–886. [Google Scholar] [CrossRef]
- Ohara, M.; Sasai, Y.; Umemoto, S.; Obata, Y.; Sugiyama, T.; Tanifuji, S.-I.; Kihara, S.-I.; Taki, K. Experimental and numerical simulation study of devolatilization in a self-wiping corotating parallel twin-screw extruder. Polymers 2020, 12, 2728. [Google Scholar] [CrossRef]
- Bravo, V.L.; Hrymak, A.N.; Wright, J.D. Numerical simulation of pressure and velocity profiles in kneading elements of a co-rotating twin screw extruder. Polym. Eng. Sci. 2000, 40, 525–541. [Google Scholar] [CrossRef]
- Ishikawa, T.; Amano, T.; Kihara, S.; Funatsu, K. Flow patterns and mixing mechanisms in the screw mixing element of a co-rotating twin-screw extruder. Polym. Eng. Sci. 2002, 42, 925–939. [Google Scholar] [CrossRef]
- Russell, K. How to Configure Your Twin-Screw Extruder-Part 2. Plast. Technol. 2023, 69, 24–26+28. [Google Scholar]
- Potente, H.; Schultheis, S.M. Investigations of the Residence Time and the Longitudinal Mixing Behavior in Counter-rotating Twin Screw Extruders. Int. Polym. Process. 1989, 4, 255–261. [Google Scholar] [CrossRef]
- Oberlehner, J.; Cassagnau, P.; Michel, A. Local residence time distribution in a twin screw extruder. Chem. Eng. Sci. 1994, 49, 3897–3907. [Google Scholar] [CrossRef]
- Kaushal, A.; Singh, V. Analysis of mechanical, thermal, electrical and EMI shielding properties of graphite/carbon fiber reinforced polypropylene composites prepared via a twin screw extruder. J. Appl. Polym. Sci. 2021, 139, 51444. [Google Scholar] [CrossRef]
- Brzoskowski, R.; Kubota, K.; Chung, K.; White, J.L.; Weissert, F.C.; Nakajima, N.; Min, K. Experimental and Theoretical Study of the Flow Characteristics of Rubber Compounds in an Extruder Screw. Int. Polym. Process. 1987, 2, 130–136. [Google Scholar] [CrossRef]
- Charasseangpaisarn, T.; Wiwatwarrapan, C.; Thunyakitpisal, P.; Srimaneepong, V. Development of poly(methyl methacrylate)/poly(lactic acid) blend as sustainable biomaterial for dental applications. Sci. Rep. 2023, 13, 16904. [Google Scholar] [CrossRef]
- Ren, J.; Zhao, J.; Liu, X. The application of genetic algorithm for the design of screw in twin-screw extruder. World J. Eng. 2017, 14, 451–458. [Google Scholar] [CrossRef]
- Robinson, M.; Cleary, P.W. Flow and mixing performance in helical ribbon mixers. Chem. Eng. Sci. 2012, 84, 382–398. [Google Scholar] [CrossRef]
- Hu, D.D.; Chen, J.N. Simulation of particle trajectories and statistical analysis in twin-screw extruders. Funct. Graded Mater. Vii 2003, 423, 753–757. [Google Scholar]
- Hwang, W.R.; Kwon, T.H. Dynamical modeling of chaos single-screw extruder and its three-dimensional numerical analysis. Polym. Eng. Sci. 2000, 40, 702–714. [Google Scholar] [CrossRef]
- Kadyirov, A.; Gataullin, R.; Karaeva, J. Numerical simulation of polymer solutions in a single-screw extruder. Appl. Sci. 2019, 9, 5423. [Google Scholar] [CrossRef]
- Acur, E.; Vlachopoulos, J. Numerical simulation of a single-screw plasticating extruder. Polym. Eng. Sci. 1982, 22, 1084–1094. [Google Scholar] [CrossRef]
- Yang, H.; Manas-Zloczower, I. Flow field analysis of the kneading disc region in a co-rotating twin screw extruder. Polym. Eng. Sci. 1992, 32, 1411–1417. [Google Scholar] [CrossRef]
- Fard, A.S.; Anderson, P.D. Simulation of distributive mixing inside mixing elements of co-rotating twin-screw extruders. Comput. Fluids 2013, 87, 79–91. [Google Scholar] [CrossRef]
- Qi, D.; Li, S.; Zhao, C.; Xie, W.; Li, A. Structural optimization of multi-pipe earth to air heat exchanger in greenhouse. Geothermics 2022, 98, 102288. [Google Scholar] [CrossRef]
- Bai, H.; Qin, W.; Jia, S.; Ren, L.; An, Y.; Bao, J. A New Type of 3D Printing Molding Equipment: Overall Structural Design and the Numerical Simulation for the Flow Field Characteristics of its Screw Module. Int. J. Precis. Eng. Manuf. 2021, 22, 1639–1656. [Google Scholar] [CrossRef]
- Lv, X.; Hao, X.; Ou, R.; Liu, T.; Guo, C.; Wang, Q.; Yi, X.; Sun, L. Rheological Properties of Wood-Plastic Composites by 3D Numerical Simulations: Different Components. Forests 2021, 12, 417. [Google Scholar] [CrossRef]
- Ren, R.; Huijun, H.; Chenxi, C. Preparation method of pitch based carbon fiber and its industrialization research. Appl. Chem. Ind. 2018, 47, 2254–2259. [Google Scholar]



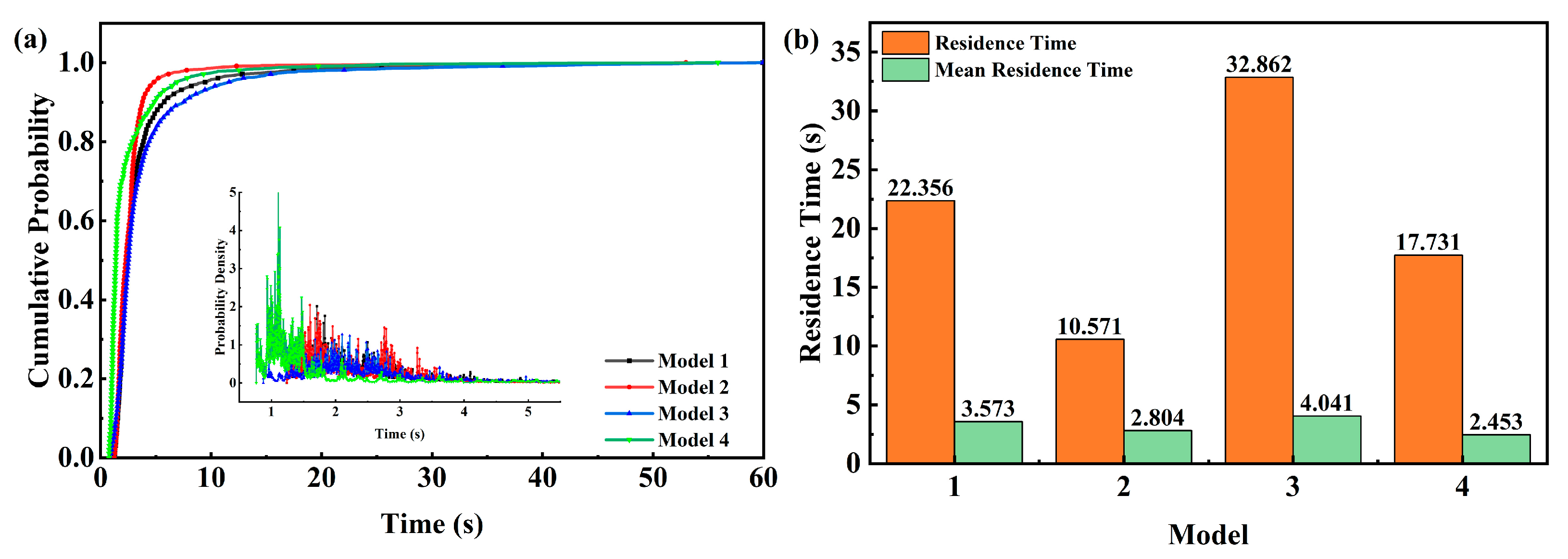




| Model Name | ts/s | t99/s | RT/s | MRT/s |
|---|---|---|---|---|
| Model 1 | 1.140 | 24.894 | 23.754 | 3.681 |
| Model 2 | 1.135 | 14.715 | 13.580 | 2.818 |
| Model 3 | 0.874 | 33.736 | 32.862 | 4.040 |
| Model 4 | 0.749 | 16.561 | 15.812 | 2.358 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Shi, Z.; Jiang, W.; Zhang, G.; Cai, H.; Zhu, B.; Qiao, K. Numerical Simulation and Optimization of Novel and Efficient Screw Structures for Spinnable Pitch. Modelling 2025, 6, 140. https://doi.org/10.3390/modelling6040140
Peng W, Shi Z, Jiang W, Zhang G, Cai H, Zhu B, Qiao K. Numerical Simulation and Optimization of Novel and Efficient Screw Structures for Spinnable Pitch. Modelling. 2025; 6(4):140. https://doi.org/10.3390/modelling6040140
Chicago/Turabian StylePeng, Wenzhen, Zhiwei Shi, Wenzheng Jiang, Guodong Zhang, Huitao Cai, Bo Zhu, and Kun Qiao. 2025. "Numerical Simulation and Optimization of Novel and Efficient Screw Structures for Spinnable Pitch" Modelling 6, no. 4: 140. https://doi.org/10.3390/modelling6040140
APA StylePeng, W., Shi, Z., Jiang, W., Zhang, G., Cai, H., Zhu, B., & Qiao, K. (2025). Numerical Simulation and Optimization of Novel and Efficient Screw Structures for Spinnable Pitch. Modelling, 6(4), 140. https://doi.org/10.3390/modelling6040140







