Spirally Coiled Tube Flocculators: A New Hydrodynamic Design for Water Treatment
Abstract
1. Introduction
2. Methodology
- (a)
- Experimental tests measured turbidity removal efficiency under controlled operating conditions. Identical inlet flow rates and coagulant dosages were applied to both geometries, enabling direct comparison of clarification performance.
- (b)
- CFD modeling simulated and analyzed internal flow behavior in each flocculator. The simulations provided detailed information on streamline distribution, axial and secondary flow patterns, and hydrodynamic indicators, clarifying the impact of geometric differences on flocculation potential.
2.1. Geometry of the Flocculators
2.2. CFD Modeling
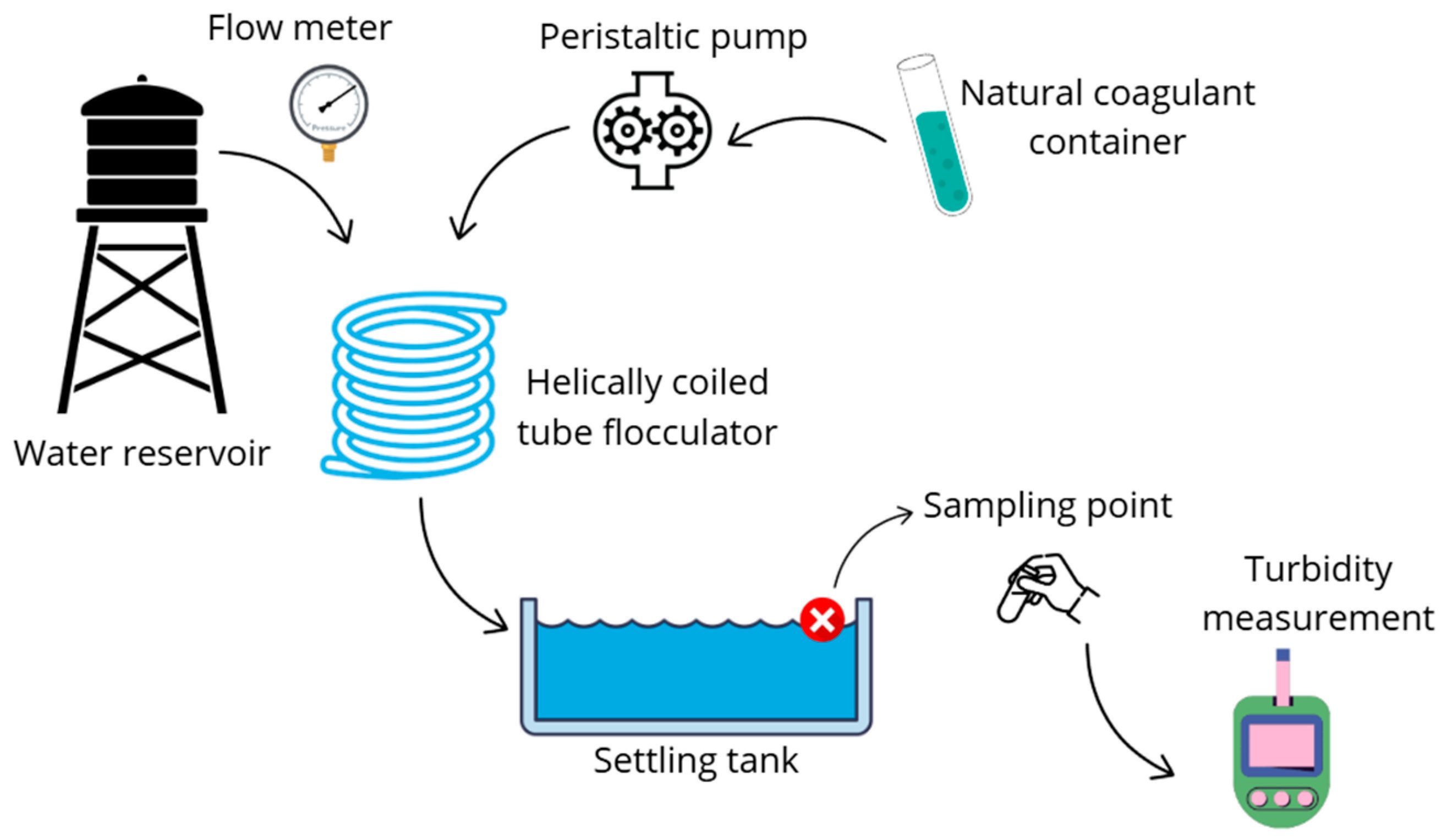
2.3. Experimental Evaluation
2.3.1. Preparation of Synthetic Water
2.3.2. Preparation of the Natural Coagulant from Moringa oleifera
2.3.3. Jar Test Assays
2.3.4. Hydraulic Circuit Tests
3. Results and Discussion
3.1. Experimental Evaluation Results
3.1.1. Jar Test Assays: Determination of Coagulant Concentration
3.1.2. Hydraulic Circuit Performance
3.2. CFD Modeling Results
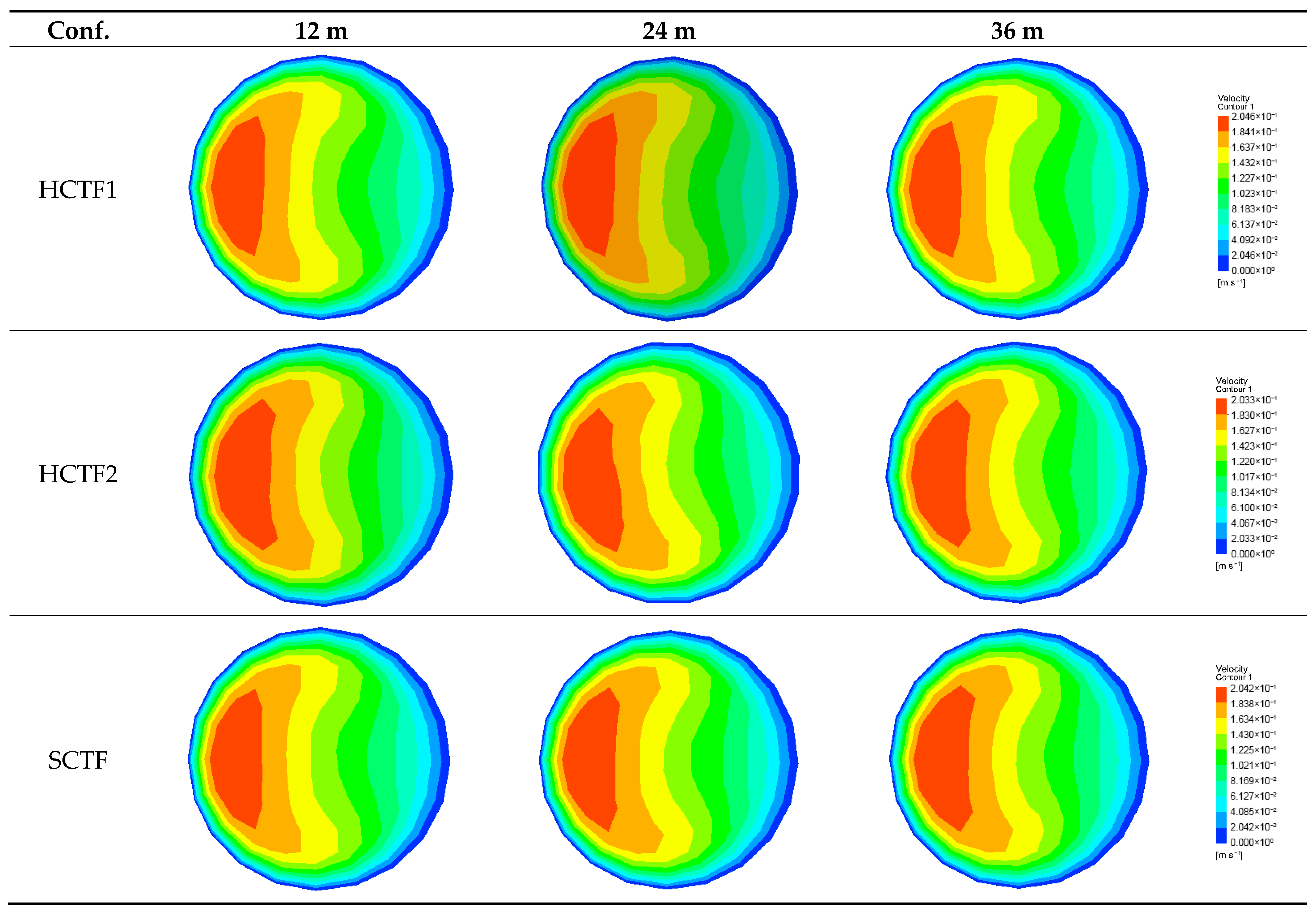
3.2.1. Axial Velocity Profiles
3.2.2. Secondary Flows
3.2.3. Streamlines
3.2.4. Head Loss and Global Velocity Gradient
3.3. Integration of Experimental and CFD Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mishra, B.K.; Kumar, P.; Saraswat, C.; Chakraborty, S.; Gautam, A. Water Security in a Changing Environment: Concept, Challenges and Solutions. Water 2021, 13, 490. [Google Scholar] [CrossRef]
- Li, X.; Yang, H.Y. A Global Challenge: Clean Drinking Water. Glob. Chall. 2021, 5, 2000125. [Google Scholar] [CrossRef]
- Pooi, C.K.; Ng, H.Y. Review of low-cost point-of-use water treatment systems for developing communities. npj Clean Water 2018, 1, 11. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, H.; Tan, C.; Lian, B.; García-Pacheco, R.; Taylor, R.A.; Fletcher, J.; Le-Clech, P.; Ranasinghe, B.; Senevirathna, T.; et al. Numerical and experimental investigation of a DC-powered RO system for Sri-Lankan villages. Renew. Energy 2022, 182, 772–786. [Google Scholar] [CrossRef]
- Gwenzi, W.; Chaukura, N.; Noubactep, C.; Mukome, F.N. Biochar-based water treatment systems as a potential low-cost and sustainable technology for clean water provision. J. Environ. Manag. 2017, 197, 732–749. [Google Scholar] [CrossRef] [PubMed]
- Hartemann, P.; Montiel, A. History and Development of Water Treatment for Human Consumption. Hygiene 2025, 5, 6. [Google Scholar] [CrossRef]
- Adams, E.A.; Stoler, J.; Adams, Y. Water insecurity and urban poverty in the Global South: Implications for health and human biology. Am. J. Hum. Biol. 2019, 32, e23368. [Google Scholar] [CrossRef] [PubMed]
- Prüss-Ustün, A.; Wolf, J.; Bartram, J.; Clasen, T.; Cumming, O.; Freeman, M.C.; Gordon, B.; Hunter, P.R.; Medlicott, K.; Johnston, R. Burden of disease from inadequate water, sanitation and hygiene for selected adverse health outcomes: An updated analysis with a focus on low- and middle-income countries. Int. J. Hyg. Environ. Health 2019, 222, 765–777. [Google Scholar] [CrossRef]
- Joy, K.; Kulkarni, S.; Roth, D.; Zwarteveen, M. Re-politicising water governance: Exploring water re-allocations in terms of justice. Local Environ. 2014, 19, 954–973. [Google Scholar] [CrossRef]
- Bolatova, Z.; Sharapatova, R.; Kabiyev, Y.; Berndtsson, R.; Tussupova, K. Towards Sustainable Solutions: Assessing Rural Access to Safe Drinking Water and Sanitation in Atyrau, Kazakhstan. Water 2025, 17, 664. [Google Scholar] [CrossRef]
- Saritha, V.; Srinivas, N.; Vuppala, N.V.S. Analysis and optimization of coagulation and flocculation process. Appl. Water Sci. 2015, 7, 451–460. [Google Scholar] [CrossRef]
- Silva, J.R.; Oliveira, D.S. Water Treatment with Clean Technologies Using Moringa oleifera Seeds in Alternative Low-Cost Clarification Units. Clean Technol. 2024, 6, 625–645. [Google Scholar] [CrossRef]
- Sharma, S.; Bhattacharya, A. Drinking water contamination and treatment techniques. Appl. Water Sci. 2017, 7, 1043–1067. [Google Scholar] [CrossRef]
- Sartori, M.; Oliveira, D.S.; Teixeira, E.C.; Rauen, W.B.; Reis, N.C. CFD modelling of helically coiled tube flocculators for velocity gradient assessment. J. Braz. Soc. Mech. Sci. Eng. 2014, 37, 187–198. [Google Scholar] [CrossRef]
- Oliveira, D.S.; Teixeira, E.C. Hydrodynamic characterization and flocculation process in helically coiled tube flocculators: An evaluation through streamlines. Int. J. Environ. Sci. Technol. 2017, 14, 2561–2574. [Google Scholar] [CrossRef]
- Oliveira, D.S.; Teixeira, E.C. Experimental evaluation of helically coiled tube flocculators for turbidity removal in drinking water treatment units. Water SA 2017, 43, 378–386. [Google Scholar] [CrossRef]
- Oliveira, D.S.; Teixeira, E.C. Swirl number in helically coiled tube flocculators: Theoretical, experimental, and CFD modeling analysis. Int. J. Environ. Sci. Technol. 2018, 16, 3735–3744. [Google Scholar] [CrossRef]
- Oliveira, D.S.; Donadel, C.B. Helically Coiled Tube Flocculators in Water Clarification Systems: Optimal Length Evaluation and Process Efficiency Probabilistic Analysis. Sustainability 2024, 16, 2172. [Google Scholar] [CrossRef]
- Garcia-Avila, F.; Cadme-Tandazo, J.; Aviles-Anazco, A.; Valdiviezo-Gonzales, L.; Cabello-Torres, R.; Cadme-Galabay, M. Experimental approach and analysis of the effectiveness of a tubular helical flow flocculator for water supply in developing communities. Heliyon 2024, 10, e33101. [Google Scholar] [CrossRef]
- Ramesh, E.; Jalali, A. Machine-learning based multi-objective optimization of helically coiled tube flocculators for water treatment. Chem. Eng. Res. Des. 2023, 197, 931–944. [Google Scholar] [CrossRef]
- Zhan, M.; You, M.; Liu, L.; Zhang, Y.; Yuan, F.; Guo, B.; Cheng, G.; Xu, W. Numerical simulation of mechanical flocculation in water treatment. J. Environ. Chem. Eng. 2021, 9, 105536. [Google Scholar] [CrossRef]
- Lazarev, S.; Protasov, D.; Konovalov, D.; Khorokhorina, I.; Abonosimov, O. Modeling of the Nanofiltration Process Based on Convective Diffusion Theory. Modelling 2024, 5, 1729–1744. [Google Scholar] [CrossRef]
- Langarudi, S.P.; Sabie, R.P.; Bahaddin, B.; Fernald, A.G. A Literature Review of Hybrid System Dynamics and Agent-Based Modeling in a Produced Water Management Context. Modelling 2021, 2, 224–239. [Google Scholar] [CrossRef]
- Manyepa, P.; Gani, K.M.; Seyam, M.; Banoo, I.; Genthe, B.; Kumari, S.; Bux, F. Removal and risk assessment of emerging contaminants and heavy metals in a wastewater reuse process producing drinkable water for human consumption. Chemosphere 2024, 361, 142396. [Google Scholar] [CrossRef]
- Han, J.-R.; Kim, H.I.; Shim, H.-W.; Choi, J.-W.; Je, J. 3D-CFD based optimization of a mixer-settler: Part I. development of a model for efficient pump-mixer system in mixer-settler. Chem. Eng. Res. Des. 2025, 220, 610–622. [Google Scholar] [CrossRef]
- Cioncolini, A.; Santini, L. An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Therm. Fluid Sci. 2006, 30, 367–380. [Google Scholar] [CrossRef]
- Oliveira, D.S.d.; Donadel, C.B. Global velocity gradient evaluation: An innovative approach using CFD modeling applied to water and wastewater treatment plants. J. Water Process Eng. 2019, 28, 21–27. [Google Scholar]
- Nhut, H.T.; Hung, N.T.Q.; Lap, B.Q.; Han, L.T.N.; Tri, T.Q.; Bang, N.H.K.; Hiep, N.T.; Ky, N.M. Use of Moringa oleifera seeds powder as bio-coagulants for the surface water treatment. Int. J. Environ. Sci. Technol. 2020, 18, 2173–2180. [Google Scholar] [CrossRef]
- Cobos, A.G.Z.; Gutiérrez, J.; Caballero, P. Use of Moringa oleifera as a Natural Coagulant in the Reduction of Water Turbidity in Mining Activities. Water 2024, 16, 2315. [Google Scholar] [CrossRef]
- Otálora, M.C.; Wilches-Torres, A.; Lara, C.R.; Castaño, J.A.G.; Cifuentes, G.R. Evaluation of Turbidity and Color Removal in Water Treatment: A Comparative Study between Opuntia ficus-indica Fruit Peel Mucilage and FeCl3. Polymers 2022, 15, 217. [Google Scholar] [CrossRef]
- Sigalotti, L.D.G.; Alvarado-Rodríguez, C.E.; Rendón, O. Fluid Flow in Helically Coiled Pipes. Fluids 2023, 8, 308. [Google Scholar] [CrossRef]
- Pourhemmati, S.; Mohammed, H.A.; Shafieian, A. The use of variable coil pitch of helical tube on the hydro-thermal performance improvement. Case Stud. Therm. Eng. 2023, 53, 103944. [Google Scholar] [CrossRef]




| Configuration | Number of Elements [-] | Skewness [-] | Orthogonal Quality [-] |
|---|---|---|---|
| SCTF | 4,201,720 | 0.13260 | 0.97620 |
| HCTF1 | 3,721,380 | 0.14199 | 0.97831 |
| HCTF2 | 4,127,906 | 0.13985 | 0.97906 |
| Test Number | Configuration (SCTF/HCTF) | Length (m) | Diameter at the Top (DT, cm) | Diameter at the Base (DB, cm) |
|---|---|---|---|---|
| 1 | SCTF | 12 | 8 | 30 |
| 2 | 24 | 41 | ||
| 3 | 36 | 50 | ||
| 4 | HCTF1 | 12 | 28 | |
| 5 | 24 | |||
| 6 | 36 | |||
| 7 | HCTF2 | 12 | 50 | |
| 8 | 24 | |||
| 9 | 36 | |||
| Jar | Coagulant Dosage (mL/L) | Average Initial Turbidity (NTU) | Average Final Turbidity (NTU) | Turbidity Removal Efficiency (%) |
|---|---|---|---|---|
| 1 | 2 | 100.20 | 10.32 | 89.70 |
| 2 | 4 | 99.81 | 10.03 | 89.95 |
| 3 | 6 | 98.54 | 8.89 | 90.98 |
| 4 | 8 | 97.93 | 4.26 | 95.65 |
| 5 | 10 | 102.20 | 6.33 | 93.81 |
| 6 | 12 | 101.80 | 11.25 | 88.95 |
| Length | Configuration | Average Initial Turbidity (NTU) | Average Final Turbidity (NTU) | Turbidity Removal Efficiency (%) |
|---|---|---|---|---|
| 12 m | HCTF1 | 101.13 | 13.04 | 87.1 |
| HCTF2 | 105.23 | 3.42 | 96.8 | |
| SCTF | 103.23 | 1.89 | 98.2 | |
| 24 m | HCTF1 | 98.90 | 16.40 | 83.4 |
| HCTF2 | 96.53 | 13.08 | 86.5 | |
| SCTF | 102.90 | 8.61 | 91.6 | |
| 36 m | HCTF1 | 99.70 | 15.20 | 84.7 |
| HCTF2 | 95.10 | 14.68 | 84.6 | |
| SCTF | 97.73 | 11.85 | 87.9 |
| Flocculator | Head Loss (Hf, m) | ||
|---|---|---|---|
| 12 m | 24 m | 36 m | |
| HCTF1 | 0.104609 | 0.209519 | 0.313246 |
| HCTF2 | 0.095433 | 0.190430 | 0.285053 |
| SCTF | 0.113628 | 0.206097 | 0.303377 |
| Flocculator | Global Velocity Gradient (G, s−1) | ||
|---|---|---|---|
| 12 m | 24 m | 36 m | |
| HCTF1 | 99.89 | 99.96 | 99.80 |
| HCTF2 | 95.41 | 95.30 | 95.20 |
| SCTF | 104.11 | 99.14 | 98.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, D.S.d.; Sartori, M.; Donadel, C.B. Spirally Coiled Tube Flocculators: A New Hydrodynamic Design for Water Treatment. Modelling 2025, 6, 139. https://doi.org/10.3390/modelling6040139
Oliveira DSd, Sartori M, Donadel CB. Spirally Coiled Tube Flocculators: A New Hydrodynamic Design for Water Treatment. Modelling. 2025; 6(4):139. https://doi.org/10.3390/modelling6040139
Chicago/Turabian StyleOliveira, Danieli Soares de, Maurício Sartori, and Clainer Bravin Donadel. 2025. "Spirally Coiled Tube Flocculators: A New Hydrodynamic Design for Water Treatment" Modelling 6, no. 4: 139. https://doi.org/10.3390/modelling6040139
APA StyleOliveira, D. S. d., Sartori, M., & Donadel, C. B. (2025). Spirally Coiled Tube Flocculators: A New Hydrodynamic Design for Water Treatment. Modelling, 6(4), 139. https://doi.org/10.3390/modelling6040139






