Equivalent Stress Model-Assisted Aero-Structural Optimization of a Compressor Rotor Using an Adjoint Method
Abstract
1. Introduction
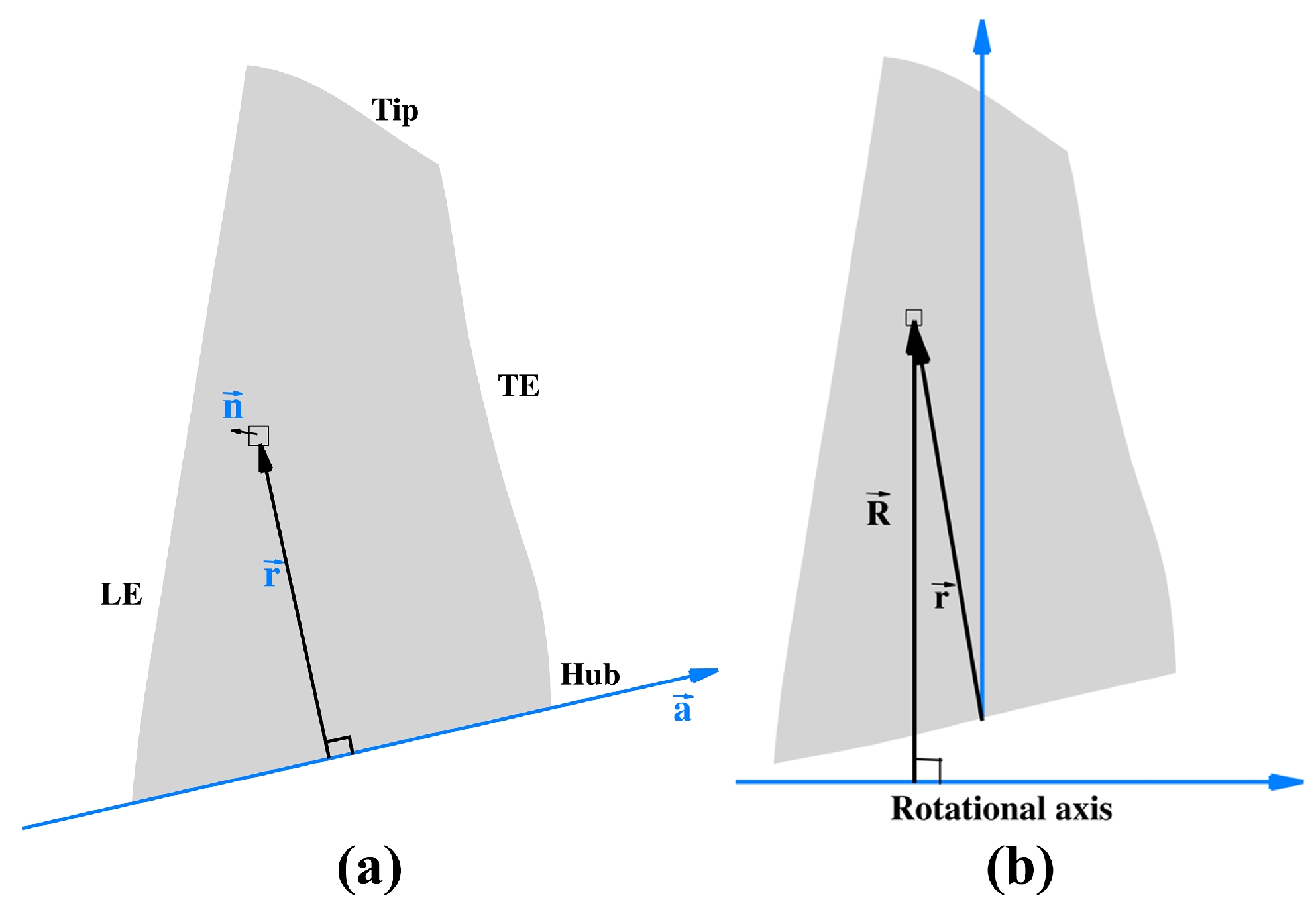
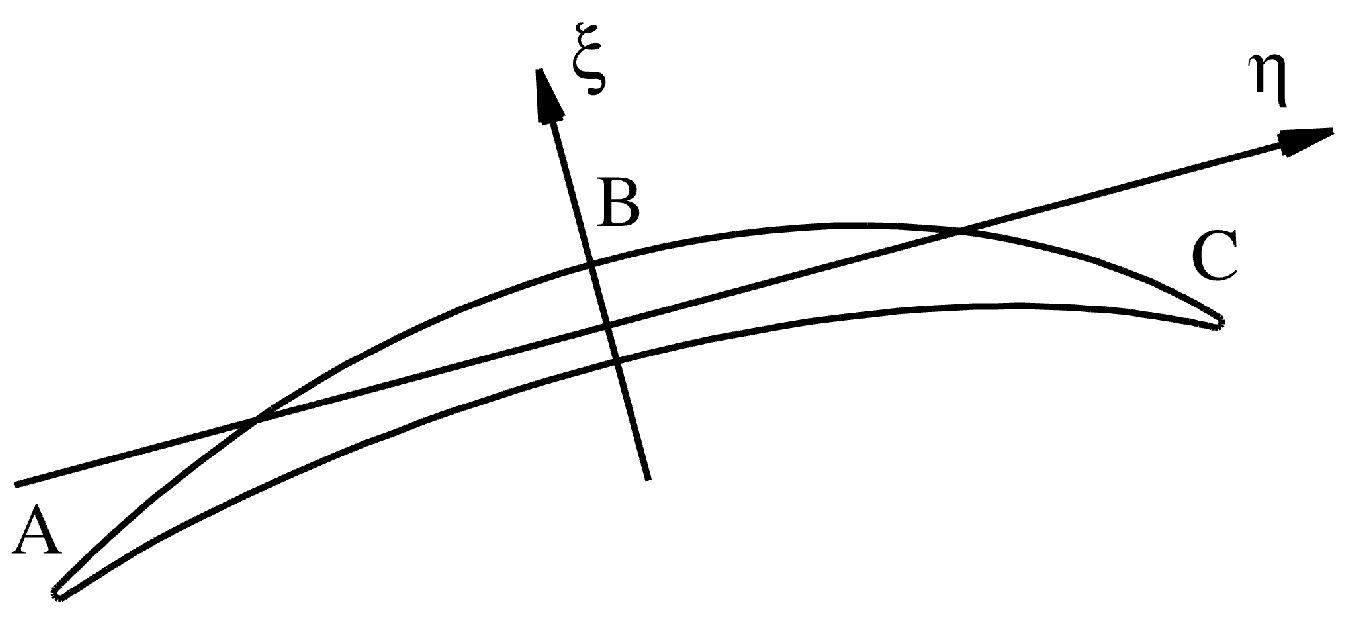
2. Equivalent Stress Model
2.1. Introduction to ESM
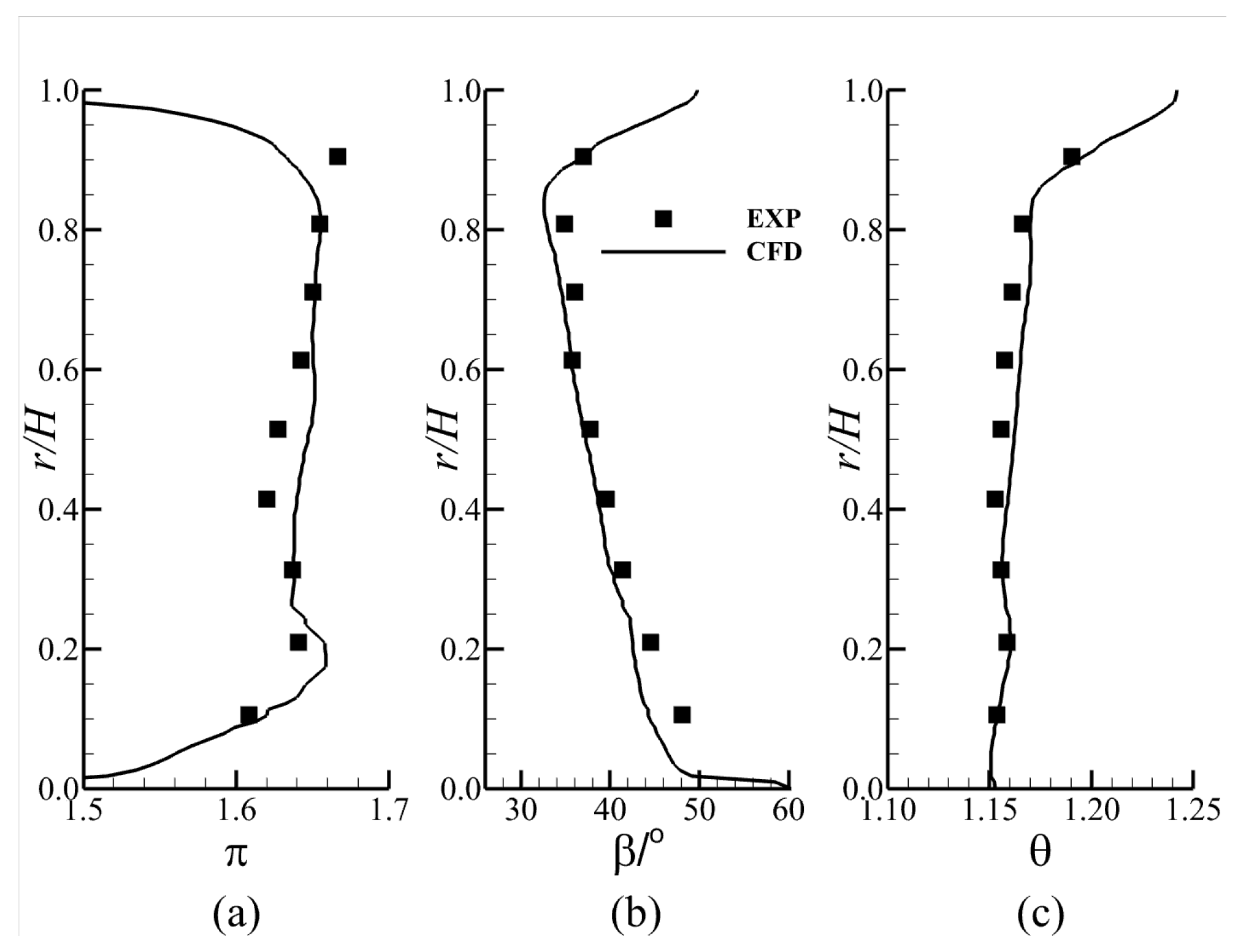
2.2. Validation of the ESM
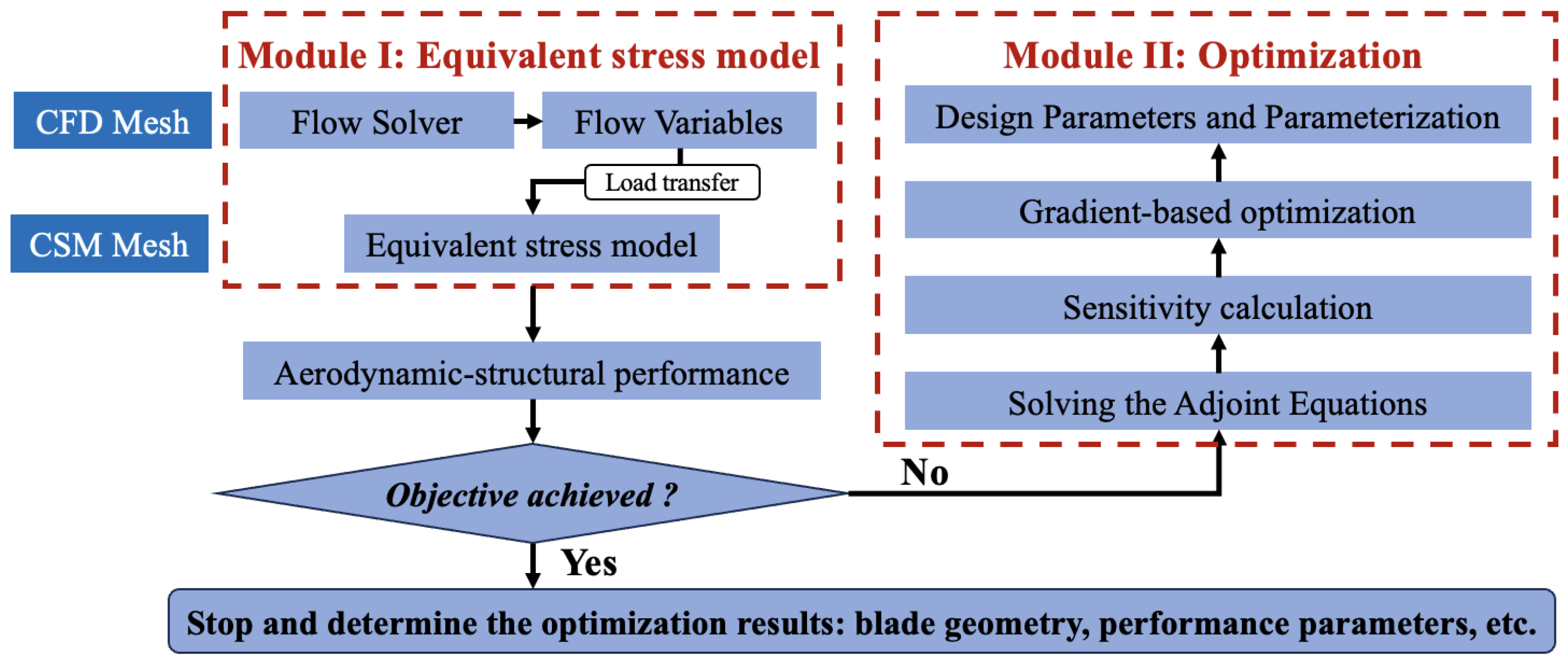
3. Methodology
3.1. Flow Simulation Method
3.2. Adjoint Method
3.3. Parameterization and Optimization Methods
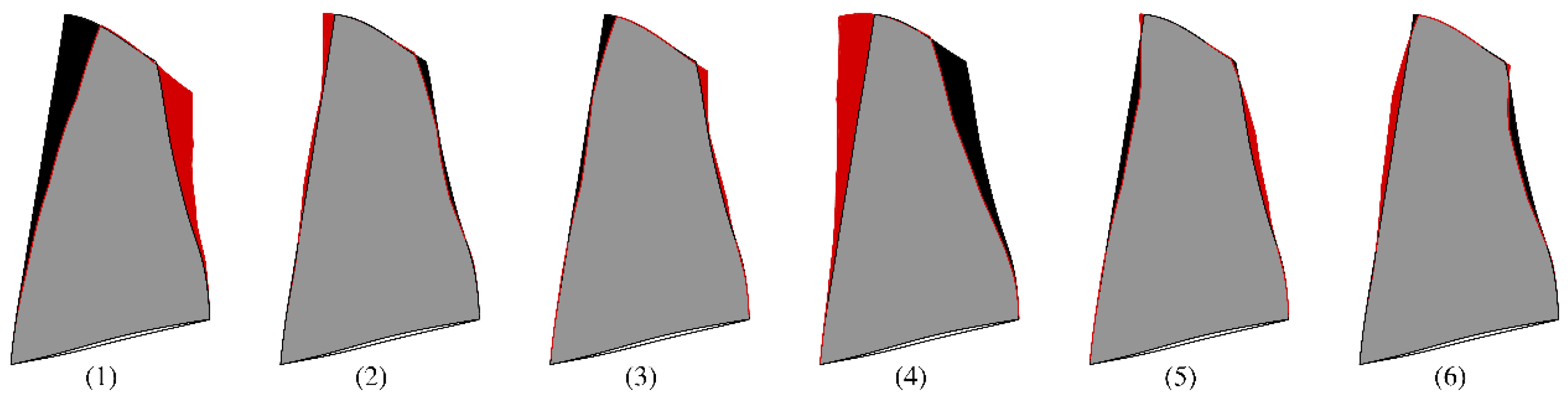
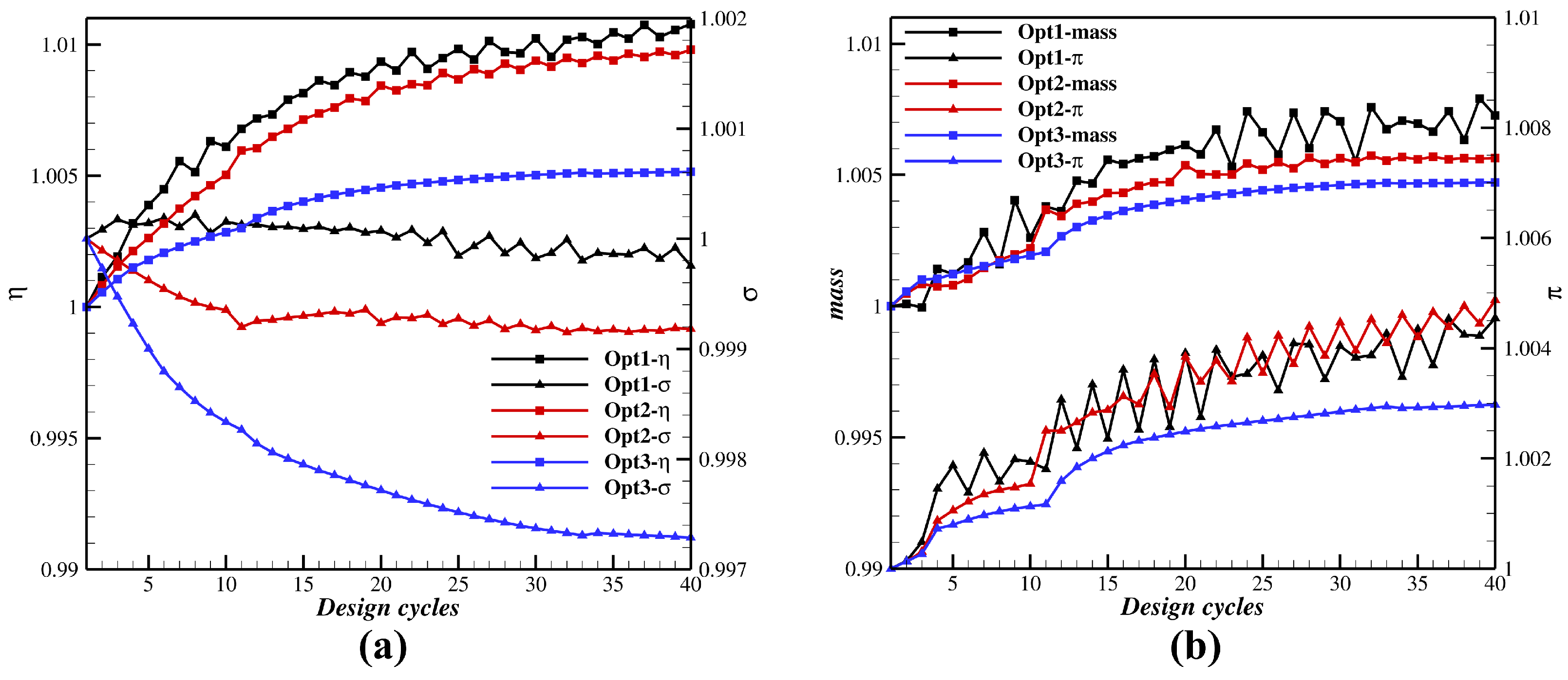
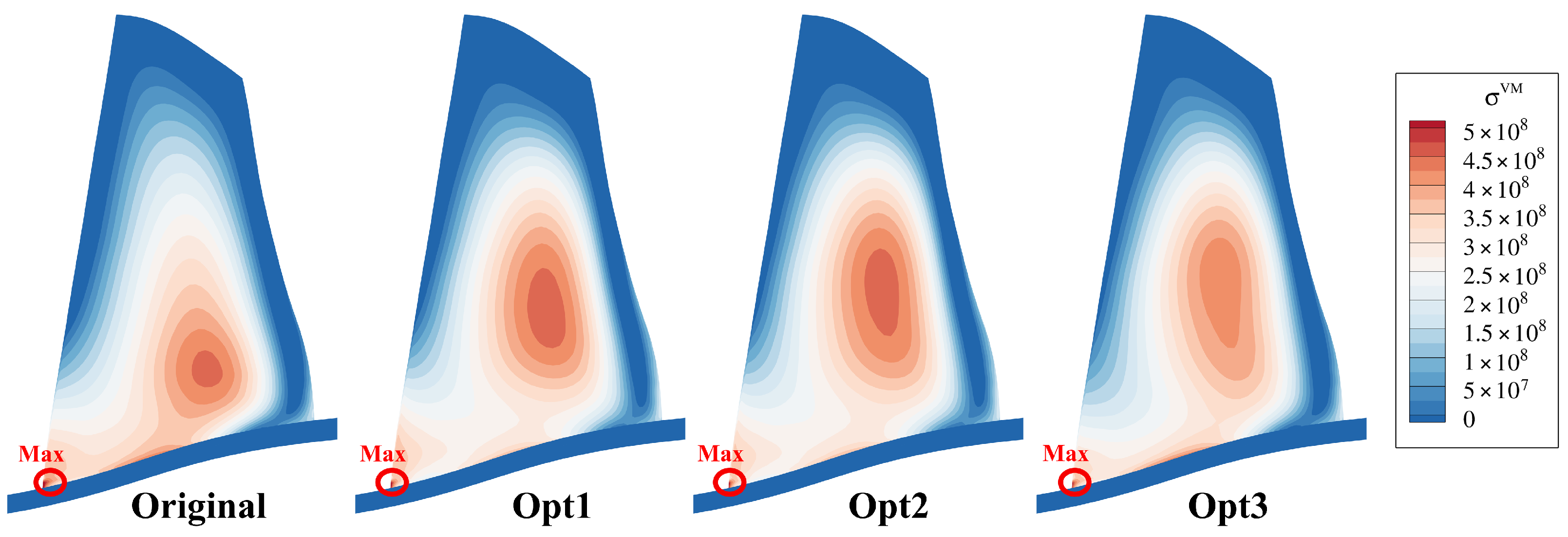
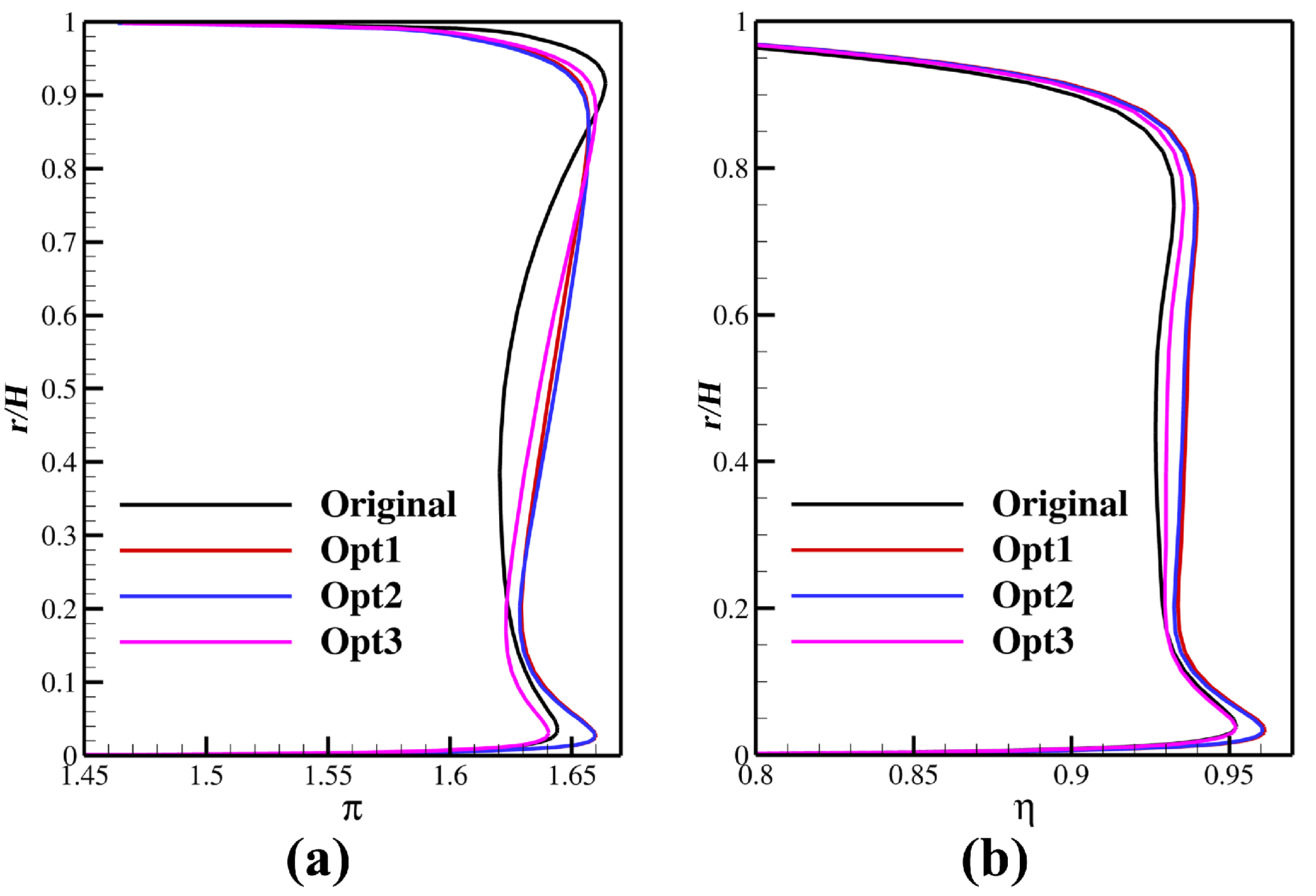
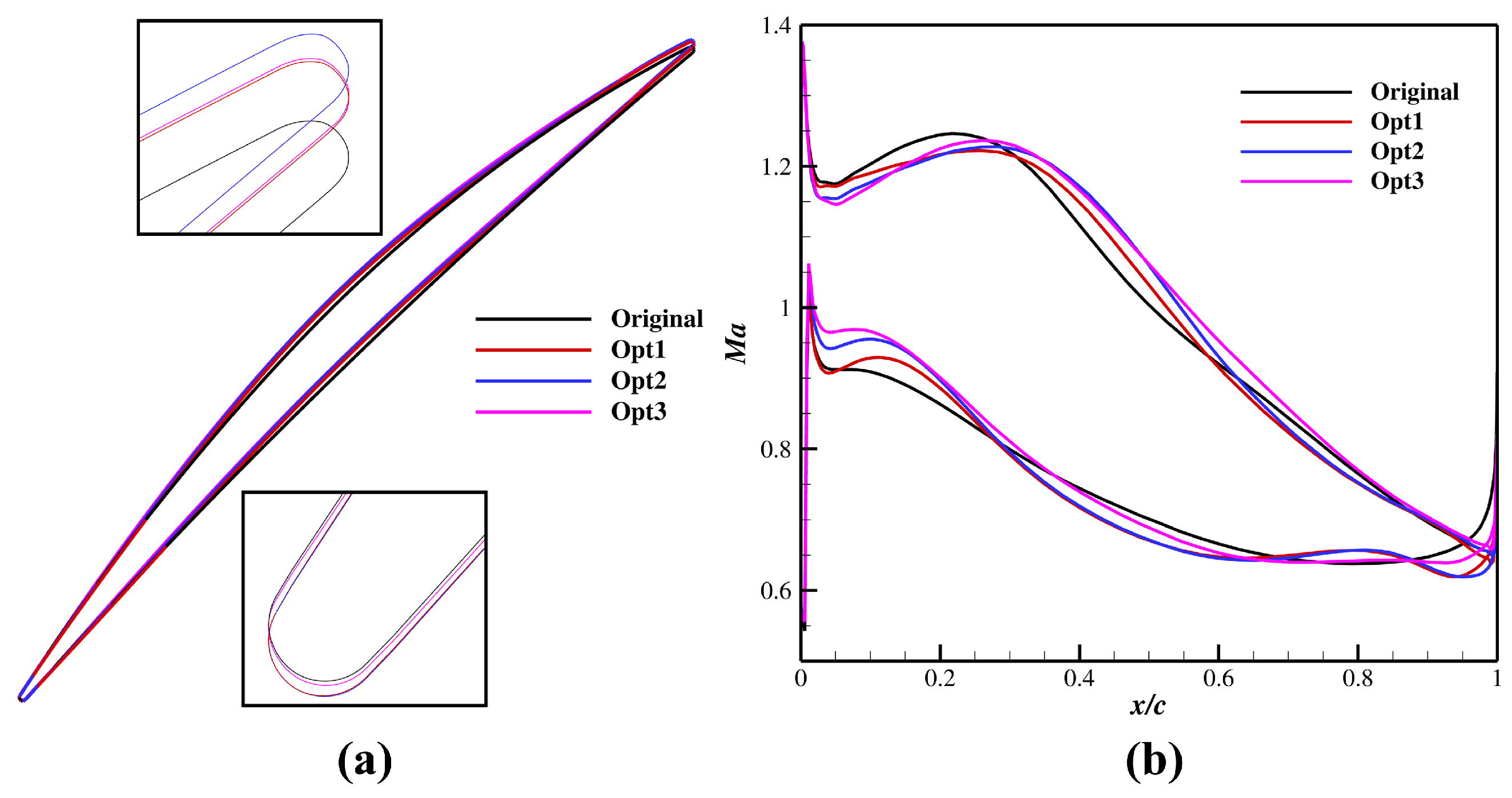
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AD | Adjoint method |
| CFD | Computational fluid dynamics |
| CSM | Computational structural mechanics |
| ESM | Equivalent stress model |
| FDM | Finite difference method |
| LE | Leading edge |
| MDO | Multi-disciplinary design optimization |
| MES | Maximum equivalent stress |
| RANS | Reynolds-averaged Navier–Stokes |
| TE | Trailing edge |
References
- Pouzadoux, F.; Reydellet, G.; Taillefer, E.; Masmoudi, M. Introduction of multi-disciplinary optimization in compressor blade design. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008. [Google Scholar]
- Li, J.; Luo, J.; Liu, Y.; Han, Z. Static aeroelasticity analysis of a rotor blade using a Gauss-Seidel fluid-structure interaction method. Adv. Aerodyn. 2023, 5, 23. [Google Scholar] [CrossRef]
- Lian, Y.; Liou, M.S. Aerostructural optimization of a transonic compressor rotor. J. Propuls. Power 2006, 22, 880–888. [Google Scholar] [CrossRef]
- Sivashanmugam, V.K.; Arabnia, M.; Ghaly, W. Aero–structural optimization of an axial turbine stage in three-dimensional flow. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar]
- Luo, C.; Chen, J.; Liu, Y.; Xiang, H. Multidisciplinary design optimization with multiple degrees of freedom for an axial compressor based on data-driven. In Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition, London, UK, 24–28 June 2024. [Google Scholar]
- Nadarajah, S.; Jameson, A. A comparison of the continuous and discrete adjoint approach to automatic aerodynamic optimization. Can. J. Earth Sci. 2013, 43, 1445–1466. [Google Scholar]
- Walther, B.; Nadarajah, S. Adjoint-based constrained aerodynamic shape optimization for multistage turbomachines. J. Propuls. Power 2015, 31, 1298–1319. [Google Scholar] [CrossRef]
- Wang, D.; He, L. Adjoint aerodynamic design optimization for blades in multistage turbomachines: Part I methodology and verification. J. Turbomach. 2010, 132, 021011. [Google Scholar] [CrossRef]
- Wu, H.; Da, X.; Wang, D. Multi-row turbomachinery aerodynamic design optimization by an efficient and accurate discrete adjoint solver. Aerospace 2023, 10, 106. [Google Scholar] [CrossRef]
- Martins, J.; Alonso, J.; Reuther, J. High-fidelity aero–structural design optimization of a supersonic business jet. J. Aircraft. 2002, 41, 523–530. [Google Scholar] [CrossRef]
- Martins, J.; Alonso, J.; Reuther, J. A coupled-adjoint sensitivity analysis method for high-fidelity aero–structural design. Optim. Eng. 2005, 6, 33–62. [Google Scholar] [CrossRef]
- Marcelet, M.; Peter, J.; Carrier, G. Sensitivity analysis of a strongly coupled aero–structural system using direct and adjoint methods. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008. [Google Scholar]
- Lei, R. Aerostructural Optimization and Design of Wing Based on Adjoint Method. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2021. [Google Scholar]
- He, L.; Wang, D. Concurrent blade aerodynamic-aero-elastic design optimization using adjoint method. J. Turbomach. 2011, 133, 011021. [Google Scholar] [CrossRef]
- Wu, H.; Yang, M.; Wang, D.; Huang, X. Efficient forced response minimization using a full-viscosity discrete adjoint harmonic balance method. AIAA J. 2024, 62, 3644–3661. [Google Scholar] [CrossRef]
- Mueller, L.; Verstraete, T.; Schwalbach, M. Adjoint-based multidisciplinary, multipoint optimization of a radial turbine considering aerodynamic and structural performances. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Cuciumita, C.; John, A.; Qin, N.; Shahpar, S. Structurally constrained aerodynamic adjoint optimisation of highly loaded compressor blades. In Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition, Virtual, 7–11 June 2021. [Google Scholar]
- Yang, H.; Gong, S.; Yi, L.; Tang, J.; Wang, D.; Huang, S.; Xu, S. Stress sensitivity analysis for a wide-chord fan blade using an adjoint method. Chin. J. Aeronaut. 2024, 37, 103–117. [Google Scholar] [CrossRef]
- Strazisar, A.J.; Powell, J.A. Laser anemometer measurements in a transonic axial-flow fan rotor. J. Eng. Power 1981, 103, 430–437. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, Y.; Tang, X.; Liu, F. Flow reconstructions and aerodynamic shape optimization of turbomachinery blades by POD-based hybrid models. Sci. China Technol. Sci. 2017, 60, 1658–1673. [Google Scholar] [CrossRef]
- Luo, J.; Fu, Z.; Li, J. Aero–structural design optimization of a transonic fan rotor using an adaptive POD-based hybrid surrogate model. Aerospace 2025, 12, 504. [Google Scholar] [CrossRef]
- Liu, F.; Jameson, A. Cascade flow calculations by a multigrid euler method. J. Propuls. Power. 1993, 9, 90–97. [Google Scholar] [CrossRef]
- Liu, F.; Jameson, A. Multigrid navier-stokes calculations for three-dimensional cascades. AIAA J. 1993, 31, 1785–1791. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Jameson, A. Solution of the euler equations for two dimensional transonic flow by a multigrid method. Appl. Math. Comput. 1983, 13, 327–355. [Google Scholar] [CrossRef]
- Li, J.; Luo, J.; Liu, F.; Zheng, Y.; Han, Z. Performance sensitivity analysis and aerodynamic optimization of compressor cascades by a turbulence adjoint method. AIP Adv. 2024, 14, 115307. [Google Scholar] [CrossRef]
- Hascoet, L.; Pascual, V. The tapenade automatic differentiation tool: Principles, model, and specification. ACM Trans. Math. Softw. 2013, 39, 20. [Google Scholar] [CrossRef]
- Hicks, R.M.; Henne, P.A. Wing design by numerical optimization. J. Aircraft. 1978, 15, 407–412. [Google Scholar] [CrossRef]








| Parameter | Value |
| Design rotation speed (rpm) | 16,043 |
| Blade number | 22 |
| Tip clearance (mm ) | 1.0 |
| Design pressure ratio | 1.63 |
| Design mass flow rate (kg/s) | 33.25 |
| Inlet total pressure (Pa) | 101,325.0 |
| Inlet total temperature (K) | 288.15 |
| /% | /Pa | /kg· s−1 | ||
|---|---|---|---|---|
| Original | 91.19 | 5.47 × 10 8 | 34.14 | 1.635 |
| Opt1 | 92.16 (1.06%) | 5.43 × 10 8 (−0.70%) | 34.37 (0.65%) | 1.643 (0.49%) |
| Opt2 | 92.09 (0.98%) | 5.31 × 10 8 (−2.96%) | 34.34 (0.59%) | 1.643 (0.49%) |
| Opt3 | 91.65 (0.51%) | 5.04 × 10 8 (−7.90%) | 34.31 (0.50%) | 1.640 (0.31%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Fu, Z.; Luo, J. Equivalent Stress Model-Assisted Aero-Structural Optimization of a Compressor Rotor Using an Adjoint Method. Modelling 2025, 6, 125. https://doi.org/10.3390/modelling6040125
Li J, Fu Z, Luo J. Equivalent Stress Model-Assisted Aero-Structural Optimization of a Compressor Rotor Using an Adjoint Method. Modelling. 2025; 6(4):125. https://doi.org/10.3390/modelling6040125
Chicago/Turabian StyleLi, Jiaxing, Zhen Fu, and Jiaqi Luo. 2025. "Equivalent Stress Model-Assisted Aero-Structural Optimization of a Compressor Rotor Using an Adjoint Method" Modelling 6, no. 4: 125. https://doi.org/10.3390/modelling6040125
APA StyleLi, J., Fu, Z., & Luo, J. (2025). Equivalent Stress Model-Assisted Aero-Structural Optimization of a Compressor Rotor Using an Adjoint Method. Modelling, 6(4), 125. https://doi.org/10.3390/modelling6040125






