An Analytical Thermal Model for Coaxial Magnetic Gears Considering Eddy Current Losses
Abstract
1. Introduction
2. Materials and Methods
2.1. Principles of CMGs
- For a fixed modulator ring (considered in this study), the output is in the opposite direction of the input and the gear ratio () is
- For a fixed outer rotor, the output is in the same direction of the input and the gear ratio () is
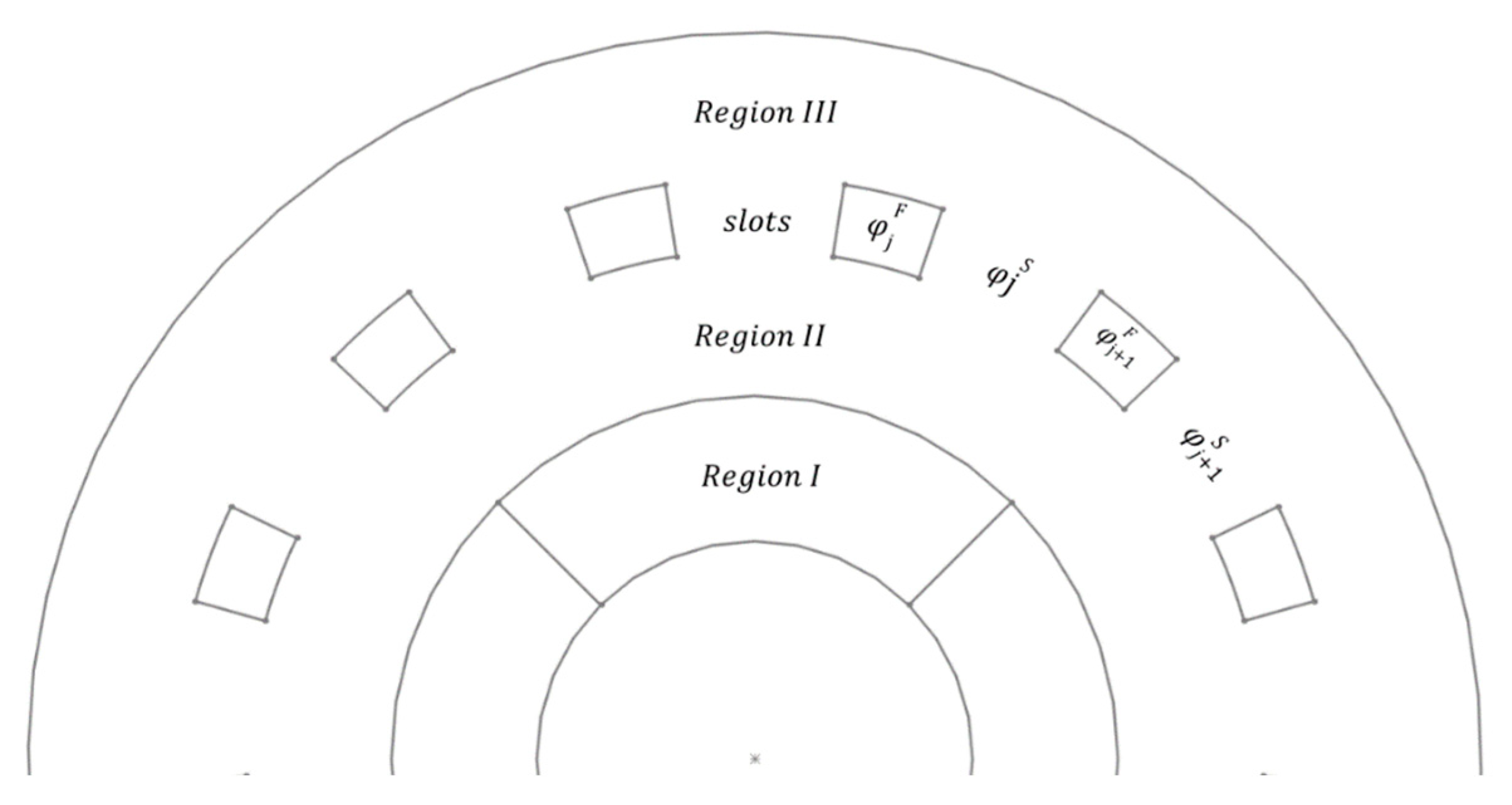
2.2. Two-Dimensional Analytical Model for Eddy Current Loss Calculation
- 1.
- Zero magnetic potential in radii () and ().
- 2.
- Continuity on both the magnetic potential and its radial derivative at the boundaries between regions.
- 3.
- Continuity of the magnetic flux density through the slots at () and ().
- 4.
- The magnetic flux through the inner surface of the modulator ring should match the flux through the outer surface.
- 5.
- The magnetic flux entering each ferromagnetic segment must equal the flux exiting it.
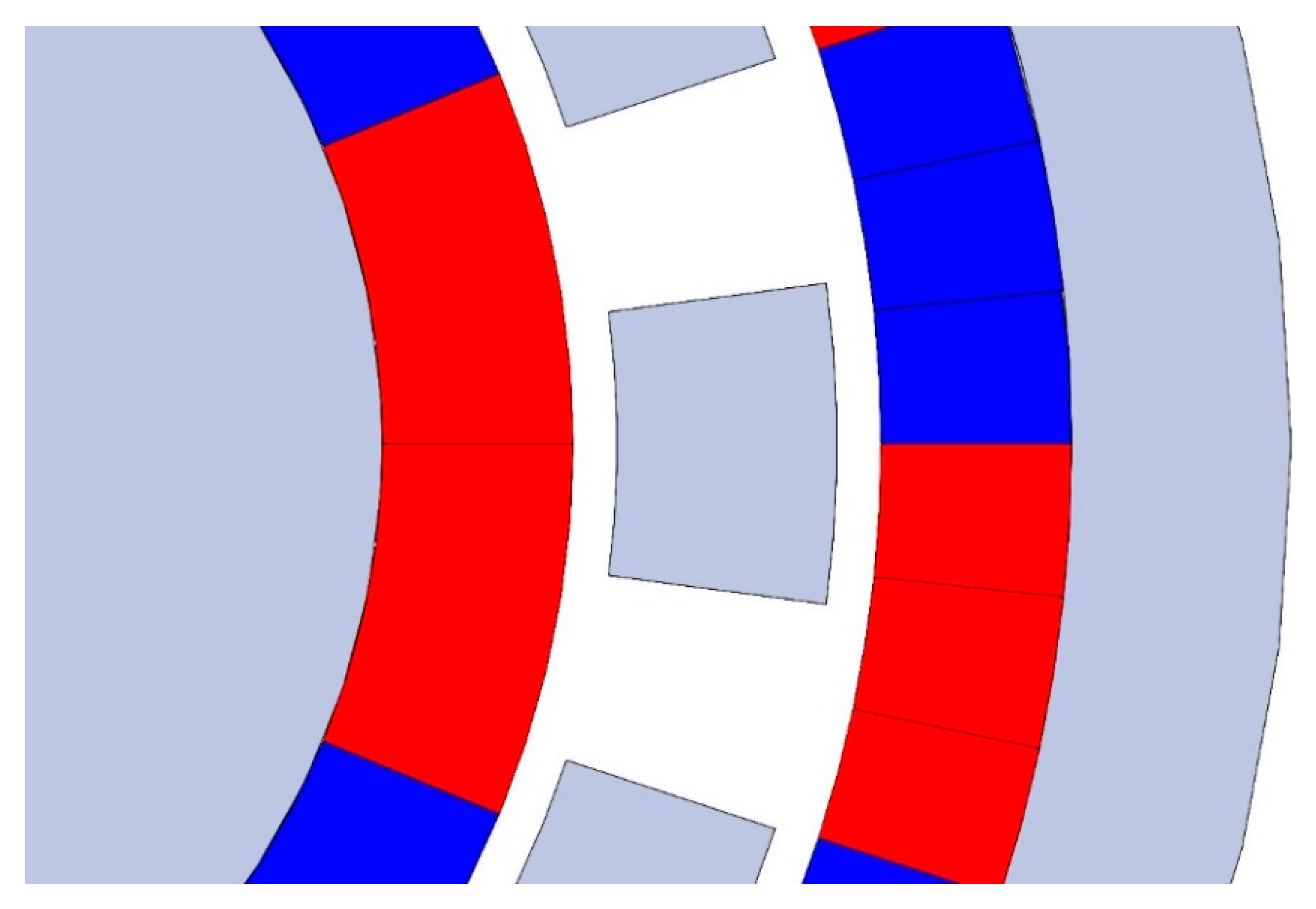
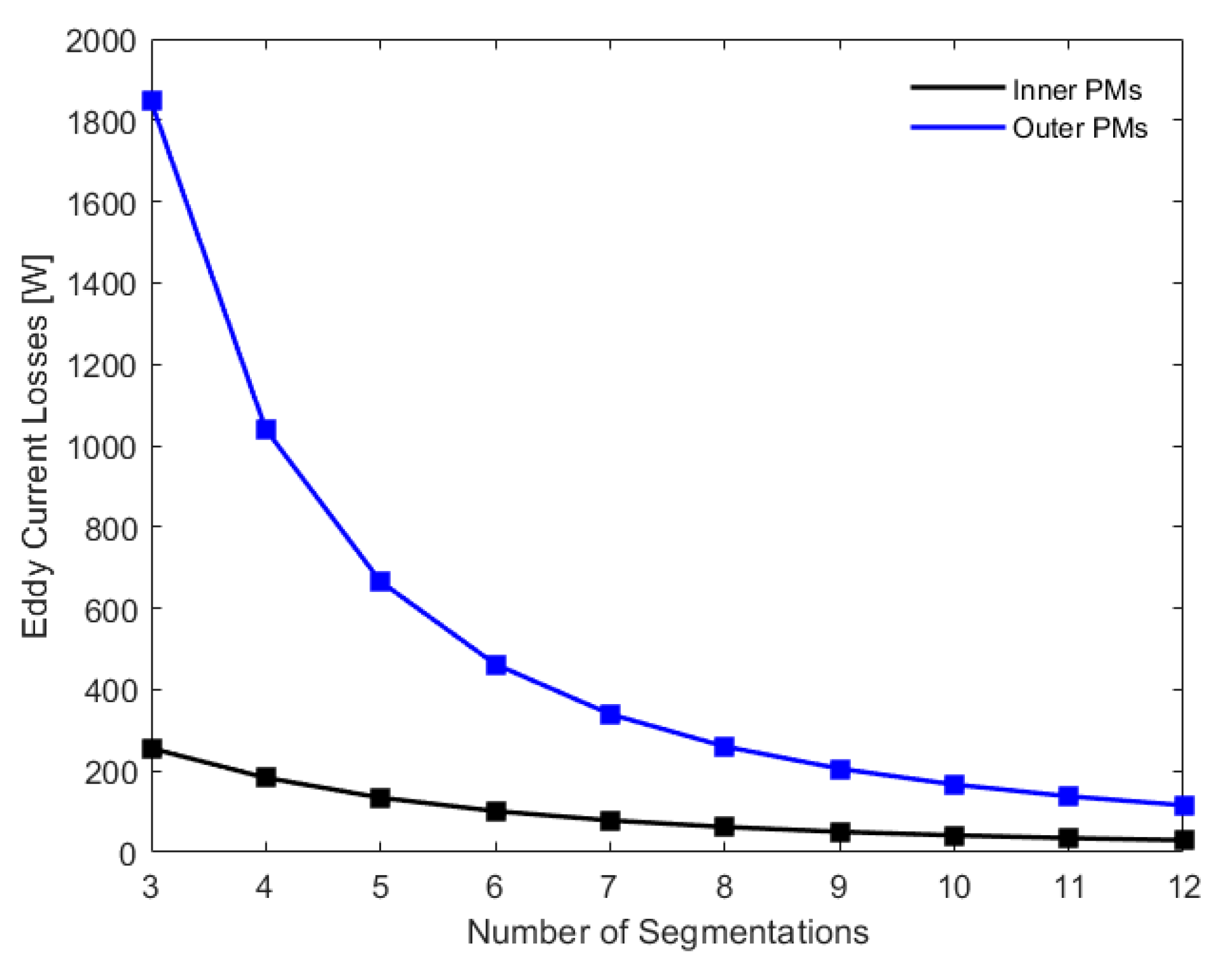
2.3. Circumferential Segmentation of PMs
2.4. Eddy Current Losses in a CMG-Empirical Formula
2.5. Thermal Model
2.6. Methodology
3. Results and Discussion
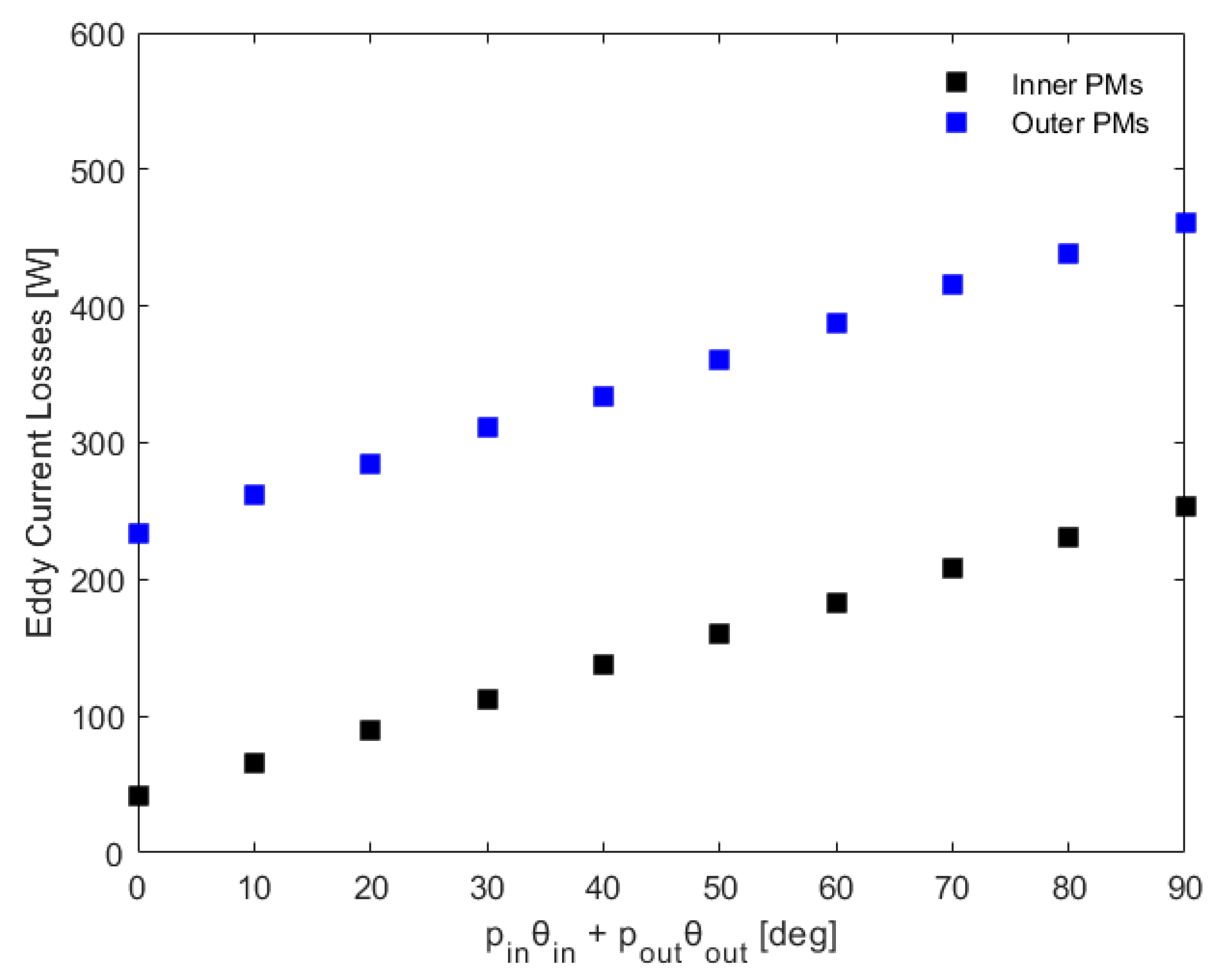
3.1. Eddy Current Loss Calculation and Comparison with FEA
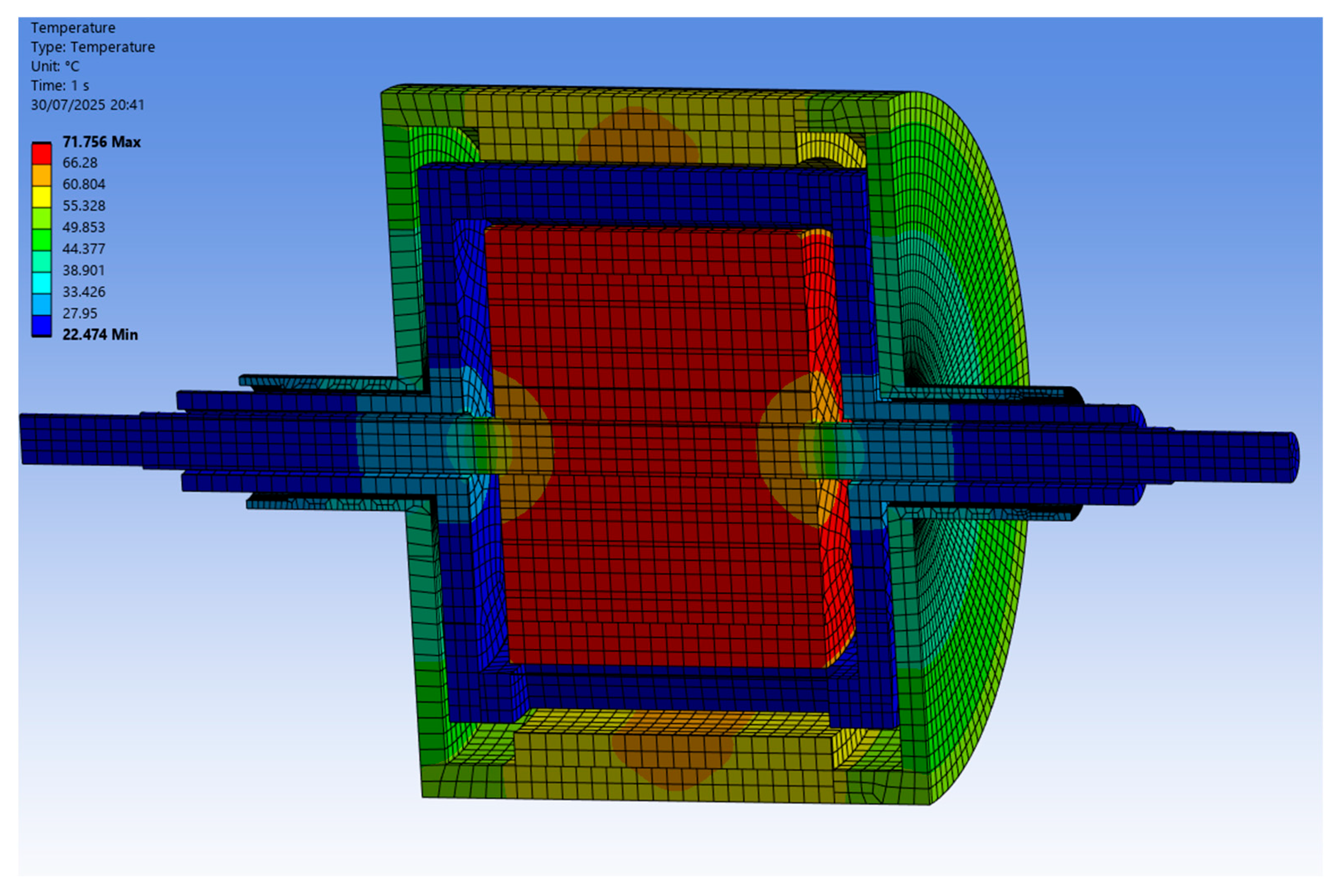
3.2. Steady-State Temperature Calculation and Comparison with FEA
4. Discussion and Future Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tlali, P.M.; Wang, R.-J.; Gerber, S. Magnetic gear technologies: A review. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 544–550. [Google Scholar]
- Ruiz-Ponce, G.; Arjona, M.A.; Hernandez, C.; Escarela-Perez, R. A Review of Magnetic Gear Technologies Used in Mechanical Power Transmission. Energies 2023, 16, 1721. [Google Scholar] [CrossRef]
- Atallah, K.; Howe, D. A Novel High-Performance Magnetic Gear. IEEE Trans. Magn. 2001, 37, 2844–2846. [Google Scholar] [CrossRef]
- Belkhir, K.S.; Khenfer, N. Magnetic Gear Generator for Wind Energy. Prz. Elektrotechniczny 2013, 89, 72–75. [Google Scholar]
- Johnson, M.; Gardner, M.C.; Toliyat, H.A.; Englebretson, S.; Ouyang, W.; Tschida, C. Design, construction, and analysis of a large-scale inner stator radial flux magnetically geared generator for wave energy conversion. IEEE Trans. Ind. Appl. 2018, 54, 3305–3314. [Google Scholar] [CrossRef]
- Scheidler, J.J.; Asnani, V.M.; Tallerico, T.F. NASA’s Magnetic gearing research for electrified aircraft propulsion. In Proceedings of the 2018 AIAA/IEEE Electric Aircraft Technologies Symposium (EATS), Cincinnati, OH, USA, 12–14 July 2018; pp. 1–12. [Google Scholar]
- Tzouganakis, P.; Gakos, V.; Kalligeros, C.; Tsolakis, A.; Spitas, V. Fast and efficient simulation of the dynamical response of coaxial magnetic gears through direct analytical torque modelling. Simul. Model. Pract. Theory 2023, 123, 102699. [Google Scholar] [CrossRef]
- Jian, L.; Chau, K.T. Analytical Calculation of Magnetic Field Distribution in Coaxial Magnetic Gears. Prog. Electromagn. Res. 2009, 92, 1–16. [Google Scholar] [CrossRef]
- Jian, L.; Chau, K.T. A Coaxial Magnetic Gear with Halbach Permanent-Magnet Arrays. IEEE Trans. Energy Convers. 2010, 25, 319–328. [Google Scholar] [CrossRef]
- Rasmussen, P.O.; Frandsen, T.V.; Jensen, K.K.; Jessen, K. Experimental evaluation of a motor-integrated permanent-magnet gear. IEEE Trans. Ind. Appl. 2013, 49, 850–859. [Google Scholar] [CrossRef]
- Desvaux, M.; Sire, S.; Hlioui, S.; Ahmed, H.B.; Multon, B. Development of a hybrid analytical model for a fast computation of magnetic losses and optimization of coaxial magnetic gears. IEEE Trans. Energy Convers. 2019, 34, 25–35. [Google Scholar] [CrossRef]
- Wang, J.; Atallah, K.; Chin, R.; Arshad, W.; Lendenmann, H. Rotor eddy-current loss in permanent-magnet brushless AC machines. IEEE Trans. Magn. 2010, 46, 2701–2707. [Google Scholar] [CrossRef]
- Lubin, T.; Mezani, S.; Rezzoug, A. Analytical Computation of the Magnetic Field Distribution in a Magnetic Gear. IEEE Trans. Magn. 2010, 46, 2611–2621. [Google Scholar] [CrossRef]
- Desvaux, M.; Traulle, B.; le Goff Latimier, R.; Sire, S.; Multon, B.; ben Ahmed, H. Computation Time Analysis of the Magnetic Gear Analytical Model. IEEE Trans. Magn. 2017, 53, 1–9. [Google Scholar] [CrossRef]
- Nikolarea, N.; Tzouganakis, P.; Gakos, V.; Papalexis, C.; Tsolakis, A.; Spitas, V. Detailed investigation of the eddy current and core losses in coaxial magnetic gears through a two-dimensional analytical model. Math. Comput. Appl. 2024, 29, 38. [Google Scholar] [CrossRef]
- Mateev, V.; Marinova, I. Loss estimation of magnetic gears. Electr. Eng. 2020, 102, 387–399. [Google Scholar] [CrossRef]
- Filippini, M. Magnetic Gears Numerical Modelling and Optimization. Available online: https://www.research.unipd.it/handle/11577/3425766 (accessed on 31 July 2025).
- Elghnam, R.I. Experimental and numerical investigation of heat transfer from a heated horizontal cylinder rotating in still air around its axis. Ain Shams Eng. J. 2014, 5, 177–185. [Google Scholar] [CrossRef]






| Parameter | Unit | Value |
|---|---|---|
| [-] | 4 | |
| [-] | 10 | |
| [-] | 14 | |
| [-] | ||
| [-] | ||
| [mm] | 53 | |
| [mm] | 66 | |
| [mm] | 69 | |
| [mm] | 84 | |
| [mm] | 87 | |
| [mm] | 97 | |
| [mm] | 100 | |
| [deg] | 15 |
| Parameter | Units | Value |
|---|---|---|
| Thermal conductivity of N52 magnets | [W/m/K] | 7.8 |
| Thermal conductivity of iron | [W/m/K] | 75 |
| Thermal conductivity of air | [W/m/K] | 0.026 |
| Kinematic viscosity of air | [m2/s] | 1.510−5 |
| Ambient temperature | [°C] | 20 |
| Parameter | Inner Rotor | Outer Rotor |
|---|---|---|
| 1.1210−5 | 0.0014 | |
| 6.410−7 | 1.510−5 | |
| 0.115 | 0.031 | |
| 0.039 | 0.215 | |
| 0.016 | 0.280 |
| Area | Temperature [°C] |
|---|---|
| Inner PMs Outer PMs | 84 100 |
| Modulator ring | 20 |
| Inner yoke | 83 |
| Outer yoke | 99.6 |
| Area | Temperature [°C] |
|---|---|
| Inner PMs Outer PMs | 71.8 61.4 |
| Modulator ring | 23.5 |
| Inner yoke | 70.3 |
| Outer yoke | 61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzouganakis, P.; Gakos, V.; Papalexis, C.; Kalligeros, C.; Tsolakis, A.; Spitas, V. An Analytical Thermal Model for Coaxial Magnetic Gears Considering Eddy Current Losses. Modelling 2025, 6, 114. https://doi.org/10.3390/modelling6040114
Tzouganakis P, Gakos V, Papalexis C, Kalligeros C, Tsolakis A, Spitas V. An Analytical Thermal Model for Coaxial Magnetic Gears Considering Eddy Current Losses. Modelling. 2025; 6(4):114. https://doi.org/10.3390/modelling6040114
Chicago/Turabian StyleTzouganakis, Panteleimon, Vasilios Gakos, Christos Papalexis, Christos Kalligeros, Antonios Tsolakis, and Vasilios Spitas. 2025. "An Analytical Thermal Model for Coaxial Magnetic Gears Considering Eddy Current Losses" Modelling 6, no. 4: 114. https://doi.org/10.3390/modelling6040114
APA StyleTzouganakis, P., Gakos, V., Papalexis, C., Kalligeros, C., Tsolakis, A., & Spitas, V. (2025). An Analytical Thermal Model for Coaxial Magnetic Gears Considering Eddy Current Losses. Modelling, 6(4), 114. https://doi.org/10.3390/modelling6040114






