Non-Fourier Thermoelastic Peridynamic Modeling of Cracked Thin Films Under Short-Pulse Laser Irradiation

Abstract

In this paper, we develop a peridynamic computational framework to analyze thermomechanical interactions in fractured thin films subjected to ultrashort-pulsed laser excitation, employing nonlocal discrete material point discretization to eliminate mesh dependency artifacts. The generalized Cattaneo–Fourier thermal flux formulation uncovers contrasting dynamic responses: hyperbolic heat propagation ($F_T=0$) generates intensified temperature localization and elevates transient crack-tip stress concentrations relative to classical Fourier diffusion ($F_T=1$). A GSSSS (Generalized Single Step Single Solve) i-Integration temporal scheme achieves oscillation-free numerical solutions across picosecond-level laser–matter interactions, effectively resolving steep thermal fronts through adaptive stabilization. These findings underscore hyperbolic conduction’s essential influence on stress-mediated fracture evolution during ultrafast laser processing, providing critical guidelines for thermal management in micro-/nano-electromechanical systems.

1. Introduction

The rapid advancement of micro-/nano-devices has propelled the study of thermodynamic behaviors under short-pulse laser heating to the forefront of research. Short-pulse lasers enable localized heating domains and controllable surface recast layers through high-peak-power material vaporization within ultrashort interaction timescales. Due to the massive advantages of short-pulse laser heating, it has been exploited to achieve the fabrication of sophisticated microstructures, the measurement of thin-film properties, and surface hardening, etc. [1,2]. This is in such a way that the thermoelastic response in such structures becomes increasingly significant with respect to practical engineering systems.

Recent experimental and modeling studies have shown that under ultrafast laser excitation, traditional Fourier-based thermal models fail to capture localized and time-delayed heat propagation accurately. Notably, works such as Xu et al. [3] demonstrate that at the microscale, thermal response timescales are non-negligible, requiring the incorporation of finite thermal wave speeds. Jiang et al. [4,5,6] focus on the microstructure and corrosion resistance of the thin films of aluminum titanate. The films exhibit a dense and uniform morphology with nano-sized grains (10 nm) at 750 °C and grain growth to 120 nm at 1350 °C. Larger grains lead to fewer grain boundaries and the disappearance of amorphous phases, greatly improving resistance to fused sodium nitrite corrosion. The research highlights how microstructural evolution critically influences the protective performance of thin films. Similarly, the study in [7] emphasizes the importance of thermal lag behavior in nano-engineered materials, reinforcing the need for advanced heat conduction formulations. Moreover, fracture behavior under coupled thermomechanical loading has been extensively discussed in classical frameworks, but the challenges in representing dynamic crack initiation and coalescence remain. The use of peridynamic theory for such systems has been preliminarily explored in [8], highlighting its potential to resolve discontinuities without mesh distortion or remeshing strategies. However, these efforts often neglect the role of heat conduction modeling in fracture evolution under ultrafast laser processing—an aspect this study directly addresses.

The theoretical basis of heat conduction relies heavily upon the underlying heat flux constitutive models, and the fusion of the mechanisms associated with heat conduction to those of elasticity leads to the fundamental description of the thermodynamic behavior of solids [9,10]. The conventional thermoelasticity theory [11] was formulated on the principles of the classical theory of heat conduction (Fourier’s heat conduction) [12], which has been acknowledged to be unphysical since the heat propagates with infinite speed. To address the issue of infinite propagation speed, Cattaneo-type thermal flux [13], which admits finite speeds for the thermal signal, was introduced to formulate the associated thermoelastic model by associating relaxations with respect to either temperature or thermal flux [14]. Another thermal flux model, namely, the dual-phase-lag heat flux, has also been extended to formulate its associated thermoelastic theory of solids [15]; however, it has several fundamental deficiencies. These thermal flux models have been widely exploited to handle the short-pulse laser heating problems, and remarkable studies regarding the thermodynamic response of solids under the short-pulse laser have been carried out in [1,2,16,17].

The expanding utilization of micro-/nano-devices, coupled with the emergence of unconventional thermomechanical phenomena in systems featuring material discontinuities, has driven significant advancements in nonlocal computational methodologies to resolve crack-induced modeling complexities. Within this context, peridynamics (PDs), a paradigm-shifting framework in continuum mechanics, offers a unified solution by reformulating constitutive laws through nonlocal interactions based on integrals, inherently bypassing the limitations of spatial derivative dependence in classical continuum theories [18,19].

In general, peridynamics, a nonlocal reformulation of continuum mechanics, has emerged as a transformative approach to modeling discontinuous deformation phenomena by redefining constitutive interactions through integral-type governing equations [20]. This mesh-free methodology discretizes the domain into interacting material points, each exchanging forces with neighbors within a predefined horizon, thereby naturally capturing spontaneous crack nucleation, branching, and coalescence without requiring ad hoc fracture criteria or predefined crack paths. Such intrinsic advantages over local continuum-based methods, such as finite element analysis, become particularly pronounced in scenarios involving dynamic fracture, impact-induced damage, or phase-transition-driven failure. To effectively simulate crack initiation and propagation, Li et al. [21] developed a strain-based extended PD model (XPDM) with enhanced multi-crack handling capabilities, validated through classical fracture benchmarks. Furthermore, peridynamics have demonstrated significant potential in thermomechanical coupling analysis. The foundational work of [22] established a state-based thermal diffusion PD framework, later extended to fully coupled thermomechanical modeling [23]. Subsequent advances include [24,25] developing fully coupled bond-based and state-based models, respectively. Recent applications highlight the PD capability in simulating thermal cracking phenomena, exemplified by rock fracture analysis and [26] in fuel pellet failure studies.

For numerically approximating the solution to multiphysics and multidisciplinary problems, such as fluid–structure interaction simulation, thermoelasticity, and the like, the monolithic/simultaneous scheme [27,28,29] and the staggered/partitioned scheme [30] have been widely exploited. For the monolithic algorithm, the time-stepping schemes are implemented concurrently with the full system of equations coupling different physical phenomena, and all the unknowns need to be evaluated simultaneously [31]. For the staggered algorithm, the coupled system of equations is solved separately with regards to different fields. Each field is allowed to be treated with different time-stepping algorithms (first and second order in time systems); consequently, the staggered algorithm may lead to the lack of stability over the whole system, in spite of different unconditionally stable time-stepping algorithms being implemented in the different fields.

In this work, the thermodynamic response of a cracked thin film under short-pulse laser heating is formulated in the framework of the generalized C- and F-thermal flux model under the Lagrangian configuration. Building upon these foundations, this study extends peridynamic theory to address coupled thermomechanical responses in thin-film systems subjected to short-pulse laser irradiation. A generalized non-Fourier thermal transport model is integrated with fracture dynamics to resolve transient thermal shocks and associated stress evolution at picosecond timescales. The proposed framework overcomes the limitations of classical thermoelasticity in handling steep thermal gradients and localized heat flux discontinuities near propagating cracks, offering new insights into the multiscale failure mechanisms of advanced micro-/nano-devices under extreme thermal loading. Additionally, a unified time integration that can readily solve the first-order and/or second-order time-dependent multiphysics-coupled problems is exploited to carry out the time stepping.

2. Theory

2.1. Generalized Thermoelastic Theory Based on C- and F-Heat Flux

As evidenced in [9,13], non-Fourier thermal transport must be considered for ultrafast energy deposition processes. This study addresses the thermomechanical behavior of metallic thin films subjected to picosecond laser pulses, where high-energy photon absorption induces non-equilibrium electron excitation prior to lattice thermalization. The transient energy localization, usually at a time level of picoseconds, necessitates hyperbolic heat conduction modeling with intrinsic thermal relaxation mechanisms. In the present work, we are attempting to introduce the non-Fourier effect to study the thermal and mechanical responses of the thin film under short-pulse laser heating. The fundamental constitutive law of thermal flux is described by a generalized thermal flux model that considers the coexistence of both the Fourier-type and the Cattaneo-type flux. The specific model of this generalized heat flux is given by

$$\begin{array}{cc}& {\mathit{q}}_F=-k{F}_T{\nabla }_{x}T\hfill \\ & {\mathit{q}}_C+\tau {\displaystyle \frac{\partial {\mathit{q}}_C}{\partial t}}=-(1-F_T)k{\nabla }_{x}T\hfill \\ & \mathit{q}={\mathit{q}}_F+{\mathit{q}}_C\hfill \end{array}$$

(1)

where $\mathit{q}$, ${\mathit{q}}_F$, and ${\mathit{q}}_C$ are the total heat flux, the fast heat flux (Fourier-type), and the slow heat flux (Cattaneo-type), respectively. The corresponding heat conductivities of $\mathit{q}$, ${\mathit{q}}_F$, and ${\mathit{q}}_C$ are k, $k_F$, and $k_C$, respectively. $F_T={\displaystyle \frac{K_F}{k_C+k_F}}$ is defined as a macroscale heat conduction model number to physically illustrate different types of heat conduction processes.

In spite of the simple formulation, this C- and F-generalized heat flux model actually emanated from the Boltzmann transport equation of heat carriers, where the high frequent motion of heat carriers leads to a fast heat process (Fourier-type) and the low frequent motion of heat carriers leads to a slow heat process (Cattaneo-type).

This constitutive hypothesis regarding coexisting Fourier–Cattaneo contributions in thermal transport emerges from the stochastic transport characteristics of thermal carriers, where their Brownian motion fundamentally manifests through spectral decomposition in phonon-scattering regimes, comprising diffusive low-frequency modes and propagative high-frequency components (Figure 1 shows the distribution of thermal carriers at different frequencies, indicating that the Fourier component is mainly dominated by high-frequency motion (fast processes), while the Cattaneo component is mainly dominated by low-frequency motion (slow processes)). The superposition mechanism inherently satisfies thermodynamic irreversibility requirements while preserving wave-diffusion duality at mesoscopic scales.

Depending on the heat parameter $F_T$, the following types of heat flux models are obtained:

• $F_T=0$
  The C- and F-model asymptotically converges to hyperbolic heat transfer dynamics, characterized by a finite thermal propagation velocity through intrinsic relaxation time scaling, thereby eliminating the non-physical infinite-speed paradox inherent in classical Fourier diffusion. The governing equation with respect to temperature is given by

  $${\displaystyle \frac{1}{c_T^2}}{\displaystyle \frac{{\partial }^{2}T}{\partial t^2}}+{\displaystyle \frac{1}{\alpha }}{\displaystyle \frac{\partial T}{\partial t}}={\nabla }^{2}T+{\displaystyle \frac{1}{k}}\left(S+\tau {\displaystyle \frac{\partial S}{\partial t}}\right)$$

  (2)
• $F_T\in (0,1)$
  The C- and F-model converges to Jeffreys-type parabolic heat conduction, wherein inherent wavefront discontinuities are regularized through Fourier-type diffusive coupling, ensuring physically consistent thermal field continuity. The temperature field is governed by

  $${\displaystyle \frac{1}{c_T^2}}{\displaystyle \frac{{\partial }^{2}T}{\partial t^2}}+{\displaystyle \frac{1}{\alpha }}{\displaystyle \frac{\partial T}{\partial t}}={\nabla }^{2}T+\tau F_T{\displaystyle \frac{\partial {\nabla }^{2}T}{\partial t}}+{\displaystyle \frac{1}{k}}\left(S+\tau {\displaystyle \frac{\partial S}{\partial t}}\right)$$

  (3)
  It is worth noting that the acknowledged Jeffrey-type heat conduction model is also classified as a generalized formulation; however, it essentially reduces to a Fourier-like diffusive model with an additional relaxation term.
• $F_T=1$
  The C- and F-model degenerates to the Fourier-type (parabolic) heat conduction processes, which has an infinite heat propagation speed. The evolution of temperature satisfies the equation

  $${\displaystyle \frac{1}{\alpha }}{\displaystyle \frac{\partial T}{\partial t}}={\nabla }^{2}T+{\displaystyle \frac{1}{k}}S$$

  (4)

  where $\alpha =k/\rho c$, and $\rho$ and c represent the material density and specific heat, respectively; S and $\tau$ are the external heat source or sink and relaxing time, respectively; and $c_T=\sqrt{\alpha /\tau }$ in the Cattaneo (Equation (2))- and Jeffrey (Equation (3))-type models. The hyperbolic model ($F_T$ = 0) produces significantly more intense stress localization at the crack tips compared to the Fourier model ($F_T$ = 1) due to its wave-like heat propagation that creates steeper thermal gradients. The intermediate Jeffreys-type model ($F_T\in (0,1)$) exhibits transitional behavior between these two extremes. For picosecond-scale laser pulses, the ($F_T$ = 0) model is crucial as it captures the strong transient thermal shocks that drive crack propagation, while the ($F_T$ = 1) model substantially underestimates these dynamic effects. The choice of $F_T$ therefore critically determines the accuracy of predicted crack behavior under ultrafast heating conditions.

The constitutive model of the thermoelastic system in the Lagrangian configuration is given by

$$\begin{array}{cc}& \mathit{S}=\mathit{C}:\mathit{E}-{\displaystyle \frac{{\rho }_{0}c}{2T_0}}T\hfill \\ & {\rho }_{0}S={\displaystyle \frac{{\rho }_{0}c}{2T_0}}T+(3\lambda +2\mu )\alpha \mathit{E}\hfill \end{array}$$

(5)

where $\mathit{S}$ represents the second Piola–Kirchhoff stress tensor with the consideration of thermal effect, respectively; $\mathit{E}$ represents the Green–Lagrange strain tensor; T and S represent the temperature and internal energy, respectively; $\lambda$ and $\mu$ represent Lamé parameters, and $\alpha$ is the coefficient of linear thermal expansion of the material; ${\rho }_0$ and c are the mass density and the specific heat at constant stain, respectively; and $T_0$ represents the reference temperature for zero stress. Moreover, $\mathit{C}$ and $\mathit{E}$ are given by

$$\begin{array}{cc}& \mathit{C}=\lambda \mathit{I}\otimes \mathit{I}+2\mu \mathit{I}\hfill \\ & \mathit{E}={\displaystyle \frac{1}{2}}\left({\mathit{F}}^T\mathit{F}-\mathit{I}\right)\hfill \end{array}$$

(6)

in which $\mathcal{I}$ is a fourth-order tensor and is defined by a function of the Kronecker delta (${\delta }_{ij}$) as follows

$${\mathcal{I}}_{ijkl}={\delta }_{ik}{\delta }_{jl}$$

(7)

and $\mathit{F}$ represents the tensor of the deformation gradient.

Based on the C-and F-heat condition model, the associated generalized dynamic themoelasticity model in Lagrangian configuration is given by

$$\begin{array}{cc}& \rho {\displaystyle \frac{{\partial }^2\mathbf{u}}{\partial t^2}}=\mathit{C}:\mathit{E}-(3\lambda +2\mu )\alpha \mathit{I}\nabla T+\rho \mathit{b}\hfill \\ & \rho c{\displaystyle \frac{\partial T}{\partial t}}+\nabla ·\left({\mathit{q}}_C+{\mathit{q}}_F\right)=T_0(3\lambda +2\mu )\alpha \nabla {\displaystyle \frac{\partial \mathit{x}}{\partial t}}+\rho Q\hfill \end{array}$$

(8)

where $\mathbf{u}$ and T represent the displacement and temperature, respectively; $\mathit{I}$ is an identity tensor; Q and $\mathit{b}$ are the external heat source or sink in the thermal field and the external body force in the deformation field, respectively; and the thermal flux terms ${\mathit{q}}_C$ and ${\mathit{q}}_F$ are given in Equation (1).

In the present work, the external heat Q is introduced via the laser pulse [1,32], which is given by

$$Q(\mathbf{u},t)=g_{0}F\left(\mathbf{u}\right)G\left(\mathbf{u}\right)$$

(9)

in which $g_0$ is the intensity of the laser absorption and is a constant, $G\left(t\right)$ is the light intensity of the laser beam, and

$$F\left(\mathbf{u}\right)=e^{-\left|\mathbf{u}\right|/\delta }$$

(10)

with $\delta$ being the laser penetration depth. In the present work, the specific formulation of $Q(\mathit{x},t)$ is given by

$$Q(\mathbf{u},t)={\displaystyle \frac{2J(1-R)}{t_p\delta \sqrt{\pi /ln\left(2\right)}}}{e}^{-x/\delta }{e}^{-a|t-2t_p|/t_p}$$

(11)

Under the action of an ultrashort pulse laser, the material rapidly heats up locally and undergoes uneven thermal expansion, thereby generating significant thermal stress. When the thermal stress exceeds the strength limit of the material, cracks begin to form. As the laser energy continues to be input, the high-temperature gradient at the crack tip causes uneven thermal-stress distribution, resulting in greater stress at this point and significantly accelerating the crack propagation process. Due to the generality of the C- and F-generalized heat flux model, a different $F_T$ leads to different existing thermoelastic models.

• $F_T=0$: Equation (8) degenerates to the Lord–Shulman thermoelasticity model [14] in a Lagrangian configuration

  $$\begin{array}{cc}& \rho {\displaystyle \frac{{\partial }^2\mathbf{u}}{\partial t^2}}=\mathit{C}:\mathit{E}-(3\lambda +2\mu )\alpha \mathit{I}\nabla T+\rho \mathit{b}\hfill \\ & \mathcal{L}\left(\rho c{\displaystyle \frac{\partial T}{\partial t}}-T_0(3\lambda +2\mu )\alpha \nabla {\displaystyle \frac{\partial \mathbf{u}}{\partial t}}-\rho Q\right)=\nabla ·k\nabla T\hfill \end{array}$$

  (12)

  where $\mathcal{L}$ is defined as the following operator:

  $$\mathcal{L}:=1+\tau {\displaystyle \frac{\partial }{\partial t}}$$

  (13)
• $F_T\in (0,1)$: Equation (8) degenerates to a thermoelastic model wherein Jefferys-type thermal flux describes the thermal field:

  $$\begin{array}{cc}& \rho {\displaystyle \frac{{\partial }^2\mathbf{u}}{\partial t^2}}=\mathit{C}:\mathit{E}-(3\lambda +2\mu )\alpha \mathit{I}\nabla T+\rho \mathit{b}\hfill \\ & \mathcal{L}\left(\rho c{\displaystyle \frac{\partial T}{\partial t}}-T_0(3\lambda +2\mu )\alpha \nabla {\displaystyle \frac{\partial \mathbf{u}}{\partial t}}-\rho Q\right)=\nabla ·k\nabla T+\tau F_T{\displaystyle \frac{\partial \nabla ·k\nabla T}{\partial t}}\hfill \end{array}$$

  (14)
• $F_T=1$: Equation (8) degenerates to the classical linear thermoelasticity model in a Lagrangian configurationL

  $$\begin{array}{cc}& \rho {\displaystyle \frac{{\partial }^2\mathbf{u}}{\partial t^2}}=\mathit{C}:\mathit{E}-(3\lambda +2\mu )\alpha \mathit{I}\nabla T+\rho \mathit{b}\hfill \\ & \rho c{\displaystyle \frac{\partial T}{\partial t}}-T_0(3\lambda +2\mu )\alpha \nabla {\displaystyle \frac{\partial \mathbf{u}}{\partial t}}=\nabla ·(k\nabla T)+\rho Q\hfill \end{array}$$

  (15)

The generalized Cattaneo–Fourier thermal flux model improves accuracy by accounting for finite heat propagation speeds and nonlocal effects, which are critical during ultrafast laser irradiation of thin films. Unlike the classical Fourier model, it captures wave-like heat transfer and spatial dispersion, providing better predictions of thermoelastic behavior and stress distributions under rapid heating and cooling cycles.

2.2. Mathematical Formulation of Coupled Thermomechanical Analysis

In peridynamics, any continuum structure is discretized into material points that interact within a nonlocal framework. Each material point at reference position $\mathbf{x}$ interacts with neighboring points ${\mathbf{x}}^{\prime }$ contained within a finite spherical domain of radius $\delta$-termed the “horizon” $H\left(\mathbf{x}\right)$. The nonlocal peridynamic framework plays a crucial role in capturing crack initiation and propagation in thermally shocked thin films by naturally handling discontinuities without remeshing, unlike traditional finite element methods. These neighboring points, collectively referred to as family members, exert pairwise forces that govern the nonlocal interactions in the PD formulation. Specifically, a material point at $\mathbf{x}$ with volume $V_{\mathbf{x}}$ experiences a bond force density $\mathbf{t}$ from its family member at ${\mathbf{x}}^{\prime }$, while simultaneously exerting an equal and opposite force density $-\mathbf{t}$ on ${\mathbf{x}}^{\prime }$ through Newton’s third law.

2.2.1. Mechanical Formulations

The governing equation for linear momentum conservation in PDs is expressed as follows [33]:

$$\rho \left(\mathbf{x}\right)\ddot{\mathbf{u}}(\mathbf{x},t)={\int }_{H\left(\mathbf{x}\right)}\left[\mathbf{t}\left({\mathbf{u}}^{\prime }-\mathbf{u},{\mathbf{x}}^{\prime }-\mathbf{x},t\right)-{\mathbf{t}}^{\prime }\left(\mathbf{u}-{\mathbf{u}}^{\prime },\mathbf{x}-{\mathbf{x}}^{\prime },t\right)\right]d{V}_{{\mathbf{x}}^{\prime }}+\mathbf{b}(\mathbf{x},t)$$

(16)

where $\rho \left(\mathbf{x}\right)$ denotes the mass density, $\mathbf{b}(\mathbf{x},t)$ represents the body force density, and $\ddot{\mathbf{u}}(\mathbf{x},t)$ corresponds to the acceleration field. The displacement vector ${\mathbf{u}}^{\prime }\equiv \mathbf{u}({\mathbf{x}}^{\prime },t)$ describes the motion of family members within the horizon, with primed coordinates (${\mathbf{x}}^{\prime }$) indicating spatial positions of neighboring material points relative to the reference point $\mathbf{x}$.

As a specialized formulation within peridynamics, bond-based PDs impose kinematic constraints on pairwise interactions. The force density vectors $\mathbf{t}$ and ${\mathbf{t}}^{\prime }$ between bonded material points satisfy

$$\mathbf{t}({\mathbf{u}}^{\prime }-\mathbf{u},{\mathbf{x}}^{\prime }-\mathbf{x},t)=-{\mathbf{t}}^{\prime }({\mathbf{u}}^{\prime }-\mathbf{u},{\mathbf{x}}^{\prime }-\mathbf{x},t)$$

(17)

where the forces maintain equal magnitude, opposite direction, and colinearity with the deformed bond vector ${\mathbf{y}}^{\prime }-\mathbf{y}$. This formulation inherently restricts the material Poisson’s ratio to $\nu =1/3$ for plane stress and $\nu =1/4$ for plane strain and 3D configurations [18].

The constitutive response is governed by the pairwise force function:

$$\mathbf{t}={\displaystyle \frac{1}{2}}f\left(s\right){\displaystyle \frac{{\mathbf{y}}^{\prime }-\mathbf{y}}{\parallel {\mathbf{y}}^{\prime }-\mathbf{y}\parallel }}$$

(18)

where the scalar response function f relates to bond stretch through

$$f\left(s\right)=cs$$

(19)

with s denoting the bond stretch:

$$s={\displaystyle \frac{\parallel {\mathbf{y}}^{\prime }-\mathbf{y}\parallel -\parallel {\mathbf{x}}^{\prime }-\mathbf{x}\parallel }{\parallel {\mathbf{x}}^{\prime }-\mathbf{x}\parallel }}$$

(20)

The micromodulus constant c bridges PD parameters with classical continuum mechanics through energy equivalence [34]:

$$c=\left\{\begin{array}{cc}{\displaystyle \frac{2E}{A{\delta }^2}}\hfill & \mathrm{for}1\mathrm{D}\hfill \\ {\displaystyle \frac{9E}{\pi h{\delta }^3}}\hfill & \mathrm{for}2\mathrm{D}\hfill \\ {\displaystyle \frac{12E}{\pi {\delta }^4}}\hfill & \mathrm{for}3\mathrm{D}\hfill \end{array}\right.$$

(21)

where E represents Young’s modulus, $\delta$ the horizon radius, A the cross-sectional area, and h the thickness for 2D analyses.

2.2.2. Non-Fourier Thermal Formulations

The classical peridynamic thermal framework is extended to incorporate non-Fourier effects by introducing a finite relaxation time $\tau$, which governs the delayed response of the heat flux. The governing equations are derived as follows.

$$\rho \left(\mathbf{x}\right)c_v\left(\mathbf{x}\right)\left[\dot{\Theta }(\mathbf{x},t)+\tau \ddot{\Theta }(\mathbf{x},t)\right]={\int }_{H\left(\mathbf{x}\right)}\left[\underline{\mathbf{h}}({\mathbf{x}}^{\prime },\mathbf{x},t)-\underline{\mathbf{h}}(\mathbf{x},{\mathbf{x}}^{\prime },t)\right]d{V}_{{\mathbf{x}}^{\prime }}+h_s(\mathbf{x},t)$$

(22)

where $\tau$ denotes the thermal relaxation time, and $\ddot{\Theta }\equiv {\partial }^2\Theta /\partial t^2$ represents the second-order temperature rate. The additional $\tau \ddot{\Theta }$ term captures the phase-lagged energy accumulation characteristic of non-Fourier conduction.

The reciprocal heat flux density vector adopts a rate-dependent formulation:

$$\underline{\mathbf{h}}({\mathbf{x}}^{\prime },\mathbf{x},t)=-\underline{\mathbf{h}}(\mathbf{x},{\mathbf{x}}^{\prime },t)={\displaystyle \frac{1}{2}}\left[f_h+\tau {\displaystyle \frac{\partial f_h}{\partial t}}\right]$$

(23)

where the transient term $\partial f_h/\partial t$ introduces memory effects into the bond-based interaction.

For isotropic materials, the thermal response function extends to

$$f_h=\kappa \left[{\displaystyle \frac{{\Theta }^{\prime }-\Theta }{\parallel \mathbf{r}\parallel }}+\tau {\displaystyle \frac{\partial }{\partial t}}\left({\displaystyle \frac{{\Theta }^{\prime }-\Theta }{\parallel \mathbf{r}\parallel }}\right)\right]$$

(24)

with $\mathbf{r}={\mathbf{x}}^{\prime }-\mathbf{x}$ being the bond vector. This formulation reduces to the Fourier-type PD model when $\tau \to 0$.

The micro-conductivity $\kappa$ maintains its original dimensional relationship with classical conductivity k [22]:

$$\kappa =\left\{\begin{array}{cc}{\displaystyle \frac{2k}{\pi {\delta }^3}}\hfill & \mathrm{for}1\mathrm{D}\hfill \\ {\displaystyle \frac{6k}{\pi h{\delta }^3}}\hfill & \mathrm{for}2\mathrm{D}\hfill \\ {\displaystyle \frac{6k}{\pi {\delta }^4}}\hfill & \mathrm{for}3\mathrm{D}\hfill \end{array}\right.$$

(25)

ensuring equivalence with classical continuum theory under local thermal equilibrium. Here, $\delta$ represents the horizon radius, and h denotes the thickness for 2D analyses, maintaining dimensional consistency in the nonlocal thermal formulation.

The generalized framework extends peridynamics to ultrafast thermal processes by incorporating relaxation times into Equation (22), enabling the modeling of finite-speed heat propagation. Furthermore, Equation (23) introduces Cattaneo–Vernotte-type flux phase-lagging at the bond level, capturing non-Fourier thermal behavior through microscale lagged heat flux interactions. This formulation preserves peridynamics’ key strengths—its natural ability to handle discontinuities and long-range interactions without spatial derivatives. By integrating these features, the framework bridges ultrafast thermal dynamics with classical Fourier models, ensuring macroscopic compatibility while capturing microscale non-equilibrium effects. This advancement establishes a unified approach for multiscale thermal analysis, seamlessly linking microscale phenomena to macroscopic heat transfer regimes.

2.2.3. Thermomechanical Coupling

The fully coupled thermomechanical framework is extended to incorporate non-Fourier thermal effects, introducing bidirectional energy transduction between deformation and thermal fields. Let ${\Theta }_0$ denote the reference temperature at the stress-free state. The temperature variation field is defined as

$$T(\mathbf{x},t)=\Theta (\mathbf{x},t)-{\Theta }_0,$$

(26)

with the bond-averaged temperature variation:

$$T_{\mathrm{ave}}={\displaystyle \frac{1}{2}}\left(T({\mathbf{x}}^{\prime },t)+T(\mathbf{x},t)\right).$$

(27)

The momentum balance equation accounts for both mechanical and thermal interactions:

$$\rho \left(\mathbf{x}\right)\ddot{\mathbf{u}}(\mathbf{x},t)={\int }_{H\left(\mathbf{x}\right)}\left[(c\mathbf{s}-\beta T_{\mathrm{ave}}){\displaystyle \frac{{\mathbf{y}}^{\prime }-\mathbf{y}}{\parallel {\mathbf{y}}^{\prime }-\mathbf{y}\parallel }}\right]d{V}_{{\mathbf{x}}^{\prime }}+\mathbf{b}(\mathbf{x},t),$$

(28)

where c is the micromodulus constant (Equation (21)), s denotes the bond stretch (Equation (20)), and $\beta =c\alpha$ represents the thermomechanical coupling modulus with $\alpha$ being the thermal expansion coefficient.

The energy balance equation is generalized to include non-Fourier heat conduction with relaxation time $\tau$:

$$\rho \left(\mathbf{x}\right)c_v\left(\mathbf{x}\right)\left[\dot{\Theta }(\mathbf{x},t)+\tau \ddot{\Theta }(\mathbf{x},t)\right]={\int }_{H\left(\mathbf{x}\right)}\left[\kappa \left({\displaystyle \frac{{\Theta }^{\prime }-\Theta }{\parallel \mathbf{r}\parallel }}+\tau {\displaystyle \frac{\partial }{\partial t}}\left({\displaystyle \frac{{\Theta }^{\prime }-\Theta }{\parallel \mathbf{r}\parallel }}\right)\right)-{\displaystyle \frac{\beta }{2}}\dot{e}\Theta \right]d{V}_{{\mathbf{x}}^{\prime }}+h_s(\mathbf{x},t),$$

(29)

where the bond extension rate $\dot{e}$, quantifying the temporal evolution of relative displacement between material points $\mathbf{x}$ and ${\mathbf{x}}^{\prime }$, is defined as follows:

$$\dot{e}={\displaystyle \frac{{\mathbf{y}}^{\prime }-\mathbf{y}}{\parallel {\mathbf{y}}^{\prime }-\mathbf{y}\parallel }}·({\dot{\mathbf{u}}}^{\prime }-\dot{\mathbf{u}}),$$

(30)

with $\mathbf{y}=\mathbf{x}+\mathbf{u}(\mathbf{x},t)$ representing the deformed position vector.

The thermomechanical interactions manifest through three fundamental mechanisms: (i) the thermal stress term $-\beta T_{\mathrm{ave}}$ in Equation (28) couples temperature variations to mechanical deformation by introducing a temperature-dependent force density proportional to the bond-averaged temperature deviation; (ii) heat generation arising from mechanical work is captured by the term $-{\displaystyle \frac{\beta }{2}}\dot{e}\Theta$ in Equation (29), which quantifies the thermal energy production rate due to bond extension dynamics; and (iii) the incorporation of phase-lagged thermal transport governed by the relaxation time $\tau$ in the modified heat flux formulation enables finite heat propagation speeds, a hallmark of non-Fourier conduction.

This generalized framework preserves peridynamics’ inherent capability to model discontinuities and long-range interactions while extending its applicability to ultrafast thermomechanical processes. The classical Fourier-based coupled solution is naturally recovered as a limiting case when $\tau \to 0$, ensuring backward compatibility with conventional thermal-stress analyses.

3. Numerical Implementations

In the present work, the numerical implementation employs a nonlocal peridynamic discretization framework, where bond-based particle interactions replace conventional mesh formulations, embedding coupled thermomechanical responses within integral-form constitutive relations while preserving nonlocal continuum physics and eliminating mesh dependency artifacts. The differential operators of peridynamics such as the gradient and Laplacian are directly implemented to carry out the spatial discretization of Equation (8). Due to the feasibility of the meshless method, the solid body is not required to be smooth enough and can have cracks in the system.

3.1. Laser Heating-Imposing Technique in Peridynamic

The specific techniques of imposing different boundary conditions (Type I, $II$, and $III$) in the heat conduction problem have been thoroughly investigated in [35]; herein, in order to investigate the thermoelastic response of solids due to laser heating, the approach of introducing an external thermal load is given as follows.

Let the energy from the external heat source be $E_k$ at the k-th particle such that the heat generated per unit volume, per unit time, can be obtained as

$${\displaystyle \frac{d{E}_k}{dt}}={\displaystyle \frac{{\int }_S{Q}_{k}dS}{V_A}}\approx -{\displaystyle \frac{1}{d_A}}{Q}_k$$

(31)

Due to this thermal effect, the governing equation of the heat process in the solid body, Equation (8), at the k-th particle considers to add the following heat source term

$$S_k=-{\displaystyle \frac{1}{d_A}}\sum _{k\in \Omega }{Q}_k{W}_{Ak}/\sum _{k\in \Omega }{W}_{Ak}$$

(32)

where the $Q_k$ is evaluated from Equation (8) at the k-th particle.

3.2. Time Integration Scheme

The numerical resolution of this strongly coupled thermomechanical system requires a rigorous temporal integration scheme, with particular attention to enforcing energy and momentum conservation at discrete time steps via a staggered operator-splitting approach. As shown in Equations (1) and (15), these governing equations of the coupled system comprise a first-order time-dependent system (${\mathit{q}}_C$ and heat conduction model) and second-order time-dependent system (equation of motion). After the spatial discretization of these equations, the associated time-continuous ordinary differential equations can be obtained in the following form

$$\begin{array}{cc}& \mathit{M}\ddot{\mathit{X}}={\mathit{f}}_X(\mathit{X},\dot{\mathit{X}},\mathit{Y},\dot{\mathit{Y}})\hfill \\ & \mathit{C}\dot{\mathit{Y}}={\mathit{f}}_Y(\mathit{X},\dot{\mathit{X}},\mathit{Y},\dot{\mathit{Y}})\hfill \end{array}$$

(33)

where $\mathit{X}$ represents the primary unknowns in the second-order time-dependent system and $\mathit{Y}$ represents the primary unknowns in the first-order time-dependent system; specifically, $\mathit{X}$ is the displacement $\mathit{x}$ of the mechanical field while $\mathit{Y}$ includes the temperature T and Cattaneo-type flux ${\mathit{q}}_C$.

In the present work, a unified time integration framework, GSSSS i-Integration, is exploited to achieve the time marching of Equation (33). In contrast to the traditional techniques that require implementing altogether different algorithmic platforms for the altogether different 1st/2nd-order systems. The GSSSS i-Integration can be simultaneously used in these two systems without resorting to each individual system and yield a family of second-order accurate, implicit, unconditionally stable algorithms with controllable numerical dissipation on the zeroth-, first-, and second-order time derivatives and zero-order overshooting behavior. The GSSSS i-Integration scheme is highly effective in maintaining numerical stability and the resolution of steep thermal gradients during picosecond-scale simulations. By accurately capturing rapid thermal changes, it ensures stable computations while preserving fine details, making it well suited for high-resolution modeling under ultrafast conditions. These numerical features of GSSSS i-Integration have been investigated; here, instead of repeating the previous work regarding the illustration of GSSSS i-Integration, we only briefly show the algorithm generated from the GSSSS i-Integration that is used in the present work.

Consider the temporal discretization of the governing equations for a time interval $\mathbb{I}=\left[t_0,t_f\right]$ split into sub-intervals, $\mathbb{I}={\bigcup }_{n=0}^{f-1}\left[t_n,t_{n+1}\right]$. The time-step size is defined as $\Delta t=t_{n+1}-t_n$ and assumed to be constant for simplicity. Via a novel normalized time-weighted residual methodology, the algorithmic time step ($t_{n+W_1}$) is introduced and the algorithmic variables are as follows:

$$\begin{array}{cc}& \widetilde{\ddot{\mathit{X}}}={\dot{X}}_n+W_1{V}_6\Delta \ddot{\mathit{X}}\hfill \\ & \widetilde{\dot{\mathit{X}}}={\dot{X}}_n+W_1{V}_4\Delta t{\ddot{\mathit{X}}}_n+W_2{V}_5\Delta t\Delta \ddot{\mathit{X}}\hfill \\ & \tilde{\mathit{X}}={\mathit{X}}_n+W_1{V}_1\Delta t{\dot{\mathit{X}}}_n+W_2{V}_2\Delta t^2{\ddot{\mathit{X}}}_n+W_3{V}_3\Delta t^2\Delta \ddot{\mathit{X}}\hfill \\ & \widetilde{\ddot{\mathit{Y}}}={\dot{Y}}_n+W_1{V}_6\Delta \ddot{\mathit{Y}}\hfill \\ & \widetilde{\dot{\mathit{Y}}}={\dot{Y}}_n+W_1{V}_4\Delta t{\ddot{\mathit{Y}}}_n+W_2{V}_5\Delta t\Delta \ddot{\mathit{Y}}\hfill \end{array}$$

(34)

Substituting Equation (34) into Equation (33) yields the increments of $\Delta \ddot{\mathit{X}}$ and $\Delta \dot{Y}$ as follows:

$$\begin{array}{c}\hfill \Delta \ddot{\mathit{X}}=\left[{\mathit{f}}_X(\tilde{\mathit{X}},\widetilde{\dot{\mathit{X}}},\tilde{\mathit{Y}},\widetilde{\dot{\mathit{Y}}})-\mathit{M}{\ddot{\mathit{X}}}_n\right]/W_1{V}_6\\ \hfill \Delta \dot{\mathit{Y}}=\left[{\mathit{f}}_Y(\tilde{\mathit{X}},\widetilde{\dot{\mathit{X}}},\tilde{\mathit{Y}},\widetilde{\dot{\mathit{Y}}})-\mathit{C}{\dot{\mathit{X}}}_n\right]/W_1{V}_6\end{array}$$

(35)

and the updated variables at the end of each time step are

$$\begin{array}{cc}& {\mathit{X}}_{n+1}={\mathit{X}}_n+{\lambda }_1{\dot{\mathit{X}}}_n\Delta t+{\lambda }_2{\ddot{\mathit{X}}}_n\Delta t^2+{\lambda }_3\Delta \ddot{\mathit{X}}\Delta t^2\hfill \\ & {\dot{\mathit{X}}}_{n+1}={\dot{\mathit{X}}}_n+{\lambda }_4\Delta \ddot{\mathit{X}}\Delta t\hfill \\ & {\ddot{\mathit{X}}}_{n+1}={\ddot{\mathit{X}}}_n+\Delta \ddot{\mathit{X}}\hfill \\ & {\mathit{Y}}_{n+1}={\mathit{Y}}_n+{\lambda }_4\Delta \dot{\mathit{Y}}\Delta t\hfill \\ & {\dot{\mathit{Y}}}_{n+1}={\dot{\mathit{Y}}}_n+\Delta \ddot{\mathit{Y}}\hfill \end{array}$$

(36)

The algorithmic parameters are as follows:

$$\begin{array}{cc}\hfill & W_1{\Lambda }_1=W_1{\Lambda }_4={\displaystyle \frac{3+{\rho }_{\infty }^{\min }+{\rho }_{\infty }^{\max }-{\rho }_{\infty }^{\min }{\rho }_{\infty }^{\max }}{2(1+{\rho }_{\infty }^{\min })(1+{\rho }_{\infty }^{\max })}},W_2{\Lambda }_2={\displaystyle \frac{1}{(1+{\rho }_{\infty }^{\min })(1+{\rho }_{\infty }^{\max })}}\hfill \\ \hfill & W_1{\Lambda }_6={\displaystyle \frac{2+{\rho }_{\infty }^{\min }+{\rho }_{\infty }^{\max }+{\rho }_{\infty }^{\mathrm{s}}-{\rho }_{\infty }^{\min }{\rho }_{\infty }^{\max }{\rho }_{\infty }^{\mathrm{s}}}{(1+{\rho }_{\infty }^{\min })(1+{\rho }_{\infty }^{\max })(1+{\rho }_{\infty }^{\mathrm{s}})}},W_2{\Lambda }_5={\displaystyle \frac{2}{(1+{\rho }_{\infty }^{\min })(1+{\rho }_{\infty }^{\max })(1+{\rho }_{\infty }^{\mathrm{s}})}}\hfill \\ \hfill & {\lambda }_1={\lambda }_4=1,{\lambda }_2={\displaystyle \frac{1}{2}},{\lambda }_3={\displaystyle \frac{1}{2(1+{\rho }_{\infty }^{\mathrm{s}})}},{\lambda }_5={\displaystyle \frac{1}{1+{\rho }_{\infty }^{\mathrm{s}}}}\hfill \end{array}$$

(37)

where $(1,{\rho }_{\infty }^{\min },{\rho }_{\infty }^{\mathrm{s}})$ are the input algorithmic real parameters that represent the principal and spurious roots.

Due to the flexibility of the GSSSS i-Integration, numerous schemes can be obtained by changing the algorithmic parameters $({\rho }_{\infty }^{\max },{\rho }_{\infty }^{\min },{\rho }_{\infty }^{\mathrm{s}})$. In this work, we attempt to introduce the max dissipation to the time integration schemes such that $(1,{\rho }_{\infty }^{\min },{\rho }_{\infty }^{\mathrm{s}})=(1,0,0)$. This is in such a way,

$$\begin{array}{cc}\hfill & W_1{\Lambda }_1=W_1{\Lambda }_4=1,W_2{\Lambda }_2=0.5\hfill \\ \hfill & W_1{\Lambda }_6=1.5,W_2{\Lambda }_5=1,{\lambda }_3=0.5,{\lambda }_5=1\hfill \end{array}$$

(38)

This particular scheme has the maximal dissipation with respect to $\ddot{\mathit{X}}$, $\dot{\mathit{X}}$ in the second-order time-dependent system and to $\dot{\mathit{Y}}$, $\mathit{Y}$ in the first-order time-dependent system. It recovers the optimal algorithm with zero-order displacement and zero-order velocity overshoot with maximal dissipation for the second-order dynamic system and Gear’s method for the first-order transient system.

4. Numerical Examples

4.1. Numerical Validations: 1D Danilovskakya Problem with Non-Fourier Effect

Danilovskaya’s problem, analyzing thermally induced shock wave propagation under abrupt boundary heating, serves as a classical benchmark for validating coupled thermomechanical formulations in dynamic elasticity theory. Detailed descriptions of this problem can be found in [36]. To validate the numerical performance of the proposed method, a generalized version of the governing equations with extension of non-Fourier heat flux is given as follows:

$$\begin{array}{cc}& {\displaystyle \frac{{\partial }^{2}u}{\partial {\xi }^2}}-{\displaystyle \frac{{\partial }^{2}u}{\partial {\tau }^2}}-{\displaystyle \frac{\partial \theta }{\partial \xi }}=0\hfill \\ & F_T{\tau }_0{\displaystyle \frac{{\partial }^2\dot{\theta }}{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2\theta }{\partial {\xi }^2}}-{\displaystyle \frac{\partial \theta }{\partial \tau }}-{\tau }_0{\displaystyle \frac{{\partial }^2\theta }{\partial {\tau }^2}}=0\hfill \end{array}$$

(39)

and the normal stress is

$$\sigma ={\displaystyle \frac{\partial u}{\partial \xi }}-\theta$$

(40)

where u and $\theta$ represent the displacement and temperature, respectively; $\xi$ and $\tau$ represent the space and time dimensions, respectively. Note that the governing equations of the original Danilovskaya problem are a one-way coupled thermoelastic model with ($ta{u}_0=0$) since the contribution from the deformation to the thermal field is ignored. The specific initial and boundary conditions are given as follows:

• Initial Conditions:

  $$\begin{array}{cc}& u(\xi ,0)=0,\dot{u}(\xi ,0)=0,\theta (\xi ,0)=0,\hfill \\ & u(\xi \to \infty ,\tau )\to 0,{\displaystyle \frac{\partial u}{\partial \xi }}(\xi \to \infty ,\tau )\to 0,\theta (\xi \to \infty ,\tau )\to 0\hfill \end{array}$$

  (41)
• Boundary Conditions:

  $$\theta (0,\tau )={\theta }_0$$

  (42)

The proposed method is exploited for the spatial discretization and the time marching in this thermal-elastic model, respectively. The system is assumed to be a 1D bar with a length $\xi =4$ and is discretized by 1000 particles. All the numerical examples in this case are simulated with a time-step size ($\Delta \tau$) ${10}^{-4}$ implicitly and an end time $\tau =1$ with $F_T=0.02$ and ${\tau }_0=0.1$ in equation (39). In addition, the local results are obtained via setting $R_d=1.01r$, in which $R_d$ represents the cut-off radius (“horizon” in peridynamics) and r represents the particle radius. Figure 2 gives the distribution of the displacement, temperature, and stress at different time instants, where the numerical results of the proposed model are represented by solid lines and those of the finite element methods proposed in [36] are represented by symbols.

Figure 2, bottom, presents the associated fully coupled thermoelastic field with that of the Fourier’s thermal flux model. In contrast to Figure 2, top, in which the temperature field does not consider the influence due to material deformation, the temperature and displacement fields affect each other concurrently, such that the distinct physics can be observed.

4.2. Numerical Validations: Thermodynamics of a Cracked Plate with Fixed Temperature Boundaries

In this part, the proposed approach is first validated by a two-dimensional cracked square (1 × 1) with fixed temperature boundaries (essential boundary condition) on the top and bottom edges and the initial temperature is taken as 1. The square is discretized by 50 × 50 particles and the time interval is taken as ${10}^{-4}$. To better illustrate the deformation and thermal fields, the material properties are artificially selected as follows:

$$\rho =3000;E=5000;\mu =0.3;c=0.1;k=10;\tau =1;\alpha ={10}^{-6}$$

(43)

Figure 3 delineates the fundamental divergence between Fourier-type ($F_T=1$) and Cattaneo-type ($F_T=0$) heat conduction mechanisms. The Fourier model exhibits parabolic thermal diffusion, with instantaneous heat signal propagation across the entire domain—evidenced by a 25% temperature attenuation ($T/T_0\approx 0.75$) at $t=0.015$ and persistent crack-induced thermal perturbations throughout the simulation. In contrast, the Cattaneo-type model demonstrates hyperbolic wave behavior, preserving 85% of the initial thermal energy ($T/T_0\approx 0.85$) at equivalent timeframes due to localized wavefront propagation. This wave-mediated mechanism delays crack interaction until post-wave passage, as manifested by a 15–20% stronger retained thermal gradient compared to the Fourier case. The von Mises stress distributions in Figure 4 further corroborate this phenomenon. The Cattaneo-type model leads to the rapid development of the stress concentration at the tip of the crack, and the Fourier-type conduction reduces the stress accumulation by about 15% under equivalent conditions at $t=0.0075$ and by approximately 20% at $t=0.015$. These quantitative trends are consistent with the existing thermal-stress coupling computational framework [37], validating the observed thermomechanical synergy.

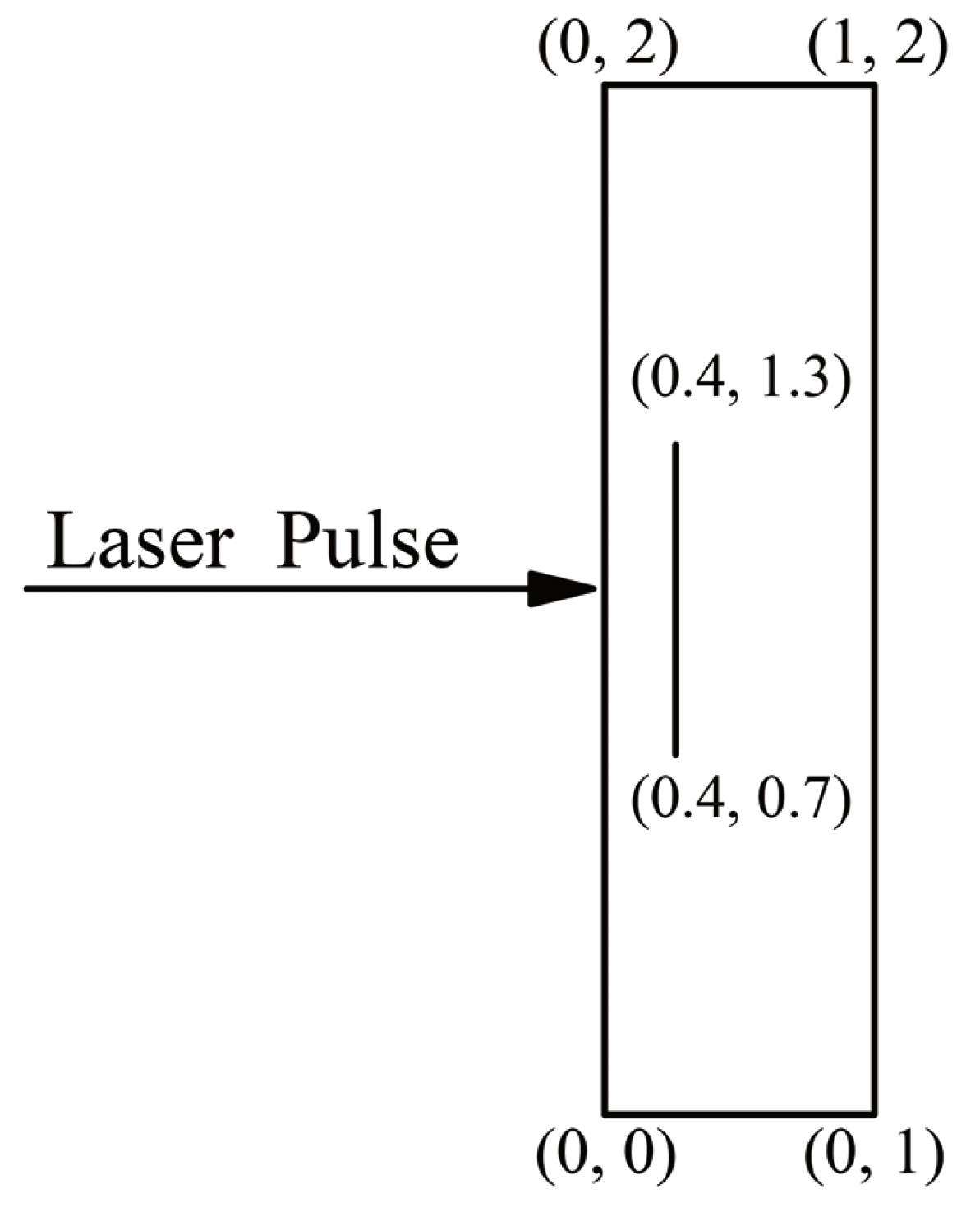
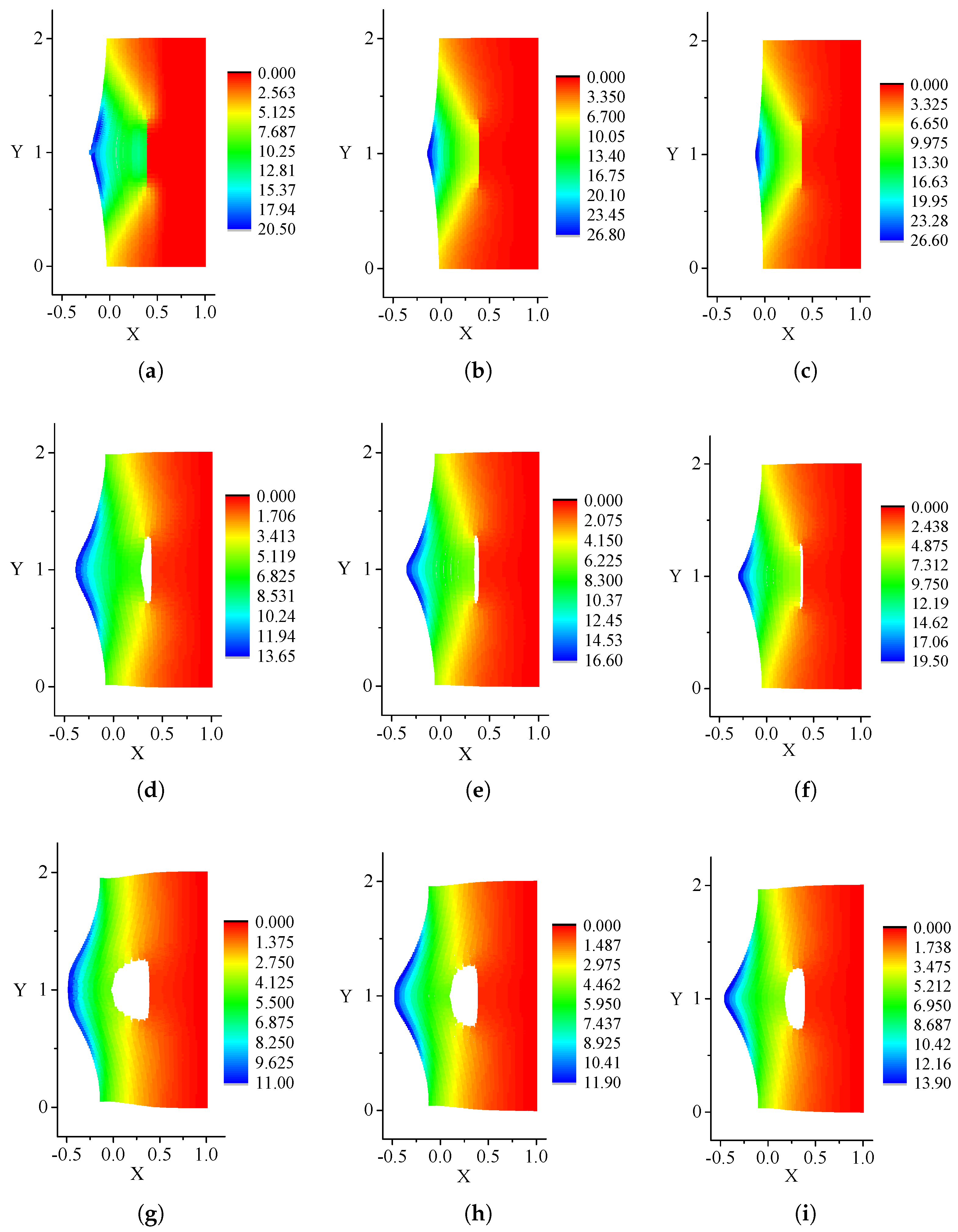
4.3. Thermodynamics of a Thin Film Under Short-Pulse Laser Heating

This section investigates the transient thermal behavior of a thin film subjected to pulsed laser irradiation. The numerical model proposed in this study is universal, with its generalized heat conduction equation and thermomechanical coupling mechanism applicable to various material systems. While the current examples validate the model using metal films as the subject, different materials have varying thermal properties. For example, non-metallic materials may exhibit stronger non-Fourier effects. Although the current model does not directly simulate the formation of other structural defects or film changes induced by ultrashort pulse lasers, it reveals the different degrees of deformation and the evolution of temperature and stress fields in films under different heat conduction mechanisms.

The system is initially equilibrated at ambient temperature ($T_{\infty }$) before experiencing rapid laser excitation, with operational parameters consistent with established models in ultrafast laser–matter interactions [1,32]. Specifically, the laser energy and material properties of the film are given as

$$\begin{array}{cc}& \delta =15.3\times {10}^{-9}\mathrm{m},J=13.4\mathrm{J}/{\mathrm{m}}^2,a=1.992,t_p={10}^{-13},R=0.93\hfill \\ & L=1\mathsf{\mu }\mathrm{m},k=315\mathrm{W}/\mathrm{m}·\mathrm{K},\alpha =1.2\times {10}^{-1}{\mathrm{m}}^2/\mathrm{s},\tau =8.5\times {10}^{-12}\mathrm{s}\hfill \end{array}$$

(44)

It is worth noting that the $\alpha$ in the present work is magnified to 1000 times that of gold to amplify the laser-induced deformation effects in the thin-film structure. The specific geometry and crack location are given in Figure 5. The film is discretized by 50 × 100 particles and the weighted function is taken to be 1 in the influence domain $R=2.5r$ in which r represents the particle radius. All the numerical simulations are carried out via the GSSSS i-Integration scheme V0 (1, 0, 0) and the time interval is taken as 1 ps.

The thermomechanical response of the laser-irradiated thin film is systematically analyzed through coupled thermal-stress modeling. As depicted in Figure 6 and Figure 7, three thermal transport regimes are examined: hyperbolic ($F_T=0$), dual-phase-lag ($F_T=0.5$), and Fourier diffusion ($F_T=1$).

The temporal evolution of von Mises stress, as depicted in Figure 6 and Figure 7, demonstrates a marked increase in stress magnitudes over time for all heat conduction models. Under the hyperbolic heat model ($F_T=0$), the stress growth rate exceeds that of the parabolic models ($F_T=0.5$ and $F_T=1$), with peak stress amplitudes reduced by up to $35\%$ for $F_T=1$ compared to $F_T=0$ at $t=100$ ps. This trend persists across all time instants, highlighting the transient stress accumulation in hyperbolic systems due to steep temperature gradients (Figure 6). Additionally, crack tips exhibit localized stress concentrations, with $F_T=0$ consistently producing higher stress magnitudes than parabolic models (e.g., $1.3$ times greater at $t=150$ ps).

The relationship between temperature gradients and stress magnitudes further clarifies these differences in Figure 7. Hyperbolic heat conduction ($F_T=0$) generates sharper temperature gradients near thermal wavefronts, directly correlating with elevated stress amplitudes. In contrast, parabolic models ($F_T=0.5$ and $F_T=1$) exhibit smoother temperature distributions, reducing peak stresses by approximately 20–$30\%$ compared to $F_T=0$. These observations emphasize the critical role of heat conduction mechanisms in thermomechanical coupling: hyperbolic models amplify transient stress concentrations, while parabolic models promote stress relaxation. The quantitative reduction in stress amplitudes underscores the importance of thermal management strategies in mitigating fracture risks during laser-driven processes.

5. Conclusions

The present study developed a peridynamic-based nonlocal computational framework to explicitly resolve thermomechanical coupling in cracked thin films under ultrashort- pulsed laser irradiation. This approach employs discrete material points to model nonlocal continuum interactions, effectively addressing crack-induced thermal perturbations and stress concentrations while overcoming mesh dependency limitations of traditional methods. The main discoveries of this study are outlined as follows:

• The thermomechanical response of thin films under short-pulse laser heating demonstrates distinct heat propagation mechanisms governed by the selected thermal flux model. For the hyperbolic Cattaneo-type formulation ($F_T=0$), thermal energy propagates at finite speeds, generating localized temperature gradients that induce pronounced structural deformation. In contrast, Fourier-type diffusion ($F_T=1$) assumes instantaneous heat distribution, resulting in smoother thermal fields and comparatively reduced mechanical distortions.
• A unified GSSSS i-Integration algorithm successfully synchronized first-order thermal and second-order mechanical fields, enabling stable simulations at picosecond timescales ($\Delta t=1$ ps). By configuring algorithmic parameters (${\rho }_{\infty }^{\min },{\rho }_{\infty }^{\mathrm{s}}$) = (0, 0), maximal numerical dissipation was achieved, suppressing oscillations while preserving accuracy in resolving steep thermal gradients and stress localization. This approach proved robust for modeling ultrafast laser-induced phenomena, where conventional staggered schemes often fail due to tight multiphysics coupling.
• In the cracked plate, Cattaneo-type flux temperature propagation is hysteretic and shows wave-like propagation. For laser-irradiated films, Fourier models reduced peak stresses by 25% compared to hyperbolic models at $t=100$ ps, underscoring the dominance of hyperbolic conduction in high-gradient scenarios. These results align with experimental observations of stress-driven failures in ultrafast laser processing.

The findings emphasize the need to select heat flux models ($F_T$) based on operational timescales. Hyperbolic models ($F_T=0$) are indispensable for simulating picosecond laser interactions, where transient stress concentrations dominate failure mechanisms. Future studies will integrate the two-temperature theory with the generalized Cattaneo–Fourier heat flux model to address electron–lattice thermal non-equilibrium in metallic thin films under ultrashort laser pulses, particularly focusing on transient energy partitioning. This hybrid approach aims to reveal picosecond-scale thermomechanical coupling mechanisms, enabling an accurate prediction of stress evolution and damage thresholds in advanced micro-/nano-electronic devices under extreme thermal transients.