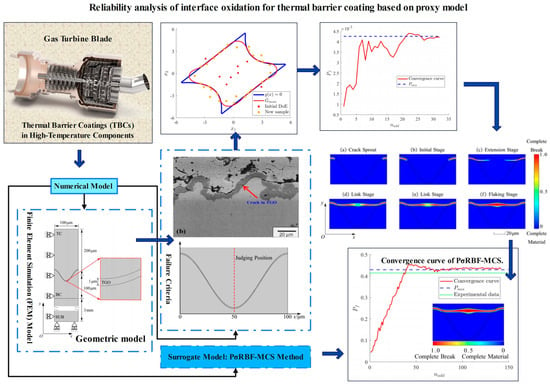
Reliability Analysis of Interface Oxidation for Thermal Barrier Coating Based on Proxy Model
Abstract
1. Introduction
2. Surrogate Model Based on Radial Basis Function
2.1. Construction of a Radial Basis Function Model
2.2. K-Fold Cross-Validation
3. RBF-MCS Method
3.1. Multiple Predictions Based on Different Shape Parameters and Multiple-Subset Initiation
3.2. Comparison of Predicted Variance Significance
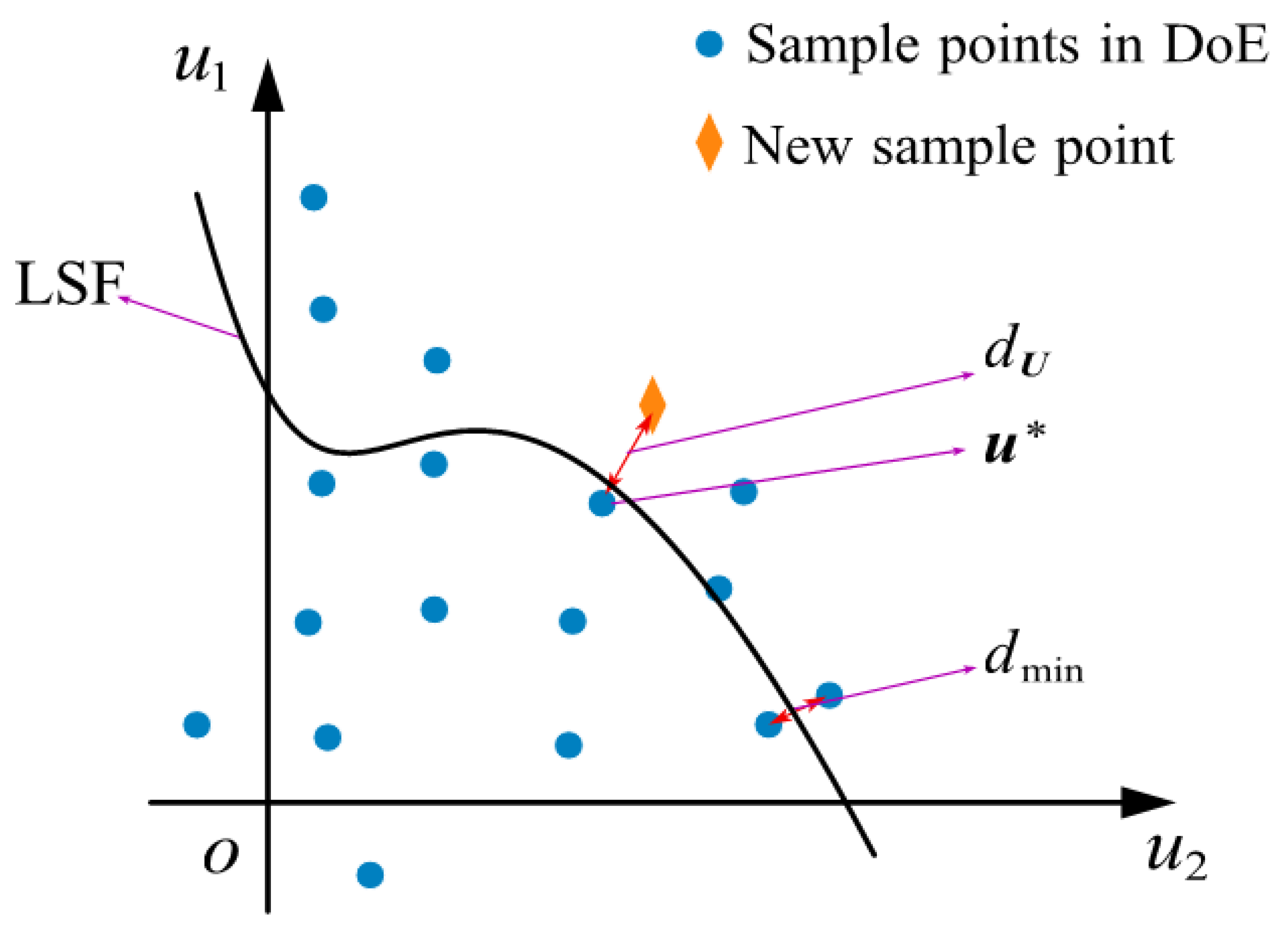
3.3. Construction of the Learning Function
3.4. Failure Probability
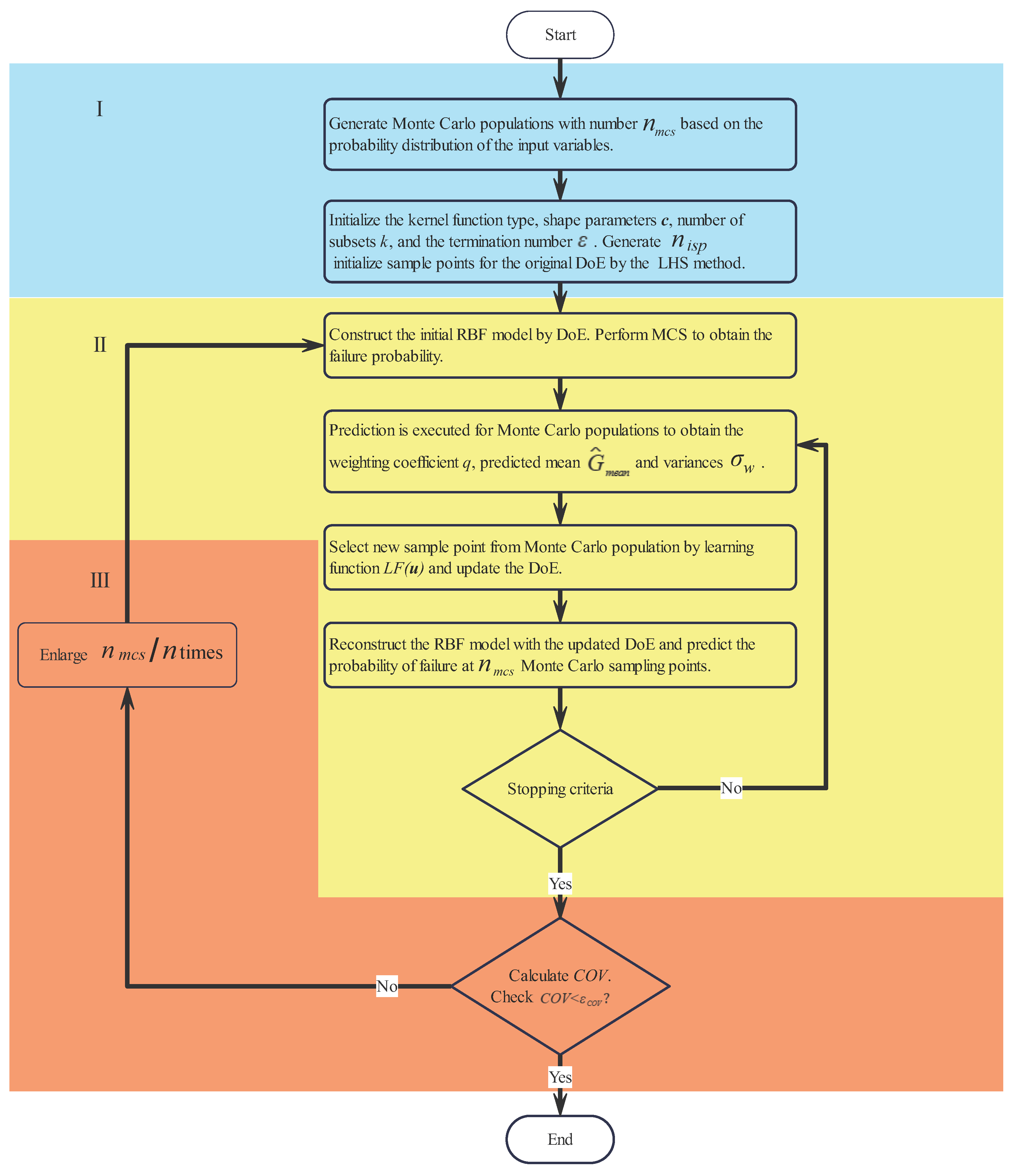
3.5. Main Steps of Active Learning Process
- Step 1: Generating an MC population with a size of based on the probability distribution of the input variables.
- Step 2: Initializing the kernel function type, shape parameters c, subset number k, and termination number of the RBF model, and generating P initial sample points that form the initial DoE by using the Limit State Function (LSF) method.
- Step 3: Constructing the initial RBF model through initial DoE, and then obtaining the failure probability by MCS.
- Step 4: Predicting MC populations to obtain weighted coefficients , predicted mean , and predicted mean variance .
- Step 5: Selecting new sample points from MC population by using learning functions and updating DoE.
- Step 6: Reconstructing the RBF model based on Equation (1) by using the updated DoE, and predicting the failure probabilities of MC sampling points.
- Step 7: Executing stop criteria judgment. If satisfied, going to the next step of judgment, otherwise, returning to step 4 to continue iterating.
- Step 8: Calculating and determining if it is less than . If satisfied, ending iteration; otherwise, expanding by 10 times and returning to step 3.
3.6. Implementation Details
4. Example Verification
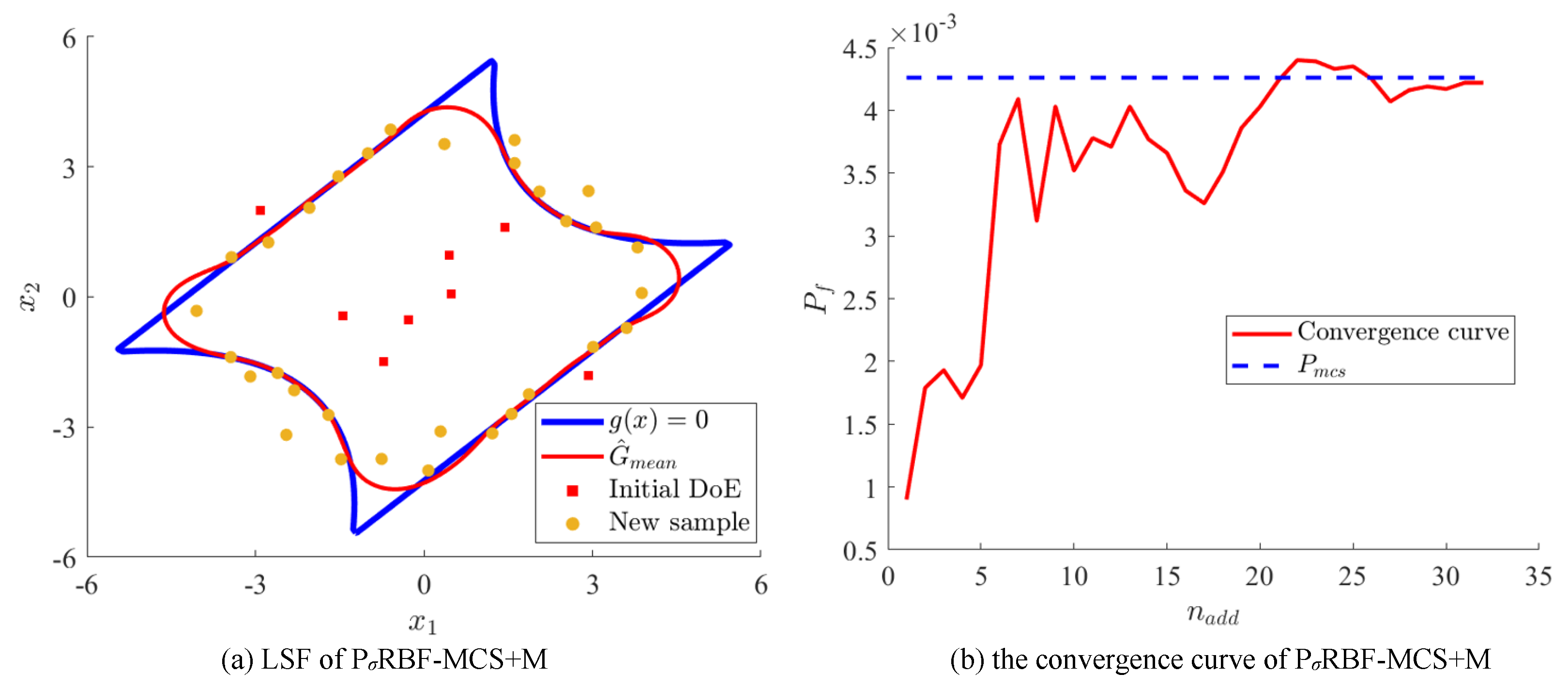

| Results of MCS or References | Method | (%) | (%) | |
|---|---|---|---|---|
| MCS | 0.4324 | / | ||
| Reference [24] | ARBFM-MCS | 60.1 | 0.4466 | 1.13 |
| Reference [24] | CVRBF-MCS () | 65.4 | 0.4480 | 1.44 |
| Reference [32] | RBF-GA | 33.3 | 0.4367 | 1.10 |
| Reference [26] | MCRBF-MCS | 36.3 | 0.4479 | 1.43 |
| RBF method | RBF+IM (, ) | 73.4 | 0.4473 | 3.44 |
| RBF+G (, ) | 35.6 | 0.4382 | 1.36 | |
| (, ) | 41.8 | 0.4383 | 1.02 | |
| (, ) | 42.3 | 0.4374 | 0.96 | |
| RBF+M (, ) | 58.9 | 0.4197 | 2.94 | |
| (, ) | 64.2 | 0.4267 | 1.32 | |
| (, ) | 38.2 | 0.4251 | 1.68 | |
| (, ) | 43.3 | 0.4300 | 1.26 | |
| (, ) | 40.8 | 0.4365 | 0.94 |
5. Reliability Assessment of TBC Interface Oxidation Failure
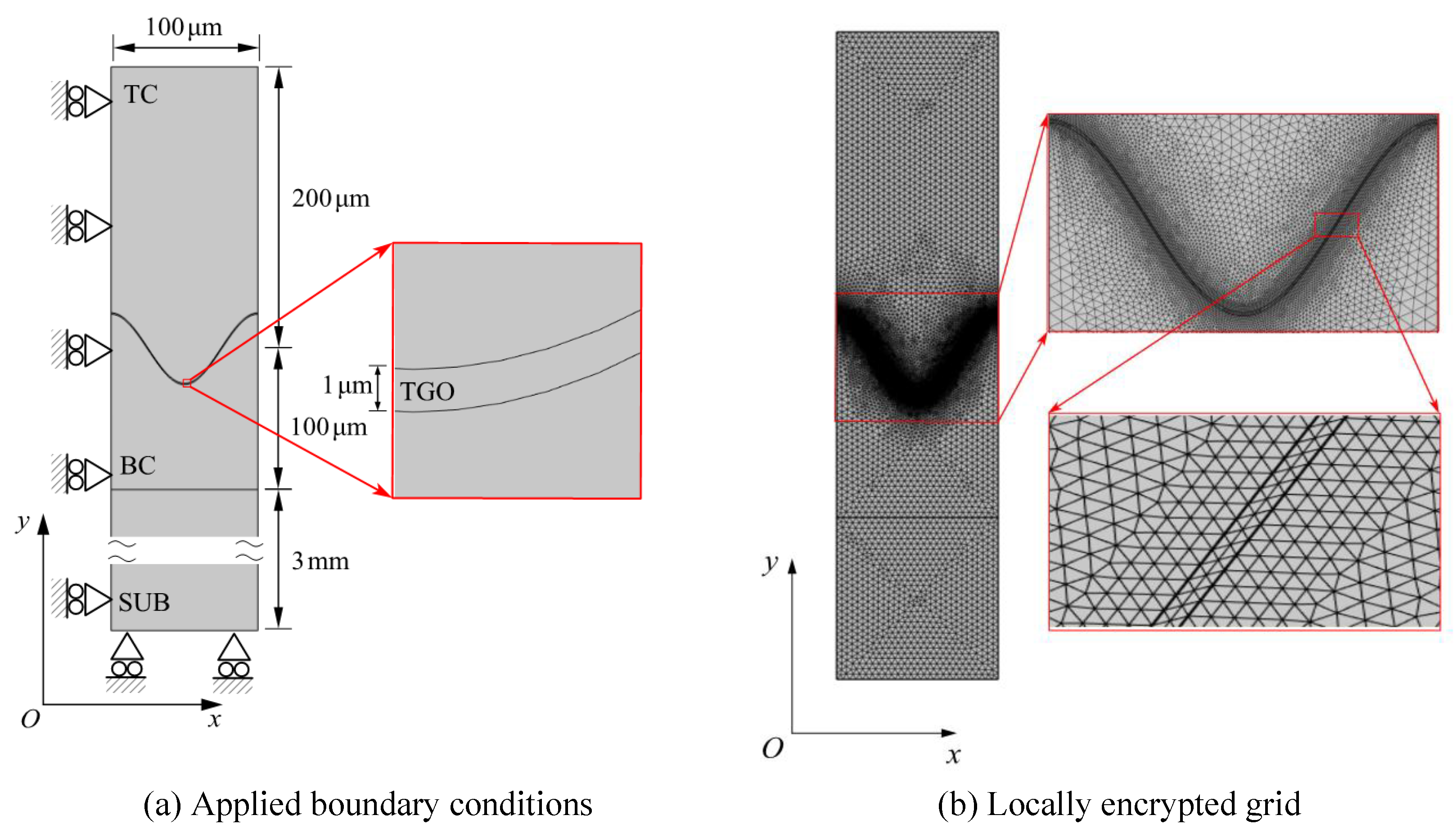
5.1. Finite Element Model and Boundary Conditions
| Ceramic Layer | Oxide Layer | Bonding Layer | Substrate | |
|---|---|---|---|---|
| Young’s modulus E (GPa) | 35 | 375 | 120 | 160 |
| Poisson’s ratio v | 0.1 | 0.25 | 0.32 | 0.33 |
| density (kg/) | 5650 | 3978 | 8100 | 8100 |
| tensile strength (GPa) | 0.2 | 0.38 | 0.5 | / |
| Fracture energy (J/) | 61 | 49 | 47 | / |
| Coefficient of thermal expansion () | 9.8 × | 9.2 × | 1.4 × | 1.5 × |
| Critical energy release rate (N/mm) | 50 | 40 | 2700 | 2700 |
| Thermal conductivity coefficient () | 1.16 | 4.4 | 14.5 | 26 |
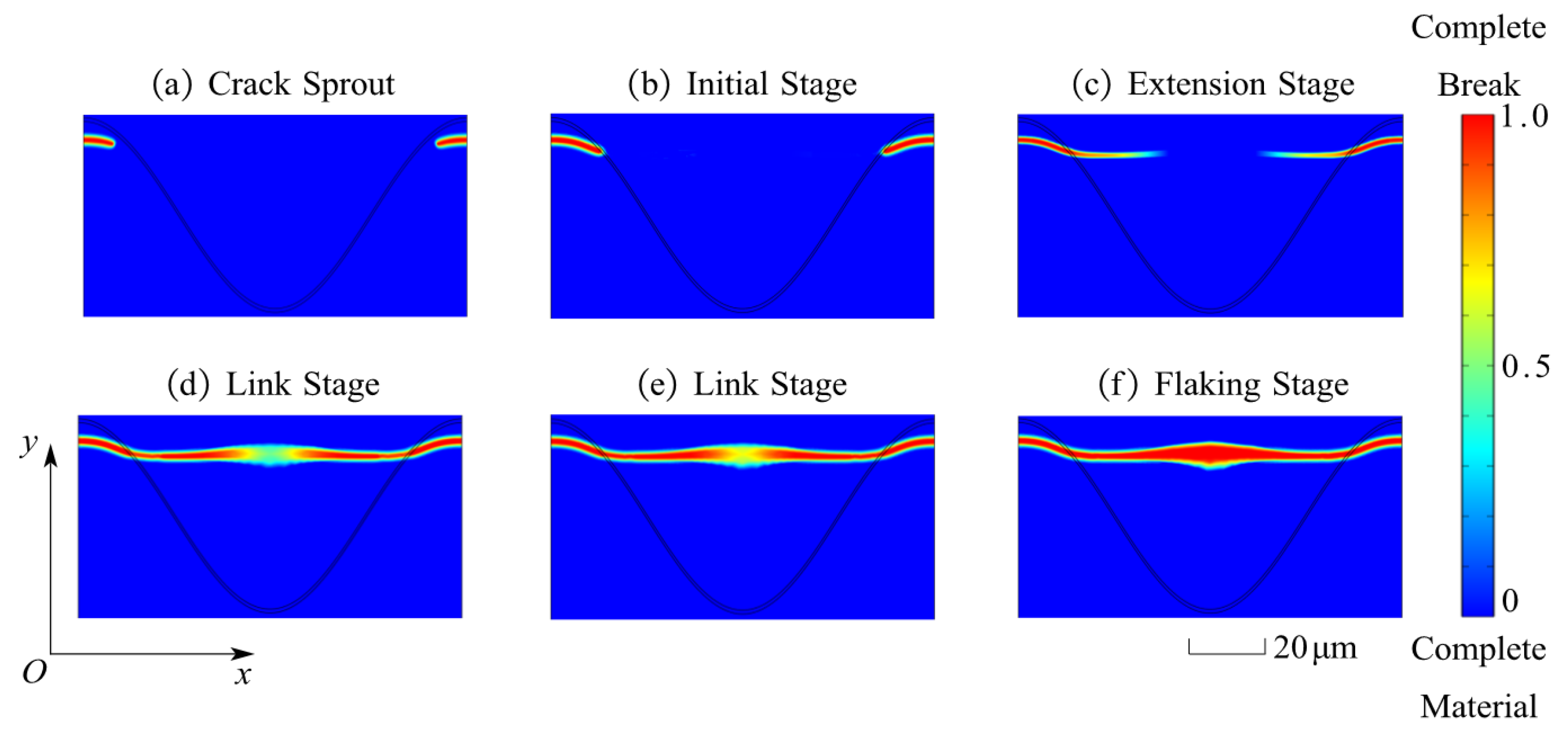
5.2. Numerical Simulation Results
5.3. Construction of Failure Criteria
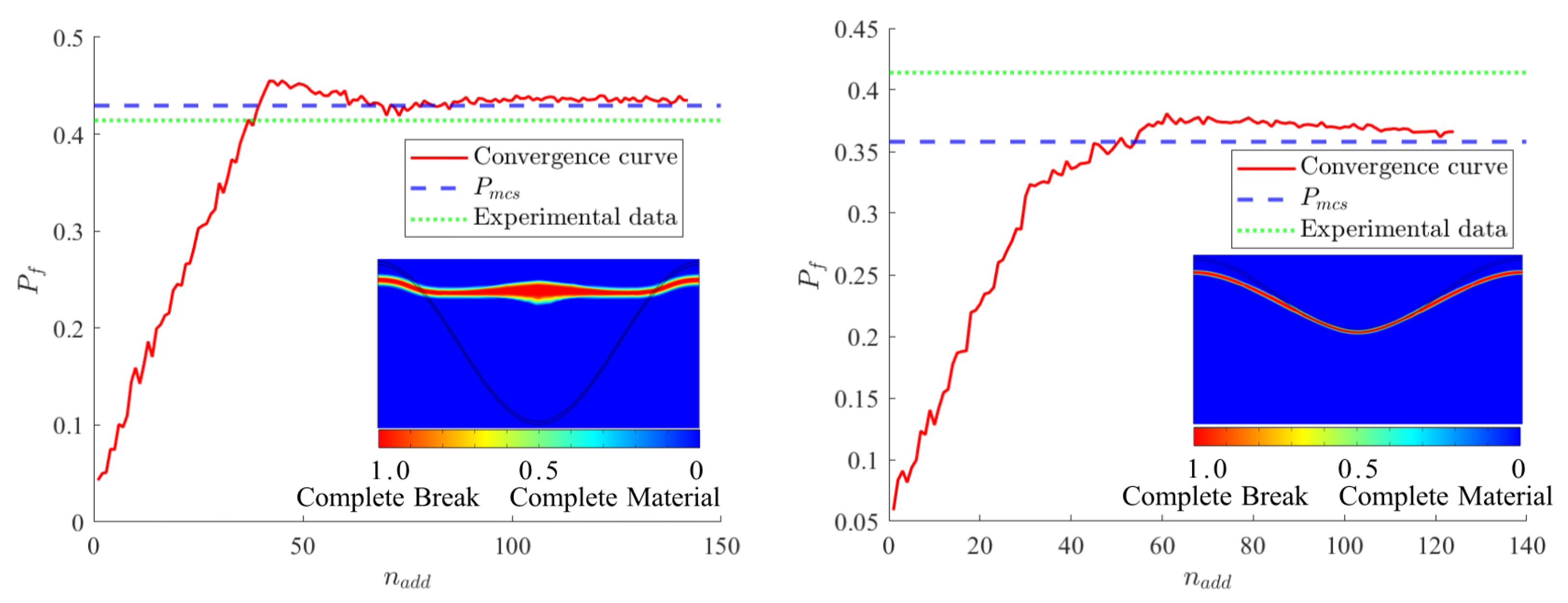
5.4. Reliability Calculation of TBC Interface Oxidation Failure Based on RBF-MCS Method
6. Conclusions
- When constructing multiple predictions with different numbers of DoE subsets , the number of subsets has a significant impact on the sequential sampling used for updating the RBF model, since the quantity of affects the local uncertainty. Simultaneously adjusting the coefficient also has an impact on the efficiency of the active learning function. When is small, the influence of local uncertainty is reduced, which also reduces the differences among the candidate sample points. Therefore, for the RBF-MCS method, the performance is the best when and in the example.
- The acceptable results under different subset numbers and adjustment coefficients can be obtained with the RBF-MCS method. The comparison with other methods in the literature can demonstrate the advantage of the proposed method in terms of accuracy.
- The accuracy and efficiency of reliability calculation for TBC oxidation failure problems can be improved via the proposed RBF-MCS method, and the results obtained are within the acceptable error range.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TBC | Thermal Barrier Coating |
| TGO | Thermally Grown Oxide |
| MCS | Monte Carlo Simulation |
| RBF | Radial Basis Function |
| PRBF-MCS | Predicted Variance RBF-MCS Method |
| DoE | Design of Experiments |
| COV | Coefficient of Variation |
| LSF | Limit State Function |
| IM | Inverse Multi-quadratic |
References
- Khajezadeh, M.H.; Mohammadi, M.; Ghatee, M. Hot corrosion performance and electrochemical study of CoNiCrAlY/YSZ/YSZ-La2O3 multilayer thermal barrier coatings in the presence of molten salt. Mater. Chem. Phys. 2018, 220, 23–34. [Google Scholar] [CrossRef]
- Clarke, D.; Levi, C. Materials design for the next generation thermal barrier coatings. Annu. Rev. Mater. Res. 2003, 33, 383–417. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, W.; Wang, W.; Zhang, W.; Yang, T.; Li, K.; Li, H.; Tang, Z.; Liu, C.; Zhang, C. Deposition characteristics, sintering and CMAS corrosion resistance, and mechanical properties of thermal barrier coatings by atmospheric plasma spraying. Surf. Coat. Technol. 2024, 482, 130623. [Google Scholar] [CrossRef]
- Liu, L.; Liu, D.; Cai, H.; Mu, R.; Yang, W.; He, L. Failure of Electron Beam Physical Vapor Deposited Thermal Barrier Coatings System under Cyclic Thermo-Mechanical Loading with a Thermal Gradient. Coatings 2024, 14, 902. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Y.; Li, L.; Yang, D.; Liu, X.; Huang, A.; Zhang, X.; Lu, J.; Zhao, X. Unraveling the CMAS corrosion mechanism of APS high-yttria-stabilized zirconia thermal barrier coatings. J. Eur. Ceram. Soc. 2024, 44, 5154–5165. [Google Scholar] [CrossRef]
- Liu, Y.; Balakrishnan, G.; Hatnean, M.C.; Xiao, P.; Chen, Y. Anisotropic fracture in gadolinium zirconate single crystal: Micromechanical testing and modelling. Acta Mater. 2025, 289, 120944. [Google Scholar] [CrossRef]
- Cheng, B.; Zhang, Y.M.; Yang, N.; Zhang, M.; Chen, L.; Yang, G.J.; Li, C.X.; Li, C.J. Sintering-induced delamination of thermal barrier coatings by gradient thermal cyclic test. J. Am. Ceram. Soc. 2017, 100, 1820–1830. [Google Scholar] [CrossRef]
- Nordhorn, C.; Mücke, R.; Mack, D.E.; Vaßen, R. Probabilistic lifetime model for atmospherically plasma sprayed thermal barrier coating systems. Mech. Mater. 2016, 93, 199–208. [Google Scholar] [CrossRef]
- Guo, J.W.; Yang, L.; Zhou, Y.C.; He, L.M.; Zhu, W.; Cai, C.Y.; Lu, C.S. Reliability assessment on interfacial failure of thermal barrier coatings. Acta Mech. Sin. 2016, 32, 915–924. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, X.; Li, Y. Structural reliability with credibility based on the non-probabilistic set-theoretic analysis. Aerosp. Sci. Technol. 2022, 127, 107730. [Google Scholar] [CrossRef]
- Arndt, C.; Crusenberry, C.; Heng, B.; Butler, R.; TerMaath, S. Reduced-dimension surrogate modeling to characterize the damage tolerance of composite/metal structures. Modelling 2023, 4, 485–514. [Google Scholar] [CrossRef]
- Luo, C.; Keshtegar, B.; Zhu, S.P.; Niu, X. EMCS-SVR: Hybrid efficient and accurate enhanced simulation approach coupled with adaptive SVR for structural reliability analysis. Comput. Methods Appl. Mech. Eng. 2022, 400, 115499. [Google Scholar] [CrossRef]
- Alban, A.; Darji, H.A.; Imamura, A.; Nakayama, M.K. Efficient Monte Carlo methods for estimating failure probabilities. Reliab. Eng. Syst. Saf. 2017, 165, 376–394. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Xu, G.; Li, Y.; Kareem, A. Efficient structural reliability analysis based on adaptive Bayesian support vector regression. Comput. Methods Appl. Mech. Eng. 2021, 387, 114172. [Google Scholar] [CrossRef]
- Teixeira, R.; Nogal, M.; O’Connor, A. Adaptive approaches in metamodel-based reliability analysis: A review. Struct. Saf. 2021, 89, 102019. [Google Scholar] [CrossRef]
- Salazar-Rojas, T.; Cejudo-Ruiz, F.R.; Calvo-Brenes, G. Comparison between machine linear regression (MLR) and support vector machine (SVM) as model generators for heavy metal assessment captured in biomonitors and road dust. Environ. Pollut. 2022, 314, 120227. [Google Scholar] [CrossRef]
- ALKannad, A.A.; Smadi, A.A.; AL-Makhlafi, M.; Yang, S.; Feng, Z. CrackVisionX: A Fine-Tuned Framework for Efficient Binary Concrete Crack Detection. IEEE Trans. Intell. Transp. Syst. 2025, 1–20. [Google Scholar] [CrossRef]
- Deng, J.; Gu, D.; Li, X.; Yue, Z.Q. Structural reliability analysis for implicit performance functions using artificial neural network. Struct. Saf. 2005, 27, 25–48. [Google Scholar] [CrossRef]
- Alkannad, A.A.; Al Smadi, A.; Yang, S.; Al-Smadi, M.K.; Al-Makhlafi, M.; Feng, Z.; Yin, Z. CrackVision: Effective Concrete Crack Detection with Deep Learning and Transfer Learning. IEEE Access 2025, 13, 29554–29576. [Google Scholar] [CrossRef]
- Bai, G.; Fei, C. Distributed collaborative response surface method for mechanical dynamic assembly reliability design. Chin. J. Mech. Eng. 2013, 26, 1160–1168. [Google Scholar] [CrossRef]
- Tamilarasan, A.; Rajamani, D. Metaheuristic Prediction Models for Kerf Deviation in Nd-YAG Laser Cutting of AlZnMgCu1.5 Alloy. Modelling 2025, 6, 17. [Google Scholar] [CrossRef]
- Chen, Z.; Li, G.; He, J.; Yang, Z.; Wang, J. Adaptive structural reliability analysis method based on confidence interval squeezing. Reliab. Eng. Syst. Saf. 2022, 225, 108639. [Google Scholar] [CrossRef]
- Singh, V.; Harursampath, D.; Dhawan, S.; Sahni, M.; Saxena, S.; Mallick, R. Physics-Informed Neural Network for Solving a One-Dimensional Solid Mechanics Problem. Modelling 2024, 5, 1532–1549. [Google Scholar] [CrossRef]
- Shi, L.; Sun, B.; Ibrahim, D.S. An active learning reliability method with multiple kernel functions based on radial basis function. Struct. Multidiscip. Optim. 2019, 60, 211–229. [Google Scholar] [CrossRef]
- Hong, L.; Li, H.; Peng, K. A combined radial basis function and adaptive sequential sampling method for structural reliability analysis. Appl. Math. Model. 2021, 90, 375–393. [Google Scholar] [CrossRef]
- Du, W.; Ma, J.; Yue, P.; Gong, Y. An efficient reliability method with multiple shape parameters based on radial basis function. Appl. Sci. 2022, 12, 9689. [Google Scholar] [CrossRef]
- Wei, Y.; Bai, G.; Song, L.K. A novel reliability analysis approach with collaborative active learning strategy-based augmented RBF metamodel. IEEE Access 2020, 8, 199603–199617. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An improved particle swarm optimization (PSO)–based MPPT for PV with reduced steady-state oscillation. IEEE Trans. Power Electron. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Dubourg, V.; Sudret, B.; Bourinet, J.M. Reliability-based design optimization using kriging surrogates and subset simulation. Struct. Multidiscip. Optim. 2011, 44, 673–690. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M. AK-MCS: An active learning reliability method combining Kriging and Monte Carlo simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- COMSOL AB. AC/DC Module User’s Guide, Version 6.3 ed.; COMSOL AB: Stockholm, Sweden, 2024. [Google Scholar]
- Jing, Z.; Chen, J.; Li, X. RBF-GA: An adaptive radial basis function metamodeling with genetic algorithm for structural reliability analysis. Reliab. Eng. Syst. Saf. 2019, 189, 42–57. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, Z.; Peng, X.; Zhu, W.; Zhou, Y.; Yang, L. Spallation mechanism of thermal barrier coatings with real interface morphology considering growth and thermal stresses based on fracture phase field. Surf. Coat. Technol. 2023, 458, 129356. [Google Scholar] [CrossRef]
- Zhou, Q.; Yang, L.; Luo, C.; Chen, F.; Zhou, Y.; Wei, Y. Thermal barrier coatings failure mechanism during the interfacial oxidation process under the interaction between interface by cohesive zone model and brittle fracture by phase-field. Int. J. Solids Struct. 2021, 214, 18–34. [Google Scholar] [CrossRef]
- Shen, Q.; Yang, L.; Zhou, Y.; Wei, Y.; Zhu, W. Effects of growth stress in finite-deformation thermally grown oxide on failure mechanism of thermal barrier coatings. Mech. Mater. 2017, 114, 228–242. [Google Scholar] [CrossRef]
- Xiao, Y.; Yang, L.; Zhu, W.; Zhou, Y.; Pi, Z.; Wei, Y. Delamination mechanism of thermal barrier coatings induced by thermal cycling and growth stresses. Eng. Fail. Anal. 2021, 121, 105202. [Google Scholar] [CrossRef]
- Min, L.; Wang, Z.; Hu, X.; Zhao, D.; Sun, Z.; Zhang, P.; Yao, W.; Bui, T.Q. A chemo-thermo-mechanical coupled phase field framework for failure in thermal barrier coatings. Comput. Methods Appl. Mech. Eng. 2023, 411, 116044. [Google Scholar] [CrossRef]
- Shen, Q.; Li, S.; Yang, L.; Zhou, Y.; Wei, Y.; Yuan, T. Coupled mechanical-oxidation modeling during oxidation of thermal barrier coatings. Comput. Mater. Sci. 2018, 154, 538–546. [Google Scholar] [CrossRef]
- Al-Athel, K.; Loeffel, K.; Liu, H.; Anand, L. Modeling decohesion of a top-coat from a thermally-growing oxide in a thermal barrier coating. Surf. Coat. Technol. 2013, 222, 68–78. [Google Scholar] [CrossRef]
- Rabiei, A.; Evans, A. Failure mechanisms associated with the thermally grown oxide in plasma-sprayed thermal barrier coatings. Acta Mater. 2000, 48, 3963–3976. [Google Scholar] [CrossRef]
- Nie, J.Y.; Li, D.Q.; Cao, Z.J.; Zhou, B.; Zhang, A.J. Probabilistic characterization and simulation of realistic particle shape based on sphere harmonic representation and Nataf transformation. Powder Technol. 2020, 360, 209–220. [Google Scholar] [CrossRef]
- Busso, E.P.; Wright, L.; Evans, H.; McCartney, L.; Saunders, S.; Osgerby, S.; Nunn, J. A physics-based life prediction methodology for thermal barrier coating systems. Acta Mater. 2007, 55, 1491–1503. [Google Scholar] [CrossRef]
- Guo, S.; Kagawa, Y. Young’s moduli of zirconia top-coat and thermally grown oxide in a plasma-sprayed thermal barrier coating system. Scr. Mater. 2004, 50, 1401–1406. [Google Scholar] [CrossRef]
- Jackson, R.D. The Effect of Bond Coat Oxidation on the Microstructure and Endurance of Two Thermal Barrier Coating Systems. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2010. [Google Scholar]
- Sfar, K.; Aktaa, J.; Munz, D. Numerical investigation of residual stress fields and crack behavior in TBC systems. Mater. Sci. Eng. A 2002, 333, 351–360. [Google Scholar] [CrossRef]
- Wan, J.; Zhou, M.; Yang, X.; Dai, C.; Zhang, Y.; Mao, W.; Lu, C. Fracture characteristics of freestanding 8 wt% Y2O3–ZrO2 coatings by single edge notched beam and Vickers indentation tests. Mater. Sci. Eng. A 2013, 581, 140–144. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Z.; Zhang, T.; Guo, W.; Dai, H.; Ding, K. Reliability evaluation of thermal barrier coatings for engine combustion chambers based on Monte-Carlo simulation. Surf. Coat. Technol. 2022, 448, 128923. [Google Scholar] [CrossRef]




| Kernel Function | |
|---|---|
| Gaussian Kernel function | |
| Multi-quadratic Kernel function | |
| Inverse Multi-quadratic Kernel function | |
| Cubic Kernel function |
| Material Properties | Values |
|---|---|
| Oxygen diffusion coefficient in bonding layer (/s) | 2 × |
| Oxygen diffusion coefficient in oxide layer (/s) | 2 × |
| Oxygen reaction rate ( ) | 1 × |
| Molar concentration of oxygen M (mol ) | 1.11 × |
| Random Variable | Distribution Type | Mean Value | Standard | |
|---|---|---|---|---|
| Young’s modulus | (GPa) | Normal distribution | 380 | 100 |
| (GPa) | Normal distribution | 120 | 30 | |
| Thermal expansion coefficient | (/K) | Normal distribution | 9.2 | 0.37 |
| (/K) | Normal distribution | 9.8 | 0.39 | |
| Fracture energy | (J/) | Weibull distribution | 60 | 6 |
| (J/) | Weibull distribution | 50 | 5 | |
| Temperature difference | (°C) | Normal distribution | 1050 | 5 |
| Method | Failure Probability (%) | Efficiency | Accuracy (%) |
|---|---|---|---|
| Experiment [47] | 41.4 | / | / |
| MC () | 42.9 | 5 × | / |
| MC () | 35.8 | 5 × | / |
| RBF-MC () | 43.7 | 143.3 | 1.92 |
| RBF-MC () | 36.6 | 126.4 | 2.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Wang, A.; Junker, P.; Alshawawreh, A.W.; Li, Q.; Xu, H.; Xue, R. Reliability Analysis of Interface Oxidation for Thermal Barrier Coating Based on Proxy Model. Modelling 2025, 6, 61. https://doi.org/10.3390/modelling6030061
Ma J, Wang A, Junker P, Alshawawreh AW, Li Q, Xu H, Xue R. Reliability Analysis of Interface Oxidation for Thermal Barrier Coating Based on Proxy Model. Modelling. 2025; 6(3):61. https://doi.org/10.3390/modelling6030061
Chicago/Turabian StyleMa, Juan, Anyi Wang, Philipp Junker, Anas W. Alshawawreh, Qingya Li, Haoqi Xu, and Runzhuo Xue. 2025. "Reliability Analysis of Interface Oxidation for Thermal Barrier Coating Based on Proxy Model" Modelling 6, no. 3: 61. https://doi.org/10.3390/modelling6030061
APA StyleMa, J., Wang, A., Junker, P., Alshawawreh, A. W., Li, Q., Xu, H., & Xue, R. (2025). Reliability Analysis of Interface Oxidation for Thermal Barrier Coating Based on Proxy Model. Modelling, 6(3), 61. https://doi.org/10.3390/modelling6030061