Stochastic Blade Pitch Angle Analysis of Controllable Pitch Propeller Based on Deep Neural Networks
Abstract
1. Introduction
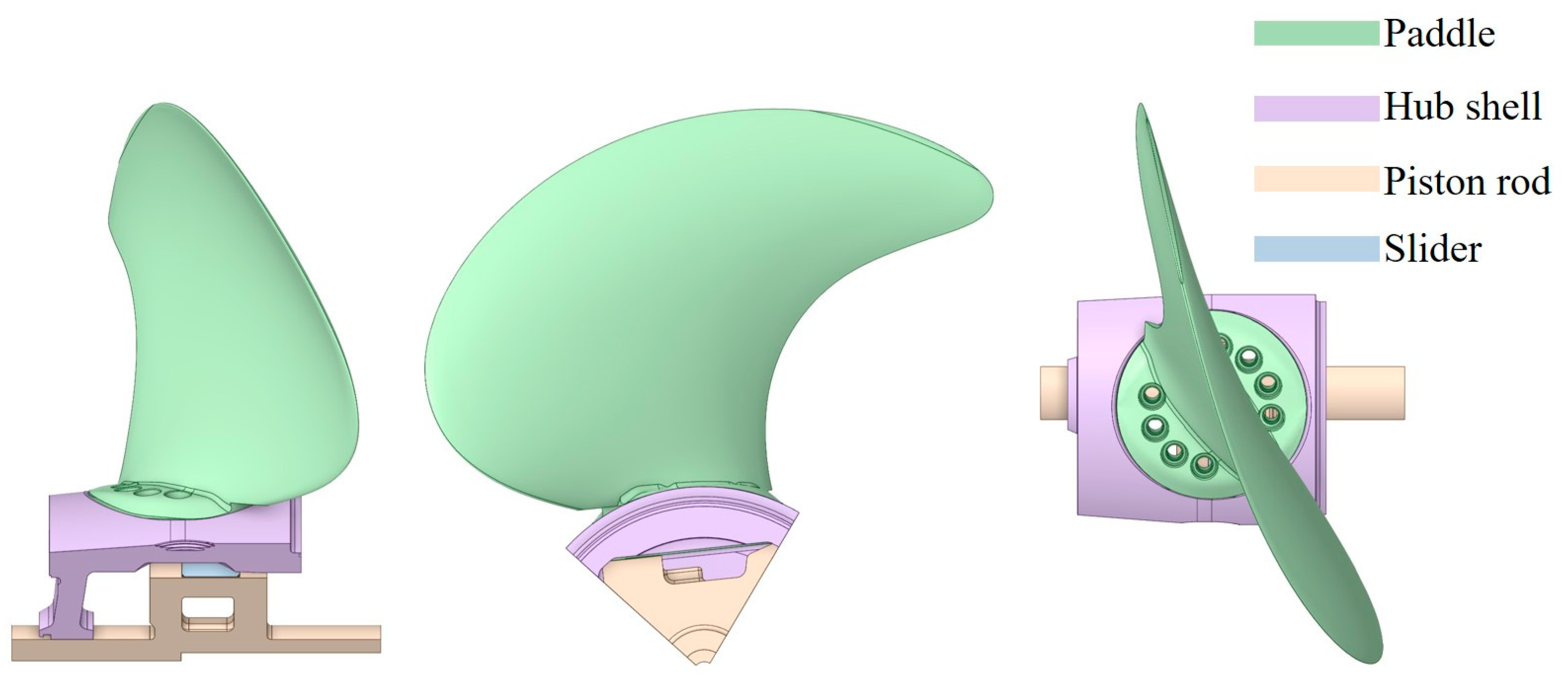
2. Kinematic Simulation Analysis
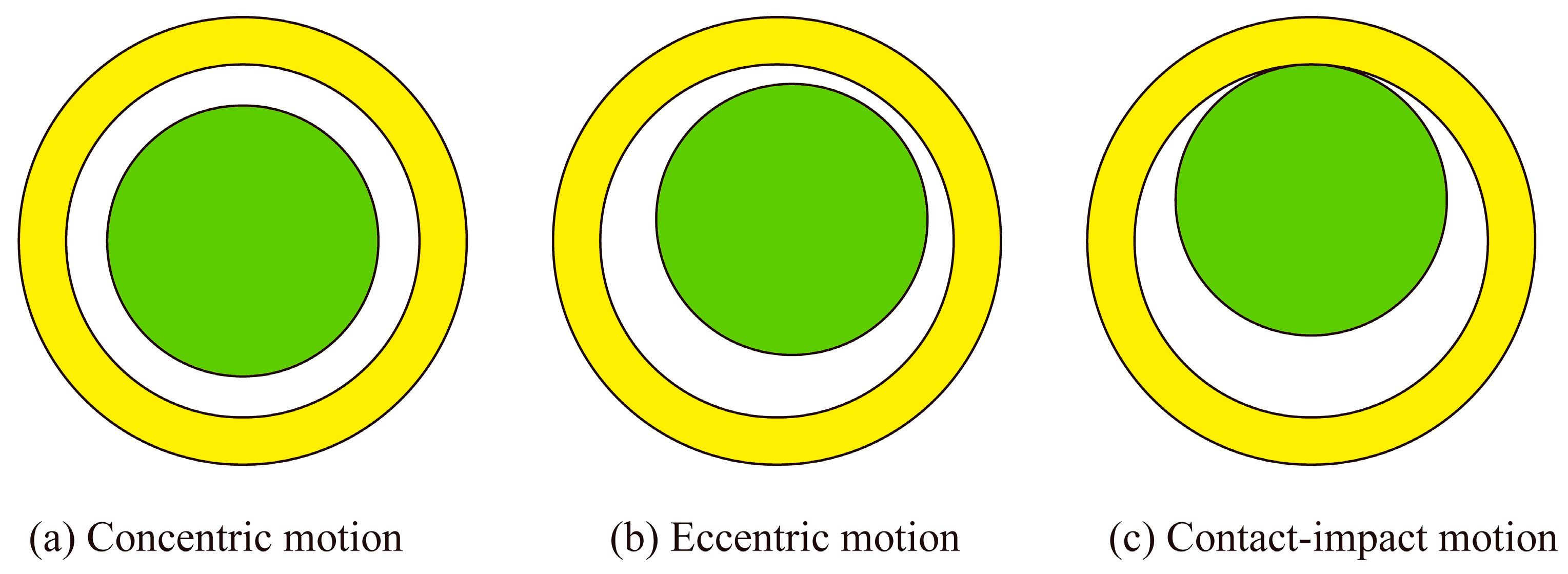
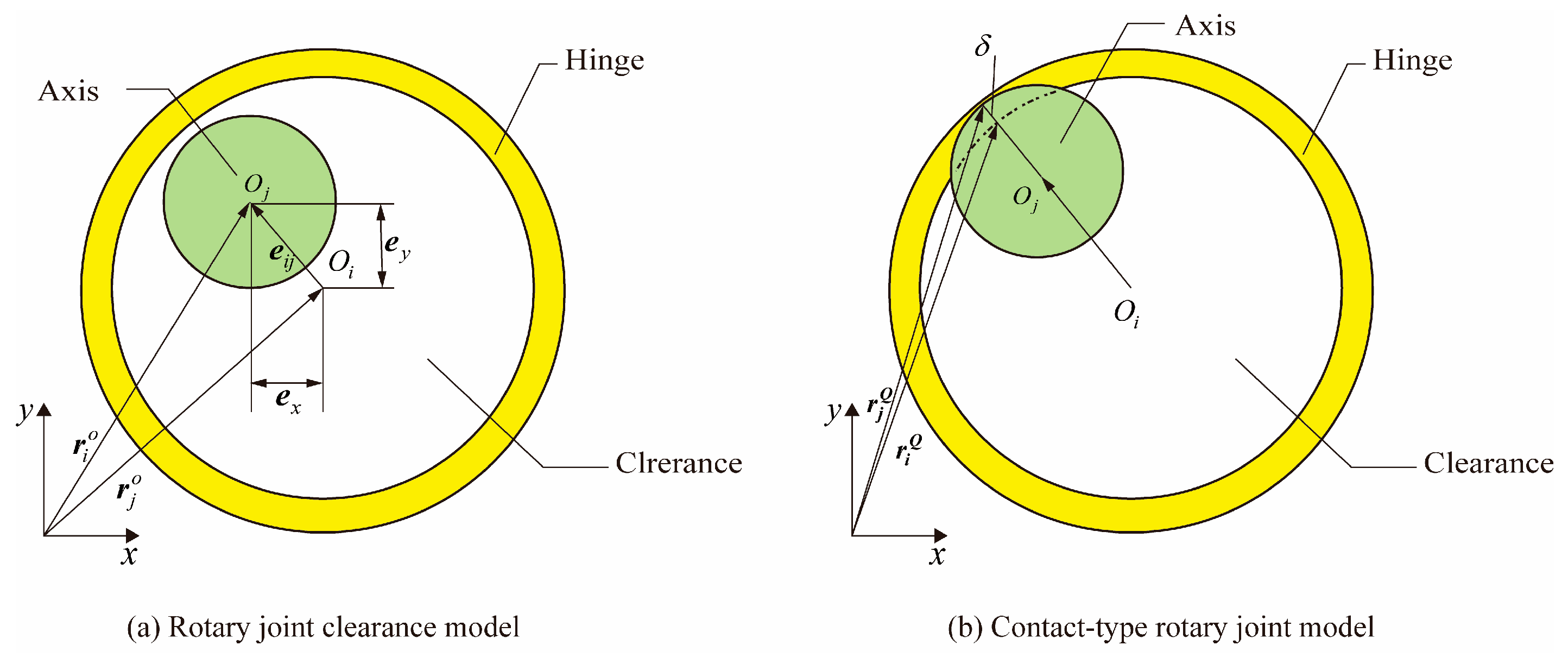
2.1. Rotary Clearance Joint Model
2.2. Contact Force Model
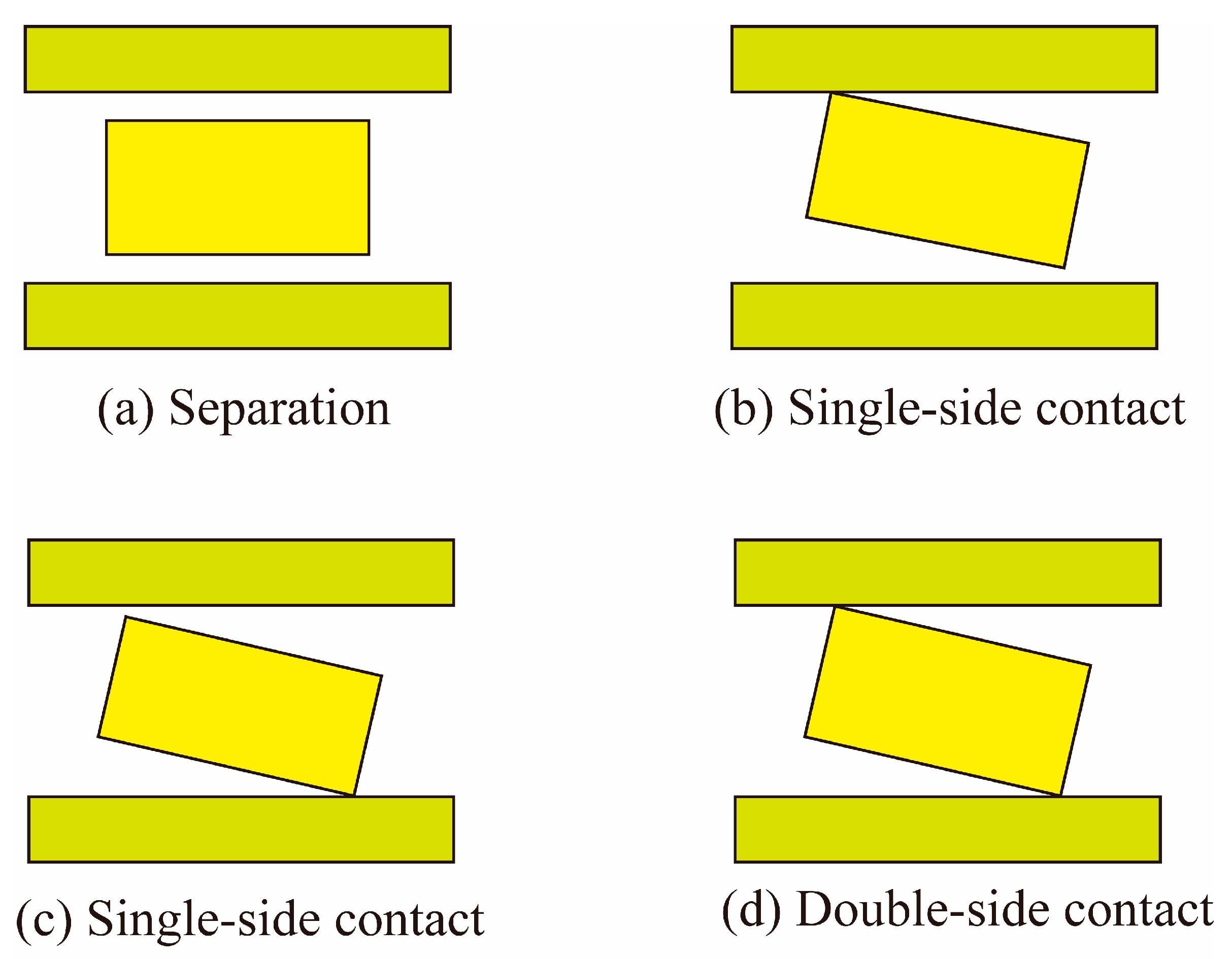
2.3. Friction Model
3. Methodology
3.1. Deep Neural Networks
3.2. Other Surrogate Models
4. Results and Discussion
4.1. Data Sets
4.2. Comparison of the Precision of Different Surrogate Models
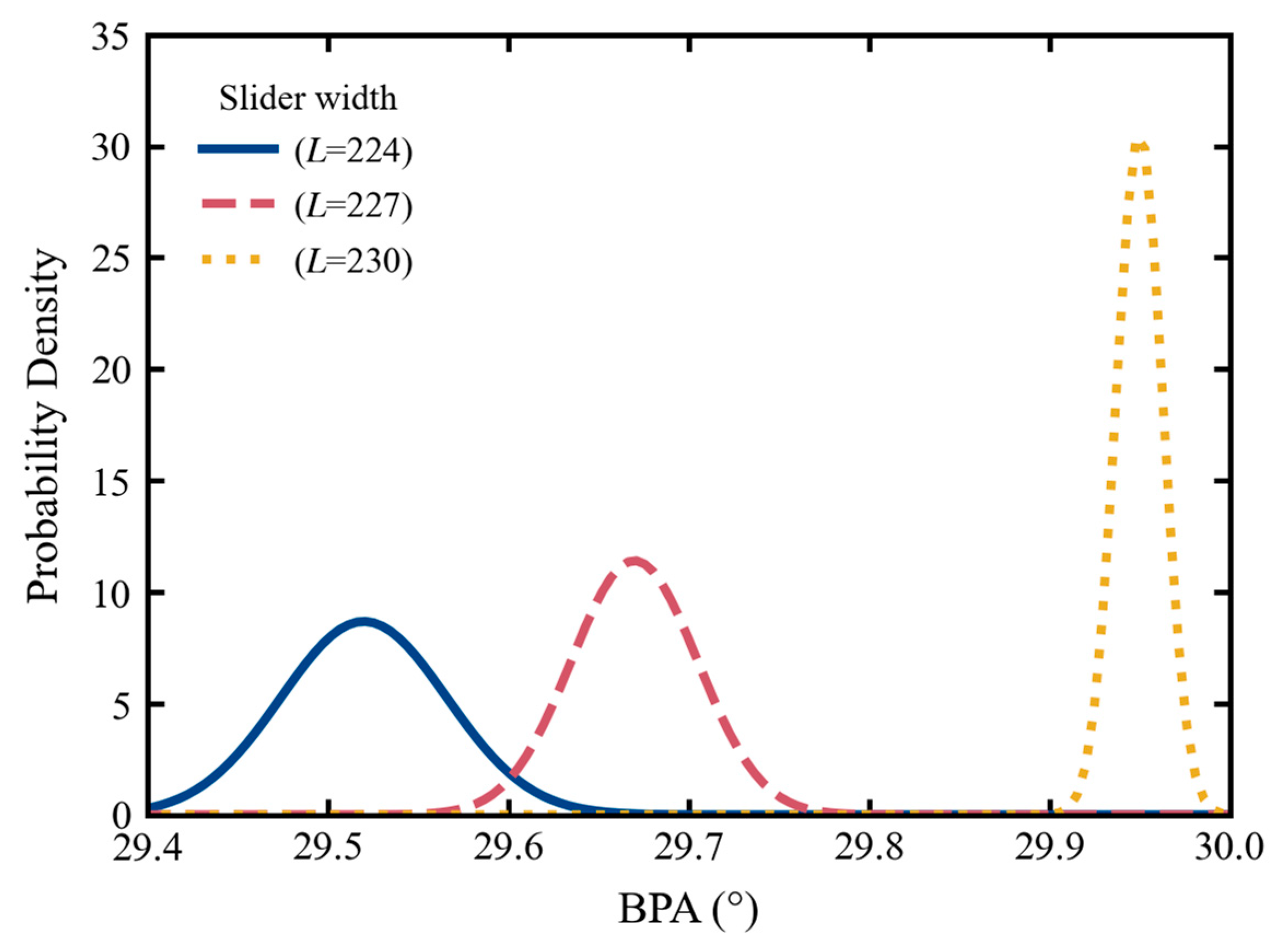
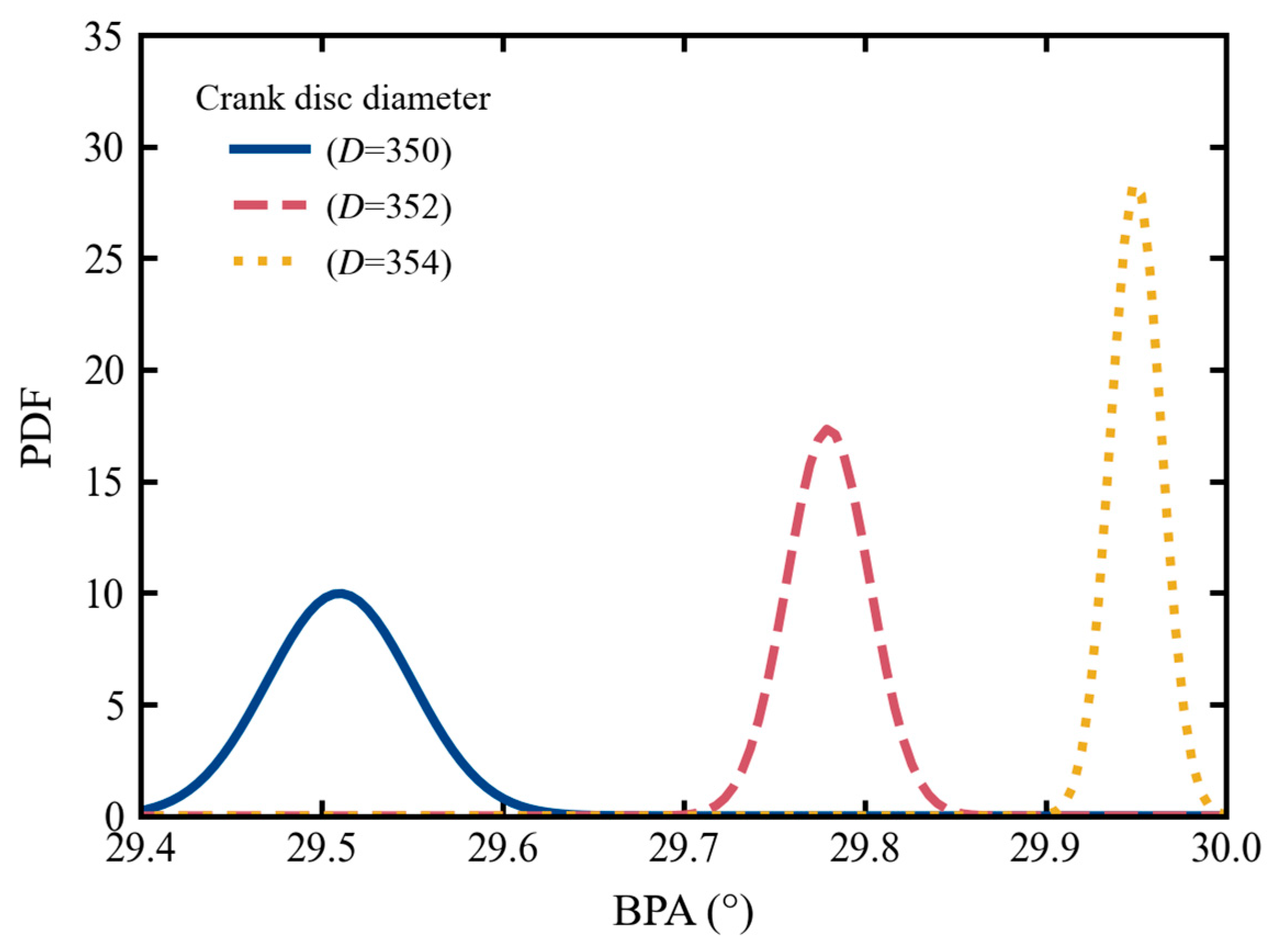
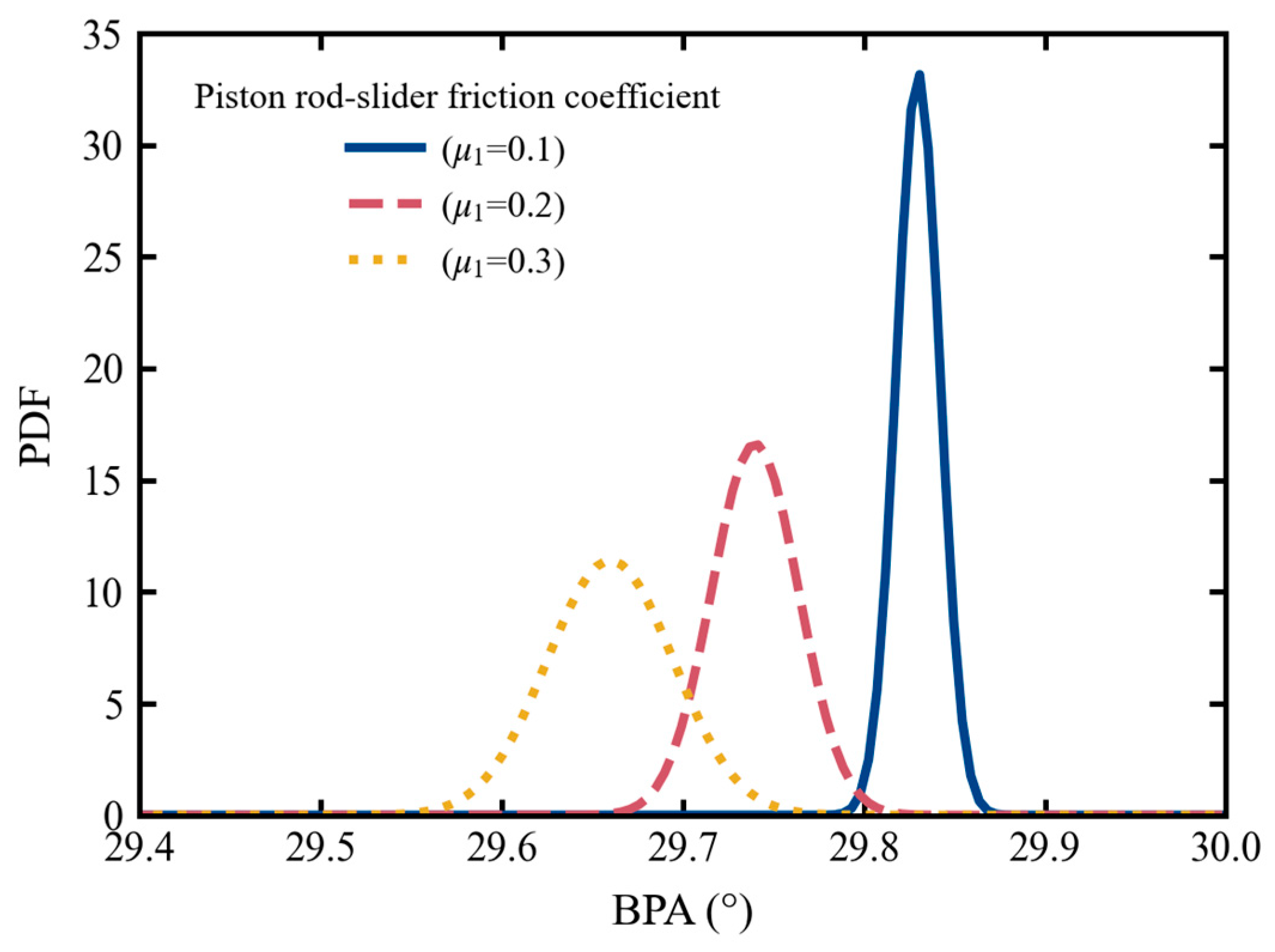
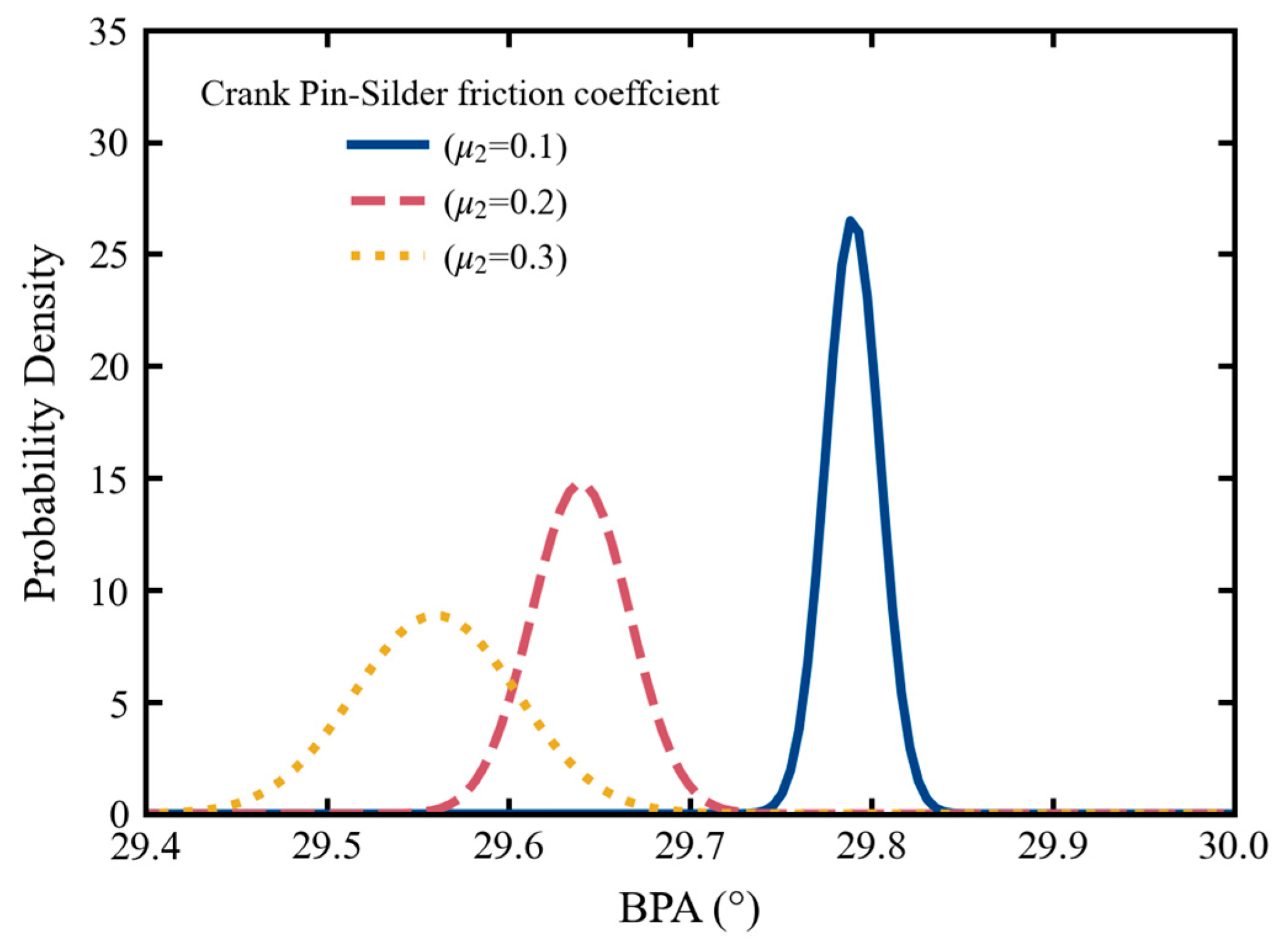
4.3. Results of Uncertainties on the BPA
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPP | Controllable Pitch Propeller |
| BPA | Blade Pitch Angle |
| DNN | Deep Neural Network |
| SVR | Support Vector Regression |
| RF | Random Forest |
| PCK | Polynomial Chaos Expansion Kriging |
References
- Tian, W.; Lang, X.; Zhang, C.; Yan, S.; Li, B.; Zang, S. Optimization of Controllable-Pitch Propeller Operations for Yangtze River Sailing Ships. JMSE 2024, 12, 1579. [Google Scholar] [CrossRef]
- Zhu, W.; Li, Z.; Ding, R. Effect of Pitch Ratio on the Cavitation of Controllable Pitch Propeller. Ocean Eng. 2024, 293, 116692. [Google Scholar] [CrossRef]
- Bacalja Bašić, B.; Krčum, M.; Jurić, Z. Propeller Optimization in Marine Power Systems: Exploring Its Contribution and Correlation with Renewable Energy Solutions. JMSE 2024, 12, 843. [Google Scholar] [CrossRef]
- Yurtseven, A.; Aktay, K. The Numerical Investigation of Spindle Torque for a Controllable Pitch Propeller in Feathering Maneuver. brod 2023, 74, 95–108. [Google Scholar] [CrossRef]
- Pan, W.; Peng, L.; Xing, J. Simulation Study on Controllable Pitch Propeller’s Simulation Based on Virtual Prototype. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 15–17 July 2011. [Google Scholar]
- Yan, T.; Li, X. The Kinematics Analytical Method and Simulation with ADAMS Based on Bias Slider-Crank Mechanism. Appl. Mech. Mater. 2014, 602–605, 185–188. [Google Scholar] [CrossRef]
- Dang, Z.; Wu, M.; He, X.; Huang, Z.; Ying, Z.; Chen, Z.; Zheng, C. An Amphibious Propeller Design Optimization Framework Based on Deep Neural Network Surrogate Model. Aerosp. Sci. Technol. 2025, 159, 109967. [Google Scholar] [CrossRef]
- Gebauer, J.; Wagnerová, R.; Smutný, P.; Podešva, P. Controller Design for Variable Pitch Propeller Propulsion Drive. IFAC-Pap. 2019, 52, 186–191. [Google Scholar] [CrossRef]
- Wang, J.; Meng, B.; Zhang, L.; Yu, C. Degradation Modeling and Reliability Estimation for Mechanical Transmission Mechanism Considering the Clearance between Kinematic Pairs. Reliab. Eng. Syst. Saf. 2024, 247, 110093. [Google Scholar] [CrossRef]
- Huang, P.; Wen, C.; Fu, L.; Peng, Q.; Tang, Y. A Deep Learning Approach for Multi-Attribute Data: A Study of Train Delay Prediction in Railway Systems. Inf. Sci. 2020, 516, 234–253. [Google Scholar] [CrossRef]
- Li, L.; Chen, Y.; Xie, S.; Xiao, Y.; Fang, T.; Wang, C. Comprehensive Feature-Based Machine Learning for Fast Prediction of Marine Propeller’s Open-Water Performance. Appl. Ocean Res. 2025, 154, 104310. [Google Scholar] [CrossRef]
- Lee, J.; Park, S.-K.; Bazher, S.A.; Seo, D. Development of a Fault Prediction Algorithm for Marine Propulsion Energy Storage System. Energies 2025, 18, 1687. [Google Scholar] [CrossRef]
- Ye, Y.; Huang, P.; Sun, Y.; Shi, D. MBSNet: A Deep Learning Model for Multibody Dynamics Simulation and Its Application to a Vehicle-Track System. Mech. Syst. Signal Process. 2021, 157, 107716. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, Y.J.; Park, H.-G. Mechanics-Based Machine Learning for Failure Classification of Load-Bearing Walls. Eng. Struct. 2025, 322, 119110. [Google Scholar] [CrossRef]
- Santos, V.B.; Cardoso-Ribeiro, F.L.; Brugnoli, A. Surrogate Modeling of a Lumped-Mass Multibody Structure Using Hamiltonian Neural Networks. IFAC-Pap. 2024, 58, 48–53. [Google Scholar] [CrossRef]
- Fan, X.; Yang, X.; Liu, Y. Two-Stage Failure Probability Function Estimation Method Based on Improved Cross-Entropy Importance Sampling and Adaptive Kriging. Reliab. Eng. Syst. Saf. 2025, 263, 111272. [Google Scholar] [CrossRef]
- Fan, X.; Yang, X.; Liu, Y. A Kriging-Assisted Adaptive Improved Cross-Entropy Importance Sampling Method for Random-Interval Hybrid Reliability Analysis. Struct. Multidisc. Optim. 2024, 67, 158. [Google Scholar] [CrossRef]
- Tian, W.; Yang, X.; Liu, Y.; Shi, X.; Fan, X. Efficient Damage Prediction and Sensitivity Analysis in Rectangular Welded Plates Subjected to Repeated Blast Loads Utilizing Deep Learning Networks. Acta Mech. 2024, 235, 7223–7244. [Google Scholar] [CrossRef]
- Han, X.; Liu, L.; Xia, Q.; Liu, D.; Tian, J. Physical-Based Surrogate Model and Its Application in 3D-1D Fusion Optimization of a Marine Two-Stroke Engine. Appl. Therm. Eng. 2025, 271, 126387. [Google Scholar] [CrossRef]
- Geng, Z.; Zhang, C.; Ren, Y.; Zhu, M.; Chen, R.; Cheng, H. An Uncertainty Weighted Kriging-Random Forest Model for Real-Time Ground Property Prediction during Earth Pressure Balance Shield Tunneling. Appl. Soft Comput. 2025, 180, 113417. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, X.; Liu, B.; Zhao, L.; Kong, X.; Alhudhaif, A.; Alenezi, F. Multi-View Support Vector Ordinal Regression with Data Uncertainty. Inf. Sci. 2022, 589, 516–530. [Google Scholar] [CrossRef]
- Liu, B.; Wang, R.; Guan, Z.; Li, J.; Xu, Z.; Guo, X.; Wang, Y. Improved Support Vector Regression Models for Predicting Rock Mass Parameters Using Tunnel Boring Machine Driving Data. Tunn. Undergr. Space Technol. 2019, 91, 102958. [Google Scholar] [CrossRef]
- Tahir, Z.U.R.; Mandal, P.; Adil, M.T.; Naz, F. Application of Artificial Neural Network to Predict Buckling Load of Thin Cylindrical Shells under Axial Compression. Eng. Struct. 2021, 248, 113221. [Google Scholar] [CrossRef]
- Nguyen, N.-H.; Nguyen, V.P.; Wu, J.-Y.; Le, T.-H.-H.; Ding, Y. Mesh-Based and Meshfree Reduced Order Phase-Field Models for Brittle Fracture: One Dimensional Problems. Materials 2019, 12, 1858. [Google Scholar] [CrossRef]

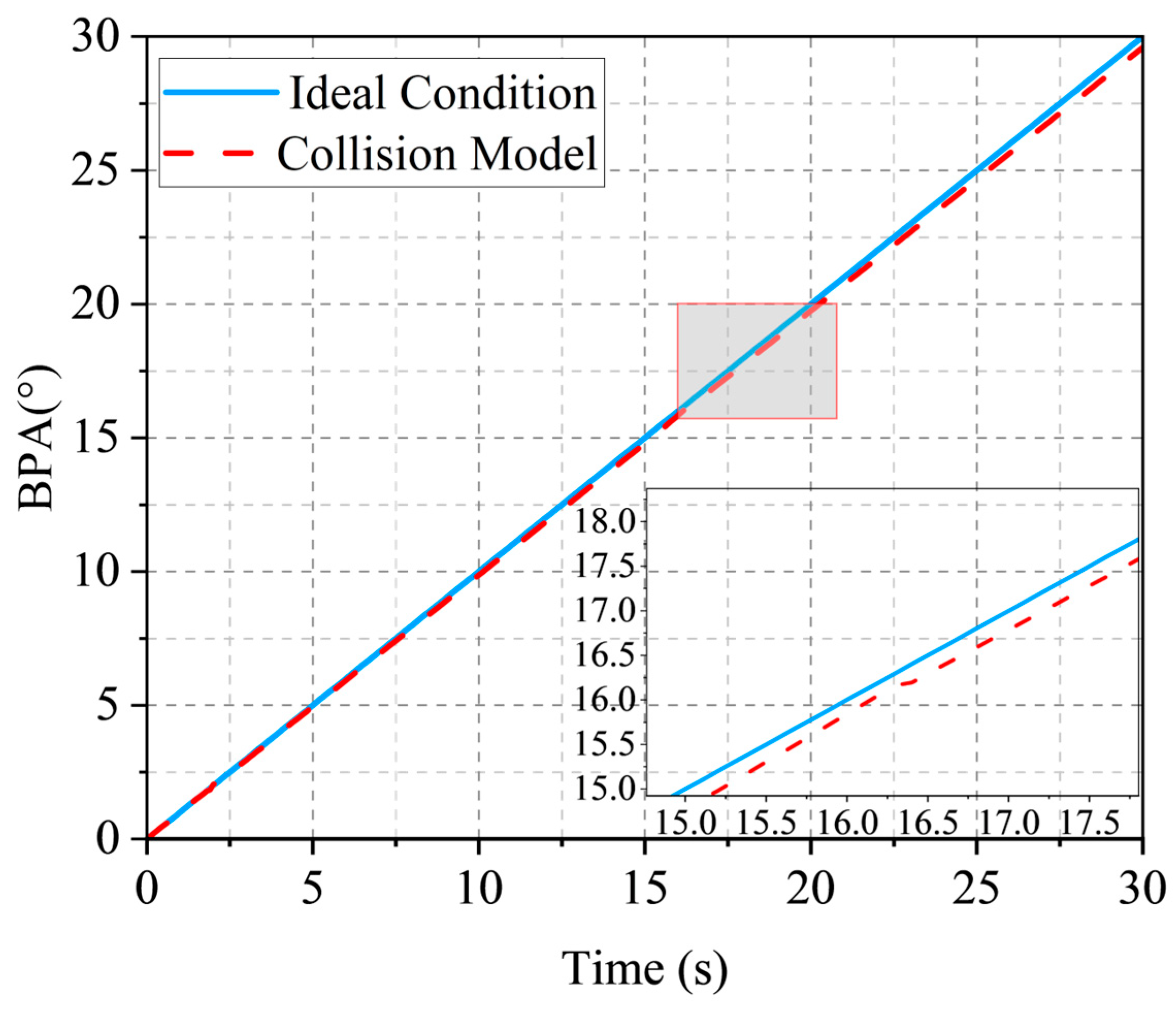
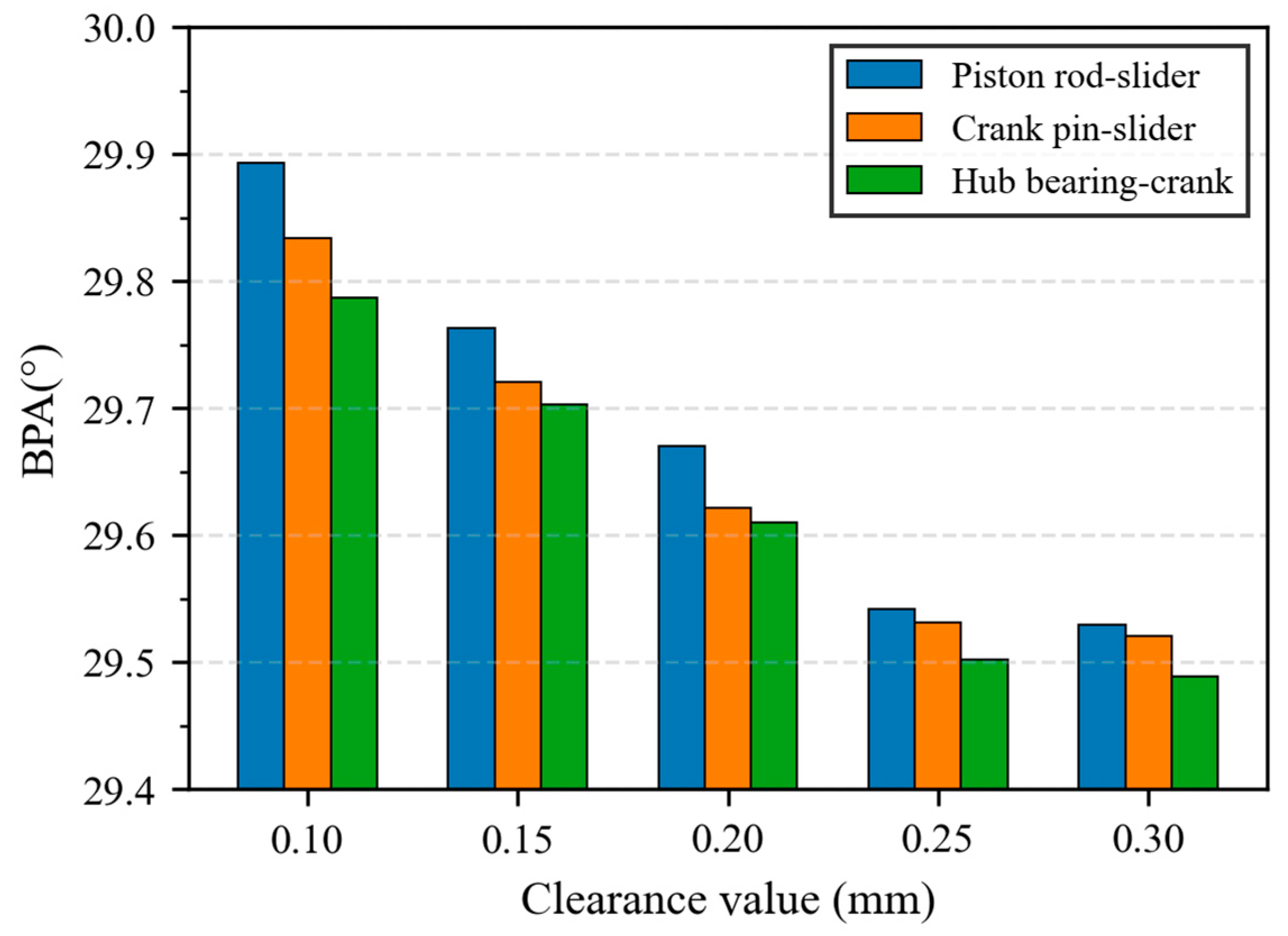


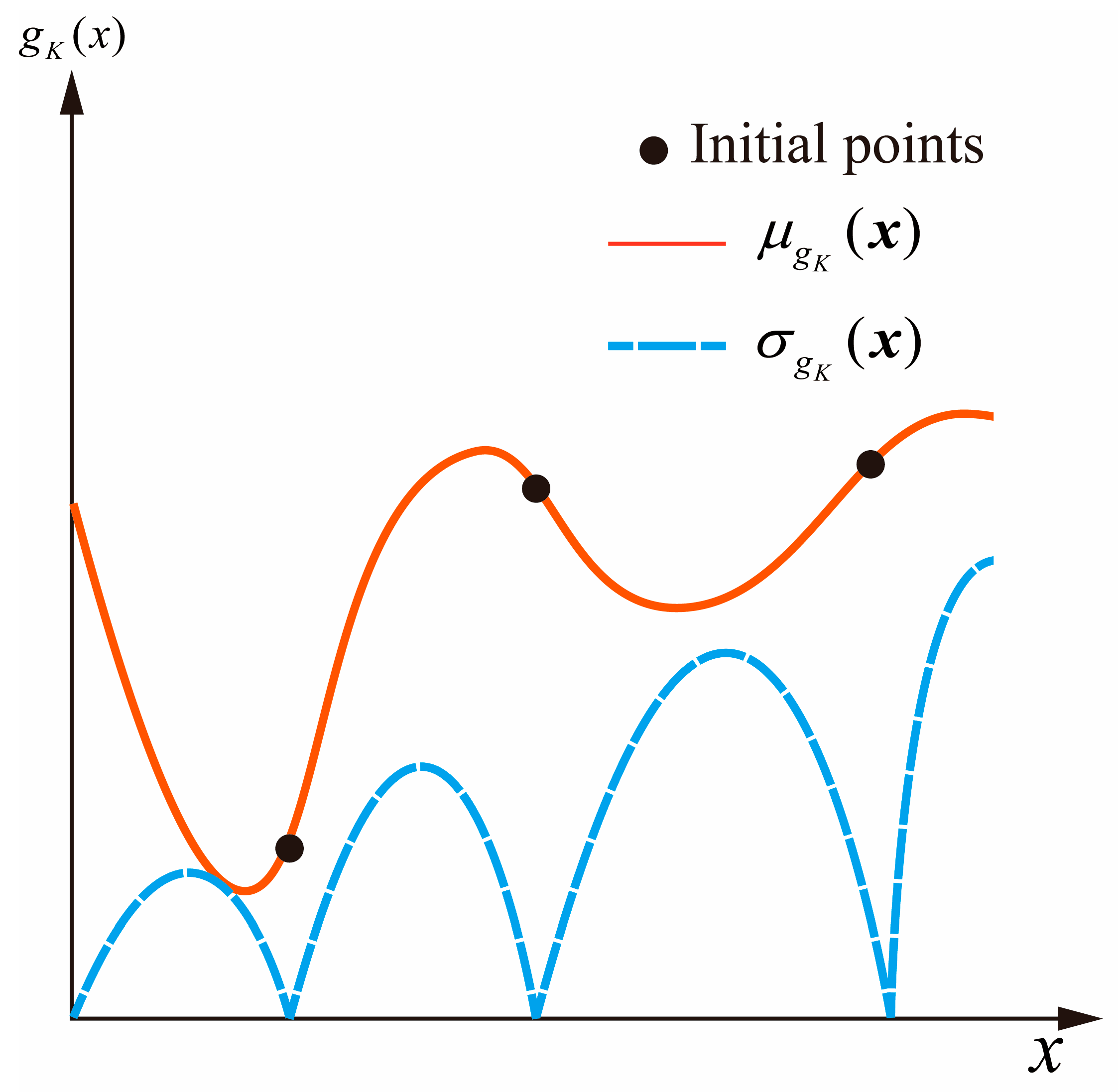




| Number | Component | Initial Range of Clearance/mm |
|---|---|---|
| Clearance I | Piston Rod | [0.025, 0.075] |
| Slider | ||
| Clearance II | crank pin | [0.015, 0.100] |
| Slider | ||
| Clearance III | Hub Bearing | [0.160, 0.320] |
| Crank Disc |
| Model Parameters | Symbol | Value |
|---|---|---|
| Slider width (mm) | 230 | |
| Stiffness coefficient (N/m) | ||
| Damping coefficient (N·(s/m)) | 10.0 | |
| Restitution coefficient | 2.2 | |
| Coefficient of maximum static friction | 0.3 | |
| Coefficient of kinetic friction | 0.1 |
| Variable | Symbol | Distribution Type | Mean | Coefficient of Variation |
|---|---|---|---|---|
| Slider width | L | Normal distribution | 230 | 0.03 |
| Crank pin diameter | d | Normal distribution | 75 | 0.03 |
| Crank disc diameter | D | Normal distribution | 354 | 0.03 |
| Piston rod–slider friction coefficient | µ1 | Normal distribution | 0.15 | 0.03 |
| Crank pin–slider friction coefficient | µ2 | Normal distribution | 0.15 | 0.03 |
| Hub bearing–crank disc friction coefficient | µ3 | Normal distribution | 0.15 | 0.03 |
| Dataset Split (Training Set:Test Set) | ||
|---|---|---|
| 7:3 | 0.934 | 1.5 × 10−5 |
| 8:2 | 0.942 | 1.42 × 10−5 |
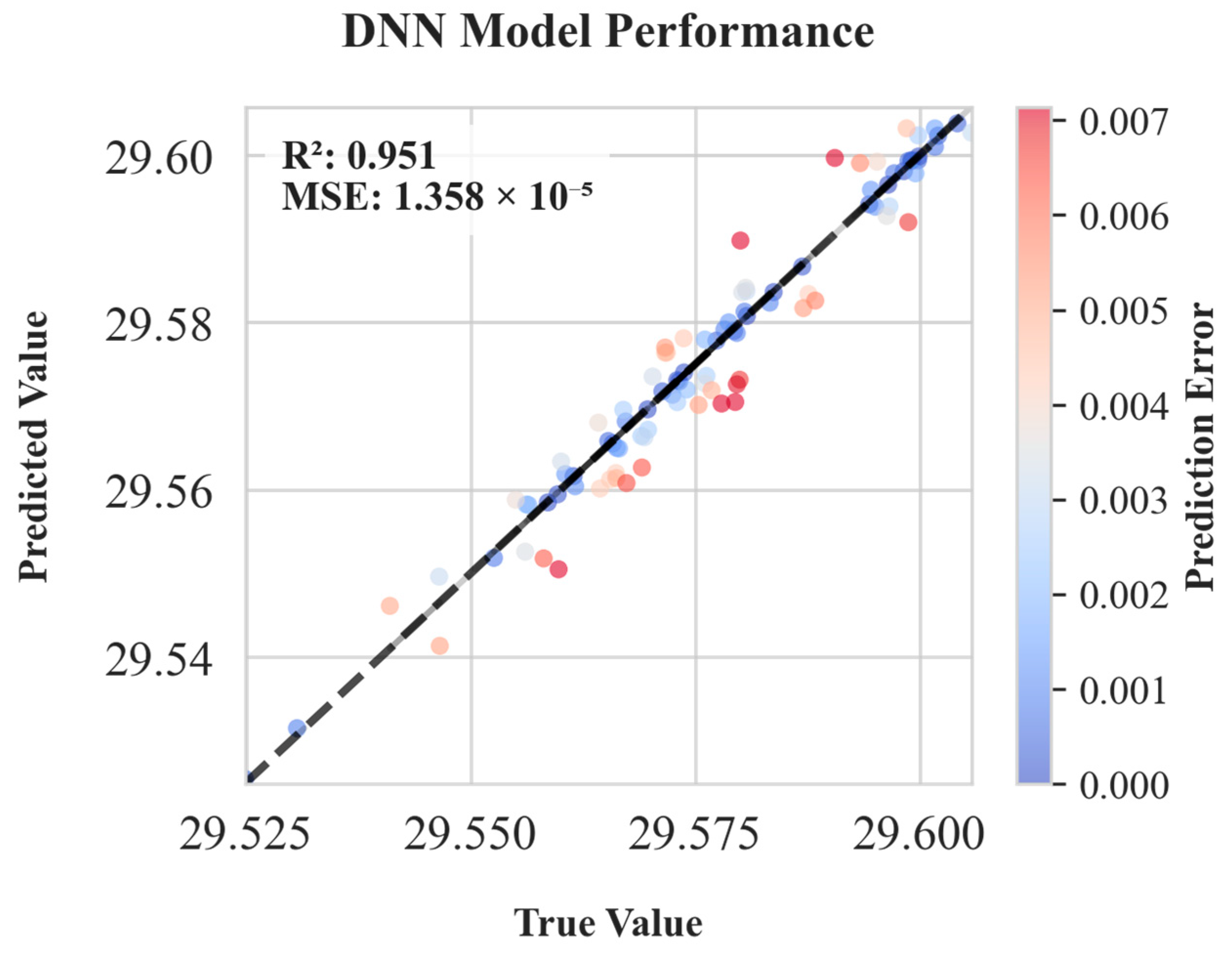
| 9:1 | 0.951 | 1.4 × 10−5 |
| Method | ||
|---|---|---|
| DNN | 0.951 | 1.4 × 10−5 |
| SVR | 0.872 | 3.53 × 10−5 |
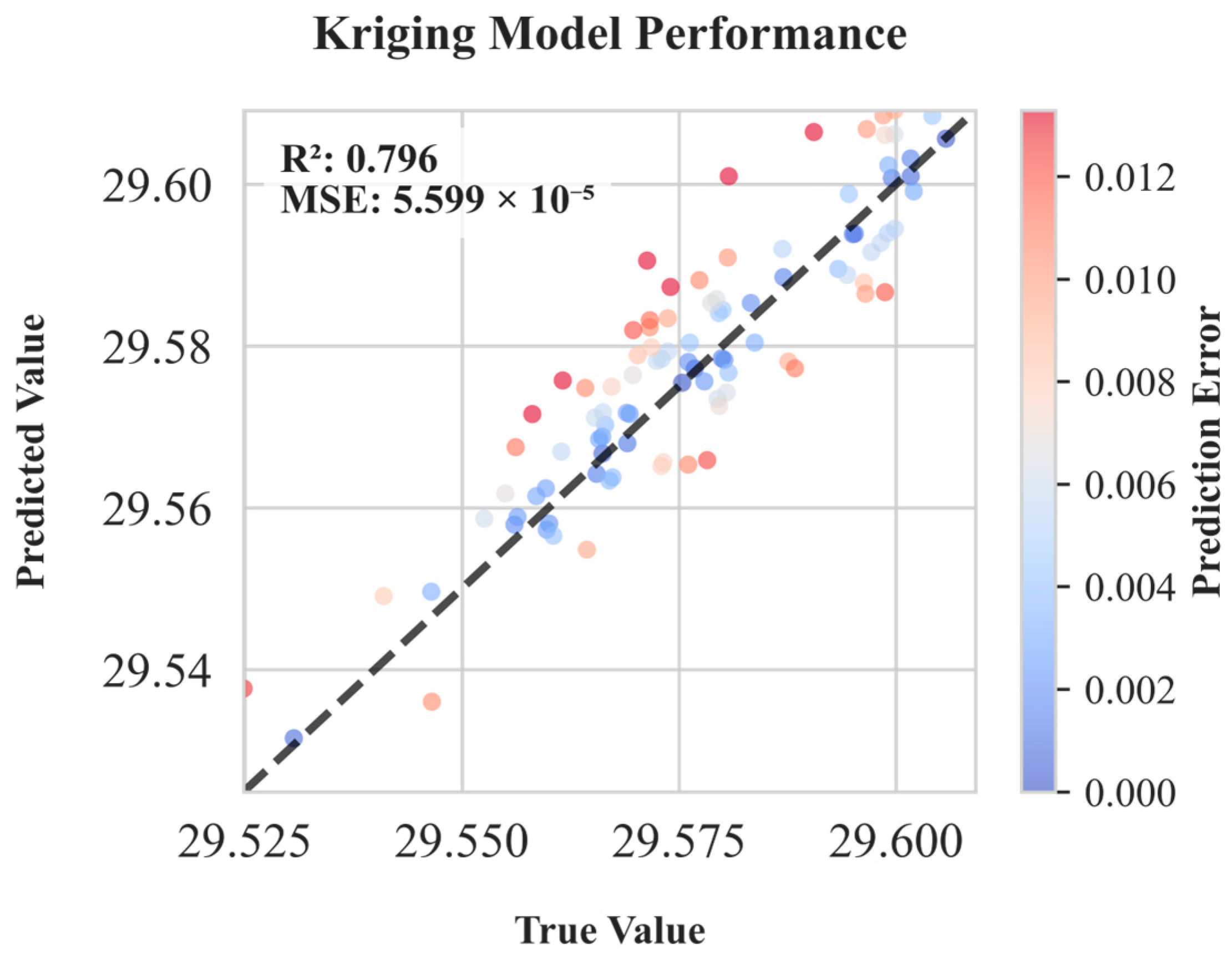
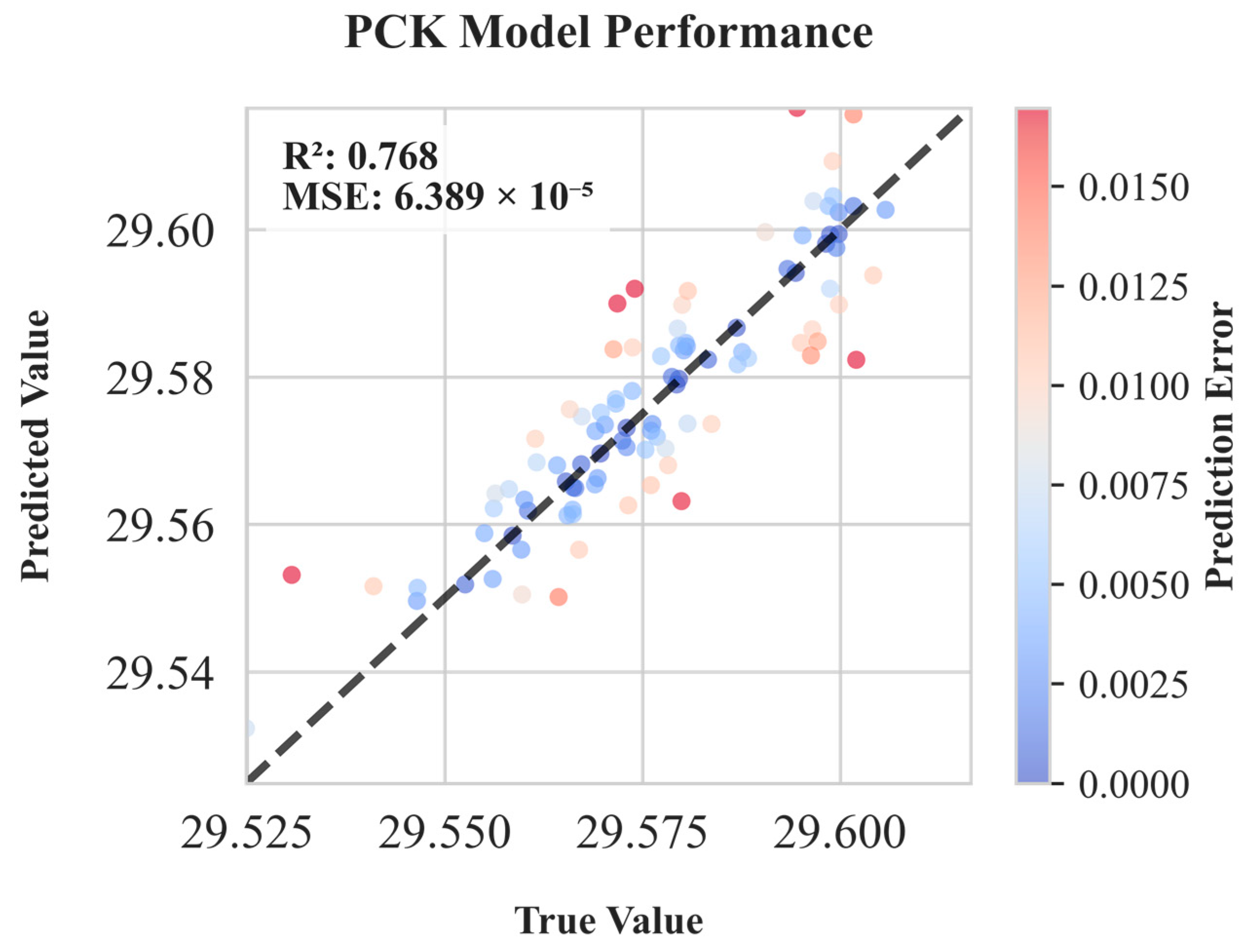
| Kriging | 0.796 | 5.599 × 10−5 |
| RF | 0.855 | 3.992 × 10−5 |
| PCK | 0.768 | 6.389 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Shao, W.; Liu, Y.; Fan, X.; Shi, R. Stochastic Blade Pitch Angle Analysis of Controllable Pitch Propeller Based on Deep Neural Networks. Modelling 2025, 6, 54. https://doi.org/10.3390/modelling6030054
Zhang X, Shao W, Liu Y, Fan X, Shi R. Stochastic Blade Pitch Angle Analysis of Controllable Pitch Propeller Based on Deep Neural Networks. Modelling. 2025; 6(3):54. https://doi.org/10.3390/modelling6030054
Chicago/Turabian StyleZhang, Xuanqi, Wenbin Shao, Yongshou Liu, Xin Fan, and Ruiyun Shi. 2025. "Stochastic Blade Pitch Angle Analysis of Controllable Pitch Propeller Based on Deep Neural Networks" Modelling 6, no. 3: 54. https://doi.org/10.3390/modelling6030054
APA StyleZhang, X., Shao, W., Liu, Y., Fan, X., & Shi, R. (2025). Stochastic Blade Pitch Angle Analysis of Controllable Pitch Propeller Based on Deep Neural Networks. Modelling, 6(3), 54. https://doi.org/10.3390/modelling6030054





