Enhancing Mathematical Knowledge Graphs with Large Language Models
Abstract
1. Introduction
1.1. Context and Importance of the Study
1.2. State of the Research Field and Objectives
1.3. Purpose, Aims, and Contributions
- The combined use of LLMs and ontology-driven KGs can significantly reduce the manual effort involved in constructing domain-specific knowledge repositories.
- Ontology-driven KGs improve the reasoning capabilities of LLMs by enforcing logical consistency and domain-specific constraints.
- The integrated approach provides a solution for validating mathematical curricula, demonstrating feasibility for handling large document sets through automated extraction and offering measurable consistency checks.
- A methodology that integrates KGs and LLMs for the extraction, validation, and management of mathematical knowledge.
- The design of a lightweight ontology to represent the structure of mathematical statements and proofs, thereby enabling advanced reasoning tasks.
- An automated extraction pipeline that processes structured LaTeX documents, allowing large-scale repositories—such as those from arXiv—to be efficiently incorporated into MKM systems.
2. Materials and Methods
2.1. KG Construction and Maintenance
2.2. Validation, Quality, and Reasoning
2.3. Interfaces
- An interactive web-based interface for querying, visualizing, and editing the KG.
- Mechanisms for detecting and correcting errors in the extracted information, incorporating a basic human-in-the-loop approach.
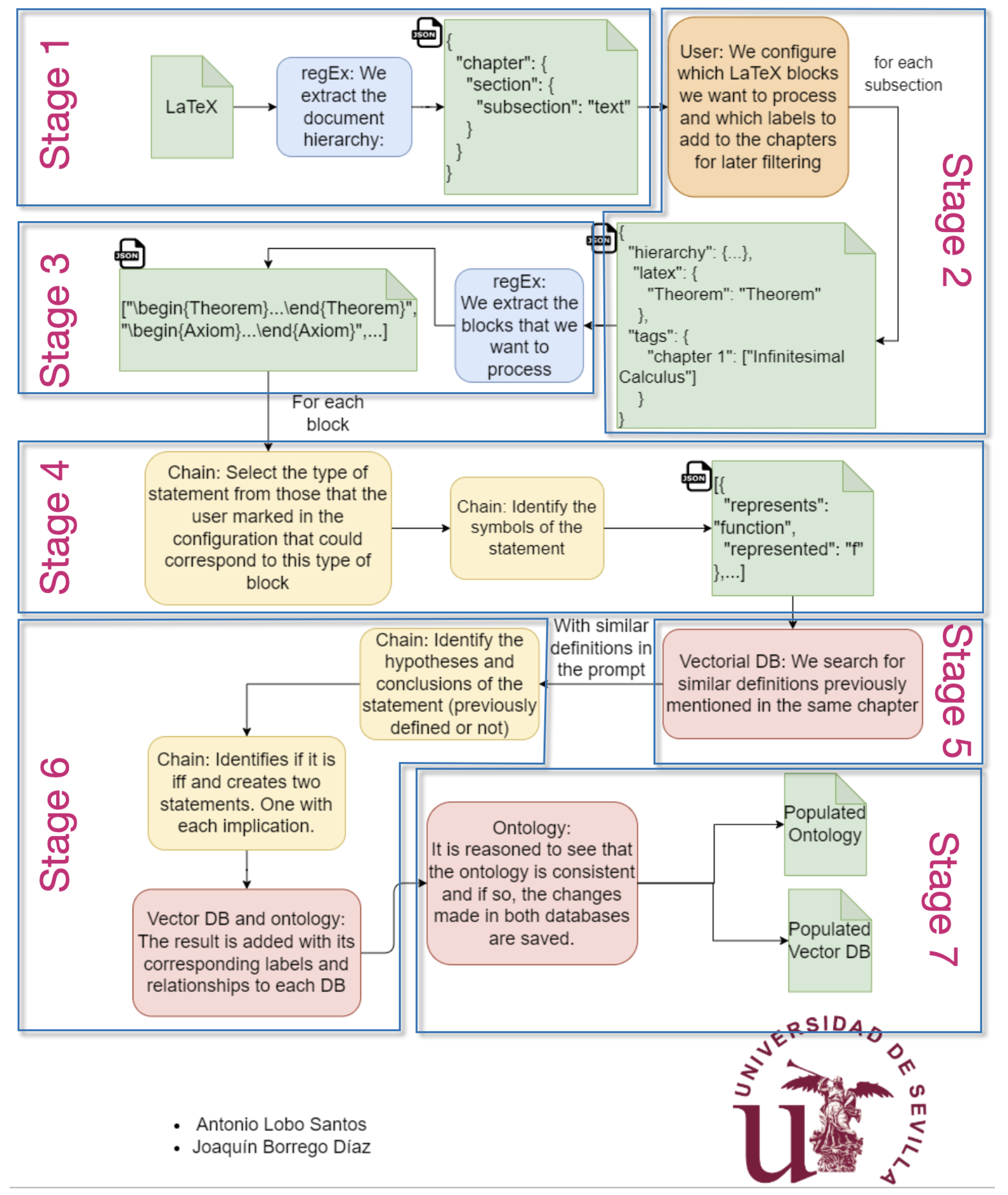
2.4. Information Extraction Process
2.4.1. Stage 1: LaTeX Document Input Processing
- A regular expression (RegEx) approach to identify structural elements, such as chapters, sections, and subsections.
- A hierarchical JSON representation is created to capture the document’s organization. For example:{“chapter1": {“sectionA": {“subsectionA1": "text of that subsection"}}}
2.4.2. Stage 2: User Configuration
- Which LaTeX blocks to extract (e.g., Theorem, Axiom, and Definition).
- Tags or labels to be assigned to specific chapters or sections for subsequent filtering.
- {“hierarchy": { … },“latex": {“theorem": ["Theorem", "Corollary"]},“tags": {“chapter1": ["Infinitesimal Calculus"]}}
2.4.3. Stage 3: Text Block Extraction
- A targeted RegEx to detect the user-specified blocks, such as\begin{Theorem}…\end{Theorem}.
- The extracted blocks are returned as an array of strings:["\\begin{Theorem} … \\end{Theorem}","\\begin{Axiom} … \\end{Axiom}", …]
2.4.4. Stage 4: Mathematical Formula Retrieval
- Notational Assumptions: We assume consistent notation is maintained throughout the document—at least within the same mathematical domain—to ensure clarity and coherence.
- Semantic Representation: LaTeX expressions are transformed into semantic forms by mapping symbolic expressions to generalized tokens (e.g., set_1, set_2, element_1).
- Vector Representations: The preprocessed text is encoded into dense vectors using BERT-based models [25], including
- Structure-Based Filtering: While symbolic layout trees or operator trees have been shown to improve retrieval precision [29], our approach prioritizes dense retrieval and does not rely on deep structural matching.
2.4.5. Stage 5: Retrieval from a Vector Database
- Indexed in a vector database, enabling efficient similarity-based searches.
- Utilized within a Retrieval-Augmented Generation (RAG) framework [30], in which the LLM is dynamically provided with the most relevant definitions or statements based on the user’s query.
2.4.6. Stage 6: Chain Process for Statement Analysis
- Detecting the Type of Statement: The system classifies each statement (e.g., theorem, axiom, and definition) based on the categories specified by the user in Stage 2.
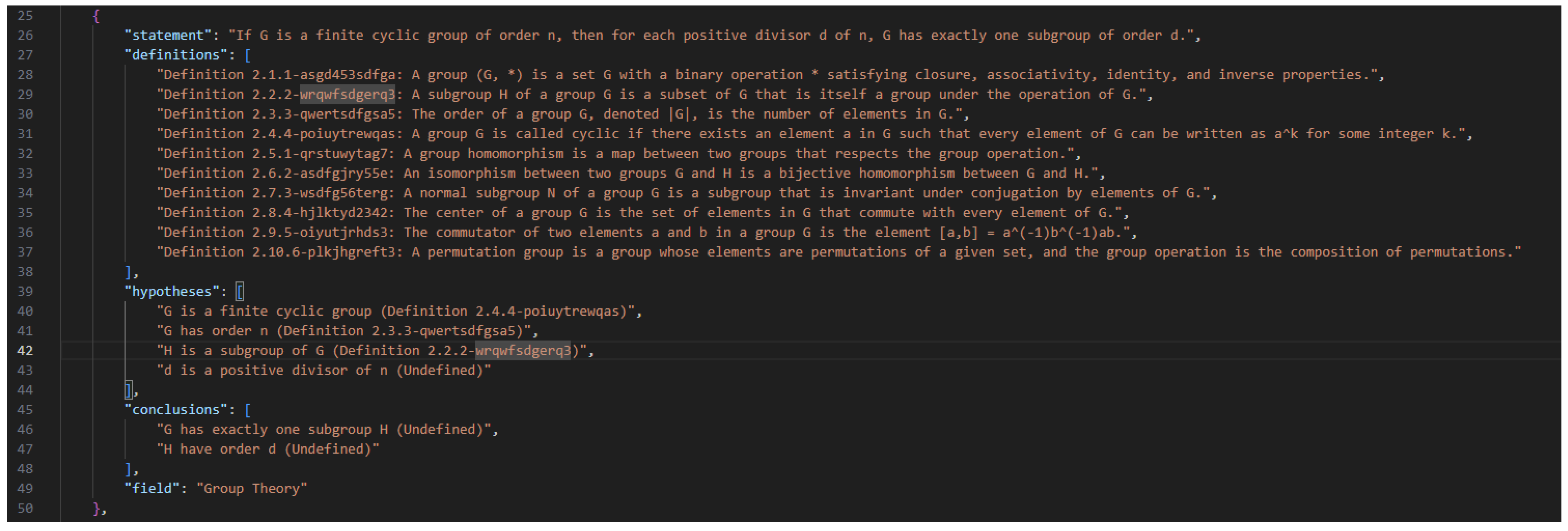
- Symbol Extraction: A JSON-formatted list of symbols is generated, linking each MathematicalObject individual to its corresponding LaTeX representation. For example:[{ "represents": "function", "represented": "f" },…]
- Identifying Hypotheses and Conclusions: For statements with an if–then structure, the system explicitly separates the premise (hypothesis) from the consequence (conclusion).
- Creating Sub-Statements: In cases involving multiple clauses, the system decomposes compound implications into separate sub-statements, enabling more granular reasoning. This chain-based analysis also checks whether a statement was previously defined. If so, it is included among the retrieved statements from Stage 5; otherwise, it is classified under the UndefinedStatement class to maintain semantic rigor and traceability.
2.4.7. Stage 7: Final Ontology Verification
- Verified against the ontology’s constraints to ensure consistency and validity.
- Stored in both the ontology and the vector database if they satisfy the consistency checks.
2.5. Front-End System Overview
2.5.1. Label Setup and Knowledge Base Population
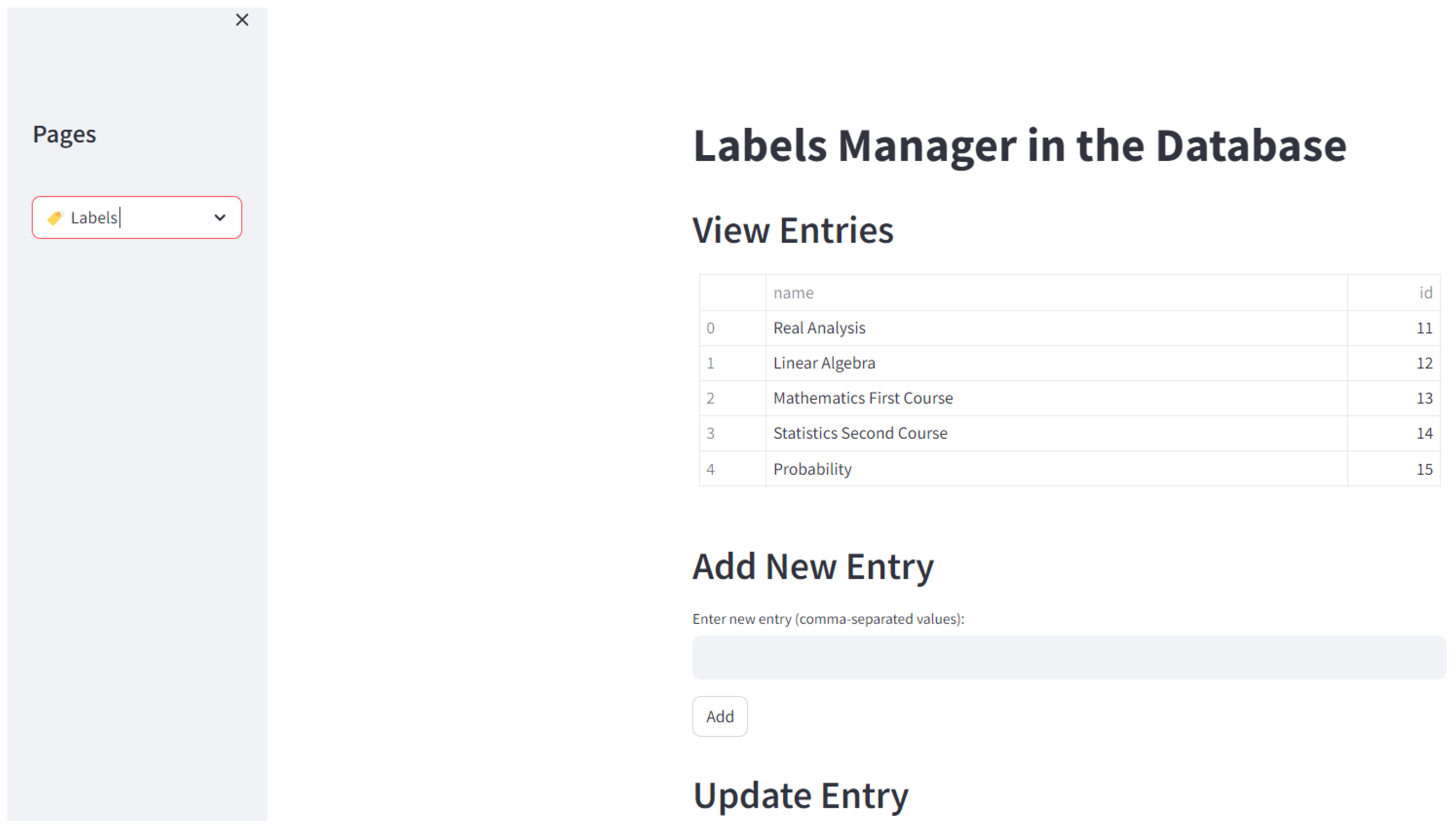
- Label Setup: Users can configure labels for mathematical statements or document sections through a dedicated web interface. An example of this functionality is illustrated in Figure 3, where existing entries can be viewed, and new entries can be added or updated within the database.Figure 3. Chatex interface for managing labels in the database, including options to view existing entries and add or update new ones.Figure 3. Chatex interface for managing labels in the database, including options to view existing entries and add or update new ones.
- Populate Knowledge Base: Users can upload LaTeX files, specify which environments to track (e.g., Theorem and Definition), configure label assignments, and monitor the extraction process in real time. Figure 4 shows the interface for uploading documents to the knowledge base. Figure 5 presents the configuration page where users select elements to extract and apply labels. Finally, Figure 6 displays the processing logs generated during information extraction.
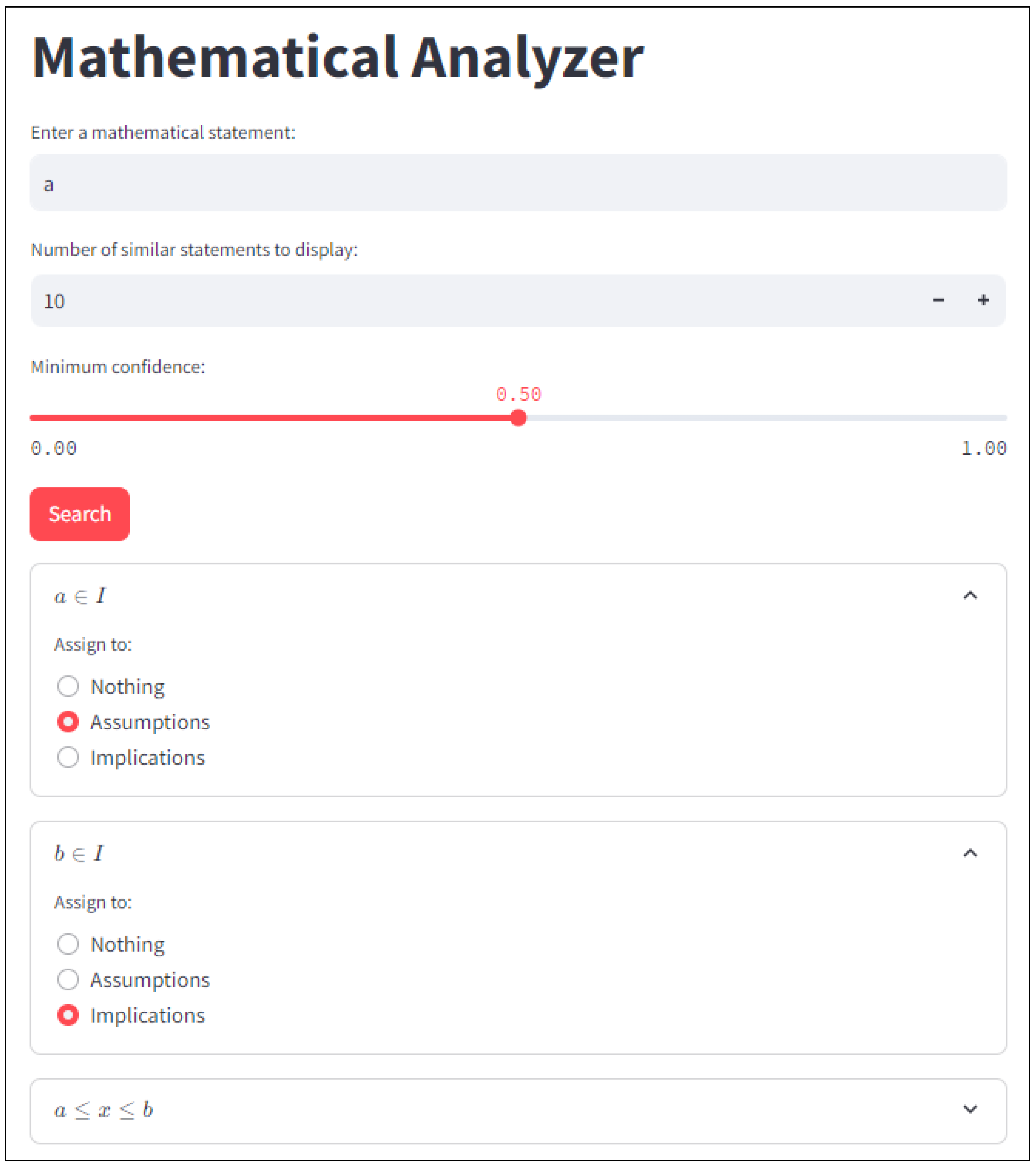
2.5.2. Similar Statements and Graph Visualizations
2.5.3. Ontology Visualization and Export
- Spring-Embedded and Shift Layouts: Spring-embedded layouts employ force-directed algorithms to emphasize clusters and reveal topological features. Shift layouts use geometric positioning to ensure planar crossing-free visualization of planar graphs.
- Hierarchical Layout: Based on the method of Sugiyama et al. [31], this layout organizes nodes into layers and reduces edge crossings, making it particularly suitable for visualizing logical inference flows.
2.6. On the Design of a Lightweight Ontology for MKM
2.6.1. Scope, Purpose, and Intended Use
- Enabling the storage and retrieval of formalized knowledge.
- Supporting logical reasoning and validation of mathematical content.
- Serving as a semantic interface between LLM-generated content and symbolic knowledge.
2.6.2. Ontology Construction and Versioning
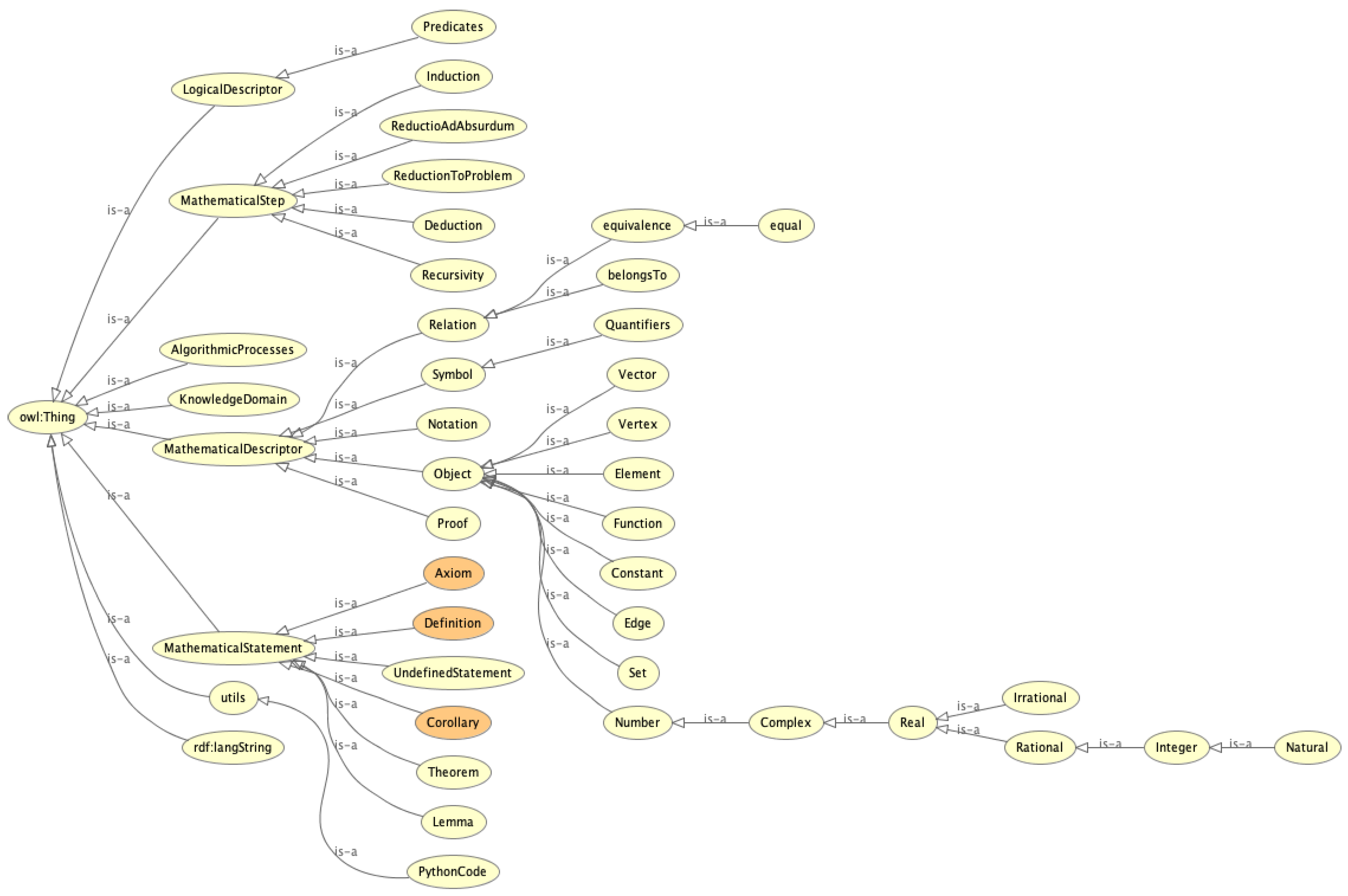
- Conceptual modeling: Identification of key conceptual categories in mathematical texts, such as Theorem, Definition, Axiom, Corollary, and ProofStep.
- Class definition: These concepts were formalized into OWL classes, organized under a root class MathematicalEntity. Core classes include
- MathematicalStatement: superclass of Theorem, Definition, Axiom, Lemma, and Corollary.
- MathematicalDescriptor: includes Symbol, Notation, and MathematicalObject (e.g., Function, Set, and Number).
- MathematicalStep: includes reasoning methods such as Deduction, Induction, and ReductionToProblem.
- Property modeling: The following object properties were defined to capture logical structure:
- assumesThat: links a statement to its hypotheses.
- impliesThat: links a statement to its conclusions.
- isProved / proves: bidirectional relation between statements and their proofs.
- hasSymbol, represents, hasNotation: to connect symbolic representations with abstract entities.
- Logical constraints: Domain and range restrictions, disjointness axioms, and inverse property assertions were added to ensure semantic consistency.
- MathematicalStatement: Represents formal mathematical statements, including axioms, theorems, definitions, corollaries, and lemmas.
- MathematicalDescriptor: Encodes components used to describe mathematical content, such as notations, mathematical objects (e.g., functions, sets, and vectors), symbols, and proofs.
- MathematicalStep: Describes individual steps in a proof, including deduction, induction, recursion, and reductio ad absurdum.
- assumesThat and impliesThat: These properties relate mathematical statements to their respective hypotheses and conclusions, enabling the representation of logical implication chains within the ontology.
- hasSymbol, hasNotation, and represents: These properties associate mathematical statements with the symbols, notations, and mathematical objects they reference, thereby supporting semantic linking and search.
- isProved and proves: These reciprocal properties establish the relationship between a mathematical statement and its proof. Specifically, isProved connects a statement to its corresponding proof, while proves asserts that a given proof validates a particular statement.
2.6.3. Ontology Versioning and Availability
| https://gitlab.com/universidad4774909/tfg/chatex-webui/-/raw/main/TFG1.owx |
| (accessed on 20 February 2025) |
2.6.4. Integration with the Information Extraction Pipeline
- Post-processing: Each extracted block is matched against the ontology schema to identify its class.
- Semantic enrichment: Statements are linked to previously defined objects and notations.
- Reasoning: Ontology reasoners are used to infer class memberships and check for logical coherence. For example, if a new Theorem is linked to undefined Function symbols, these are flagged and stored under the UndefinedEntity class for later validation.
- SPARQL queries: These are used to detect implication chains, retrieve related definitions, and assess proof completeness.
2.6.5. Ontology Reasoning and Mathematical Information Extraction
- Detection of logical inconsistencies or errors within stored statements.
- Deduction of implicit relationships and knowledge from the existing ontology structure.
- Validation of newly extracted statements by comparing them against established logical rules and semantic links.
2.7. Prompt Templates
- Prompt Format: Different LLMs (e.g., llama3.1 or command-r) may require different prompt structures and formatting conventions [32].
- Few-Shot Examples: Where possible, prompts are augmented with annotated examples that demonstrate how to parse mathematical statements or identify hypotheses.
- Symbol Delimitation: Explicit guidance is provided to help the model distinguish between symbols and text, facilitating more robust semantic extraction.
2.8. Use Case Examples and Algorithmic Implementations
2.8.1. Optimization of Hypotheses
Objective
Algorithmic Approach
- Which definitions or propositions in the ontology imply a given conclusion.
- The prerequisite assumptions needed for each implication to hold.
Output
- {“Proposition1”: [“Definition_Anonymous”,“Definition_Compact_Interval”],“Proposition3”: [“Definition_Anonymous”]}
Use Case
2.8.2. Maximization of Conclusions
Objective
Algorithmic Approach
- Initializes a queue with all hypotheses in H.
- Iteratively retrieves all conclusions implied by each hypothesis.
- Adds newly derived conclusions to the queue if they have not yet been processed.
Output
Use Case
2.8.3. Pseudo-Demonstrations
Objective
Algorithmic Approach
- Each implication edge is assigned a uniform weight of 1.
- The algorithm searches for the shortest paths from elements in H to each target conclusion in C.
- If a conclusion is unreachable, the system flags it as such.
Output
Use Case
2.8.4. Academic Coherence and Course Planning
Objective
- Identifying concepts already covered in previous courses.
- Detecting missing prerequisites necessary to meet learning outcomes.
- Constructing pseudo-demonstrations that connect prior knowledge to new objectives.
Methodology
- Minimal Known Hypotheses: Filter out derivable content already covered in prior coursework to isolate the essential hypotheses.
- Hypothesis Minimization: Apply the Optimization of Hypotheses algorithm (Section 2.8.1) to determine the minimal set of additional prerequisites needed.
- Pseudo-demonstration Construction: Use the pseudo-demonstrations algorithm (Section 2.8.3) to build a hierarchical graph linking existing knowledge to new course content.
Use Case
2.9. Model Selection Criteria
3. Results
3.1. Information Extraction Effectiveness
- High performance on the benchmark should indicate robust in-domain task performance.
- Examples must be clearly annotated and unambiguous.
- Test samples should undergo thorough validation to eliminate erroneous or ambiguous cases.
- The dataset must provide sufficient statistical power for rigorous evaluation.
- The benchmark should identify and discourage the development of biased models by exposing potential harmful biases.
3.1.1. Small LLMs
3.1.2. Medium LLMs
3.1.3. Large LLMs
3.2. Use Case Demonstration
- Label creation for filtering extracted statements.
- Ontology population from a well-structured LaTeX document.
- Visualization of the resulting KG using spring-embedded and planar layouts.
- Application of reasoning algorithms and visualization using the Sugiyama hierarchical layout.
- Ontology inspection and validation via the Protégé platform.
4. Discussion
4.1. Technological Challenges and Limitations
4.1.1. Limitations of LLMs
- Hallucinations: Fabrications of intermediate results, definitions, and proofs persisted despite meticulous prompt engineering. This behavior aligns with recent findings [5], which report pervasive hallucination across model sizes and architectures. Nevertheless, the integration of ontologies can impose domain-specific constraints, helping to delineate output boundaries in line with the Knowledge-Controlled Generation paradigm [53]. Moreover, the structured nature of the KG and subsequent validation steps offer potential mechanisms for identifying and mitigating some inconsistencies introduced by hallucinated content, although such challenges are not entirely eliminated.
- Symbolic Reasoning Deficiencies: Consistent with prior studies [10,54,55], the LLMs exhibited significant limitations in symbolic and multi-step mathematical reasoning. Their performance was often fragile, with minor semantically irrelevant changes (e.g., altering numerical values or introducing extraneous information) substantially impacting the outcomes, suggesting reliance on superficial pattern matching rather than robust logical inference [10]. Furthermore, the models frequently failed at compositional reasoning, struggling to spontaneously combine known concepts to solve novel problems involving logical traps [54]. Manual analyses confirm that these failures often stem from flawed logical chains, unwarranted assumptions, and difficulties regarding translating physical intuition into formalized steps [55]. Notably, although the expanded context windows permit the inclusion of additional relevant statements, doing so did not consistently enhance reasoning performance, underscoring a fundamental limitation in flexible knowledge integration rather than a mere context size constraint.
- Parameter and Language Constraints: Models with fewer than 5 billion parameters demonstrated limited capacity for parsing structured mathematical input and exhibited strong reliance on English-language prompts. These constraints reduced the performance robustness across diverse input scenarios. Nonetheless, recent advances in small language models suggest potential for future improvements [56].
- Dependency on Structured Input: Our system requires well-formatted LaTeX documents, limiting applicability to sources with clean standardized structures. Broader issues of unstructured document parsing, including neglect of tables, diagrams, and semantic metadata, remain challenging [57].
4.1.2. Challenges in Document Conversion and Standardization
- Conversion Quality: Many available tools and APIs generate cluttered LaTeX outputs that include unnecessary style elements, making it harder to identify structural components like theorems and definitions [58].
- OCR Limitations: Although advanced OCR models (e.g., [59]) were evaluated, they failed to provide the required precision and structure necessary for reliable extraction of complex mathematical notations.
- Heterogeneity of LaTeX Formats: The lack of a standardized LaTeX format significantly complicates automated extraction. The “ideal” LaTeX template we developed served as a controlled format to mitigate this issue, but widespread adoption of such a format remains a challenge.
4.1.3. Ontology Design and Prompt Engineering
- Enhanced consistency checking for newly extracted statements.
- Clear mapping of semantic relationships among theorems, definitions, and numerical methods.
- Integration with reasoning engines for validation, inference, and logical navigation through mathematical content.
4.1.4. Scope of Knowledge Extraction:
4.2. Cognitive Computing
- The interpretability of complex mathematical models.
- The robustness and transparency of decision-making in knowledge-intensive environments.
4.3. Expanding the Methodology to Other Domains
- Domain-specific ontology design: Replace the mathematical ontology with a structured vocabulary of entities and relations relevant to the target domain (e.g., biomedical conditions and legal concepts).
- Prompt specialization: Tailor prompt templates to reflect domain-relevant discourse structures and knowledge types using strategies like chain-of-thought prompting.
- Validation frameworks: Incorporate domain-appropriate quality checks, such as expert review for clinical safety or consistency audits for legal correctness.
4.4. Future Directions
- Ontology Expansion: Expand the ontology to include mathematical and engineering concepts that support the direct execution of simulations or numerical methods when necessary.
- Integration with Theorem Provers: Incorporate formal proof assistants (e.g., Lean and Coq) to validate and verify the correctness of extracted mathematical statements, strengthening the logical soundness of the knowledge base. Recent studies have shown impressive improvement regarding model performance when incorporating these tools into the LLM reasoning process [64,65].
- Advanced Prompt Engineering and Reasoning Model Integration: Develop and integrate prompt templates and reasoning strategies that leverage cutting-edge reasoning models [66] to perform multi-step internal planning to excel regarding advanced mathematics and science tasks and reduce LLM hallucinations [67]. This can enhance semantic fidelity, and extract richer symbolic representations.
- Bias Mitigation: Investigate and address the biases present in LLM outputs to ensure neutrality, reliability, and fairness in extracted content, particularly when deployed in educational or decision-support systems.
- Dynamic KG Maintenance: Addressing the dynamic nature of mathematical knowledge (e.g., revised definitions and evolving curricula) is crucial. Future work will explore a pipeline involving (1) versioned storage of triples with validity intervals; (2) change-triggered re-indexing based on fine-grained dependency tracking; (3) automated outdated-fact detection, potentially adapting techniques like Deep Outdated Fact Detection [68], which leverage structural and textual cues; and (4) minimal-change revision mechanisms, including archiving or consistent replacement of flagged triples to maintain KG integrity.
- KG Completion and Implicit Reasoning: A significant direction is enhancing KG completeness and inferring implicit knowledge beyond explicitly stated facts. Future work includes exploring text-enhanced KG completion methods. For instance, SimKGC [69] leverages contrastive learning on entity descriptions and is a natural baseline for our text-rich LaTeX sources. More recent neighborhood- and relation-aware models—KGC-ERC [70] and RAA-KGC [71]—set a new state of the art and should also be considered. To adapt these approaches to the mathematical domain, they should be combined with our mathematical-formula-retrieval pipeline (Section 2.4.4) so that symbols and equations provide additional domain-specific context for entities and relations.
5. Conclusions
5.1. Key Contributions
- Ontology-Driven Knowledge Modeling: We developed a lightweight yet expressive ontology capable of representing core mathematical structures, including hypotheses, theorems, and proofs. This structured representation underpins the system’s ability to perform advanced reasoning, validate curriculum coherence, and retrieve relevant methods accurately [1,2].
- Automated Information Extraction Pipeline: A robust pipeline was implemented, leveraging state-of-the-art LLMs and vector retrieval models to accurately extract and structure formal statements from LaTeX source documents. This automation is key to enabling the ingestion and management of knowledge from large-scale repositories like arXiv, benefiting MKM [9,10].
- Hybrid Cognitive Computing Framework: The integration of probabilistic LLM-based generation with symbolic ontology-based reasoning embodies a hybrid AI approach. This synergy bridges the gap between data-driven pattern recognition and formal logic, resulting in a knowledge representation framework that is potentially more robust, explainable, and suitable for knowledge-intensive applications in education and research [72].
5.2. Implications for MKM
- Curriculum Validation and Model Verification: The system provides tools to ensure the logical flow and consistency of educational materials.
- Intelligent Tutoring Systems: By enabling the generation of pseudo-demonstrations and the verification of prerequisite knowledge, the framework can serve as a valuable component in developing sophisticated AI-driven educational platforms.
- Storage and Retrieval of Precise Methods: The KG acts as a repository for rigorously defined computational methods, such as precise algorithms implementing mathematical definitions or verifying properties, explicitly linked to the corresponding formal statements. This structured storage allows for the validation of computational implementations against their specifications, facilitates reliable retrieval, and promotes reproducibility and methodological rigor.
5.3. Acknowledged Limitations and Path Forward
5.4. Final Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Prompt Template: Hypothesis Extraction
| Listing A1. Prompt template used for extracting hypotheses from mathematical theorems. |
 |
References
- Kohlhase, M. OMDoc—An Open Markup Format for Mathematical Documents, Version 1.2; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4180, pp. XIX, 432. [Google Scholar] [CrossRef]
- Elizarov, A.; Kirillovich, A.; Lipachev, E.; Nevzorova, O. Digital Ecosystem OntoMath: Mathematical Knowledge Analytics and Management. In Data Analytics and Management in Data Intensive Domains. DAMDID/RCDL 2016; Communications in Computer and Information Science; Kalinichenko, L., Kuznetsov, S., Manolopoulos, Y., Eds.; Springer: Cham, Switzerland, 2017; Volume 706, pp. 34–45. [Google Scholar] [CrossRef]
- Weikum, G.; Dong, X.L.; Razniewski, S.; Suchanek, F.M. Machine knowledge: Creation and curation of comprehensive knowledge bases. Found. Trends Databases 2021, 10, 108–490. [Google Scholar] [CrossRef]
- Xue, B.; Zou, L. Knowledge Graph Quality Management: A Comprehensive Survey. IEEE Trans. Knowl. Data Eng. 2023, 35, 4969–4988. [Google Scholar] [CrossRef]
- Tonmoy, S.M.T.I.; Zaman, S.M.M.; Jain, V.; Rani, A.; Rawte, V.; Chadha, A.; Das, A. A Comprehensive Survey of Hallucination Mitigation Techniques in Large Language Models. arXiv 2024, arXiv:2401.01313. [Google Scholar]
- Huang, L.; Yu, W.; Zhang, W.; Tian, Y.; Qiu, S.; Liu, C.; Niu, D.; Yue, D.; Wu, J.R.; Wang, J. A Survey on Hallucination in Large Language Models: Principles, Taxonomy, Challenges, and Open Questions. arXiv 2024, arXiv:2311.05232. [Google Scholar] [CrossRef]
- Gao, Y.; Xiong, Y.; Gao, X.; Jia, K.; Pan, J.; Bi, Y.; Dai, Y.; Sun, J.; Wang, M.; Wang, H. Retrieval-Augmented Generation for Large Language Models: A Survey. arXiv 2024, arXiv:2312.10997. [Google Scholar]
- Guo, T.; Yang, Q.; Wang, C.; Liu, Y.; Li, P.; Tang, J.; Li, D.; Wen, Y. KnowledgeNavigator: Leveraging large language models for enhanced reasoning over knowledge graph. Complex Intell. Syst. 2024, 10, 7063–7076. [Google Scholar] [CrossRef]
- Pan, S.; Luo, L.; Wang, Y.; Chen, C.; Wang, J.; Wu, X. Unifying Large Language Models and Knowledge Graphs: A Roadmap. arXiv 2023, arXiv:2306.08302. [Google Scholar] [CrossRef]
- Mirzadeh, I.; Alizadeh, K.; Shahrokhi, H.; Tuzel, O.; Bengio, S.; Farajtabar, M. GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models. arXiv 2024, arXiv:2410.05229. [Google Scholar]
- Luo, L.; Zhao, Z.; Haffari, G.; Gong, C.; Pan, S. Graph-constrained Reasoning: Faithful Reasoning on Knowledge Graphs with Large Language Models. arXiv 2024, arXiv:2404.12954. [Google Scholar]
- Rahman, A.M.M.; Yang, T.; Yang, M.; Zhao, H.; Yang, T. LemmaHead: RAG Assisted Proof Generation Using Large Language Models. arXiv 2025, arXiv:2501.15797. [Google Scholar]
- Xena Project. Lean in 2024. Blog Post. 2024. Available online: https://xenaproject.wordpress.com/2024/01/20/lean-in-2024/ (accessed on 20 February 2025).
- Buzzard, K. The Xena Project. Online Talk/Blog. 2021. Ongoing Project. Available online: https://xenaproject.wordpress.com/ (accessed on 20 February 2025).
- Dixit, P.; Oates, T. SBI-RAG: Enhancing Math Word Problem Solving for Students Through Schema-Based Instruction and Retrieval-Augmented Generation. arXiv 2024, arXiv:2410.13293. [Google Scholar]
- Hogan, A.; Blomqvist, E.; Cochez, M.; d’Amato, C.; de Melo, G.; Gutierrez, C.; Kirrane, S.; Gayo, J.E.L.; Navigli, R.; Neumaier, S.; et al. Knowledge graphs. ACM Comput. Surv. 2021, 54, 1–37. [Google Scholar] [CrossRef]
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Ichter, B.; Xia, F.; Chi, E.; Le, Q.; Zhou, D. Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. arXiv 2023, arXiv:2201.11903. [Google Scholar]
- Kwon, W.; Li, Z.; Zhuang, S.; Sheng, Y.; Zheng, L.; Yu, C.H.; Gonzalez, J.E.; Zhang, H.; Stoica, I. Efficient Memory Management for Large Language Model Serving with PagedAttention. arXiv 2023, arXiv:2309.06180. [Google Scholar]
- Gurajada, S.; Seufert, S.; Miliaraki, I.; Theobald, M. TriAD: A distributed shared-nothing RDF engine based on asynchronous message passing. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 22–27 June 2014; pp. 289–300. [Google Scholar]
- Schwarte, A.; Haase, P.; Hose, K.; Schenkel, R.; Schmidt, M. FedX: A Federation Layer for Distributed Query Processing on Linked Open Data. In The Semantic Web: Research and Applications, Proceedings of the 8th Extended Semantic Web Conference, (ESWC 2011), Heraklion, Greece, 29 May–2 June 2011; LNCS 6644; Springer: Berlin/Heidelberg, Germany, 2011; pp. 481–486. [Google Scholar] [CrossRef]
- Dadzie, A.S.; Rowe, M. Approaches to Visualising Linked Data: A Survey. Semant. Web 2011, 2, 89–124. [Google Scholar] [CrossRef]
- Katifori, A.; Halatsis, C.; Lepouras, G.; Vassilakis, C.; Giannopoulou, E. Ontology visualization methods—A survey. ACM Comput. Surv. 2007, 39, 10-es. [Google Scholar] [CrossRef]
- Heer, J.; Shneiderman, B. Interactive dynamics for visual analysis. Commun. ACM 2012, 55, 45–54. [Google Scholar] [CrossRef]
- Shneiderman, B. The eyes have it: A task by data type taxonomy for information visualizations. In Proceedings of the 1996 IEEE Symposium on Visual Languages, Boulder, CO, USA, 3–6 September 1996; pp. 336–343. [Google Scholar] [CrossRef]
- Wang, J.; Huang, J.X.; Tu, X.; Wang, J.; Huang, A.J.; Laskar, M.T.R.; Bhuiyan, A. Utilizing BERT for Information Retrieval: Survey, Applications, Resources, and Challenges. arXiv 2024, arXiv:2403.00784. [Google Scholar] [CrossRef]
- Reusch, A.; Thiele, M.; Lehner, W. Transformer-Encoder and Decoder Models for Questions on Math. In Proceedings of the Conference and Labs of the Evaluation Forum, CLEF 2022, Bologna, Italy, 5–8 September 2022. [Google Scholar]
- Kohlhase, A.; Kovács, L. (Eds.) Intelligent Computer Mathematics. In Proceedings of the 17th International Conference, CICM 2024, Montréal, QC, Canada, 5–9 August 2024; Proceedings, Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2024; Volume 14960. [Google Scholar]
- Novotný, V.; Štefánik, M. Combining Sparse and Dense Information Retrieval. In Working Notes of CLEF 2022, Proceedings of the Conference and Labs of the Evaluation Forum, CLEF 2022, Bologna, Italy, 5–8 September 2022; Faggioli, G., Ferro, N., Hanbury, A., Potthast, M., Eds.; CEUR-WS: Bologna, Italy, 2022; pp. 104–118. [Google Scholar]
- Zanibbi, R.; Mansouri, B.; Agarwal, A. Mathematical Information Retrieval: Search and Question Answering. arXiv 2024, arXiv:2408.11646. [Google Scholar] [CrossRef]
- Lewis, P.; Perez, E.; Piktus, A.; Petroni, F.; Karpukhin, V.; Goyal, N.; Küttler, H.; Lewis, M.; Tau Yih, W.; Rocktäschel, T.; et al. Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks. arXiv 2021, arXiv:2005.11401. [Google Scholar]
- Sugiyama, K.; Tagawa, S.; Toda, M. Methods for Visual Understanding of Hierarchical System Structures. IEEE Trans. Syst. Man, Cybern. 1981, 11, 109–125. [Google Scholar] [CrossRef]
- Mirac Suzgun, A.T.K. Meta-Prompting: Enhancing Language Models with Task-Agnostic Scaffolding. arXiv 2024, arXiv:2401.12954. [Google Scholar]
- Qi, Z.; Ma, M.; Xu, J.; Zhang, L.L.; Yang, F.; Yang, M. Mutual Reasoning Makes Smaller LLMs Stronger Problem-Solvers. arXiv 2024, arXiv:2408.06195. [Google Scholar]
- Chen, W.; Ma, X.; Wang, X.; Cohen, W.W. Program of thoughts prompting: Disentangling computation from reasoning for numerical reasoning tasks. arXiv 2022, arXiv:2211.12588. [Google Scholar]
- Khot, T.; Trivedi, H.; Finlayson, M.; Fu, Y.; Richardson, K.; Clark, P.; Sabharwal, A. Decomposed prompting: A modular approach for solving complex tasks. arXiv 2022, arXiv:2210.02406. [Google Scholar]
- Universidad de Sevilla, Facultad de Matemáticas. Plan de Estudios del Grado en Matemáticas. 2009. Available online: https://matematicas.us.es/titulaciones/grado-en-matematicas/presentacion/plan-de-estudios-del-grado-en-matematicas (accessed on 20 February 2025).
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Kahn, A.B. Topological sorting of large networks. Commun. ACM 1962, 5, 558–562. [Google Scholar] [CrossRef]
- Gao, B.; Song, F.; Yang, Z.; Cai, Z.; Miao, Y.; Dong, Q.; Li, L.; Ma, C.; Chen, L.; Xu, R.; et al. Omni-MATH: A Universal Olympiad Level Mathematic Benchmark for Large Language Models. arXiv 2024, arXiv:2410.07985. [Google Scholar]
- Ming, Y.; Purushwalkam, S.; Pandit, S.; Ke, Z.; Nguyen, X.P.; Xiong, C.; Joty, S. FaithEval: Can Your Language Model Stay Faithful to Context, Even If “The Moon is Made of Marshmallows”. arXiv 2024, arXiv:2410.03727. [Google Scholar]
- Card, D.; Henderson, P.; Khandelwal, U.; Jia, R.; Mahowald, K.; Jurafsky, D. With Little Power Comes Great Responsibility. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Virtually, 16–20 November 2020; Webber, B., Cohn, T., He, Y., Liu, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 9263–9274. [Google Scholar] [CrossRef]
- Bowman, S.R.; Dahl, G. What Will it Take to Fix Benchmarking in Natural Language Understanding? In Human Language Technologies, Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics, Online, 6–11 June 2021; Toutanova, K., Rumshisky, A., Zettlemoyer, L., Hakkani-Tur, D., Beltagy, I., Bethard, S., Cotterell, R., Chakraborty, T., Zhou, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021; pp. 4843–4855. [Google Scholar] [CrossRef]
- Meta. Introducing Meta Llama 3: The Most Capable Openly Available LLM to Date. Available online: https://ai.meta.com/blog/meta-llama-3/ (accessed on 20 February 2025).
- Abdin, M.; Aneja, J.; Awadalla, H.; Awadallah, A.; Awan, A.A.; Bach, N.; Bahree, A.; Bakhtiari, A.; Bao, J.; Behl, H.; et al. Phi-3 Technical Report: A Highly Capable Language Model Locally on Your Phone. arXiv 2024, arXiv:2404.14219. [Google Scholar]
- Team, G.; Riviere, M.; Pathak, S.; Sessa, P.G.; Hardin, C.; Bhupatiraju, S.; Hussenot, L.; Mesnard, T.; Shahriari, B.; Ramé, A.; et al. Gemma 2: Improving Open Language Models at a Practical Size. arXiv 2024, arXiv:2408.00118. [Google Scholar]
- Mistral AI. Mathstral: Accelerating Mathematical Discovery with AI. Available online: https://mistral.ai/news/mathstral/ (accessed on 31 November 2024).
- Yang, A.; Yang, B.; Hui, B.; Zheng, B.; Yu, B.; Zhou, C.; Li, C.; Li, C.; Liu, D.; Huang, F.; et al. Qwen2 technical report. arXiv 2024, arXiv:2407.10671. [Google Scholar]
- Team, Q. Qwen2.5: A Party of Foundation Models. arXiv 2024, arXiv:2412.15115. [Google Scholar]
- Dubey, A.; Dubey, A.; Jauhri, A.; Pandey, A.; Kadian, A.; Al-Dahle, A.; Letman, A.; Mathur, A.; Schelten, A.; Vaughan, A.; et al. The Llama 3 Herd of Models. arXiv 2024, arXiv:2407.21783. [Google Scholar]
- Jiang, A.Q.; Sablayrolles, A.; Roux, A.; Mensch, A.; Savary, B.; Bamford, C.; Chaplot, D.S.; de las Casas, D.; Hanna, E.B.; Bressand, F.; et al. Mixtral of Experts. arXiv 2024, arXiv:2401.04088. [Google Scholar]
- Qwen Team. Introducing Qwen1.5. Qwen Blog (Blog), 4 February 2024. Available online: https://qwenlm.github.io/blog/qwen1.5/ (accessed on 20 February 2025).
- Touvron, H.; Martin, L.; Stone, K.; Albert, P.; Almahairi, A.; Babaei, Y.; Bashlykov, N.; Batra, S.; Bhargava, P.; Bhosale, S.; et al. Llama 2: Open Foundation and Fine-Tuned Chat Models. arXiv 2023, arXiv:2307.09288. [Google Scholar]
- Agrawal, G.; Kumarage, T.; Alghamdi, Z.; Liu, H. Can Knowledge Graphs Reduce Hallucinations in LLMs? A Survey. arXiv 2023, arXiv:2311.07914. [Google Scholar]
- Zhao, J.; Tong, J.; Mou, Y.; Zhang, M.; Zhang, Q.; Huang, X. Exploring the Compositional Deficiency of Large Language Models in Mathematical Reasoning. arXiv 2024, arXiv:2405.06680. [Google Scholar]
- Boye, J.; Moell, B. Large Language Models and Mathematical Reasoning Failures. arXiv 2025, arXiv:2502.11574. [Google Scholar]
- Subramanian, S.; Elango, V.; Gungor, M. Small Language Models (SLMs) Can Still Pack a Punch: A survey. arXiv 2025, arXiv:2501.05465. [Google Scholar]
- Zhang, Q.; Wang, B.; Huang, V.S.J.; Zhang, J.; Wang, Z.; Liang, H.; He, C.; Zhang, W. Document Parsing Unveiled: Techniques, Challenges, and Prospects for Structured Information Extraction. arXiv 2025, arXiv:2410.21169. [Google Scholar]
- Mathpix. Math Pix PDF to LaTeX. Available online: https://mathpix.com/pdf-to-latex (accessed on 20 February 2025).
- HuggingFace. trOCR. Available online: https://huggingface.co/docs/transformers/model_doc/trocr (accessed on 20 February 2025).
- Hao, S.; Gu, Y.; Ma, H.; Hong, J.J.; Wang, Z.; Wang, D.Z.; Hu, Z. Reasoning with Language Model is Planning with World Model. arXiv 2023, arXiv:2305.14992. [Google Scholar]
- Arsenyan, V.; Bughdaryan, S.; Shaya, F.; Small, K.W.; Shahnazaryan, D. Large Language Models for Biomedical Knowledge Graph Construction: Information extraction from EMR notes. In Proceedings of the 23rd Workshop on Biomedical Natural Language Processing, Bangkok, Thailand, 16 August 2024; Association for Computational Linguistics: Stroudsburg, PA, USA, 2024; pp. 295–317. [Google Scholar] [CrossRef]
- Feng, X.; Wu, X.; Meng, H. Ontology-grounded Automatic Knowledge Graph Construction by LLM under Wikidata Schema. arXiv 2024, arXiv:2412.20942. [Google Scholar]
- Auer, C.; Lysak, M.; Nassar, A.; Dolfi, M.; Livathinos, N.; Vagenas, P.; Ramis, C.B.; Omenetti, M.; Lindlbauer, F.; Dinkla, K.; et al. Docling Technical Report. arXiv 2024, arXiv:2408.09869. [Google Scholar]
- Yang, K.; Swope, A.M.; Gu, A.; Chalamala, R.; Song, P.; Yu, S.; Godil, S.; Prenger, R.; Anandkumar, A. LeanDojo: Theorem Proving with Retrieval-Augmented Language Models. arXiv 2023, arXiv:2306.15626. [Google Scholar]
- Wang, R.; Zhang, J.; Jia, Y.; Pan, R.; Diao, S.; Pi, R.; Zhang, T. TheoremLlama: Transforming General-Purpose LLMs into Lean4 Experts. arXiv 2024, arXiv:2407.03203. [Google Scholar]
- Ballon, M.; Algaba, A.; Ginis, V. The Relationship Between Reasoning and Performance in Large Language Models–o3 (mini) Thinks Harder, Not Longer. arXiv 2025, arXiv:2502.15631. [Google Scholar]
- Snell, C.; Lee, J.; Xu, K.; Kumar, A. Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters. arXiv 2024, arXiv:2408.03314. [Google Scholar]
- Tu, H.; Yu, S.; Saikrishna, V.; Xia, F.; Verspoor, K. Deep Outdated Fact Detection in Knowledge Graphs. In Proceedings of the 2023 IEEE International Conference on Data Mining Workshops (ICDMW), Shanghai, China, 4 December 2023; pp. 1443–1452. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, W.; Wei, Z.; Liu, J. SimKGC: Simple Contrastive Knowledge Graph Completion with Pre-trained Language Models. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics, Dublin, Ireland, 22–27 May 2022; Volume 1, pp. 4281–4294. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, K.; Gan, A.; Tong, S.; Shen, S.; Liu, Q. Enhancing Knowledge Graph Completion with Entity Neighborhood and Relation Context. arXiv 2025, arXiv:2503.23205. [Google Scholar]
- Yuan, D.; Zhou, S.; Chen, X.; Wang, D.; Liang, K.; Liu, X.; Huang, J. Knowledge Graph Completion with Relation-Aware Anchor Enhancement. arXiv 2025, arXiv:2504.06129. [Google Scholar] [CrossRef]
- Satpute, A.; Giessing, N.; Greiner-Petter, A.; Schubotz, M.; Teschke, O.; Aizawa, A.; Gipp, B. Can LLMs Master Math? Investigating Large Language Models on Math Stack Exchange. arXiv 2024, arXiv:2404.00344. [Google Scholar]






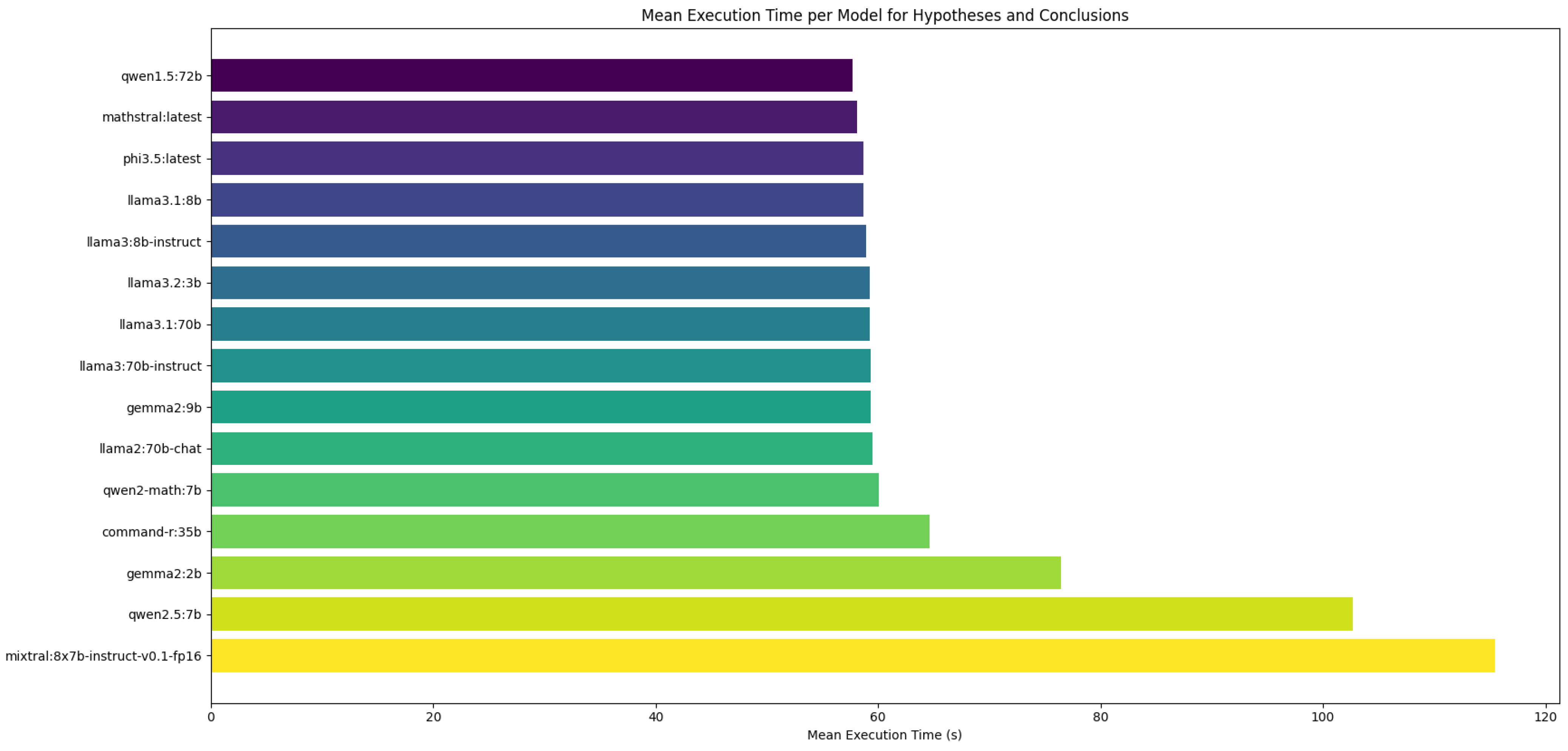
| Model | Accuracy | Recall | Execution Time (s) |
|---|---|---|---|
| Bert-MLM_arXiv-MP-class_zbMath | 0.6281 | 0.6281 | 26.8666 |
| math_pretrained_bert | 0.6377 | 0.6377 | 28.3329 |
| Bert-MLM_arXiv | 0.6706 | 0.6706 | 29.6985 |
| Model | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| gemma2:2B | 0.7415 | 0.7311 | 0.9767 | 0.7415 |
| llama3.2:3B | 0.7281 | 0.7174 | 0.9651 | 0.7281 |
| phi3.5:latest | 0.7466 | 0.7436 | 0.9690 | 0.7466 |
| Model | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| mathstral:latest | 0.7384 | 0.7308 | 0.9690 | 0.7384 |
| qwen2.5:7B | 0.7362 | 0.7291 | 0.9690 | 0.7362 |
| qwen2-math:7B | 0.7380 | 0.7238 | 0.9767 | 0.7380 |
| gemma2:9B | 0.7328 | 0.7257 | 0.9690 | 0.7328 |
| llama3:8B-instruct | 0.7336 | 0.7218 | 0.9690 | 0.7336 |
| llama3.1:8B | 0.7374 | 0.7234 | 0.9767 | 0.7374 |
| Model | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| mixtral:8x7B-instruct-v0.1-fp16 | 0.7317 | 0.7176 | 0.9767 | 0.7317 |
| command-r:35B | 0.7352 | 0.7211 | 0.9767 | 0.7352 |
| llama2:70B-chat | 0.7319 | 0.7203 | 0.9690 | 0.7319 |
| llama3:70B-instruct | 0.7247 | 0.7145 | 0.9535 | 0.7480 |
| llama3.1:70B | 0.7258 | 0.7180 | 0.9535 | 0.7491 |
| qwen1.5:72B | 0.7402 | 0.7261 | 0.9767 | 0.7402 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobo-Santos, A.; Borrego-Díaz, J. Enhancing Mathematical Knowledge Graphs with Large Language Models. Modelling 2025, 6, 53. https://doi.org/10.3390/modelling6030053
Lobo-Santos A, Borrego-Díaz J. Enhancing Mathematical Knowledge Graphs with Large Language Models. Modelling. 2025; 6(3):53. https://doi.org/10.3390/modelling6030053
Chicago/Turabian StyleLobo-Santos, Antonio, and Joaquín Borrego-Díaz. 2025. "Enhancing Mathematical Knowledge Graphs with Large Language Models" Modelling 6, no. 3: 53. https://doi.org/10.3390/modelling6030053
APA StyleLobo-Santos, A., & Borrego-Díaz, J. (2025). Enhancing Mathematical Knowledge Graphs with Large Language Models. Modelling, 6(3), 53. https://doi.org/10.3390/modelling6030053