An Analytical Solution for Energy Harvesting Using a High-Order Shear Deformation Model in Functionally Graded Beams Subjected to Concentrated Moving Loads
Abstract
1. Introduction
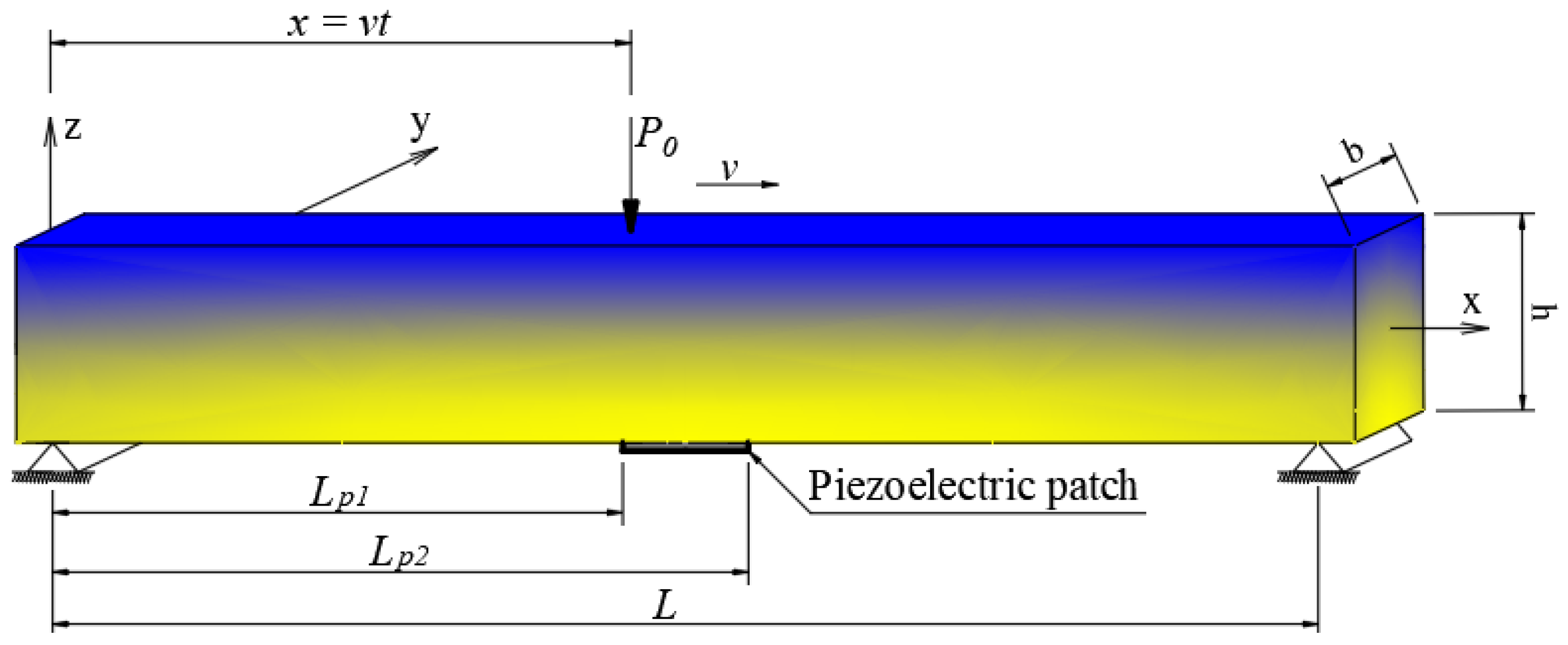
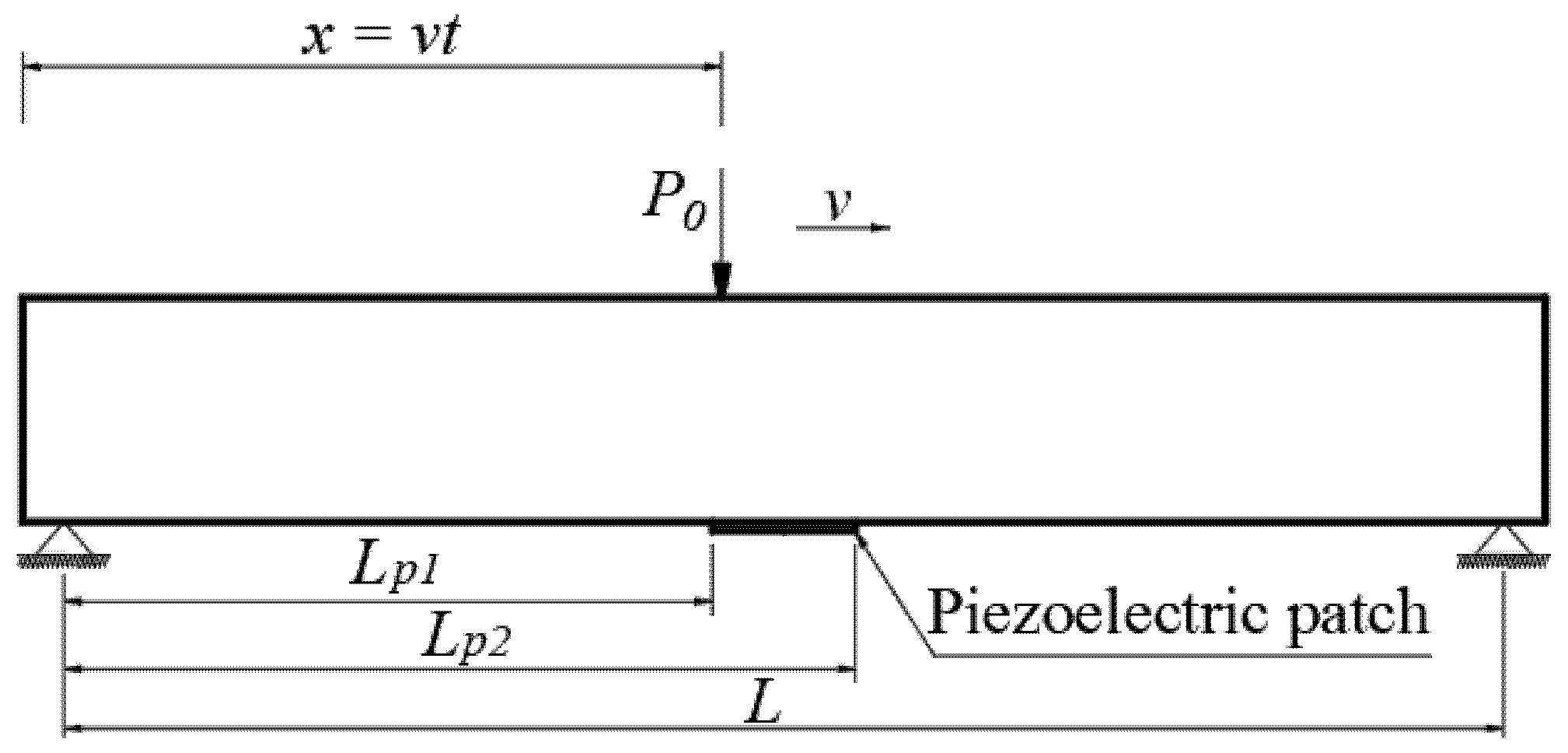
2. Formulation for a Beam
2.1. Basic Equations FGM Beam
2.2. Governing Equations of Motion
3. Method of Solution
4. Piezoelectric Energy Harvesting
5. Numerical Examples
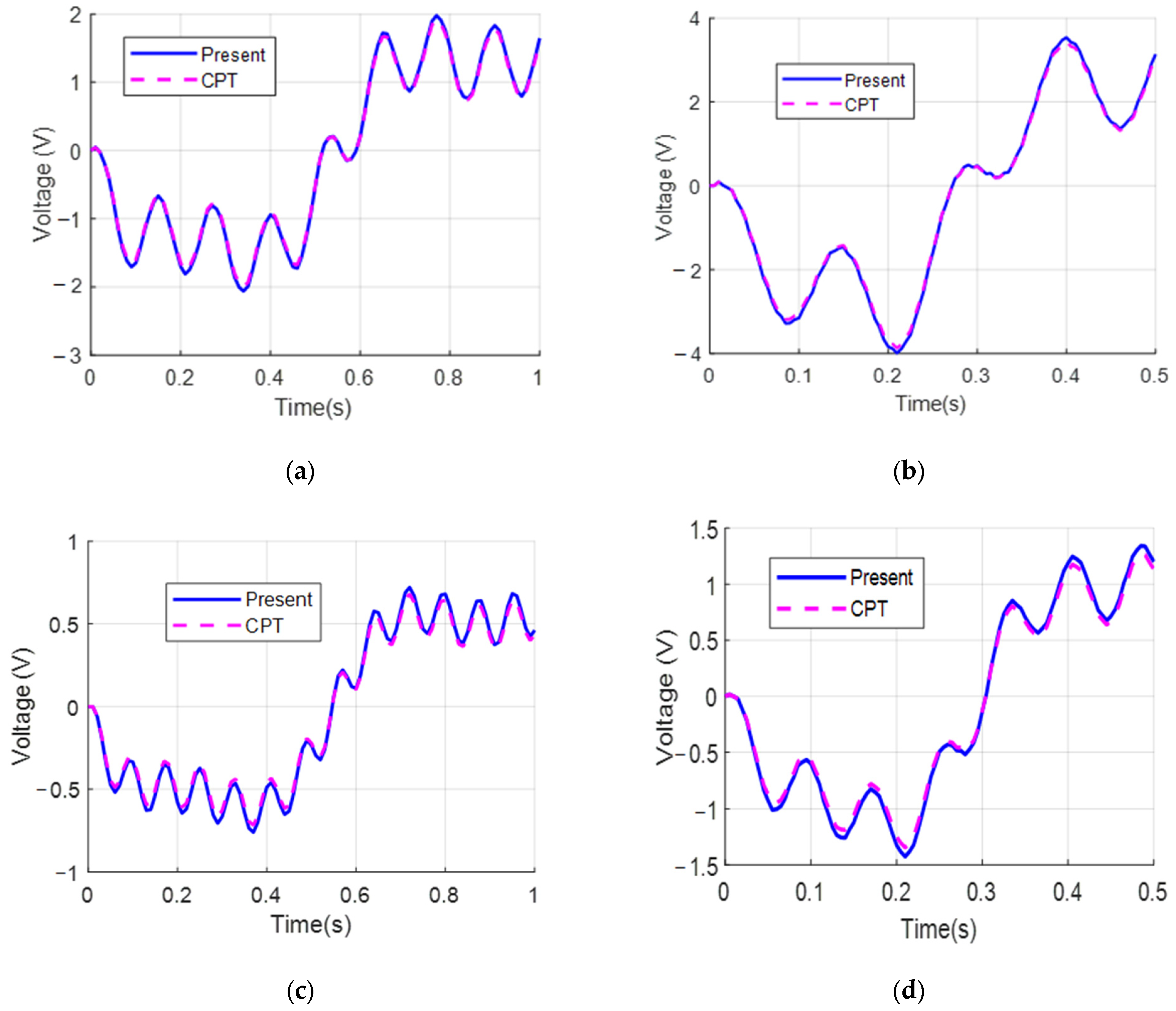
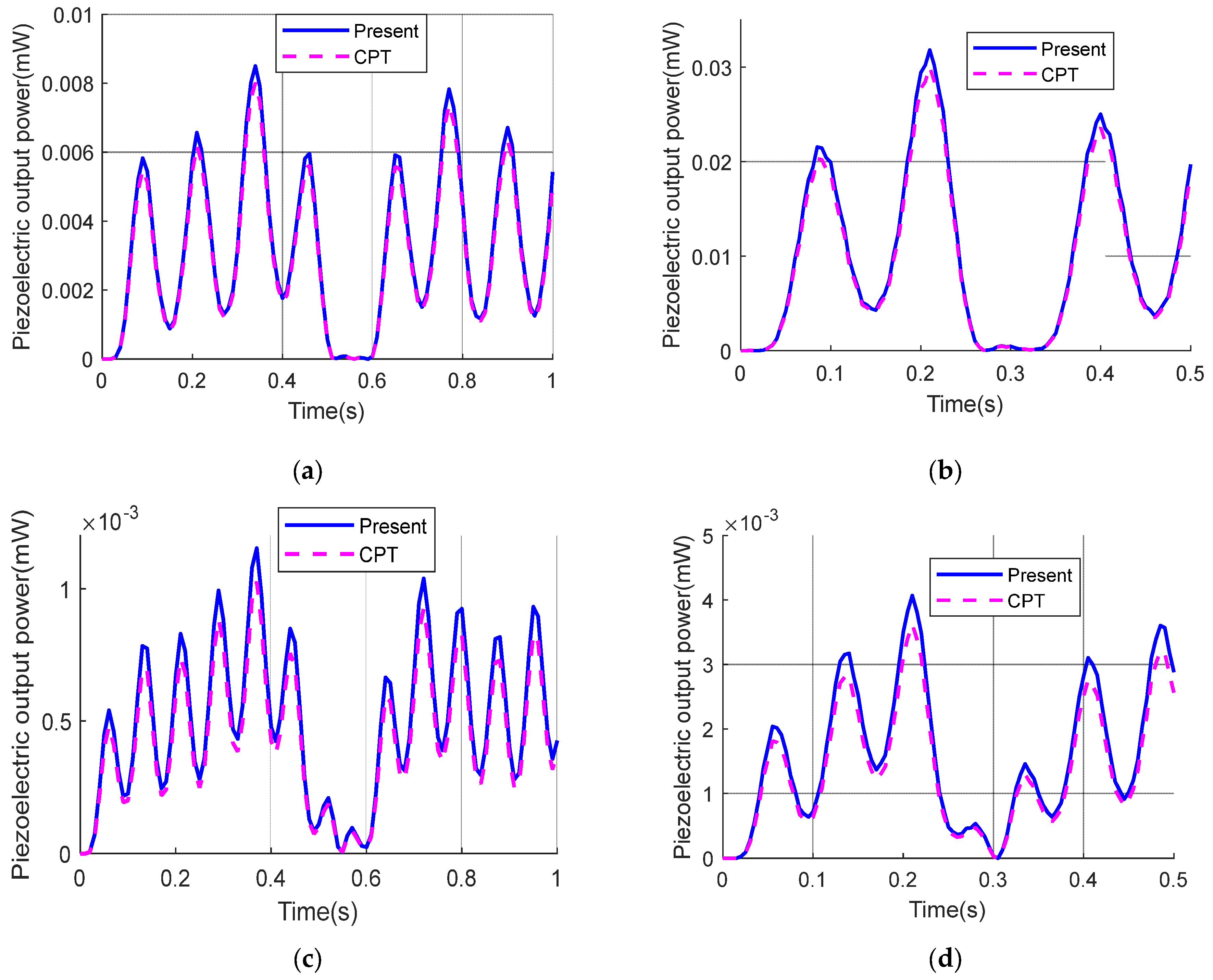
5.1. Verification Example
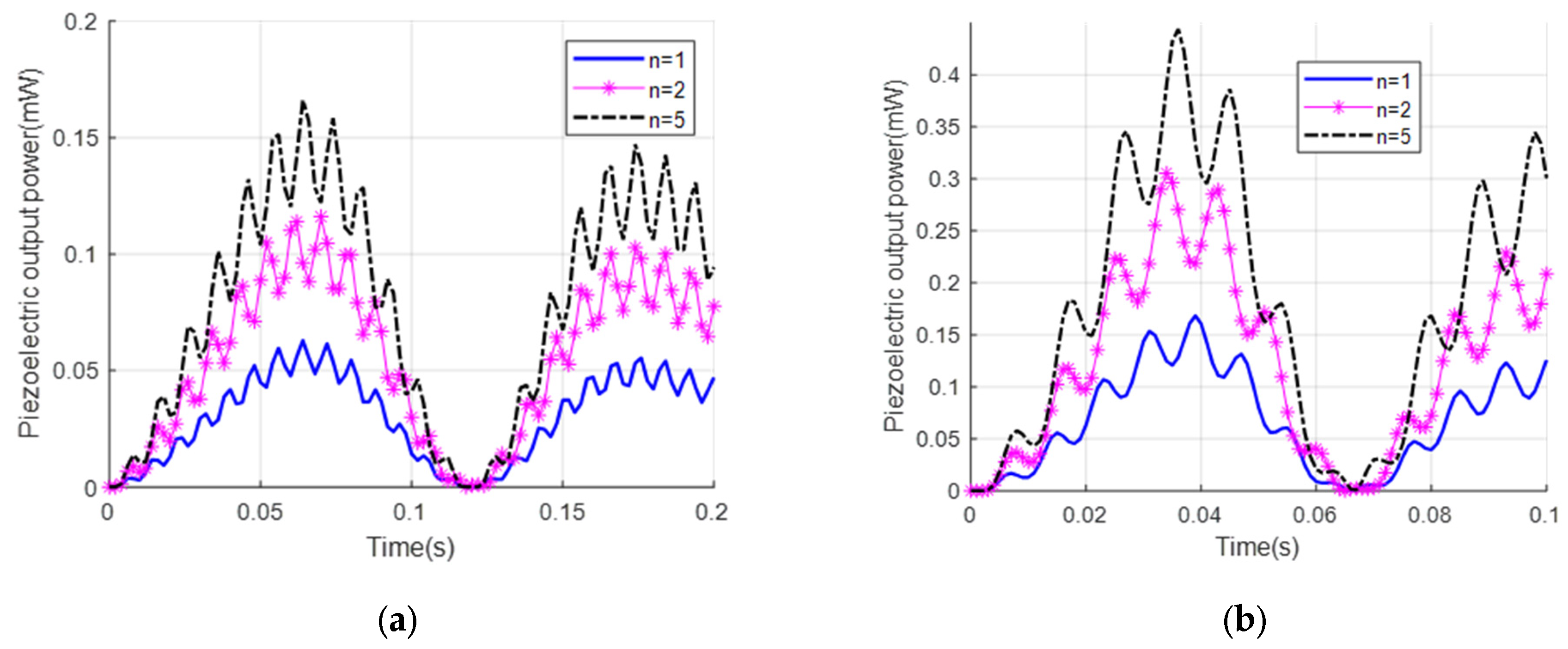
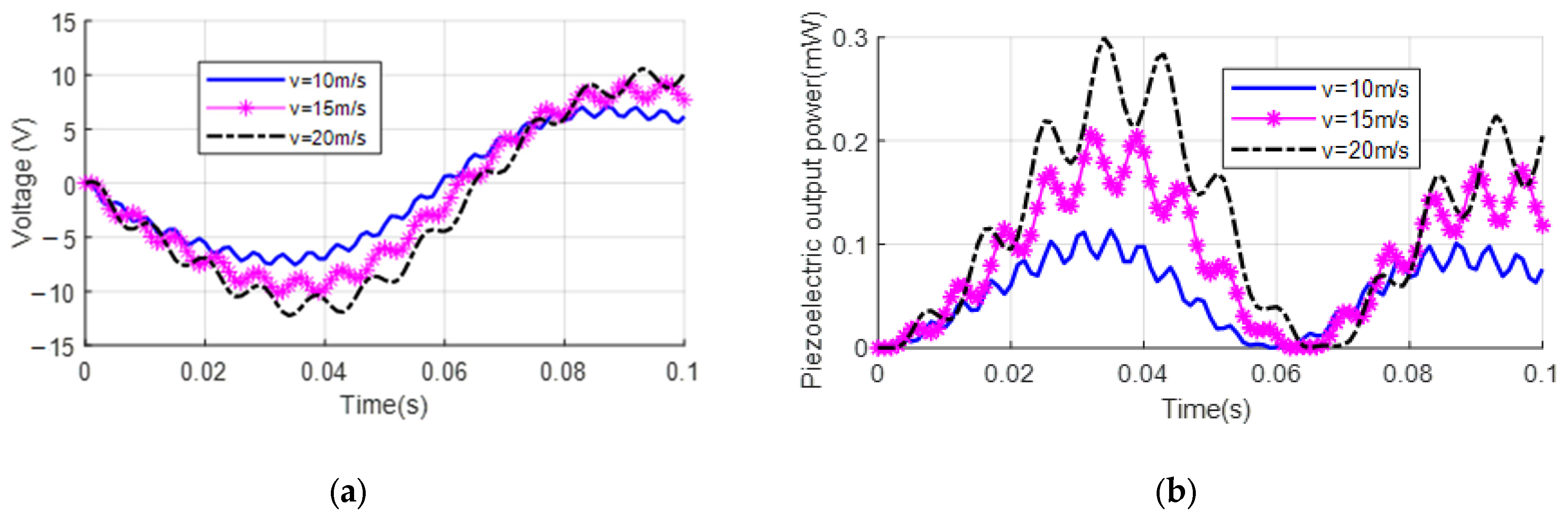
5.2. Investigation of Energy Harvesting from Vibrations of FGM Beams
- Metal phase:
- Ceramic phase:
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. List of Parameters Used in the Analytical Model
| Symbol | Description | Unit |
| x, z | Longitudinal and thickness coordinates | m |
| t | Time variable | s |
| L | Beam length | m |
| b | Beam width | m |
| h | Beam thickness | m |
| u(x,t) | Axial displacement at the neutral axis | m |
| wb(x,t) | Transverse displacement due to bending | m |
| ws(x,t) | Transverse displacement due to shear | m |
| w(x,t) | Total transverse displacement | m |
| ρ(z) | Density varying through thickness | kg/m³ |
| ρm | Density of the metal phase | kg/m³ |
| ρc | Density of the ceramic phase | kg/m³ |
| E(z) | Young’s modulus varying through thickness | Pa |
| Em | Young’s modulus of metal | Pa |
| Ec | Young’s modulus of ceramic | Pa |
| ν | Poisson’s ratio (assumed constant) | – |
| G(z) | Shear modulus varying through thickness | Pa |
| n | Material gradation index | – |
| d31 | Piezoelectric strain constant | C/N |
| e31 | Piezoelectric stress constant | C/m² |
| Permittivity at constant stress in piezoelectric material | F/m | |
| lP | Length of piezoelectric patch | m |
| bp | Width of piezoelectric patch | m |
| hp | Thickness of piezoelectric patch | m |
| Cp | Capacitance of piezoelectric patch | F |
| R | Load resistance (external circuit) | Ω |
| V(t) | Output voltage across the electrodes | V |
| P(t) | Harvested power | W |
| P0 | Magnitude of moving concentrated load | N |
| v | Velocity of moving load | m/s |
| vr | Resonance velocity | m/s |
| x(t) | Instantaneous position of the moving load | m |
| δ(x − vt) | Dirac delta function representing load location | 1/m |
References
- Alshorbagy, A.E.; Eltaher, M.A.; Mahmoud, F.F. Free vibration characteristics of a functionally graded beam by finite element method. Appl. Math. Model. 2011, 35, 412–425. [Google Scholar] [CrossRef]
- Avcar, M.; Mohammed, W.K.M. Free vibration of functionally graded beams resting on Winkler-Pasternak foundation. Arab. J. Geosci. 2018, 11, 232. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Mahesh, V.; Harursampath, D.; Sedighi, H.M. Free vibration of functionally graded beam embedded in Winkler-Pasternak elastic foundation with geometrical uncertainties using symmetric Gaussian fuzzy number. Eur. Phys. J. Plus 2022, 137, 399. [Google Scholar] [CrossRef]
- Lien, P.T.B. Free vibration of porous functionally graded sandwich beams on elastic foundation based ontrigonometric shear deformation theory. Transp. Commun. Sci. J. 2023, 74, 946–961. [Google Scholar] [CrossRef]
- Ninh, V.T.A. Fundamental frequencies of bidirectional functionally graded sandwich beams partially supported by foundation using different beam theories. Transp. Commun. Sci. J. 2021, 72, 452–467. [Google Scholar] [CrossRef]
- Aydin, K. Free vibration of functionally graded beams with arbitrary number of surface cracks. Eur. J. Mech.-A/Solids 2013, 42, 112–124. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Ananthapuvirajah, A. Free vibration of functionally graded beams and frameworks using the dynamic stiffness method. J. Sound Vib. 2018, 422, 34–47. [Google Scholar] [CrossRef]
- Ha, L.T.; Khue, N.T.K. Free vibration of functionally graded porous nano beams. Transp. Commun. Sci. J. 2019, 70, 95–103. [Google Scholar] [CrossRef][Green Version]
- Belarbi, M.-O.; Khechai, A.; Houari, M.S.A.; Bessaim, A.; Hirane, H.; Garg, A. Free Vibration Behavior of Sandwich FGM Beams: Parametric and Uncertainty Analysis. J. Vib. Eng. Technol. 2024, 12, 883–905. [Google Scholar] [CrossRef]
- Lakhdar, K.; Sadoun, M.; Addou, F.Y.; Bourada, F.; Bousahla, A.A.; Tounsi, A.; Khedher, K.M.; Tounsi, A. Free vibrational characteristics of various imperfect FG beam via a novel integral Timoshenko’s theory. Acta Mech. 2024, 235, 6287–6304. [Google Scholar] [CrossRef]
- Wei, D.; Liu, Y.; Xiang, Z. An analytical method for free vibration analysis of functionally graded beams with edge cracks. J. Sound Vib. 2012, 331, 1686–1700. [Google Scholar] [CrossRef]
- Fatehi, P.; Farid, M. Piezoelectric Energy Harvesting from Nonlinear Vibrations of Functionally Graded Beams: Finite-Element Approach. J. Eng. Mech. 2019, 145, 04018116. [Google Scholar] [CrossRef]
- Alshenawy, R.; Sahmani, S.; Safaei, B.; Elmoghazy, Y.; Al-Alwan, A.; Nuwairan, M.A. Surface stress effect on nonlinear dynamical performance of nanobeam-type piezoelectric energy harvesters via meshless collocation technique. Eng. Anal. Bound. Elem. 2023, 152, 104–119. [Google Scholar] [CrossRef]
- Amini, Y.; Emdad, H.; Farid, M. Finite element modeling of functionally graded piezoelectric harvesters. Compos. Struct. 2015, 129, 165–176. [Google Scholar] [CrossRef]
- Keshmiri, A.; Wu, N.; Wang, Q. A new nonlinearly tapered FGM piezoelectric energy harvester. Eng. Struct. 2018, 173, 52–60. [Google Scholar] [CrossRef]
- Rafiee, M.; He, X.; Liew, K. Nonlinear analysis of piezoelectric nanocomposite energy harvesting plates. Smart Mater. Struct. 2014, 23, 065001. [Google Scholar] [CrossRef]
- Brusa, E.; Carrera, A.; Delprete, C. A Review of Piezoelectric Energy Harvesting: Materials, Design, and Readout Circuits. Actuators 2023, 12, 457. [Google Scholar] [CrossRef]
- Du, W.; Xiang, Z.; Qiu, X. Stochastic analysis of an acoustic black hole piezoelectric energy harvester under Gaussian white noise excitation. Appl. Math. Model. 2024, 131, 22–32. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, W.; Zhou, Z.; Zhu, P.; Du, W. Piezomagnetoelastic energy harvesting from bridge vibrations using bi-stable characteristics. Energy 2023, 263, 125859. [Google Scholar] [CrossRef]
- Hassan, E.; Kouritem, S.A.; Amer, F.Z.; Mubarak, R.I. Acoustic energy harvesting using an array of piezoelectric cantilever plates for railways and highways environmental noise. Ain Shams Eng. J. 2023, 15, 102461. [Google Scholar] [CrossRef]
- Adoukatl, C.; Ntamack, G.E.; Azrar, L. High order analysis of a nonlinear piezoelectric energy harvesting of a piezo patched cantilever beam under parametric and direct excitations. Mech. Adv. Mater. Struct. 2023, 30, 4835–4861. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T. A semi-analytical model for energy harvesting of flexural wave propagation on thin plates by piezoelectric composite beam resonators. Mech. Syst. Signal Process. 2021, 147, 107137. [Google Scholar] [CrossRef]
- Lu, Z.-Q.; Chen, J.; Ding, H.; Chen, L.-Q. Two-span piezoelectric beam energy harvesting. Int. J. Mech. Sci. 2020, 175, 105532. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, C.; Lai, L.; Dong, X.; Li, Y. Design, Manufacture and Test of Piezoelectric Cantilever-Beam Energy Harvesters with Hollow Structures. Micromachines 2021, 12, 1090. [Google Scholar] [CrossRef]
- Amini, Y.; Heshmati, M.; Fatehi, P.; Habibi, S.E. Piezoelectric energy harvesting from vibrations of a beam subjected to multi-moving loads. Appl. Math. Model. 2017, 49, 1–16. [Google Scholar] [CrossRef]
- Paknejad, A.; Rahimi, G.; Farrokhabadi, A.; Khatibi, M.M. Analytical solution of piezoelectric energy harvester patch for various thin multilayer composite beams. Compos. Struct. 2016, 154, 694–706. [Google Scholar] [CrossRef]
- Erturk, A. Piezoelectric energy harvesting for civil infrastructure system applications: Moving loads and surface strain fluctuations. J. Intell. Mater. Syst. Struct. 2011, 22, 1959–1973. [Google Scholar] [CrossRef]
- Kumar, A.; Ansari, M.N.M.; Ibrahim, S.M.; Thomas, P.; Vaish, R. Functionally graded piezoelectric energy harvester: A numerical study. Electronics 2022, 11, 2595. [Google Scholar] [CrossRef]
- Khiem, N.T.; Huan, D.T.; Hieu, T.T. Vibration of Cracked FGM Beam with Piezoelectric Layer Under Moving Load. J. Vib. Eng. Technol. 2023, 11, 755–769. [Google Scholar] [CrossRef]
- Dehkordi, S.F.; Beni, Y.T. On the size-dependent electromechanical layered beam-type porous functionally graded flexoelectric energy harvesters. Eng. Anal. Bound. Elem. 2024, 165, 105801. [Google Scholar] [CrossRef]
- Ray, M.C.; Jha, B.K. Exact solutions for bimorph cross-ply and antisymmetric angle-ply plate piezoelectric energy harvesters. Compos. Struct. 2022, 286, 115261. [Google Scholar] [CrossRef]
- Song, J.; Sun, G.; Zeng, X.; Li, X.; Bai, Q.; Zheng, X. Piezoelectric energy harvester with double cantilever beam undergoing coupled bending-torsion vibrations by width-splitting method. Sci. Rep. 2022, 12, 583. [Google Scholar] [CrossRef] [PubMed]
- Bendine, K.; Junho Pereira, J.L.; Ferreira Gomes, G. Energy harvesting enhancement of nonuniform functionally graded piezoelectric beam using artificial neural networks and Lichtenberg algorithm. Structures 2023, 57, 105271. [Google Scholar] [CrossRef]
- Mousavi, M.; Ziaei-Rad, S.; Karimi, A.H. Piezoelectric-based energy harvesting from bridge vibrations subjected to moving successive vehicles by functionally graded cantilever beams–Theoretical and experimental investigations. Mech. Syst. Signal Process. 2023, 188, 110015. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Patel, H.G. A two variable refined plate theory for orthotropic plate analysis. Int. J. Solids Struct. 2006, 43, 6783–6799. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. Free vibration of laminated composite plates using two variable refined plate theory. Int. J. Mech. Sci. 2010, 52, 626–633. [Google Scholar] [CrossRef]
- Tounsi, A.; Houari, M.S.A.; Benyoucef, S.; Adda Bedia, E.A. A refined trigonometric shear deformation theory for thermoelastic bending of functionally graded sandwich plates. Aerosp. Sci. Technol. 2013, 24, 209–220. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Vo, T.P.; Thai, H.-T.; Nguyen, T.-K.; Inam, F. Static and vibration analysis of functionally graded beams using refined shear deformation theory. Meccanica 2014, 49, 155–168. [Google Scholar] [CrossRef]
- Khdeir, A.A.; Reddy, J.N. Exact-Solutions for the Transient-Response of Symmetric Cross-Ply Laminates Using a Higher-Order Plate-Theory. Compos. Sci. Technol. 1989, 34, 205–224. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting: Modelling and Application; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Dan, D.S. An investigation of energy harvesting from vibrations of beams subjected to concentrated moving loads using analytical methods. Viet Nam Bridge Road Mag. 2024, 28, 13–17. [Google Scholar]
- Benyoucef, S.; Mechab, I.; Tounsi, A.; Fekrar, A.; Ait Atmane, H.; Adda Bedia, E.A. Bending of thick functionally graded plates resting on Winkler–Pasternak elastic foundations. Mech. Compos. Mater. 2010, 46, 425–434. [Google Scholar] [CrossRef]


| Description | Parameter | Numerical Value |
|---|---|---|
| Permittivity component | ||
| Plane stress piezoelectric stress constant | ||
| High of piezoceramic patch | 0.0002 (m) | |
| Width of piezoceramic patch | 0.05 (m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dao, S.-D.; Nguyen, D.-D.; Nguyen, T.-H.; Nguyen, N.-L. An Analytical Solution for Energy Harvesting Using a High-Order Shear Deformation Model in Functionally Graded Beams Subjected to Concentrated Moving Loads. Modelling 2025, 6, 55. https://doi.org/10.3390/modelling6030055
Dao S-D, Nguyen D-D, Nguyen T-H, Nguyen N-L. An Analytical Solution for Energy Harvesting Using a High-Order Shear Deformation Model in Functionally Graded Beams Subjected to Concentrated Moving Loads. Modelling. 2025; 6(3):55. https://doi.org/10.3390/modelling6030055
Chicago/Turabian StyleDao, Sy-Dan, Dang-Diem Nguyen, Trong-Hiep Nguyen, and Ngoc-Lam Nguyen. 2025. "An Analytical Solution for Energy Harvesting Using a High-Order Shear Deformation Model in Functionally Graded Beams Subjected to Concentrated Moving Loads" Modelling 6, no. 3: 55. https://doi.org/10.3390/modelling6030055
APA StyleDao, S.-D., Nguyen, D.-D., Nguyen, T.-H., & Nguyen, N.-L. (2025). An Analytical Solution for Energy Harvesting Using a High-Order Shear Deformation Model in Functionally Graded Beams Subjected to Concentrated Moving Loads. Modelling, 6(3), 55. https://doi.org/10.3390/modelling6030055






