Modeling and Experimental Verification of Plasma Jet Electromagnetic Signals
Abstract
:1. Introduction
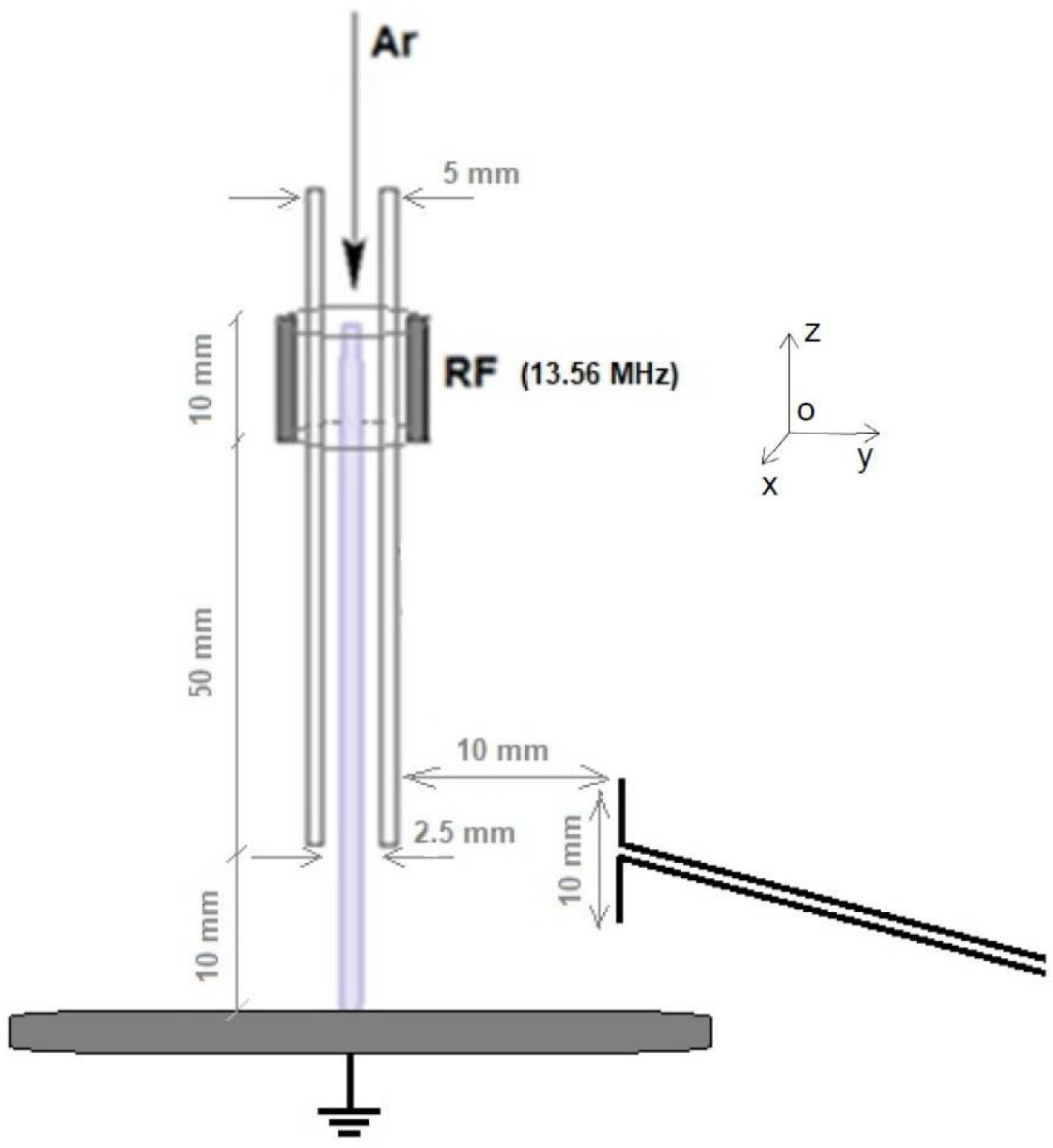
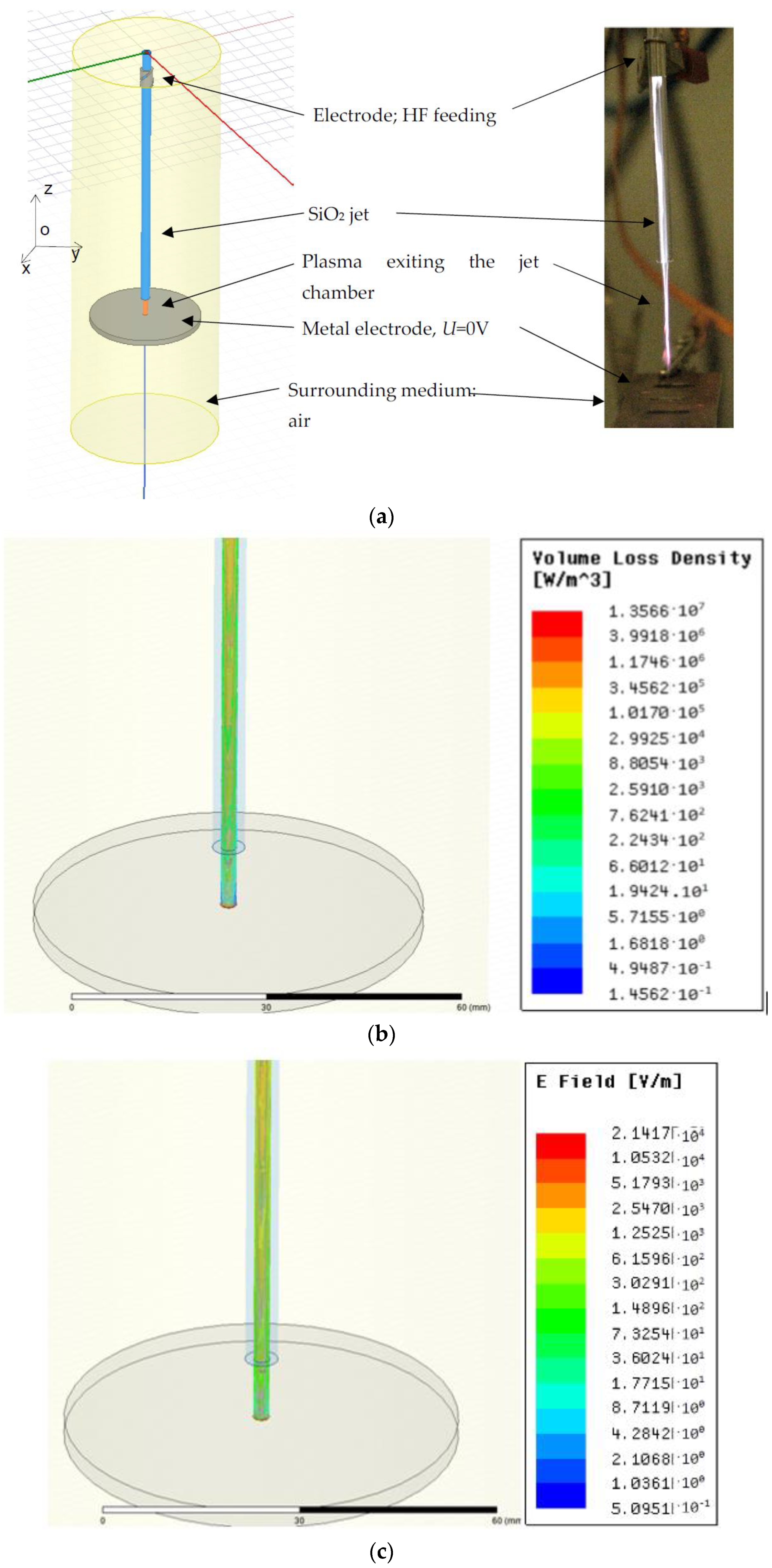
2. Numerical Model with Distributed Parameters
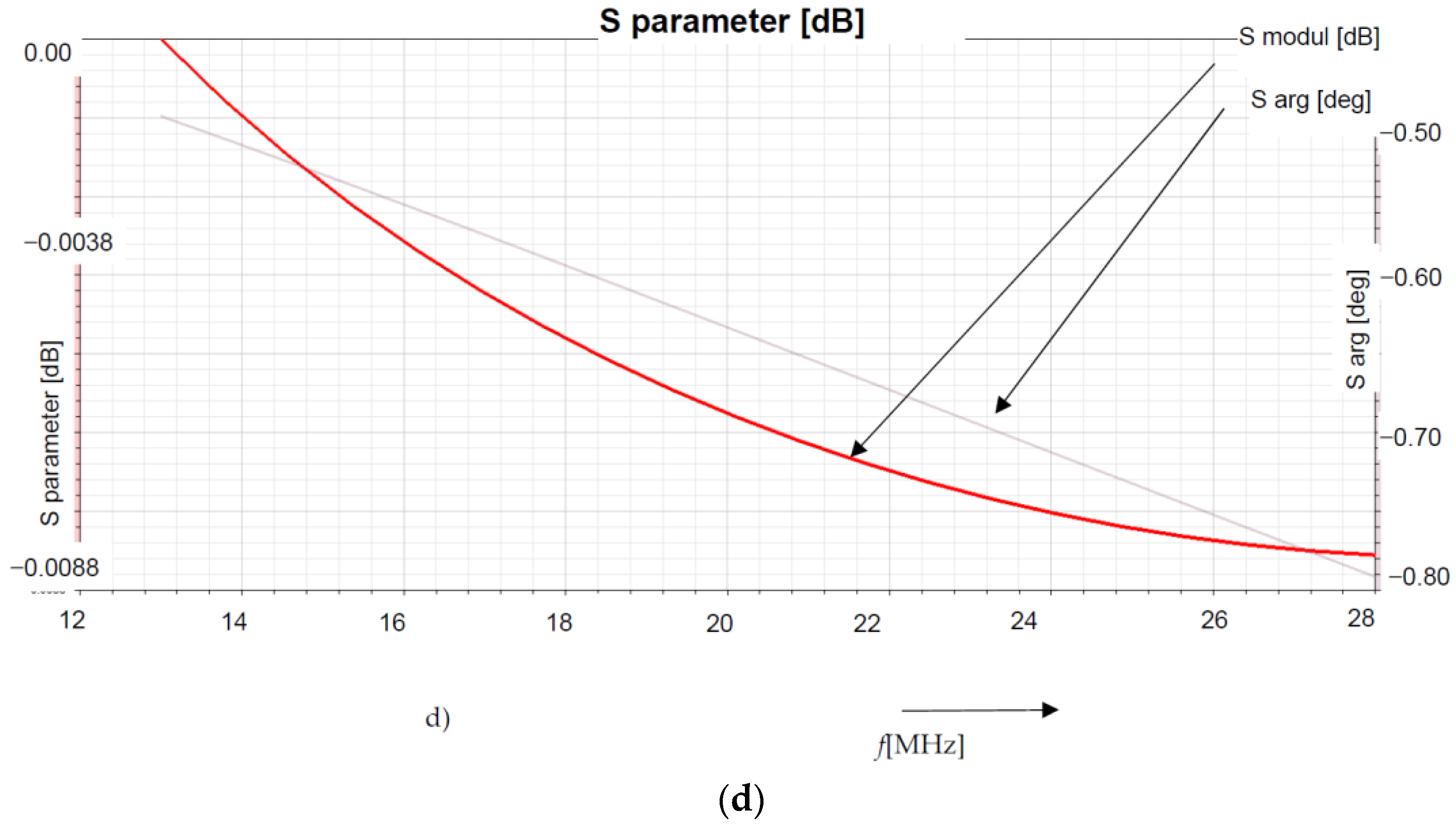
3. Numerical Model with Concentrated Parameters
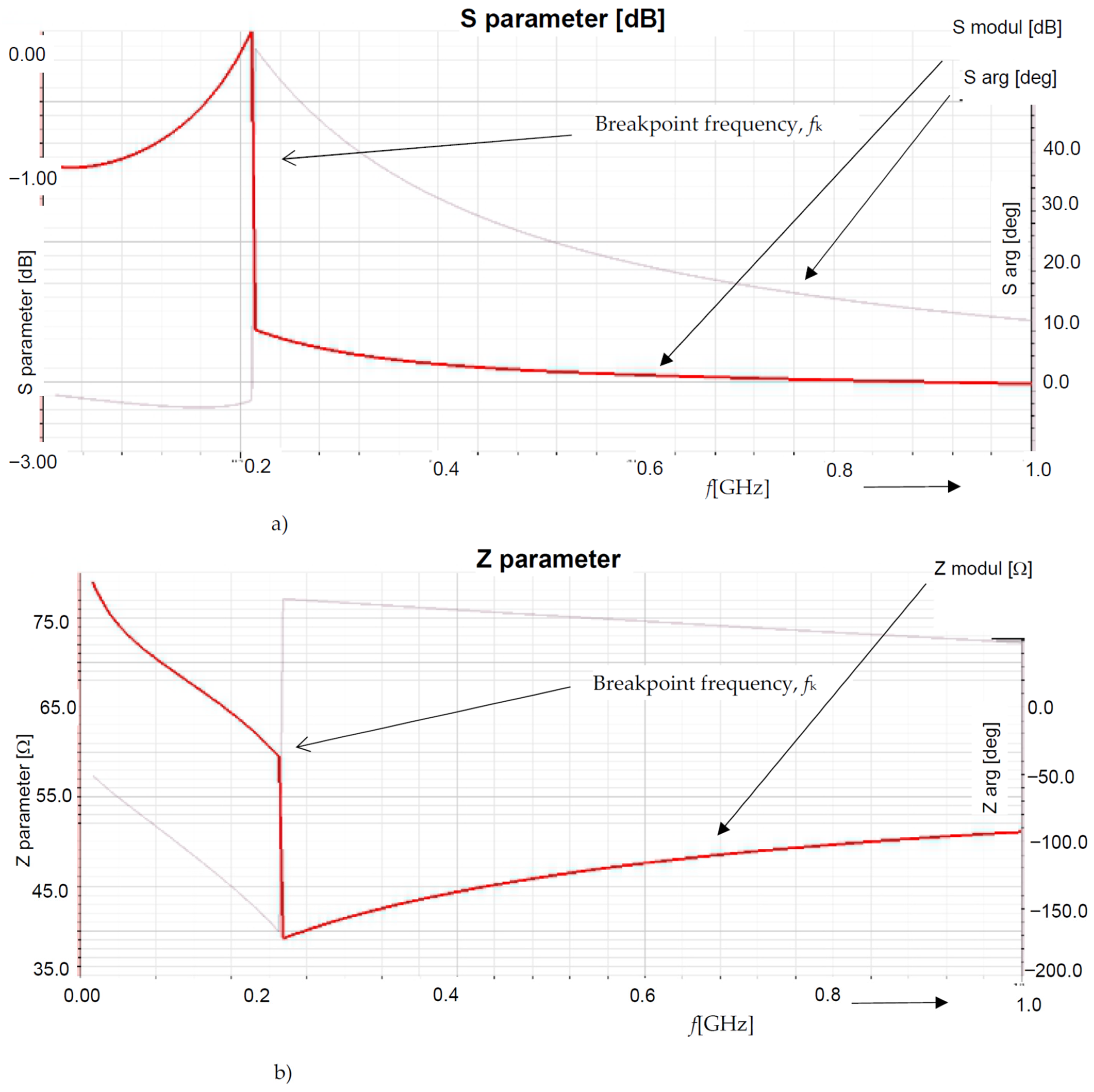
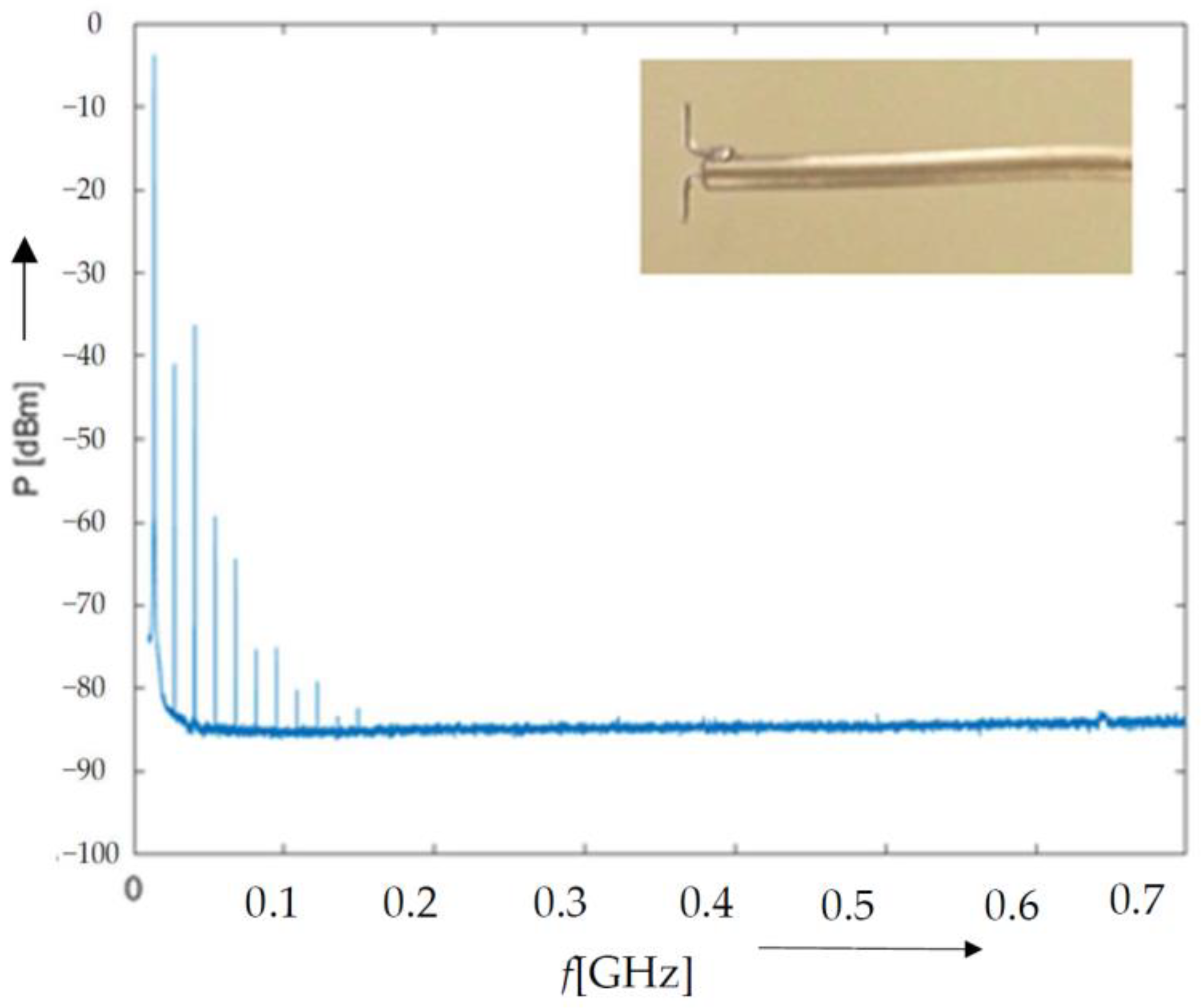
4. Comparing the Model and the Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ishikawa, K. Plasma diagnostics. In Cold Plasma in Food and Agriculture: Fundamentals and Applications; Academic Press: Cambridge, MA, USA, 2016; pp. 117–141. [Google Scholar] [CrossRef]
- Liao, L.; He, J. Discussion on laser-induced plasma diagnostics under condition of optically thick. Optik 2016, 127, 4878–4880. [Google Scholar] [CrossRef]
- Donne, A.J.H. Introduction to plasma diagnostics. Fusion Technol. 1994, 25 Pt 2, 291–296. [Google Scholar]
- Brown, N.P.; Steinberg, A.M.; Deibel, J.A.; Walker, M.L.R. Assessment of the capability of terahertz time-domain spectroscopy as a plasma diagnostic. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Virtual Event, 24–26 August 2020; pp. 1–20. [Google Scholar] [CrossRef]
- Fiala, P.; Drexler, P.; Nespor, D.; Szabo, Z.; Mikulka, J.; Polivka, J. The evaluation of noise spectroscopy tests. Entropy 2016, 18, 443. [Google Scholar] [CrossRef] [Green Version]
- Fiala, P.; Jirku, T.; Drexler, P.; Dohnal, P. Detection of partial discharge inside of HV transformer, modeling, sensors and measurement. In Proceedings of the PIERS 2010 Cambridge—Progress in Electromagnetics Research Symposium, Cambridge, MA, USA, 5–8 July 2010; pp. 1013–1016. [Google Scholar]
- Myška, R.; Drexler, P. Simulation and verification of methods for partial discharge source localization. In Proceedings of the Progress in Electromagnetics Research Symposium, Kuala Lumpur, Malaysia, 27–30 March 2012; pp. 704–708. [Google Scholar]
- Drexler, P.; Fiala, P. Methods for high-power em pulse measurement. IEEE Sens. J. 2007, 7, 1006–1011. [Google Scholar] [CrossRef]
- Guo, Y.; Guan, Y.; Xiang, Y. Diagnostic value of high-frequency color doppler in plasma cell mastitis. J. Dalian Med. Univ. 2014, 36, 556–558. [Google Scholar] [CrossRef]
- Liu, Y.; Morita, S.; Huang, X.; Oishi, T.; Goto, M.; Zhang, H. Component investigation of ionization stages on tungsten unresolved transition array spectra for plasma diagnostics based on space-resolved extreme-ultra violet spectroscopy in large helical device. J. Appl. Phys. 2017, 122, 233301. [Google Scholar] [CrossRef]
- Norberg, S.A.; Johnsen, E.; Kushner, M.J. Helium atmospheric pressure plasma jets touching dielectric and metal surfaces. J. Appl. Phys. 2015, 118, 013301. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; Wiley: New York, NY, USA, 1941; pp. 1–640. [Google Scholar]
- Kikuchi, H. Electrohydrodynamics in Dusty and Dirty Plasmas, Gravito-Electrodynamics and EHD; Kluwer: Boston, MA, USA, 2001; pp. 1–207. [Google Scholar]
- ANSYS. Ansys Multiphysics Manuals; ANSYS: Canonsburg, PA, USA, 2020; Available online: https://www.ansys.com/ (accessed on 19 January 2022).
- Weisstein, E.W. Galerkin Method; MathWorld. 2015. Available online: https://mathworld.wolfram.com/GalerkinMethod.html (accessed on 19 January 2022).
- Bartusek, K.; Drexler, P.; Fiala, P.; Kadlec, R.; Kubasek, R. Magnetoinductive Lens for Experimental Mid-field MR Tomograph. In Proceedings of the Piers 2010 Cambridge Progress in Electromagnetics Research Symposium, Cambridge, MA, USA, 5–8 July 2010; Volume 1–2, pp. 1047–1050. [Google Scholar]
- Zhang, D.; Ranjan, B.; Tanaka, T.; Sugioka, K. Multiscale hierarchical micro/nanostructures created by femtosecond laser ablation in liquids for polarization-dependent broadband antireflection. Nanomaterials 2020, 10, 1573. [Google Scholar] [CrossRef]
- Haňka, L. Teorie Elektromagnetického Pole; paperback SNTL: Praha, Czech Republic, 1971. [Google Scholar]
- Madrova, T. Supravodivost ve Čtvrtém Skupenství (Superconductivity in the Fourth State). Master’s Thesis, Brno Univerzity of Technology, Brno, Czech Republic, 2020; pp. 1–88. [Google Scholar]
- Kousal, J.; Pokorná, J.; Brablec, A.; Slavíček, P.; Klíma, M.; Janča, J. Electron concetration in atmospheric non-isotermal plasma jet. Czechoslov. J. Phys. 2002, 52, 571–575. [Google Scholar]
- Drexler, P.; Fiala, P.; Klima, M.; Gescheidtova, E.; Zajickova, L. A plasma chamber: Electromagnetic modeling and experiments. In Proceedings of the Progress in Electromagnetics Research Symposium, Rome, Italy, 17–20 June 2019; pp. 2570–2573. [Google Scholar] [CrossRef]
- Fiala, P.; Bartusek, K.; Steinbauer, M. A novel hypothesis for quantum physics, model with telegraphs equation. In Proceedings of the Progress in Electromagnetics Research Symposium, Hangzhou, China, 24–28 March 2008; Volume 2, pp. 1189–1192. [Google Scholar]
- Drexler, P.; Fiala, P. Utilization of faraday mirror in fiber optic current sensors. Radioengineering 2008, 17, 2.101–2.107. [Google Scholar]
- Fiala, P.; Drexler, P.; Nespor, D. Principal tests and verification of a resonance-based solar harvester utilizing micro/nano technology. Microsyst. Technol. 2014, 20, 845–860. [Google Scholar] [CrossRef]
- Urban, R.; Drexler, P.; Fiala, P.; NeŠpor, D. Numerical model of a large periodic structure. In Proceedings of the Progress in Electromagnetics Research Symposium, Guangzhou, China, 25–28 August 2014; pp. 2350–2354. [Google Scholar]
- Bartusek, K.; Kubasek, R.; Fiala, P. Determination of pre-emphasis constants for eddy current reduction. Meas. Sci. Technol. 2010, 21, 105601. [Google Scholar] [CrossRef]
- Steinbauer, M.; Pernica, R.; Zukal, J.; Kadlec, R.; Bachorec, T.; Fiala, P. Modeling electromagnetic nanostructures and experimenting with nanoelectric elements to form periodic structures. Inform. Autom. Pomiary W Gospod. I Ochr. Środowiska 2020, 10, 4–14. [Google Scholar] [CrossRef]
- Klíma, M.; Slavíček, P.; Šíra, M.; Čižmár, T.; Vaněk, P. HF plasma pencil and DC diaphragm discharge in liquids—diagnostics and application. Czechoslov. J. Phys. 2006, 56, B1051–B1056. [Google Scholar] [CrossRef]
- Slavíček, P.; Brablec, A.; Kapička, V.; Klíma, M.; Šíra, M. Longitudinal emission diagnostics of plasma channel in rf barrier torch discharge. Acta Phys. Slovaca 2005, 55, 573–576. [Google Scholar]
- Fiala, P.; Machac, J.; Polivka, J. Microwave noise field behaves like white light. Prog. Electromagn. Res. 2011, 111, 311–330. [Google Scholar]
- Fiala, P.; Szabó, Z.; Friedl, M. EMHD models respecting relativistic processes of trivial geometries. In Proceedings of the Progress in Electromagnetics Research Symposium, Marrakesh, Morocco, 20–23 March 2011; pp. 95–98. [Google Scholar]
- Steinbauer, M.; Fiala, P.; Szabo, Z.; Bartusek, K. Experiments with accuracy of the air ion field measurement. Adv. Electr. Electron. Eng. 2008, 8, 276–279. [Google Scholar]
- Drexler, P.; Čáp, M.; Fiala, P.; Steinbauer, M.; Kadlec, R.; Kaška, M.; Kočiš, L. A sensor system for detecting and localizing partial discharges in power transformers with improved immunity to interferences. Sensors 2019, 19, 923. [Google Scholar] [CrossRef] [Green Version]
- Fiala, P. Pulse-powered virtual cathode oscillator. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 1046–1053. [Google Scholar] [CrossRef]
- Fiala, P.; Sadek, V.; Kriz, T. Numerical modeling of electromagnetic field a tornado. In Proceedings of the Progress in Electromagnetics Research Symposium, Hangzhou, China, 24–28 March 2008; Volume 2, pp. 1180–1184. [Google Scholar]
- Moisan, M.; Pelltier, J. Microwave Excited Plasmas; Elsevier: Amsterdam, The Netherlands, 1992; ISBN 0-444-88815-2. [Google Scholar]
- AlShunaifi, I.A.; Elaissi, S.; Ghiloufi, I.; Alterary, S.S.; Alharbi, A.A. Modelling of a Non-Transferred Plasma Torch Used for Nano-Silica Powders Production. Appl. Sci. 2021, 11, 9842. [Google Scholar] [CrossRef]
- Vinoth Kumar, S.H.B.; Ibaceta-Jaña, J.; Maticuic, N.; Kowiorski, K.; Zelt, M.; Gernert, U.; Lipińska, L.; Szyszka, B.; Schlatmann, R.; Hartmann, U.; et al. Applicability of Atmospheric Pressure Plasma Jet (APPJ) Discharge for the Reduction in Graphene Oxide Films and Synthesis of Carbon Nanomaterials. C 2021, 7, 71. [Google Scholar] [CrossRef]
- Demetriades, S.T.; Argyropoulos, G.S. Ohm’s law in multicomponent nonisothermal plasmas with temperature and pressure gradients. Phys. Fluids 1966, 9, 2136–2149. [Google Scholar] [CrossRef]
- Taccogna, F.; Dilecce, G. Non-equilibrium in low-temperature plasmas. Eur. Phys. J. D 2016, 70, 251. [Google Scholar] [CrossRef]
- Kodanova, S.K.; Issanova, M.K.; Amirov, S.M.; Ramazanov, T.S.; Tikhonov, A.; Moldabekov, Z.A. Relaxation of non-isothermal hot dense plasma parameters. Matter Radiat. Extrem. 2018, 3, 40–49. [Google Scholar] [CrossRef] [Green Version]
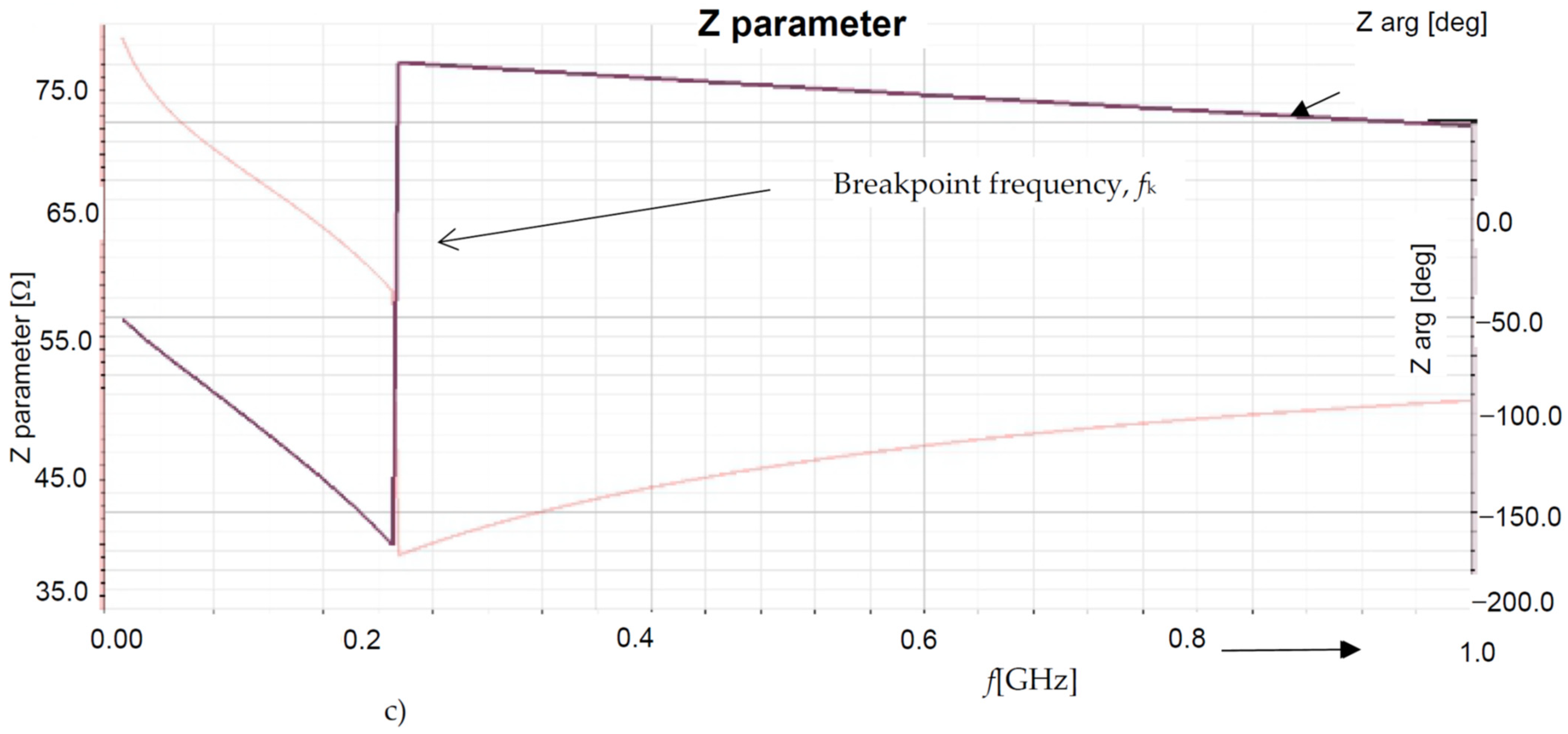

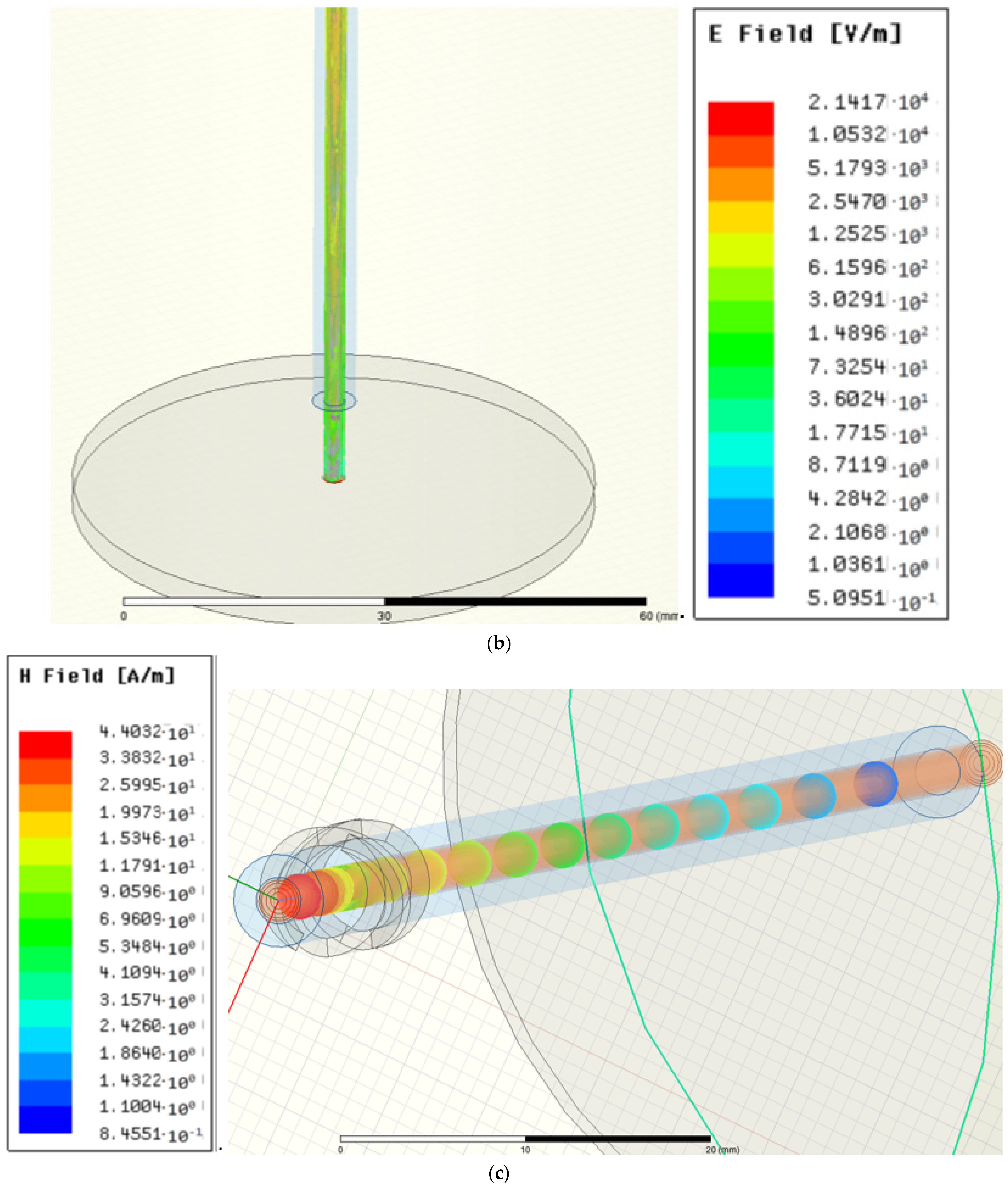
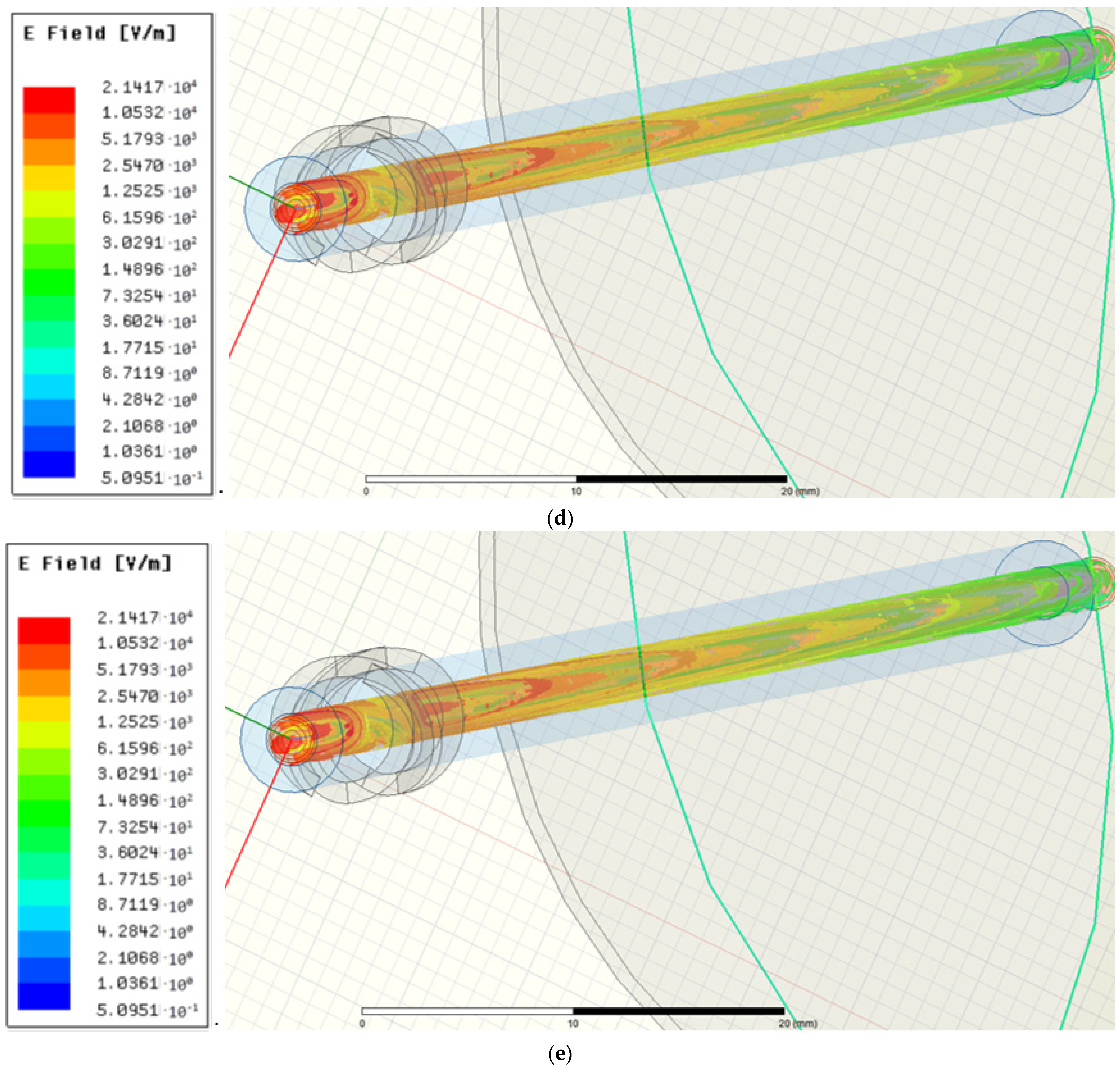
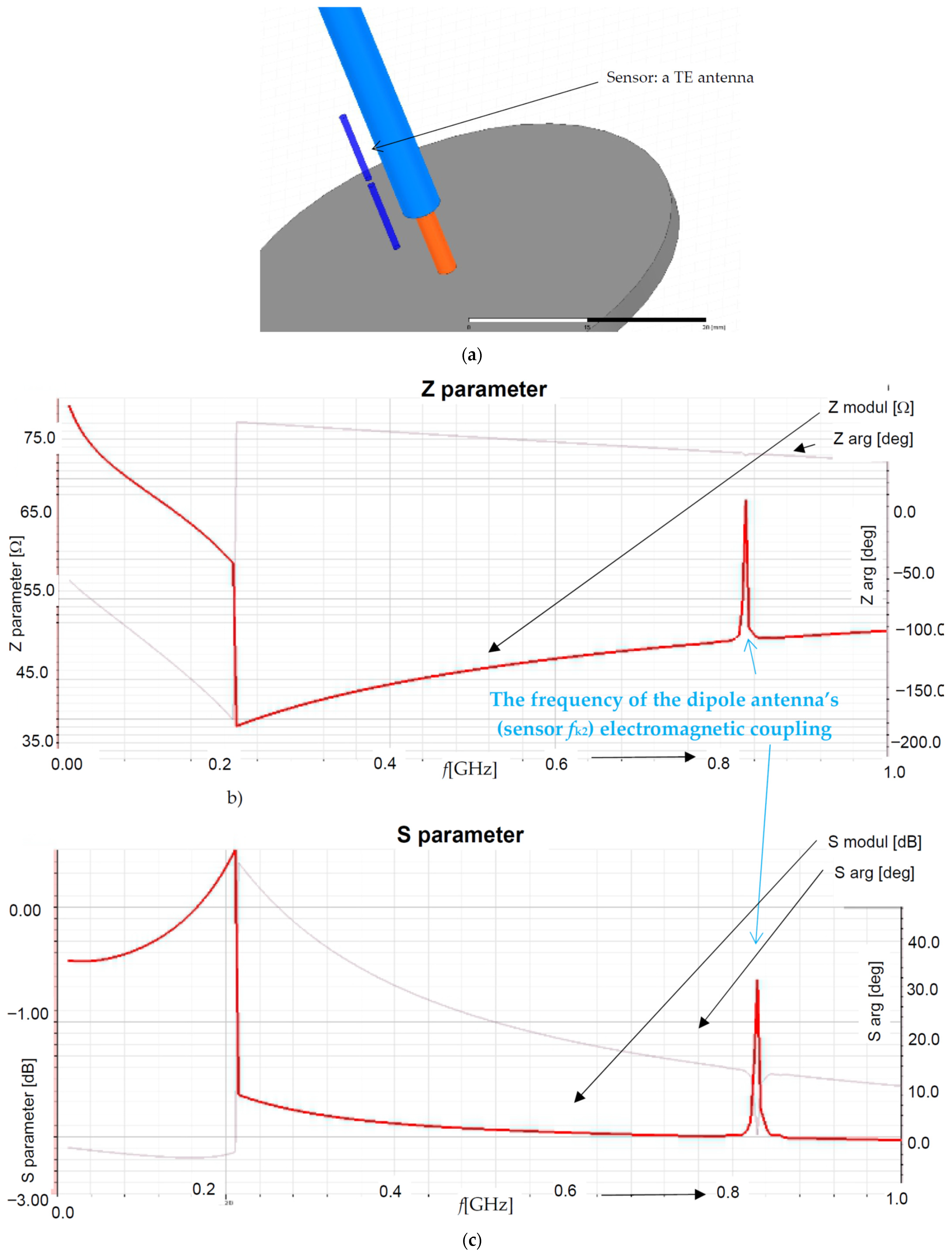
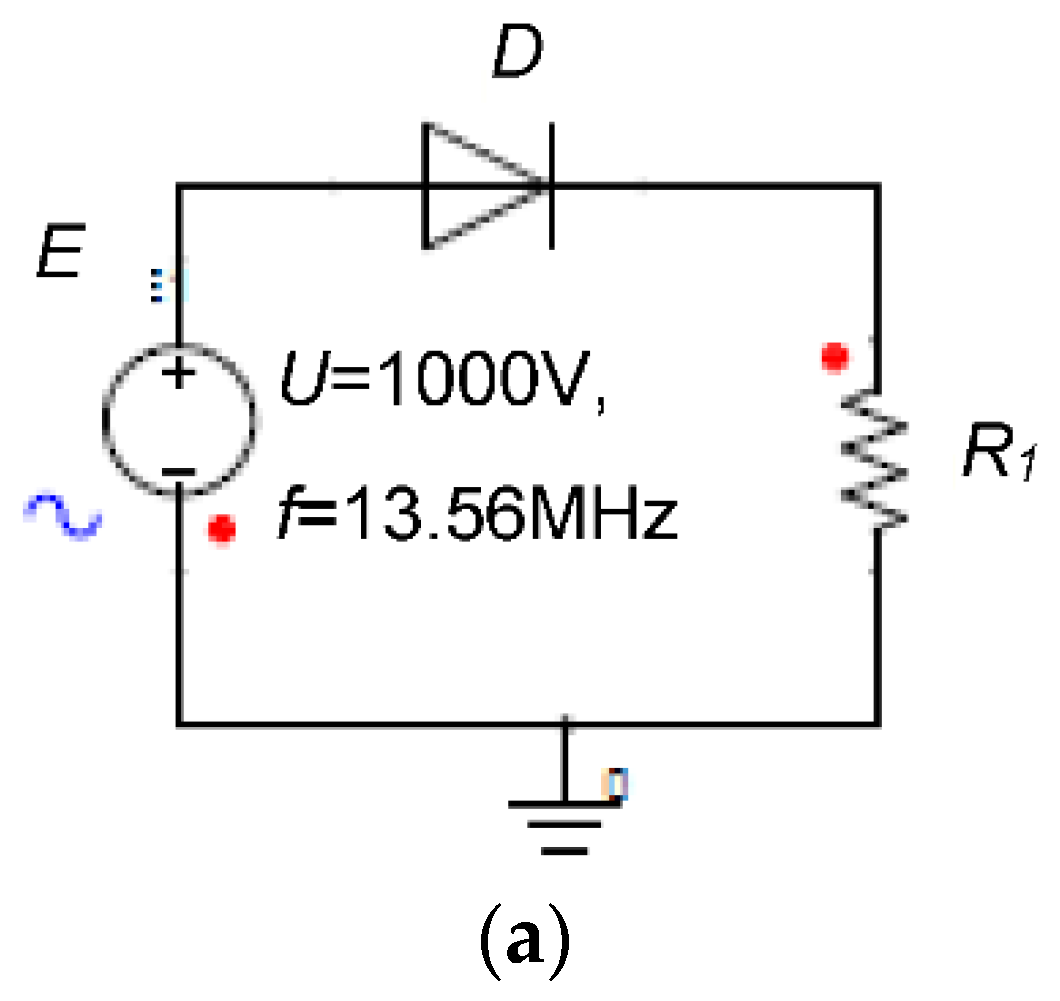
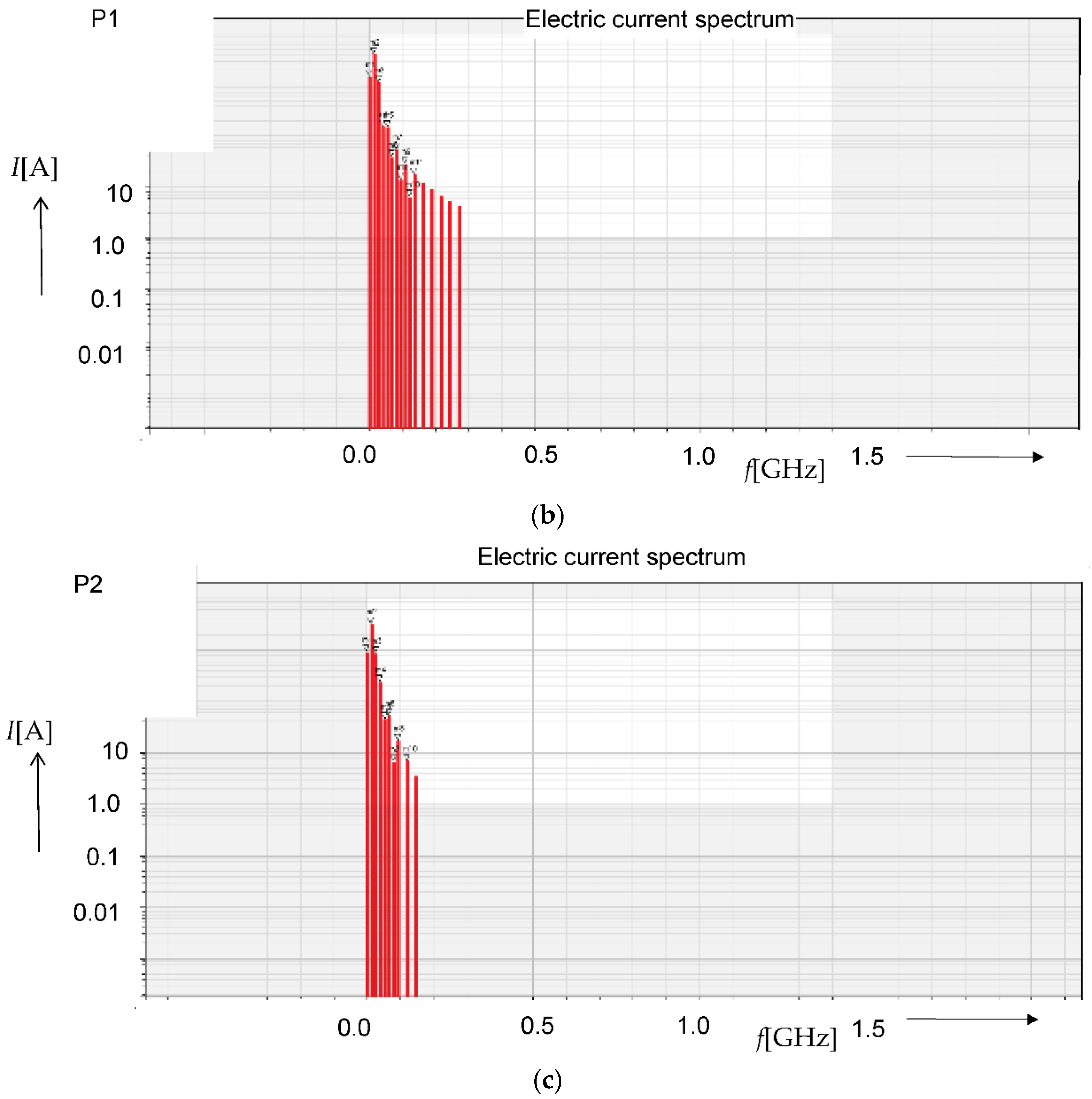

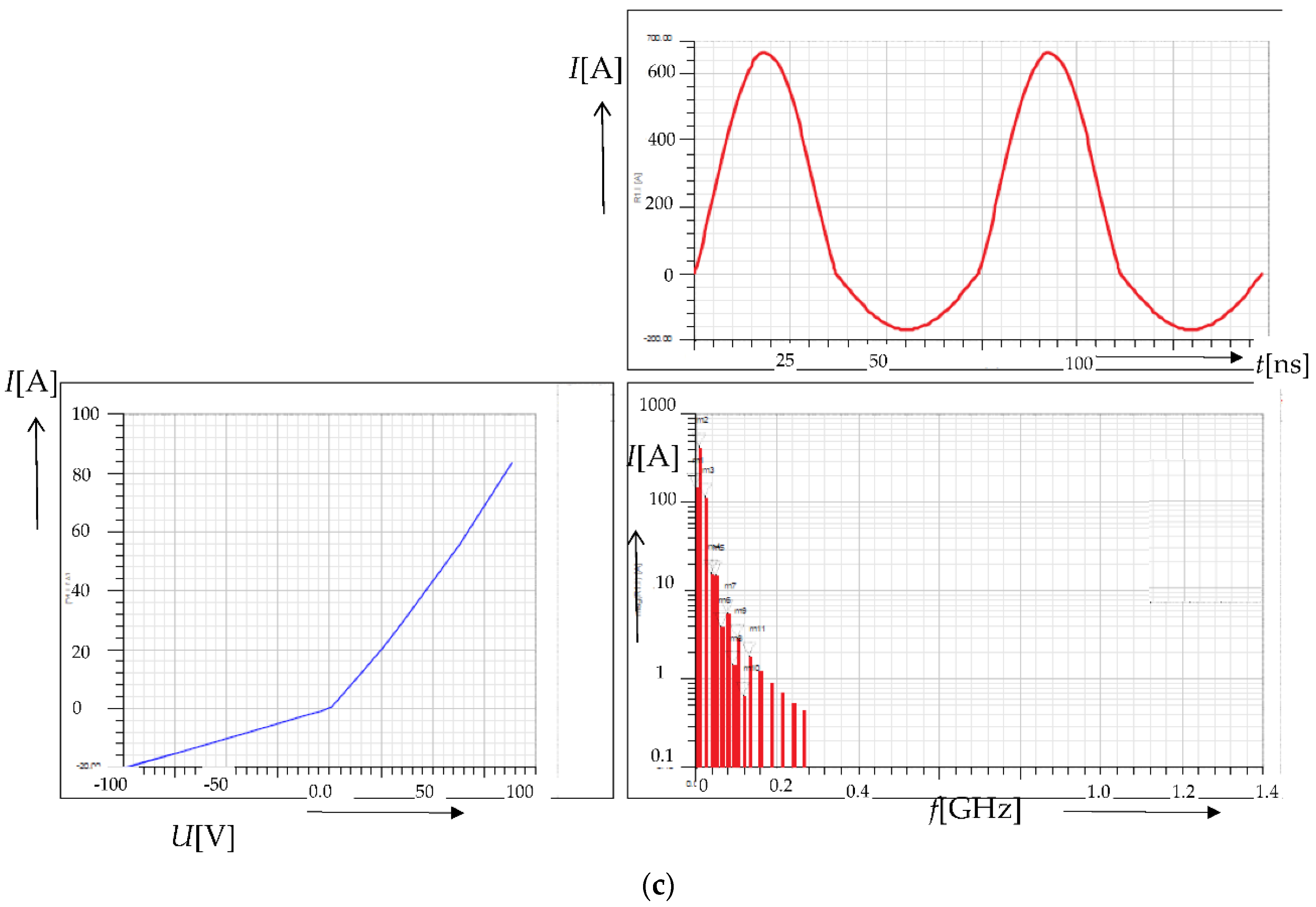

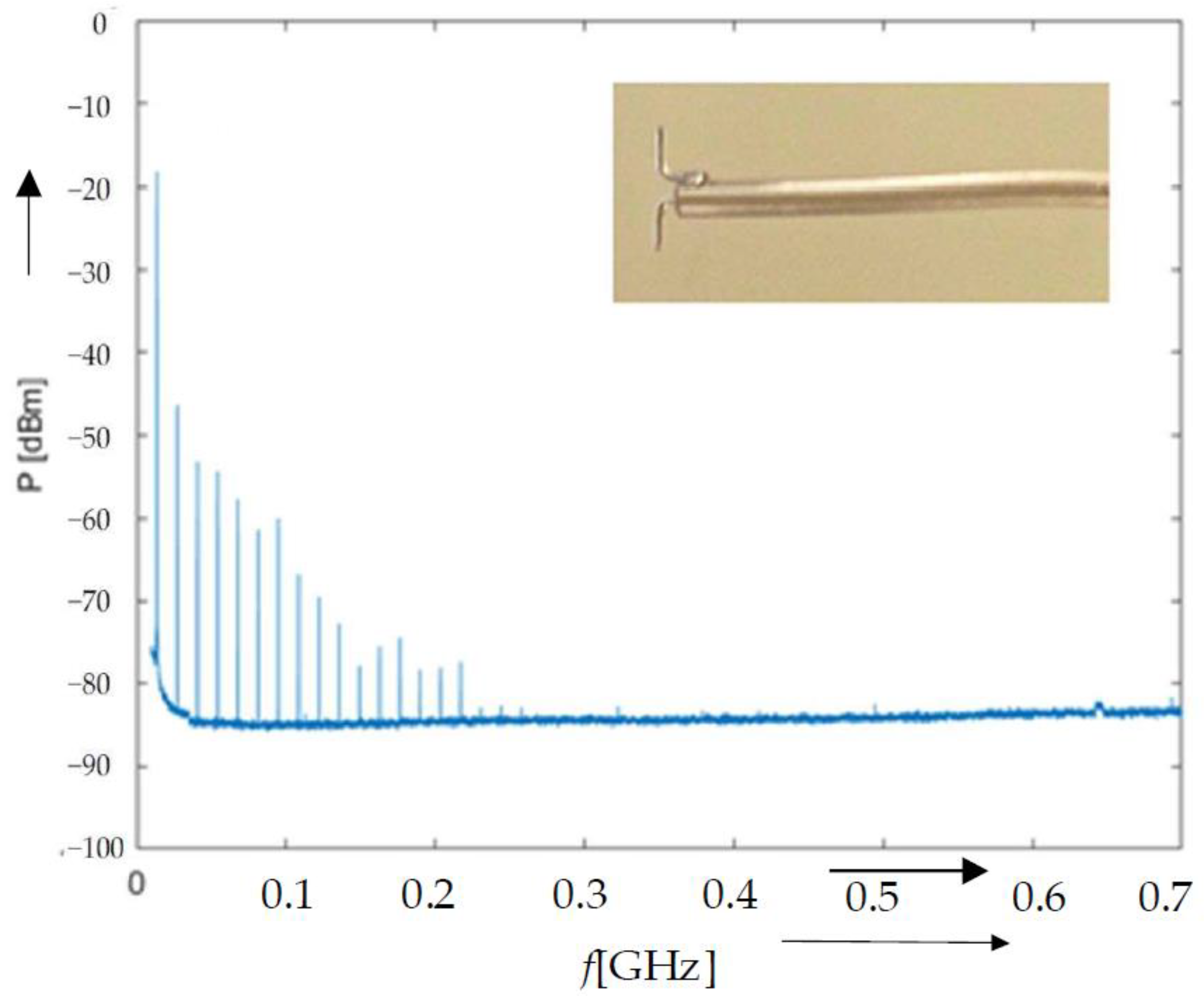
| Plasma Pencil | TrotOH [K] | TvibN2 [K] | TexcAr [K] | Ne [cm−3] |
|---|---|---|---|---|
| Values | 350–1600 | 1500–6000 | 4500–8000 | 1013–1015 |
| I [A] | P [dBm] | ||||
|---|---|---|---|---|---|
| f [MHz] | A | B | C | D | E |
| 13.56 | 362.7 | 321.0 | 401.7 | −18.1 | −4.1 |
| 27.12 | 68.1 | 86.8 | 113.2 | −46.1 | −42.4 |
| 40.68 | 23.72 | 23.7 | 15.4 | −54.2 | −36.2 |
| 54.24 | 1.055 | 4.99 | 14.86 | −56.6 | −59.0 |
| 67.8 | 5.29 | 5.29 | 3.81 | −58.1 | −64.1 |
| 81.36 | 0.851 | 0.661 | 5.42 | −61.8 | −75.0 |
| 94.92 | 1.88 | 1.88 | 1.39 | −60.1 | −73.9 |
| 108.48 | 0.608 | 0.0 * | 2.83 | −67.2 | −81.0 |
| 122.04 | 0.702 | 0.710 | 0.64 | −70.3 | −78.6 |
| 135.6 | 0.382 | 0.0 * | 1.76 | −72.5 | −82.8 |
| 149.16 | 0.0 * | 0.0 * | 0.0 * | −77.9 | −81.5 |
| 162.7 | 0.0 * | 0.380 | 1.30 | −74.8 | 0.0 * |
| 176.28 | 0.0 * | 0.0 * | 0.0 * | −73.5 | 0.0 * |
| 189.84 | 0.0 * | 0.0 * | 0.910 | −78.6 | 0.0 * |
| 203.4 | 0.0 * | 0.0 * | 0.0 * | −76.7 | 0.0 * |
| 216.96 | 0.0 * | 0.0 * | 0.610 | −74.9 | 0.0 * |
| 230.52 | 0.0 * | 0.0 * | 0.0 * | −85.1 | 0.0 * |
| 244.08 | 0.0 * | 0.0 * | 0.520 | −83.9 | 0.0 * |
| 257.64 | 0.0 * | 0.0 * | 0.0 * | −85.0 | 0.0 * |
| 271.2 | 0.0 * | 0.0 * | 0.430 | 0.0 * | 0.0 * |
| 284.76 | 0.0 * | 0.0 * | 0.0 * | 0.0 * | 0.0 * |
| 298.32 | 0.0 * | 0.0 * | 0.0 * | 0.0 * | 0.0 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drexler, P.; Szabó, Z.; Pernica, R.; Zukal, J.; Kadlec, R.; Klíma, M.; Fiala, P. Modeling and Experimental Verification of Plasma Jet Electromagnetic Signals. Modelling 2022, 3, 70-91. https://doi.org/10.3390/modelling3010005
Drexler P, Szabó Z, Pernica R, Zukal J, Kadlec R, Klíma M, Fiala P. Modeling and Experimental Verification of Plasma Jet Electromagnetic Signals. Modelling. 2022; 3(1):70-91. https://doi.org/10.3390/modelling3010005
Chicago/Turabian StyleDrexler, Petr, Zoltán Szabó, Roman Pernica, Jiri Zukal, Radim Kadlec, Miloš Klíma, and Pavel Fiala. 2022. "Modeling and Experimental Verification of Plasma Jet Electromagnetic Signals" Modelling 3, no. 1: 70-91. https://doi.org/10.3390/modelling3010005
APA StyleDrexler, P., Szabó, Z., Pernica, R., Zukal, J., Kadlec, R., Klíma, M., & Fiala, P. (2022). Modeling and Experimental Verification of Plasma Jet Electromagnetic Signals. Modelling, 3(1), 70-91. https://doi.org/10.3390/modelling3010005






