Abstract
Computer modeling of the electrophysiology of the heart has undergone significant progress. A healthy heart can be modeled starting from the ion channels via the spread of a depolarization wave on a realistic geometry of the human heart up to the potentials on the body surface and the ECG. Research is advancing regarding modeling diseases of the heart. This article reviews progress in calculating and analyzing the corresponding electrocardiogram (ECG) from simulated depolarization and repolarization waves. First, we describe modeling of the P-wave, the QRS complex and the T-wave of a healthy heart. Then, both the modeling and the corresponding ECGs of several important diseases and arrhythmias are delineated: ischemia and infarction, ectopic beats and extrasystoles, ventricular tachycardia, bundle branch blocks, atrial tachycardia, flutter and fibrillation, genetic diseases and channelopathies, imbalance of electrolytes and drug-induced changes. Finally, we outline the potential impact of computer modeling on ECG interpretation. Computer modeling can contribute to a better comprehension of the relation between features in the ECG and the underlying cardiac condition and disease. It can pave the way for a quantitative analysis of the ECG and can support the cardiologist in identifying events or non-invasively localizing diseased areas. Finally, it can deliver very large databases of reliably labeled ECGs as training data for machine learning.
Keywords:
in silico; electrophysiology; electrocardiogram; ECG; cardiac disease; arrhythmia; ischemia 1. Introduction
This article reviews research aimed at building a bridge between computerized modeling of the electrophysiology of the human heart and the analysis of the electrocardiogram (ECG). Potential applications of computer modeling for better interpretation of the ECG are demonstrated and an outlook for further research is given.
The research field of computerized modeling of the electrophysiology of the heart has reached a mature state. The healthy heart can be replicated in a computer model with various degrees of detail, starting with the ion channels and ending with the spread of a depolarization wave through the atria and the ventricles. Several diseases have been the focus of this research but many open questions remain: modeling can only be as good as our basic understanding of the pathologies of the heart.
On the other hand, after more than 100 years of ECG interpretation, the clinical knowledge about ECG and what it can tell us about cardiac diseases has reached an expert level. Most often, this knowledge is based on personal experience or empirical studies and only coarse attempts are made to relate a decisive feature in the ECG to its pathological origin inside the heart. The classical heart vector is a valuable tool for understanding the general shape of the ECG, but it is not good enough to follow details of the spatial spread of de- and repolarization.
It is astounding that the number of articles where modeling of the heart is extended to the calculation of the ECG and where this is used for better ECG interpretation is limited. Table 1 shows the result of a literature survey.

Table 1.
Literature survey of research about modeling of the heart together with the corresponding ECG.
Methods for calculation of the ECG (and the body surface potential map, BSPM) from the source distribution in the heart have been described in several articles. The main differences between the approaches are (a) the cellular models and their parameters, (b) the method to calculate the spread of depolarization (bidomain, monodomain, eikonal, reaction eikonal) and (c) the method of forward calculation (finite difference, finite element, boundary element methods; homogeneous torso versus different organs considered). The forward problem is obviously related to the inverse problem of ECG as used in ECG imaging (ECGi). Thus, all articles dealing with fast and realistic methods of calculating the lead field matrix that maps the sources in the heart to the body surface ECG are related to the topic of this article but are not discussed in detail.
Published in 2004, the software package ECGSim allows for a fast and easy relation of source patterns on the heart to the corresponding 12-lead ECG. The user can modify local activation times, repolarization times and the slope of the transmembrane voltage [64]. Thus, these source distributions can be realistic or not—no model of excitation spread is running in the background. Meanwhile, advanced software packages to simulate the electrophysiology of the heart are available: openCARP [65,66], acCELLerate [67], FEniCS [68], Chaste [69], propag-5 [70], and LifeV [71]. They all have been verified in an N-version benchmark activity initiated by Niederer [72].
The literature survey yielded several articles that do not focus on a specific disease but rather deal with the general concept of calculating the ECG from computer models of the heart. Lyon et al. gave an outline of a computational pipeline, listed examples of modeling diseases together with the ECG and showed up several applications of modeling in ECG interpretation [73]. Potse suggested a fast method for realistic ECG simulation without oversimplifying the torso model by using a lead-field approach [74]. Building upon this approach, Pezzuto et al. found an even faster method that allows for implementation on a general-purpose graphic processing unit (GPGPU) [75]. Keller et al. investigated the influence of tissue conductivities on the resulting ECG [76]. Schuler et al. [77] found a way to downsample the fine grid necessary for calculating the spread of depolarization for the forward calculation of the ECG—further reducing calculation time. Neic et al. developed a reaction eikonal algorithm that simulates the spread of depolarization very fast and still delivers realistic ECGs [78].
Calculation times for computing the spread of depolarization and repolarization, the lead field matrix and the body surface potentials including the ECG strongly depend on the methods employed: highly detailed cell models versus simplified phenomenological models, high versus low spatial resolutions, etc. They can range from one day down to one second. As an example, the calculation times of the P-waves shown in Figure 1 were 27 h for the full bidomain model and the Courtemanche cell model, 1 h and 24 min for a pseudo-bidomain model and 40 min for a monodomain simulation (heart mesh with 4.7 million elements and 920 k nodes, desktop computer with 12 cores at 1.4 GHz). Fast calculation times are important for the researcher aiming at the identification of new features in the ECG, for creating a training dataset for machine learning and for personalization of a heart model. They are not relevant any more if, for example, a machine learning algorithm is finally used in clinics.
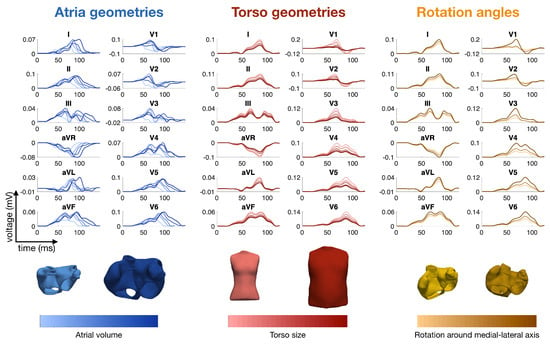
Figure 1.
Simulated P-waves of the 12-lead ECG with various atrial shapes, several orientations of the atria inside the torso and a variety of body shapes. The colors represent the total atrial volume in blue, the torso size in red and the orientation angle around the medial-lateral axis in orange [50].
2. Modeling the ECG of a Healthy Heart
2.1. The QRS Complex and the Purkinje Tree
The morphology of the QRS complex is strongly determined by the topology of the His-Purkinje system in the ventricular subendocardial layer [2]. An earlier approach to fit a Punkinje network model to a measured ECG was published by Keller et al. in 2009 [1]. In total, 744 Purkinje muscle junctions were distributed across the ventricular endocardial surface following specific rules. Other publications followed this scheme and implemented “root points” coupled to thin endocardial layers with very fast conduction [3]. Automatic and reproducible manipulation of root node locations is facilitated by chamber-specific coordinate systems [79,80,81]. Mincholé et al. investigated the impact of anatomical variability on simulated QRS complexes [6]. They found that QRS duration is mainly determined by myocardial volume and not affected by the position of the heart in the torso. The latter influences QRS morphology in the precordial leads, whereas ventricular anatomy dominates in the limb leads. Cranford et al. carried out a sensitivity study: they implemented 1 to 4 “seed stimuli” and up to 384 “regional stimuli” and observed the changes in the QRS complex while changing the number and topology of excitation sites [5]. The topology of four seed stimuli at adapted positions was more relevant than a large number of regional stimuli. Pezzuto et al. were able to reproduce the QRS complex of 11 patients using up to 11 of the earliest activation sites on the endocardium and adapted the conduction velocity in the ventricles and in a fast endocardial layer [7]. Gillette et al. proposed a comprehensive workflow to optimize the positioning of five root disks, timing, and endocardial conduction velocities (10 parameters) to reproduce the QRS complex with a personalized model [8].
The healthy QRS complex can be reproduced faithfully, meaning that adapted heart models show an ECG with high correlation to measured ECGs. This does not prove that the modeled spread of depolarization is the one present in the patient, but it is good to see that there are no inconsistencies. Some relevant questions are: Which parameters in the model are responsible for the natural variability of QRS complexes—both inter- and intra-patient wise [4,6] (see also Section 2.5)? Is the heart axis that is visible in the ECG mainly determined by the geometrical axis of the heart or by the properties of the His-Purkinje system? Which simplifications of the thorax model are acceptable and where do we need detailed models?
2.2. The T-Wave and the Repolarization
Modeling the T-wave is a challenging task. If all myocytes in the ventricles would follow the same action potential, the T-wave would have the opposite sign as the R-peak. Heterogeneity is a necessary condition for concordant T-waves. Keller et al. investigated various schemes of heterogeneity of the repolarization current (transmural, apico-basal, left–right) and found that both transmural and apico-basal gradients can lead to realistic T-waves, whereas a pure left–right heterogeneity creates a notch in the T-wave [11]. Even though the focus of an article of Bukhari et al. was on the changes in the T-wave during dialysis (see Section 3.9), this article also reported on the heterogeneity that is needed to obtain a realistic T-wave in healthy hearts. They assume a solely transmural dispersion of ion channel conductivities [13]. Xue et al. analyzed how transmural and apico-basal heterogeneities change the morphology of the T-wave. They included heterogeneities of the following ion channels: , , . They concluded that mainly apico-basal gradients contribute to a positive T-Wave [10]. The modeled heterogeneity scenarios are informed by experimental cellular data [82]. However, the available data do not allow us to draw definite conclusions and different heterogeneity patterns can lead to the similar T-wave morphologies.
While contraction of the heart happens only after the P-wave and the early QRS complex, it can influence the source distribution during the repolarization. How the contraction of the heart affects the morphology of the simulated T-wave was investigated by Moss et al. They observed an 8% increase in amplitude and a shift of the T-wave peak by 7 ms [12].
2.3. The P-Wave
A review about computerized modeling of the atria including the corresponding ECG was given by Doessel et al. in 2012 [15]. Krueger et al. were the first to set up an atrial model that included realistic fiber orientation [14,83]. They also investigated the influence of atrial heterogeneities on the morphology of the P-wave, created personalized models and compared the ECGs of several patients [16].
The contribution of the left and right atria to the P-wave was analyzed by Loewe et al. [17] and Jacquemet et al. [18]. Even in the last third of the P-wave, one-third of the signal stems from the right atrium [17]. Potse et al. discovered that a jigging morphology of the P-wave, which was observed in computer simulations, was not an artefact but could be observed in a similar way in healthy volunteers when carefully preventing smoothing through filtering or averaging [19]. Loewe et al. investigated the influence of the earliest site of activation in the right atrium (i.e., the sinus node exit site) on the morphology of the P-wave [20] and could demonstrate that small shifts in the earliest excitation site and its proximity to the inter-atrial connections can significantly change the terminal phase of the P-wave. Andlauer et al. dissected the differential effects of atrial dilation and hypertrophy on the morphology of the P-wave [21] and showed that left atrial dilation did not influence P-wave duration significantly, but instead had a strong effect on P-wave amplitude and thus P-wave Terminal Force in lead V1 (PTF-V1).
A literature survey of simulations of the P-wave and in particular of the P-wave in patients suffering from paroxysmal atrial fibrillation (AFib) was published by Filos et al. [43]. All the effects described in the literature that have an influence on the morphology of the P-wave of AFib patients are outlined. Despite the very large number of articles, we conclude that there is still a way to go before these results can be routinely used in clinical practice.
Nagel et al. analyzed the inter- and intra-patient variability of the P-wave in the Physionet ECG database, aiming at the optimization of a simulated database of P-waves [84] (see also Section 2.5). Figure 1 shows several examples of P-waves with various atrial shapes, several orientations of the atria inside the torso and a variety of body shapes.
2.4. Modeling Rhythmic Features and Heart Rate Variability
Modeling of a heart beat most often starts with a stimulation either from an area around the sinus node (atria) or from the model of the Purkinje tree (ventricles, see Section 2.1). Modeling of the sinus node is an interesting research topic that goes beyond the scope of this article.
The ECG fluctuates from beat to beat even in the healthy state. Both the RR interval and also the morphology of the P-, QRS- and T-wave are not completely periodic. The fluctuations of the RR interval are well known and analyzed by means of heart rate variability (HRV), as reviewed by Rajendra et al. [85]. HRV is high in normal hearts and low when there is a cardiac problem. The variation in the beat-to-beat RR interval is usually studied in both the time domain and frequency domain. Not many clinicians make use of this measure in daily clinical practice. On the modeling side, only few articles describe simulations of beta-adrenergic and vagal tones on the sinus node [86]. It seems as if there is still a “missing link” between computerized modeling of the heart and HRV interpretation [87].
2.5. Modeling Inter- and Intra-Patient Variability
The variety of ECG morphologies observed in a cohort of healthy humans is large. This can be explained by different geometries of the heart [88] , different rotation inside the thorax [6], and different shapes of the torso. Moreover, differences in electrophysiology also contribute to the variability (see, for example, the discussion about the QRS morphology and the Purkinje tree in Section 2.1).
As already mentioned in Section 2.3, Nagel et al. investigated the inter- and intra-patient variability of the P-wave [84]. The beat-to-beat variability of the P-wave in case of atrial fibrillation was investigated by Pezzuto et al. [42]. Already small variations (1 to 5 mm) in the location of the earliest activation site lead to changes in the morphology of the P-wave. This effect was significantly enhanced if slow conducting regions were near the earliest activation site.
3. Modeling Diseases and the Corresponding ECG
3.1. Ischemia and Infarction
Loewe at al. gave an outline of how computer modeling can support comprehension of cardiac ischemia and discussed the link to the corresponding ECG [28]. Figure 2 shows several examples of ischemic regions together with the corresponding ECG. The parameters of the ten Tusscher–Panfilov cell model which reflect the degree and temporal stage of the occlusion were summarized by Wilhelms et al. [25]. They considered the cellular effects due to hyperkalemia, acidosis and hypoxia as well as due to cellular uncoupling. After clarifying the origin of ST-segment elevation (and depression), they also demonstrated how several ischemic scenarios will not show any ST-segment change [26]. Thus, they were able to explain the large group of non-ST-segment elevation myocardial infarctions (NSTEMI). Potyagaylo et al. showed that these scenarios are not only electrically but also magnetically “silent” [89]. Loewe at al.—using computer modeling—investigated whether additional electrodes, optimized electrode placement or improved analysis of the ST segment could lead to better diagnosis of patients with acute ischemia. They suggest the deviation from baseline at the K-point as being superior to J-point analysis [27].
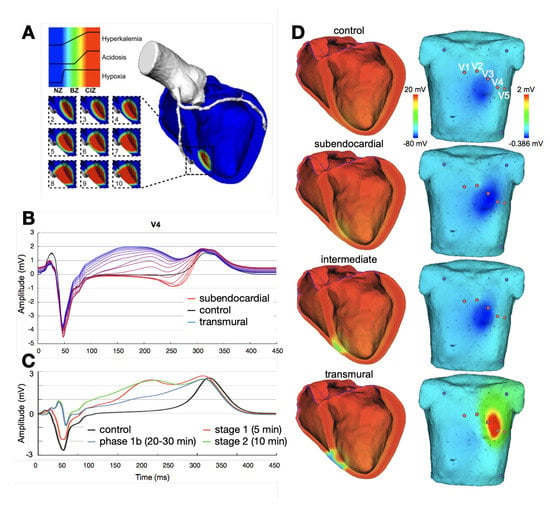
Figure 2.
Examples of ischemic regions with varying transmural extent due to occlusion of the left anterior descending coronary artery and the related levels of hyperkalemia, acidosis, and hypoxia (A). ECG lead V4 for ischemia of varying transmural extent in temporal stage 2 (B) and varying duration of a transmural ischemia (C). Ventricular transmembrane voltage and body surface potential distribution during the action potential plateau (t = 200 ms) for ischemia of varying transmural extent in stage 2 (D). The QRS complex was not optimized in this study. (Images reproduced with permission from [28].)
Ledezma et al. created populations of control and ischemic cell strands and observed the corresponding pseudo-ECGs (which is the voltage between two virtual electrodes at or near to the ends of a tissue strand immersed in an infinite homogeneous volume conductor). Based on these data, they trained an artificial neural network that was able to determine severity (mild or severe) and size of the ischemic region from the pseudo-ECG [30].
All these articles deal with ischemia and “fresh” infarctions (not older than a couple of hours). The modeling of “old” infarction scars seems to be straightforward: the scar areas cannot depolarize, they should be “switched off” during modeling. Basically. the QRS complex will change. In particular, small bridges of viable tissue within a scar area are of interest since they are likely to lead to ventricular tachycardia (VT). Lopez-Perez et al. were able to set up a personalized model of a patient with an old infarction with strong emphasis on modeling border zones. They were able to reproduce the 12-lead ECG of a patient with a history of infarction both in sinus rhythm and during VT (see Section 3.3) [29].
Electrocardiographic imaging of myocardial infarction was the subject of the Challenge of the Computing in Cardiology conference in 2007. BSPMs of patients were provided for the participants. Ghasemi et al. were very successful in finding the location and extent of the infarction using only the heart vector and a very simplified model of the distribution of depolarization during systole [90]. Farina et al. employed a model-based approach to solve the task [23] and also reached very good results; however, based on the full BSPM. Jiang et al. investigated the best electrode arrangements to localize an infarcted area in the heart [24]. A dense set of electrodes including and extending the precordial leads was essential. Optimal results were obtained when using at least 64 electrodes.
3.2. Ventricular Ectopic Beats and Extrasystoles
The localization of ventricular ectopic beats (premature ventricular contractions, PVCs) is a major topic of the inverse problem of ECG. Any knowledge about the site of origin can guide the cardiologist during an ablation procedure and thus shorten the duration of the invasive procedure. Many publications contain chapters on calculating the body surface potential map of ventricular ectopic beats using simulations of the spread of depolarization (see, for example, Potyagaylo et al. [31]). Most of them assume that the individual body shape and cardiac geometry is known, which is, however, not the setting of traditional ECG analysis.
Figure 3 shows, as an example, a fast simulation of the spread of depolarization (transmembrane voltage and epicardial potentials) and the corresponding 12-lead ECG for three different ventricular extrasystoles.
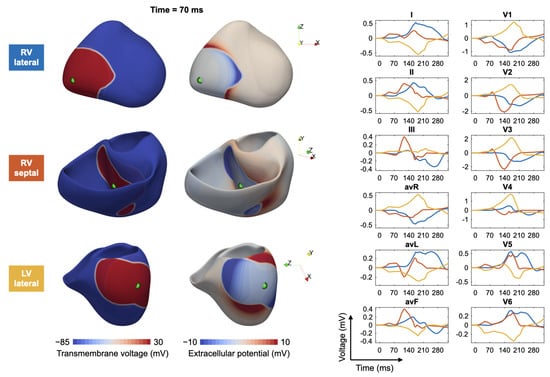
Figure 3.
Modeling of ectopic beats and the corresponding ECG: for three different trigger locations in the right ventricle (RV) and left ventricle (LV), the transmembrane voltage (left column), the extracellular potentials (middle column) and corresponding ECGs (right column) are shown. Excitation propagation was computed by solving the anisotropic Eikonal equation.
3.3. Ventricular Tachycardia
Sapp et al. were able to localize the exit point of a ventricular tachycardia (VT) from a 12-lead ECG based on an empirical study including 38 patients [91]. No modeling was employed; nevertheless, an accuracy of 10 mm was achieved. It might be that the number of patients was too small for drawing general conclusions. In 2007, Segal et al. suggested features in the ECG that point to specific areas of exit points of VT (e.g., antero-lateral, antero-apical, mid-septum, etc.) without any computer model [92]. Kania et al. localized the exit point of a ventricular tachycardia using a personalized geometry for modeling and only three ECG leads (Frank VCG) with an accuracy of 11.7 mm [35]. Additionally, in this section, the article of Lopez-Perez et al. has to be mentioned: they reproduced the ECG during VT of a personalized model of a patient with an old infarction [29].
3.4. Cardiomyopathy
Lyon et al. investigated ECG phenotypes resulting from hypertrophic cardiomyopathy using computer modeling [36]. The objective was to better identify patients at high risk of sudden cardiac death. An inverted T-wave with normal QRS was obtained with increased apico-basal repolarization gradients in the septum and the apex. Lateral QRS abnormalities were only obtained with abnormal Purkinje-myocardium coupling.
3.5. Bundle Branch Blocks
The most important feature visible in the ECG that points towards a bundle branch block is a prolonged QRS complex. Modeling in this respect is mainly aiming at optimization of cardiac resynchronization therapy. The bundle branch block is most often simulated by only stimulating the Purkinje system in the right ventricle (left bundle branch block, LBBB) or left ventricle (RBBB). Potse et al. investigated different hypotheses about activation times for the LV endocardium, morphology of electrograms and ECG features in patients with heart failure and LBBB using personalized computer modeling [37]. Simulated and measured ECGs matched quite well (correlation coefficient between measured and simulated activation times was r = 0.91 in one case and 0.87 in another case). Giffard-Roisin et al. were able to match the 12-lead ECG of a patient with LBBB in a personalized geometry by adjusting only 3 conduction velocities (CVs): in the myocardium, in the left ventricular Purkinje system and in the right ventricular Purkinje system [39]. Personalized models of five patients with heart failure and LBBB were created by Nguyen et al. [38]. They reached a very good agreement between simulated and measured 12-lead ECG and demonstrated that the correct heart position and orientation has a strong impact on several features of the ECG. A combined clinical (21 patients) and in-silico (3 simulated cases) study of LBBB was presented by Nguyen et al. in 2018 [40]: the computer models were personalized using endocardial mapping and the 12-lead ECG.
3.6. Atrial Ectopic Beats
The localization of atrial ectopic beats is of interest since the knowledge of their origin could guide an ablation procedure. Localization of ectopic foci on the left atrium was enabled by model-based computation of the spread of depolarization, forward calculation to the body surface and comparison with “measured” BSPM by Potyagaylo et al. [93]. A “full search” method was applied, which cannot only deliver the location of the focus but also a confidence region on the atria. Using only the first half of the P-wave improved results. Feng et al. optimized a method to classify atrial ectopic beats, stable re-entries and sinus rhythm in the 12-lead ECG by using simulated data [32]. Yang et al. trained a convolutional neural network with simulated ectopic beats and applied it to nine patients to localize ectopic beats from the 12-lead ECG by identifying the most likely origin from 25 cardiac segments. They achieved a localization error of 11 mm when using a personalized model of the thorax of the patient [33]. Additionally, Ferrer-Albero et al. were able to localize atrial ectopic beats using simulated body surface P-wave integral maps and a machine learning approach (support vector machine). The computed ECGs compare well with clinical ECGs. Dividing the atria in up to six regions (clusters), the origin of an ectopic beat could be localized reliably, with the best accuracy of 96% achieved with four clusters [34].
3.7. Atrial Tachycardia, Flutter and Fibrillation
Atrial flutter (AFlut) can be clearly diagnosed from the ECG. Typical and atypical AFlut can be reliably recognised from the ECG by a trained cardiologist. However, the question of which type of atypical atrial flutter the patient suffers from cannot be answered directly from the ECG up to date. Again, this knowledge would speed up ablation procedures and could inform clinical decision making. It also could inform the cardiologist about two alternating classes of AFlut that might be present. It could give evidence that the type of flutter that is observed in the electrophysiology lab is identical with the type that the patient suffers from out of hospital. Zhou et al. employed ECGi to classify several types of AFlut in seven patients based on full BSPMs and personalized torso models [41]. On the other hand, Medi et al. were able to separate a few classes of atypical AFlut just from the ECG without any modeling [94] such as, for example, focal versus macro-re-entry and right atrial versus left atrial macro-re-entry. An approach with similar objectives—classification of macro-re-entrant atrial tachycardia—but without any modeling should be mentioned: Ruiperez-Campillo et al. analyzed loops of the atrial vectorcardiogram, created “archetypes” of the loops of the four most frequent types of AFlut and determined the similarity of the vectorcardiogram loop of a patient with the archetypes [95].
Luongo et al. were able to classify 20 different types of AFlut using the 12-lead ECG based on a recurrence quantification analysis [45] in a computational study with a clinical proof of concept. Figure 4 shows two examples. They also investigated the influence of different atrial and torso geometries on the outcome of their algorithm [46]. Figure 4 shows two examples of simulated AFlut scenarios and the corresponding BSPMs and 12-lead ECGs.
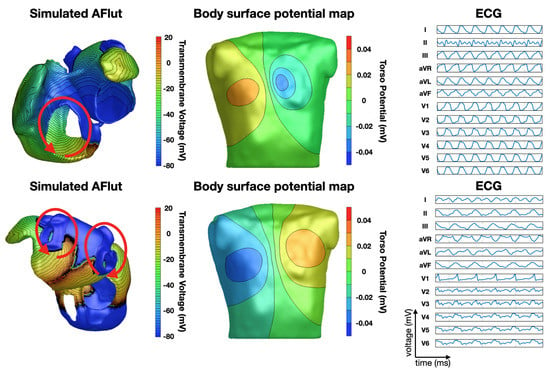
Figure 4.
Examples of simulated AFlut transmembrane voltage distributions and the corresponding BSPMs and 12-lead ECGs. Top row: AFlut around the tricuspid valve in the counter-clockwise direction. Bottom row: figure-8 macro-re-entry around the left and right pulmonary veins in the anterior direction of rotation [45].
Pezzuto et al. presented simulations of beat-to-beat variations of the P-waves in patients with paroxysmal atrial fibrillation (AFib). They suggest that variations of the exit location of the sinus node are responsible for P-wave fluctuations observed in patients [42] (see also [20]). Filos et al. conducted a literature survey of articles about simulations of the P-wave, the beat-to-beat variations with a particular focus on P-waves of patients suffering from paroxysmal AFib. They showed how advances in computer models and high performance computing could lead to the use of electrophysiological models of the heart to improve quality of life of patients with AFib and optimize AFib treatment [43] (see also Section 2.3).
Atrial fibrillation remains a challenge regarding the relation of ECG features with patterns of depolarization. In case several (more than three) re-entry mechanisms are active simultaneously, it will probably be impossible to discriminate them from the ECG only. Rodrigo et al. used BSPMs computed in personalized torso models and found that areas of high dominant frequency and areas of large rotors can be localized [48]. However, as mentioned before, this is not the setting of classical ECG interpretation. Nevertheless, if only one ectopic center or one rotor is the driver of AFib, then important characteristics can be deduced from the ECG. Luongo et al. were able to classify whether an AFib driver is located in the vicinity of the pulmonary veins or not, and if not, whether it is in the right or left atrium using a machine learning approach [51]. A decision tree was trained purely on simulated data and performed favorably when subsequently being applied to a clinical dataset comprising 46 patients.
Using computerized modeling, a method was proposed by Saha et al. that can monitor an ablation procedure [47]. In total, 20 ablation patterns were investigated. A simulated 16-lead ECG (including V3R, V4R, V8 and V9) was analyzed in respect to P-wave duration (PWD) and P-wave area. Several reconnections could be detected by comparing pre- and post-ablation ECGs, but the settings of detection thresholds were quite demanding (5 ms for PWD and 0.1 Vs for P-wave area). Regarding a real-time assessment of a typical ablation procedure in case of perimitral flutter, the anterior mitral line, was demonstrated by Lehrmann et al. in a clinical study that was enriched and mechanistically underpinned using computer simulations [44]. The time from the stimulus in the left atrial appendage to the P-wave peak in ECG lead V1 (“V1 delay”) can be used as a reliable measure for blocking of the anterior mitral line. Even more predictive is the sudden jump of the P-wave (“V1 jump”) upon completion of the line.
3.8. Genetic Diseases and Channelopathies
Modeling of genetic diseases leading to cardiac arrhythmias can be straightforward. If the affected ion channel and its modification are known, the modified model of the ion channel can be built into the computer model replacing the normal ion channel. If the dynamics of the ion channel are not affected, just the maximum channel conductance is replaced by a modified value. Sometimes, it is not as easy as that: depending on how the mutation affects the channel, a complete reparametrization or even reformulation of the model can be required. Most frequent cases are the long QT syndromes (LQT1 to LQT16), the short QT syndrome (SQT) and the Brugada syndrome. A review about the modifications of ion channels for theses channelopathies was given by Schwartz et al. [96].
In a very early article, Shimizu and Antzelevitch described the link between transmural heterogeneity in LQT1 syndrome and features of the ECG, in particular concerning the T-wave [97]. Numerous articles followed dealing with empirical clinical studies of ECG morphology in LQT, SQT and Brugada patients but with no link to computer modeling. On the other hand, many articles deal with computational studies about LQT (LQT1 to LQT16), SQT and Brugada syndrome without calculating the corresponding ECG. A computed pseudo-transmural ECG is shown sometimes but it only allows one to identify gross morphological changes but no details in the ECG (for Long QT: Seemann et al., [52], for Short QT: Weiss et al. [53]).
Seemann et al. carried out simulations of LQT1, LQT2 and LQT3 and calculated the corresponding ECGs using a realistic torso model. The T-waves of a healthy control group can clearly be distinguished from LQT patients and the simulated T-waves show good correspondence to clinical data. However, the objective to classify the type of LQT from the ECG was not achieved [54].
3.9. Imbalance of Electrolytes
Imbalance of electrolytes is dangerous in many respects. In particular, it can lead to cardiac arrhythmias. Large deviations from homeostasis can be observed in patients suffering from chronic kidney disease. A continuous monitoring of electrolyte plasma concentration via ECG could be an important aid for patients. Several changes in the ECG due to electrolyte imbalance are well known (see, for example, Wald [98]). Hyper- and hypocalcemia and hyper- and hypokalemia show typical alterations in ECGs.
Bukhari et al. investigated the changes in morphology of the T-wave during hemodialysis, both with modeling and with a clinical study [13]. They identified morphological T-wave features (e.g., amplitude, upslope, and morphological variability) to reconstruct [Ca] and [K] concentrations. They also pointed out that the heterogeneity of action potentials in the ventricles leading to the T-wave shows strong inter-individual variability [99]. This complicates quantitative analysis and it will probably require a personalized model to determine the electrolyte concentration from the ECG.
A review article about the classification and quantification of potassium and calcium disorders using an ECG was published by Pilia et al. [59]. It contains a chapter on modeling electrolyte disorders and the characteristic features in the ECG that can be derived from modeling [55]. It also points out that classical ventricular cell models are not prepared to show reasonable results for electrolyte concentrations that are far away from homeostasis—they have to be adapted [100]. This group also presented a method to estimate blood calcium concentration [58] and they suggested an optimized selection of features of the T-wave and a polynomial regression method to reconstruct the potassium concentration from the ECG [60]. Further on, they investigated various lead reduction techniques to extract the most important information from a 12-lead ECG using computer simulations [56].
Loewe at al. contributed to the comprehension of the electrolytes on the sinus node and thus on the heart rate [57]. They could demonstrate how the heart rate can be slowed down during hypocalcemia.
3.10. Drug-Induced Changes in the ECG
Several antiarrhythmic drugs used today aim at specific modifications of the ion channels. Class I agents are blockers of the fast sodium channel. Class II antiarrhythmics are known to block -receptors and thus attenuate the sympathetic nervous system. Class III drugs block one or several outward potassium currents and class IV drugs block calcium channels. These modifications can be introduced into the electrophysiological cell models of the heart and the specific changes in the action potential can be observed. Often times, integrative modeling is a means to predict the net effect of multi-channel blockers when experimental data are only available on the single channel level [101]. Predicting the effect of specific ion channel modifications on the vulnerability of the heart for arrhythmias is a very active field of research [102,103,104]. The effect on the ECG is not the major focus of most of these studies.
Since drugs that prolong the QT interval are thought to be responsible for life threatening arrhythmias (e.g., torsades de pointes), the effect of a drug on the QT interval is investigated intensively even beyond antiarrhythmic drugs [105]. For that purpose, a strongly simplified model of a strand of cells (e.g., 1 × 1 × 20 mm) representing a transmural wedge can be sufficient under specific conditions. The electric voltage measured from one end to the other is called a “transmural pseudo-ECG”. The morphology of this signal cannot be directly compared to a real ECG, but the changes in QT interval due to a drug can be represented. A prerequisite is to model the transmural heterogeneity properly, as already discussed in Section 2.2.
One of the first studies which closed the gap between modeling drug effects on the cellular and tissue level and the corresponding ECG was presented by Wilhelms et al. [61]. The effects of amiodarone and cisapride on human ventricular electrophysiology and the corresponding ECG were analyzed. For cisapride, only a block of is reported. In contrast, amiodarone affects currents through several ion channels (, , , , , ). While cisapride only prolongs the QT interval, amiodarone in addition modifies the QRS complex. Similar observations were confirmed by Zemzemi et al. [62]. They investigated the influence of a 50% hERG channel block () and of a 50% block of the fast sodium channel (). Both led to a prolongation of the QT interval but the hERG blocker did not affect the QT interval, whereas the 50% sodium channel block prolonged the QRS complex by 12%. Zemzemi et al. also investigated the effect of an blocker and the combined effect with an blocker at various combinations of doses [63]. The dose–response dependency of the degree of block on concentration is modeled using the classical Hill curve in these studies causing a pore block (by reducing ) but not representing any drug-induced changes in the channel dynamics.
A review about various approaches to additionally include the channel dynamics using Markov-type models was published by Yuan et al. [106]. The action of amiodarone and cisapride at the organ level is shown and pseudo-ECGs are presented. Several articles followed with a large variety of objectives (e.g., unmasking LQT syndrome [107], designing antiarrhythmic drugs for SQT patients [108], uncovering cardiac drug toxicity beyond QT prolongation [109], understanding the antiarrhythmic effect of dofetelide [110], analyzing the interaction of drugs with the cardiac conduction system [111], assessment of drug safety regarding late sodium current () blockers [112]) but they all end at the pseudo-ECG level. They are important building blocks for in silico drug assessment and design, but they are not in the focus of this article. The reader is also referred to the “Comprehensive In Vitro Proarrhythmia Assay”(CiPA) initiative, promoting cardiac drug safety assessments based on four approaches: ion channel data, myocyte data, human studies, and in silico investigations [113].
In summary, modeling drug effects so far most often stopped at the pseudo-ECG level and did not consider the realistic ECG derived by computing the field distribution in the thorax induced by the spatio-temporal source distribution in the full heart. The potential to validate in silico modeling with measured ECGs and the potential to enable the individual optimization of the dose via quantification of features in the ECG is not fully realized yet.
4. Options of Modeling for Better Interpretation of the ECG
Computer modeling can contribute to a better understanding of the relation between features in the ECG and the underlying cardiac condition or disease. This was demonstrated in cases of genetic diseases, effect of drugs and imbalance of electrolytes. It can pave the way for quantitative analysis of the ECG. As an example, the quantitative level of extracellular [K] can be estimated from the shape of the T-wave.
Model assisted ECG interpretation can guide the cardiologist to better localize ectopic events or diseased areas. This was demonstrated for the localization of regions of infarction, location of the origin of ectopic beats (atrial and ventricular) and the exit points of a VT.
Moreover, modeling can be a means to generate a very large database of perfectly annotated ECGs as a training dataset for machine learning. Millions of ventricular extrasystoles with exact knowledge about the site of origin can be created for the development of machine learning-based localization. Millions of atria with increasing levels of fibrosis can be created to estimate the degree of fibrosis in the atria from the P-wave. Even though it has to be stated that measured patient data would always be the ideal option for a database, we have to accept that measured data are scarce, often contain incorrect annotations and nearly always have a bias because the variety of diseases is rarely equally distributed among study populations.
The objectives of linking computer modeling with the ECG can also be classified into (a) personalization of a heart model (“digital twin”), (b) the investigation of fundamental mechanisms using generic models and (c) the investigation of cohorts of patients [50,114]. All three play their role in better ECG interpretation but considering variability will become more and more important to derive universally valid conclusions.
5. Summary and Outlook
Establishing a stronger link between computer modeling of the heart and the ECG holds great potential. To consequently add at least the calculation of endocardial electrograms and compare with clinical data from the electrophysiology lab would add more evidence to computerized modeling of the heart. Moreover, the forward calculation of the ECG on the body surface is possible and allows for a comparison with the clinical ECG that is most often available. It is a valuable test of the consistency of the modeling approach and can lead to new insights about the relation between electrophysiological phenomena in the heart and the corresponding ECG.
Likewise, if new (and most often computerized) methods of ECG analysis are proposed, it would be important to make the results explainable by mechanistically underpinning the results, e.g., by backing up the hypotheses with state-of-the-art computer simulations. In many cases, a “rule of thumb” using the classical heart vector for an explanation can be misleading. If a feature in the ECG can be clearly linked to a source pattern on the heart, the diagnostic value of ECG can be increased.
It might be possible to construct personalized models of the heart from the 12–lead ECG [7,8]. However, often there will be ambiguities and spatially higher resolved BSPMs or intracardiac electrograms will be needed. There are also other options for personalization: e.g., measuring the ECG of a patient for one or two electrolytes or drug concentrations and using computer modeling to predict (interpolate) intermediate values can enable a quantitative interpretation of the ECG.
For making general conclusions about features in the ECG that point to specific diseases, the analysis of computer simulations with just one geometry of heart and torso will not be sufficient in the long run. A variety of heart shapes and body shapes can be created using published shape models (for the atria see [22,115,116], for the ventricles see [117,118], for the torso see [119]). Features in the ECG that are discovered with computer simulations using only one heart and body geometry might easily lose their applicability due to the large inter-patient variability of ECGs. Only features that can be discriminated from the natural variety are useful.
In summary, bridging the gap between computerized modeling of the heart and ECG analysis (as well as intracardiac electrograms) holds great potential to lead to better comprehension of cardiac diseases, better diagnosis and optimized therapy planning.
Author Contributions
Conceptualization: O.D.; writing—original draft: O.D.; writing—review and editing: A.L., C.N. and G.L.; visualization: A.L., C.N. and G.L. All authors have read and agreed to the final version of the manuscript.
Funding
This work was supported by the EMPIR programme co-financed by the participating states and from the European Union’s Horizon 2020 research and innovation programme under grant MedalCare 18HLT07 and by the European Union’s Horizon 2020 programme under grant agreement No. 766082, MY-ATRIA project. We gratefully acknowledge support by Deutsche Forschungsgemeinschaft (DFG) (project ID 391128822, LO 2093/1-1). We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank Steffen Schuler for preparing Figure 3.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Keller, D.U.J.; Kalayciyan, R.; Dössel, O.; Seemann, G. Fast creation of endocardial stimulation profiles for the realistic simulation of body surface ECGs. In Proceedings of the IFMBE World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; Volume 25/4, pp. 145–148. [Google Scholar]
- Vigmond, E.J.; Stuyvers, B.D. Modeling our understanding of the His-Purkinje system. Prog. Biophys. Mol. Biol. 2016, 120, 179–188. [Google Scholar] [CrossRef]
- Cardone-Noott, L.; Bueno-Orovio, A.; Mincholé, A.; Zemzemi, N.; Rodriguez, B. Human ventricular activation sequence and the simulation of the electrocardiographic QRS complex and its variability in healthy and intraventricular block conditions. EP Eur. 2016, 18, iv4–iv15. [Google Scholar] [CrossRef]
- Kahlmann, W.; Poremba, E.; Potyagaylo, D.; Dössel, O.; Loewe, A. Modelling of patient-specific Purkinje activation based on measured ECGs. Curr. Dir. Biomed. Eng. 2017, 3, 171–174. [Google Scholar] [CrossRef]
- Cranford, J.P.; O’Hara, T.J.; Villongco, C.T.; Hafez, O.M.; Blake, R.C.; Loscalzo, J.; Fattebert, J.L.; Richards, D.F.; Zhang, X.; Glosli, J.N.; et al. Efficient Computational Modeling of Human Ventricular Activation and Its Electrocardiographic Representation: A Sensitivity Study. Cardiovasc. Eng. Technol. 2018, 9, 447–467. [Google Scholar] [CrossRef]
- Mincholé, A.; Zacur, E.; Ariga, R.; Grau, V.; Rodriguez, B. MRI-Based Computational Torso/Biventricular Multiscale Models to Investigate the Impact of Anatomical Variability on the ECG QRS Complex. Front. Physiol. 2019, 10, 1103. [Google Scholar] [CrossRef]
- Pezzuto, S.; Prinzen, F.W.; Potse, M.; Maffessanti, F.; Regoli, F.; Caputo, M.L.; Conte, G.; Krause, R.; Auricchio, A. Reconstruction of three-dimensional biventricular activation based on the 12-lead electrocardiogram via patient-specific modelling. EP Eur. 2021, 23, 640–647. [Google Scholar] [CrossRef]
- Gillette, K.; Gsell, M.A.; Prassl, A.J.; Karabelas, E.; Reiter, U.; Reiter, G.; Grandits, T.; Peyer, C.; Štern, D.; Urschler, M.; et al. A Framework for the Generation of Digital Twins of Cardiac Electrophysiology from Clinical 12-leads ECGs. Med. Image Anal. 2021, 71, 102080. [Google Scholar] [CrossRef] [PubMed]
- Grandits, T.; Effland, A.; Pock, T.; Krause, R.; Plank, G.; Pezzuto, S. GEASI: Geodesic-based Earliest Activation Sites Identification in cardiac models. arXiv 2021, arXiv:2102.09962v1. [Google Scholar]
- Xue, J.; Chen, Y.; Han, X.; Gao, W. Electrocardiographic morphology changes with different type of repolarization dispersions. J. Electrocardiol. 2010, 43, 553–559. [Google Scholar] [CrossRef]
- Keller, D.U.J.; Weiss, D.L.; Dossel, O.; Seemann, G. Influence of I(Ks) heterogeneities on the genesis of the T-wave: A computational evaluation. IEEE Trans. Biomed. Eng. 2012, 59, 311–322. [Google Scholar] [CrossRef]
- Moss, R.; Moritz Wülfers, E.; Seemann, G. T-Wave Changes Due to Cardiac Deformation Are Dependent on the Temporal Relationship Between Repolarization and Diastolic Phase. Comput. Cardiol. 2018, 45, 1–4. [Google Scholar] [CrossRef]
- Bukhari, H.A.; Palmieri, F.; Ramirez, J.; Laguna, P.; Ruiz, J.E.; Ferreira, D.; Potse, M.; Sanchez, C.; Pueyo, E. Characterization of T Wave Amplitude, Duration and Morphology Changes During Hemodialysis: Relationship with Serum Electrolyte Levels and Heart Rate. IEEE Trans. Biomed. Eng. 2020, 1, ahead of print. [Google Scholar] [CrossRef]
- Krueger, M.W.; Schmidt, V.; Tobón, C.; Weber, F.M.; Lorenz, C.; Keller, D.U.J.; Barschdorf, H.; Burdumy, M.; Neher, P.; Plank, G.; et al. Modeling atrial fiber orientation in patient-specific geometries: A semi-automatic rule-based approach. In Functional Imaging and Modeling of the Heart 2011; Lecture Notes in Computer Science; Axel, L., Metaxas, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6666, pp. 223–232. [Google Scholar] [CrossRef]
- Dössel, O.; Krueger, M.W.; Weber, F.M.; Wilhelms, M.; Seemann, G. Computational modeling of the human atrial anatomy and electrophysiology. Med. Biol. Eng. Comput. 2012, 50, 773–799. [Google Scholar] [CrossRef]
- Krueger, M.W.; Dorn, A.; Keller, D.U.J.; Holmqvist, F.; Carlson, J.; Platonov, P.G.; Rhode, K.S.; Razavi, R.; Seemann, G.; Dössel, O. In-silico modeling of atrial repolarization in normal and atrial fibrillation remodeled state. Med. Biol. Eng. Comput. 2013, 51, 1105–1119. [Google Scholar] [CrossRef] [PubMed]
- Loewe, A.; Krueger, M.W.; Platonov, P.G.; Holmqvist, F.; Dössel, O.; Seemann, G. Left and Right Atrial Contribution to the P-wave in Realistic Computational Models. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9126, pp. 439–447. [Google Scholar] [CrossRef]
- Jacquemet, V. Modeling left and right atrial contributions to the ECG: A dipole-current source approach. Comput. Biol. Med. 2015, 65, 192–199. [Google Scholar] [CrossRef]
- Potse, M.; Lankveld, T.A.R.; Zeemering, S.; Dagnelie, P.C.; Stehouwer, C.D.A.; Henry, R.M.; Linnenbank, A.C.; Kuijpers, N.H.L.; Schotten, U. P-wave complexity in normal subjects and computer models. J. Electrocardiol. 2016, 49, 545–553. [Google Scholar] [CrossRef]
- Loewe, A.; Krueger, M.W.; Holmqvist, F.; Dössel, O.; Seemann, G.; Platonov, P.G. Influence of the earliest right atrial activation site and its proximity to interatrial connections on P-wave morphology. EP Eur. 2016, 18, iv35–iv43. [Google Scholar] [CrossRef]
- Andlauer, R.; Seemann, G.; Baron, L.; Dössel, O.; Kohl, P.; Platonov, P.; Loewe, A. Influence of left atrial size on P-wave morphology: Differential effects of dilation and hypertrophy. EP Eur. 2018, 20, iii36–iii44. [Google Scholar] [CrossRef]
- Nagel, C.; Schuler, S.; Dössel, O.; Loewe, A. A bi-atrial statistical shape model for large-scale in silico studies of human atria: Model development and application to ECG simulations. arXiv 2021, arXiv:2102.10838. [Google Scholar]
- Farina, D.; Dössel, O. Model-based approach to the localization of infarction. Comput. Cardiol. 2007, 34, 173–176. [Google Scholar] [CrossRef]
- Jiang, Y.; Qian, C.; Hanna, R.; Farina, D.; Dössel, O. Optimization of the electrode positions of multichannel ECG for the reconstruction of ischemic areas by solving the inverse electrocardiographic problem. Int. J. Bioelectromagn. 2009, 11, 27–37. [Google Scholar]
- Wilhelms, M.; Dössel, O.; Seemann, G. Comparing Simulated Electrocardiograms of Different Stages of Acute Cardiac Ischemia. In Proceedings of the International Conference on Functional Imaging and Modeling of the Hear, LNCS, New York, NY, USA, 25–27 May 2011; Volume 6666, pp. 11–19. [Google Scholar] [CrossRef]
- Wilhelms, M.; Dössel, O.; Seemann, G. In silico investigation of electrically silent acute cardiac ischemia in the human ventricles. IEEE Trans. Biomed. Eng. 2011, 58, 2961–2964. [Google Scholar] [CrossRef]
- Loewe, A.; Schulze, W.H.W.; Jiang, Y.; Wilhelms, M.; Luik, A.; Dössel, O.; Seemann, G. ECG-Based Detection of Early Myocardial Ischemia in a Computational Model: Impact of Additional Electrodes, Optimal Placement, and a New Feature for ST Deviation. BioMed Res. Int. Artic. 2014, 2015, 530352. [Google Scholar] [CrossRef]
- Loewe, A.; Wülfers, E.M.; Seemann, G. Cardiac ischemia-insights from computational models. Herzschrittmachertherapie Elektrophysiologie 2018, 29, 48–56. [Google Scholar] [CrossRef]
- Lopez-Perez, A.; Sebastian, R.; Izquierdo, M.; Ruiz, R.; Bishop, M.; Ferrero, J.M. Personalized Cardiac Computational Models: From Clinical Data to Simulation of Infarct-Related Ventricular Tachycardia. Front. Physiol. 2019, 10, 580. [Google Scholar] [CrossRef]
- Ledezma, C.A.; Zhou, X.; Rodríguez, B.; Tan, P.J.; Díaz-Zuccarini, V. A modeling and machine learning approach to ECG feature engineering for the detection of ischemia using pseudo-ECG. PLoS ONE 2019, 14, e0220294. [Google Scholar] [CrossRef] [PubMed]
- Potyagaylo, D.; Chmelevsky, M.; van Dam, P.; Budanova, M.; Zubarev, S.; Treshkur, T.; Lebedev, D. ECG Adapted Fastest Route Algorithm to Localize the Ectopic Excitation Origin in CRT Patients. Front. Physiol. 2019, 10, 183. [Google Scholar] [CrossRef]
- Feng, Y.; Roney, C.; Hocini, M.; Niederer, S.; Vigmond, E. Robust Atrial Ectopic Beat Classification From Surface ECG Using Second-Order Blind Source Separation. Comput. Cardiol. 2020, 47. [Google Scholar] [CrossRef]
- Yang, T.; Yu, L.; Jin, Q.; Wu, L.; He, B. Localization of Origins of Premature Ventricular Contraction by Means of Convolutional Neural Network From 12-Lead ECG. IEEE Trans. Biomed. Eng. 2018, 65, 1662–1671. [Google Scholar] [CrossRef]
- Ferrer-Albero, A.; Godoy, E.J.; Lozano, M.; Martínez-Mateu, L.; Atienza, F.; Saiz, J.; Sebastian, R. Non-invasive localization of atrial ectopic beats by using simulated body surface P-wave integral maps. PLoS ONE 2017, 12, e0181263. [Google Scholar] [CrossRef] [PubMed]
- Kania, M.; Coudière, Y.; Cochet, H.; Haissaguerre, M.; Jais, P.; Potse, M. Prediction of the Exit Site of Ventricular Tachycardia Based on Different ECG Lead Systems. Comput. Cardiol. 2017, 44. [Google Scholar] [CrossRef]
- Lyon, A.; Bueno-Orovio, A.; Zacur, E.; Ariga, R.; Grau, V.; Neubauer, S.; Watkins, H.; Rodriguez, B.; Mincholé, A. Electrocardiogram phenotypes in hypertrophic cardiomyopathy caused by distinct mechanisms: Apico-basal repolarization gradients vs. Purkinje-myocardial coupling abnormalities. EP Eur. 2018, 20, iii102–iii112. [Google Scholar] [CrossRef]
- Potse, M.; Krause, D.; Kroon, W.; Murzilli, R.; Muzzarelli, S.; Regoli, F.; Caiani, E.; Prinzen, F.W.; Krause, R.; Auricchio, A. Patient-specific modelling of cardiac electrophysiology in heart-failure patients. EP Eur. 2014, 16 (Suppl. 4), iv56–iv61. [Google Scholar] [CrossRef]
- Nguyen, U.C.; Potse, M.; Regoli, F.; Caputo, M.L.; Conte, G.; Murzilli, R.; Muzzarelli, S.; Moccetti, T.; Caiani, E.G.; Prinzen, F.W.; et al. An in-silico analysis of the effect of heart position and orientation on the ECG morphology and vectorcardiogram parameters in patients with heart failure and intraventricular conduction defects. J. Electrocardiol. 2015, 48, 617–625. [Google Scholar] [CrossRef] [PubMed]
- Giffard-Roisin, S.; Fovargue, L.; Webb, J.; Molléro, R.; Lee, J.; Delingette, H.; Ayache, N.; Razavi, R.; Sermesant, M. Estimation of Purkinje Activation from ECG: An Intermittent Left Bundle Branch Block Study. Lect. Notes Comput. Sci. 2017, 10124, 135–142. [Google Scholar] [CrossRef]
- Nguyên, U.C.; Potse, M.; Vernooy, K.; Mafi-Rad, M.; Heijman, J.; Caputo, M.L.; Conte, G.; Regoli, F.; Krause, R.; Moccetti, T.; et al. A left bundle branch block activation sequence and ventricular pacing influence voltage amplitudes: An in vivo and in silico study. EP Eur. 2018, 20, iii77–iii86. [Google Scholar] [CrossRef]
- Zhou, Z.; Jin, Q.; Yu, L.; Wu, L.; He, B. Noninvasive Imaging of Human Atrial Activation during Atrial Flutter and Normal Rhythm from Body Surface Potential Maps. PLoS ONE 2016, 11, e0163445. [Google Scholar] [CrossRef] [PubMed]
- Pezzuto, S.; Gharaviri, A.; Schotten, U.; Potse, M.; Conte, G.; Caputo, M.L.; Regoli, F.; Krause, R.; Auricchio, A. Beat-to-beat P-wave morphological variability in patients with paroxysmal atrial fibrillation: An in silico study. EP Eur. 2018, 20, iii26–iii35. [Google Scholar] [CrossRef]
- Filos, D.; Tachmatzidis, D.; Maglaveras, N.; Vassilikos, V.; Chouvarda, I. Understanding the Beat-to-Beat Variations of P-Waves Morphologies in AF Patients During Sinus Rhythm: A Scoping Review of the Atrial Simulation Studies. Front. Physiol. 2019, 10, 742. [Google Scholar] [CrossRef]
- Lehrmann, H.; Jadidi, A.S.; Minners, J.; Chen, J.; Müller-Edenborn, B.; Weber, R.; Dössel, O.; Arentz, T.; Loewe, A. Novel Electrocardiographic Criteria for Real-Time Assessment of Anterior Mitral Line Block. JACC Clin. Electrophysiol. 2018, 4, 920–932. [Google Scholar] [CrossRef]
- Luongo, G.; Schuler, S.; Luik, A.; Almeida, T.P.; Soriano, D.C.; Dossel, O.; Loewe, A. Non-Invasive Characterization of Atrial Flutter Mechanisms Using Recurrence Quantification Analysis on the ECG: A Computational Study. IEEE Trans. Biomed. Eng. 2021, 68, 914–925. [Google Scholar] [CrossRef]
- Luongo, G.; Schuler, S.; Rivolta, M.W.; Dössel, O.; Sassi, R.; Loewe, A. Automatic ECG-based Discrimination of 20 Atrial Flutter Mechanisms: Influence of Atrial and Torso Geometries. Comput. Cardiol. 2020. [Google Scholar] [CrossRef]
- Saha, M.; Conte, G.; Caputo, M.L.; Regoli, F.; Krause, R.; Auricchio, A.; Jacquemet, V. Changes in P-wave morphology after pulmonary vein isolation: Insights from computer simulations. Europace 2016, 18, iv23–iv34. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, M.; Climent, A.M.; Liberos, A.; Fernández-Avilés, F.; Berenfeld, O.; Atienza, F.; Guillem, M.S. Highest dominant frequency and rotor positions are robust markers of driver location during noninvasive mapping of atrial fibrillation: A computational study. Heart Rhythm 2017, 14, 1224–1233. [Google Scholar] [CrossRef]
- Irakoze, E.; Jacquemet, V. Simulated P wave morphology in the presence of endo-epicardial activation delay. EP Eur. 2018, 20, iii16–iii25. [Google Scholar] [CrossRef] [PubMed]
- Nagel, C.; Luongo, G.; Azzolin, L.; Schuler, S.; Dössel, O.; Loewe, A. Non-Invasive and Quantitative Estimation of Left Atrial Fibrosis Based on P Waves of the 12-Lead ECG—A Large-Scale Computational Study Covering Anatomical Variability. J. Clin. Med. 2021, 10, 1797. [Google Scholar] [CrossRef]
- Luongo, G.; Azzolin, L.; Schuler, S.; Rivolta, M.W.; Almeida, T.P.; Martínez, J.P.; Soriano, D.C.; Luik, A.; Müller-Edenborn, B.; Jadidi, A.; et al. Machine learning enables noninvasive prediction of atrial fibrillation driver location and acute pulmonary vein ablation success using the 12-lead ECG. Cardiovasc. Digit. Health J. 2021, 2, 126–136. [Google Scholar] [CrossRef]
- Seemann, G.; Weiß, D.L.; Sachse, F.B.; Dössel, O. Simulation of the Long-QT Syndrome in a Model of Human Myocardium. Comput. Cardiol. 2003, 30, 287–290. [Google Scholar]
- Weiss, D.L.; Seemann, G.; Sachse, F.B.; Dössel, O. Modelling of the short QT syndrome in a heterogeneous model of the human ventricular wall. EP Eur. 2005, 7s2, 105–117. [Google Scholar] [CrossRef]
- Seemann, G.; Alvarez de Eulate, M.; Konrad, N.; Maier, J.; Wilhelms, M.; Keller, D.; Dössel, O.; Scholz, E. Evaluating body surface ECG differences of simulated long-QT syndromes. Comput. Cardiol. 2013, 40, 345–348. [Google Scholar]
- Hernández Mesa, M.; Pilia, N.; Dössel, O.; Severi, S.; Loewe, A. Effects of Serum Calcium Changes on the Cardiac Action Potential and the ECG in a Computational Model. Curr. Dir. Biomed. Eng. 2018, 4, 251–254. [Google Scholar] [CrossRef]
- Hernández Mesa, M.; Pilia, N.; Dössel, O.; Loewe, A. Influence of ECG Lead Reduction Techniques for Extracellular Potassium and Calcium Concentration Estimation. Curr. Dir. Biomed. Eng. 2019, 5, 69–72. [Google Scholar] [CrossRef]
- Loewe, A.; Lutz, Y.; Nairn, D.; Fabbri, A.; Nagy, N.; Toth, N.; Ye, X.; Fuertinger, D.H.; Genovesi, S.; Kotanko, P.; et al. Hypocalcemia-Induced Slowing of Human Sinus Node Pacemaking. Biophys. J. 2019, 117, 2244–2254. [Google Scholar] [CrossRef] [PubMed]
- Pilia, N.; Hernandez Mesa, M.; Dössel, O.; Loewe, A. ECG-based Estimation of Potassium and Calcium Concentrations: Proof of Concept with Simulated Data. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 2610–2613. [Google Scholar] [CrossRef]
- Pilia, N.; Severi, S.; Raimann, J.G.; Genovesi, S.; Dössel, O.; Kotanko, P.; Corsi, C.; Loewe, A. Quantification and classification of potassium and calcium disorders with the electrocardiogram: What do clinical studies, modeling, and reconstruction tell us? APL Bioeng. 2020, 4, 041501. [Google Scholar] [CrossRef]
- Pilia, N.; Corsi, C.; Severi, S.; Dössel, O.; Loewe, A. Reconstruction of Potassium Concentrations with the ECG on Imbalanced Datasets. arXiv 2020, arXiv:2006.05212. [Google Scholar]
- Wilhelms, M.; Rombach, C.; Scholz, E.P.; Doessel, O.; Seemann, G. Impact of amiodarone and cisapride on simulated human ventricular electrophysiology and electrocardiograms. EP Eur. 2012, 14, v90–v96. [Google Scholar] [CrossRef] [PubMed]
- Zemzemi, N.; Bernabeu, M.O.; Saiz, J.; Cooper, J.; Pathmanathan, P.; Mirams, G.R.; Pitt-Francis, J.; Rodriguez, B. Computational assessment of drug-induced effects on the electrocardiogram: from ion channel to body surface potentials. Br. J. Pharmacol. 2013, 168, 718–733. [Google Scholar] [CrossRef]
- Zemzemi, N.; Rodriguez, B. Effects of L-type calcium channel and human ether-a-go-go related gene blockers on the electrical activity of the human heart: A simulation study. EP Eur. 2015, 17, 326–333. [Google Scholar] [CrossRef] [PubMed]
- Oosterom, A.V.; Oostendorp, T.F. ECGSIM: An interactive tool for studying the genesis of QRST forms. Heart 2004, 90, 165–168. [Google Scholar] [CrossRef]
- Plank, G.; Loewe, A.; Neic, A.; Augustin, C.; Huang, Y.L.; Gsell, M.A.; Karabelas, E.; Nothstein, M.; Prassl, A.J.; Sánchez, J.; et al. The openCARP simulation environment for cardiac electrophysiology. Comput. Methods Programs Biomed. 2021, 208, 106223. [Google Scholar] [CrossRef]
- Sánchez, J.; Nothstein, M.; Neic, A.; Huang, Y.L.; Prassl, A.J.; Klar, J.; Ulrich, R.; Bach, F.; Zschumme, P.; Selzer, M.; et al. openCARP: An Open Sustainable Framework for In-Silico Cardiac Electrophysiology Research. Comput. Cardiol. 2020, 47. [Google Scholar] [CrossRef]
- Seemann, G.; Sachse, F.B.; Karl, M.; Weiss, D.L.; Heuveline, V.; Dössel, O. Framework for modular, flexible and efficient solving the cardiac bidomain equation using PETSc. Math. Ind. 2010, 15, 363–369. [Google Scholar] [CrossRef]
- Sundnes, J.; Nielsen, B.F.; Mardal, K.A.; Cai, X.; Lines, G.T.; Tveito, A. On the computational complexity of the bidomain and the monodomain models of electrophysiology. Ann. Biomed. Eng. 2006, 34, 1088–1097. [Google Scholar] [CrossRef] [PubMed]
- Cooper, F.; Baker, R.; Bernabeu, M.; Bordas, R.; Bowler, L.; Bueno-Orovio, A.; Byrne, H.; Carapella, V.; Cardone-Noott, L.; Cooper, J.; et al. Chaste: Cancer, Heart and Soft Tissue Environment. J. Open Source Softw. 2020, 5, 1848. [Google Scholar] [CrossRef]
- Krause, D.; Potse, M.; Dickopf, T.; Krause, R.; Auricchio, A.; Prinzen, F. Hybrid Parallelization of a Large-Scale Heart Model. Lect. Notes Comput. Sci. 2012, 7174, 120–132. [Google Scholar] [CrossRef]
- Quarteroni, A.; Manzoni, A.; Vergara, C. The cardiovascular system: Mathematical modelling, numerical algorithms and clinical applications. Acta Numer. 2017, 26, 365–590. [Google Scholar] [CrossRef]
- Niederer, S.A.; Kerfoot, E.; Benson, A.P.; Bernabeu, M.O.; Bernus, O.; Bradley, C.; Cherry, E.M.; Clayton, R.; Fenton, F.H.; Garny, A.; et al. Verification of cardiac tissue electrophysiology simulators using an N-version benchmark. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 4331–4351. [Google Scholar] [CrossRef]
- Lyon, A.; Mincholé, A.; Martínez, J.P.; Laguna, P.; Rodriguez, B. Computational techniques for ECG analysis and interpretation in light of their contribution to medical advances. J. R. Soc. Interface 2018, 15, 20170821. [Google Scholar] [CrossRef] [PubMed]
- Potse, M. Scalable and Accurate ECG Simulation for Reaction-Diffusion Models of the Human Heart. Front. Physiol. 2018, 9, 370. [Google Scholar] [CrossRef] [PubMed]
- Pezzuto, S.; Kal’avský, P.; Potse, M.; Prinzen, F.W.; Auricchio, A.; Krause, R. Evaluation of a Rapid Anisotropic Model for ECG Simulation. Front. Physiol. 2017, 8, 265. [Google Scholar] [CrossRef] [PubMed]
- Keller, D.U.J.; Weber, F.M.; Seemann, G.; Dössel, O. Ranking the Influence of Tissue Conductivities on Forward-Calculated ECGs. IEEE Trans. Biomed. Eng. 2010, 57, 1568–1576. [Google Scholar] [CrossRef]
- Schuler, S.; Tate, J.D.; Oostendorp, T.F.; MacLeod, R.S.; Dössel, O. Spatial Downsampling of Surface Sources in the Forward Problem of Electrocardiography. In Functional Imaging and Modeling of the Heart; Lecture Notes in Computer Science; Coudière, Y., Ozenne, V., Vigmond, E., Zemzemi, N., Eds.; Springer International Publishing: Berlin, Germany, 2019; Volume 11504, pp. 29–36. [Google Scholar] [CrossRef]
- Neic, A.; Campos, F.O.; Prassl, A.J.; Niederer, S.A.; Bishop, M.J.; Vigmond, E.J.; Plank, G. Efficient computation of electrograms and ECGs in human whole heart simulations using a reaction-eikonal model. J. Comput. Phys. 2017, 346, 191–211. [Google Scholar] [CrossRef] [PubMed]
- Schuler, S.; Pilia, N.; Potyagaylo, D.; Loewe, A. Cobiveco: Consistent biventricular coordinates for precise and intuitive description of position in the heart—With MATLAB implementation. arXiv 2021, arXiv:2102.02898. [Google Scholar]
- Bayer, J.; Prassl, A.J.; Pashaei, A.; Gomez, J.F.; Frontera, A.; Neic, A.; Plank, G.; Vigmond, E.J. Universal ventricular coordinates: A generic framework for describing position within the heart and transferring data. Med. Image Anal. 2018, 45, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Roney, C.H.; Pashaei, A.; Meo, M.; Dubois, R.; Boyle, P.M.; Trayanova, N.A.; Cochet, H.; Niederer, S.A.; Vigmond, E.J. Universal atrial coordinates applied to visualisation, registration and construction of patient specific meshes. Med. Image Anal. 2019, 55, 65–75. [Google Scholar] [CrossRef] [PubMed]
- Opthof, T.; Remme, C.A.; Jorge, E.; Noriega, F.; Wiegerinck, R.F.; Tasiam, A.; Beekman, L.; Alvarez-Garcia, J.; Munoz-Guijosa, C.; Coronel, R.; et al. Cardiac activation-repolarization patterns and ion channel expression mapping in intact isolated normal human hearts. Heart Rhythm 2017, 14, 265–272. [Google Scholar] [CrossRef]
- Wachter, A.; Loewe, A.; Krueger, M.W.; Dössel, O.; Seemann, G. Mesh structure-independent modeling of patient-specific atrial fiber orientation. Curr. Dir. Biomed. Eng. 2015, 1, 409–412. [Google Scholar] [CrossRef]
- Nagel, C.; Pilia, N.; Loewe, A.; Dössel, O. Quantification of Interpatient 12-lead ECG Variabilities within a Healthy Cohort. Curr. Dir. Biomed. Eng. 2020, 6, 493–496. [Google Scholar] [CrossRef]
- Rajendra Acharya, U.; Paul Joseph, K.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart rate variability: A review. Med. Biol. Eng. Comput. 2006, 44, 1031–1051. [Google Scholar] [CrossRef]
- Wilders, R.; Hoekstra, M.; van Ginneken, A.C.G.; Verkerk, A.O. Beta-adrenergic modulation of heart rate: Contribution of the slow delayed rectifier K+ current (IKs). Comput. Cardiol. 2010, 37, 629–631. [Google Scholar]
- Dössel, O.; Reumann, M.; Seemann, G.; Weiss, D. The missing link between cardiovascular rhythm control and myocardial cell modeling. Biomed Tech. 2006, 51, 205–209. [Google Scholar] [CrossRef]
- Rodero, C.; Strocchi, M.; Marciniak, M.; Longobardi, S.; Whitaker, J.; O’Neill, M.D.; Gillette, K.; Augustin, C.; Plank, G.; Vigmond, E.J.; et al. Linking statistical shape models and simulated function in the healthy adult human heart. PLoS Comput. Biol. 2021, 17, e1008851. [Google Scholar] [CrossRef]
- Potyagaylo, D.; Seemann, G.; Schulze, W.; Dössel, O. Magnetocardiography did not uncover electrically silent ischemia in an in-silico study case. Comput. Cardiol. 2015, 42, 1145–1148. [Google Scholar]
- Ghasemi, M. Electrocardiographic imaging of myocardial infarction using heart vector analysis. Comput. Cardiol. 2007. [Google Scholar] [CrossRef]
- Sapp, J.L.; Bar-Tal, M.; Howes, A.J.; Toma, J.E.; El-Damaty, A.; Warren, J.W.; MacInnis, P.J.; Zhou, S.; Horáček, B.M. Real-Time Localization of Ventricular Tachycardia Origin From the 12-Lead Electrocardiogram. JACC Clin. Electrophysiol. 2017, 3, 687–699. [Google Scholar] [CrossRef] [PubMed]
- Segal, O.R.; Chow, A.W.C.; Wong, T.; Trevisi, N.; Lowe, M.D.; Davies, D.W.; Della Bella, P.; Packer, D.L.; Peters, N.S. A novel algorithm for determining endocardial VT exit site from 12-lead surface ECG characteristics in human, infarct-related ventricular tachycardia. J. Cardiovasc. Electrophysiol. 2007, 18, 161–168. [Google Scholar] [CrossRef]
- Potyagaylo, D.; Loewe, A.; van Dam, P.; Dössel, O. ECG imaging of focal atrial excitation: Evaluation in a realistic simulation setup. Comput. Cardiol. 2016, 43, 113–116. [Google Scholar] [CrossRef]
- Medi, C.; Kalman, J.M. Prediction of the atrial flutter circuit location from the surface electrocardiogram. EP Eur. 2008, 10, 786–796. [Google Scholar] [CrossRef]
- Ruipérez-Campillo, S.; Castrejón, S.; Martínez, M.; Cervigón, R.; Meste, O.; Merino, J.L.; Millet, J.; Castells, F. Non-invasive characterisation of macroreentrant atrial tachycardia types from a vectorcardiographic approach with the slow conduction region as a cornerstone. Comput. Methods Programs Biomed. 2021, 200, 105932. [Google Scholar] [CrossRef]
- Schwartz, P.J.; Ackerman, M.J.; Antzelevitch, C.; Bezzina, C.R.; Borggrefe, M.; Cuneo, B.F.; Wilde, A.A.M. Inherited cardiac arrhythmias. Nat. Rev. Dis. Prim. 2020, 6, 767–779. [Google Scholar] [CrossRef]
- Shimizu, W.; Antzelevitch, C. Cellular basis for the ECG features of the LQT1 form of the long-QT syndrome: Effects of [beta]-adrenergic agonists and antagonists and sodium channel blockers on transmural dispersion of repolarization and torsade de pointes. Circulation 1998, 98, 2314–2322. [Google Scholar] [CrossRef]
- Wald, D.A. ECG manifestations of selected metabolic and endocrine disorders. Emerg. Med. Clin. N. Am. 2006, 24, 145–157. [Google Scholar] [CrossRef]
- Bukhari, H.A.; Palmieri, F.; Ferreira, D.; Potse, M.; Ramírez, J.; Laguna, P.; Sánchez, C.; Pueyo, E. Transmural Ventricular Heterogeneities Play a Major Role in Determining T-Wave Morphology at Different Extracellular Potassium Levels. Comput. Cardiol. 2019, 1–4. [Google Scholar] [CrossRef]
- Loewe, A.; Hernandez Mesa, M.; Pilia, N.; Severi, S.; Dössel, O. A heterogeneous formulation of the Himeno et al. human ventricular myocyte model for simulation of Body Surface ECGs. Comput. Cardiol. 2018, 45. [Google Scholar] [CrossRef]
- Cavero, I.; Holzgrefe, H. CiPA: Ongoing testing, future qualification procedures, and pending issues. J. Pharmacol. Toxicol. Methods 2015, 76, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Corrias, A.; Jie, X.; Romero, L.; Bishop, M.J.; Bernabeu, M.; Pueyo, E.; Rodriguez, B. Arrhythmic risk biomarkers for the assessment of drug cardiotoxicity: From experiments to computer simulations. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2010, 368, 3001–3025. [Google Scholar] [CrossRef] [PubMed]
- Passini, E.; Britton, O.J.; Lu, H.R.; Rohrbacher, J.; Hermans, A.N.; Gallacher, D.J.; Greig, R.J.H.; Bueno-Orovio, A.; Rodriguez, B. Human Drug Trials Demonstrate Higher Accuracy than Animal Models in Predicting Clinical Pro-Arrhythmic Cardiotoxicity. Front. Physiol. 2017, 8, 668. [Google Scholar] [CrossRef] [PubMed]
- Loewe, A.; Lutz, Y.; Wilhelms, M.; Sinnecker, D.; Barthel, P.; Scholz, E.P.; Dössel, O.; Schmidt, G.; Seemann, G. In-silico assessment of the dynamic effects of amiodarone and dronedarone on human atrial patho-electrophysiology. EP Eur. 2014, 16, iv30–iv38. [Google Scholar] [CrossRef]
- Mamoshina, P.; Rodriguez, B.; Bueno-Orovio, A. Toward a broader view of mechanisms of drug cardiotoxicity. Cell Rep. Med. 2021, 2, 100216. [Google Scholar] [CrossRef]
- Yuan, Y.; Bai, X.; Luo, C.; Wang, K.; Zhang, H. The virtual heart as a platform for screening drug cardiotoxicity. Br. J. Pharmacol. 2015, 172, 5531–5547. [Google Scholar] [CrossRef]
- Romero, L.; Trenor, B.; Yang, P.C.; Saiz, J.; Clancy, C.E. In silico screening of the impact of hERG channel kinetic abnormalities on channel block and susceptibility to acquired long QT syndrome. J. Mol. Cell. Cardiol. 2014, 72, 126–137. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Luo, C.; Wang, K.; Zhang, H. Modelling the effects of chloroquine on KCNJ2-linked short QT syndrome. Oncotarget 2017, 8, 106511–106526. [Google Scholar] [CrossRef] [PubMed]
- Jie, X.; Rodriguez, B.; Pueyo, E. A new ECG biomarker for drug toxicity: A combined signal processing and computational modeling study. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 2565–2568. [Google Scholar] [CrossRef]
- Saiz, J.; Gomis-Tena, J.; Monserrat, M.; Ferrero, J.M.J.; Cardona, K.; Chorro, J. Effects of the antiarrhythmic drug dofetilide on transmural dispersion of repolarization in ventriculum. A computer modeling study. IEEE Trans. Biomed. Eng. 2011, 58, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Dux-Santoy, L.; Sebastian, R.; Felix-Rodriguez, J.; Ferrero, J.M.; Saiz, J. Interaction of specialized cardiac conduction system with antiarrhythmic drugs: A simulation study. IEEE Trans. Biomed. Eng. 2011, 58, 3475–3478. [Google Scholar] [CrossRef]
- Trenor, B.; Gomis-Tena, J.; Cardona, K.; Romero, L.; Rajamani, S.; Belardinelli, L.; Giles, W.R.; Saiz, J. In silico assessment of drug safety in human heart applied to late sodium current blockers. Channels 2013, 7, 249–262. [Google Scholar] [CrossRef]
- Park, J.S. Introduction to in silico model for proarrhythmic risk assessment under the CiPA initiative. Transl. Clin. Pharmacol. 2019, 27, 12–18. [Google Scholar] [CrossRef]
- Niederer, S.A.; Aboelkassem, Y.; Cantwell, C.D.; Corrado, C.; Coveney, S.; Cherry, E.M.; Delhaas, T.; Fenton, F.H.; Panfilov, A.V.; Pathmanathan, P.; et al. Creation and application of virtual patient cohorts of heart models. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2020, 378, 20190558. [Google Scholar] [CrossRef]
- Nagel, C.; Schuler, S.; Dössel, O.; Loewe, A. A Bi-atrial Statistical Shape Model and 100 Volumetric Anatomical Models of the Atria. Zenodo 2020. [Google Scholar] [CrossRef]
- Corrado, C.; Razeghi, O.; Roney, C.; Coveney, S.; Williams, S.; Sim, I.; O’Neill, M.; Wilkinson, R.; Oakley, J.; Clayton, R.H.; et al. Quantifying atrial anatomy uncertainty from clinical data and its impact on electro-physiology simulation predictions. Med. Image Anal. 2020, 61, 101626. [Google Scholar] [CrossRef]
- Schuler, S.; Loewe, A. Biventricular statistical shape model of the human heart adapted for computer simulations. Zenodo 2021. [Google Scholar] [CrossRef]
- Bai, W.; Shi, W.; de Marvao, A.; Dawes, T.J.; O’Regan, D.P.; Cook, S.A.; Rueckert, D. A bi-ventricular cardiac atlas built from 1000+ high resolution MR images of healthy subjects and an analysis of shape and motion. Med. Image Anal. 2015, 26, 133–145. [Google Scholar] [CrossRef] [PubMed]
- Pishchulin, L.; Wuhrer, S.; Helten, T.; Theobalt, C.; Schiele, B. Building statistical shape spaces for 3D human modeling. Pattern Recognit. 2017, 67, 276–286. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).