Abstract
In the context of a full-potential orbital-free approach for the modeling of multi-atomic systems we investigated the dependence of the cohesive energies and bulk elastic modules of the large nanosystems Cn (n is up to 4096 atoms), Aln (n is up to 23,328 atoms) and tin (n is up to 2160 atoms). It was shown that the cohesive energies and elastic modules tend towards bulk crystal values at n ≈ 3000 for Cn systems, at n ≈ 1500 for Tin and at n ≈ 20,000 for Aln. The execution time for one energy iteration for Ti23328 was only 23 min.
1. Introduction
Modern technologies—nanotechnologies, bio-engineering, drug production and so on—need powerful tools to predict the properties of systems containing hundreds of thousands or millions of atoms. Traditional quantum-mechanical approaches, such as the Kohn–Sham (KS) version of the density functional theory (DFT), do not provide an opportunity to operate with large amounts of atoms; their limits do not exceed several thousand atoms, even using pseudopotentials, not to mention full-electron calculations. Methods using empirical potentials allow operation with large systems, but they do not provide reliable results. On the other hand, opportunities for increasing computer speed are nearing their physical limit; thus, it is useless to hope for a solution to the problem this way. A new modeling method is urgently needed, one which could combine quantum-mechanical accuracy with the possibility of operating with an enormous number of atoms. The idea of such a method arose in 1964 when Hohenberg and Kohn formulated a theorem [1] that suggested the ground state energy of any quantum system is completely defined by its electronic density. In the same work, they declared that there is a certain universal functional Ee[ρ], through which minimization leads to the equilibrium of the electronic density ρ and total electron energy Ee. The functional Ee[ρ] has been written in the following form:
where ε(ρ) is the density of total electron energy, V(r) is an external potential, φ(r) is the electrostatic Hartree potential and εex−c(ρ) and εkin(ρ) are the exchange-correlation and kinetic energies (per electron).
Minimization of (1) with a condition indicates the solution has the following equation (Nel is the number of electrons in the system):
where μ(r) is the electron chemical potential, which depends on coordinates in finite systems.
It follows from (2):
In our case the external potential V(r) is a sum of full-electron atomic potentials: , where Zi is a nuclear charge of the i-atom. The Hartree potential may be calculated using Fourier transformations or Poisson equations.
There are some realistic approximations for the exchange-correlation energy εex−c(ρ) (for example the local density approximation (LDA) [2,3]). The only real problem is the kinetic energy εkin(ρ). There were attempts to use the Thomas and Fermi (TF) approximation [4,5] based on the free electron approach:
This functional was found to be absolutely inadequate (all molecules were unstable); the von Weizsacker (W) gradient correction [6] added to the TF did not solve the problem either (binding energies were incorrect).
Kohn and Sham offered an approach to act as a compromise [7]. They proposed to find the kinetic energy Ekin by solving a one-electron equation, which is known now as the Kohn–Sham (KS) equation. This approach has become widely popular; many effective computing programs were created on its basis, and many tasks of modeling of multi-atomic systems were solved. However, as has been mentioned above, its potential in the full-electron approach are almost exhausted.
The orbital-free (OF) approach as a version of the density functional theory could present an alternative to the KS method. The advantage of this approach is obvious: operating only with an electronic density instead of numerous wave functions, it allows for sharply increasing the speed of calculations and the inclusion of a huge number of atoms.
The first attempts to develop the OF method of modeling began about 20 years ago with simulations of liquid metals in the jellium approximation [8]. Then, works by other researchers (see, for example, reviews and original papers [9,10,11,12]) were applied to some simple molecules and solids. All of these works were based on the use of special pseudopotentials, with most of them trying to use the TF and W approximations for the kinetic energy in different combinations. However, these attempts did not have a large degree of success and were not widely adopted. In addition, there has not been a single work that proposes an OF full-electron modeling method. It seems to us that the main reason for this is that researchers try to use some universal functional of kinetic energy for all systems. It was recently shown [13,14] that the Hohenberg–Kohn idea about the existence of a universal density functional leading to the energy minimum was not strictly proved. Therefore, the search for specific types of kinetic potentials is necessary and justified.
In our recent work [15] we described an orbital-free full-potential (OF-FP) approach that works without pseudopotentials and demonstrated that it is possible to use this approach for modeling atomic systems on the basis of single-atomic kinetic potentials obtained from KS calculations. We found equilibrium bond lengths and binding energies for homoatomic dimers from Li2 up to Cl2 as well as for some heteroatomic dimers. We analyzed our results and concluded that they corresponded well with experimental data results received by means of full-electrons calculations using the KS method. Now we describe the OF-FP approach developed for large multi-atomic systems and demonstrate how it is suitable for objects comprising thousands of atoms.
2. The Main Details of the Approach
For some multi-atomic systems we can introduce
Our aim is to find the density ρ(r) that satisfies the equation
To find this density we use the iteration procedure:
where K is a numeral parameter controlling convergence. The sum of atomic densities can be taken as the initial density .
There are two problems concerning Equation (6). First, we do not know the kinetic potential μkin(ρ), including that of F(ρ). Second, we do not know the chemical potential µ(r). The second problem is simple: we have to find the equilibrium F(ρ) and then obtain µ(r) from the equation . The first problem is a principal one. It was proposed in our work [15] that the kinetic potential for a two-atomic system could be defined through the single-atomic potential :
where f is a function of the interatomic distance d. Now, for multi-atomic systems, we propose using the same approximation for but with f depending on the average nearest-neighbor distance dav.; a special type of f (dav) must be determined for each system type.
The single-atomic potential can be easily found from a usual KS calculation. If we know the equilibrium atomic total density ρa we can write:
where we have taken µa = 0.
Therefore, the atomic kinetic potential can be found:
Then, as we know ρa(r) we can easily transform to .
If we found the equilibrium ρ(r) of the system we can calculate the total energy Etot:
where is the Hartree energy; is the Coulomb energy; is the exchange-correlation energy; is the kinetic energy; and is the energy of interatomic repulsion, . In this work we used the LDA approximation for the exchange-correlation energy for simplicity’s sake.
To find the equilibrium atomic geometry of the system we calculated atomic forces as minus derivatives of the total energy with respect to the coordinates of the atoms, and then we moved atoms until the energy change was less than 0.01 eV per atom near the energy minimum. After that we were able to find the equilibrium density ρ following the iteration procedure Equation (6) and calculate the equilibrium total energy from Equation (10).
3. Cohesive Energy
To test our approach for large systems we performed calculations for the cohesive energy for carbon (covalent material), aluminum (simple metal) and titanium (transition metal). Carbon systems were taken as diamond cubic fragments, aluminum was tested in the form of face-centered cube fragments and titanium was studied as particles with a hexagonal close-packed structure. To find the equilibrium electronic densities of single C, Al and Ti atoms we used the FHI98pp code [16] that usually is applied to construct pseudopotentials; however, in the process of pseudopotential construction, this code calculates the full electronic structure of the atom and the total density. Knowing the equilibrium densities, we found single atomic kinetic potentials according to Equation (5).
Omitting the technical details of the calculations, we emphasize the fundamental point: to calculate kinetic potentials for various materials, our approach requires specifying some functions f(dav) (see Equation (7)), which should ensure that the results obtained are comparable to experimental ones. However, as was mentioned in [17], the energy of the system should depend not only on dav, but also on how many of the nearest neighbors each atom has. Taking these considerations into account, we propose the following types of functions f for the materials we investigated:
Here, Nn is average number of the nearest neighbors, which depend on the structure of the system and usually increase with increasing of the system; the numerical parameters included in the functions do not depend on the number of atoms. We understand that careful work should be carried out to identify the relationship between the interatomic density and kinetic functional. In this work, we identified only a simple semi-empirical connection. We hope that in following research we will be able to move forward in this direction.
All the systems were studied in the cubic cell with the sides of 55 Ǻ for carbon, 88 Ǻ for aluminum and 85 Ǻ for titanium; the number of atoms varied, reaching up to 4096 for carbon, up to 2196 for titanium and up to 23,328 for aluminum; a standard personal computer was used for calculations.
The speed of the calculations depends on the density of the three-dimensional grid, which divides the work cell to perform the needed integrations. For each material, we aimed to use a mesh with the lowest density possible, which still gave results with reasonable accuracy. For carbon, with its compact atoms, we used a mesh of 130 × 130 × 130. A mesh of 50 × 50 × 50 was sufficient for diffusive aluminum, and for d-metal titanium the best results were obtained with a mesh of 150 × 150 × 150. We investigated the dependence of the cohesive energy Ecoh and the average nearest-neighbor distance dav on the size of the system. All studied systems had ideal crystal structures as initial states for structure optimization. Density optimization was performed after reaching structural equilibrium. The results of the calculations are presented in Figure 1.
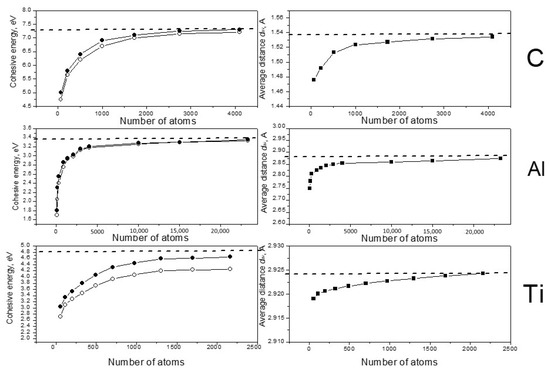
Figure 1.
Dependence of the cohesive energy Ecoh (the left column) and the average nearest-neighbor distance dav (the right column) on the system size. Open circles demonstrate energy results without optimization of the density; solid circles show the cohesive energy for the equilibrium density. Dashed lines present experimental values of Ecoh and dav for bulk crystal materials [18,19].
One can see that in all cases the calculated values of Ecoh and dav increased with the increasing of the systems in accordance with known data for small clusters of carbon [20,21], aluminum [22,23] and titanium [17,24]. In the case of carbon, the cohesive energy approached the crystal experimental value very well when the number of atoms neared 3000. Good convergence was found for titanium; the Ti energy results reached saturation for the 1300-atom system and reached the experimental value after density optimization. Aluminum demonstrated inferior convergence; it needed near 15,000–20,000 atoms to obtain cohesive energy results close the experimental value. It must be noted that the energy of titanium clusters changed in the process of the density optimization much more drastically than the energies of C and Al. For titanium we also observed another feature: the dav values increased very little as number of atoms increased, and the total change was less than 0.01 Ǻ. This result correlates with the conclusion of Houqian Sun et al. [17], who found that the distance values become nearly reach those of the bulk crystal in the 20-atom titanium cluster interatomic.
4. Bulk Elastic Modules
The main disadvantage of modeling polyatomic systems using the orbital-free approach is that it cannot be used to obtain information about the electronic structure of the system or about its electrical and optical properties. However, it can be effectively used to study mechanical properties. To do this, we must make sure that with its help it is possible not only to find the correct energy values, but also to correctly describe the forces of interatomic interactions, and the latter is most clearly manifested in elastic properties. Typically, this testing involves calculating the bulk modulus B.
To find the elastic modulus, we calculated the total energy of cubic particles Cn, Aln and Tin, which are fragments of the corresponding crystals, by changing the value of the crystal lattice parameter and fixing the position of all boundary atoms. When calculating the moduli of elasticity, the mesh density was increased to ensure the required accuracy. For carbon we used a mesh of 170 × 170 × 170, for aluminum a mesh of 100 × 100 × 100 was sufficient, and for titanium a mesh of 250 × 250 × 250 was used. Having thus found the dependence of the energy on the volume of the particle, we approximated the minimum value of this dependence using a parabola and found the quantity B using the formula , where Ea and va are the energy and volume per atom.
Figure 2 shows the dependence of the bulk modulus of the elasticity of the investigated materials on the particle size.
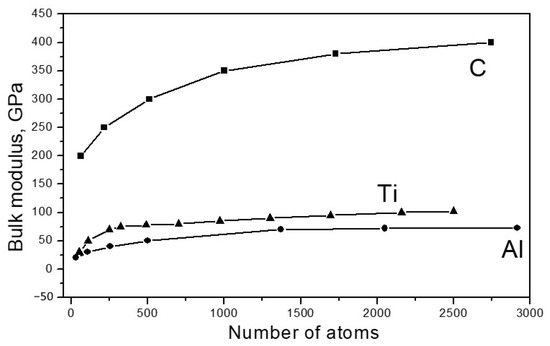
Figure 2.
Dependence of the value of the bulk modulus of elasticity B for particles Cn, Aln and Tin, on the number of atoms n.
As seen from Figure 2, for all materials under study, the modulus of elasticity increased with an increase in the particle size, approaching the values of Bcr typical for bulk crystals. For carbon, Bcr = 445 GPa, for aluminum, Bcr 72 = GPa and for titanium, Bcr = 120 GPa. There are a number of publications (for example [25,26,27,28,29]) that provide data indicating that the values of the elastic moduli of nanoparticles significantly exceed the corresponding values of the same moduli in bulk crystals. However, there is no contradiction to this in our results. The fact is that the structure of the nanoparticles, which are discussed in such works, significantly differs from the structure of a massive crystal; the atoms are better connected with each other energetically, which leads to an increase in elastic forces. In [30], where the dependence of the elastic properties of carbon, silicon and germanium, taken in the form of fragments of diamond lattices, was studied, results similar to ours were obtained; the elastic modulus increased with an increase in the size of the fragment.
One of the authors of this work (Zavodinsky) performed earlier calculations of the elastic properties (Young’s modulus) of silicon particles. In the case of [25], in which particles with an optimized structure were investigated, it was found that the environment of atoms had nothing to do with their environment in the crystal; the modulus of elasticity significantly exceeded its value in the crystal. When a fragment of a silicon crystal was taken as the object of investigation [31], the modulus of elasticity turned out to be much lower.
Thus, we can assert that our method adequately describes the elastic properties of large nano-objects and is suitable for studying their mechanical characteristics.
5. Speed, Convergence and Mesh Influence
The main characteristics of every modeling method are the speed of calculations and the possible maximum size of studied systems. As a rule, these quantities are interrelated, and ideally one would like to have a method that allows him to quickly explore huge systems. These characteristics are especially important for the OF approach, the meaning of which is to operate with large nanosystems. Figure 3 shows the dependence of calculation time per one structure optimization iteration on the system size. One can see that this dependence is linear, and the one iteration for 23 thousand of Al atoms only requires 23 min. For comparison, we calculated a cluster of five aluminum atoms using the ELK full-electronic package. The execution time of one iteration was 40 min. We hope that with further optimization of this method, we will be able to achieve even higher computational speed without the loss of accuracy.
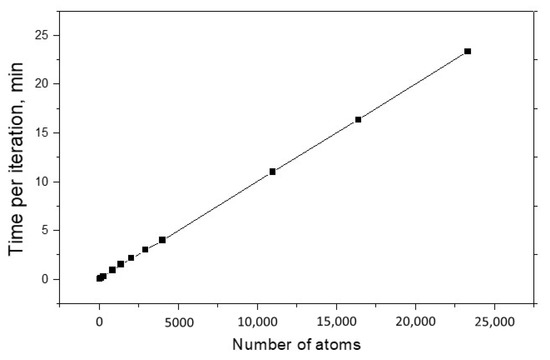
Figure 3.
The structure optimization time for the Al nano objects as a function of number of atoms.
Figure 4 demonstrates the convergence of energy calculations in the example of carbon systems. It can be seen that total number of iterations required for the full energy convergence is very realistic.
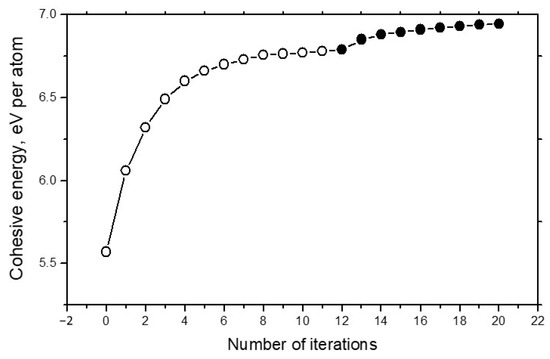
Figure 4.
Dependence of the cohesive energy Ecoh for the 1000-atom carbon system on number of iterations. Open circles concern the structure optimization, and solid circles show results of the density calculations.
As previously mentioned, the speed of calculations depends on the density of the mesh; the lower the density, the higher the speed. However, a decrease in density can lead to a loss in the accuracy of calculations. The dependence of energy results on the density of the three-dimensional mesh is shown in Figure 5 using Ti systems as an example. It is clear that the 125 × 125 × 125 mesh can be used for quick calculations; however, the 150 × 150 × 150 mesh leads to more accurate results.
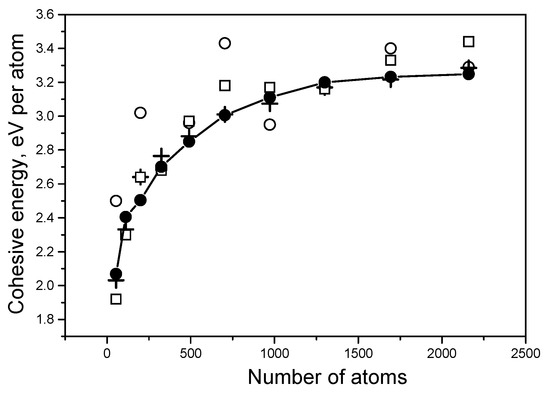
Figure 5.
Dependence of the cohesive energy Ecoh for Ti systems on the mesh density. Open circles concern the 50 × 50 × 50 mesh, and open squares correspond to the 100 × 100 × 100 mesh. Crosses show the results for the 125 × 125 × 125 mesh, and a solid curve with solid circles demonstrates calculations with the 150 × 150 × 150 mesh.
6. Conclusions
Using the examples of carbon, aluminum and titanium we demonstrated that our OF-FP approach allows us to describe the energy of large nanosystems up to tens of thousands of atoms in size. It was shown that the cohesive energies, interatomic distances and elastic modules tend towards bulk crystal values at n ≈ 3000 for Cn systems, at n ≈ 1500 for Tin and at n ≈ 20,000 for Aln. Our method has a high computational speed with a linear dependence of the computational time on the size of the system. The execution time enquired for one energy iteration to find the energy of Ti23328 is only 23 min. We hope that with further optimization of this method, we will be able to achieve even higher computational speed without a loss of accuracy.
In this paper we presented calculations for homogenous systems only. However, in our work [15] we described how to extend our approach for heterogeneous systems by using several weight functions, which construct kinetic potentials in the space between atoms of different types. We plan to calculate the elastic properties of heterogeneous systems, as well as explore the potential of our approach in the study of the processes of the mechanical processing of materials: cutting, fracturing and the like.
Author Contributions
Conceptualization, V.G.Z.; methodology, V.G.Z.; software, O.A.G.; investigation, V.G.Z.; formal analysis, O.A.G.; writing—original draft preparation, V.G.Z.; project administration, V.G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hohenberg, H.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Zunger, A.S. Self-interaction correction to density functional approximation for many-electron systems. Phys. Rev. 1981, 23, 5048–5079. [Google Scholar] [CrossRef] [Green Version]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. 1980, 45, 566–569. [Google Scholar]
- Thomas, L.H. The calculation of atomic field. Math. Proc. Camb. Philos. Soc. 1927, 23, 542–548. [Google Scholar] [CrossRef] [Green Version]
- Fermi, E. Un metodo statistic per la determinazione di alcune priorieta dell’atomo. Rend. Accad. Lincei 1927, 6, 602607. [Google Scholar]
- Weizsacker, C.F.v. Theorie de Kernmassen. Z. Physik 1935, 96, 431458. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, J.L. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 40, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Gomez, S.; Gonzalez, L.E.; Gonzalez, D.J.; Stott, M.J.; Dalgic, S.; Silbert, M.J. Orbital free ab initio molecular dynamic study of expanded liquid Cs. Non-Cryst. Solids 1999, 250–252, 163–167. [Google Scholar] [CrossRef]
- Wang, Y.A.; Carter, E.A. Orbital-free kinetic-energy density functional theory. In Theoretical Methods in Condensed Phase Chemistry; Schwartz, S.D., Ed.; Springer: Dordrecht, The Netherlands, 2002; pp. 117–184. [Google Scholar]
- Chen, H.; Zhou, A. Orbital-free density functional theory for molecular structure calculations. Numer. Math. Theory Methods Appl. 2008, 1, 1–28. [Google Scholar]
- Hung, L.; Carter, E.A. Accurate Simulations of Metals at the Mesoscale: Explicit Treatment of 1 Million Atoms with Quantum Mechanics. Chem. Phys. Lett. 2009, 475, 163–170. [Google Scholar] [CrossRef]
- Karasiev, V.V.; Chakraborty, D.; Trickey, S.B. Progress on New Approaches to Old Ideas: Orbital-Free Density Functionals. In Many-Electron Approaches in Physics, Chemistry and Mathematics. Mathematical Physics Studies; Bach, V., Delle, S.L., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 113–135. [Google Scholar]
- Sarry, A.M.; Sarry, M.F. To the density functional theory. Phys. Solid State 2012, l54, 1315–1322. [Google Scholar] [CrossRef]
- Bobrov, V.B.; Trigger, S.A. The problem of the universal density functional and the density matrix functional theory. J. Exp. Theor. Phys. 2013, 116, 635–640. [Google Scholar] [CrossRef]
- Zavodinsky, V.G.; Gorkusha, O.A. On a possibility to develop a full-potential orbital-free modelling approach. Nanosyst. Phys. Chem. Math. 2019, 9, 402–409. [Google Scholar] [CrossRef]
- Fuchs, M.; Scheffler, M. Ab initio pseudopotentials for electronic structure calculations of poly-atomic systems using density-functional theory. Comp. Phys. Commun. 1999, 119, 67–98. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Ren, Y.; Wu, Z.; Xu, N. Density functional calculation of the growth, electronic and bonding properties of titanium clusters Tin (n = 2–20). Comput. Theor. Chem. 2015, 1062, 74–83. [Google Scholar] [CrossRef]
- KnowledgeDoor. Available online: https://www.knowledgedoor.com/ (accessed on 12 October 2021).
- Wiley Online Library. Available online: https://onlinelibrary.wiley.com (accessed on 12 October 2021).
- Waschi, H.P.; Stoll, H.; Preuß, H. Ab-initio and PCILO Calculations of Diamond Clusters and the Corresponding Saturated Hydrocarbons. Z. Naturforsch. 1978, 83, 358–365. [Google Scholar] [CrossRef]
- Robertson, J. Diamond-like amorphous carbon. Mater. Sci. Eng. R 2002, 37, 129–281. [Google Scholar] [CrossRef] [Green Version]
- Ahlrichs, R.; Elliott, S.D. Clusters of aluminium, a density functional study. Phys. Chem. Chem. Phys. 1999, 1, 13–21. [Google Scholar] [CrossRef]
- Kiohara, V.O.; Carvalho, E.F.; Paschoal, C.W.; Machado, F.B.; Roberto-Neto, O. DFT and CCSD(T) electronic properties and structures of aluminum clusters: Alnx (n = 1–9, x = 0, ±1). Chem. Phys. Lett. 2013, 568–569, 42–48. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.H.; Zeng, Z.; You, J.Q.; Yan, X.H.; Gong, X.G. A density-functional study of small titanium clusters. J. Chem. Phys. 2000, 113, 11127–11133. [Google Scholar] [CrossRef] [Green Version]
- Zavodinsky, V.G.; Chibisov, A.N.; Gnidenko, A.A.; Alejnikova, M.A. Theoretical study of elastic properties of small nanoparticles with different types of interatomic bonds. Mekhanika Kompozitsionnykh Materialov i Ronstruktsij 2005, 11, 337–346. (In Russian) [Google Scholar]
- Vakhrushev, A.V.; Shushkov, A.A. Modeling of elastic reaction of nanoparticles on the force action. Izvestiya Instituta matematiki i informatiki. Ishevsk 2006, 2, 125–128. (In Russian) [Google Scholar]
- Celine, G.; Laurent, P. Mechanical behavior of nanoparticles: Elasticity and plastic deformation mechanisms. Pramana 2015, 84, 1041–1048. [Google Scholar]
- Nysten, B.; Frétigny, C.; Cuenot, S. Elastic modulus of nanomaterials: Resonant contact-AFM measurement and reduced-size effect. In Proceedings of the SPIE Conference Volume 5766′ Testing, Reliability, and Application of Micro- and Nano-Material Systems III, San Diego, CA, USA, 6–10 March 2005; Geer, R.E., Meyendorf, N., Baaklini, G.Y., Michel, B., Eds.; SPIE: Bellingham, WA, USA, 2005; pp. 78–88. [Google Scholar]
- Wu, Q.; Miao, W.S.; Gao, H.J.; Hui, D. Mechanical properties of nanomaterials: A review. Nanotechnol. Rev. 2020, 9, 259–273. [Google Scholar] [CrossRef]
- Magomedov, M.N. Dependence of elastic properties on the size and the shape of diamond, silicon and germany nanocrystals. Zhurnal Tekhnicheskoj Fiziki 2014, 84, 80–90. (In Russian) [Google Scholar]
- Zavodinsky, V.G.; Kuyanov, I.A.; Holavkin, M.N. Soft elastic behavior of nanometer silicon particles: Computer simulation. Phys. Low-Dim. Struct. 1999, 9, 49–56. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).