Defect Engineering and Na-Ion Transport in NaMnPO4: A Computational Perspective
Abstract
1. Introduction
2. Computational Methods
3. Results
3.1. Crystal Structure of NaMnPO4
3.2. Intrinsic Defect Properties
3.3. Na-Ion Diffusion
3.4. Solution of Dopants
3.4.1. Monovalent Dopants
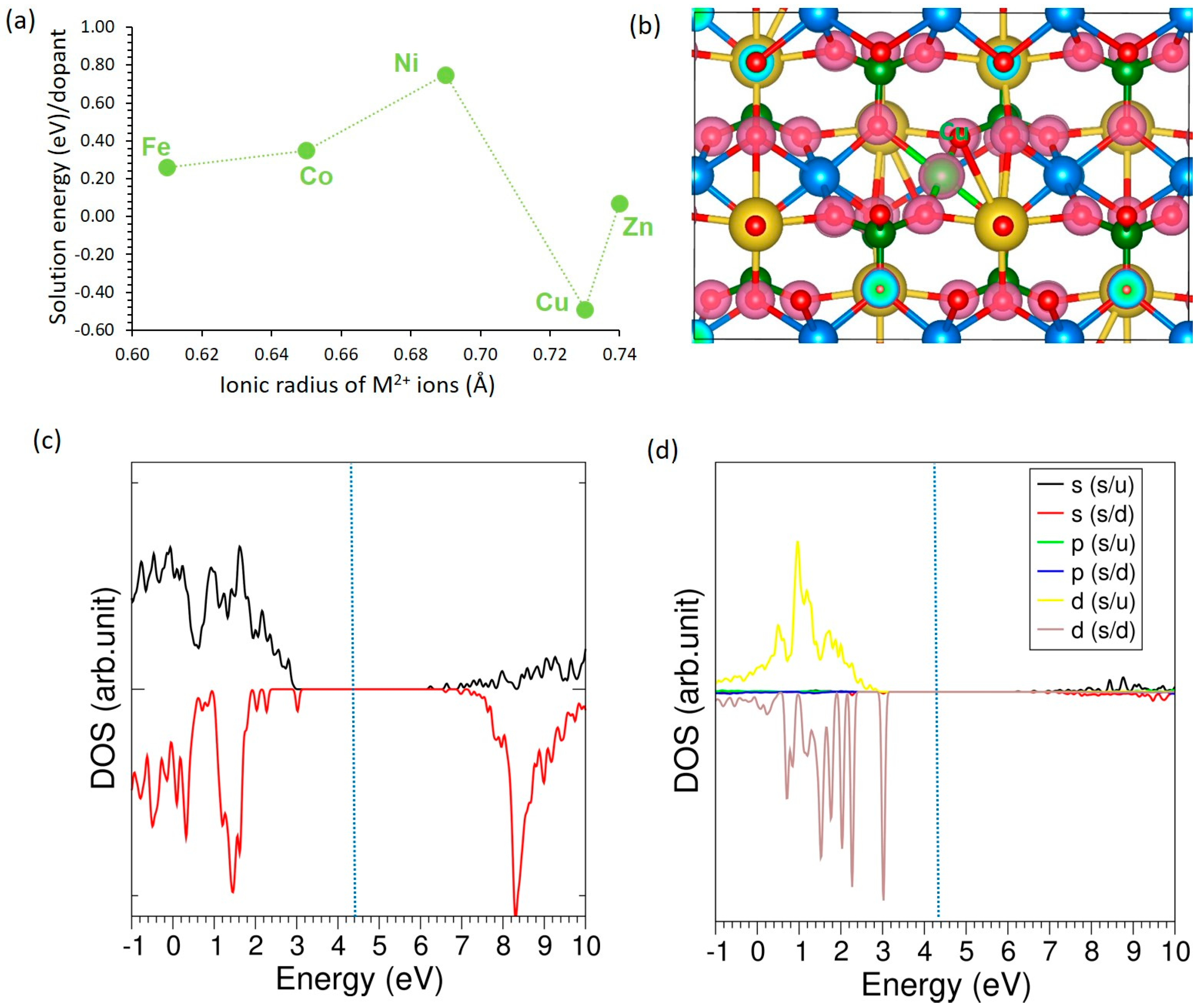
3.4.2. Divalent Dopants
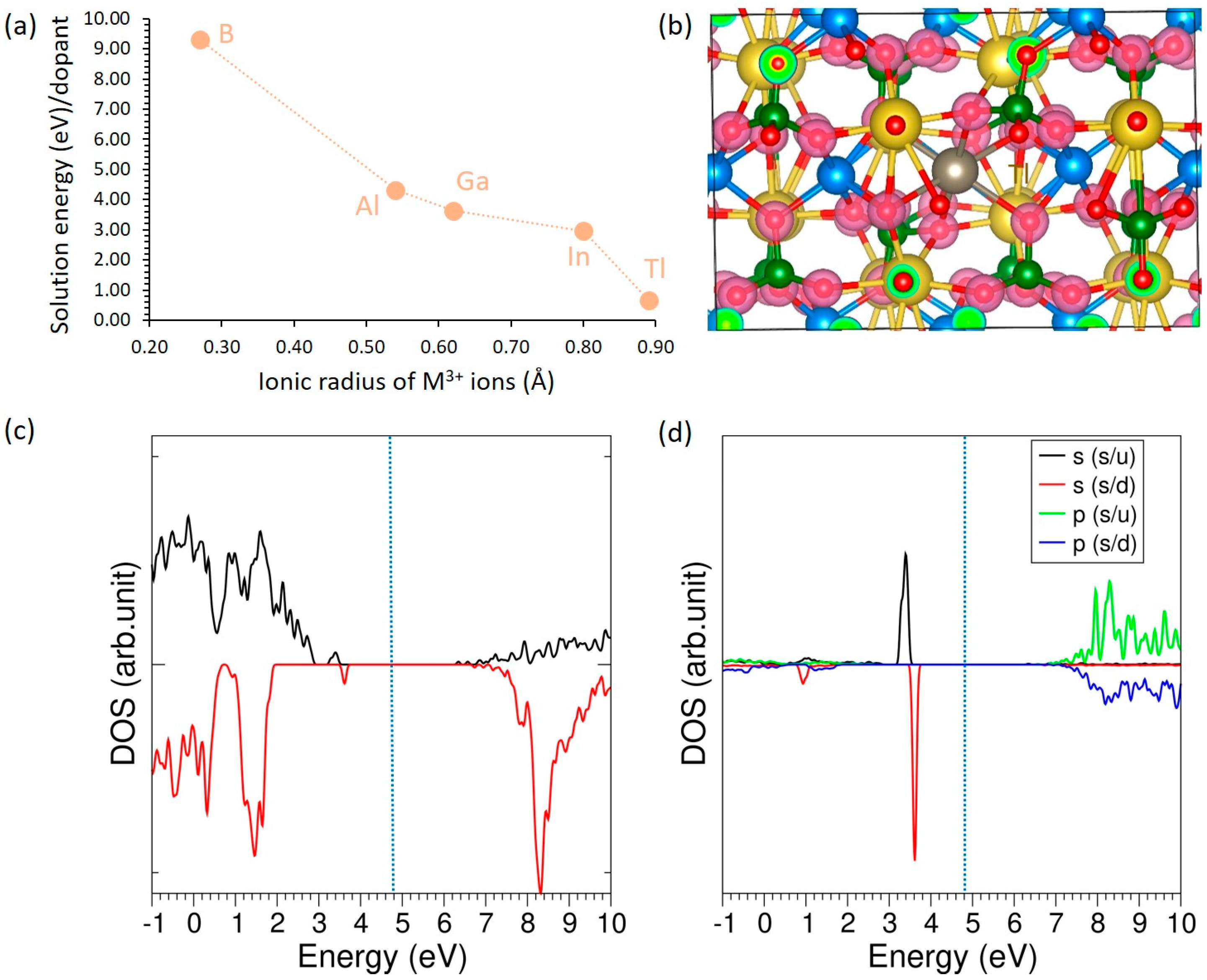
3.4.3. Trivalent Dopants
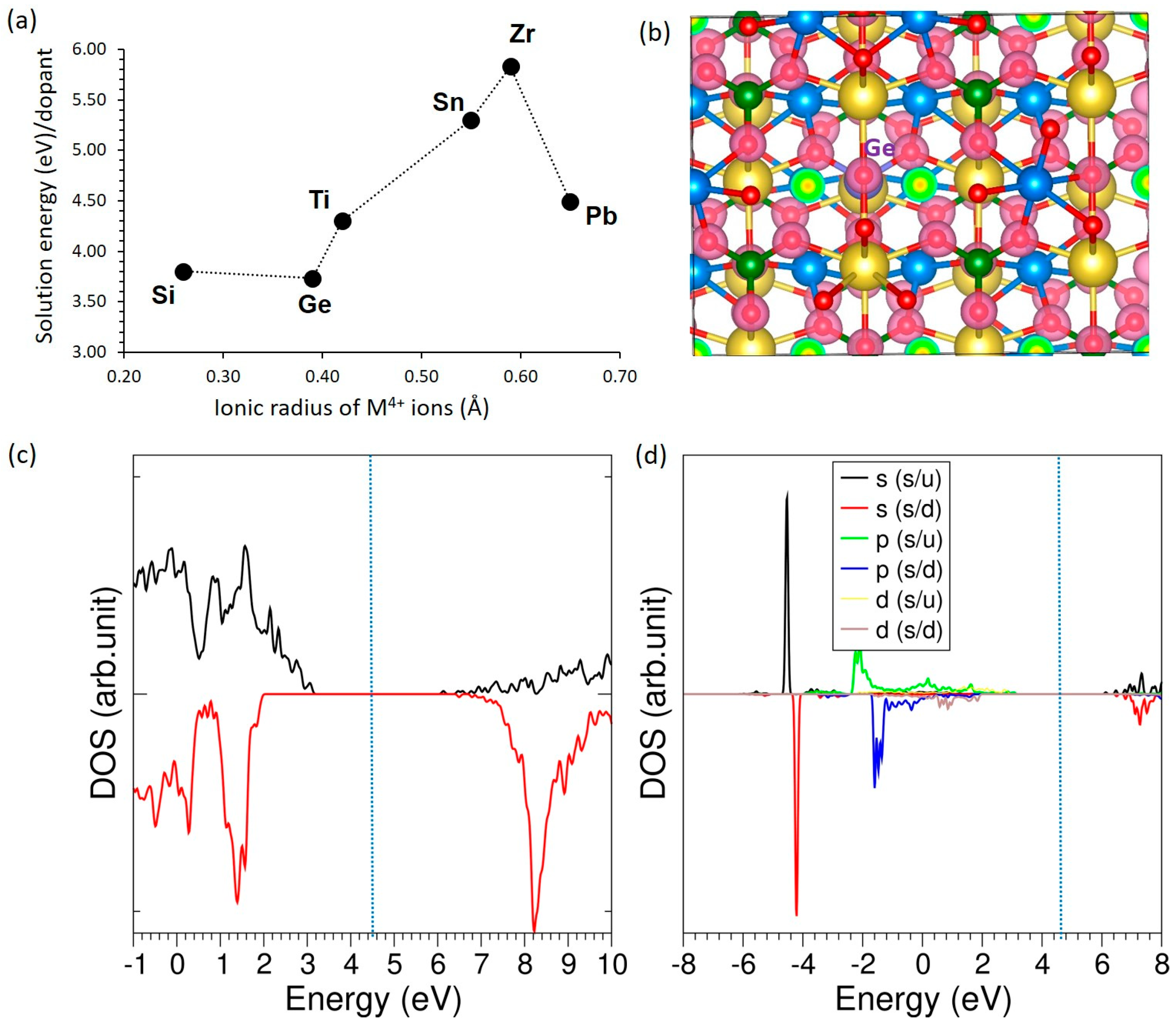
3.4.4. Tetravalent Dopants
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hasan, M.M.; Haque, R.; Jahirul, M.I.; Rasul, M.G.; Fattah, I.M.R.; Hassan, N.M.S.; Mofijur, M. Advancing energy storage: The future trajectory of lithium-ion battery technologies. J. Energy Storage 2025, 120, 116511. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, T.; Chen, J.; Gao, B.; Yu, M.; Zhu, J. Advances in safety of lithium-ion batteries for energy storage: Hazard characteristics and active suppression techniques. Energy Rev. 2025, 4, 100117. [Google Scholar] [CrossRef]
- Njema, G.G.; Ouma, R.B.O.; Kibet, J.K. A Review on the Recent Advances in Battery Development and Energy Storage Technologies. J. Renew. Energy 2024, 2024, 2329261. [Google Scholar] [CrossRef]
- Mizushima, K.; Jones, P.C.; Wiseman, P.J.; Goodenough, J.B. LixCoO2 (0 < x < −1): A new cathode material for batteries of high energy density. Mater. Res. Bull. 1980, 15, 783–789. [Google Scholar]
- Zhao, T.; Mahandra, H.; Marthi, R.; Ji, X.; Zhao, W.; Chae, S.; Traversy, M.; Li, W.; Yu, F.; Li, L.; et al. An overview on the life cycle of lithium iron phosphate: Synthesis, modification, application, and recycling. Chem. Eng. J. 2024, 485, 149923. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Q.; Wei, J.; Hu, Y.; Liu, X.; Huang, S.; Pang, C. Advances and industrialization of LiFePO4 cathodes in electric vehicles: Challenges, innovations, and future directions. J. Mater. Chem. A 2025, 13, 17271–17283. [Google Scholar] [CrossRef]
- Konar, R.; Maiti, S.; Shpigel, N.; Aurbach, D. Reviewing failure mechanisms and modification strategies in stabilizing high-voltage LiCoO2 cathodes beyond 4.55 V. Energy Storage Mater. 2023, 63, 103001. [Google Scholar] [CrossRef]
- Dou, Y.; Zhao, L.; Liu, Y.; Zhang, Z.; Zhang, Y.; Li, R.; Liu, X.; Zhou, Y.; Wang, J.; Wang, J. High-abundance and low-cost anodes for sodium-ion batteries. Carbon Neutralization 2024, 3, 954–995. [Google Scholar] [CrossRef]
- Phogat, P.; Dey, S.; Wan, M. Comprehensive review of Sodium-Ion Batteries: Principles, Materials, Performance, Challenges, and future Perspectives. Mater. Sci. Eng. B 2025, 312, 117870. [Google Scholar] [CrossRef]
- Hwang, J.-Y.; Myung, S.-T.; Sun, Y.-K. Sodium-ion batteries: Present and future. Chem. Soc. Rev. 2017, 46, 3529–3614. [Google Scholar] [CrossRef]
- Wu, Y.; Shuang, W.; Wang, Y.; Chen, F.; Tang, S.; Wu, X.-L.; Bai, Z.; Yang, L.; Zhang, J. Recent Progress in Sodium-Ion Batteries: Advanced Materials, Reaction Mechanisms and Energy Applications. Electrochem. Energy Rev. 2024, 7, 17. [Google Scholar] [CrossRef]
- Bača, P.; Libich, J.; Gazdošová, S.; Polkorab, J. Sodium-Ion Batteries: Applications and Properties. Batteries 2025, 11, 61. [Google Scholar] [CrossRef]
- Yabuuchi, N.; Kubota, K.; Dahbi, M.; Komaba, S. Research Development on Sodium-Ion Batteries. Chem. Rev. 2014, 114, 11636–11682. [Google Scholar] [CrossRef]
- Yadav, P.; Shelke, V.; Patrike, A.; Shelke, M. Sodium-based batteries: Development, commercialization journey and new emerging chemistries. Oxf. Open Mater. Sci. 2023, 3, itac019. [Google Scholar] [CrossRef]
- Balaouras, V.; Kelaidis, N.; Daskalopulu, A.; Kuganathan, N.; Chroneos, A. Ionic diffusion in post-lithium batteries. J. Solid State Electrochem. 2025, 29, 3553–3565. [Google Scholar] [CrossRef]
- Zhu, L.; Li, L.; Wen, J.; Zeng, Y.-R. Structural stability and ionic transport property of NaMPO4 (M = V, Cr, Mn, Fe, Co, Ni) as cathode material for Na-ion batteries. J. Power Sources 2019, 438, 227016. [Google Scholar] [CrossRef]
- Liao, H.; Zhang, Z.; Zheng, Y.; Gao, Y. NaFePO4 for sodium-ion batteries: Mechanism, synthesis and optimization strategies toward commercialization. Energy Storage Mater. 2024, 65, 103157. [Google Scholar] [CrossRef]
- Pan, M.-Y.; Lu, S.-T.; Zhang, M.-Y.; Li, C.; Zou, G.-D.; Cao, K.-Z.; Fan, Y. Synthesis of olivine NaMnPO4 single crystals and electrochemical performance as anode material for Li-ion batteries. J. Solid State Chem. 2023, 321, 123929. [Google Scholar] [CrossRef]
- Akçay, T.; Häringer, M.; Pfeifer, K.; Anhalt, J.; Binder, J.R.; Dsoke, S.; Kramer, D.; Mönig, R. Na3V2(PO4)3—A Highly Promising Anode and Cathode Material for Sodium-Ion Batteries. ACS Appl. Energy Mater. 2021, 4, 12688–12695. [Google Scholar] [CrossRef]
- Zhang, X.; Rui, X.; Chen, D.; Tan, H.; Yang, D.; Huang, S.; Yu, Y. Na3V2(PO4)3: An advanced cathode for sodium-ion batteries. Nanoscale 2019, 11, 2556–2576. [Google Scholar] [CrossRef]
- Banerjee, S.; Choudhary, R.B.; Ansari, S. Na3V2(PO4)3 derived cathode materials for sodium-ion batteries (SIBs): A review. Future Batter. 2024, 4, 100010. [Google Scholar] [CrossRef]
- Li, S.; Guo, J.; Ye, Z.; Zhao, X.; Wu, S.; Mi, J.-X.; Wang, C.-Z.; Gong, Z.; McDonald, M.J.; Zhu, Z.; et al. Zero-Strain Na2FeSiO4 as Novel Cathode Material for Sodium-Ion Batteries. ACS Appl. Mater. Interfaces 2016, 8, 17233–17238. [Google Scholar] [CrossRef] [PubMed]
- Law, M.; Ramar, V.; Balaya, P. Na2MnSiO4 as an attractive high capacity cathode material for sodium-ion battery. J. Power Sources 2017, 359, 277–284. [Google Scholar] [CrossRef]
- Treacher, J.C.; Wood, S.M.; Islam, M.S.; Kendrick, E. Na2CoSiO4 as a cathode material for sodium-ion batteries: Structure, electrochemistry and diffusion pathways. Phys. Chem. Chem. Phys. 2016, 18, 32744–32752. [Google Scholar] [CrossRef]
- Blesa, M.C.; Moran, E.; León, C.; Santamaria, J.; Tornero, J.D.; Menéndez, N. α-NaFeO2: Ionic conductivity and sodium extraction. Solid State Ion. 1999, 126, 81–87. [Google Scholar] [CrossRef]
- Satrughna, J.A.K.; Kanwade, A.R.; Rajore, S.M.; Tiwari, M.K.; Ito, Y.; Ogura, A.; Lee, H.; Ohshita, Y.; Shirage, P.M. Sol-gel-based synthesis of high-capacity-NaCoO2 cathode for advanced sodium-ion batteries. Electrochim. Acta 2024, 507, 145201. [Google Scholar] [CrossRef]
- Wadhwa, P.; Cappellini, G.; Teles, L.K.; Filippetti, A. Fundamentals of NaMnO2, the cathode material for Na-ion rechargeable batteries. J. Mater. Chem. C 2025, 13, 12483–12493. [Google Scholar] [CrossRef]
- An, S.; Karger, L.; Dreyer, S.L.; Hu, Y.; Barbosa, E.; Zhang, R.; Lin, J.; Fichtner, M.; Kondrakov, A.; Janek, J.; et al. Improving cycling performance of the NaNiO2 cathode in sodium-ion batteries by titanium substitution. Mater. Futures 2024, 3, 035103. [Google Scholar] [CrossRef]
- Thirupathi, R.; Kumari, V.; Chakrabarty, S.; Omar, S. Recent progress and prospects of NASICON framework electrodes for Na-ion batteries. Prog. Mater. Sci. 2023, 137, 101128. [Google Scholar] [CrossRef]
- Wang, J.; He, T.; Yang, X.; Cai, Z.; Wang, Y.; Lacivita, V.; Kim, H.; Ouyang, B.; Ceder, G. Design principles for NASICON super-ionic conductors. Nat. Commun. 2023, 14, 5210. [Google Scholar] [CrossRef]
- Song, W.; Ji, X.; Wu, Z.; Zhu, Y.; Yang, Y.; Chen, J.; Jing, M.; Li, F.; Banks, C.E. First exploration of Na-ion migration pathways in the NASICON structure Na3V2(PO4)3. J. Mater. Chem. A 2014, 2, 5358–5362. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, B.; Liu, J.; He, X.; Xiao, Z.; Qin, H.; Liu, T.; Amine, K.; Ou, X. NaSICON-type materials for lithium-ion battery applications: Progress and challenges. Nano Energy 2024, 127, 109730. [Google Scholar] [CrossRef]
- Mohsin, I.U.; Schneider, L.; Yu, Z.; Cai, W.; Ziebert, C. Enabling the Electrochemical Performance of Maricite-NaMnPO4 and Maricite-NaFePO4 Cathode Materials in Sodium-Ion Batteries. Int. J. Electrochem. 2023, 2023, 6054452. [Google Scholar] [CrossRef]
- Xiao, H.; Fang, H. Rapid synthesis of olivine NaMnPO4. Chem. Lett. 2024, 53, upae125. [Google Scholar] [CrossRef]
- Jana, S.; Lingannan, G.; Ishtiyak, M.; Panigrahi, G.; Sonachalam, A.; Prakash, J. Syntheses, crystal structures, optical, Raman spectroscopy, and magnetic properties of two polymorphs of NaMnPO4. Mater. Res. Bull. 2020, 126, 110835. [Google Scholar] [CrossRef]
- Zhu, L.; Xie, J.-Y.; Zhou, G.-M.; Zhang, D.-A.; Du, A. First principles investigation of voltage, structure, ionic and electronic conduction of olivine and maricite NaMnPO4. Solid State Ion. 2023, 398, 116274. [Google Scholar] [CrossRef]
- Koleva, V.; Boyadzhieva, T.; Zhecheva, E.; Nihtianova, D.; Simova, S.; Tyuliev, G.; Stoyanova, R. Precursor-based methods for low-temperature synthesis of defectless NaMnPO4 with an olivine- and maricite-type structure. CrystEngComm 2013, 15, 9080–9089. [Google Scholar] [CrossRef]
- Priyanka, V.; Savithiri, G.; Subadevi, R.; Sivakumar, M. An emerging electrochemically active maricite NaMnPO4 as cathode material at elevated temperature for sodium-ion batteries. Appl. Nanosci. 2020, 10, 3945–3951. [Google Scholar] [CrossRef]
- Kuganathan, N.; Srikaran, R.; Fossati, P.C.M.; Chroneos, A. Theoretical Modeling of Defects, Dopants, and Diffusion in the Mineral Ilmenite. Minerals 2019, 9, 610. [Google Scholar] [CrossRef]
- Kuganathan, N. DFT Modelling of Li6SiO4Cl2 Electrolyte Material for Li-Ion Batteries. Batteries 2022, 8, 137. [Google Scholar] [CrossRef]
- Kuganathan, N.; Baiutti, F.; Morata, A.; Tarancon, A.; Chroneos, A. Interstitial lithium doping in SrTiO3. AIP Adv. 2021, 11, 075029. [Google Scholar] [CrossRef]
- Suthaharan, S.; Iyngaran, P.; Kuganathan, N.; Chroneos, A. Defects, diffusion and dopants in the ceramic mineral “Lime-Feldspar”. J. Asian Ceram. Soc. 2021, 9, 570–577. [Google Scholar] [CrossRef]
- Dutra, A.C.C.; Goldmann, B.A.; Islam, M.S.; Dawson, J.A. Understanding solid-state battery electrolytes using atomistic modelling and machine learning. Nat. Rev. Mater. 2025, 10, 566–583. [Google Scholar] [CrossRef]
- Poletayev, A.D.; Dawson, J.A.; Islam, M.S.; Lindenberg, A.M. Defect-driven anomalous transport in fast-ion conducting solid electrolytes. Nat. Mater. 2022, 21, 1066–1073. [Google Scholar] [CrossRef]
- Wood, S.M.; Eames, C.; Kendrick, E.; Islam, M.S. Sodium Ion Diffusion and Voltage Trends in Phosphates Na4M3(PO4)2P2O7 (M = Fe, Mn, Co, Ni) for Possible High-Rate Cathodes. J. Phys. Chem. C 2015, 119, 15935–15941. [Google Scholar] [CrossRef]
- Clark, J.M.; Barpanda, P.; Yamada, A.; Islam, M.S. Sodium-ion battery cathodes Na2FeP2O7 and Na2MnP2O7: Diffusion behaviour for high rate performance. J. Mater. Chem. A 2014, 2, 11807–11812. [Google Scholar] [CrossRef]
- Whiteside, A.; Fisher, C.A.J.; Parker, S.C.; Saiful Islam, M. Particle shapes and surface structures of olivine NaFePO4 in comparison to LiFePO4. Phys. Chem. Chem. Phys. 2014, 16, 21788–21794. [Google Scholar] [CrossRef]
- Tripathi, R.; Wood, S.M.; Islam, M.S.; Nazar, L.F. Na-ion mobility in layered Na2FePO4F and olivine Na[Fe,Mn]PO4. Energy Environ. Sci. 2013, 6, 2257–2264. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Binks, D.J.; Grimes, R.W. Incorporation of Monovalent Ions in ZnO and Their Influence on Varistor Degradation. J. Am. Ceram. Soc. 1993, 76, 2370–2372. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects, Dopants and Sodium Mobility in Na2MnSiO4. Sci. Rep. 2018, 8, 14669. [Google Scholar] [CrossRef]
- Gale, J.D.; Henson, N.J. Derivation of interatomic potentials for microporous aluminophosphates from the structure and properties of berlinite. J. Chem. Soc. Faraday Trans. 1994, 90, 3175–3179. [Google Scholar] [CrossRef]
- Lewis, D.W.; Catlow, C.R.A.; Sankar, G.; Carr, S.W. Structure of Iron-Substituted ZSM-5. J. Phys. Chem. 1995, 99, 2377–2383. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C, 2nd ed.; The art of scientific computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Bader, R.F.W. The zero-flux surface and the topological and quantum definitions of an atom in a molecule. Theor. Chem. Acc. 2001, 105, 276–283. [Google Scholar] [CrossRef]
- Dima, R.S.; Maleka, P.M.; Maluta, E.N.; Maphanga, R.R. First principles study on sodium de-intercalation from NaMnPO4. Mater. Today Proc. 2022, 62, S7–S11. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Ong, S.P.; Chevrier, V.L.; Hautier, G.; Jain, A.; Moore, C.; Kim, S.; Ma, X.; Ceder, G. Voltage, stability and diffusion barrier differences between sodium-ion and lithium-ion intercalation materials. Energy Environ. Sci. 2011, 4, 3680–3688. [Google Scholar] [CrossRef]
- Seshan, V.; Iyngaran, P.; Abiman, P.; Kuganathan, N. Atomic-Scale Study of NASICON Type Electrode Material: Defects, Dopants and Sodium-Ion Migration in Na3V2(PO4)3. Physchem 2025, 5, 1. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects, diffusion, dopants and encapsulation of Na in NaZr2(PO4)3. Materialia 2021, 16, 101039. [Google Scholar] [CrossRef]
- El Kacemi, Z.; Mansouri, Z.; Benyoussef, A.; El Kenz, A.; Balli, M.; Mounkachi, O. First principle calculations on pristine and Mn-doped iron fluorophosphates as sodium-ion battery cathode materials. Comput. Mater. Sci. 2022, 206, 111292. [Google Scholar] [CrossRef]
- Xiao, H.; Fang, H. On the thermal stability of olivine NaMnPO4. Dalton Trans. 2025, 54, 9049–9056. [Google Scholar] [CrossRef]
- Jang, D.; Palanisamy, K.; Yoon, J.; Kim, Y.; Yoon, W.-S. Crystal and local structure studies of LiFe0.48Mn0.48Mg0.04PO4 cathode material for lithium rechargeable batteries. J. Power Sources 2013, 244, 581–585. [Google Scholar] [CrossRef]
- Drezen, T.; Kwon, N.-H.; Bowen, P.; Teerlinck, I.; Isono, M.; Exnar, I. Effect of particle size on LiMnPO4 cathodes. J. Power Sources 2007, 174, 949–953. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, N.; Wang, F.; Liu, X.; Jiao, L.; Fan, L.-Z. Approaching the Downsizing Limit of Maricite NaFePO4 toward High-Performance Cathode for Sodium-Ion Batteries. Adv. Funct. Mater. 2018, 28, 1801917. [Google Scholar] [CrossRef]
- Hu, W.; Tang, Y.; Zhang, Y.; Yu, L.; Liu, H.; Cao, Y.; Li, B.; Liu, L. Carbon-Coated Maricite NaFePO4 Nanospheres Embedded in Graphene Nanosheets as Cathodes for Sodium-Ion Batteries. ACS Appl. Nano Mater. 2025, 8, 13238–13245. [Google Scholar] [CrossRef]
- Song, A.; Li, Y.; Yuan, D.; Wu, J.; Gu, H.; Zhang, G.; Wu, A.; Xu, J. Recent progress in carbon-based composite materials for advanced sodium ion batteries: From storage mechanism to structural design to applications as flexible electrodes. Green Energy Environ. 2025, 10, 1437–1460. [Google Scholar] [CrossRef]
- Lee, K.T.; Ramesh, T.N.; Nan, F.; Botton, G.; Nazar, L.F. Topochemical Synthesis of Sodium Metal Phosphate Olivines for Sodium-Ion Batteries. Chem. Mater. 2011, 23, 3593–3600. [Google Scholar] [CrossRef]
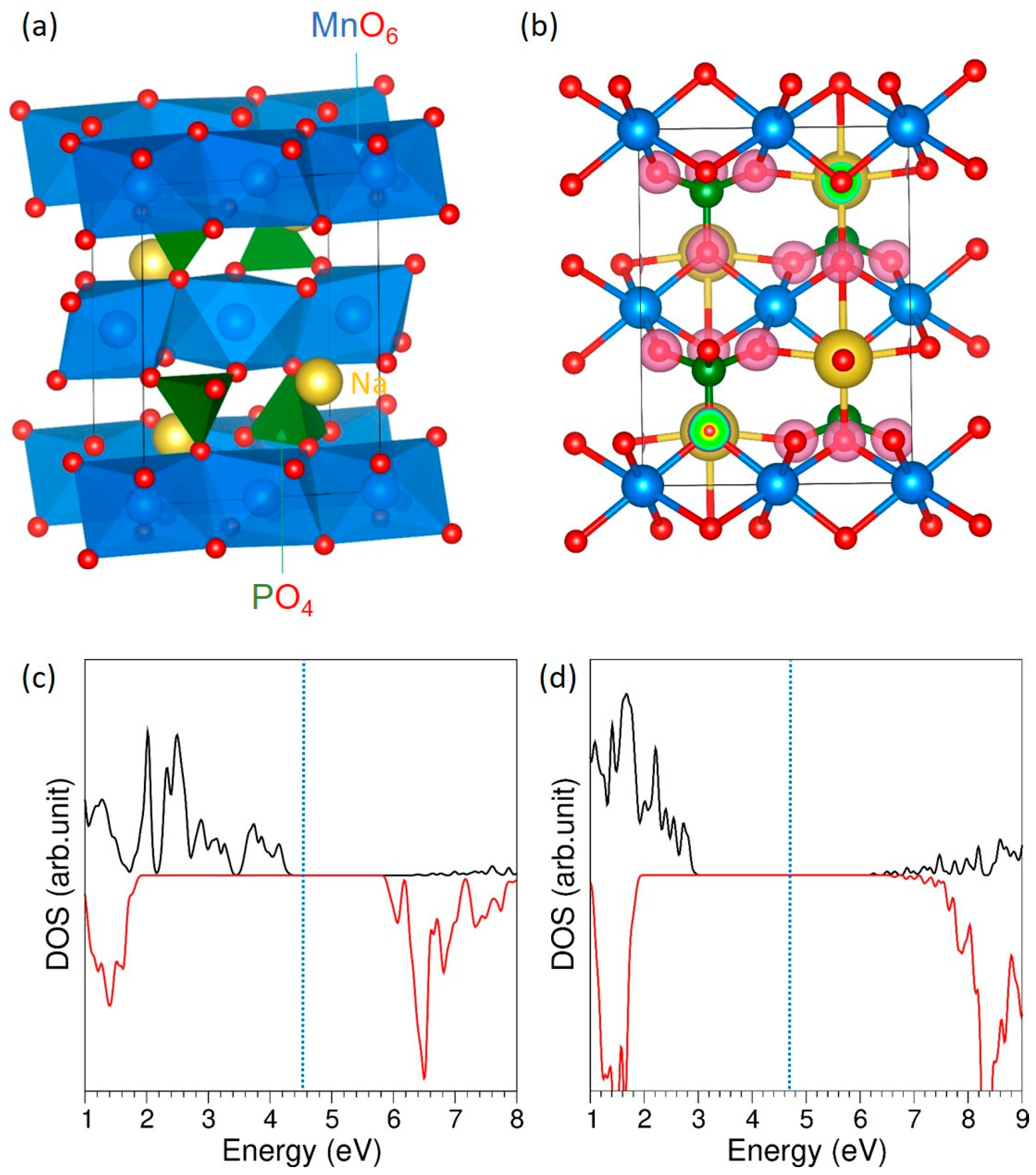
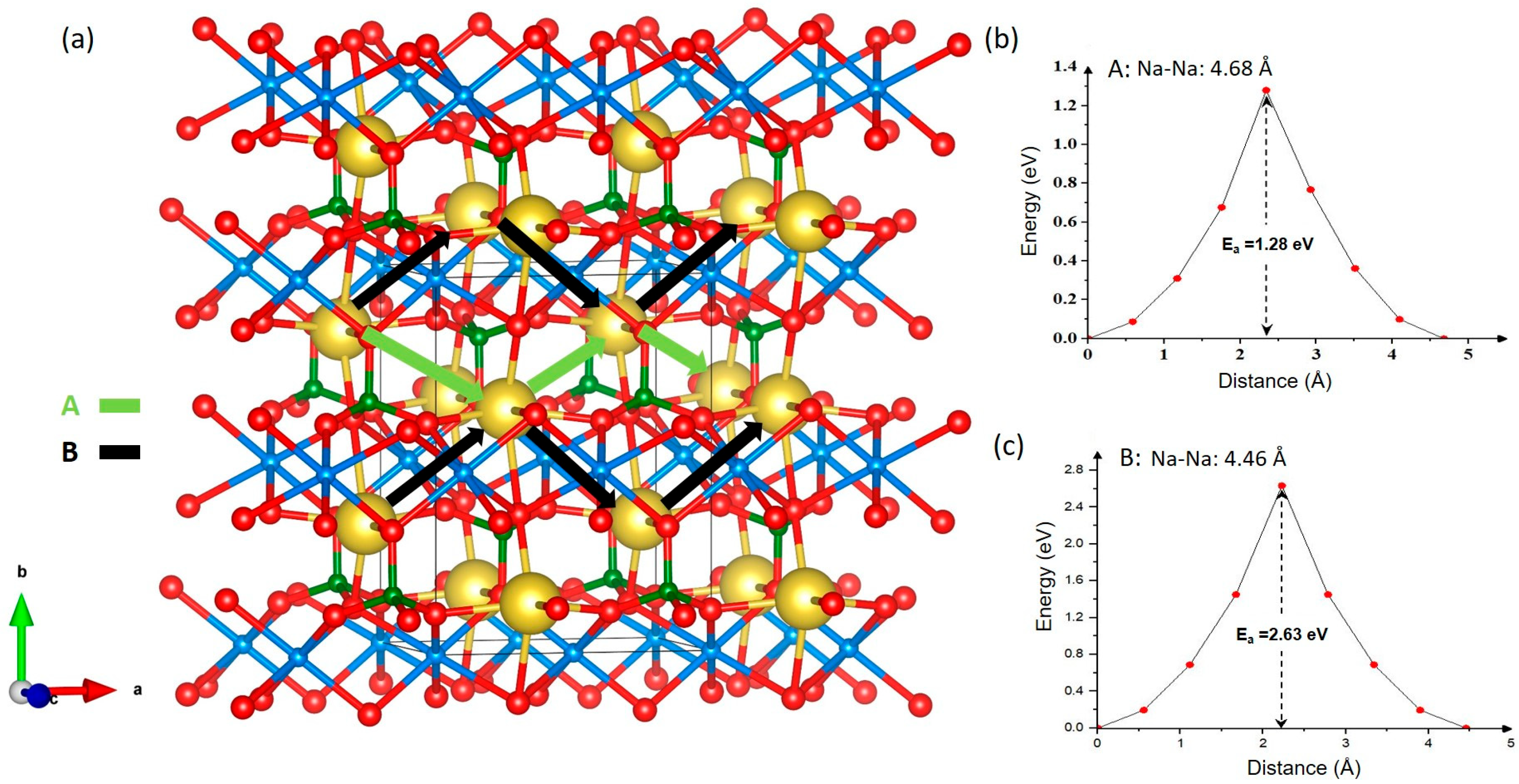
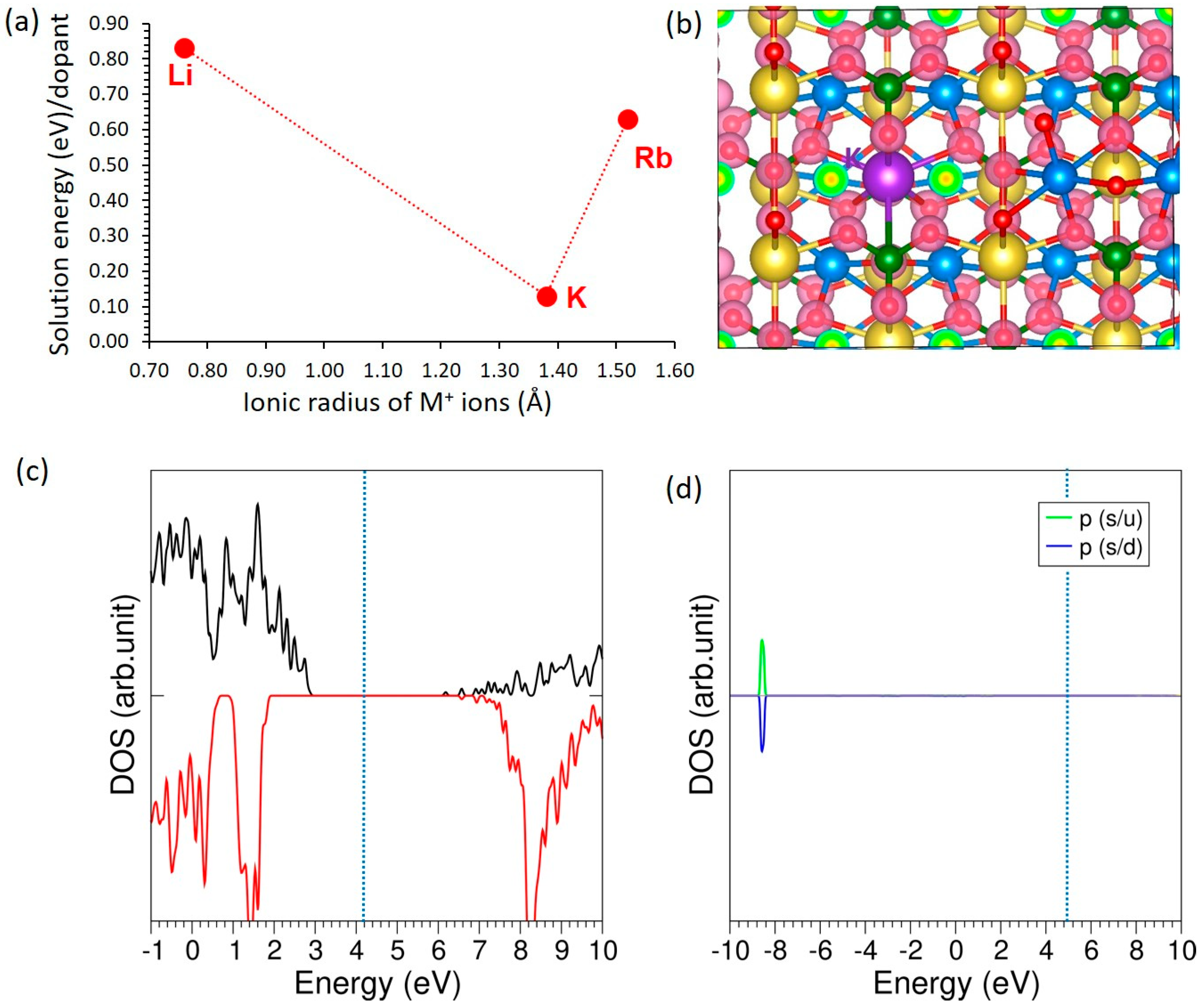
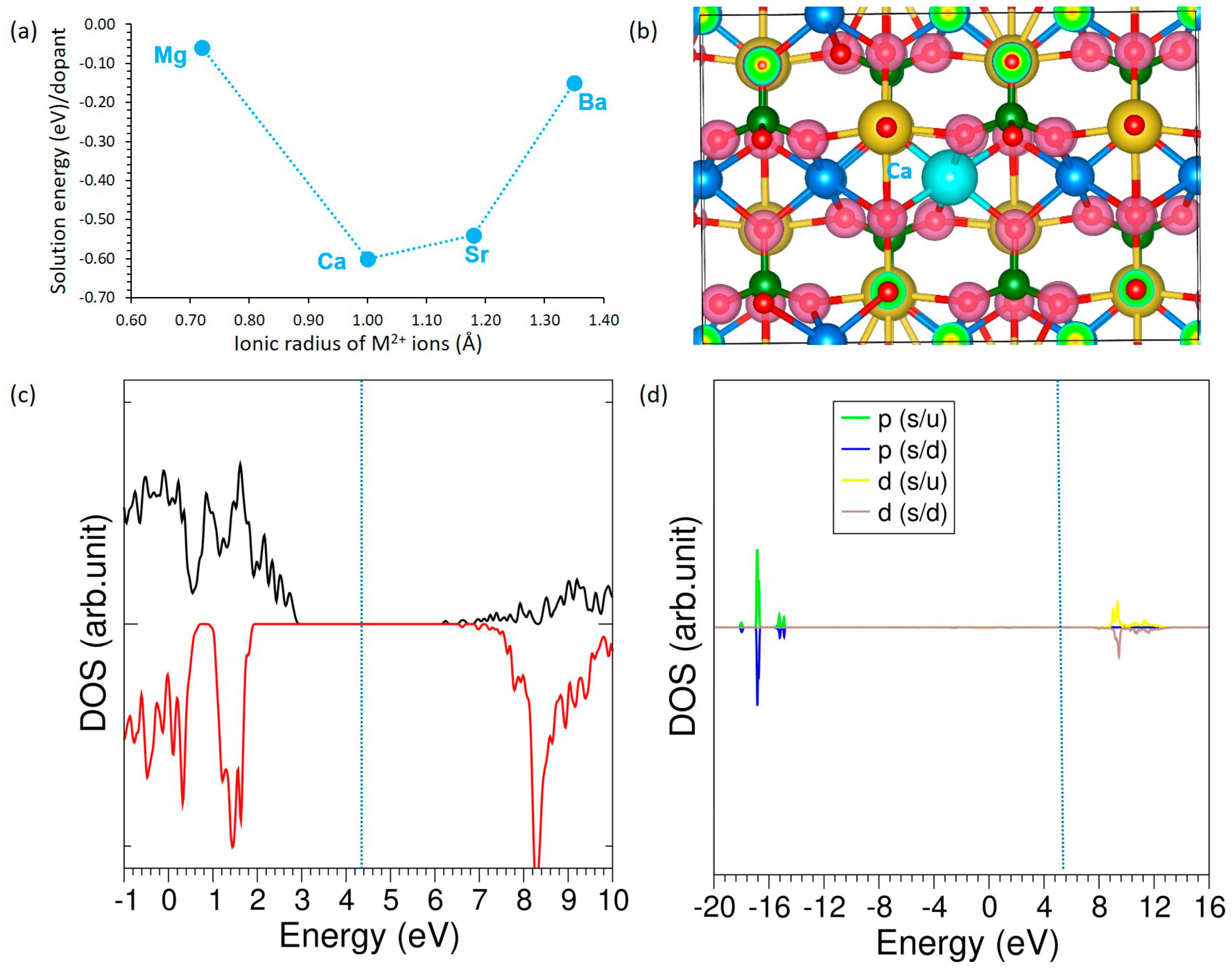
| Interaction | A/eV | ρ/Å | C/eV·Å6 | Y/e | K/eV·Å−2 |
|---|---|---|---|---|---|
| Na+–O2− | 1677.830 | 0.2934 | 0.00 | 1.0000 | 292.430 |
| Mn2+–O2− | 2601.394 | 0.2780 | 0.00 | 2.0000 | 148.0 |
| O2−–O2− | 22,764.0 | 0.149 | 27.88 | −2.820 | 74.92 |
| P5+–O2− | 877.340 | 0.35940 | 0.00 | 5.0000 | 99,999 |
| Lattice Parameters | Calculated | Experiment [35] | |∆|(%) | ||
|---|---|---|---|---|---|
| Classical | DFT | Classical | DFT | ||
| a (Å) | 6.946 | 6.937 | 6.892 | 0.78 | 0.65 |
| b (Å) | 9.099 | 9.195 | 9.079 | 0.22 | 1.28 |
| c (Å) | 5.177 | 5.125 | 5.108 | 1.02 | 0.33 |
| α = β = γ (°) | 90.0 | 90.0 | 90.0 | 0.00 | 0.00 |
| V (Å3) | 327.24 | 326.89 | 319.62 | 2.38 | 2.27 |
| Defect Process | Equation Number | Defect Energy/Defect (eV) |
|---|---|---|
| Na-Frenkel | 1 | 1.93 |
| Mn-Frenkel | 2 | 2.97 |
| P-Frenkel | 3 | 15.98 |
| O-Frenkel | 4 | 4.07 |
| Schottky | 5 | 4.85 |
| Na2O-Schottky | 6 | 2.65 |
| MnO-Schottky | 7 | 3.13 |
| P2O5-Schottky | 8 | 7.48 |
| Na-Mn anti-site (isolated) | 9 | 0.53 |
| Na-Mn (cluster) | 10 | 0.12 |
| Dopant (M) | Ionic Radius (Å) | M-O (Å) | Bader Charge on M (|e|) | Magnetic Moment (µ) | (%) |
|---|---|---|---|---|---|
| Li | 0.76 | 2.29 | +1.00 | 5.00 | ─0.26 |
| K | 1.38 | 2.77 | +0.82 | 5.00 | +0.79 |
| Rb | 1.52 | 2.81 | +0.82 | 5.00 | +1.27 |
| Dopant (M) | Ionic Radius (Å) | M-O (Å) | Bader Charge on M (|e|) | Magnetic Moment (µ) | (%) |
|---|---|---|---|---|---|
| Mg | 0.72 | 2.17 | +2.00 | 4.69 | −0.43 |
| Ca | 1.00 | 2.33 | +1.60 | 4.69 | +0.77 |
| Sr | 1.18 | 2.42 | +1.63 | 4.69 | +1.38 |
| Ba | 1.35 | 2.59 | +1.62 | 4.69 | +2.36 |
| Dopant (M) | Ionic Radius (Å) | M-O (Å) | Bader Charge on M (|e|) | Magnetic Moment (µ) | (%) |
|---|---|---|---|---|---|
| Fe | 0.61 | 2.12 | +1.52 | 4.94 | −0.20 |
| Co | 0.65 | 2.11 | +1.34 | 4.86 | −0.38 |
| Ni | 0.69 | 2.05 | +1.11 | 4.64 | −0.34 |
| Cu | 0.73 | 2.15 | +0.98 | 4.63 | −0.18 |
| Zn | 0.74 | 2.21 | +1.42 | 4.69 | −0.20 |
| Dopant (M) | Ionic Radius (Å) | M-O (Å) | Bader Charge on M (|e|) | Magnetic Moment (µ) | (%) |
|---|---|---|---|---|---|
| B | 0.27 | 2.39 | +0.60 | 4.63 | +0.59 |
| Al | 0.54 | 1.95 | +3.00 | 4.63 | −0.29 |
| Ga | 0.62 | 2.21 | +2.66 | 4.63 | +0.99 |
| In | 0.80 | 2.36 | +3.00 | 4.63 | +2.19 |
| Tl | 0.89 | 2.64 | +0.92 | 4.63 | +2.84 |
| Dopant (M) | Ionic Radius (Å) | M-O (Å) | Bader Charge on M (|e|) | Magnetic Moment (µ) | |
|---|---|---|---|---|---|
| Si | 0.26 | 1.65 | +4.00 | 4.94 | −0.38 |
| Ge | 0.39 | 1.78 | +4.00 | 4.94 | +0.30 |
| Ti | 0.42 | 1.84 | +2.52 | 4.94 | +0.55 |
| Sn | 0.55 | 1.96 | +3.82 | 4.94 | +1.03 |
| Zr | 0.59 | 1.98 | +3.08 | 4.94 | +1.37 |
| Pb | 0.65 | 2.22 | +2.42 | 4.94 | +1.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galappaththi, G.M.P.D.; Abiman, P.; Iyngaran, P.; Kuganathan, N. Defect Engineering and Na-Ion Transport in NaMnPO4: A Computational Perspective. Electrochem 2025, 6, 39. https://doi.org/10.3390/electrochem6040039
Galappaththi GMPD, Abiman P, Iyngaran P, Kuganathan N. Defect Engineering and Na-Ion Transport in NaMnPO4: A Computational Perspective. Electrochem. 2025; 6(4):39. https://doi.org/10.3390/electrochem6040039
Chicago/Turabian StyleGalappaththi, G. M. P. Dananjana, Poobalasingam Abiman, Poobalasuntharam Iyngaran, and Navaratnarajah Kuganathan. 2025. "Defect Engineering and Na-Ion Transport in NaMnPO4: A Computational Perspective" Electrochem 6, no. 4: 39. https://doi.org/10.3390/electrochem6040039
APA StyleGalappaththi, G. M. P. D., Abiman, P., Iyngaran, P., & Kuganathan, N. (2025). Defect Engineering and Na-Ion Transport in NaMnPO4: A Computational Perspective. Electrochem, 6(4), 39. https://doi.org/10.3390/electrochem6040039







