Chemical Stability of PFSA Membranes in Heavy-Duty Fuel Cells: Fluoride Emission Rate Model

Abstract

Laboratory data from in-cell tests at and near open circuit potentials (OCV) and ex-situ H₂O₂ vapor exposure tests are used to develop a fluoride emission rate (FER) model for a state-of-the-art 12-µm thin, low equivalent weight, long-chain perfluorosulfonic acid (PFSA) ionomer membrane that is mechanically reinforced with expanded PTFE and chemically stabilized with 2 mol% cerium as an anti-oxidant. The anode FER at OCV linearly correlates with O₂ crossover from the cathode and the high yield of H₂O₂ at anode potentials, as observed in rotating ring disk electrode (RRDE) studies. The cathode FER may be linked to the energetic formation of reactive hydroxyl radicals (·OH) from the decomposition of H₂O₂ produced as an intermediate in the two-electron ORR pathway at high cathode potentials. Both anode and cathode FERs are significantly enhanced at low relative humidity and high temperatures. The modeled FER is strongly influenced by the gradients in water activity and cerium concentration that develops in operating fuel cells. Membrane stability maps are constructed to illustrate the relationship between the cell voltage, temperature, and relative humidity for FER thresholds that define H₂ crossover failure by chemical degradation over a specified lifetime.

1. Introduction

Low-temperature polymer electrolyte membrane fuel cells (PEMFCs) are being considered for many heavy-duty (HD) transport applications [1,2,3,4,5,6]. Marcinkoski et al. established interim targets for PEMFC systems to compete with the performance, durability, and cost of class-8 diesel trucks: 68% peak efficiency, 25,000-h lifetime, and a cost of 80 USD/kW [7]. Padgett et al. formulated a unified cell-level target for performance and durability in a single metric: 2.5 kW/g_PGM Pt group metal (PGM) utilization at 0.7 V, 90 °C, 2.5 atm, and 2/1.5 anode/cathode stoichiometry after a 25,000 h-equivalent accelerated stress test (AST) [8]. Ahluwalia et al. investigated several catalyst systems for oxygen reduction reaction (ORR) and operational strategies to achieve 25,000-h electrode lifetime on a HD truck duty cycle [9,10,11]: load sharing with hybrid batteries, regulating the radiator fan power to preferentially maintain the stack temperature below 65 °C, clipping the maximum cell voltage to 850 mV, overloading the cathode catalyst, limiting the loss of electrochemical surface area (ECSA), and oversizing the active membrane area.

Besides the ORR catalyst, stability of perfluorosulfonic acid (PFSA) membranes in low-temperature PEMFCs is also of concern in heavy-duty applications that have aggressive duty cycles and long service life [12,13,14,15]. Despite recent advances in backbone fluorination, mechanical reinforcement of 8–20 µm thin membranes, and chemical stabilization with anti-oxidants [16,17,18], PFSA membranes remain subject to chemical and mechanical degradation under harsh conditions. Chemical degradation is initiated by the formation of hydrogen peroxide and subsequent radicals that attack the main and side chains of the polymer, leading to fragmentation of the structure [19,20,21,22]. Mechanical degradation occurs due to hygrothermal stresses on a constrained membrane caused by dynamically varying membrane humidification levels during operation over a vehicle duty cycle [23,24]. Synergistic chemical–mechanical degradation significantly shortens the membrane lifetime in vehicular applications with frequent load cycling and start–stop events [25,26,27].

Chemical degradation is stimulated through the combination of metal contaminants, fuel impurities, and radical attacks on the Nafion polymer [28,29]. Specifically, a radical attack occurs through the initial formation of peroxide as a side reaction intermediate in the 2-electron ORR at the fuel cell electrodes [30,31]. Although H₂O₂ can attack the polymer structure, conversion of H₂O₂ into highly reactive radical species is generally considered the dominant degradation pathway under typical fuel cell operating conditions. Metal ion contaminants from bipolar plate degradation such as Fe²⁺ and Fe³⁺ catalyze the decomposition of H₂O₂ under acidic conditions into more reactive radical species such as hydroxyl (⋅OH) and hydroperoxyl (⋅OOH) through a Fenton reaction [32,33,34].

$$\mathrm{F}{\mathrm{e}}^{2+}+{\mathrm{H}}_2{\mathrm{O}}_{2 }⟶ \mathrm{F}{\mathrm{e}}^{3+}+\cdot \mathrm{OH}+{}^{-}\mathrm{OH}$$

$$\cdot \mathrm{OH}+{ \mathrm{H}}_2{\mathrm{O}}_2 ⟶ {\mathrm{H}}_2\mathrm{O}+\cdot \mathrm{OOH}$$

$$\cdot \mathrm{OH}+{ \mathrm{H}}_2 ⟶ {\mathrm{H}}_2\mathrm{O}+\cdot \mathrm{H}$$

$$\mathrm{F}{\mathrm{e}}^{3+}+{ \mathrm{H}}_2{\mathrm{O}}_2 ⟶ \mathrm{F}{\mathrm{e}}^{2+}+\cdot \mathrm{OOH}+{ \mathrm{H}}^{+}$$

The $\cdot \mathrm{OH}$ radicals rapidly react with fluoride atoms from the main and side chains of Nafion, breaking C-F and C-S bonds and releasing HF [19,35]. A radical attack primarily occurs through the unzipping of the terminal end groups, side chain degradation, and random scission along the Nafion backbone [34]. Unzipping occurs on the carboxylic end groups to produce CO₂ and HF. Subsequent radical attack and hydrolysis result in the regeneration of the carboxylic end group with one carbon removed.

$$\begin{gathered} {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+\cdot \mathrm{OH} ⟶ \\ {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\cdot +\mathrm{ }\mathrm{C}{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O} \end{gathered}$$

$$\begin{gathered} {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\cdot +\cdot \mathrm{OH}+{\mathrm{H}}_2\mathrm{O} ⟶ \\ {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{COOH}+2 \mathrm{HF} \end{gathered}$$

On the side chain of Nafion, radical attack can initiate at the C-S bond, generating a CF₂ radical group that undergoes radical-driven hydrolysis forming a carboxylic end group and releasing HF.

$$\begin{gathered} {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+\cdot \mathrm{OH} ⟶ \\ {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\cdot \right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+\mathrm{S}{\mathrm{O}}_3+{\mathrm{H}}_2\mathrm{O} \end{gathered}$$

$$\begin{gathered} {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\cdot \right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+{\cdot \mathrm{OH}+\mathrm{H}}_2\mathrm{O} ⟶ \\ {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+2\mathrm{HF} \end{gathered}$$

Hydrogen radicals can also abstract fluorine from the carbon connected to the side chain, forming a $\mathrm{C}\cdot \text{-}\mathrm{O}$ bond that undergoes beta scission by reacting with hydroxyl radicals and separates the side chain from the backbone neighboring carbon. In this process, a radicalized -CF₂⋅ is formed in the main chain, which may be oxidized to form -CF₂OH or -COOH groups. The production of HF accelerates as the concentration of -COOH end groups regeneratively increases and the main chains become available for unzipping and further degradation [36].

$$\begin{gathered} {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{CF}\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+\cdot \mathrm{H} ⟶ \\ {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{C}\cdot \text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+\mathrm{HF}\hspace{0.25em} \end{gathered}$$

$$\begin{gathered} {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\left(\mathrm{C}\cdot \text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+2\cdot \mathrm{OH} ⟶ \\ {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\cdot +\left(\mathrm{COO}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CF}\left(\mathrm{C}{\mathrm{F}}_3\right)\text{-}\mathrm{O}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{S}{\mathrm{O}}_3\mathrm{H}\right)\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{COOH}+{\mathrm{H}}_2\mathrm{O} \end{gathered}$$

$${\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\cdot +\cdot \mathrm{OH}+{\mathrm{H}}_2\mathrm{O} ⟶ {\left[\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{C}{\mathrm{F}}_2\right]}_{\mathrm{m}}\text{-}\mathrm{C}{\mathrm{F}}_2\text{-}\mathrm{CO}\mathrm{O}\mathrm{H}\mathrm{ }+2\mathrm{H}\mathrm{F}\hspace{1em}\hspace{1em}$$

Membrane lifetime can be enhanced by incorporating radical scavengers, such as cerium and manganese ions [37,38,39]. For example, Ce³⁺ scavenges ·OH to form Ce⁴⁺; which is subsequently reduced back to Ce³⁺ upon reacting with H₂O₂, mitigating radical formation and attack [38,40,41,42]. This leads to a regenerative sink process in which cerium ions reduce the presence of peroxide and radical species.

$$\mathrm{C}{\mathrm{e}}^{3+}+\cdot \mathrm{OH}+{ \mathrm{H}}^{+}⟶ \mathrm{C}{\mathrm{e}}^{4+}+{\mathrm{H}}_2\mathrm{O}$$

$$\mathrm{C}{\mathrm{e}}^{4+}+{ \mathrm{H}}_2{\mathrm{O}}_2 ⟶ \mathrm{C}{\mathrm{e}}^{3+}+\cdot \mathrm{OOH}+{ \mathrm{H}}^{+}$$

$$\mathrm{C}{\mathrm{e}}^{4+}+\cdot \mathrm{OOH} ⟶ \mathrm{C}{\mathrm{e}}^{3+}+{\mathrm{O}}_2+{ \mathrm{H}}^{+}$$

The purpose of this work is to discuss the chemical stability of a mechanically reinforced, chemically stabilized, long-chain PFSA membrane with commercially relevant electrodes and Pt loadings. The scope is limited to low temperature PEMFC systems that operate below 90–95 °C and are equipped with a cathode humidifier to maintain relative humidities above 30% [22,23]. The overall approach is to characterize the chemical stability in terms of fluoride emission rate (FER) at steady-state and to develop a model using experimental data at or near OCV, where it can be measured with high fidelity. The model can then be used to calculate FER in differential cells and map operating conditions to limit fluoride emission rates for postulated failure scenarios.

2. Materials and Methods

2.1. Data Sources

The experimental data supporting the FER model development pertains to a state-of-the-art, thin (12 μm), low equivalent weight (800 EW) PFSA membrane that is mechanically reinforced with an expanded PTFE skeleton layer and chemically stabilized with 9.7 mg/cm² Ce [43]. It is incorporated into a membrane electrode assembly (MEA) in which the cathode electrode has 30% PtCo/HSC ORR catalyst with 0.1 mg/cm² Pt and 825 EW ionomer with 0.9 I/C. The anode electrode has 10% Pt/GrV HOR catalyst with 0.025 mg/cm² Pt and 900 EW ionomer with 0.6 I/C. The data sources are briefly described below.

Cell Tests: A series of 270–300 h tests were conducted on a 44-cm² single cell hardware to examine the effect of operating conditions on FER measured by ion exchange chromatography of water samples collected over 24-h time intervals. Figure 1a presents the data from one series of tests on the effect of temperature on anode and cathode FERs at 250 kPa_abs backpressure and 100% RH. The cell voltage was held at 0.9 V or OCV if it could not be maintained at the set point. No specific cell recovery operation was attempted during the course of the test, and the cell voltage dropped to an OCV of 0.86 V after 265 h at 95 °C but stayed at the set point of 0.9 V at 80 °C. The membrane remained healthy, as evidenced by no obvious change in the measured H₂ crossover.

In another series of tests, the cells were subjected to catalyst-specific, membrane-specific, and combined catalyst–membrane H₂/air-accelerated stress tests (AST) in a counterflow configuration [45]. The 125-h catalyst AST consisted of 30,000 square wave (SW) potential cycles at 90 °C and 100% RH. Each potential cycle was of 15-s duration with 5 s at 0.675 V lower potential limit (LPL) and 10 s at 0.925 V upper potential limit (UPL). The 500-h membrane AST consisted of 30,000 SW current cycles at 95 °C and 20% RH. Each current cycle was of 60-s duration with 30 s at 0.01 A/cm² lower current density (LCD) and 30 s at 1.5 A/cm² upper current density (UCD). The 625-h combined AST consisted of the 125-h catalyst AST as Part I and the 500-h membrane AST as Part II. Post-test transmission electron microscopic (TEM) examination of specimens revealed that the membrane thickness had decreased by 22% at the air inlet, 30% in the middle, and 38% at the air outlet after the combined AST. The membrane remained healthy in the tests, with no significant change In the measured H₂ crossover. More complete information on test protocols and data will be published in a separate paper.

OCV Tests: Coms et al. investigated the effect of membrane thickness on chemical degradation in a 38-cm² active area cell hardware with the catalysts coated on the anode and cathode gas diffusion media [43]. The tests were performed at OCV and 90 °C for 2-mol% Ce loading and three levels of four variables: membrane thickness, RH, cathode pressure, and anode differential pressure. A design-of-experiments approach was used to reduce the number of tests from 3⁴ to 3^(4–1). The tests were 270 h long, and the measured FERs are summarized in Figure 1b as steady-state values after exposure for 200 h at different RH. The OCV is not constant during the test and declines at a rate that depends on the operating conditions. For example, it declined rapidly to 0.860 V for an MEA with a 20-µm membrane held at 90% RH, 210 kPa anode, and 150 kPa cathode pressure, and gradually to 0.792 V for an MEA with a 12-µm membrane held at 30% RH, 220 kPa anode, and 200 kPa cathode pressure. The variability in FER for a given RH in Figure 1b is a measure of the combined effect of membrane thickness and gas pressures.

Hydrogen Peroxide Vapor Test: Ex-situ tests were conducted by Kumaraguru [44] and Coms [43] to investigate the chemical stability of membranes exposed to 30-ppm of H₂O₂ vapor in a N₂ carrier stream at 90 °C. A three-step protocol was developed to baseline the membrane degradation rate via unzipping at 91–95% RH in step 1, measure the accelerated degradation rate at 22–23% RH in step 2, and kinetically characterize the damage in the low-RH excursion in step 2 by holding at 91–95% RH in step 3. Each step had a 20-h duration. The tests were performed for three membrane thicknesses (8, 12, 20 µm) and three levels of Ce loading. Figure 1c summarizes the 3-step FER data for the 12-µm membrane with 0, 2, and 8 mol% Ce loading. It indicates that the unmitigated membrane has much higher degradation rates and, as detected by FTIR, also suffers chain scission during low-RH excursion. Even at low 2 mol% loading, cerium is very effective in mitigating chemical degradation and, as confirmed by FTIR, arresting main chain scission.

2.2. Theoretical

Differential Cell Model: A 1-D model was developed to calculate the potential gradients and other variables that affect Ce transport in operating differential cells. Neglecting current transport in the axial direction, the ionic ($E_i$) and electric potential ($E_e$) distributions in the through-plane (anode to cathode, y) are determined by the following equations:

$${\displaystyle \frac{\partial }{\partial y}}\left({\sigma }_i{\displaystyle \frac{\partial E_i}{\partial y}}\right)=-\left(j_a-j_c\right)$$

(1)

$${\displaystyle \frac{\partial }{\partial y}}\left({\sigma }_e{\displaystyle \frac{\partial E_e}{\partial y}}\right)=\left(j_a-j_c\right)$$

(2)

$$i_i=-{\sigma }_i{\displaystyle \frac{\partial E_i}{\partial y}}$$

(3)

$$i_e=-{\sigma }_e{\displaystyle \frac{\partial E_e}{\partial y}}$$

(4)

$${i=i}_i+i_e$$

(5)

We use the Butler–Volmer equation for the HOR kinetics and the Tafel equation for the ORR kinetics as follows:

$$j_a=2i_{0a}{S}_{Pt}^{a}sinh\left({\displaystyle \frac{{\mathsf{\eta }}_a}{b_a}}\right)$$

(6)

$$i_{0a}=i_{0a}^r{\left({\displaystyle \frac{C_{H_2}}{C_{H_2}^r}}\right)}^{{\gamma }_a}{e}^{{\displaystyle \frac{{\Delta H}_s^a}{R}}\left({\displaystyle \frac{1}{353}}-{\displaystyle \frac{1}{T}}\right)}$$

(7)

$${\eta }_a=E_e-E_i+E_N^a$$

(8)

$$E_N^a={\displaystyle \frac{RT}{2F}}ln\left({\displaystyle \frac{C_{H_2}}{C_{H_2}^r}}\right)$$

(9)

$$j_c+j_x=i_{0c}{S}_{Pt}^c\left(1-\theta \right)e^{-{\displaystyle \frac{\omega \theta }{RT}}}{e}^{{\displaystyle \frac{{\mathsf{\eta }}_c}{b_c}}}$$

(10)

$$i_{0c}=i_{0c}^r{\left({\displaystyle \frac{C_{O_2}}{C_{O_2}^r}}\right)}^{{\gamma }_c}{a}_w^{\beta }\left(1-S\right)e^{{\displaystyle \frac{{\Delta H}_s^c}{R}}\left({\displaystyle \frac{1}{353}}-{\displaystyle \frac{1}{T}}\right)}$$

(11)

$${\eta }_c=E_N^c-(E_e-E_i)$$

(12)

$$E_N^c=E_N^0+{\displaystyle \frac{\mathrm{RT}}{2\mathrm{F}}}\ln \left[{\left({\displaystyle \frac{C_{O_2}}{C_{O_2}^r}}\right)}^{0.5}/a_w\right]$$

(13)

Water Transport: Assuming a local equilibrium between water uptake in ionomer (${\lambda }_m$) and vapor concentration (${\rho }_v$) in the electrode, the following equations define water concentration (${\rho }_w$), effective diffusivity ($D_w^e$), and water transport in the through-plane [46]:

$$(\epsilon +{\epsilon }_m){\rho }_w={\epsilon }_m\left({\displaystyle \frac{M_w}{M_m}}\right){\rho }_m {\lambda }_m+\epsilon {\rho }_v$$

(14)

$$(\epsilon +{\epsilon }_m){\rho }_w{D}_w^e={\epsilon }_m\left({\displaystyle \frac{M_w}{M_m}}\right){\rho }_m {\lambda }_m{D}_{\lambda }^e+\epsilon {{\rho }_{v}D}_v^e$$

(15)

$${\displaystyle \frac{\partial }{\partial t}}[\left(\epsilon +{\epsilon }_m\right){\rho }_w]={\displaystyle \frac{\partial }{\partial y}}[\left(\epsilon +{\epsilon }_m\right)D_w^e{\displaystyle \frac{\partial {\rho }_w}{\partial y}}-{M_w\beta }_{\lambda }{\displaystyle \frac{i_i}{F}}]+{\dot{S}}_w$$

(16)

$${\dot{S}}_w={\displaystyle \frac{j_c}{2F}}{M}_w$$

(17)

The water transport equation can be conveniently recast in terms of ${\rho }_v$ as the dependent variable:

$$(\epsilon +{\epsilon }_m^{\prime }){\displaystyle \frac{\partial {\rho }_v}{\partial t}}={\displaystyle \frac{\partial }{\partial y}}[(\epsilon +{\epsilon }_m^{\prime })D_w^e{\displaystyle \frac{\partial {\rho }_v}{\partial y}}-{M_w\beta }_{\lambda }{\displaystyle \frac{i_i}{F}}]+{\dot{S}}_w$$

(18)

$${\epsilon }_m^{\prime }={\epsilon }_m\left({\displaystyle \frac{M_w}{M_m}}\right)\left({\displaystyle \frac{{\rho }_m}{{\rho }_s}}\right)\left({\displaystyle \frac{\partial {\lambda }_m}{\partial {\mathrm{a}}_m}}\right)$$

(19)

For computational expediency, Lai’s relationship between ${\lambda }_m$ and water activity ($a_m$) is extrapolated beyond the saturation limit ($a_m=1$) as follows:

$${\lambda }_m=\mathrm{ }\left(1+0.2352{\alpha }_m^2\left({\displaystyle \frac{T-303}{30}}\right)\right)\left(14.22a_m^3-18.92a_m^2+13.41a_m\right),\mathrm{ }{a}_m\le 1$$

(20)

$${\lambda }_m={\left({\displaystyle \frac{a_m-1}{a_{ml}-1}}\right)}^{0.1}\left({\lambda }_{ml}-{\lambda }_s\right)+{\lambda }_s,\mathrm{ }{1<a}_m<{(a}_{ml}=3)$$

(21)

$${\lambda }_{ml}=7.633+0.1779\left(T-273\right),\mathrm{ }298\mathrm{ }K<T<373\mathrm{ }K$$

(22)

Cerium Transport: Ce is mobile and moves rapidly in the through-plane under applied potential. The following conservation equation describes the dynamics of Ce transport between the membrane and the electrodes by electromigration and diffusion:

$${ϵ}_m{\displaystyle \frac{\partial c_{Ce}}{\partial t}}=\mathrm{ }{\displaystyle \frac{\partial }{\partial y}}(D_{Ce}{\displaystyle \frac{\partial c_{Ce}}{\partial y}}+u_{Ce}{c}_{Ce}{\displaystyle \frac{\partial V_i}{\partial y}})$$

(23)

Following Baker et al., Ce diffusivity ($D_{Ce}$) and mobility ($u_m$) are correlated with temperature and water uptake [47]:

$$D_{Ce}={ϵ}_m^{1.5}{D}_{Ce}({\lambda }_s,T_r)e^{{\displaystyle \frac{{∆H}_d}{R}}\left({\displaystyle \frac{1}{T}}-{\displaystyle \frac{1}{T_r}}\right)}{\left({\displaystyle \frac{{\lambda }_m-{\lambda }_0}{{\lambda }_s-{\lambda }_0}}\right)}^{1.75}, D_{Ce}\left({\lambda }_s,T_r\right)=2\times {10}^{-6}\mathrm{ }\mathrm{c}{\mathrm{m}}^2/\mathrm{s},\mathrm{ }{\lambda }_0=2.3$$

(24)

$$u_{Ce}={{ϵ}_m^{1.5}u}_{Ce}\left({\lambda }_s,T_r\right)e^{{\displaystyle \frac{{∆H}_m}{R}}\left({\displaystyle \frac{1}{T}}-{\displaystyle \frac{1}{T_r}}\right)}{\left({\displaystyle \frac{{\lambda }_m-{\lambda }_0}{{\lambda }_s-{\lambda }_0}}\right)}^{1.4}, u_{Ce}\left({\lambda }_s,T_r\right)=1.5\times {10}^{-2}\mathrm{ }\mathrm{c}{\mathrm{m}}^2/\mathrm{V}.\mathrm{s}$$

(25)

Solution Method: The foregoing set of equations governing potential distribution, water transport, cerium transport, and fluoride emission rate for the differential cell models were solved simultaneously using COMSOL Multiphysics (version 6.0) [48]. The computational domain defined as the gas diffusion layers, catalyst layers, and membrane was discretized on a non-uniform rectangular grid providing appropriate spatial variation in through-plane gradients. The simulations were performed using the time-dependent COMSOL solver, with adaptive time stepping to ensure numerical stability. The output data was processed to extract crossover rates, cerium retention, and relative humidity at the anode and cathode interfaces of the membrane. The transient equations are integrated for multiple time steps until convergence, defined as repeat solutions with negligible differences, is obtained.

3. Results

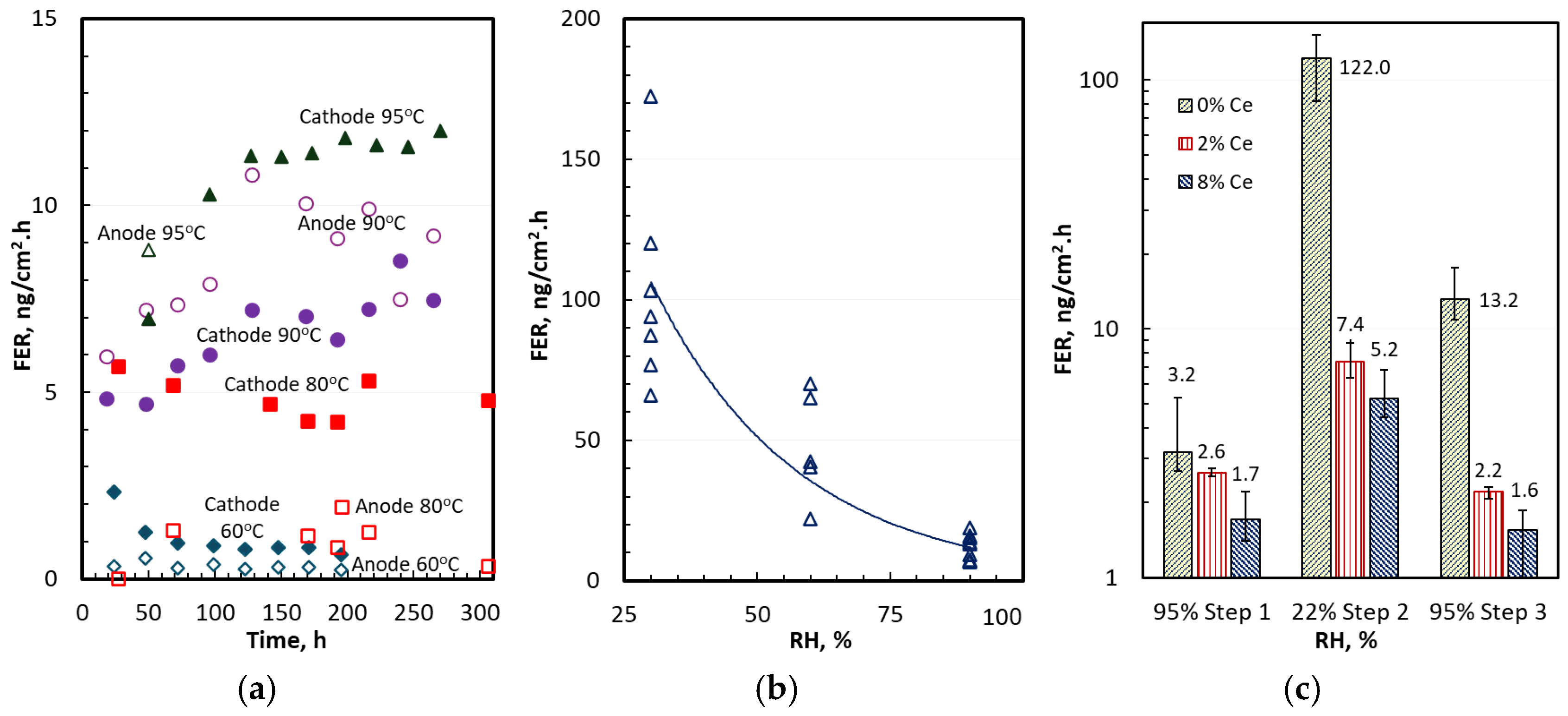
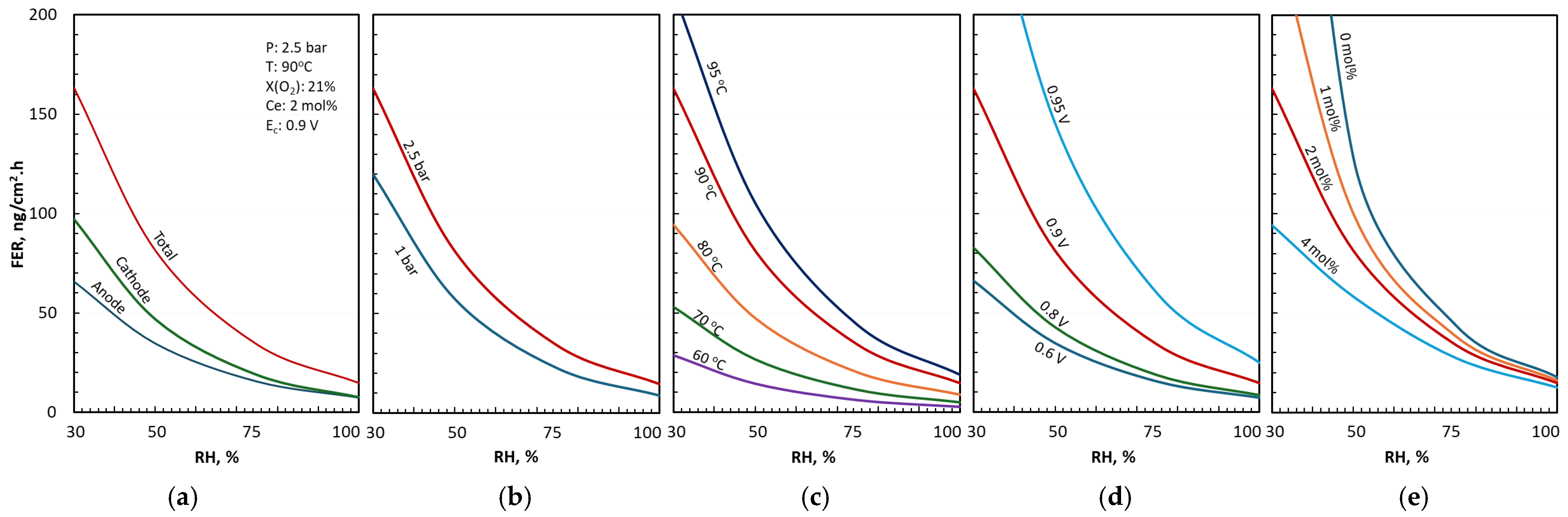
3.1. Anode and Cathode FERs

Coms et al. obtained 27 data points for FERs at OCV for different combinations of membrane thickness (8, 12, and 20 µm thicknesses), relative humidity (30%, 60%, 90%), cathode pressure (150 kPa, 200 kPa, 250 kPa), and differential pressure between anode and cathode (−20 kPa, +20 kPa, +60 kPa) [43]. We digitized the measured total (anode plus cathode) FERs that were reported as discrete data points, plotted in terms of single variables: RH, membrane thickness, cathode pressure, and anode pressure. We were able to pair the digitized data with reasonable certainty and extract the complete information for FERs in terms of all four experimental variables for each data point. Figure 2a presents the digitized FER as a function of the O₂ crossover (${\dot{N}}_{O_2}$) that is known to depend on T, water uptake, membrane EW, $P_{O_2}$, and ${\delta }_m$.

$${\dot{N}}_{O_2}={\psi }_{O_2}{\displaystyle \frac{P_{O_2}}{{\delta }_m}}$$

(26)

Figure 2a includes least-square linear fits of FER (${\dot{r}}_F$) at 30%, 60%, and 90% RH, in which the x-intercept represents the cathode FER (${\dot{r}}_{Fc}$) and the slope is a measure of the anode FER selectivity ($S_F$), i.e., moles of fluorine produced per mole of O₂ crossover to anode. The choice of intercepts (i.e., ${\dot{r}}_{Fc}$) was constrained by the measured cathode FERs of 4.6 ng/cm²·h at 90% RH for a 20-µm membrane at 210 kPa anode and 150 kPa cathode pressure, and 44.3 ng/cm²·h at 30% RH for a 12-µm membrane at 220 kPa anode and 200 kPa cathode pressure. Most data points are within 1 standard deviation of 9, 9.8, and 4.8 ng/cm²·h at 30%, 60%, and 90% RH, respectively. The mean errors are 10% for 30% RH, 24% for 60% RH, and 39% for 90% RH.

$${\dot{r}}_F={\dot{r}}_{Fc}+{\dot{r}}_{Fa}$$

(27)

$${\dot{r}}_{Fa}={\dot{N}}_{O_2}{S_{F}M}_F$$

(28)

Figure 2b presents the derived and modeled cathode FER as a function of RH. The derived ${\dot{r}}_{Fc}$ is well correlated with an exponential function considering that R² is 99.91%, the standard deviation is 0.75 ng/cm²·h, and the mean error is 3.9%. We also investigated the possible relationship between cathode FER and H₂ crossover from anode (${\dot{N}}_{H_2}$) by plotting ${\dot{r}}_{Fc} \left(={\dot{r}}_F-{\dot{r}}_{Fa}\right)$ against ${\dot{N}}_{H_2}$ and found no correlation between them.

$${\dot{N}}_{H_2}={\psi }_{H_2}{\displaystyle \frac{P_{H_2}}{{\delta }_m}}$$

(29)

Figure 2c presents the derived anode FER selectivity as a function of RH and shows that $S_F$ decreases from 0.19 mol-F/1000 mol-O₂ at 30% RH to 0.01 mol-F/1000 mol-O₂ at 90% RH. The derived $S_F$ is fairly well correlated with an exponential function considering that R² is 96.52%, the standard deviation is 0.018 mol-F/1000 mol-O₂, and the mean error is 20%. H₂O₂ produced from the parasitic 2-electron ORR of proton–electron couples and crossover O₂ is the likely source of anode FER since experiments on rotating ring disk electrodes (RRDE) exhibit a high yield of peroxide at anode potentials [49]. The cathode FER may be linked to the energetic formation of reactive hydroxyl radicals (·OH) from the decomposition of H₂O₂ produced as an intermediate in the 2-electron ORR pathway at high cathode potentials. Production of radicals is also catalyzed by metal contaminants through the Fenton reaction.

$${\mathrm{O}}_2+2\hspace{0.17em}{\mathrm{H}}^{+}+2\hspace{0.17em}{\mathrm{e}}^{-} ⟶ {\mathrm{H}}_2{\mathrm{O}}_2$$

(30)

$${\mathrm{H}}_2{\mathrm{O}}_2+2\hspace{0.17em}{\mathrm{H}}^{+}+2\hspace{0.17em}{\mathrm{e}}^{-} ⟶ {2 \mathrm{H}}_2\mathrm{O}$$

(31)

$${\mathrm{H}}_2{\mathrm{O}}_2 ⟶ \cdot \mathrm{OH}+{}^{-}\mathrm{OH}$$

(32)

Figure 3a is a parity plot of modeled and measured FER for the 24 data points that could be digitized and paired with reasonable accuracy. The coefficient of determination (R²) from a statistical analysis is 91.7%, and the standard deviation is 12.3 ng/cm²·h or 23.5%. The mean errors are 11%, 18%, and 37% for 30%, 60%, and 90% RH, respectively.

Figure 3b is a parity plot showing results from a regression analysis for the same 24 data points assuming that ${\dot{r}}_F$ is only a function of RH. With this assumption, R² is smaller: 71.93%; the standard deviation is larger: 22.6 ng/cm²·h or 43.2%; and the mean errors are much larger: 33%, 31%, and 39% for 30%, 60%, and 90% RH, respectively. Coms’ analysis with all 27 data points shows a reported R² of 82.30% for RH-only and 85.31% for combined RH and ΔP regression [43].

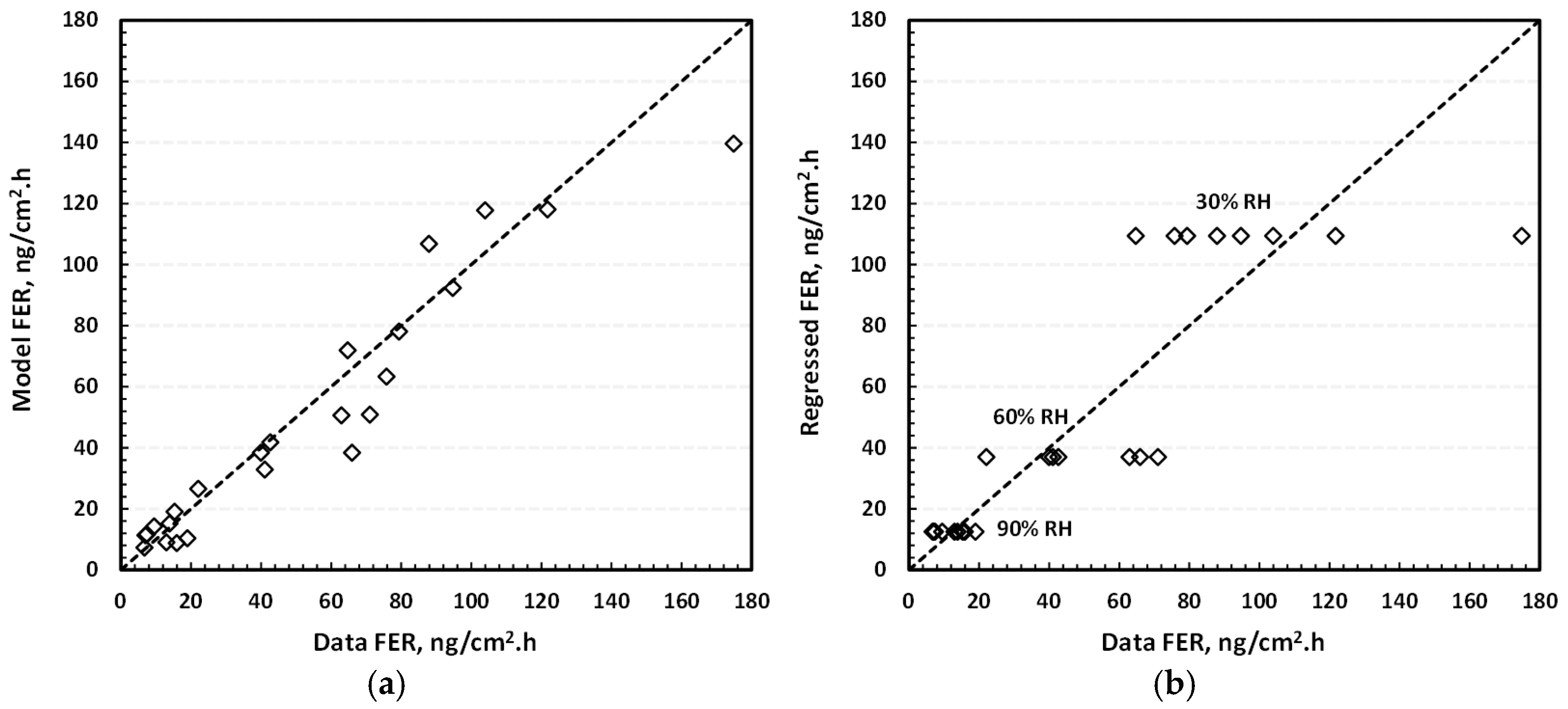
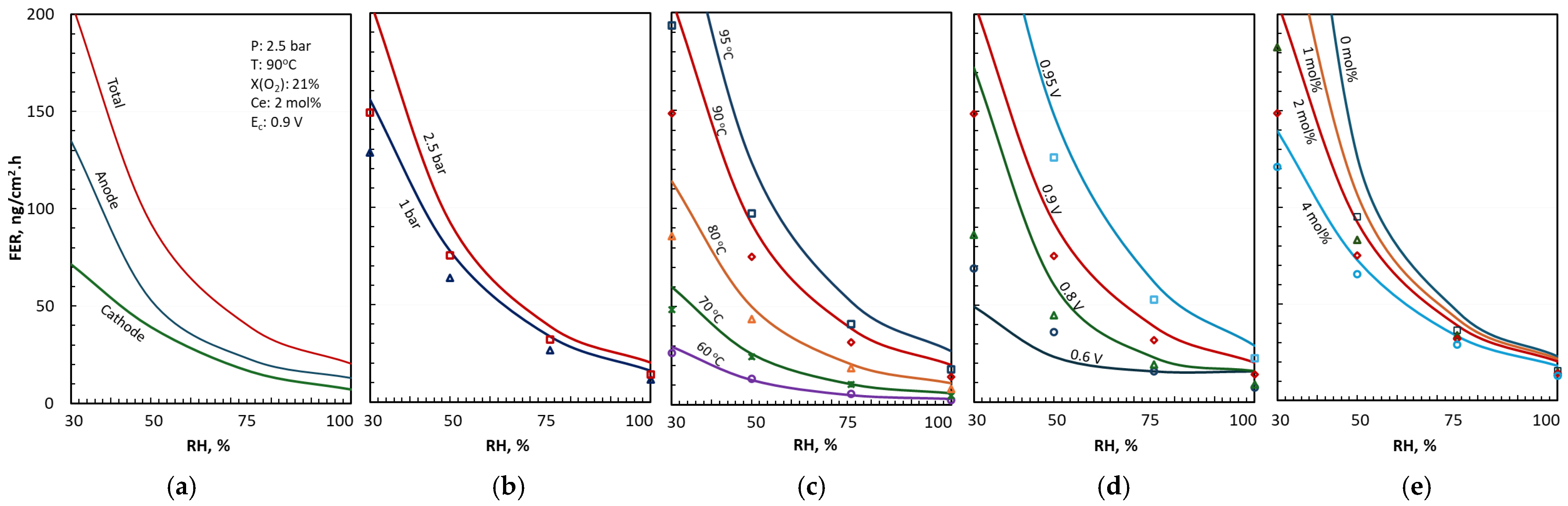
3.2. FER Correlation

We developed separate correlations for anode and cathode FER by combining the data in Figure 1 and Figure 2, and assuming that ${\dot{r}}_{Fc}$ is a function of the cathode potential ($E_c$), but, because HOR is facile and the anode overpotentials are small, the anode potential generally remains below 10 mV vs. SHE under all conditions, so the potential dependence of ${\dot{r}}_{Fa}$ can be neglected.

Both ${\dot{r}}_{Fc}$ and ${\dot{r}}_{Fa}$ are functions of the water activity in membrane ($a_m$), Ce loading ($C_{Ce}$), and temperature ($T$). Following Chandesris [21], the equivalent transfer coefficient (${\alpha }_F$) for the dependence of ${\dot{r}}_{Fc}$ on cathode potential is assigned a value of 0.54, which translates into a factor of 5 increase in FER if the cathode potential is raised to 0.95 V from 0.85 V (see Figure 4a).

$${\dot{r}}_{Fc}=A_c(a_m){\chi }_c({a_m,C_{Ce})e}^{{\displaystyle \frac{{∆H}_c}{R}}\left({\displaystyle \frac{1}{T_r}}-{\displaystyle \frac{1}{T}}\right)}{e}^{{\displaystyle \frac{{\alpha }_{F}F}{RT}}(E_c-E_r)}$$

(33)

$$A_c\left(a_m\right)=A_{c0}{e}^{-{\beta }_c{a}_m}$$

(34)

$$S_F=A_a(a_m){\chi }_a({a_m,C_{Ce})e}^{{\displaystyle \frac{{∆H}_a}{R}}\left({\displaystyle \frac{1}{T_r}}-{\displaystyle \frac{1}{T}}\right)}$$

(35)

$$A_a\left(a_m\right)=A_{a0}{e}^{-{\beta }_a{a}_m}$$

(36)

Figure 4a presents the effect of temperature on the measured anode, cathode, and total FER from which we derive apparent activation energies for temperature dependence at 0.9 V of 99 kJ/mol for ${\dot{r}}_{Fa}$ and 71 kJ/mol for ${\dot{r}}_{Fc}$.

Table 1. Model constants and parameters adapted from previous work on a distributed ORR kinetic model applied to differential cells with the same material set and MEA [50]. The model constants for FER have been determined in this study.

Symbol		Symbol		Symbol
$i_{0a}^r$	248 $\mathrm{m}\mathrm{A}/{\mathrm{c}\mathrm{m}}_{\mathrm{P}\mathrm{t}}^2$	${\gamma }_a$	1.25	${\Delta H}_s^a$	30.2 kJ/mol
$b_a$	22.6 mV	$S_{Pt}^a$	$5.6\times {10}^6 {\mathrm{m}}_{\mathrm{P}\mathrm{t}}^2/{\mathrm{m}}^3$
$i_{0c}^r$	3.1 $\mathrm{m}\mathrm{A}/{\mathrm{c}\mathrm{m}}_{\mathrm{P}\mathrm{t}}^2$	${\gamma }_c$	0.65	${\Delta H}_s^c$	28.1 kJ/mol
$b_c$	60.8 mV	$S_{Pt}^c$	$12\times {10}^6 {\mathrm{m}}_{\mathrm{P}\mathrm{t}}^2/{\mathrm{m}}^3$	$\omega$	2.9 kJ/mol
ε	0.4	${\epsilon }_m$	0.26	β	0.9
${∆H}_d$	51.6 kJ/mol	${∆H}_m$	46.5 kJ/mol
$A_{c0}$	123.3 ng/cm2·h	${\beta }_c$	3.7	${∆H}_c$	71 kJ/mol
${\alpha }_F$	0.54	$E_r$	0.85 V	$T_r$	363 K
$A_{a0}$	$6.5\times {10}^{-4}$	${\beta }_a$	4.1	${∆H}_a$	78 kJ/mol

lists the actual values of ${∆H}_c$ and ${∆H}_a$ from Equations (33) and (35). It also includes the coefficients, ${\beta }_a$ and ${\beta }_c$, that determine the effect of water activity on ${\dot{r}}_{Fc}$ and ${\dot{r}}_{Fa}$ as derived from the modeled curves in Figure 2b,c.

The effect of Ce on FER is incorporated by analyzing the peroxide data in Figure 1c, which indicates that Ce³⁺ mitigates the effect of H₂O₂ vapor, especially under dry conditions. As suggested by Coms, the hydroxyl radical (∙OH) produced from H₂O₂ decomposition is responsible for abstracting hydrogen atoms by unzipping PFSA chains and releasing fluoride at a rate that depends on temperature, RH, and anti-oxidant loading in a stabilized membrane [43]. Scission of a polymer chain in an unmitigated membrane can also occur, but it does not directly release fluoride; however, the scission rate can be measured by FTIR. We built an empirical function using data in Figure 1c to capture the effect of Ce loading and RH on relative FER from a 12-µm membrane. The function is valid from 0 to 4 mol% Ce and 30% to 100% RH:

$${\chi }_c\left(a_m,C_{Ce}\right)={\chi }_a\left(a_m,C_{Ce}\right)={\chi }_0\left(a_m\right){\left[C_{Ce}+C_0\left(a_m\right)\right]}^{-}$$

(37)

$${\chi }_0\left(a_m\right)=32.49a_m-5.82$$

(38)

$$C_0\left(a_m\right)=16.46a_m-3.68$$

(39)

$$={\displaystyle \frac{ln\left({\chi }_0\right)}{ln(2+C_0)}}$$

(40)

Figure 4c shows that adding a small amount of Ce to an unmitigated membrane can significantly reduce FER under dry conditions, and the benefit is progressively smaller at higher Ce loading and under wet conditions.

A single-variable sensitivity analysis was conducted to illustrate the effect of the operating and design variables on FER correlation. The baseline conditions are 2.5 bar, 90 °C, 21 mol% O₂, 0.9 V cathode potential, 2 mol% Ce loading, and other MEA characteristics listed in Table 1. Figure 5a indicates that at 0.9 V cathode potential, the anode and cathode FERs are nearly equal at 100% RH, but the cathode FER is about 50% larger at 30% RH. Raising the operating pressure in Figure 5b increases FER because of the higher oxygen crossover and hence, the anode FER. Figure 5c shows that FER is extremely sensitive to temperature, especially under drier conditions, and increases ten-fold on raising the temperature from 60 °C to 95 °C. Figure 5d points to a similar sensitivity of FER to cathode potentials above 0.8 V; note that the cathode potential only affects ${\dot{r}}_{Fc}$ and not ${\dot{r}}_{Fa}$. Figure 5e confirms that Ce³⁺ is more effective in mitigating FER under dry conditions than under wet conditions. We conclude that FER is extremely sensitive to RH, T, $E_c$, and cerium loading, and prolonged excursions near OCV and high T under dry conditions accelerate chemical degradation of the membrane.

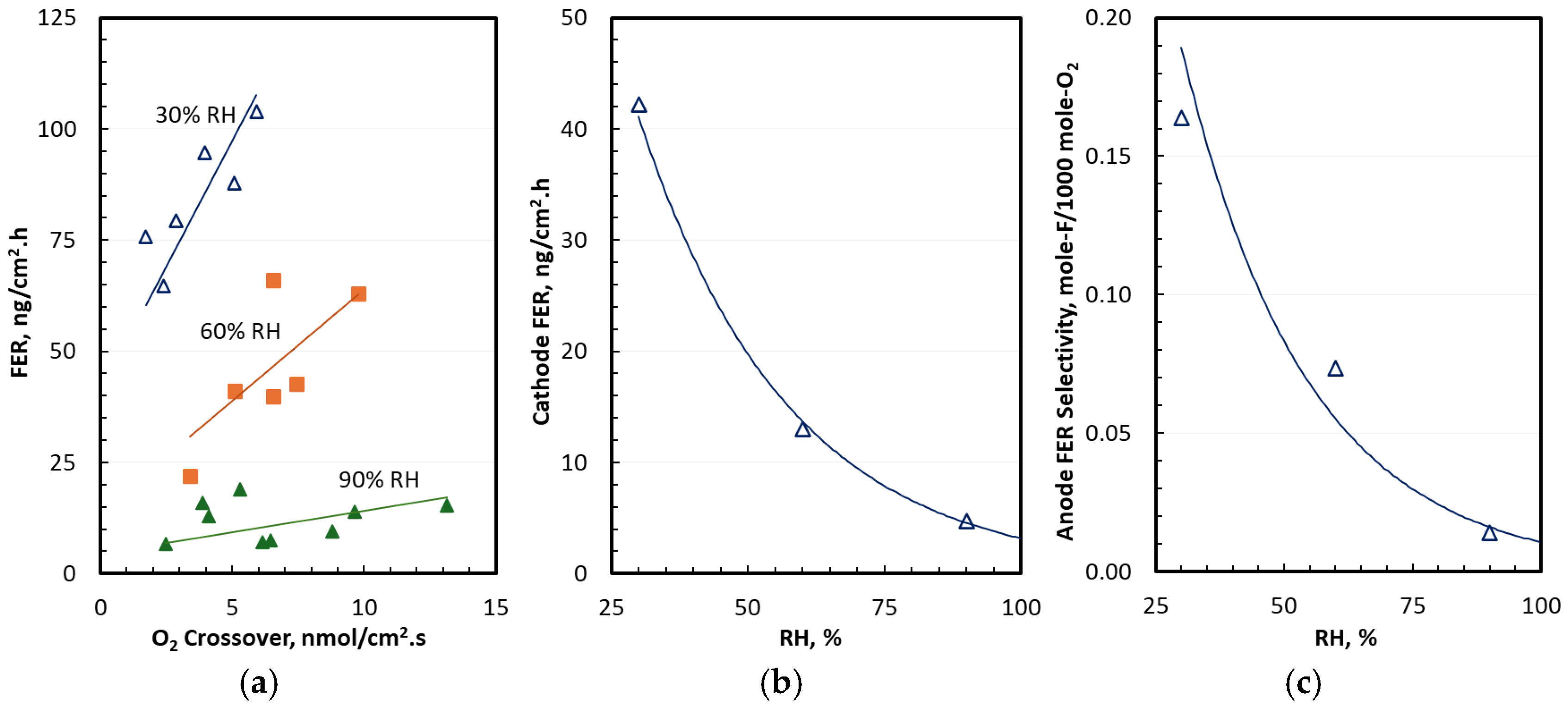
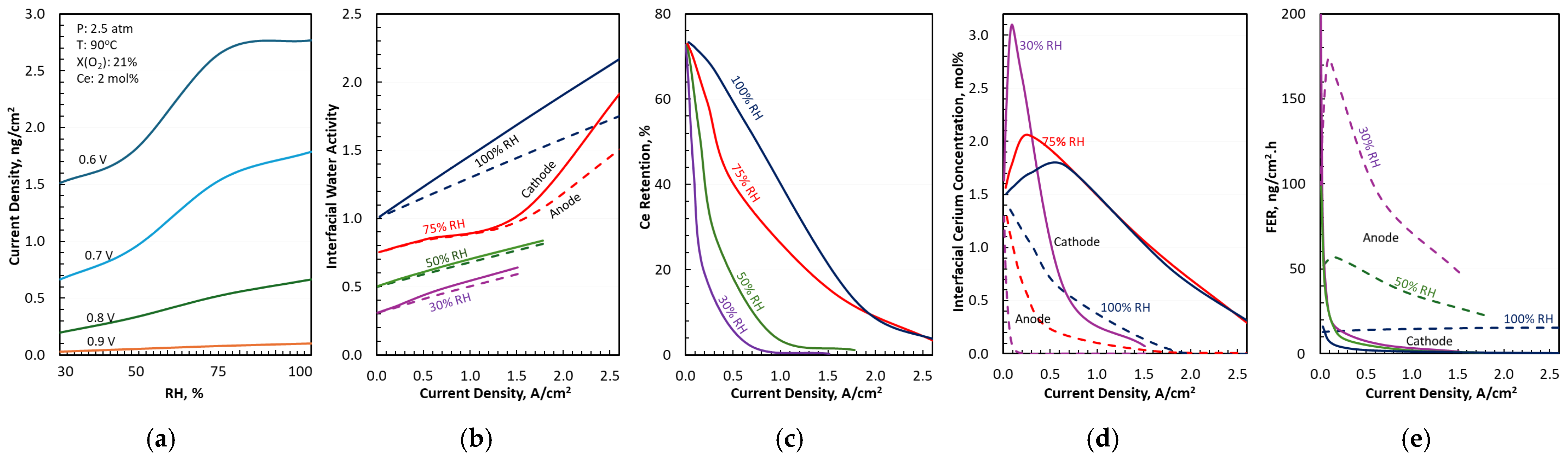
3.3. Water and Cerium Transport in Differential Cells

Gradients in water activity and cerium concentration develop in operating cells that affect FER. We used our models to characterize these gradients under the same baseline conditions as in Figure 5, except that the cell voltage is treated as a variable.

Figure 6a depicts the modeled relationship between the cell voltage and current density as a function of RH in the gas channel. At the lowest cell voltage of interest in this study, 0.6 V, the current density varies between 1.5 A/cm² at 30% RH and 2.7 A/cm² at 100% RH. Figure 6b presents the resulting gradients in interfacial activity due to water production in the cathode, electroosmotic drag that transports water from the anode to the cathode, and diffusion in the membrane. The higher the current density, the larger the differential between the activities at cathode and anode interfaces and between the gas channel and the membrane interfaces.

Figure 6c presents the modeled steady-state Ce retention, defined as the fraction of total Ce loading remaining in the membrane under applied potential. At OCV, diffusion redistributes cerium equally between the membrane, anode, and cathode, and limits the retention in the membrane to <72%. As voltage is applied, Ce is also transported by electromigration with flux proportional to the potential gradient ($\partial E_i/\partial y$) and, therefore, the current density ($i_i/{\sigma }_i$), and Ce retention is determined by the balance between electromigration and diffusion. The higher the current density, the lower the retention, which drops to <20% at 0.6 V (1.5–2.5 A/cm²). For a given current density, Ce diffusivity decreases faster at lower RH than electromobility, and Ce retention decreases, becoming <5% at 1.5 A/cm² for RH < 50%.

Figure 6d portrays the dynamics of cerium migration. Under applied potential, Ce depletes in the anode and segregates at the cathode–membrane interface at low current density before accumulating in the cathode at higher current density. Under drier conditions, Ce depletes to a greater extent at the anode interface, and segregates more at low current density and depletes more at high current density at the cathode interface.

Figure 6e presents FER calculated using interfacial water activity and Ce concentration in Figure 5b,d. Only near OCV is FER higher at the cathode than the anode. The cross-over cell voltage at which anode FER exceeds cathode FER depends on the RH in the gas channel: 907 mV at 30% RH and 925 mV at 100% RH. At lower cell voltage (i.e., higher current density), higher water activity at the cathode interface suppresses cathode FER, and Ce depletion at the anode interface accelerates anode FER.

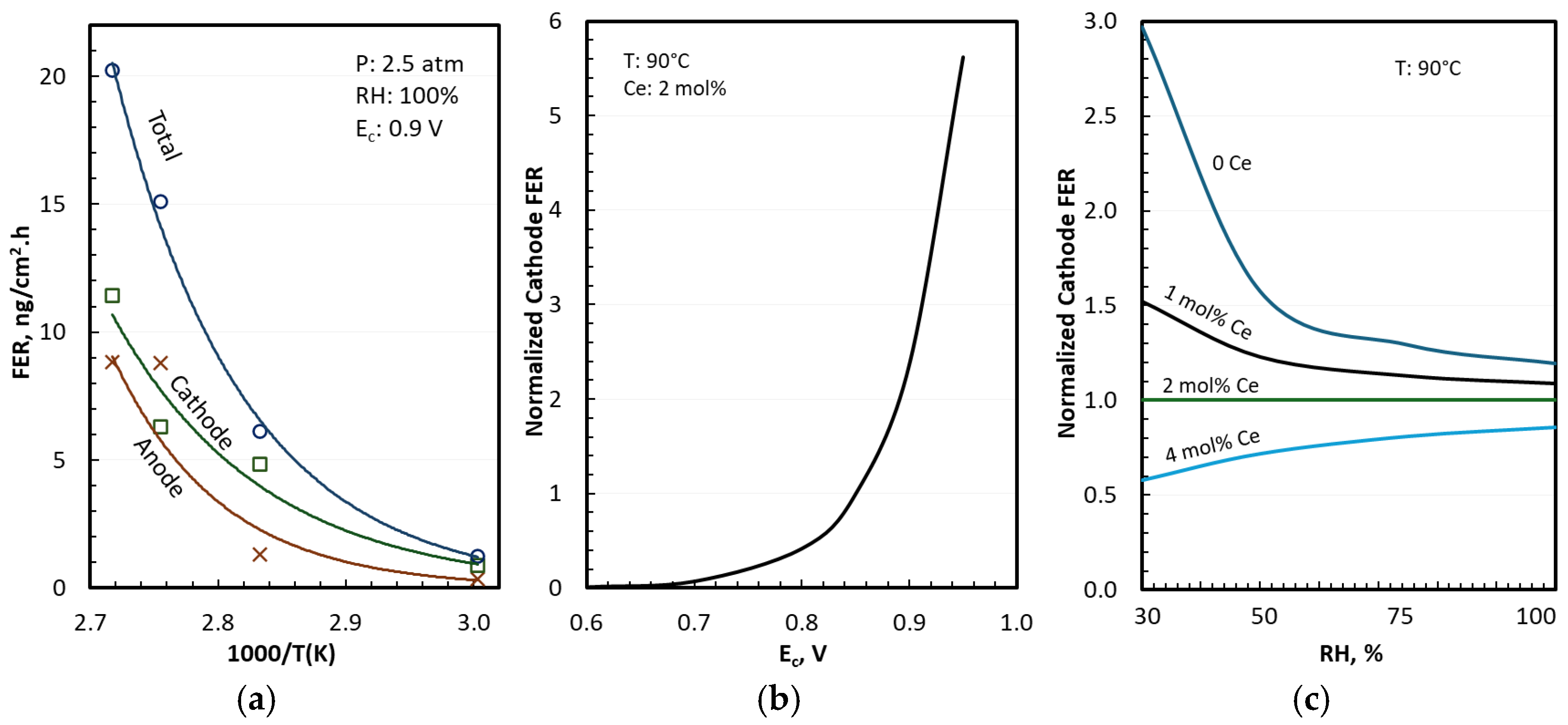
3.4. FER in Differential Cells

Figure 7 summarizes results from a single-variable sensitivity analysis conducted to quantify the effects of activity and Ce gradients on FER. The solid lines in Figure 7 are FERs with gradients, and the symbols are FERs at the same cathode potentials but without gradients.

Figure 7a indicates that the anode FER is comparable to but higher than the cathode FER at 0.9 V and other baseline conditions listed in the legend. As seen previously in Figure 6e, the difference between anode and cathode FERs grows at lower cell voltages. Cathode FER is higher than the anode FER for cell voltages above a threshold, 925 mV at 2.5 bar and for pressures below 2 bar at 0.9 V.

The main message from the sensitivity analysis Is that the gradients In Ce concentration generally accelerate FER at lower RH (Figure 7b–e), higher pressures (Figure 7b), higher temperatures (Figure 7c), lower cell voltages (Figure 7d), and lower Ce loading in the membrane (Figure 7e). Increased interfacial water activity at higher current density tends to offset or even reverse the effect of Ce segregation, as manifested in lower FER at 0.6 V in Figure 7d.

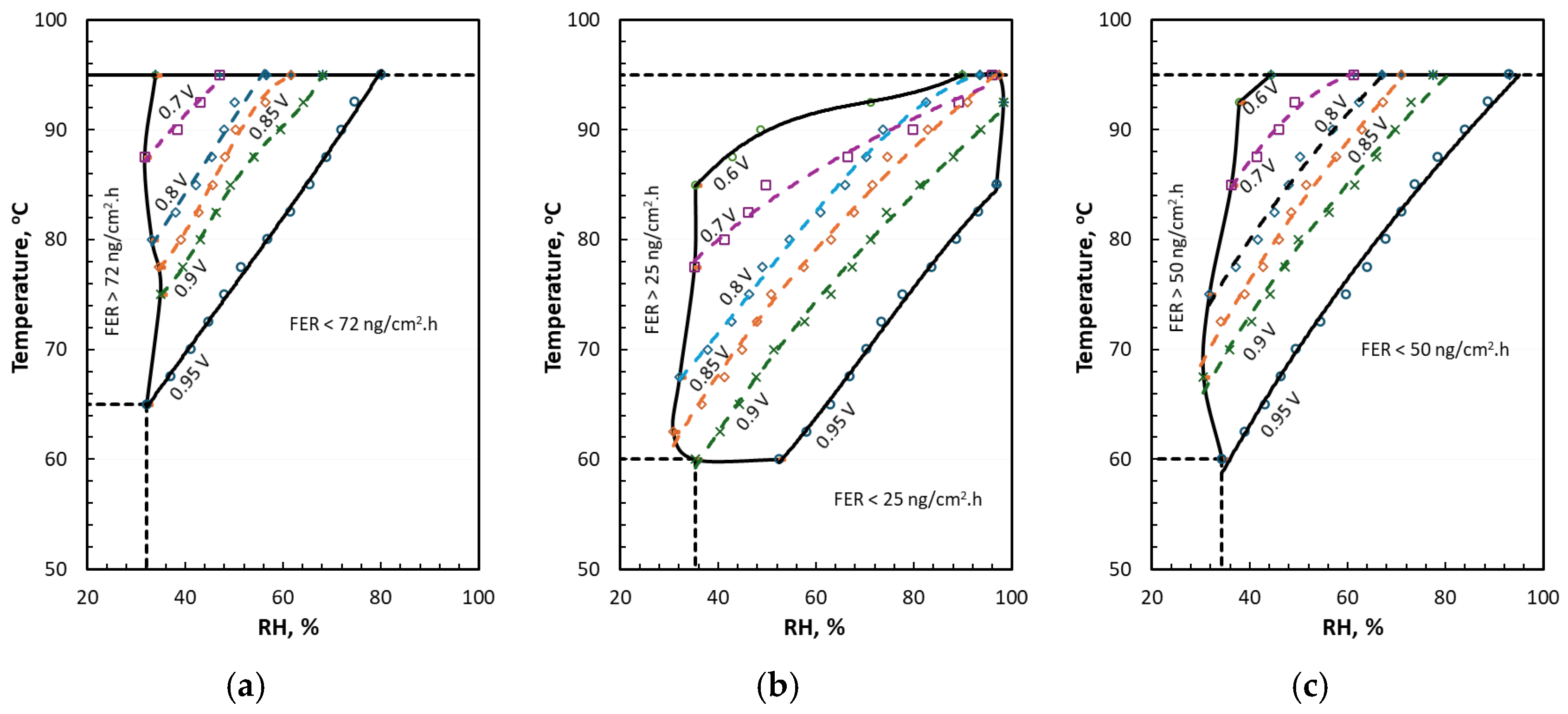
4. Discussion

For a perspective on results obtained in this study, we calculate average FER for membrane failure by chemical degradation within 25,000 h. The actual membrane lifetime may be further limited by synergistic mechanical stresses and manufacturing defects [51]. We postulate three scenarios and refer to them as theoretical failure limit (TFL), safe limit (SL), and design limit (DL). TFL identifies absolute membrane failure by hole formation and corresponds to 100% cumulative fluoride release (CFR) in 25,000 h. In this limit, the average FER is 72 ng/cm²·h for a 12-µm membrane with 75% fluorine content, as in a (CF₂)_m polymer chain (excluding the PTFE reinforcement). The average FER in SL is 25 ng/cm²·h corresponding to 33% CFR in 25,000 h and was selected to coincide with the results from TEM analysis of specimens exposed to the combined catalyst–membrane AST. DL is a compromise between TFL and SL, with an average FER of 50 ng/cm²·h corresponding to 70% CFR in 25,000 h. It may be regarded as a 50% probability of H₂ crossover failure by chemical degradation of membrane.

Figure 8 presents stability maps for TFL, SL, and DL over a range of 60 to 95 °C temperature, 30 to 100% RH, and 0.6 to 0.95 V cell voltage. Each iso-potential line in Figure 8 represents combinations of RH and temperature at a specified cell voltage for which the FER equals the average that defines the failure limit. All operating points below and to the right of an iso-potential line have an average FER below the failure limit and are deemed safe, i.e., have a membrane lifetime >25,000 h. All operating points above and to the left of an iso-potential line have an average FER exceeding the failure limit and are deemed unsafe, i.e., have a membrane lifetime <25,000 h. As expected, the operating conditions are less restrictive at lower cell voltages. For example, the two DL end points are 60 °C, 34% RH and 95 °C, 90% RH for 0.95 V iso-potential line, and these relax to 85 °C, 34% RH and 95 °C, 60% RH for 0.7 V iso-potential line.

5. Conclusions

The main conclusion of this study is that the chemical stability of PFSA membranes can be characterized by fluoride emission due to attacks by radicals such as $\cdot \mathrm{OH}$ produced from decomposition of H₂O₂ that forms on the anode by reaction between H₂ and crossover O₂ and on the cathode as an intermediate in the 2-electron ORR pathway. Thus, the anode FER depends on ${\dot{N}}_{O_2}$ and the cathode FER is not related to ${\dot{N}}_{H_2}$ but depends on the cathode potential. Both anode and cathode FERs are significantly enhanced at low relative humidity and are strongly influenced by the gradients in water activity and cerium concentration that develop in operating fuel cells. The cathode FER exceeds anode FER at potentials near open circuit voltage, and vice versa at lower cell voltages.

The following are some prospective areas of research that may be worthy of future investigations:

(a)

Cerium mobility, water transport, and FER under dynamically varying loads representative of duty cycles for different applications

(b)

Effect of Fe impurities on FER from Ce-doped membranes

(c)

Experimental measurements of anode and cathode FERs in operating cells at 0.6–0.85 V and 60–80 °C

(d)

Relationship between cumulative fluoride emission and membrane failure mode

(e)

Development of accelerated stress tests that can simulate membrane failure in a reasonable time without altering the degradation mechanism

(f)

Synergism between mechanical stresses and chemical degradation

(g)

Enhanced membrane stability by immobilization of cerium

(h)

Ionomer stability and its effect on ORR catalyst activity