Abstract
Determining the oxidation potential (OP) of lithium-ion battery (LIB) electrolytes using theoretical methods will significantly speed up and simplify the process of creating a new generation high-voltage battery. The algorithm for calculating OP should be not only accurate but also fast. Our work proposes theoretical principles for evaluating the OP of LIB electrolytes by considering LiDFOB solutions with different salt concentrations in EC/DMC solvent mixtures. The advantage of the new algorithm compared to previous versions of the theoretical determination of the oxidation potential of electrolyte solutions used in lithium-ion batteries for calculations of statistically significant complexes, the structure of which was determined by the molecular dynamics method. This approach significantly reduces the number of atomic–molecular systems whose geometric parameters need to be optimized using quantum chemical methods. Due to this, it is possible to increase the speed of calculations and reduce the power requirements of the computer performing the calculations. The theoretical calculations included a set of approaches based on the methods of classical molecular mechanics and quantum chemistry. To select statistically significant complexes that can make a significant contribution to the stability of the electrochemical system, a thorough analysis of molecular dynamics simulation trajectories was performed. Their geometric parameters (including oxidized forms) were optimized by QM methods. As a result, oxidation potentials were assessed, and their dependence on salt concentration was described. Here, we once again emphasize that it is difficult to obtain, by calculation methods, the absolute OP values that would be equal (or close) to the OP values estimated by experimental methods. Nevertheless, a trend can be identified. The results of theoretical calculations are in full agreement with the experimental ones.
1. Introduction
Lithium-ion batteries (LIB) are currently the most common electrochemical power supply widely used in portable electronics, electric vehicles, energy storage systems, etc. In recent years, many attempts have been made to further increase the energy density of LIB. At the end of the 1990s, cathode materials operating above 4.5 V (vs. Li/Li+) were developed. These materials include layered cathode materials with high nickel, lithium and manganese content [1,2,3,4,5,6], LiCoPO4 [7,8,9,10] LiCoPO4F [11,12], LiF-MO nanocomposites (M = Mn, Fe, Co) [3,13], LiNiO2 [14,15] and others.
The electrolytes used in the production of LIB are 1–1.5 M solutions of LiPF6 in base mixtures of linear and cyclic carbonates, additionally containing functional additives [16,17,18]. However, commercial electrolytes are electrochemically stable up to 4.3 V and cannot provide operability for high-voltage cathode materials [19]. Thus, the development of electrolyte compositions resistant to oxidation at potentials higher than 5 V is underway around the world [20].
In recent years, lithium difluoro(oxalato)borate LiBF2(C2O4) (abbreviated as LiDFOB) has been recognized by high-voltage lithium-ion batteries due to its excellent performance [21,22]. Unlike LiPF6, the decomposition of LiDFOB does not produce HF [23]. LiDFOB is also involved in the formation of SEI films on anodes and suppresses the reactivity of lithiated graphite toward electrolytes [24,25]. More importantly, LiDFOB can passivate the aluminum current collector of the positive electrode [26] and promote the formation of cathode electrolyte interfacial passivation layers (CEI) at high potentials [27,28].
The properties of an electrochemical system depend on the structure of complexes of different types formed as a result of salt dissolution. The involvement of computational chemistry methods to investigate the physicochemical properties and structural features of various complexes formed in LiDFOB solutions in different solvents was previously described. In their article [29], the structure and oxidizing ability of anionic complexes of the {DFOB−}(EC1) type were examined depending on the different coordination of the anion and the solvent molecule with respect to each other. The evaluation of redox potentials for the ionic species {Li+DFOB−} and {Li+(DFOB−)2− by quantum chemistry methods was presented in [30]. In [31], systems based on LiDFOB in a mixture of three solvents (EMC, EC, ADN and EMC, SL, ADN) were investigated. However, the authors here limited themselves to studying the structural features of cationic complexes in a 1 to 1 solvent-to-lithium cation ratio, estimating the HOMO-LUMO gap and the dipole moment for the solvents. In addition, the authors evaluated the affinity of lithium cation to different solvents and showed that among solvents such as SL, EC, ES, DMC, DMC and ADN, lithium cation shows the highest affinity to SL.
The estimation of HOMO LUMO by QC methods was used in the paper [32]. The authors concluded that LiDFOB can decompose at the cathode prior to the decomposition of EC, EMC and DEC solvents and is most likely to reduce at the anode prior to their reduction. This is due to high HOMO energy and low LUMO energy.
Molecular dynamics methods were used in [33] to estimate the radial distribution function and describe the surroundings of lithium cation in 1 M LiDFOB DME solution.
In all cases, attention is drawn to the fact that the authors of the above-mentioned works investigated the structural features of individual complexes, usually in a 1-to-1 ratio (ion pair and one molecule of solvent), both in the case of cationic complexes and in the case of solvated ion pairs. In this case, the coordination number value of the lithium cation is determined. Depending on the environment, this can be from four to eight [34]. Meanwhile, using 1 M LiBF4 in EC/DMC and SL/DMC solvent mixtures as an example, we [35] showed that the formation of various complexes, namely cationic, anionic and solvated ion pairs, is possible in the systems. The structural features of all systems must be considered in order to evaluate the redox potential. The environment of lithium cation can be studied by molecular dynamics methods. The analysis of the results suggests the most probable structure of possible complexes.
Here, the optimization of geometric parameters by the QM method is necessary for many atomic–molecular systems. For example, we need to evaluate the oxidation potential (OP) of 1 m LiBF4 salt in a solvent mixture (EC/DMC). We have to optimize the geometrical parameters of all possible solvated anion complexes and solvated contact ion pairs, including their oxidized forms. This is about 40–50 structures. And the optimization procedure should be completed successfully. There should be no imaginary units in the matrix of the second derivatives of the wave function. Moreover, we use the Born–Haber cycle for OP calculation. This means we must further optimize the complexes, considering the presence of solvent. Then, the total number of calculated structures increases to 80–90. In addition, methodological shortcomings in QM methods can cause difficulties in the convergence of the wave function.
Our new algorithm includes a thorough analysis of particle trajectory after molecular–dynamic simulation. This makes it possible to estimate the composition and environment of each lithium cation and identify statistically significant complexes, the contribution of which to electrochemical stability may be greatest. In the results of this analysis, the atom–molecular systems for the next QM optimization are significantly reduced. This work investigated LiDFOB-based systems with different salt concentrations using baseline solvent mixtures EC/DMC. In our case, we optimized only 12 structures (including the oxidized form in the gas phase and with a polarizable continuum model (PCM)) for one type of salt concentration. This approach significantly reduces calculation time. The results of theoretical calculations are in full agreement with the experimental ones.
2. Materials and Methods
2.1. Theoretical Parts
LiDFOB solution in a mixed solvent EC/DMC (1:1, wt.) was considered as a model system in this work. The following salt concentrations were regarded: 0.5, 0.75 and 1 mol/kg.
2.1.1. Molecular Dynamic Simulations
Virtual cubic models containing a certain number of lithium cations, DFOB anions and solvent molecules were constructed for molecular–dynamic simulations (Figure 1).
Figure 1.
Structural parameters of components of studied systems.
The numerical composition of the particles corresponded to the specified experimental values of salt concentration of 1.0, 0.75 and 0.5 mol/kg (Table S1). The molecules were placed in the cube in random order. An example of visualization of the model systems is presented in SM (Figure S1). The protocol for preparing the system for modeling included preliminary minimization (conjugate gradient method) and the balancing of components in the NVT ensemble for 0.1 ns at 10 K, 0.1 ns at 298 K, 0.2 ns at 700 K sequentially.
The systems were balanced in the NPT (P − 1 atm.) for 10 ns at 298 K. The period of the recorded simulation was 50 ns in the NVT ensemble at 298 K. To maintain a constant temperature of the systems, a Nose–Hoover thermostat was used [36]. To calculate the density of the system, an MD simulation was performed in the NPT ensemble for 100 ns at 1 atm and 293.15 K. Density is expressed in g/cm3 and is computed for each frame over the course of the trajectory. Inspection of the convergence of density gives important feedback on the degree of system convergence. With the OPLS force fields, the fully equilibrated density can be computed to within 3% of experimental values. Molecular dynamic simulations were performed using Desmond-v7.2 MD simulation software [37] and OPLS4 [38].
The structural features of substances, in particular to describe the composition and structure of complexes, were assessed through the radial distribution function (RDF) and its integral component N (R). MD trajectory analysis and visualization were performed using the VMD program [39]. A statistical analysis of all variants of the interaction of lithium cations with other components of the electrolyte was carried out in order to assess the composition of the complexes in the mixture.
2.1.2. Quantum Chemistry Calculations
Optimization of the geometric parameters of atomic–molecular systems with subsequent solution of the vibrational problem was carried out at the DFT level using the M052X functional [40] with the TZVP basis set [41]. The absence of an imaginary unit in the matrix of second derivatives of the wave function was considered evidence of the establishment of a stationary point on the potential energy surface. Thermodynamic parameters were calculated in the gas phase approximation at 298 K and atmospheric pressure, as well as taking into account implicit solvation [42]. As a solvent, PCM models used acetone with ε = 20.5, which is close to the permittivity value of most electrolyte mixtures [43]. All calculations were performed using GAUSSIAN 09 rev C software.
In order to assess the thermodynamic stability of the complexes studied, incremental (step by step) values of the energies of formation (ΔfG°inc) were considered as the Gibbs energy of the reaction of successive addition of a solvent molecule to the complexes [34] based on the second consequence of the Hess law.
The adiabatic oxidation potential Ead for the complexes was estimated according to the Born–Haber cycle [44], as described in the previous work [35].
2.2. Experimental Part
Ethylene carbonate (battery grade, Sigma Aldrich, St. Louis, MO, USA), dimethyl carbonate (anhydrous, ≥99%, Sigma Aldrich) and LiDFOB (≥98%, Sigma Aldrich) were used to prepare electrolytes. The solvent mixture was incubated over Molecular Sieve 3Å for 1 week in order to remove traces of water from ethylene carbonate and dimethyl carbonate. The concentrations of the solutions studied were 0.5, 0.75 and 1 m. The electrolytes were prepared and stored in a dry argon box.
The electrochemical stability window of the electrolyte was measured and determined by the linear sweep potential technique method. Two-electrode electrochemical cells were used for measurements. Glass-carbon was used as the working electrode, and metallic lithium was used as the counter electrode. In order to determine the oxidation potential, the experiment was carried out in the range from 2.5 V (open circuit voltage) to 5.99 V vs. Li0/Li+. The potentiostat P-20 × 8 (Elins LLC, Chernogolovka, Russia) was used for measurements. Sweep rate was 0.02 mV∙s−1.
The density of the electrolyte solution was determined using pycnometers with a nominal volume of 5 mL, pre-calibrated at 25 °C. Measurements were performed in three parallels at 20 °C.
The compositions of predominant ionic species were confirmed by high-resolution NMR. The spectra on the cores 1H, 7Li, 11B, 13C, 17O, 19F were captured on the Bruker Avance III 500 MHz NMR spectrometer. The spectra were recorded at room temperature (24 °C), at frequencies of 500, 194, 160, 126, 68, 471 MHz for 1H, 7Li, 11B, 13C, 17O, 19F, respectively. Liquid samples were placed in standard 5 mm ampoules without the addition of deuteron solvent. To calibrate the chemical shift scale, an additional magnetic field was set from the DMSO-d6 signal as an external standard (2.50 ppm for 1H).
3. Results
3.1. Molecular–Dynamic Results
The main goal of molecular dynamic simulations is to assess the environment of the lithium cation and describe the composition of the complexes that dominate in the electrolyte solution based on this assessment. In the first stage, we estimated the density values of model systems and compared the data with the experiment. The results assessed based on QC calculations correlate with the experimental data (Figure 2). This result suggests that the computational model is adequate and the molecular dynamics simulation protocol is suitable for studying such systems.
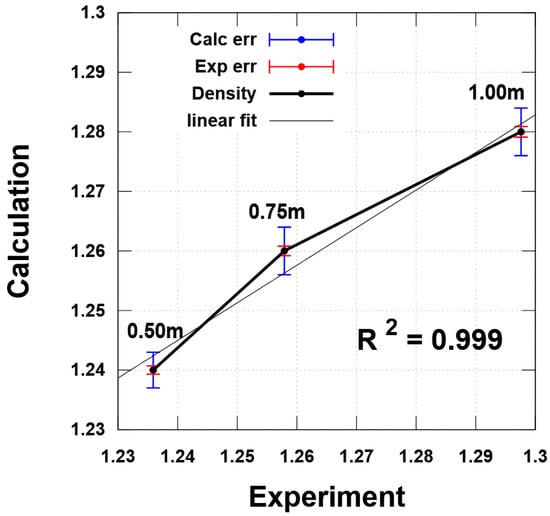
Figure 2.
Correlation of density values obtained as a result of experiment and theoretical calculation.
The analysis of particle behavior during molecular dynamic simulations enables us to estimate the qualitative and quantitative composition of the coordination sphere of the lithium cation depending on the salt concentration. Our previous work [33] showed that the lithium cation preferentially coordinates with the carbonyl oxygen atom of EC and DMC. The Li+ cation can coordinate with the asymmetric DFOB− anion in two ways (Figure 3): through an oxalic acid residue forming a five-membered ring (II, III) or through fluorine atoms (I, IV). In both cases, both the monodentate (I, II) and bidentate (III, IV) coordination of Li+ relative to the anion are possible. In addition to the expected coordination of Li+ with highly polar carbonyl groups of the oxalic acid residue, coordination with the ether oxygen of the ring or some intermediate coordination with ether and carbonyl oxygens simultaneously cannot be excluded (V). In [45], the analysis of molecular dynamic simulations shows the coordination of the lithium cation relative to the DFOB- anion between the carbonyl oxygen atom and the ring oxygen. The salt concentration is likely to be an important factor influencing the location of the cation relative to the anion.

Figure 3.
(I–V)—versions for coordination of lithium cation relative to solvents and anion.
We estimated the number of contacts registered between lithium cations and anion atoms in a 1 m salt solution in the solvent mixture being studied (Figure 4a). The contacts are registered at a distance of 3.3 Å or more between the cation and a particular atom. If the atom is located from the cation at a distance greater than 3.3 Å, then the number of such contacts will correspond to the coordination number 0. Value 3.3 Å was chosen with a margin based on calculations that were published in article [35]. Analyzing the structural parameters of complexes formed in electrochemical systems shows that the solvent atoms are located within a radius of 2 to 3 Å relative to the lithium cation. During the analysis of molecular dynamics data, we used a radius of 3.3 Å relative to the lithium cation. This value is taken with a margin to ensure that all molecules fall within this radius. The analysis of the histograms enables us to draw the following conclusions: one or two anions are most often located around the lithium cation. The ion pair may dissociate, and then the anion “floats away” from the cation at a distance exceeding 3.3 Å. In general, Li+ is located relative to atoms B and F at distances greater than 3.3 Å. Contacts at smaller distances are registered between cations and oxygen atoms. Both monodentate and bidentate coordination are probably possible.
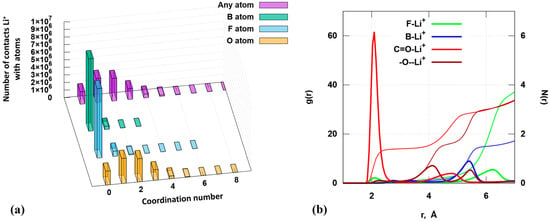
Figure 4.
Analysis of molecular dynamic simulations of 1.0 m LiDFOB EC/DMC (1:1, wt.): (a)—estimation of the number of contacts between lithium cations and anion atoms at distance of 3.3 Å («Any atom» is the sum of B, F and O atoms); (b)—radial distribution function and structural factor.
The analysis of the radial distribution function (RDF) and its structure factor (N(r)) suggest that lithium cations preferentially contact specifically carbonyl oxygen at distances between 1.8 and 2.7 Å. This is evidenced by the height of the peak (Figure 4b, bright red curve). The first step of the N(r) curve corresponds to 1.5 units, which also suggests two likely coordinations of the cation relative to the carbonyl oxygen of the anion, as indicated in Figure 4.
Histograms characterizing contacts of lithium cations with oxygen atoms of the anion and solvent molecules are presented in Figure 5a–c. Contacts between cations and oxygen atoms are registered at distances up to 3.3 Å. If the oxygen atom under consideration is located from the cation at a distance greater than 3.3 Å, the number of such contacts will correspond to the coordination number 0. Radial distribution functions describing the surrounding of cations by particles present in solution are also given (Figure 5d–f). The coordination number of Li+ tends to be 6 in all cases.
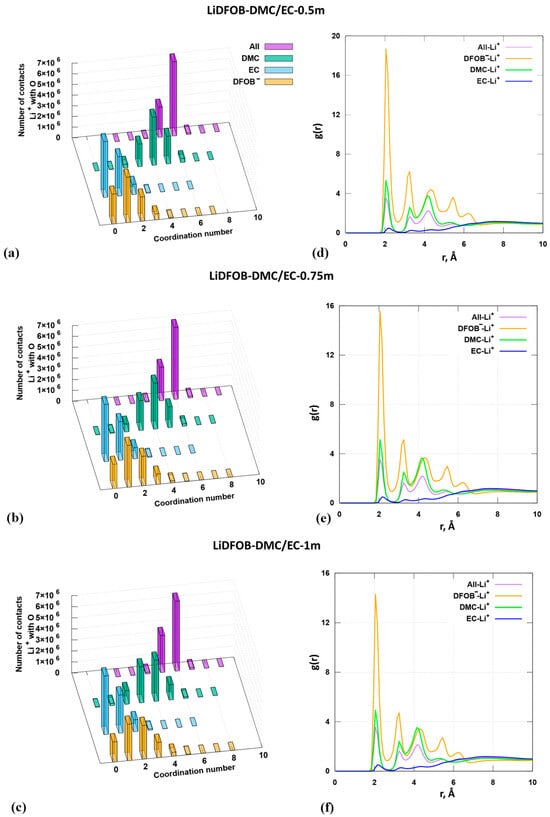
Figure 5.
Analysis of molecular dynamic simulations: (a)—estimation of the number of contacts between lithium cations and oxygen atoms of solvent molecules and anions at distance of 3.3 Å of 0.5 m LiDFOB EC/DMC (1:1, wt.); (b)—estimation of the number of contacts between lithium cations and oxygen atoms of solvent molecules and anions at distance 3.3 Å of 0.75 m LiDFOB EC/DMC (1:1, wt.); (c)—estimation of the number of contacts between lithium cations and oxygen atoms of solvent molecules and anions at distance 3.3 Å of 1.0 m LiDFOB EC/DMC (1:1, wt.); (d)—radial distribution functions 0.5 m LiDFOB EC/DMC (1:1, wt.); (e)—radial distribution functions 0.75 m LiDFOB EC/DMC (1:1, wt.); (f)—radial distribution functions 1.0 m LiDFOB EC/DMC (1:1, wt.). («All» means the sum of all molecules).
At concentrations of 0.5 and 0.75 m, the lithium cation preferentially interacts with one oxygen anion, corresponding to monodentate coordination (Figure 5a,b). At the same time, we do not exclude bidentate coordination or the possibility of contact of a cation with two anions. The height of the columns corresponding to coordination number 1 is slightly higher than the column corresponding to coordination number 2. At a concentration of 1 m (Figure 5c), the column heights are equalized. The number of registered contacts between cations and oxygen atoms of the anion corresponding to coordination numbers 1 and 2 is equally probable. According to the analysis of the radial distribution function, lithium cations are more often in contact with the carbonyl oxygen of the anion than with the carbonyl oxygen of solvent molecules. This is evidenced by the height of the peak in Figure 5d–f (yellow curve).
The frequency of Li+ contacts with EC oxygen atoms is practically independent of the salt concentration. By analyzing the histograms in Figure 5a–c, we can assume that the first coordination sphere of the cation will preferentially include no more than one EC molecule. This conclusion is in agreement with the analysis of radial distribution function curves (Figure 5d–f). The height of the columns characterizing the frequency of contacts of DMC oxygen atoms with the cation varies with concentration. At a minimum concentration of 0.5 m, Li+ preferentially contacts with four oxygen atoms of DMC. With increasing concentration, the height of the column corresponding to coordination number 4 slightly decreases, while the height of the column corresponding to c.n. 3 increases.
Thus, a statistical analysis of molecular dynamic simulations enables us to estimate the composition and structure of probable complexes formed in the studied systems with different salt concentrations. According to the statistical analysis, the c.n. of the cation corresponds to six units. Using Maxwell–Boltzmann statistics, we numerically evaluated the composition and statistical significance of complexes in the LiDFOB-EC/DMC system as a function of concentration (Table 1).

Table 1.
Statistical significance of complexes recorded during molecular dynamic simulations.
Statistically significant complexes were analyzed by a trajectory analysis of molecular dynamic simulations. The structural analysis of molecular dynamics simulation trajectories analyzes every frame registered within 50 ns and the environment of every lithium atom. Then, all these frames were summed up, and we obtained those complexes that appear most often. These complexes are called statistically significant.
This statistical analysis takes into account the dynamic contacts between lithium cations and oxygen atoms of solvent molecules and anions. It should be noted here that, according to the RDF analysis, the lithium cation preferentially contacts carbonyl oxygen atoms. This fact was taken into account when creating complexes for the following QC calculations.
Then, at concentrations of 0.5 and 0.75, the dominant complex is {Li+DFOB−}(DMC)1(EC)1. In this case, the statistical frequency of such a complex decreases as a function of concentration, and at 1 m, the probability of its detection is 24%, while the complex of composition {Li+DFOB−}(DMC)1(EC)2 is registered in 76% of cases. Changing the salt concentration affects the composition of the first coordination sphere of the lithium cation, and as a consequence, the structure of the solvated complexes differs.
The geometrical parameters of the most frequently occurring complexes listed in Table 1 were downloaded for the estimation of their thermostability and oxidizing potential by quantum chemistry methods. The possibility of monodentate and bidentate coordination of the cation relative to the carboxyl oxygen atom was taken into account in the calculation.
3.2. QC Calculations Results
3.2.1. Structures of Complexes and Thermodynamic Parameters
Complexes {Li+DFOB−}(DMC)n(EC)m (n, m = 1, 2)
The geometrical parameters of statistically significant complexes (Table 1) of the solvated ion pair, of the form {Li+DFOB−}(DMC)n(EC)m, where n, m = 1, 2, were optimized by quantum chemistry methods. Gibbs free energy of formation values were estimated (Figure 6). The incremental Gibbs free energy values are presented in Table A1.
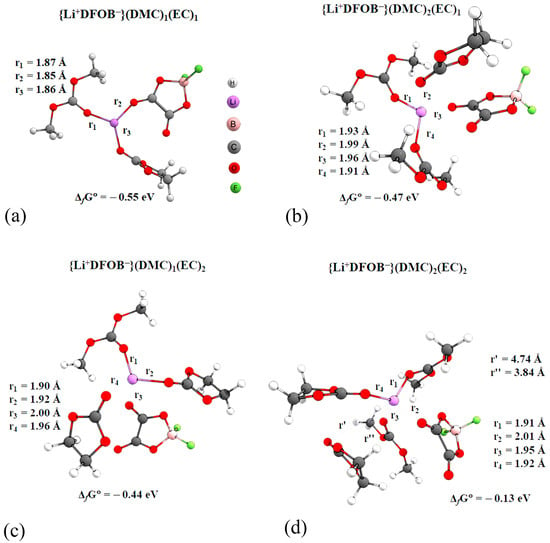
Figure 6.
Structural parameters of complexes (M052X/TZVP, PCM, acetone): (a)—{Li+DFOB−}(DMC)1(EC)1; (b)—{Li+DFOB−}(DMC)2(EC)1; (c)—{Li+DFOB−}(DMC)1(EC)2; (d)—{Li+DFOB−}(DMC)2(EC)2.
The lithium cation is surrounded by bulk solvent molecules. Thus, the lithium cation can form sufficiently strong coordination bonds with four (maximum five) oxygen atoms of the surrounding particles (solvent molecules and anions). The most symmetrical (Li-O bond lengths have approximately equal values) resembles the complex {Li+DFOB−}(DMC)1(EC)1. From a thermodynamic point of view, this complex is more stable than the others (Figure 6a). The lithium cation and the surrounding three oxygen atoms are arranged in the same plane. The complexes of composition {Li+DFOB−}(DMC)2(EC)1 (Figure 6b) and {Li+DFOB−}(DMC)1(EC)2 (Figure 6c) have a pyramidal structure. The distances between the lithium cation and the surrounding oxygen are longer than in the complex of composition {Li+DFOB−}(DMC)1(EC)1. In both cases, one of the EC molecules is coordinated to the anion: the minimum distance between the hydrogen and fluorine atoms barely exceeds 2.3 Å, suggesting the presence of a bonding point. Gibbs free energy formation of {Li+DFOB−}(DMC)2(EC)1 complex is 0.03 eV lower than the formation energy of {Li+DFOB−}(DMC)1(EC)2.
The analysis of incremental values of Gibbs energies (Table A1) also indicates that the coordination of the DMC molecule relative to the lithium cation is thermodynamically more favorable than contact of the cation with the EC. These observations are consistent with the RDF analysis (Figure S2). In the complex of composition {Li+DFOB−}(DMC)2(EC)2, one of the EC molecules is more than 3.7 Å away from the lithium cation by the distance between Li+ and the EC oxygen. Thermodynamically, this complex (Figure 6d) is less stable than the others.
In the above complexes, the lithium cation is coordinated to only one carbonyl oxygen atom of the anion. At the same time, according to statistical analysis at a concentration of 0.5 mol/kg, we also considered the probability of forming a complex {Li+DFOB−}*(DMC)1(EC)2 (Table 1), bidentate coordination.
However, the optimization of the geometrical parameters of such a complex was not successful. During calculation, the coordination of particles relative to the cation leads to the formation of a complex {Li+DFOB−}(DMC)1(EC)2 (Figure 6c). It is probable that such an arrangement of anion relative to cation is thermodynamically more stable.
Complexes {Li+(DFOB−)2}(DMC)n(EC)m (n, m = 1, 2)
The statistical analysis of molecular dynamic simulations showed that negatively charged ionic triplets may be present in the studied systems (triple ions)—complexes in which two anions, in addition to solvent molecules, are coordinated relative to the lithium cation. Using methods of quantum chemistry, the geometrical parameters of complexes {Li+(DFOB−)2−}(DMC)1(EC)1 (Figure 7a) and {Li+(DFOB−)2−}(DMC)1(EC)2 (Figure 7b) were optimized. The Gibbs formation energy of the latter complex is positive, i.e., it is unstable.
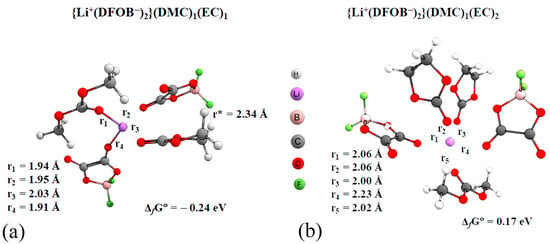
Figure 7.
Structural parameters and Gibbs formation free energy of complexes (M052X/TZVP, PCM, acetone) (a)—{Li+(DFOB−)2−}(DMC)1(EC)1; (b)—{Li+(DFOB−)2−}(DMC)1(EC)2.
In the {Li+(DFOB−)2−}(DMC)1(EC)1 complex, four oxygen atoms are “stacked” in a pseudo-pyramid with the cation in the center. In the {Li+(DFOB−)2−}(DMC)1(EC)2 complex, all the particles are arranged relatively evenly with the cation. The furthest away is one of the anions.
NMR Study
The molecular structure of the complexes as a function of salt concentration was studied using NMR. Chemical shifts in NMR spectra at the nuclei 1H, 7Li, 11B, 13C, 17O, 19F were obtained. The values of chemical shifts are presented in SM (Tables S2–S4). The chemical shifts of statistically significant complexes were calculated by quantum chemistry methods. The correlation index of calculated and experimental values of chemical shifts does not exceed 0.98 units in both systems (Figure 8). Here, we can observe that the proposed structures of the complexes are correct. Thus, the composition and structure of the complexes proposed on the basis of theoretical calculations are in full agreement with the analysis of NMR spectra. It should be noted that chemical shifts in NMR spectra are practically independent of salt concentration. This indicates that the environment of the nuclei does not change, and no exchange processes occur in the studied systems.
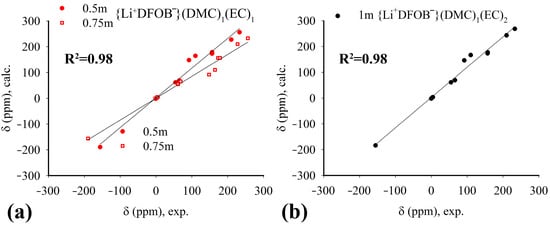
Figure 8.
Correlation of chemical shift values in NMR spectra at nuclei 1H, 7Li, 11B, 13C, 17O, 19F, obtained by experimental and theoretical (QC) method: (a)—0.5 and 0.75 m solutions, complex {Li+DFOB−}(DMC)1(EC)1; (b)—1 m solution, complex {Li+DFOB−}(DMC)1(EC)2. The solid lines on the graphs show direct matches of experimental and theoretical values of chemical shifts.
3.2.2. Oxidation Potential
The oxidation process is accompanied by a change in the geometrical parameters of the complexes. Figure 9 shows the oxidation reactions of complexes characterized by minimum adiabatic OD values (Eox) (Table A1). In the system with the lowest salt concentration of 0.5 m, oxidation probably starts from the negatively charged ionic triplet {Li+(DFOB−)2−}(DMC)1(EC)2, which seems logical. As a result of oxidation, the particles are observed to regroup in relation to the cation. The distance r1 between the oxygen atom of the anion and Li+ increases by more than 1.2 Å; the other particles (anion, two EC molecules and one DMC) conversely approach the cation. The distance between the carbons in one of the anions increases to 1.9 Å as a result of the breaking of the five-membered cycle (Figure 9a). In systems with higher salt concentrations of 0.75 m and 1 m, ionic triplets were not detected by statistical analysis; they are dominated by electrically neutral ion pairs (see Table 1). At a concentration of 0.75 m, the complex {Li+DFOB−}(DMC)2(EC)2 starts to oxidize first. Here, a slight change in the coordination of the particles relative to the cation is observed. The geometrical parameters of the anion change noticeably. The distance between the oxygen atom and Li+ increases, as well as the distance between carbons, which is again associated with the rupture of the five-membered cycle (Figure 9b). The statistically significant complex {Li+DFOB−}(DMC)1(EC)2 in 1 m of salt solution rearranges upon oxidation. The anion moves away from the cation by a greater distance. The distance between the carbon atoms in DFOB− increases as a consequence of cycle breaking. The oxygen atoms of two EC molecules and one DMC molecule are located in the same plane with Li+ (Figure 9c).
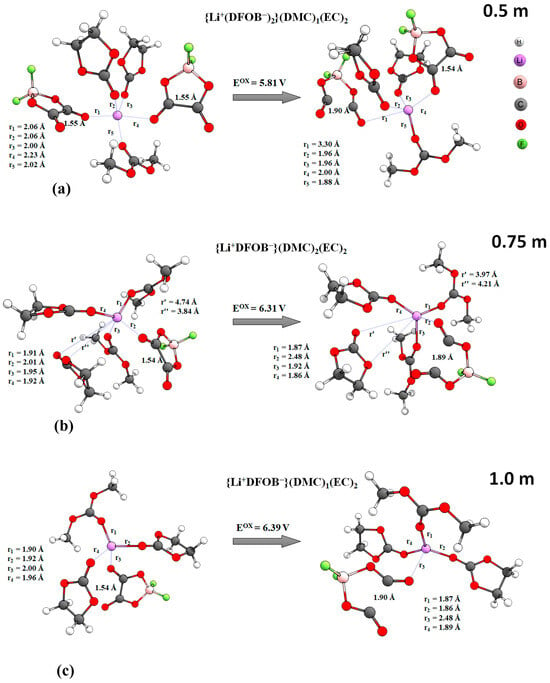
Figure 9.
Change of structural parameters at oxidation of some complexes (M052X/TZVP, PCM, acetone. Complexes with minimal OP value are shown): (a)—{Li+(DFOB−)2−}(DMC)1(EC)2, 0.5 m LiDFOB EC/DMC (1:1, wt.); (b)—{Li+DFOB−}(DMC)2(EC)2, 0.75 m LiDFOB EC/DMC (1:1, wt.); (c)—{Li+DFOB−}(DMC)1(EC)2, 1.0 m LiDFOB EC/DMC (1:1, wt.).
Taking into account the statistical significance of the complexes obtained from molecular dynamics simulation analysis, we calculated the additive value of OP (Eoxadd). In addition, using the Maxwell–Boltzmann distribution of Gibbs formation free energy values (ΔfG°) and incremental energy component values (ΔfG°inc calculated by quantum chemistry methods, additive OP values were also estimated: Eoxadd(form)—based on ΔfG° and Eoxadd(inc)—based on ΔfG°inc. The additive values of oxidation potentials calculated by the three methods are shown in Figure 10a, depending on the salt concentration in the model system. The numerical values are summarized in Table S5 (see. SM). As can be seen from the figure and table, all three methods of Eoxadd calculation give very close numerical results (the maximum discrepancy between the obtained values is 0.12 V) and reflect the same tendency. With increasing salt concentration, Eoxadd grows and reaches a plateau (Figure 10a). In addition to the additive values of the oxidation potentials, Figure 10a shows the Eox values for the least stable complexes in each solution as dots. For a solution with a concentration of 0.50 m, these are the negatively charged ionic triplets {Li+(DFOB−)2−}(DMC)1(EC)2, with the lowest electrochemical stability among all ionic particles considered above (Eox = 5.81 V). Such complexes are absent in the model systems at higher salt concentrations. This is most significant for the increase in the values of Eoxadd. In the system with a concentration of 0.75 m, the neutral complex is least stable {Li+(DFOB−)−}(DMC)2(EC)2 (Eox = 6.31 V), whereas at 1.00 m, the neutral complex is the least stable {Li+(DFOB−)−}(DMC)1(EC)2 (Eox = 6.39 V). A decrease in the number of molecules in the solvate shell seems to make the neutral ion pair more resistant to oxidation. It is important to take into account the Eox values of the least stable complexes when predicting the electrochemical stability of an electrolyte solution, along with the analysis of Eoxadd values.
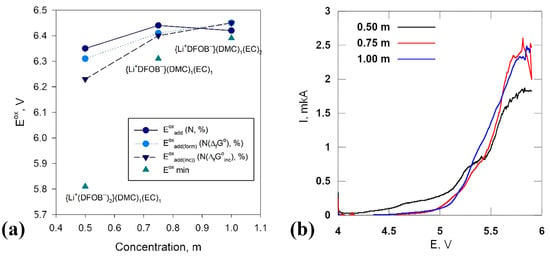
Figure 10.
Results of theoretical calculations and experiments: (a)—additive OP values estimated by combined methods of quantum chemistry and molecular dynamics. Triangles indicate minimum values OP (Eox), corresponding to the specified complexes; (b)—linear sweep voltammograms of LIDFOB in EC:DMC (1:1, wt.) solutions with salt concentrations of 0.50, 0.75 and 1.00 m, scan rate: 0.02 mV s−1.
The curves obtained by the linear sweep potential method for LiDFOB solutions in EC/DMC mixed solvent (1:1) with salt concentrations of 0.50, 0.75 and 1.00 m are shown in Figure 10b. As can be seen from the figure, the current growth in the solution with a concentration of 0.50 m begins at E ≈ 4.55 V. The increase in salt concentration up to 0.75 and 1.00 m leads to a shift in the beginning of oxidation processes towards higher values of potential, and both these solutions give very close curves, in full accordance with the prediction (Figure 10a).
4. Discussion
The thermodynamic stability of the complexes under consideration can be evaluated on the basis of the energy component of each particle included in the complex, for example, from the perspective of the free energy of Gibbs formation (ΔfG°). The processes of the sequential addition of solvent molecules to an ion pair can also be considered, i.e., thermodynamic stability can be evaluated from the perspective of incremental Gibbs energy (ΔfG°inc). The results of our calculations indicate that the additive value of the OP can be estimated based on the Maxwell–Boltzmann distribution of both the formation energy and the incremental energy. In both cases, we observed an insignificant difference in the OP values. On the other hand, the use of the incremental component requires the optimization of the geometric parameters of intermediate complexes, which can increase the calculation time. Therefore, we recommend estimating additive OP values based on the Gibbs energy of complex formation (ΔfG°) in order to simplify the prediction procedure.
The analysis of additive OP values (Figure 10a), estimated by quantum chemistry methods, enables us to note that the oxidation of the electrolyte in the model system with the lowest salt concentration (0.50 m) occurs at lower OP values. As the salt concentration increases, the additive OP values increase, and the values corresponding to salt concentrations of 0.75 and 1.00 m differ by no more than 0.04 V (Table S5). In other words, the 0.50 m LiDFOB system in DMC/EC can be considered the least stable. At high concentrations, the oxidative stability of solutions is practically independent of concentration. This is completely consistent with the experimental results (Figure 10b). Here, we once again emphasize that it is difficult to obtain, by calculation methods, the absolute OP values that would be equal (or close) to the OP values estimated by experimental methods. Nevertheless, a trend can be identified. Confirmation of the adequacy of the model is the presence of a corresponding trend. The cumulative analysis of the results indicates the adequacy of the theoretical algorithm used.
5. Conclusions
The main goal of this work was to develop a theoretical algorithm to enable the fast evaluation of trends dependent upon the oxidation potential of an electrolyte solution on its composition. Our new algorithm allows for reducing the time for oxidation potential estimation by theoretical methods. This is achieved through a careful analysis of the trajectory of molecular dynamic simulations, the correct selection of statistically significant complexes and the optimization of the geometric parameters of a smaller number of systems using QM methods. At the same time, the accuracy of the calculations is sufficient to predict the composition of the electrolyte. LiDFOB solutions with different concentrations in baseline mixed solvent EC/DMC (1:1, wt) were used as an example.
Our algorithm involves the following stages of the OP assessment procedure:
- (1)
- Creation of a model system based on experimental data.
- (2)
- Molecular dynamic simulations for each model system for at least 50 ns, including system equilibration. The adequacy of the models used can be assessed by calculating the system density.
- (3)
- A thorough analysis of molecular dynamic simulations to evaluate the environment of each lithium cation throughout the simulation time.
- (4)
- Selection of statistically significant complexes, optimization of their geometric parameters and calculation of energy parameters using quantum chemistry methods.
- (5)
- Assessment of the additive value of the oxidative potential, taking into account the proportion of complexes of each type.
Testing such an algorithm for assessing the oxidation potential using the selected model system LiDFOB in EC/DMC (1:1, wt) produced encouraging results. The composition and structure of the complexes assumed in theoretical calculations are consistent with the data of NMR spectra for electrolyte solutions with the same concentration. The calculated OP values are in satisfactory agreement with the experimentally observed values. They quite correctly reflect the trend of changes in Eox with increasing salt concentration. For this reason, we believe that the calculation algorithm proposed herein can be applied to assess the OP of other electrochemical systems.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/electrochem5010007/s1, Figure S1: Visualization virtual cubes of systems 1 m LiDFOB (DMC/EC): lithium cations are shown as violet balls; DFOB− anions as green molecules, and molecules of DMC and EC are shown in blue and orange colors, respectively; Figure S2: Radial distribution function; Table S1: Particle ratio in virtual cube; Table S2: Chemical shifts (ppm) in 1H NMR spectra; Table S3: Chemical shifts (ppm) in 13C NMR spectra; Table S4: Chemical shifts (ppm) in 7Li, 11B, 17O, 19F NMR spectra; Table S5: Values of the oxidative potential of the complexes.
Author Contributions
Conceptualization, Y.A.D. and S.S.B.; methodology, E.Y.E., T.A.P. and O.V.B.; software, E.M.K. and S.S.B.; validation, E.Y.E. and V.G.K.; formal analysis, M.G.I., E.M.K. and A.V.C.; investigation, S.S.B.; resources, E.Y.E.; writing—original draft preparation, E.Y.E.; writing—review and editing, Y.A.D. and O.V.B.; supervision, S.S.B.; project administration, E.Y.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 22-23-00846, “Prediction of the stability of lithium-conducting electrolytes”.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data are not publicly available due to privacy or ethical reasons.
Acknowledgments
The authors are grateful to the theoretical group “Quanta and Dynamics”: https://monrel.ru/ accessed on 31 July 2023.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A

Table A1.
Thermodynamic and oxidative parameters of solvent molecules and various complexes existing in the system LiDFOB DMC/EC: ΔfG0inc—incremental (stepped) Gibbs energy of formation (eV); ΔEox—adiabatic oxidation potential estimated in this work (M052X/TZVP); IP—ionization potential, eV.
Table A1.
Thermodynamic and oxidative parameters of solvent molecules and various complexes existing in the system LiDFOB DMC/EC: ΔfG0inc—incremental (stepped) Gibbs energy of formation (eV); ΔEox—adiabatic oxidation potential estimated in this work (M052X/TZVP); IP—ionization potential, eV.
| Complex | ΔfGoinc, eV | IP, eV | ΔEox, V |
|---|---|---|---|
| Nonsolvent ionic pair {Li+DFOB−} | −0.64 | 10.50 | 6.95 |
| {Li+DFOB−}(DMC)1 | −0.20 | 9.99 | 6.91 |
| {Li+DFOB−}(EC)1 | −0.23 | 9.74 | 7.52 |
| {Li+DFOB−}(DMC)2 {Li+DFOB−}(DMC)1 + DMC ⮀ {Li+DFOB−}(DMC)2 | −0.28 | 9.55 | 6.78 |
| {Li+DFOB−}(DMC)1(EC)1 {Li+DFOB−}(EC)1 + DMC ⮀ {Li+DFOB−}(EC)1(DMC)1 | 0.05 | 9.25 | 6.50 |
| {Li+DFOB−}(DMC)1 + EC ⮀ {Li+DFOB−}(DMC)1(EC)1 | 0.03 | ||
| {Li+DFOB−}(DMC)2(EC)1 {Li+DFOB−}(DMC)1(EC)1 + DMC ⮀ {Li+DFOB−}(DMC)2(EC)1 | 0.09 | 9.05 | 6.32 |
| {Li+DFOB−}(DMC)1(EC)2 {Li+DFOB−}(DMC)1(EC)1 + EC ⮀ {Li+DFOB−}(DMC)1(EC)2 | 0.11 | 8.95 | 6.39 |
| {Li+DFOB−}(DMC)2(EC)2 {Li+DFOB−}(DMC)1(EC)2 + DMC ⮀ {Li+DFOB−}(DMC)2(EC)2 | 0.31 | 8.83 | 6.31 |
| {Li+DFOB−}(DMC)2(EC)1 + EC ⮀ {Li+DFOB−}(DMC)2(EC)2 | 0.33 | ||
| {Li+(DFOB−)2−}(DMC)1(EC)1 {Li+(DFOB−)2−} (DMC)1 + EC ⮀ {Li+(DFOB−)2−}(DMC)1(EC)1 | 0.10 | 5.94 | 6.14 |
| {Li+DFOB−} (DMC)1(EC)1 + DFOB− ⮀ {Li+(DFOB−)2−}(DMC)1(EC)1 | 0.31 | ||
| {Li+(DFOB−)2−} (EC)1 + DMC ⮀ {Li+(DFOB−)2−}(DMC)1(EC)1 | 0.20 | ||
| {Li+(DFOB−)2−}(DMC)1(EC)2 {Li+DFOB−} (DMC)1(EC)2 + DFOB− ⮀ {Li+(DFOB−)2−}(DMC)1(EC)1 | 0.61 | 5.94 | 5.81 |
| {Li+(DFOB−)2−} (DMC)1(EC)1 + EC ⮀ {Li+(DFOB−)2−}(DMC)1(EC)2 | 0.41 |
References
- Choi, J.W.; Aurbach, D. Promise and reality of post-lithium-ion batteries with high energy densities. Nat. Rev. Mater. 2016, 1, 16013. [Google Scholar] [CrossRef]
- Xiang, J.; Wei, Y.; Zhong, Y.; Yang, Y.; Cheng, H.; Yuan, L.; Xu, H.; Huang, Y. Building Practical High-Voltage Cathode Materials for Lithium-Ion Batteries. Adv. Mater. 2022, 34, e2200912. [Google Scholar] [CrossRef]
- Lee, W.; Muhammad, S.; Sergey, C.; Lee, H.; Yoon, J.; Kang, Y.; Yoon, W. Advances in the Cathode Materials for Lithium Rechargeable Batteries. Angew. Chemie Int. Ed. 2020, 59, 2578–2605. [Google Scholar] [CrossRef]
- Guo, K.; Qi, S.; Wang, H.; Huang, J.; Wu, M.; Yang, Y.; Li, X.; Ren, Y.; Ma, J. High-Voltage Electrolyte Chemistry for Lithium Batteries. Small Sci. 2022, 2, 2100107. [Google Scholar] [CrossRef]
- Zhong, Q.; Bonakdarpour, A.; Zhang, M.; Gao, Y.; Dahn, J.R. Synthesis and Electrochemistry of LiNixMn2−xO4. J. Electrochem. Soc. 1997, 144, 205–213. [Google Scholar] [CrossRef]
- Santhanam, R.; Rambabu, B. Research progress in high voltage spinel LiNi0.5Mn1.5O4 material. J. Power Sources 2010, 195, 5442–5451. [Google Scholar] [CrossRef]
- Amine, K. Olivine LiCoPO4 as 4.8 V Electrode Material for Lithium Batteries. Electrochem. Solid-State Lett. 1999, 3, 178. [Google Scholar] [CrossRef]
- Brutti, S.; Panero, S. Recent Advances in the Development of LiCoPO4 as High Voltage Cathode Material for Li-Ion Batteries. In Nanotechnology for Sustainable Energy; ACS Publications: Washington, DC, USA, 2013; pp. 67–99. [Google Scholar] [CrossRef]
- Wu, J.; Tsai, C.-J. Qualitative modeling of the electrolyte oxidation in long-term cycling of LiCoPO4 for high-voltage lithium-ion batteries. Electrochim. Acta 2021, 368, 137585. [Google Scholar] [CrossRef]
- Sreedeep, S.; Natarajan, S.; Aravindan, V. Recent advancements in LiCoPO4 cathodes using electrolyte additives. Curr. Opin. Electrochem. 2022, 31, 100868. [Google Scholar] [CrossRef]
- Okada, S.; Ueno, M.; Uebou, Y.; Yamaki, J. Fluoride phosphate Li2CoPO4F as a high-voltage cathode in Li-ion batteries. J. Power Sources 2005, 146, 565–569. [Google Scholar] [CrossRef]
- Wu, X.; Gong, Z.; Tan, S.; Yang, Y. Sol–gel synthesis of Li2CoPO4F/C nanocomposite as a high power cathode material for lithium ion batteries. J. Power Sources 2012, 220, 122–129. [Google Scholar] [CrossRef]
- Jung, S.-K.; Kim, H.; Cho, M.G.; Cho, S.-P.; Lee, B.; Kim, H.; Park, Y.-U.; Hong, J.; Park, K.-Y.; Yoon, G.; et al. Lithium-free transition metal monoxides for positive electrodes in lithium-ion batteries. Nat. Energy 2017, 2, 16208. [Google Scholar] [CrossRef]
- Kothalawala, V.N.; Devi, A.A.S.; Nokelainen, J.; Alatalo, M.; Barbiellini, B.; Hu, T.; Lassi, U.; Suzuki, K.; Sakurai, H.; Bansil, A. First Principles Calculations of the Optical Response of LiNiO2. Condens. Matter 2022, 7, 54. [Google Scholar] [CrossRef]
- Kothalawala, V.N.; Suzuki, K.; Nokelainen, J.; Hyvönen, A.; Makkonen, I.; Barbiellini, B.; Hafiz, H.; Tynjälä, P.; Laine, P.; Välikangas, J.; et al. Compton scattering study of strong orbital delocalization in a LiNiO2 cathode. Phys. Rev. B 2024, 109, 035139. [Google Scholar] [CrossRef]
- Zhao, W.; Ji, Y.; Zhang, Z.; Lin, M.; Wu, Z.; Zheng, X.; Li, Q.; Yang, Y. Recent advances in the research of functional electrolyte additives for lithium-ion batteries. Curr. Opin. Electrochem. 2017, 6, 84–91. [Google Scholar] [CrossRef]
- Han, J.; Kim, K.; Lee, Y.; Choi, N. Scavenging Materials to Stabilize LiPF6-Containing Carbonate-Based Electrolytes for Li-Ion Batteries. Adv. Mater. 2019, 31, e1804822. [Google Scholar] [CrossRef]
- Xu, K. Electrolytes and Interphases in Li-Ion Batteries and Beyond. Chem. Rev. 2014, 114, 11503–11618. [Google Scholar] [CrossRef]
- Aurbach, D.; Markovsky, B.; Salitra, G.; Markevich, E.; Talyossef, Y.; Koltypin, M.; Nazar, L.; Ellis, B.; Kovacheva, D. Review on electrode–electrolyte solution interactions, related to cathode materials for Li-ion batteries. J. Power Sources 2007, 165, 491–499. [Google Scholar] [CrossRef]
- Fan, X.; Wang, C. High-voltage liquid electrolytes for Li batteries: Progress and perspectives. Chem. Soc. Rev. 2021, 50, 10486–10566. [Google Scholar] [CrossRef]
- Chen, M.; Huang, Y.; Shi, Z.; Luo, H.; Liu, Z.; Shen, C. Effect of High-Voltage Additives on Formation of Solid Electrolyte Interphases in Lithium-Ion Batteries. Materials 2022, 15, 3662. [Google Scholar] [CrossRef]
- Zhang, K.; Tian, Y.; Wei, C.; An, Y.; Feng, J. Building stable solid electrolyte interphases (SEI) for microsized silicon anode and 5 V-class cathode with salt engineered nonflammable phosphate-based lithium-ion battery electrolyte. Appl. Surf. Sci. 2021, 553, 149566. [Google Scholar] [CrossRef]
- Zhou, H.; Xiao, K.; Li, J. Lithium difluoro(oxalate)borate and LiBF4 blend salts electrolyte for LiNi0.5Mn1.5O4 cathode material. J. Power Sources 2016, 302, 274–282. [Google Scholar] [CrossRef]
- Zhang, S.S. Electrochemical study of the formation of a solid electrolyte interface on graphite in a LiBC2O4F2-based electrolyte. J. Power Sources 2007, 163, 713–718. [Google Scholar] [CrossRef]
- Nie, M.; Lucht, B.L. Role of Lithium Salt on Solid Electrolyte Interface (SEI) Formation and Structure in Lithium Ion Batteries. J. Electrochem. Soc. 2014, 161, A1001–A1006. [Google Scholar] [CrossRef]
- Park, K.; Yu, S.; Lee, C.; Lee, H. Comparative study on lithium borates as corrosion inhibitors of aluminum current collector in lithium bis(fluorosulfonyl)imide electrolytes. J. Power Sources 2015, 296, 197–203. [Google Scholar] [CrossRef]
- Shkrob, I.A.; Zhu, Y.; Marin, T.W.; Abraham, D.P. Mechanistic Insight into the Protective Action of Bis(oxalato)borate and Difluoro(oxalate)borate Anions in Li-Ion Batteries. J. Phys. Chem. C 2013, 117, 23750–23756. [Google Scholar] [CrossRef]
- Xiang, J.; Wu, F.; Chen, R.; Li, L.; Yu, H. High voltage and safe electrolytes based on ionic liquid and sulfone for lithium-ion batteries. J. Power Sources 2013, 233, 115–120. [Google Scholar] [CrossRef]
- Borodin, O.; Behl, W.; Jow, T.R. Oxidative Stability and Initial Decomposition Reactions of Carbonate, Sulfone, and Alkyl Phosphate-Based Electrolytes. J. Phys. Chem. C 2013, 117, 8661–8682. [Google Scholar] [CrossRef]
- Delp, S.A.; Borodin, O.; Olguin, M.; Eisner, C.G.; Allen, J.L.; Jow, T.R. Importance of Reduction and Oxidation Stability of High Voltage Electrolytes and Additives. Electrochim. Acta 2016, 209, 498–510. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, P.; Cui, X.; Mao, L.; Li, C.; Li, S. Robust and sulfur-containing ingredient surface film to improve the electrochemical performance of LiDFOB-based high-voltage electrolyte. Electrochim. Acta 2018, 260, 536–548. [Google Scholar] [CrossRef]
- Li, B.; Shao, Y.; He, J.; Chen, R.; Huang, S.; Wu, Z.; Li, J.; Wang, Z.; Liu, G. Cyclability improvement of high voltage lithium cobalt oxide/graphite battery by use of lithium difluoro(oxalate)borate electrolyte additive. Electrochim. Acta 2022, 426, 140783. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Deng, L.; Yang, Y.; Tan, L.; Niu, X.; Chen, Y.; Zeng, L.; Fan, X.; Zhu, Y. An additive-enabled ether-based electrolyte to realize stable cycling of high-voltage anode-free lithium metal batteries. Energy Storage Mater. 2023, 54, 450–460. [Google Scholar] [CrossRef]
- Sanginov, E.A.; Borisevich, S.S.; Kayumov, R.R.; Istomina, A.S.; Evshchik, E.Y.; Reznitskikh, O.G.; Yaroslavtseva, T.V.; Melnikova, T.I.; Dobrovolsky, Y.A.; Bushkova, O.V. Lithiated Nafion plasticised by a mixture of ethylene carbonate and sulfolane. Electrochim. Acta 2021, 373, 137914. [Google Scholar] [CrossRef]
- Dobrovolsky, Y.A.; Ilyina, M.G.; Evshchik, E.Y.; Khamitov, E.M.; Chernyak, A.V.; Shikhovtseva, A.V.; Melnikova, T.I.; Bushkova, O.V.; Borisevich, S.S. QC and MD Modelling for Predicting the Electrochemical Stability Window of Electrolytes: New Estimating Algorithm. Batteries 2022, 8, 292. [Google Scholar] [CrossRef]
- Ikeguchi, M. Partial rigid-body dynamics in NPT, NPAT and NPγT ensembles for proteins and membranes. J. Comput. Chem. 2004, 25, 529–541. [Google Scholar] [CrossRef]
- Bowers, K.J.; Chow, E.; Xu, H.; Dror, R.O.; Eastwood, M.P.; Gregersen, B.A.; Klepeis, J.L.; Kolossvary, I.; Moraes, M.A.; Sacerdoti, F.D.; et al. Scalable algorithms for molecular dynamics simulations on commodity clusters. In Proceedings of the 2006 ACM/IEEE Conference on Supercomputing, Tampa, FL, USA, 11–17 November 2006. [Google Scholar] [CrossRef]
- Lu, C.; Wu, C.; Ghoreishi, D.; Chen, W.; Wang, L.; Damm, W.; Ross, G.A.; Dahlgren, M.K.; Russell, E.; Bargen, C.D.; et al. OPLS4: Improving Force Field Accuracy on Challenging Regimes of Chemical Space. J. Chem. Theory Comput. 2021, 17, 4291–4300. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Borodin, O.; Jow, T.R. Quantum Chemistry Study of the Oxidation-Induced Decomposition of Tetramethylene Sulfone (TMS) Dimer and TMS/BF4−. ECS Trans. 2013, 50, 391–398. [Google Scholar] [CrossRef]
- Chatfield, D.; Christopher, J. Cramer: Essentials of Computational Chemistry: Theories and Models. Theor. Chem. Accounts Theory Comput. Model. 2002, 108, 367–368. [Google Scholar] [CrossRef]
- Li, S.; Liu, Q.; Zhang, W.; Fan, L.; Wang, X.; Wang, X.; Shen, Z.; Zang, X.; Zhao, Y.; Ma, F.; et al. High-Efficacy and Polymeric Solid-Electrolyte Interphase for Closely Packed Li Electrodeposition. Adv. Sci. 2021, 8, 2003240. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).