Double-Layer Capacitances Caused by Ion–Solvent Interaction in the Form of Langmuir-Typed Concentration Dependence
Abstract
:1. Introduction
2. Materials and Methods
3. Theory
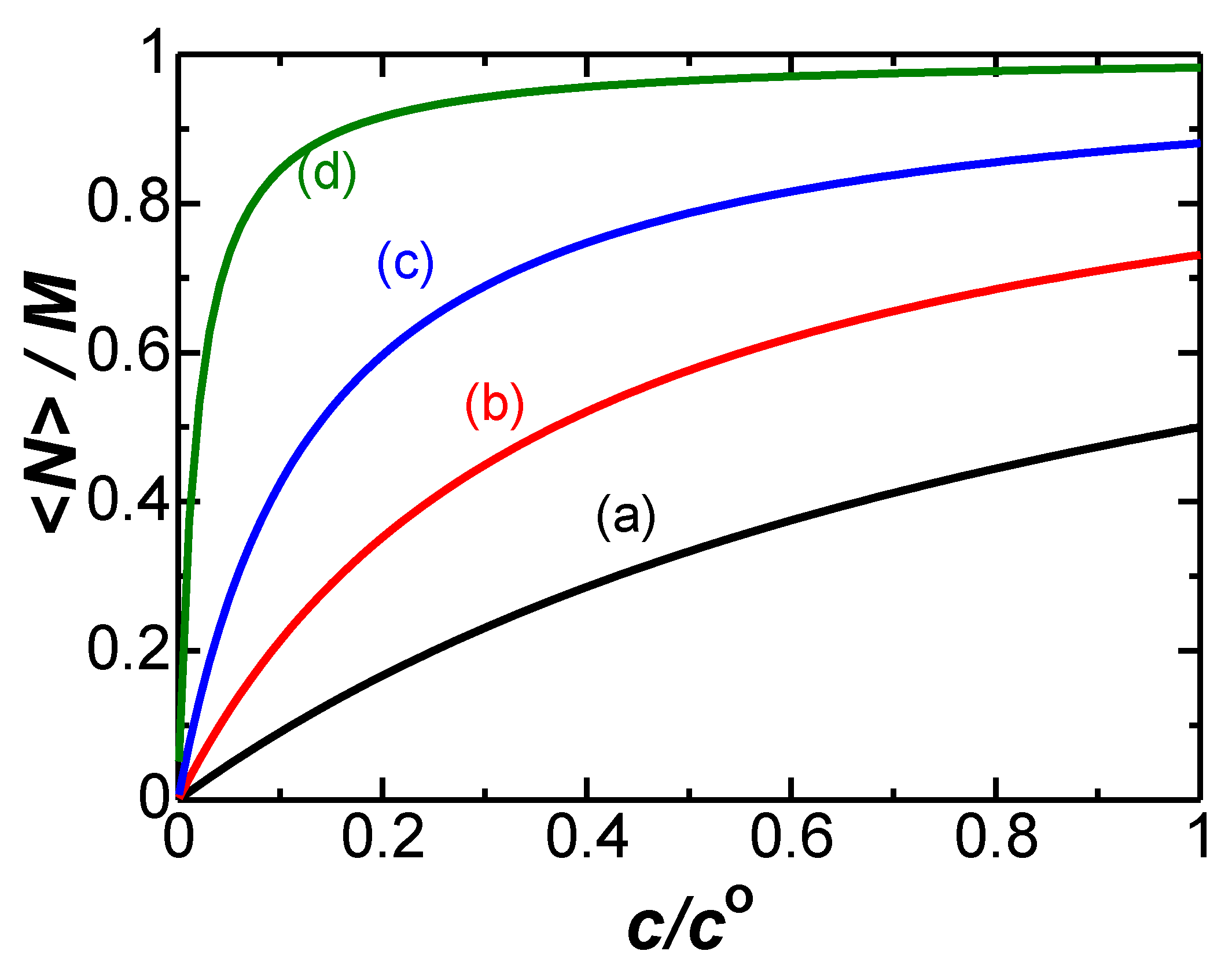
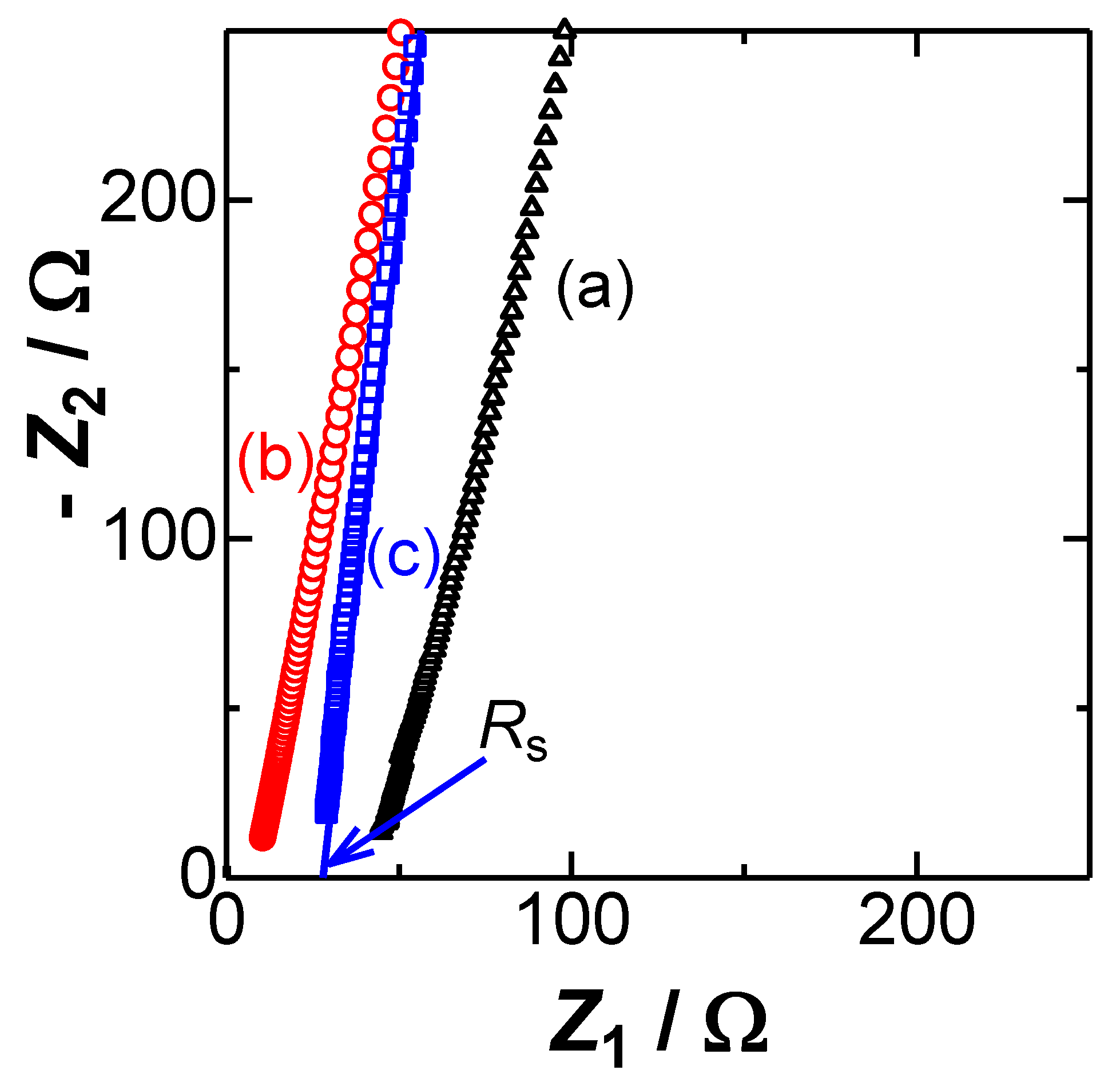
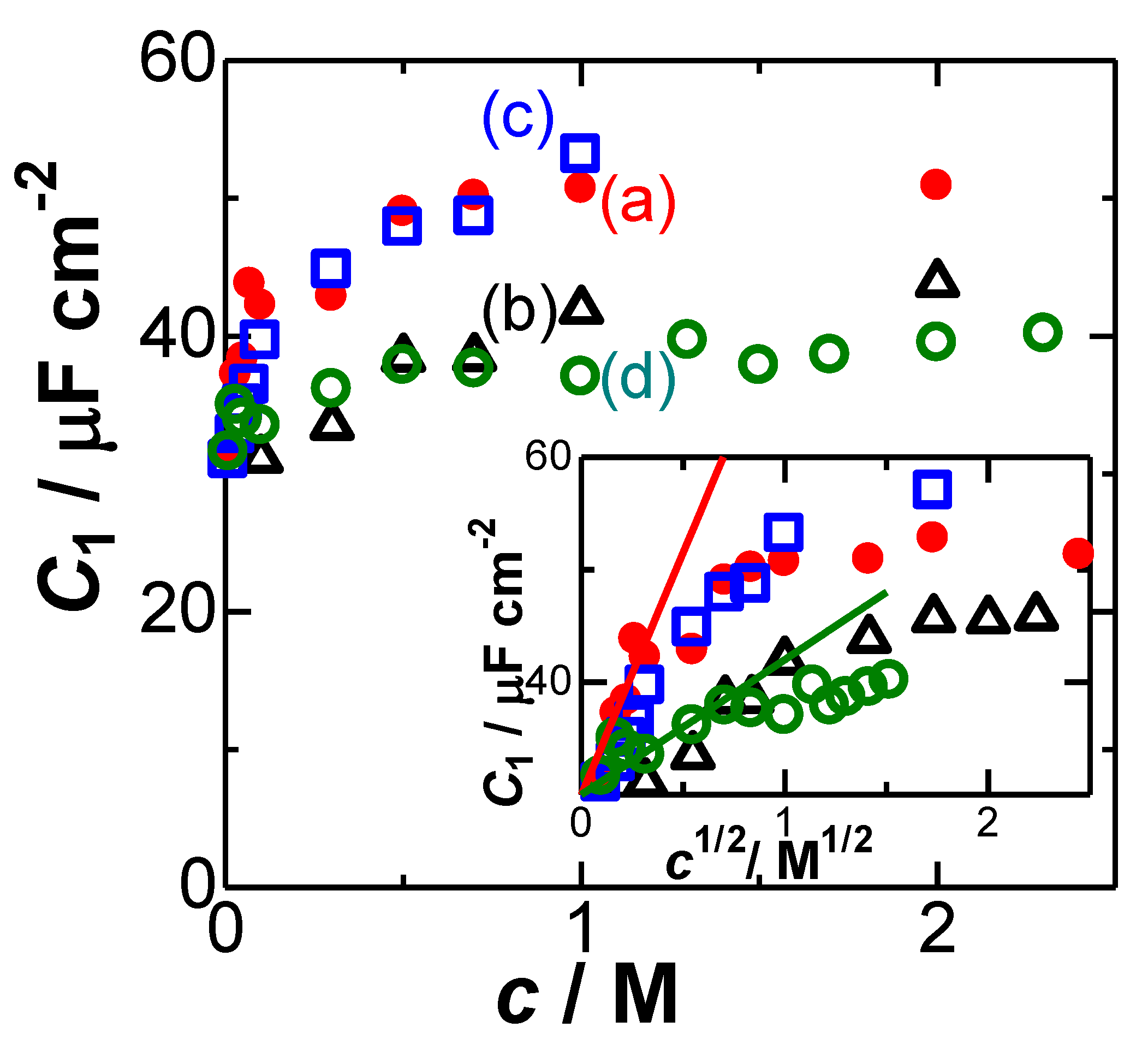
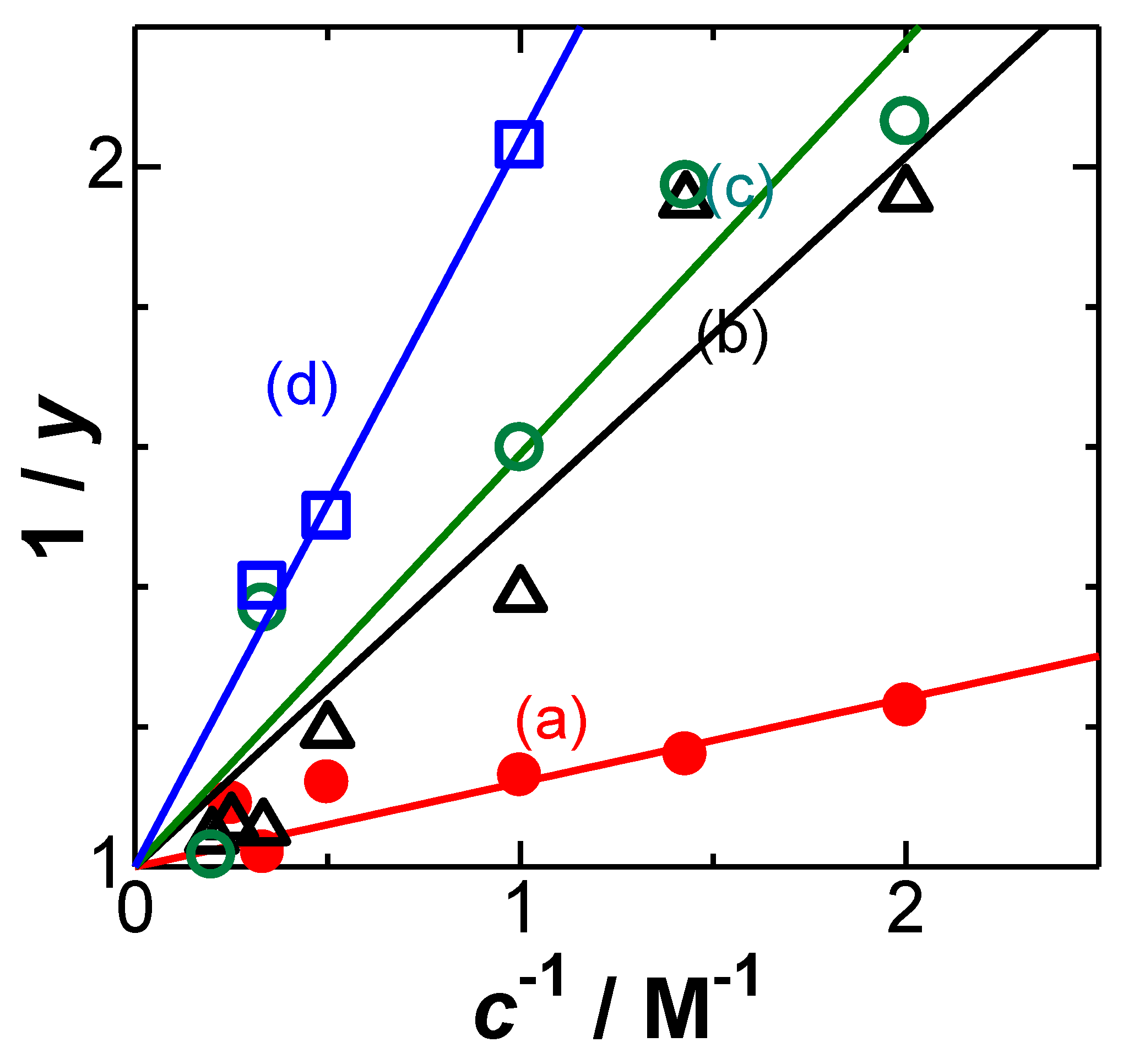
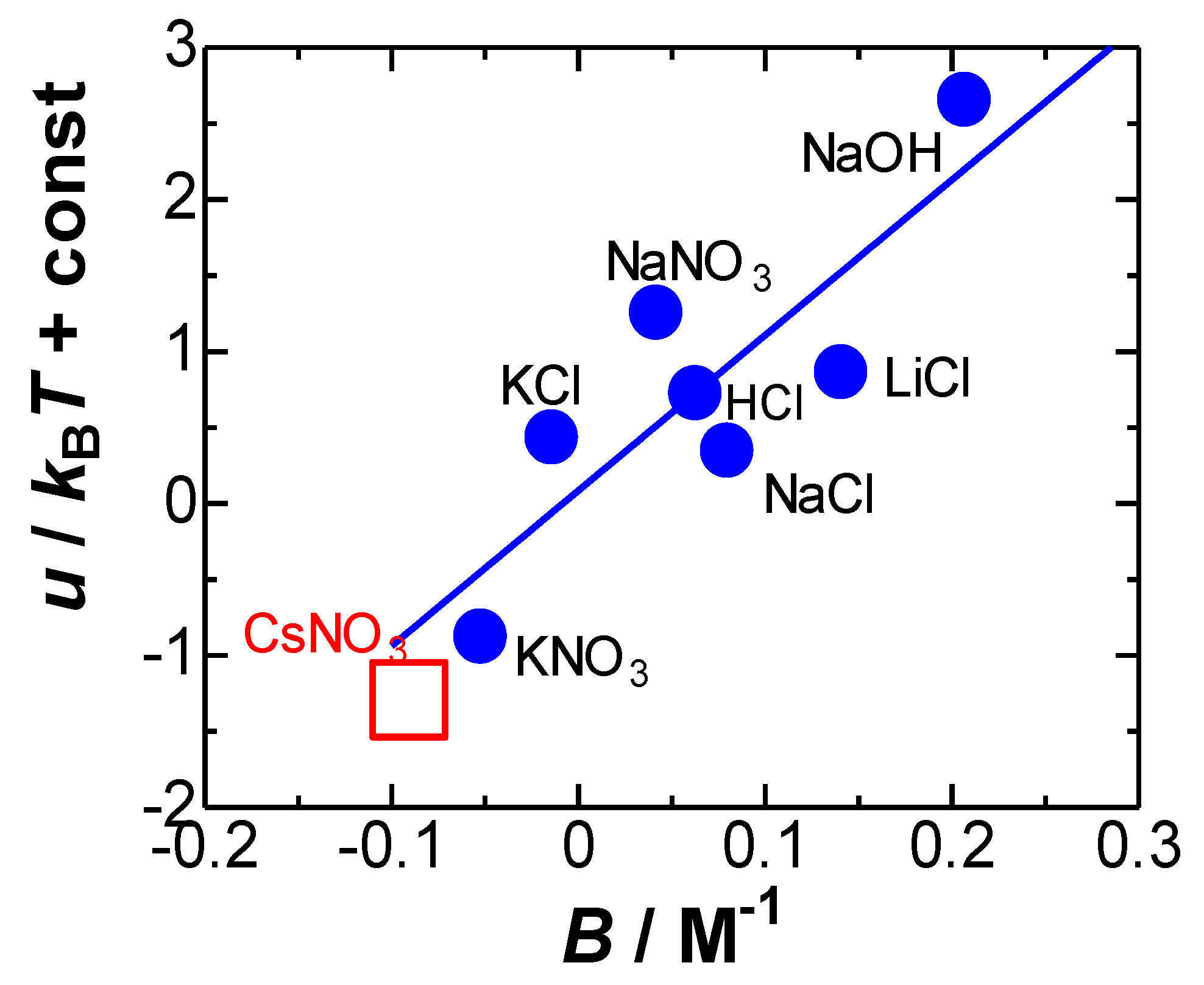
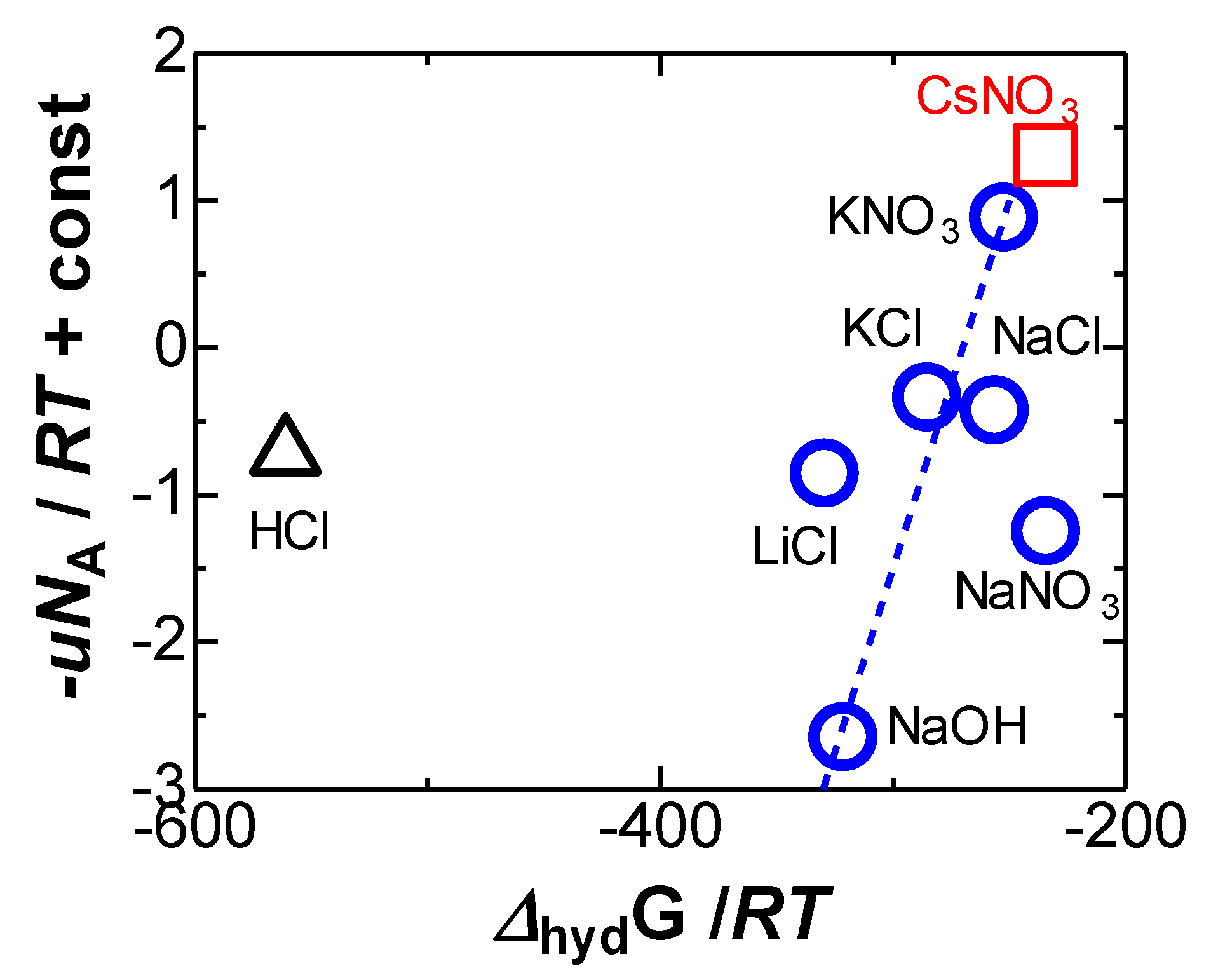
4. Results and Discussion
5. Conclusions
- (i)
- values of DLCs increase with ionic concentrations and reach saturated values at most 1.5 times as large as the ion-free value;
- (ii)
- the values are not at all proportional to c1/2 by the GC theory;
- (iii)
- the Stern model is not valid in the context of the concentration dependence;
- (iv)
- ionic effects are caused by ion–solvent interaction rather than ion-ion interaction;
- (v)
- variation of C1 with c depends on ionic properties.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Conway, B.E. Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications; Plenum Press: New York, NY, USA, 1999. [Google Scholar]
- Lu, M.; Beguin, F.; Frackowiak, E. Supercapacitors: Materials, Systems, and Applications, 1st ed.; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Kötz, R.; Carlen, M. Principles and applications of electrochemical capacitors. Electrochim. Acta 2000, 45, 2483–2498. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, L.; Zhang, J. A review of electrode materials for electrochemical supercapacitors. Chem. Soc. Rev. 2012, 41, 797–828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ho, J.; Jow, E.; Boggs, S. Historical Introduction to Capacitor Technology. IEEE Elect. Ins. Mag. 2010, 26, 20–25. [Google Scholar] [CrossRef] [Green Version]
- Namisnyk, A.M. A Survey of Electrochemical Supercapacitor Technology 2007. Available online: https://www.semanticscholar.org/paper/A-SURVEY-OF-ELECTROCHEMICAL-SUPERCAPACITOR-Namisnyk-Zhu/d9018594f7d9a6cc36b7b0a11ebea8fe55190a90 (accessed on 1 October 2021).
- Evans, D.A. High Energy Density Electrolytic-Electrochemical Hybrid Capacitor. In 14th Capacitor & Resistor Technology Symposium; Components Technology Institute Inc.: Jupiter, FL, USA, 22 March 1994. [Google Scholar]
- Viswanathan, A.; Shetty, A.N. Enhancement of supercapacitance of reduced graphene oxide, copper oxide and polyaniline using the mixture of methane sulphonic acid and sulphuric acid as electrolyte. Chem. Eng. Sci. 2021, 229, 116020. [Google Scholar] [CrossRef]
- He, R.; Aoki, K.J.; Chen, J. Electric Field-Dependence of Double Layer Capacitances by Current-Controlled Charge-Discharge Steps. Electrochem 2020, 1, 217–225. [Google Scholar] [CrossRef]
- Hou, Y.; Aoki, K.J.; Chen, J.; Nishiumi, T. Solvent Variables Controlling Electric Double Layer Capacitance at Metal-Solution Interface. J. Phys. Chem. C 2014, 118, 10153–10158. [Google Scholar] [CrossRef]
- Hou, Y.; Aoki, K.J.; Chen, J.; Nishiumi, T. Invariance of double layer capacitance to polarized potential in halide solutions. Univ. J. Chem. 2013, 1, 162–169. [Google Scholar] [CrossRef]
- Zhao, X.; Aoki, K.J.; Chen, J.; Nishiumi, T. Examination of the Gouy–Chapman theory for double layer capacitance in deionized latex suspensions. RSC Adv. 2014, 4, 63171–63181. [Google Scholar] [CrossRef]
- Khademi, M.; Barz, D.P.J. Structure of the Electrical Double Layer Revisited: Electrode Capacitance in Aqueous Solutions. Langmuir 2020, 36, 4250–4260. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications; John Wiley & Sons, Inc.: New York, NY, USA, 2001; p. 551. [Google Scholar]
- Aoki, K.J.; Chen, J. Effects of the dipolar double layer on elemental electrode processes at micro- and macro-interfaces. Faraday Discus. 2018, 210, 219–234. [Google Scholar] [CrossRef] [PubMed]
- Prehal, C.; Koczwara, C.; Amenitsch, H.; Presser, V.; Paris, O. Salt concentration and charging velocity determine ion charge storage mechanism in nanoporous supercapacitors. Nat. Commun. 2018, 9, 4145. [Google Scholar] [CrossRef] [Green Version]
- Ramachandran, R.; Wang, F. Electrochemical Capacitor Performance: Influence of Aqueous Electrolytes; IntechOpen: London, UK, 2017. [Google Scholar]
- Pohlmann, S.; Balducci, A. A new conducting salt for high voltage propylene carbonate-based electrochemical double layer capacitors. Electrochim. Acta 2013, 110, 221–227. [Google Scholar] [CrossRef]
- Galek, P.; Frackowiak, E.; Fi, K. Interfacial aspects induced by saturated aqueous electrolytes in electrochemical capacitor applications. Electrochim. Acta 2020, 20, 135572. [Google Scholar] [CrossRef]
- Li, J.; Pham, P.H.Q.; Zhou, W.; Pham, T.D.; Burke, P.J. Carbon-Nanotube–Electrolyte Interface: Quantum and Electric Double Layer Capacitance. ACS Nano 2018, 12, 9763–9774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kortschot, R.J.; Philipse, A.P.; Erné, B.H. Debye Length Dependence of the Anomalous Dynamics of Ionic Double Layers in a Parallel Plate Capacitor. J. Phys. Chem. C 2014, 118, 11584–11592. [Google Scholar] [CrossRef]
- Lust, E.; Jänes, A.; Sammelselg, V.; Miidla, P. Influence of charge density and electrolyte concentration on the electrical double layer characteristics at rough cadmium electrodes. Electrochim. Acta 2000, 46, 185–191. [Google Scholar] [CrossRef]
- Zhang, X.; Kuhnel, R.-S.; Passerini, S.; Balducci, A. Double-Salt Electrolytes for High Voltage Electrochemical Double-Layer Capacitors. J. Sol. Chem. 2015, 44, 528–537. [Google Scholar] [CrossRef]
- Krummacher, J.; Balducci, A. Al(TFSI)3 as a Conducting Salt for High-Voltage Electrochemical Double-Layer Capacitors. Chem. Mater. 2018, 30, 4857–4863. [Google Scholar] [CrossRef]
- Uchida, S.; Masese, T. Electric Double-Layer Capacitors Based on Non-Aqueous Electrolytes: A Comparative Study of Potassium and Quaternary Ammonium Salts. Batter. Supercaps 2020, 3, 392–396. [Google Scholar] [CrossRef]
- Zheng, J.P.; Jow, T.R. The Effect of Salt Concentration in Electrolytes on the Maximum Energy Storage for Double Layer Capacitors. J. Electrochem. Soc. 1997, 144, 2417–2420. [Google Scholar] [CrossRef]
- Noel, R.L.; Hampson, A. The dispersion of double-layer capacitance with frequency I. Smooth solid electrodes. Surf. Tech. 1978, 7, 151–155. [Google Scholar]
- Nyikos, L.; Pajkossy, T. Fractal dimension and fractional power frequency-dependent impedance of blocking electrodes. Electrochim. Acta 1985, 30, 1533–1540. [Google Scholar] [CrossRef]
- Brug, G.J.; Van Den Eeden, A.L.G.; Sluyters-Rehbach, M.; Sluyters, J.H. The analysis of electrode impedances complicated by the presence of a constant phase element. J. Electroanal. Chem. 1984, 176, 275–295. [Google Scholar] [CrossRef]
- Zoltowski, P. On the electrical capacitance of interfaces exhibiting constant phase element behavior. J. Electroanal. Chem. 1998, 443, 149–154. [Google Scholar] [CrossRef]
- Lasia, A. Electrochemical Impedance Spectroscopy and its Applications. In Modern Aspects of Electrochemistry; Conway, B.E., Bockris, J.O.M., White, R.E., Eds.; Springer: Boston, MA, USA; Volume 32. [CrossRef]
- Wang, H.; Aoki, K.J.; Chen, J.; Nishiumi, T.; Zeng, X.; Ma, X. Power law for frequency-dependence of double layer capacitance of graphene flakes. J. Electroanal. Chem. 2015, 741, 114–119. [Google Scholar] [CrossRef]
- Aoki, K.J. Molecular interaction model for frequency-dependence of double layer capacitors. Electrochim. Acta 2016, 188, 545–550. [Google Scholar] [CrossRef]
- Jiang, G.; Cheng, C.; Li, D.; Liu, J.Z. Molecular dynamics simulations of the electric double layer capacitance of graphene electrodes in mono-valent aqueous electrolytes. Nano Res. 2016, 9, 174–186. [Google Scholar] [CrossRef] [Green Version]
- Welch, D.A.; Mehdi, B.L.; Hatchell, H.J.; Faller, R.; Evans, J.E.; Browning, N.D. Using molecular dynamics to quantify the electrical double layer and examine the potential for its direct observation in the in-situ TEM. Adv. Struct. Chem. Imag. 2015, 1, 1. [Google Scholar] [CrossRef] [Green Version]
- Katakura, S.; Nishi, N.; Kobayashi, K.; Amano, K.; Sakka, T. An electric double layer structure and differential capacitance at the electrode interface of tributylmethylammonium bis(trifluoromethanesulfonyl)amide studied using a molecular dynamics simulation. Phys. Chem. Chem. Phys. 2020, 22, 5198–5210. [Google Scholar] [CrossRef]
- Kong, X.; Lu, D.; Liu, Z.; Wu, J. Molecular dynamics for the charging behavior of nanostructured electric double layer capacitors containing room temperature ionic liquids. Nano Res. 2014, 8, 931–940. [Google Scholar] [CrossRef]
- Burt, R.; Birkett, G.; Zhao, X.S. A review of molecular modelling of electric double layer capacitors. Phys. Chem. Chem. Phys. 2014, 16, 6519–6538. [Google Scholar] [CrossRef]
- Frank, H.S.; Wen, W.-Y. Ion-Solvent Interaction. Structural Aspects of Ion-Solvent Interaction in Aqueous Solutions: A Suggested Picture of Water Structure. Discuss. Faraday Soc. 1957, 44, 133–140. [Google Scholar] [CrossRef]
- Samoilov, O.Y. A new approach to the study of hydration of ions in aqueous solutions. Discuss. Faraday Soc. 1957, 44, 141–146. [Google Scholar] [CrossRef]
- Feakins, D.; Lawrence, K.G. The relative viscosities of solutions of sodium and potassium chlorides and bromides in N-methylformamide at 25, 35, and 45°. J. Chem. Soc. A 1966, 212–219. [Google Scholar] [CrossRef]
- Jenkins, H.D.B.; Marcus, Y. Viscosity B-Coefficients of Ions in Solution. Chem. Rev. 1995, 95, 2695–2724. [Google Scholar] [CrossRef]
- Talekar, S.V. Temperature dependence of activation energies for self-diffusion of water and of alkali ions in aqueous electrolyte solutions. A model for ion selective behavior of biological cells. Int. J. Quantum Chem. 1977, 12, 459–469. [Google Scholar] [CrossRef]
- Marcus, Y. Thermodynamics of Solvation of Ions, Part 5. Gibbs Free Energy of Hydration at 298.15 K. J. Chem. Soc. Faraday Trans. 1991, 87, 2995–2999. [Google Scholar] [CrossRef]
- Plambec, J.A. Solvation thermodynamics of ions: Free energies in water, ammonia, and fused LiCl-KC1 eutectic. Can. J. Chem. 1969, 47, 1401–1410. [Google Scholar] [CrossRef]
- Setschenow, J. Uber die Konstitution der Salzlosungen auf Grund ihres Verhaltens zu Kohlensaure. Z. Physik. Chem. 1889, 4, 117–125. [Google Scholar] [CrossRef]
- Ni, N.; Yalkowsky, S.H. Prediction of Setschenow constants. Int. J. Pharm. 2003, 254, 167–172. [Google Scholar] [CrossRef]
- Aoki, K.J.; Chen, J.; Zeng, X.; Wang, Z. Decrease in double layer capacitance by Faradaic current. RSC Adv. 2017, 7, 22501–22509. [Google Scholar] [CrossRef] [Green Version]
- Lust, E.; Jänes, A.; Arulepp, M. Influence of solvent nature on the electrochemical parameters of electrical double layer capacitors. J. Electroanal. Chem. 2004, 562, 33–42. [Google Scholar] [CrossRef]
- Kim, I.-T.; Egashira, M.; Yoshimoto, N.; Morita, M. Effects of electrolytic composition on the electric double-layer capacitance at smooth-surface carbon electrodes in organic media. Electrochim. Acta 2010, 55, 6632–6638. [Google Scholar] [CrossRef]
- Rampolla, R.; Miller, R.; Smyth, C. Microwave Absorption and Molecular Structure in Liquids. XXV. Measurements of Dielectric Constant and Loss at 3.1-mm Wavelength by an Interferometric Method. J. Chem. Phys. 1959, 30, 566. [Google Scholar] [CrossRef]
- Aoki, K.J. Frequency-dependence of electric double layer capacitance without Faradaic reactions. J. Electroanal. Chem. 2016, 779, 117–125. [Google Scholar] [CrossRef]
- Aoki, K.J.; He, R.; Chen, J. Parallel Combination of Inner Capacitance and Ionic Capacitance, Apparently Inconsistent with Stern’s Model. Electrochem 2021, 2, 71–82. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aoki, K.J.; He, R.; Chen, J. Double-Layer Capacitances Caused by Ion–Solvent Interaction in the Form of Langmuir-Typed Concentration Dependence. Electrochem 2021, 2, 631-642. https://doi.org/10.3390/electrochem2040039
Aoki KJ, He R, Chen J. Double-Layer Capacitances Caused by Ion–Solvent Interaction in the Form of Langmuir-Typed Concentration Dependence. Electrochem. 2021; 2(4):631-642. https://doi.org/10.3390/electrochem2040039
Chicago/Turabian StyleAoki, Koichi Jeremiah, Ridong He, and Jingyuan Chen. 2021. "Double-Layer Capacitances Caused by Ion–Solvent Interaction in the Form of Langmuir-Typed Concentration Dependence" Electrochem 2, no. 4: 631-642. https://doi.org/10.3390/electrochem2040039
APA StyleAoki, K. J., He, R., & Chen, J. (2021). Double-Layer Capacitances Caused by Ion–Solvent Interaction in the Form of Langmuir-Typed Concentration Dependence. Electrochem, 2(4), 631-642. https://doi.org/10.3390/electrochem2040039







