Abstract
It is essential to understand the adsorption of guest molecules on carbon-based materials for both theoretical and practical reasons. It is crucial to analyze the surface properties of carbon-based materials with a wide range of applications (e.g., catalyst supports, hydrogen storage, sensors, adsorbents, separation media, etc.). Inverse gas chromatography (IGC) as a powerful and sensitive technique can be used to characterize the surface physicochemical properties (i.e., Brunauer-Emmett-Teller (BET) surface area, surface energy heterogeneity, heat of adsorption, specific interaction of adsorption, work of cohesion, glass transition temperatures, solubility, and so forth) of various types of materials such as powders, films, and fibers. In this review, the principles, common methods, and application of IGC are discussed. In addition, the examples of various experiments developed for the IGC to characterize the carbonaceous materials (such as carbon nanotubes, graphite, and activated carbon) are discussed.
1. Introduction
Gas chromatography is a method often used to investigate gas–adsorbent and gas–liquid equilibria. A variant of this method is inverse gas chromatography. The term inverse indicates that the material studied is a nonvolatile stationary phase that is either liquid or solid. This modification of the classical chromatographic approach was first introduced by Davis and Petersen [1]. There are a lot of research studies in the literature describing the physicochemical characteristics derived from inverse gas chromatography (IGC) experiments of silica, alumina, polymer and their blends, commercial stationary phases, paper fillers, wood, minerals, carbon fibers, carbon blacks and graphite, and activated carbons. Therefore, a review of the literature could help researchers’ better understanding and useful application of the IGC method. Using this method is promising in the investigation of the surface activity of porous material, which is challenging to measure by conventional methods such as contact angle. The effect of modification on surface properties as well as the effect of the IGC experiment conditions such as temperature and humidity can be evaluated [2].
Two different conditions may apply to perform IGC: infinite dilution (ID) and finite concentration (FC). In IGC-FC, the small amount of injected salutes leads to deformation of the chromatographic peaks, and the measurement is based on the calculation of the peak deformation, adsorption isotherms, and adsorption energies distribution. The IGC-ID is based on the calculation of the interaction level of solid surface and probe molecules by the injection of very small amounts of probe molecules into a chromatographic column. The degree of dilution is such that intermolecular interactions between the adsorbed molecules can be neglected. A pulse of a very diluted vapor of probe molecules is injected into the column, pushed by the carrier gas, after which the probe molecules explore the whole surface of the solid statistically before leaving the column. The flow of solute molecules leaving the column is detected and recorded [3,4]. In this review, a theoretical background of IGC and methods to calculate the dispersive surface energy are described and compared. In addition, examples of application of IGC to characterize the physicochemical properties (such as surface energy, acid–base properties, solubility, etc.) of carbonaceous material (activated carbon, carbon nanotubes, carbon fiber, graphite, etc.) are described.
2. Theoretical Background of Inverse Gas Chromatography
Characterization of the surface properties of solid materials is the main application of the IGC. The measurement is based on the retention volume or retention time, which are the carrier gas volume and time required to create a peak as a result of interactions of the probe molecule and the solid surface. Different features of a material such as dispersive surface energy and acid–base properties can be determined using IGC. The surface energy of the solid material is a combination of dispersive and specific components.
2.1. Dispersive Component of Surface Free Energy
Two methods are used to calculate the dispersive component of the surface free energy, including the Schultz method [5] and Dorris–Gray method [6], which are discussed in the next sections.
2.1.1. Schultz Method
Schultz and Lavielle [7] suggested a method to calculate the surface dispersive free energy. In this method, the calculation of the surface-dispersive free energy () is based on the retention time or volume of series of linear liquid n-alkane (non-polar) probe molecules at infinite dilution at the Henry’s Law region [8]. While using the non-polar alkanes, there are no interactions between the probe molecules; thus, the IGC chromatograms are symmetrical Gaussian [9]. The required time for the non-adsorbing probe molecule to pass the column after injection into the column, the dead time (t0), is typically determined using methane as an inert gas. The solute gross retention time is the required time to pass the column completely (tR). The net retention volume (VN) of the probe is determined by [9]:
where j is the James–Martin correction factor, and Fc is the flow rate of carrier gas in the column. The value of j is determined using Equation (2) [6,10]:
where is the entering pressure and is the atmospheric pressure. The net retention time is an average required time for the probe molecules in the adsorbed state. The value of the retention of the test solutes () is the difference between the retention time of the peak of the probe (tR) and the gas hold-up time (), which can be calculated using the Grobler–Balizs procedure [11,12].
VN = j·Fc·(tR − t0)
The value of corresponds to the first-order moment of the peak of the probe. The specific retention volume () is the required volume of the carrier gas to push the probe molecules out of the GC column. The exact quantity in terms of the experimental variable is [6]:
where T is the measurement temperature, is the mass of the stationary phase. At infinite dilution, the net retention volume (VN) value of one or several probes is related to the concentration of the adsorbate in the gas phase, and it can be determined as [10]:
where is the surface partition coefficient, and S is the specific surface area of the examined material. The standard free energy change of adsorption of the probe on a solid surface can be shown as:
where R is the gas constant, S is the specific surface area of the adsorbate, and g is the weight of the adsorbate in the column. Depending on the reference state Kemball and Rideal (= 1.013 × 105 Pa and = 6.08 × 10−5 Nm−1) or DeBoer (P0 = 1.013 × 105 Pa and = 3.38 × 10−4 Nm−1), can be written as [10,13]:
where K is a constant for the chromatographic column.
where N is Avogadro’s number, a is the surface area of the probe molecule, and is the adhesion energy between probe molecules and solid per unit surface area of the solid adsorbate. When n-alkanes are used as probes and dispersion interactions are only being exchanged, the energy of adhesion can be obtained based on the Fowkes relation [10]:
For n-alkanes , thus:
where is the dispersive free surface energy of the probe molecule, is a dispersive component of the surface free energy of the solid, and is the surface free energy for non-polar hydrocarbons. The is a linear function of the quantity , and the slope of the straight line leads to the values.
When two alkanes of n and (n + 1) are used as probe molecules, the can be expressed as:
2.1.2. Dorris–Gray Method
Dorris and Gray [6] suggested another method to calculate the dispersive component of the surface free energy. The can be calculated by considering the increment of free energy of adsorption per CH2 group. The increase per CH2 in the free energy of adsorption between two alkanes of n and n+1 can be determined using [9]:
By applying Foweks principle, Equation (14) can be expressed as:
where is the cross-sectional area of a CH2 group, and is the surface energy of a CH2 group at the given temperature of T (K), which can be calculated by:
2.1.3. Comparison of Schultz and Dorris–Gray Methods
Generally, the dispersive results calculated from two methods of Dorris–Gray and Schultz are different in a similar condition of measurement. A comparison of two methods can help find the differences in their results. The ratio of and can be calculated from Equations (13) and (19):
If the ratio value is higher than one, it means that the calculated dispersive free energy by the Dorris–Gray method is bigger than that calculated using the Schultz method. Shi et al. [14] reported that increasing the temperature resulted in an increment of the ratio. They have also reported that the values of were bigger than those calculated by the Dorris–Gray method. In comparison with the parameters in the solvents handbook, the calculated surface free energy parameters using the Schultz method were not accurate enough. Another study by Ylä-Mäihäniemi [15] confirmed that compared to the calculated with the Schultz method, the obtained value with Dorris–Gray is more accurate with a much lower experimental error. On the other hand, Kołodziejek et al. [16] reported that the values calculated with the Dorris–Gray and Schultz methods for different hybrid materials were without a certain difference.
2.2. Specific Component of Surface Free Energy
During the polar probes injection, both dispersive and specific interactions are established with the solid surface, thus:
Based on the theory of Good-Van Oss:
where and are the acidic and basic parameters of the solid surface, and are the acidic and basic parameters of the probe molecules. For non-polar probes, , and can be provided by the literature. Thus,
Therefore,
Similarly, the can be written as:
and the total surface energy () is calculated as follows:
The adsorption enthalpy, , assigned to the acid–base interactions can be determined as follows [10]:
where is the adsorption entropy of acid–base interactions. Following Papirer’s approach [17], the values of and were calculated using:
The and are describing the acid and base characteristics of the solids, while DN and are Gutmann’s numbers for the acceptor and donor probes. The and values can be calculated from the plot of versus :
IGC is a powerful, sensitive, and quick method to evaluate the surface properties of different kinds of materials such as films, fiber, and powder in crystalline or amorphous structures such as copolymers, polymer blends, pharmaceutical materials, and nanomaterials [18]. By increasing the interest in material science, the IGC was invented in 1967, and the theory and methodology of IGC were developed at the beginning of 1976 [10]. Various surface characterization and a wide range of information about physicochemical properties can be obtained using this technique, such as solubility, thermodynamic interaction parameters, glass transition temperatures, surface area, surface energy heterogeneity, diffusion kinetics, acid–base properties, work of cohesion, work of adhesion, adsorption isotherms, and polar functionality on the materials surface.
3. Applications of IGC for Carbonaceous Materials
Since carbonaceous materials are broadly used in many fields of industry, especially as adsorbents and catalysts, the investigation of surface properties and interface characterization, interfacial tension, and surface energy are attracting more attention. IGC is an accurate and well-established method to study the physicochemical properties of the surface of various materials such as pharmaceutical materials, nanomaterials, fibers, porous materials, and carbonaceous materials.
Table 1 summarizes the results of different investigations on the surface properties of carbonaceous materials such as surface area, sorption free energy, surface energy, enthalpy, entropy, and acid–base properties. The application of IGC to analyze the surface properties of carbon nanotubes (CNTs), carbon fibers, and activated carbons is discussed in the following sections.

Table 1.
Surface properties of carbonaceous materials.
3.1. Carbon Nanotubes
Carbon nanotubes (CNTs) with unique and remarkable intrinsic chemical and physical properties such as a large specific surface area, mechanical strength, stiffness, and high electrical conductivity have high potential for use in a wide range of applications in various field such as filtration, heterogeneous catalyst, energy storage, gas sensors, and hybrid nanocomposites.
Their main applications were noncovalent adsorption or the wrapping of various functional molecules and the covalent attachment of chemical groups through reactions onto the π-conjugated polymers of CNTs. CNTs are ideal candidates as advanced reinforcing materials in composite materials, owing to their outstanding mechanical and electrical properties [55]. The investigation of CNTs’ surface properties using analytical techniques are crucial. In nanocomposite applications, the chemical modification of CNTs is an effective method to increase the dispersion uniformity and strong bond to the matrix to enable effective stress transfer. Furthermore, their low concentration of surface groups, heterogeneity, low solubility, high optical absorbance, high surface area, and small size limited many characterization techniques. In this area, IGC is a powerful technique. The surface characterization of CNTs has been investigated by different conventional analytical methods such as scanning electron microscopy (SEM) [56], transmission electronic microscopy (TEM) [57], X-ray photoelectron spectroscopy (XPS) [58], scanning tunneling microscopy [59,60], photoluminescence spectroscopy [61], neutron diffraction [62], infrared spectroscopy [63], Raman spectroscopy [64], electrophoretic zeta-potential measurements [65], and Boehm’s titration [66]. Applying IGC as a powerful method combined with other techniques such as Fourier-transform infrared spectroscopy (FTIR), transmission electron microscopy (TEM), and thermal gravimetric analysis (TGA) can provide useful complementary information on the surface characterization of materials. Researchers have used IGC as a method to measure the surface energy and acid/base properties of the gas diffusion layer of proton exchange membrane fuel cells [67,68] and to identify relative humidity effects on the hydrophobic nature of gas diffusion layer (GDL) [69].
The IGC technique has been applied to investigate the adsorption of different alkanes, aromatics, and chlorohydrocarbons onto three kinds of nonmicroporous carbons, including multi-walled carbon nanotubes (MWCNTs), carbon nanofibers (CNFs), and high surface area graphite (HSAGs) [25]. The enthalpy of adsorption of HSAG is higher than that of CNTs and CNFs; hence, adsorption on CNTs and CNFs is less energetically favorable than adsorption on HGAS. Thus, HSAG had considerably higher adsorption capacity compared to CNTs and CNFs. The surface energy and acid/base properties of MWCNTs and their derivatives using different probe molecules and conditions of near-zero surface coverage of MWCNTs were investigated by Zhang et al. [70] and found that the surface modification of MWCNT is strongly affecting the acid/base characters.
The IGC analysis is mainly considered as one of the standard methods for the surface characterization of CNTs with polymer blends. Gerencser et al. [43] reported that the IGC is an efficient technique to characterize the surface properties of untreated and treated MWCNTs with the olefin maleic–anhydride–ester–amide copolymer (OMAEA) coupling agent. They have investigated the specific and dispersive surface energy ( and ) and acidic and basic component of the surface energy (γs+ and γs-) by using n-hexane, n-heptane, n-octane, n-nonane, chloroform, and toluene as test probe molecules. The IGC experiments were carried out at a column temperature of 353 K. The Dorris–Gray method was used to calculate the , and van Oss–Chaudhury–Good theory with the Della Volpe scale was applied to calculate . As shown in Figure 1a, the dispersive surface energy () of modified MWCNTs decreased considerably.
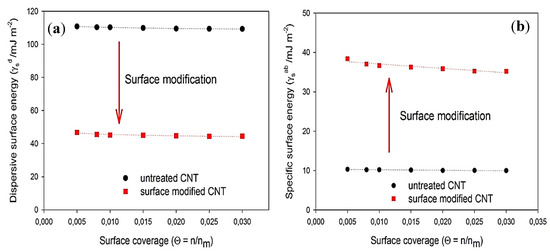
Figure 1.
(a) profiles, and (b) profiles of untreated multi-walled carbon nanotubes (MWCNTs) and modified MWCNTs with olefin maleic–anhydride–ester–amide copolymer (OMAEA) [45].
Debey, Kessom, and London ascribed the strong physical attraction of untreated MWCNTs to their high dispersive surface energy and high agglomeration tendency. The attachment of OMAEA on the surface of MWCNTs caused a reduction in the dispersive surface energy of MWCNTs, indicating that the coupling agents are affecting the dispersive surface energy. The specific surface energy () of modified MWCNTs increased by more than fourfold compared with that of untreated MWCNTs, which confirmed the enhancement in the connection between polar probes and modified MWCNTs (Figure 1b).
As shown in Figure 2a, the dispersive surface energy probability function of the MWCNTs became more spread out by surface modification, indicating a higher degree of energetic surface heterogeneity. The small changes in the surface energies of untreated MWCNTs indicate that its surface is energetically homogeneous. Surface modification led to a greater variation in , suggesting that the surface of the OMAEA-modified MWCNTs is energetically heterogeneous (Figure 2b). The of treated MWCNTs showed a higher value compared to untreated MWCNTs, which was due to increasing the concentration of polar clusters on the surface of MWCNTs [45].
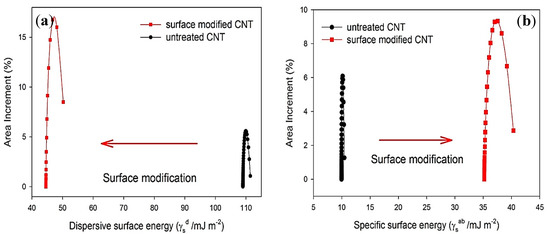
Figure 2.
(a) probability functions, and (b) probability functions of untreated MWCNTs and modified MWCNTs with OMAEA [45].
Menzel et al. [71] investigated the surface properties of the as-received and surface-modified CNTs using IGC (Dorris–Gray method, measurement temperature of 100 C, and probe molecules of C6–C8, ethanol, ethyl acetate, butanone, benzene, dioxane) in terms of specific free energy values, KA and KD numbers, and Henry’s constant. They found that the results obtained using IGC were in good agreement with the available data obtained from conventional methods to analyze the surface.
A potential problem in measuring the thermodynamic properties of carbon nanomaterials is the convolution of the surface chemistry and surface structure effects. The effect of the structural and chemical surface properties of the solid on the adsorption can be investigated by using the probe molecules with different structures but similar cross-sections and chemical functionality. The surface chemistry of the solid can be studied by employing the chemically different probe molecules with similar structures and similar cross-sections. Menzel et al. [28] introduced a method to study the structural and chemical properties of the solids separately to deconvolute and separately quantify the contribution of both surface structure and surface chemistry to the retention behavior of organic vapors. They have used the following equation to harmonize the units of the dispersive component of surface energy () and specific free energy () [20,72,73]:
where a is the molecular cross-section of the adsorbate, NA is the Avogadro constant, and Isp (mJ/m2) is stated as the specific interaction parameter for a polar probe molecule.
The surface properties of different carbon nanomaterial samples, including commercial, annealed, and oxidized MWCNTs, have been studied by Menzel et al. [28]. The samples had different chemical and structural surface properties, but other properties such as the porosity, mean diameter, and curvature were similar. The measurements were conducted using different structural probes of n-hexane (C6), 2-methyl pentane (C5Me), and 2,3-dimethyl butane (C4Me2), and different chemical probes of 2-pentanone and 2-pentanol (Figure 3). The higher value of the specific interaction parameter of 2-pentanol by the oxidized CNTs (shown in Table 2) suggested the large concentration of polar surface groups and noticeable chemical heterogeneity. Similar values of dispersive surface energies of around 94 mJ/m2, which is a typical value for the of graphitic carbon materials [74], show that the potential of the CNTs to interact with probe molecules through dispersive van der Waals forces were retained after modification. The surface chemistry and type of probe molecules affect the ability of CNTs to interact through specific forces [75]. As shown in Table 2, the specific interaction parameter of oxidized CNTs is higher than as-received and annealed CNTs. The higher values of the specific interaction parameter Isp are correlated with the higher micropore volume of the carbonaceous material after treatment. Díaz et al. [20] reported that the Isp of activated carbon is not correlated with the functional groups such as oxygenated groups but rather influenced by their organic and topographical structures.
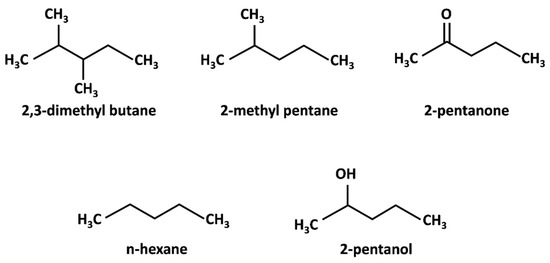
Figure 3.
Structural probes (2,3-dimethyl butane (C4Me2), 2-methyl pentane (C5Me), n-hexane (C6)) and chemical probes (2-pentanone (C5=O), 2-pentanol (C5-OH)).

Table 2.
Net retention time, dispersive component of surface energy, and specific interaction parameter of CNTs (C4Me2: 2,3-dimethyl butane, C5Me: 2-methyl pentane, C6: n-hexane, C5=O: 2-pentanone, C5-OH: 2-pentanol) [28].
The differences in the retention time of three structural probes (C4Me2, C5Me, C6) of different samples of CNT were small. The weakest adsorption (shortest net retention time) was observed for the most branched isomer of C4Me2 probe, while slightly stronger adsorption was seen for C5Me, while the unbranched C6 molecules experienced the strongest retention. The small differences in retention time, tn, between hexane isomers are likely because the unbranched hexane molecules are more flexible and therefore able to adjust their conformation upon adsorption to increase their contact area with the high-energy surface of the CNTs, while the branched molecules are more rigid and less able to adapt upon adsorption. The consistent retention of the three structural probes by all three samples strongly indicates that there are no major differences in the geometric surface structure of the CNT materials.
The difference in the retention time of the chemical probes can be due to the chemical functionality of the solid surface. As a result of the analogous molecular structure of these adsorbates, the differences in the adsorption/desorption behavior of these chemical probes cannot be affected by the minor structural differences, and therefore, they can be directly related. The retention of the two chemical probes differed significantly, indicating specific interactions between the carbonyl and hydroxyl groups of the probes and the polar functional groups on the CNT surface. Among these samples, the annealed CNTs had smaller net retention times, indicating a more homogeneous surface structure which is probably because of the lower concentration of polar surface groups.
3.2. Graphite and Graphene
After graphene discovery, it was demonstrated that graphene can be a promising material for a variety of applications such as electronics to medicine. The potential application of graphene can be broadened by various modes of functionalization, such as the noncovalent binding of molecules and nanoparticles. The investigation of dispersive surface energy and enthalpies of adsorption of polar compounds indicated that the dispersive contribution of the enthalpy of adsorption is more important than a specific one. The nature of high surface energy sites in few-layer graphene and graphite nanopowders as a function of surface coverage was investigated by IGC [38]. Compared with the few-layer graphene, the graphite powder showed considerably more high-energy sites; hence, by increasing the surface coverage in the range between 0.1% and 20%, the adsorption enthalpy of graphite increase more slowly. The adsorption enthalpies measured at the surface coverage lower than 3% corresponded to adsorption to surface steps and edge cavities; although for the higher surface coverage, the adsorption enthalpies were attributed to the flat surface. Another study by Lazar et al. [76] indicated that the combination of the experimental and theoretical quantification of adsorption of organic molecules on the surface of graphene showed that the adsorption enthalpies were controlled mostly by the interaction energy [76]. The theoretical adsorption enthalpies obtained from ab initio molecular dynamics were in good agreement with the experimental results.
Lazar et al. [50] measured the dispersive component of the surface energy of graphite fluoride (CF)n using IGC. They have reported that the van der Waals force, which is weaker than the corresponding forces in graphite, was responsible for holding the individual CF layers together. The comparison of the computational data with experimental results showed good agreement for fluoride graphite with the C/F ratio close to one [50]. The isostatic adsorption enthalpies and entropies of volatile organic compounds to 2D dimensional carbon-based materials, including graphene and fluorographene, as a function of surface coverage, were studied by Otyepková et al. [34]. Applying FC-IGC and ID-IGC to investigate a series of milled graphite in the function of the milling time parameter and oxygen content proved that the IGC is a powerful method to analyze the surface [77]. Increasing the milling time caused a considerable increase in dispersiveness of the surface energy (). The milling of graphite induced the formation of high-energy sites and increased the nano-roughness surface characteristic of the lateral surface of lamellar solids.
The solubility parameters theory has been used to study the solubility and dispersibility. The interaction of nanomaterials, such as graphene, and solvents, occur at their surface. Therefore, for these materials, the Hansen-like solubility parameters based on surface energy seem to be more applicable than Hildebrand parameters based on cohesive energy densities. The surface energy is an important parameter to determine the interaction of nanomaterials and solvents [54]. The surface energy is a combination of dispersive interactions, which are representative of van der Waals forces and polar interactions, which themselves are representative of acid–base interactions, hydrogen bonding, and π–π stacking [78]. Dai et al. [29] studied the surface properties of graphene oxides samples. The surface energies and dispersibility of different types of graphene oxide (GO) have been investigated. They found the relation between dispersion state and polar component (δP) and hydrogen-bonding component (δH) of solvents.
The surface energy and the C/O ratios, which are dependent on the surface groups and degree of the modification, affect the δP and δH. As shown in Figure 4, the is increased by increasing the C/O ratios. The number of oxygen-containing groups of reduced graphene oxide (rGO) is lower than that of GO, which results in a higher value of of rGO. The contact angle measurement results showed that the hydrophilicity of the GO samples is as follows: rGO < EG-rGO < GO < COOH-GO. The considerable decrease in the hydrophilicity of rGO can be attributed to the presence of less oxygen-containing groups on the surface compared with carboxylated GO, which contains several oxygen-containing groups (such as –C–OH, –OH, C=O, and C–O–C). They have reported that the lower amount of polar oxygen-containing groups of the materials resulted in the smaller values of polar and total surface energies. The dispersibility of all GO samples was dependent on the degree of modification, surface groups, and Hansen solubility parameters of solvents.
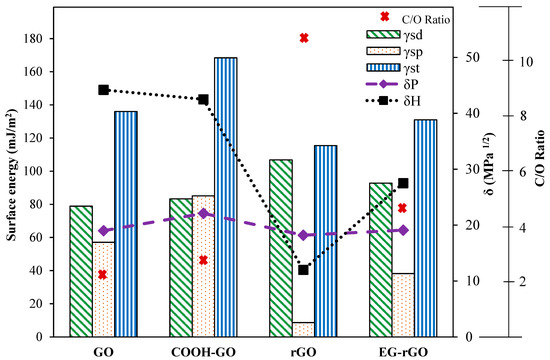
Figure 4.
Correlation of surface free energy and solubility parameter and C/O ratio.
The surface properties of thiourea and melamine-derived graphitic carbon nitrides (T-GCN/M-GCN) have been evaluated using IGC by Sreekanth et al. [24]. The dispersive surface free energies () evaluated using both Schultz and Dorris–Gray methods showed a linear reduction by increasing temperature (Table 3), indicating that the surface of the solid polymeric materials undergoes a structural change, and the probe molecules penetrate the solid polymeric materials. Increasing the temperature resulted in an increase in the molecules distance in the polymer, and consequently, the negative temperature gradient of was observed.

Table 3.
Surface properties of surface-modified graphitic carbon nitrides.
The dispersive energy is inversely proportional to the sixth power of the separation distance between the molecules. Thus, raising the temperature resulted in increased distance between molecules and consequently reduced dispersive energy [24,79]. Gutmann’s Lewis acid–base parameters, KA and KD, of M-GCN and T-GCN were calculated using the surface free energy through various methods. The comparison of the KA, KD, and KD/KA values shown in Table 3 indicated that the surface of both samples has more basic sites than acidic, which could make a strong interaction between the basic sites and acidic media.
3.3. Activated Carbon and Carbon Fibers
Activated carbon is extensively used in different industries. IGC was used to investigate the surface properties such as surface energy and surface area of different activated carbons to investigate the effect of various treatments on their characteristics. Examples include changes in the pore structure as a result of heat treatment, the development of porosity in carbons, changes in surface structure and surface chemistry as a result of oxidation, changes in surface heterogeneity due to chemical modifications, and the suitability of carbons for removing certain pollutants [13].
IGC was used to study activated carbons in various terms such as surface chemistry, surface heterogeneity, surface area, and pore structure changes. Capillary column, flame ionization detector (FID), and thermal conductivity detector (TCD) were used in IGC to have a fast and sensitive measurement and separate the probe’s component before entering the IGC column. Thus, the modified IGC is an appropriate and fast method compared to the conventional IGC method in the characterization of porous materials [4]. Thielmann and Pearse [80] used finite concentration IGC (IGC-FC) to determine the surface heterogeneity of different types of graphite. They have reported that IGC is a quick and accurate technique to determine the adsorption of probes at the surface of graphite samples and provides additional information on different adsorption mechanisms and polar sorption sites in order to have a better understanding of the interaction process in blends quality control.
Pal et al. [23] investigated the surface energy and acid–base properties of surface-treated AC with KOH and H2 using IGC. Compared with the other samples, H2-treated AC showed the highest surface energy due to the higher basicity and lower oxygen content after H2 treatment, which was confirmed by CHN and XPS analysis. The treatment of AC using H2 and KOH resulted in a decrease in surface energy. It is observed that the dispersive surface energy dominates for all AC samples. The Gutmann base constant (KD) of all samples was higher than the Gutmann acid constant (KA), which was attributed to the high concentration of basic functional groups on their surfaces [23].
Huber et al. [80] prepared the monolithic, nitrogen-doped carbon adsorbent from resorcinol–urea–formaldehyde resins. The synthesized material was physically activated with CO2. The physicochemical characteristics and water sorption behavior of the materials at various activation times were investigated. The results revealed that the value of the energy of adsorption and surface energy is the highest for the non-activated carbon and the lowest for the carbon activated in CO2. Singh et al. [39] observed the maximum value for the free energy of adsorption, and the surface energy for the sample occurs when the sample was activated in CO2 for the shortest period. Longer activation times lead to a slight decrease in the free energy of adsorption, which may be due to the pore widening during activation. These observations are in agreement with the results of the study by Huber et al. [81].
The surface characteristics of granular activated carbon (GAC), such as porous structure, surface chemistry, and free energy distribution, are affecting its adsorption behaviors [21]. The chemical heterogeneity and free energy distribution of GAC, affected by functional groups on the surface of AGC, are changing the adsorption of organic and inorganic compounds [21,82,83]. The acid properties of GAC are influenced by carboxylic, phenolic (hydroxyl), carbonyl, lactone, and carboxylic acid [84], and the basic features are affected by chromen and pyron [85,86]. The presence of other functional groups may be predicted because the surface chemical structures of GAC were not clarified entirely (Figure 5).
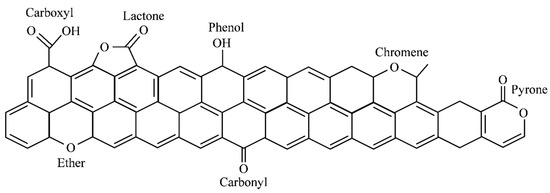
Figure 5.
Surface functional group on carbonaceous materials.
Contaminated carbon fiber (CF) may affect their end-use in reinforced composite materials. Li et al. [43] investigated the surfaces of CFs, which were stored in polyolefin zip-lock bags for possible contamination at different storage times. The and profiles of the CFs at different storage times are shown in Figure 6. In comparison with the zip-lock bag stored fibers, the CFs from the spool with higher dispersive and specific surface energy are energetically more active and more heterogeneous and decreased by increasing the storage time.
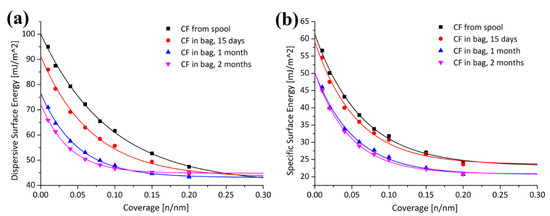
Figure 6.
Time sequences depicting the change in (a) and (b) values of carbon fibers (CFs) [43].
Jäger et al. [41] evaluated the , , and , as well as the specific free energy of desorption () of unsized and sized carbon fiber composite (CFs) using IGC, and found that the changes in the surface energy of CFs affected the interfacial adhesion and wettability of CFs. Kafi et al. [42] investigated the physicochemical properties of the CFs and found that higher oxygen content and high surface polarity is associated with their surface chemical homogeneities.
Huson et al. [40] measured the dispersive surface energy of different carbon fibers (CFs) using polar and non-polar probes at 70 and 120 °C. The higher temperature of 120 °C was used for the oxidized sample due to its higher total surface energy. Both the unsized fibers exhibit high maximum values in excess of 90 mJ/m2, which is typical of graphitic carbon materials. Oxidation results in an increase in polar groups on the surface of the fiber and a slight decrease in . The energetic heterogeneity of the unoxidized fiber is solely due to a range of dispersive energies, whereas the oxidized fiber is heterogeneous in both dispersive and acid–base surface energies (Figure 7). Sized fibers exhibited an increased specific and total surface energy leading to increased polarity. The overall polarity of the carbon fibers is reported as follows: unoxidized < oxidized < sized. This increased polarity in the sized fiber is consistent with the fact that sizing is known to improve the wettability of carbon fibers due to the polar species in the epoxy polymers.
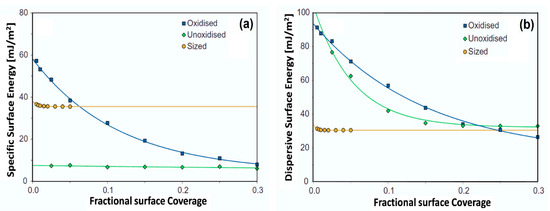
Figure 7.
(a) Dispersive surface energy and (b) specific surface energy for the oxidized, unoxidized, and sized carbon fiber [40].
Table 4 shows the surface energy of different carbonaceous materials with surface modification. The surface modification resulted in changes in surface energy heterogeneity [45]. Pal et al. [23] investigated surface unmodified and modified Maxsorb III and found that the dispersive surface energy for carbon samples is very high, which is above 200 mJ/m2. Higher surface energy values are obtained at higher surface coverage. At first, at very low surface coverage, the higher energy sites were occupied by probe molecules, and then at higher surface coverage, the lower energy sites were occupied. Higher values of H2-Maxsorb III are ascribed to the presence of oxygen content and functional groups on its surface, which is lower than that of untreated Maxsorb III. The same trends were observed for . Luo et al. [27] reported that the amino-functionalization of the MWCNTs surface resulted in reduced values. The dispersive component of the surface energy is related to the surface density of the atoms, polarizability, and ionization energy of MWCNTs. The high of MWCNTs (122.95 mJ/m2) indicates its high agglomeration tendency. After modification, the surface polar groups are replaced by amino-organics with lower polarity. Thus, amino-organics grafted MWCNTs had lower dispersive surface energy of 18.65 and 25.69 mJ/m2 for different amine-modified MWCNTs, respectively.

Table 4.
Surface energy of different carbonaceous materials.
The specific component of surface energy is correlated with the functional groups and sites of polar probes; hence, some amendment with the surface wettability is expected. Niu et al. [19] used IGC to study the surface energy and hydrophilicity of different samples of coal and introduced the hydrophilicity index. The hydrophilicity index was calculated using:
The surface energies and the hydrophilicity index of the coal samples are shown in Table 5 and Figure 8. The flotation of coal samples increased in the following order: SBL > CJT > AY > SHM > JJ, while the hydrophilicity index decreased in the same order. The JJ coal with the highest flotation concentrate yield owns the lowest hydrophilicity index. They also reported that the work of adhesion of samples had a similar trend with the hydrophilicity index that can indicate the wettability of the samples. There is a good correlation between the hydrophilicity index, which is calculated from the surface energy of the coals and their flotation yield, and the introduced parameter can be used as a promoting factor to predict the flotation recovery of fine coal in industry.

Table 5.
The results of , , , and hydrophilicity index of the coal samples [19].
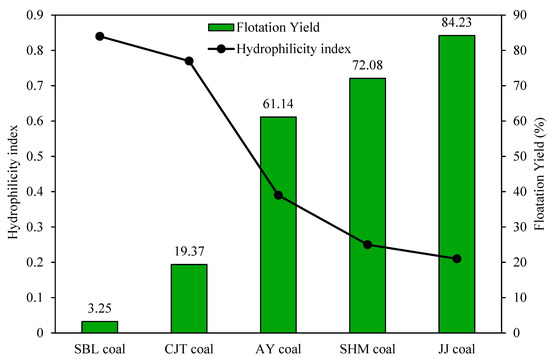
Figure 8.
Flotation yield and hydrophilicity index of coal samples.
Darmstadt et al. [87] investigated the surface properties of commercial carbon blacks and carbon blacks obtained by vacuum pyrolysis of different types of used rubbers. They found a correlation between the dispersive components of the surface energy and the specific interaction of carbon blacks. The specific interaction for the different probes changed similarly, and for all samples, the same trend was observed for the free energies of adsorption. Strzemiecka et al. [37] characterized the carbon black and correlated the surface chemistry using IGC, TGA, and XPS. The results indicated that the carbon black samples with lower specific surface areas (Corax N774 and Corax N326) had lower KA/KD values that reveal the basic character mostly due to the C–O and C=O groups on their surface. In contrast, Corax N220, with the highest specific surface area, had an acidic character with a high value of KA/KD, owing to its high –OH content (Figure 9). They have also reported that the and of all samples, except Corax N326, with the highest content of oxygen and C–O groups, increased by increasing their specific surface area [37].
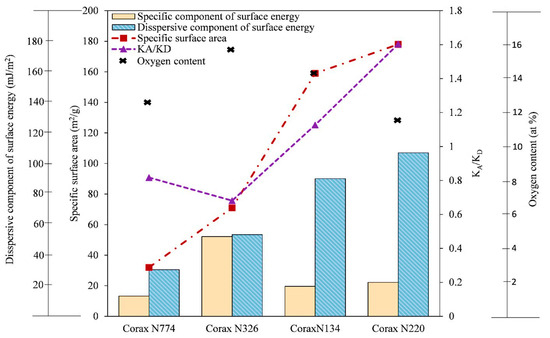
Figure 9.
Chemical statistical analysis of the surface chemistry of carbon black samples.
4. Conclusions
Inverse gas chromatography (IGC), as a sensitive technique, is undoubtedly helpful to many industries. In spite of numerous research and publications in the last decades, the IGC technique, which is attractive to scientists in various fields, is still developing. The results of research experiments on a wide range of carbonaceous materials in different shapes and morphologies have evidenced that IGC is successfully applied to characterizing different surface properties. Its versatility, as well as high accuracy and simplicity, can establish its position as an indispensable part of analytical laboratories. As reviewed in this work, IGC as a versatile, highly accurate and simple technique is a complementary tool to provide additional information on the solid-state properties, in particular, the surface properties of materials to aid the understanding of material changes under various conditions, as well as their behavior during processing.
Author Contributions
Conceptualization, F.G.; Investigation, F.G., M.T.; and Z.G.; Writing—Original Draft Preparation, F.G., M.T., Z.G., S.M., and M.V.; Writing—Review & Editing, F.G.; Funding Acquisition, F.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Ministry of Education, Youth and Sports (Czech Republic)] grant number [LO1402].
Acknowledgments
The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, cofunded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI programme and, in the follow-up sustainability stage, supported through CENTEM PLUS (LO1402) by financial means from the Ministry of Education, Youth and Sports under the ”National Sustainability Programme I.”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Davis, T.C.; Petersen, J.C. Adaptation of inverse gas-liquid chromatography to asphalt oxidation studies. Anal. Chem. 1966, 38, 1938–1940. [Google Scholar] [CrossRef]
- Voelkel, A. Inverse gas chromatography in characterization of surface. Chemom. Intell. Lab. 2004, 72, 205–207. [Google Scholar] [CrossRef]
- Balard, H. Notes on Inverse Gas Chromatography. 2015. Available online: https://www.researchgate.net/publication/279955104_Notes_on_Inverse_Gas_Chromatography (accessed on 1 August 2020). [CrossRef]
- Mohammadi-Jam, S.; Waters, K. Inverse gas chromatography applications: A review. Adv. Colloid Interface Sci. 2014, 212, 21–44. [Google Scholar] [CrossRef]
- Schultz, J.A.; Lavielle, L.; Martin, C. The role of the interface in carbon fibre-epoxy composites. J. Adhes. 1987, 23, 45–60. [Google Scholar] [CrossRef]
- Dorris, G.M.; Gray, D.G. Adsorption of n-alkanes at zero surface coverage on cellulose paper and wood fibers. J. Colloid. Interface Sci. 1980, 77, 353–362. [Google Scholar] [CrossRef]
- Schultz, J.; Lavielle, L. Interfacial Properties of Carbon Fiber—Epoxy Matrix Composites; ACS Publications: Washington, DC, USA, 1989. [Google Scholar]
- Voelkel, A. Physicochemical measurements (inverse gas chromatography). In Gas Chromatography; Elsevier: Amsterdam, The Netherlands, 2012; pp. 477–494. [Google Scholar]
- Ho, R.; Heng, J.Y. A review of inverse gas chromatography and its development as a tool to characterize anisotropic surface properties of pharmaceutical solids. KONA Powder Part J. 2013, 30, 164–180. [Google Scholar] [CrossRef]
- Lloyd, D.R.; Ward, T.C.; Schreiber, H.P. Inverse Gas Chromatography; American Chemical Society: Washington, DC, USA, 1989. [Google Scholar]
- Grobler, A.; Balizs, G. Computer program for a statistical calculation of retention indices. J. Chromatogr. Sci. 1974, 12, 57–58. [Google Scholar] [CrossRef]
- Milczewska, K.; Voelkel, A. Inverse Gas Chromatography in Characterization of Composites Interaction. Advanced Gas Chromatography-Progress in Agricultural, Biomedical and Industrial Applications; InTech: Rijeka, Croatia, 2012; pp. 421–436. [Google Scholar]
- Bandosz, T. Inverse Gas Chromatography to Determine the Structural and Chemical Features of Activated Carbon Surfaces. In Encyclopedia of Surface and Colloid Science, 3rd ed.; Taylor & Francis, CRC press: Boca Raton, FL, USA, 2015; pp. 3365–3378. [Google Scholar]
- Shi, B.; Wang, Y.; Jia, L. Comparison of Dorris–Gray and Schultz methods for the calculation of surface dispersive free energy by inverse gas chromatography. J. Chromatogr. A 2011, 1218, 860–862. [Google Scholar] [CrossRef]
- Ylä-MäIhäNiemi, P.P.; Heng, J.Y.; Thielmann, F.; Williams, D.R. Inverse gas chromatographic method for measuring the dispersive surface energy distribution for particulates. Langmuir 2008, 24, 9551–9557. [Google Scholar] [CrossRef] [PubMed]
- Kołodziejek, J.; Voelkel, A.; Heberger, K. Characterization of hybrid materials by means of inverse gas chromatography and chemometrics. J. Pharm. Sci. 2013, 102, 1524–1531. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Papirer, E.; Perrin, J.M.; Siffert, B.; Philipponneau, G. Surface characteristics of aluminas in relation with polymer adsorption. J. Colloid Interface Sci. 1991, 144, 263–270. [Google Scholar] [CrossRef]
- Dimopoulou, M.; Ritzoulis, C.; Panayiotou, C. Surface characterization of okra hydrocolloid extract by inverse gas chromatography (IGC). Colloids Surf. A Physicochem. Eng. Asp. 2015, 475, 37–43. [Google Scholar] [CrossRef]
- Niu, C.; Xia, W.; Peng, Y. Analysis of coal wettability by inverse gas chromatography and its guidance for coal flotation. Fuel 2018, 228, 290–296. [Google Scholar] [CrossRef]
- Díaz, E.; Ordóñez, S.; Vega, A.; Coca, J. Comparison of adsorption properties of a chemically activated and a steam-activated carbon, using inverse gas chromatography. Microporous Mesoporous Mater. 2005, 82, 173–181. [Google Scholar] [CrossRef]
- Fulazzaky, M.A. Study of the dispersion and specific interactions affected by chemical functions of the granular activated carbons. Environ. Nanotechnol. Monit. Manag. 2019, 12, 100230. [Google Scholar] [CrossRef]
- Wang, W.; Hua, Q.; Sha, Y.; Wu, D.; Zheng, S.; Liu, B. Surface properties of solid materials measured by modified inverse gas chromatography. Talanta 2013, 112, 69–72. [Google Scholar] [CrossRef]
- Pal, A.; Kondor, A.; Mitra, S.; Thu, K.; Harish, S.; Saha, B.B. On surface energy and acid–base properties of highly porous parent and surface treated activated carbons using inverse gas chromatography. J. Ind. Eng. Chem. 2019, 69, 432–443. [Google Scholar] [CrossRef]
- Sreekanth, T.; Basivi, P.K.; Nagajyothi, P.; Dillip, G.; Shim, J.; Ko, T.; Yoo, K. Determination of surface properties and Gutmann’s Lewis acidity–basicity parameters of thiourea and melamine polymerized graphitic carbon nitride sheets by inverse gas chromatography. J. Chromatogr. A 2018, 1580, 134–141. [Google Scholar] [CrossRef]
- Díaz, E.; Ordóñez, S.; Vega, A. Adsorption of volatile organic compounds onto carbon nanotubes, carbon nanofibers, and high-surface-area graphites. J. Colloid Interface Sci. 2007, 305, 7–16. [Google Scholar] [CrossRef]
- Keru, G.; Ndungu, P.G.; Nyamori, V.O. Effect of boron concentration on physicochemical properties of boron-doped carbon nanotubes. Mater. Chem. Phys. 2015, 153, 323–332. [Google Scholar] [CrossRef]
- Luo, Y.; Zhao, Y.; Cai, J.; Duan, Y.; Du, S. Effect of amino-functionalization on the interfacial adhesion of multi-walled carbon nanotubes/epoxy nanocomposites. Mater. Des. 2012, 33, 405–412. [Google Scholar] [CrossRef]
- Menzel, R.; Bismarck, A.; Shaffer, M.S. Deconvolution of the structural and chemical surface properties of carbon nanotubes by inverse gas chromatography. Carbon 2012, 50, 3416–3421. [Google Scholar] [CrossRef]
- Dai, J.; Wang, G.; Ma, L.; Wu, C. Study on the surface energies and dispersibility of graphene oxide and its derivatives. J. Mater. Sci. 2015, 50, 3895–3907. [Google Scholar] [CrossRef]
- Dai, J.; Wang, G.J.; Wu, C.K. Investigation of the surface properties of graphene oxide and graphene by inverse gas chromatography. Chromatographia 2014, 77, 299–307. [Google Scholar] [CrossRef]
- Grajek, H. The optimisation of chromatographic conditions for the determination of acceptor-donor properties of graphene oxide and reduced graphene oxide. Acta Innov. 2018, 26, 5–20. [Google Scholar] [CrossRef]
- Yuan, X.; Zhu, B.; Cai, X.; Zhao, S.; Qiao, K.; Zhang, M. Effects of particle size and distribution of the sizing agent on carbon fiber/epoxy composites interfacial adhesion. Polym. Compos. 2018, 39, E2036–E2045. [Google Scholar] [CrossRef]
- Lim, H.J.; Lee, K.; Cho, Y.S.; Kim, Y.S.; Kim, T.; Park, C.R. Experimental consideration of the Hansen solubility parameters of as-produced multi-walled carbon nanotubes by inverse gas chromatography. Phys. Chem. Chem. Phys. 2014, 16, 17466–17472. [Google Scholar] [CrossRef]
- Otyepková, E.; Lazar, P.; Čépe, K.; Tomanec, O.; Otyepka, M. Organic adsorbates have higher affinities to fluorographene than to graphene. Appl. Mater. Today 2016, 5, 142–149. [Google Scholar] [CrossRef]
- Karlický, F.E.; Otyepkova, E.; Lo, R.; Pitoňák, M.; Jurečka, P.; Pykal, M.; Otyepka, M. Adsorption of organic molecules to van der Waals materials: Comparison of fluorographene and fluorographite with graphene and graphite. J. Chem. Theory Comput. 2017, 13, 1328–1340. [Google Scholar] [CrossRef]
- Karlický, F.E.; Otyepková, E.; Banáš, P.; Lazar, P.; Kocman, M.S.; Otyepka, M. Interplay between ethanol adsorption to high-energy sites and clustering on graphene and graphite alters the measured isosteric adsorption enthalpies. J. Phys. Chem. C 2015, 119, 20535–20543. [Google Scholar] [CrossRef]
- Strzemiecka, B.; Voelkel, A.; Donate-Robles, J.; Martín-Martínez, J.M. Assessment of the surface chemistry of carbon blacks by TGA-MS, XPS and inverse gas chromatography using statistical chemometric analysis. Appl. Surf. Sci. 2014, 316, 315–323. [Google Scholar] [CrossRef]
- Lazar, P.; Otyepkova, E.; Banáš, P.; Fargašová, A.; Šafářová, K.; Lapčík, L.; Otyepka, M. The nature of high surface energy sites in graphene and graphite. Carbon 2014, 73, 448–453. [Google Scholar] [CrossRef]
- Singh, G.; Lal, D.; Tripathi, V. Study of microporosity of active carbon spheres using inverse gas chromatographic and static adsorption techniques. J. Chromatogr. A 2004, 1036, 189–195. [Google Scholar] [CrossRef] [PubMed]
- Huson, M.G.; Church, J.S.; Kafi, A.A.; Woodhead, A.L.; Khoo, J.; Kiran, M.; Fox, B.L. Heterogeneity of carbon fibre. Carbon 2014, 68, 240–249. [Google Scholar] [CrossRef]
- Jäger, M.; Zabihi, O.; Ahmadi, M.; Li, Q.; Depalmeanar, A.; Naebe, M. Nano-enhanced interface in carbon fibre polymer composite using halloysite nanotubes. Compos. Part A Appl. Sci. Manuf. 2018, 109, 115–123. [Google Scholar] [CrossRef]
- Kafi, A.; Li, Q.; Chaffraix, T.; Khoo, J.; Gengenbach, T.; Magniez, K.J.C. Surface treatment of carbon fibres for interfacial property enhancement in composites via surface deposition of water soluble POSS nanowhiskers. Polymer 2018, 137, 97–106. [Google Scholar] [CrossRef]
- Li, Q.; Woodhead, A.L.; Church, J.S.; Naebe, M. On the detection of carbon fibre storage contamination and its effect on the fibre–matrix interface. Sci. Rep. 2018, 8, 16446. [Google Scholar] [CrossRef]
- Zabihi, O.; Ahmadi, M.; Li, Q.; Shafei, S.; Huson, M.G.; Naebe, M. Carbon fibre surface modification using functionalized nanoclay: A hierarchical interphase for fibre-reinforced polymer composites. Compos. Sci. Technol. 2017, 148, 49–58. [Google Scholar] [CrossRef]
- Gerencsér, F.; Rieder, N.; Varga, C.; Hancsók, J.; Dallos, A. Surface Energy Heterogeneity Profiles of Carbon Nanotubes with a Copolymer-Modified Surface Using Surface Energy Mapping by Inverse Gas Chromatography. Hung. J. Ind. Chem. 2017, 45, 61–66. [Google Scholar] [CrossRef]
- Mezgebe, M.; Jiang, L.H.; Shen, Q.; Du, C.; Yu, H.R. Studies and comparison of the liquid adsorption behavior and surface properties of single-and multiwall carbon nanotubes by capillary rise method. Colloids Surf. A Physicochem. Eng. Asp. 2012, 415, 86–90. [Google Scholar] [CrossRef]
- Ombaka, L.M.; Ndungu, P.G.; Nyamori, V.O. Tuning the nitrogen content and surface properties of nitrogen-doped carbon nanotubes synthesized using a nitrogen-containing ferrocenyl derivative and ethylbenzoate. J. Mater. Sci. 2015, 50, 1187–1200. [Google Scholar] [CrossRef]
- Ferguson, A.; Harvey, A.; Godwin, I.J.; Bergin, S.D.; Coleman, J.N. The dependence of the measured surface energy of graphene on nanosheet size. 2D Mater. 2016, 4, 015040. [Google Scholar] [CrossRef]
- Ferguson, A.; Caffrey, I.T.; Backes, C.; Coleman, J.N.; Bergin, S.D. Differentiating defect and basal plane contributions to the surface energy of graphite using inverse gas chromatography. Chem. Mater. 2016, 28, 6355–6366. [Google Scholar] [CrossRef]
- Lazar, P.; Otyepková, E.; Karlický, F.; Čépe, K.; Otyepka, M. The surface and structural properties of graphite fluoride. Carbon 2015, 94, 804–809. [Google Scholar] [CrossRef]
- Speltini, A.; Merli, D.; Quartarone, E.; Profumo, A. Separation of alkanes and aromatic compounds by packed column gas chromatography using functionalized multi-walled carbon nanotubes as stationary phases. J. Chromatogr. A 2010, 1217, 2918–2924. [Google Scholar] [CrossRef]
- Fakhrhoseini, S.M.; Li, Q.; Unnikrishnan, V.; Naebe, M. Nano-magnetite decorated carbon fibre for enhanced interfacial shear strength. Carbon 2019, 148, 361–369. [Google Scholar] [CrossRef]
- Kim, Y.S.; Oh, J.Y.; Kim, J.H.; Shin, M.H.; Jeong, Y.C.; Sung, S.J.; Park, C.R. Crucial role of oxidation debris of carbon nanotubes in subsequent end-use applications of carbon nanotubes. ACS Appl. Mater. 2017, 9, 17552–17564. [Google Scholar] [CrossRef]
- Bergin, S.D.; Sun, Z.; Rickard, D.; Streich, P.V.; Hamilton, J.P.; Coleman, J.N. Multicomponent solubility parameters for single-walled carbon nanotube—Solvent mixtures. ACS Nano 2009, 3, 2340–2350. [Google Scholar] [CrossRef] [PubMed]
- Basivi, P.K.; Sreekanth, T.; Sivalingam, R.; Thota, C.; Pasupuleti, V.R. Surface characterization and London dispersive surface free energy of functionalized single-walled carbon nanotubes with a blend of polytetrafluoroethylene by inverse gas chromatography. Surf. Interface Anal. 2019, 51, 516–524. [Google Scholar] [CrossRef]
- Lehman, J.H.; Terrones, M.; Mansfield, E.; Hurst, K.E.; Meunier, V. Evaluating the characteristics of multiwall carbon nanotubes. Carbon 2011, 49, 2581–2602. [Google Scholar] [CrossRef]
- Ismagilov, Z.R.; Shalagina, A.E.; Podyacheva, O.Y.; Ischenko, A.V.; Kibis, L.S.; Boronin, A.I.; Anikeeva, O.B. Structure and electrical conductivity of nitrogen-doped carbon nanofibers. Carbon 2009, 47, 1922–1929. [Google Scholar] [CrossRef]
- Wepasnick, K.A.; Smith, B.A.; Bitter, J.L.; Fairbrother, D.H. Chemical and structural characterization of carbon nanotube surfaces. Anal. Bioanal. Chem. 2010, 396, 1003–1014. [Google Scholar] [CrossRef] [PubMed]
- Yao, Z.; Ge, L.; Yang, W.; Xia, M.; Ji, X.; Jin, M.; Dienstmaier, J.R. Finite dilution inverse gas chromatography as a versatile tool to determine the surface properties of biofillers for plastic composite applications. Anal. Chem. 2015, 87, 6724–6729. [Google Scholar] [CrossRef] [PubMed]
- Meunier, V.; Lambin, P. Scanning tunneling microscopy and spectroscopy of topological defects in carbon nanotubes. Carbon 2000, 38, 1729–1733. [Google Scholar] [CrossRef]
- Maciel, I.O.; Anderson, N.; Pimenta, M.A.; Hartschuh, A.; Qian, H.; Terrones, M.; Novotny, L. Electron and phonon renormalization near charged defects in carbon nanotubes. Nat. Mater. 2008, 7, 878. [Google Scholar] [CrossRef]
- Bauer, B.J.; Hobbie, E.K.; Becker, M.L. Small-angle neutron scattering from labeled single-wall carbon nanotubes. Macromolecules 2006, 39, 2637–2642. [Google Scholar] [CrossRef]
- Branca, C.; Frusteri, F.; Magazu, V.; Mangione, A. Characterization of carbon nanotubes by TEM and infrared spectroscopy. J. Phys. Chem. B 2004, 108, 3469–3473. [Google Scholar] [CrossRef]
- Dresselhaus, M.; Jorio, A.; Saito, R. Characterizing graphene, graphite, and carbon nanotubes by Raman spectroscopy. Annu. Rev. Condens. Matter Phys. 2010, 1, 89–108. [Google Scholar] [CrossRef]
- Hu, H.; Yu, A.; Kim, E.; Zhao, B.; Itkis, M.E.; Bekyarova, E.; Haddon, R.C. Influence of the zeta potential on the dispersability and purification of single-walled carbon nanotubes. J. Phys. Chem. B 2005, 109, 11520–11524. [Google Scholar] [CrossRef]
- Scheibe, B.; Borowiak-Palen, E.; Kalenczuk, R.J. Oxidation and reduction of multiwalled carbon nanotubes—Preparation and characterization. Mater. Charact. 2010, 61, 185–191. [Google Scholar] [CrossRef]
- Kannan, A.M.; Munukutla, L. Carbon nano-chain and carbon nano-fibers based gas diffusion layers for proton exchange membrane fuel cells. J. Power Sources 2007, 167, 330–335. [Google Scholar] [CrossRef]
- Seidenberger, K.; Wilhelm, F.; Haußmann, J.; Markötter, H.; Manke, I.; Scholta, J. Grand canonical Monte Carlo study on water agglomerations within a polymer electrolyte membrane fuel cell gas diffusion layer. J. Power Sources 2013, 239, 628–641. [Google Scholar] [CrossRef]
- Borup, R.; Davey, J.; Garzon, F.; Wood, D.; Welch, P.; More, K. PEM fuel cell durability with transportation transient operation. ECS Trans. 2006, 3, 879–886. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, D.; Xu, P.; Wang, C.; Du, Q. Characterizing the surface properties of carbon nanotubes by inverse gas chromatography. J. Mater. Sci. 2007, 42, 7069–7075. [Google Scholar] [CrossRef]
- Menzel, R.; Lee, A.; Bismarck, A.; Shaffer, M.S. Inverse gas chromatography of as-received and modified carbon nanotubes. Langmuir 2009, 25, 8340–8348. [Google Scholar] [CrossRef]
- Shih, Y.H.; Li, M.S. Adsorption of selected volatile organic vapors on multiwall carbon nanotubes. J. Hazard. Mater. 2008, 154, 21–28. [Google Scholar] [CrossRef]
- Zhou, J.; Yu, T.; Wu, S.; Xie, Z.; Yang, Y. Inverse gas chromatography investigation of rubber reinforcement by modified pyrolytic carbon black from scrap tires. Ind. Eng. Chem. Res. 2010, 49, 1691–1696. [Google Scholar] [CrossRef]
- Papirer, E.; Brendle, E.; Ozil, F.; Balard, H. Comparison of the surface properties of graphite, carbon black and fullerene samples, measured by inverse gas chromatography. Carbon 1999, 37, 1265–1274. [Google Scholar] [CrossRef]
- Brandao, S.; Andrada, D.; Mesquita, A.; Santos, A.; Gorgulho, H.; Paniago, R.; Furtado, C. The influence of oxygen-containing functional groups on the dispersion of single-walled carbon nanotubes in amide solvents. J. Phys. Condens. Matter 2010, 22, 334222. [Google Scholar] [CrossRef]
- Lazar, P.; Karlicky, F.; Jurečka, P.; Kocman, M.S.; Otyepková, E.; Šafářová, K.R.; Otyepka, M. Adsorption of small organic molecules on graphene. J. Am. Chem. Soc. 2013, 135, 6372–6377. [Google Scholar] [CrossRef]
- Balard, H.; Maafa, D.; Santini, A.; Donnet, J. Study by inverse gas chromatography of the surface properties of milled graphites. J. Chromatogr. A 2008, 1198, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Das, S.C.; Larson, I.; Morton, D.A.; Stewart, P.J. Determination of the polar and total surface energy distributions of particulates by inverse gas chromatography. Langmuir 2011, 27, 521–523. [Google Scholar] [CrossRef] [PubMed]
- Kondor, A.; Quellet, C.; Dallos, A. Surface characterization of standard cotton fibres and determination of adsorption isotherms of fragrances by IGC. Surf. Interface Anal. 2015, 47, 1040–1050. [Google Scholar] [CrossRef]
- Thielmann, F.; Pearse, D. Determination of surface heterogeneity profiles on graphite by finite concentration inverse gas chromatography. J. Chromatogr. A 2002, 969, 323–327. [Google Scholar] [CrossRef]
- Huber, L.; Hauser, S.B.; Brendlé, E.; Ruch, P.; Ammann, J.; Hauert, R.; Yoon, S. The effect of activation time on water sorption behavior of nitrogen-doped, physically activated, monolithic carbon for adsorption cooling. Microporous Mesoporous Mater. 2019, 276, 239–250. [Google Scholar] [CrossRef]
- Madhu, R.; Veeramani, V.; Chen, S.M. Heteroatom-enriched and renewable banana-stem-derived porous carbon for the electrochemical determination of nitrite in various water samples. Sci. Rep. 2014, 4, 4679. [Google Scholar] [CrossRef]
- Ania, C.O.; Bandosz, T.J. Importance of structural and chemical heterogeneity of activated carbon surfaces for adsorption of dibenzothiophene. Langmuir 2005, 21, 7752–7759. [Google Scholar] [CrossRef]
- Sajjadi, B.; Chen, W.Y.; Egiebor, N.O. A comprehensive review on physical activation of biochar for energy and environmental applications. Rev. Chem. Eng. 2019, 35, 735–776. [Google Scholar] [CrossRef]
- Kern, A.M.; Zierath, B.; Fey, T.; Etzold, B.J. Adsorption of Nickel Ions on Oxygen-Functionalized Carbons. Chem. Eng. Technol. 2016, 39, 715–722. [Google Scholar] [CrossRef]
- Shafeeyan, M.S.; Daud, W.; Ma, W.; Houshmand, A.; Shamiri, A. A review on surface modification of activated carbon for carbon dioxide adsorption. J. Anal. Appl. Pyrolysis 2010, 89, 143–151. [Google Scholar] [CrossRef]
- Darmstadt, H.; Roy, C.; Kaliaguine, S.; Cormier, H. Surface energy of commercial and pyrolytic carbon blacks by inverse gas chromatography. Rubber Chem. Technol. 1997, 70, 759–768. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).