Some Questionable Approaches in Interfacial Electrochemistry—The Charged State of Adsorbed Species and Their Involvement in Redox Processes

Abstract

On the basis of a survey on the relevant literature it can be stated that some views and approaches concerning the charged state of adsorbed species and the charge transfer processes occurring with them are far from being unambiguous even in some respect they contradict fundamental physical and physicochemical principles. The meaning of the electrosorption valency, the misleading formulation of the Gibbs adsorption equation, and the interpretation of redox processes occurring with adsorbed species, is discussed in detail. It has been concluded that although the electrosorption valency of an adsorbed species as usually defined is an extra-thermodynamic and self-contradictory concept, experimental determined formal partial charge numbers can be a useful tool for scientists investigating adsorption phenomena, since the observed deviation between its value and the charge number of the same species in the solution phase unequivocally indicates a non-simple mechanism of the adsorption process, which should be taken into account in theoretical interpretation of the experimental data. It has been emphasized that the evaluation of voltammetric curves obtained in the presence of adsorbed redox partners requires a cautious analysis of the accompanying chemical transformations. In the framework of a critical analysis it is demonstrated that probably one of the most important sources of the misinterpretations and misunderstandings is the inadequate approach to the concept of electrode charge. The possibility of a general and straightforward presentation of the Gibbs adsorption equation has also been discussed.

1. Introduction

The interfacial energetics of electrodes is an important aspect in understanding the relationships between surface morphology and electrochemical activity. As a matter of fact, most electrochemical systems involving solids are capillary systems, because any interaction between the bulk solid and the remainder of the system takes place via the interfacial region. Thermodynamic properties of the surface region are directly related to the electrochemical processes taking place there. Therefore, it is not surprising, that over the last century several attempts have been made to derive thermodynamic equations which are valid for electrified interfaces. It should be noted here, that in electrochemistry, there are currently two main usages for the term “electrode”, namely either a heterogeneous electrochemical system in which an electronic conductor phase is in intimate contact with an ionic conductor phase, simply the electron conductor connected to the external leads [1,2,3]. On the other hand, the following relatively simple definition may also be relevant: “An electrode is a heterogeneous electrochemical system including one interface, or interfaces which are connected in parallel, at which the type of electrical conduction changes from electronic to ionic or to mixed, or vice versa” [3].

Interfacial thermodynamics is addressing topics including adsorption, interfacial energies, interfacial tension, and superficial charge, and about relations between them, as such it can be defined as the study of the application of thermodynamics to interfacial phenomena. “Adsorption” of one or more “components” or “constituents”, at one or more of the phase boundaries of a multicomponent, multiphase system takes place if the concentrations in the interfacial layers are different from those in the adjoining bulk phases. The primary goals of all thermodynamic treatments are to describe systems containing interfaces in terms of experimentally observable quantities and to derive relationships which relate the thermodynamic properties of a system described by a complete set of physicochemical parameters to those in different circumstances. It is quite evident that an interface does not exist in isolation. It is rather an interfacial region between two homogeneous phases whose thickness cannot be determined experimentally, and valid thermodynamic conclusions can only be drawn by considering the whole system, i.e., the interface and the two regions adjacent to the interface. The words “interface” and “surface” are sometimes used synonymously, nevertheless the first term is preferred for the boundary between two condensed phases and particularly in cases where the two phases are explicitly named, e.g., the solid/liquid interface [4].

Unfortunately, especially for electrodes containing conducting solid phase(s), the correct thermodynamic treatment of interfaces is not straightforward, and the thermodynamic theory of solid/liquid interfaces cannot be accepted as conclusively proven. For instance, concerning the variables of the fundamental functions, the question may arise whether the area of the interface can be regarded as an appropriate variable of state or not. Theoretical debates on the derivation of several pertinent equations (e.g., the Couchman–Everett equation or the so-called “generalized Lippmann equation” [5]) provide good examples of these problems. Even after many years of disputes, a consensus regarding the different approaches is still being sought. Some of these issues have been discussed recently in excellent articles and reviews [6,7,8,9,10]. When considering which model is most appropriate to apply to the solid/liquid interfaces, one may argue that the results of the theoretical work can be proved experimentally. Unfortunately, the measurement of surface energies of solid electrodes is difficult, and the results obtained so far are rather inconsistent [3,11,12,13].

On the other hand, based on a survey on the relevant literature it can be stated that the different views concerning the charged state of adsorbed entities and the charge transfer processes taking place with them are also far from being without contradictions. It is well known that from equilibrium adsorption measurements or, more generally, from measurements of thermodynamic nature no information related to the state of adsorbed species can be obtained [14,15]. In principle, the latter problem can be solved only by application of direct methods (for instance, spectroscopy) furnishing information about the structure and composition of adsorbed species. On the other hand, it is well known (even from textbooks) that an appropriate combination of thermodynamic and non-thermodynamic assumptions may lead to the solution of certain problems which cannot be solved by thermodynamic reasoning alone. However, in such cases a critical analysis of all assumptions involved cannot be avoided.

From the electrochemical point of view, the problem could be considered from two interrelated aspects.

(a) what is the charged state of adsorbed entities (i.e., the adsorbed species are neutral, or they are bearing some electric charge).

(b) what kind of charge transfer processes could occur with them.

If we try to interpret the term “charge of an electrode” we encounter, very often, contradictions in the electrochemical literature. Two different concepts can be distinguished.

One is the so called “double layer model approach”, where the charge is a real electrostatic charge located in both sides of a (hypothetical) double layer formed at the interface. This charge is the so called “free charge” (σ) [16]. This consideration means that the behavior of the interface is like that of a capacitor. The “free charge” approach implicates that when continuous current is flowing through the interface a clear distinction should be made between the so-called “Faradaic” and “capacitive” (non-Faradaic) currents. The capacitive current is responsible for the charging/discharging of the double layer capacitor while the Faradaic current is the charge flow related to the charge transfer processes taking place at the interface.

The total charge or thermodynamic charge (Q) is the charge flown through the outer electric circuit to the electrode under consideration. This current flow, however, should be accompanied by material changes occurring in the interfacial region and, as a consequence, in the bulk phase. In order to keep the concentration of all bulk phase components constant, the amounts of components appearing in the interface should be added to the bulk phase. The term “component” refers here to the so-called thermodynamic components, and not to the constituents or material species present in the system. For that reason, the number of independent components (i.e., the number of the independent variables in the equilibrium relationships) is less than that of the number of entities involved in the equilibrium processes, and we have some liberty in the choice of “independent” components. More details concerning the definitions of σ and Q can be found in Appendix A.

At constant pressure (p) and temperature (T) the state of an interface can be changed by two means.

(a) by altering the concentration of some components (or a single species) in the bulk phases.

(b) by constructing an electrochemical cell containing a counter electrode to create a closed electrical circuit and allowing a current to flow through the circuit, i.e., through the electrode under test.

It is evident that independently from the character and nature of the processes taking place at the interfaces, any current flowing in the system is accompanied by equivalent material changes. Nevertheless, from a thermodynamic point of view both of them can be treated in terms of concentration changes.

The aim of the present study is to review three selected concepts and approaches which were discussed and debated in various publications (including scientific papers and book chapters) over the past decades, apparently without reaching a broad consensus. More specifically, the controversial concept of electrosorption valency, the disputable interpretation of redox processes occurring with adsorbed species, and the misleading formulation of the Gibbs adsorption equation are reviewed in detail. In the framework of a critical analysis it is demonstrated that one of the most important sources of the misinterpretations and misunderstandings is the inadequate approach to the notion of the electrode charge

2. The Problem of Electrosorption Valency and Partial Charge Transfer

In a paper published some years ago [17] de Levie discussed the problems regarding the concepts of electrosorption valency and partial charge transfer. He arrived at the conclusion that the electrosorption valency is an extra-thermodynamic and self-contradictory concept (“the electrosorption valency… has no valid scientific interpretation in terms of partial charge transfer, and is, therefore, best left alone” [17]). A similar criticism and concerns with regard to the serious problems related to electrosorption valency had been already formulated in [18]. The argumentation presented in reference [17] is thermodynamically straightforward and consistent, however, the term is still used in the literature, see [19,20,21,22,23,24,25,26]. Nevertheless, the self-contradictory character of the concept of electrosorption valency can also be demonstrated by using the elementary laws of electrochemistry, that is, without thermodynamic considerations [27,28].

The roots of the problem go back to the early 1960’s when Lorenz and co-workers have suggested [29,30,31,32,33,34] that a purely electrostatic bond between the ion and the metal is not a reality, and that, in case of specific adsorption, there is a degree of charge transfer, i.e., electrons are shared by atoms, like in covalent bonding. This suggestion raises the possibility that the charge on the adsorbed ion is not the same as the charge it carries in the solution phase, and equations in surface thermodynamics in which the chemical amount of adsorbed ions is related to the surface charge may be incorrect.

The specific adsorption on the basis of this concept was formulated as follows

$${\mathrm{R}}^z={\mathrm{R}}_{\mathrm{ads}}^{z\left(1‒\lambda \right)}+\lambda z\mathrm{e}$$

(2.1)

where R^z is the adsorbing species of charge ze and λ is a dimensionless coefficient, denoted as the partial-charge coefficient. In the classical model of adsorption λ = 0, in contrary to this λ = 1 implies a purely covalent bond. This concept of partial charge transfer was subject to general criticism by many authors. These critical views are adequately summarized in the relevant IUPAC recommendations [35].

According to [35]: “the quantity accessible experimentally is the formal partial charge number” defined as

$$l_{\mathrm{B}}=\frac{-{\left(\partial q_{\mathrm{m}}/\partial {\Gamma }_{\mathrm{B}}\right)}_{E,{\mu }_{\mathrm{i}}\ne {\mu }_{\mathrm{B}}}}{F}=\frac{-{\left(\partial {\mu }_{\mathrm{B}}/\partial E\right)}_{{\Gamma }_{\mathrm{B}},{\mu }_{\mathrm{i}}\ne {\mu }_{\mathrm{B}}}}{F}$$

(2.2)

where q_m is the surface charge density electrode, Γ_B is the surface excess of the specifically adsorbed substance B, E is the electrode potential, and F is the Faraday constant, respectively. On the other hand, using the partial charge concept, in [36,37] an adsorption equilibrium was assumed as

$$v\mathrm{M}-{\mathrm{OH}}_2+{\mathrm{S}}_{\mathrm{aq}}^{z_{\mathrm{S}}}\hspace{0.17em}\rightleftharpoons {\mathrm{M}}_v-{\mathrm{S}}^{z_{\mathrm{S}}+\lambda }+v{\mathrm{H}}_2\mathrm{O}+\lambda {\mathrm{e}}^{-}$$

(2.3)

where λ is a non-integer number, S is a species with the charge number z, and M represents the surface (surface atoms) of the electrode. According to this approach the “electrosorption valency” (γ) is given by

$${\left(\partial q_{\mathrm{m}}/\partial {\Gamma }_{\mathrm{S}}\right)}_{\Delta \phi }=-\gamma F$$

(2.4)

or by

$${\left(\partial q_{\mathrm{m}}/\partial {\Gamma }_{\mathrm{S}}\right)}_E=-\gamma F$$

(2.5)

when excess supporting electrolyte is present [38]. In Equations (2.4) and (2.5) Γ_S stands for the surface excess of the specifically adsorbed species S^zs+λ, q_m is the “electrode charge density”, E is the electrode potential, and Δφ represents “the potential difference of the compact double layer” [36]. It follows from the above equations that l_s and γ are equivalent.

The i electrosorption current density was given in [36] as

$$i={\left(\frac{\partial q_{\mathrm{m}}}{\partial t}\right)}_{\Delta \phi }={\left(\frac{\partial q_{\mathrm{m}}}{\partial {\Gamma }_{\mathrm{S}}}\right)}_{\Delta \phi }{\left(\frac{\partial {\Gamma }_{\mathrm{S}}}{\partial t}\right)}_{\Delta \phi }=-\gamma F{v}_{\mathrm{ad}}$$

(2.6)

and at constant electrode potential (E) in the presence of excess supporting electrolyte as

$$i={\left(\frac{\partial q_{\mathrm{m}}}{\partial t}\right)}_E=-\gamma F{v}_{\mathrm{ad}}$$

(2.7)

where v_ad is the rate of adsorption of the species S.

Equations (2.4)–(2.7) are clearly equivalent with

$$i={\left(\frac{\partial q_{\mathrm{m}}}{\partial t}\right)}_{\Delta \varphi }=-\gamma F{\left(\frac{\partial {\Gamma }_{\mathrm{S}}}{\partial t}\right)}_{\Delta \varphi }$$

(2.8)

and

$$i={\left(\frac{\partial q_{\mathrm{m}}}{\partial t}\right)}_E=-\gamma F{\left(\frac{\partial {\Gamma }_{\mathrm{S}}}{\partial t}\right)}_E$$

(2.9)

Which equations form the basis of the method frequently used for the determination of the electrosorption valency from the charge flow. The essence of this method is that coulometric measurements for the determination of the charge density (q_m) are combined with analytical measurements for the determination of Γ_S.

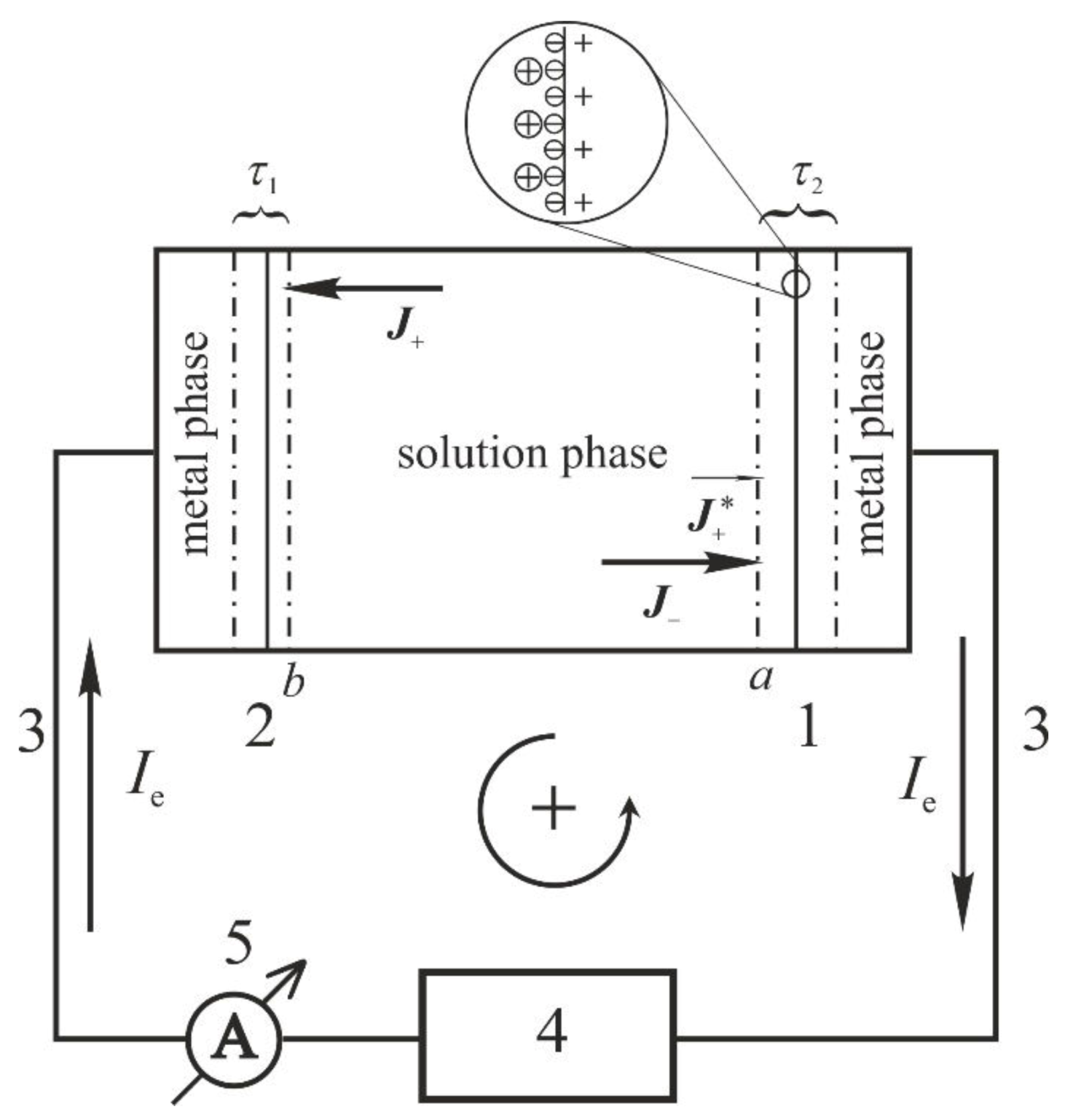
The principle of the experimental determination can be understood on the basis of the “surface layer” (or “interfacial layer”) model. According to this model the surface layer or interfacial layer is the region of space adjoining and comprising the phase boundary within which the physicochemical properties of matter are significantly differ from those of the adjoining bulk phases [39] (see Figure 1). In addition, it is customary to define a surface or interfacial layer (s) of finite thickness (τ) (sometimes called a Guggenheim layer) bordered by two suitably chosen surfaces (one in each of the adjacent homogeneous bulk phases) parallel to the phase boundary [40].

Usually, in the presence of a great excess of a supporting electrolyte under potentiostatic conditions, the use of Equation (2.9) is suggested for the determination of γ. In this treatment it is assumed that AΓ_S (where A is the area of the electrode interface) equals the total chemical amount of S^zs+λ in the interfacial layer. If this requirement is fulfilled, the derivative of the Γ_S function with respect to time can be given as

$$\mathrm{d}{\Gamma }_{\mathrm{S}}/\mathrm{d}t=A^{-1}\mathrm{d}{n}_{\mathrm{S}}^{\mathrm{s}}/\mathrm{d}t$$

(2.10)

where n_S^s is the amount of component S in the interfacial layer. Integrating Equation (2.9), the following relationship can be obtained when Γ_S = 0 at t = 0:

$${\displaystyle \underset{0}{\overset{t}{\int }}\hspace{0.17em}i\hspace{0.17em}\mathrm{d}\hspace{0.17em}t}=q_{\mathrm{m}}=-\gamma F{\Gamma }_{\mathrm{S}}\left(t\right)$$

(2.11)

Furthermore,

$$q_{\mathrm{m}}={\displaystyle \underset{0}{\overset{t}{\int }}\hspace{0.17em}i\hspace{0.17em}\mathrm{d}\hspace{0.17em}t}=\frac{1}{A}\gamma F\left(n_{\mathrm{S}}^0-n_{\mathrm{S}}\right)$$

(2.12)

where n_S⁰ and n_S are the chemical amounts of species S in the solution phase at the beginning and end of the experiment, respectively.

In several cases values for γ have been determined on the basis of Equations (2.5), (2.11), and (2.12) (for example, q_m was determined by means of coulometric measurements and the Γ_S values were then calculated based on thermodynamic considerations [41,42], or analytical methods were used for the determination of Γ_S), and

$$\gamma \ne z_{\mathrm{S}}$$

(2.13)

has been found. In Equation (2.13) z_S means the charge number of the species S in the solution.

The processes occurring in an electrochemical cell may be most easily understood if we imagine an observer located in the bulk solution phase who records the entire sequence of events during a typical adsorption experiment.

In such experiments, the cell contains a supporting electrolyte XY (dissociated into its respective ions ${\mathrm{X}}^{z_{\mathrm{X}}+}$ and ${\mathrm{Y}}^{{\mathrm{z}}_{\mathrm{Y}}-}$) and the electrosorption of ${\mathrm{S}}^{z_{\mathrm{S}}-}$ ions is studied. The ${\mathrm{S}}^{z_{\mathrm{S}}-}$ ions are added to the system in the form of a salt (electrolyte) such as ${\mathrm{C}}_{v_{\mathrm{C}}}{\mathrm{S}}_{v_{\mathrm{S}}}$.

At the beginning of the experiment the potential of the working electrode is set to E(t = 0), e.g., with the help of a potentiostat. At time t = 0 a potential step E−E(t = 0) is applied to the working electrode and the electrode potential is held at a constant value (E) thereafter. The surface charge is determined based on Equation (2.11), i.e., by integrating the current vs. time curves recorded after stepping the electrode potential to E.

The net current flowing through an electrochemical cell can be measured only in the “outer circuit”, i.e., outside the cell (see Figure 1), where the instantaneous current flowing through the ammeter and through the metal wires connected to the electrodes is equal with that of flowing through the electrochemical cell. It should be pointed out that all metals are (purely) electronic conductors.

For the observer in the bulk solution phase Faraday’s law should be valid, no matter what happens at the electrodes. The classical Faraday laws involve the following fundamental axioms:

• The discreteness of material objects and charge (ions, electrons, and other charged matter).
• There can be no electric charge without matter: It is not possible to separate the (discrete) charges from the (discrete) material objects.
• Conservation laws of mass and charge.

Equation (2.3) infers, that only one kind of charged species participates in the adsorption process. It means, that according to the above principles at boundary “a” the observer situated in the bulk solution phase recognizes that the flux of ${\mathrm{S}}^{z_{\mathrm{S}}-}$ ions during the adsorption process (Figure 1) is [27]

$${\mathit{J}}_{-}\left(t\right)=-A_{\mathrm{a}}^{-1}\mathrm{d}{n}_{\mathrm{S}}/\mathrm{d}t$$

(2.14)

and the current flowing towards electrode 1 (working electrode) can be given as

$$I_{-}\left(t\right)=-z_{\mathrm{S}}F{A}_{\mathrm{a}}{\mathit{J}}_{-}$$

(2.15)

For the sake of simplicity, in the above equations and in the following we denote ${\mathrm{S}}^{z_{\mathrm{S}}-}$ by S, and we suppose, that the surface area of the working electrode is equal with the area of boundary “a” (A_a). By considering Equation (2.10), we have

$$I_{-}\left(t\right)=z_{\mathrm{S}}F\left(\mathrm{d}{n}_{\mathrm{S}}/\mathrm{d}t\right)=z_{\mathrm{S}}{A}_{\mathrm{a}}F\left(\mathrm{d}{\Gamma }_{\mathrm{S}}/\mathrm{d}t\right)$$

(2.16)

Nevertheless, as a matter of fact, only the electronic current $I_{\mathrm{e}}$ flowing in the “outer circuit” (for which, in compliance with the usual definition in physics $-I_{\mathrm{e}}\left(t\right)=I\left(t\right)$) is directly measurable. According to Kirchhoff’s nodal rule:

$$I_{-}\left(t\right)=I_{\mathrm{e}}\left(t\right)=-I\left(t\right)$$

(2.17)

To complete the electrochemical cell, we can choose an auxiliary (counter) electrode (electrode 2 in Figure 1) where the reaction

$${\mathrm{C}}^{z_{\mathrm{C}}+}+z_{\mathrm{C}}{\mathrm{e}}^{-}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}\mathrm{C}(\mathrm{or}{\mathrm{X}}^{z_{\mathrm{X}}+}+z_{\mathrm{X}}{\mathrm{e}}^{-}\hspace{0.17em}=\hspace{0.17em}\mathrm{X})$$

(2.18)

can take place unhindered under the given conditions. Assuming, that the surface area of the auxiliary (counter) electrode is equal with that of boundary “b”, the observer located in the solution phase can determine the flux

$${\mathit{J}}_{+}\left(t\right)=A_{\mathrm{b}}^{-1}\mathrm{d}{n}_{C^{z_{\mathrm{c}}+}}/\mathrm{d}t$$

(2.19)

at boundary “b” (or ${\mathit{J}}_{+}\left(t\right)=A_{\mathrm{b}}^{-1}\mathrm{d}{n}_{X^{z_{\mathrm{x}}+}}/\mathrm{d}t$), and the current

$$I_{+}\left(t\right)=z_{\mathrm{C}}F\left(\mathrm{d}{n}_{C^{z_{\mathrm{c}}+}}/\mathrm{d}t\right)$$

(2.20)

(or $I_{+}\left(t\right)=z_{\mathrm{X}}F\left(\mathrm{d}{n}_{X^{z_{\mathrm{x}}+}}/\mathrm{d}t\right)$) flowing towards electrode 2 (Figure 1). $n_{C^{z_{\mathrm{c}}+}}$ and $n_{X^{z_{\mathrm{x}}+}}$ are the amounts of component ${\mathrm{C}}^{z_{\mathrm{C}}+}$ and ${\mathrm{X}}^{z_{\mathrm{X}}+}$, respectively.

Because of the electroneutrality condition in the bulk solution phase and due to the mass conservation law

$$v_{\mathrm{C}}\mathrm{d}{n}_{\mathrm{S}}/\mathrm{d}t=v_{\mathrm{S}}\mathrm{d}{n}_{{\mathrm{C}}^{z_{\mathrm{c}}+}}/\mathrm{d}t$$

(2.21)

or

$$\left|v_{\mathrm{C}}{A}_{\mathrm{a}}{\mathit{J}}_{-}\left(t\right)\right|=\left|v_{\mathrm{S}}{A}_{\mathrm{b}}{\mathit{J}}_{+}\left(t\right)\right|$$

(2.22)

is also true.

According to Kirchhoff’s first law, at electrode 2:

$$I_{+}\left(t\right)=I_e\left(t\right)=-I\left(t\right)$$

(2.23)

It follows from Equations (2.17) and (2.23), that $I_{-}\left(t\right)=I_{+}\left(t\right)$, i.e., the currents at boundary “a” and boundary “b” are equal.

Considering the working electrode (electrode 1) and comparing Equations (2.7) and (2.9), we get

$$I\left(t\right)=A_{\mathrm{a}}i\left(t\right)=A_{\mathrm{a}}{\left(\frac{\partial q_{\mathrm{m}}}{\partial t}\right)}_E=-\gamma F{A}_{\mathrm{a}}{\left(\frac{\partial {\Gamma }_{\mathrm{S}}}{\partial t}\right)}_E=-\gamma F{A}_{\mathrm{a}}{v}_{\mathrm{ad}}$$

(2.24)

It means, that the equation

$$-I_{-}\left(t\right)=-z_{\mathrm{S}}F{\left(\frac{\partial {\Gamma }_{\mathrm{S}}}{\partial t}\right)}_E=I\left(t\right)=-\gamma F{\left(\frac{\partial {\Gamma }_{\mathrm{S}}}{\partial t}\right)}_E=-I_{+}\left(t\right)$$

(2.25)

can only be true if $\gamma =z_{\mathrm{S}}$, which contradicts Equation (2.13).

It can be shown that we can arrive at the same conclusion if we consider Equations (2.12), (2.20), and (2.22). According to the derivation presented in [27], in case of $\gamma \ne z_{\mathrm{S}}$ the electroneutrality condition is violated as well.

However, there are many published results showing that the $l_{\mathrm{S}}=\frac{-{\left(\partial q_{\mathrm{m}}/\partial {\Gamma }_{\mathrm{S}}\right)}_{E,{\mu }_{\mathrm{i}}\ne {\mu }_{\mathrm{S}}}}{F}$ values calculated from the experimentally determined qm and Γ_S data differs from z_S. Usually $l_{\mathrm{S}}=\gamma <z_{\mathrm{S}}$ was found by different authors. In line with the above results and the arguments presented in reference [27], some other processes should also be taken into account in order to resolve the contradictions between experimental and theoretical results.

Some possible explanations are based on the simultaneous adsorption (coadsorption) of other ions besides ${\mathrm{S}}^{z_{\mathrm{S}}-}$ [43].

For instance:

(1) $\frac{z_{\mathrm{S}}}{z_{\mathrm{C}}}\left(\frac{1}{\gamma }-\frac{1}{z_{\mathrm{S}}}\right)\frac{q_{\mathrm{m}}{A}_{\mathrm{a}}}{F}$ moles of ${\mathrm{C}}^{z_{\mathrm{C}}+}$ ions (or $\frac{z_{\mathrm{S}}}{z_{\mathrm{X}}}\left(\frac{1}{\gamma }-\frac{1}{z_{\mathrm{S}}}\right)\frac{q_{\mathrm{m}}{A}_{\mathrm{a}}}{F}$ moles of ${\mathrm{X}}^{z_{\mathrm{X}}+}$ ions) are co-adsorbed with ${\mathrm{S}}^{z_{\mathrm{S}}-}$.

(2) $\frac{z_{\mathrm{S}}}{z_{\mathrm{Y}}}\left(\frac{1}{\gamma }-\frac{1}{z_{\mathrm{S}}}\right)\frac{q_{\mathrm{m}}{A}_{\mathrm{a}}}{F}$ moles of ${\mathrm{Y}}^{{\mathrm{z}}_{\mathrm{Y}}-}$ enter the solution from the interphase.

(3) Desorption of ${\mathrm{Y}}^{{\mathrm{z}}_{\mathrm{Y}}-}$ and simultaneous adsorption of ${\mathrm{C}}^{z_{\mathrm{C}}+}$ and/or ${\mathrm{X}}^{z_{\mathrm{X}}+}$, etc. Several mechanisms of rearrangement can be imagined, however, charge balance (electroneutrality) should be maintained in all macroscopic domains of the solution phase.

Case (1) above is illustrated in Figure 2. Since ${\mathrm{C}}^{z_{\mathrm{C}}+}$ or ${\mathrm{X}}^{z_{\mathrm{X}}+}$ ions adsorb simultaneously with the ${\mathrm{S}}^{z_{\mathrm{S}}-}$ ions (co-adsorption), besides the fluxes $J_{+}$ and $J_{-}$ shown in Figure 1, the observer located in the solution phase perceives the $J_{+}^{\ast }$ flux of ${\mathrm{C}}^{z_{\mathrm{C}}+}$ or ${\mathrm{X}}^{z_{\mathrm{X}}+}$ ions at boundary “a”, as well. In the following quantities characteristic of ${\mathrm{C}}^{z_{\mathrm{C}}+}$ are denoted by subscript C.

The current corresponding to the ionic fluxes at boundary “a” is therefore

$$I_{-}\left(t\right)=z_{\mathrm{S}}{A}_{\mathrm{a}}F\left(\mathrm{d}{\Gamma }_{\mathrm{S}}/\mathrm{d}t\right)-z_{\mathrm{C}}{A}_{\mathrm{a}}F\left(\mathrm{d}{\Gamma }_C/\mathrm{d}t\right)$$

(2.26)

By comparing Equations (2.9), (2.10), (2.17), and (2.20) we obtain

$$I\left(t\right)=-z_{\mathrm{S}}{A}_{\mathrm{a}}F\left(\mathrm{d}{\Gamma }_{\mathrm{S}}/\mathrm{d}t\right)+z_{\mathrm{C}}{A}_{\mathrm{a}}F\left(\mathrm{d}{\Gamma }_C/\mathrm{d}t\right)=-\gamma A_{\mathrm{a}}F\left(\mathrm{d}{\Gamma }_{\mathrm{S}}/\mathrm{d}t\right)$$

(2.27)

From radiotracer experiments it is known (see e.g., [18,44]), that in numerous cases I(t) and dΓ_C/dt are proportional, and so $\frac{\mathrm{d}{\Gamma }_C}{\mathrm{d}t}=\frac{p}{A_{\mathrm{a}}}I\left(t\right)$, where $0<p<1$.

With Equation (2.26)

$$I\left(t\right)=-\frac{z_{\mathrm{S}}{A}_{\mathrm{a}}F\left(\mathrm{d}{\Gamma }_{\mathrm{S}}/\mathrm{d}t\right)}{1+p{z}_{\mathrm{C}}F}$$

(2.28)

By substituting the above expression into Equation (2.27)

$$\gamma =\frac{z_{\mathrm{S}}}{1+p{z}_{\mathrm{C}}F}$$

(2.29)

is obtained.

It can be seen from Equation (2.29) that under these circumstances the inequality $\gamma <z_{\mathrm{S}}$ is really fulfilled if we consider the experimentally determined value of γ or l_S.

3. On the Alternative Formulations of the Gibbs Adsorption Equation in Electrochemistry

Adsorption of one or more of the components of a multicomponent, multiphase system is the enrichment or depletion of one or more components at one or more of the phase boundaries. This means that adsorption occurs if the concentrations in the interfacial layers differ from those in the adjoining bulk phases. If adsorption occurs in a multiphase system, the overall stoichiometry of the system differs from that of a (hypothetical) reference system built up of homogeneous bulk phases whose volumes and/or amounts are defined by suitably chosen dividing surfaces.

Gibbs found it mathematically convenient to consider an idealized system in which a real interface layer is replaced by a dividing surface [45]. Gibbs introduced also the notion of “surface excess”, the physical interpretation of which is far from easy. This question was discussed later by Guggenheim and Adam [46]. Guggenheim [47] gave an excellent summary of interfacial thermodynamics from a point of view somewhat different from that of Gibbs, e.g., in his model two dividing surfaces, one at each boundary, is employed and it is assumed that there is a “surface” or “interfacial” layer (“interphase”) of finite thickness (τ) bounded by two appropriately chosen surfaces parallel to the phase boundary, one in each of the adjacent homogeneous bulk phases.

Summary of the main features of the above models and general derivations of the Gibbs adsorption equation together with the mathematical background behind them can be found e.g., in references [3,14,35,40,48,49].

Nevertheless, a generalized form of the Gibbs adsorption equation is quite complicated as it was demonstrated by Mohilner [50]. According to Mohilner [50]: “Electrocapillary measurements, like any other electrochemical measurements, require the use of a complete cell, that is, one with two electrodes. One electrode is the ideal polarized electrode; the other electrode is a reversible charge-transfer electrode… However, it is important to realize from the outset that this second electrode is not an ordinary “constant-potential” reference electrode like the saturated calomel electrode (SCE). Rather, it is simply some electrode dipping into the solution S, which is reversible (in the Nernstian sense) to one of the ions of that solution… This second electrode of the electrocapillary cell will be called the indicator electrode and denoted by the symbol IN. The particular ion of the solution to which electrode IN is reversible will be called the indicator ion… A solution S containing c cationic species and an anionic species could be prepared in many different ways. However, for the purpose of the thermodynamic treatment, the most general electrocapillary equation can be derived if we assume that the ions of the solution are furnished by neutral binary salts. Of the c × a different binary salts that could be chosen, we shall select c + a − 1 binary salts in the following way.

If the indicator electrode IN is reversible to cation j’, we arbitrarily select an anion, say k’. If the indicator electrode is reversible to anion k’, we arbitrarily select a cation, say j’. In either case we have selected a binary salt containing ions j’ and k’. We call this salt the indicator salt. The electrolyte solution is then considered to have been made up by dissolving c + a − 2 additional binary salts of which c − 1 have anion k’ in common with the indicator salt; the remaining a − 1 salts have cation j’ in common with the indicator salt.”

Thus, at constant temperature T and pressure p the Gibbs adsorption equation for an ideally polarizable electrode and a cation-reversible indicator electrode can be expressed as [50,51]:

$$\begin{array}{l}\mathrm{d}\gamma =-q_{\mathrm{M}}\mathrm{d}{E}_{+}-{\displaystyle \sum _{i\ne i^{\prime }}{\Gamma }_{i{i}^{\prime }}\mathrm{d}{\mu }_i}-{\displaystyle \sum _{j\ne j^{\prime }}{\Gamma }_{j{h}^{\prime }}/{\nu }_{j{k}^{\prime }}^{+}}\mathrm{d}{\mu }_{j{k}^{\prime }}-{\displaystyle \sum _{k\ne k^{\prime }}{\Gamma }_{k{h}^{\prime }}/{\nu }_{j^{\prime }k}^{-}}\mathrm{d}{\mu }_{j^{\prime }k}\\ -{\displaystyle \sum _{h\ne h^{\prime }}{\Gamma }_{h{h}^{\prime }}\mathrm{d}{\mu }_h}-\left[\left({\Gamma }_{k^{\prime }{h}^{\prime }}/{\nu }_{j^{\prime }{k}^{\prime }}^{-}\right)-\left(\frac{1}{\left|z_{k^{\prime }}\right|{\nu }_{j^{\prime }{k}^{\prime }}^{-}}\right){\displaystyle \sum _{j\ne j^{\prime }}{\Gamma }_{j{h}^{\prime }}{z}_j}\right]\hspace{0.17em}\mathrm{d}{\mu }_{j^{\prime }{k}^{\prime }}\end{array}$$

(3.1)

where γ is the interfacial intensive parameter, q_M is the charge density on the metal side of the interface, E₊ is the electrode potential with respect to the cation-reversible indicator electrode, subscript i indicates the components (metals) in the metallic phase (a single phase alloy), subscript h designates the neutral molecular species in the solution, the z-s are the ionic charges, the Γ and μ values are the surface excesses and chemical potentials of the various components, respectively, and the ν-s indicate the number of moles of cations (or anions) per formula weight of the salt.

Equation (3.1) or the equation given as

$$\begin{array}{l}\mathrm{d}\gamma =-s^{\mathsf{\sigma }}\mathrm{d}T-q_{\mathrm{M}}\mathrm{d}{E}_{+}-{\displaystyle \sum _{i\ne i^{\prime }}{\Gamma }_{i{i}^{\prime }}\mathrm{d}{\mu }_i}-{\displaystyle \sum _{j\ne j^{\prime }}{\Gamma }_{j{h}^{\prime }}/{\nu }_{j{k}^{\prime }}^{+}}\mathrm{d}{\mu }_{j{k}^{\prime }}-{\displaystyle \sum _{k\ne k^{\prime }}{\Gamma }_{k{h}^{\prime }}/{\nu }_{j^{\prime }k}^{-}}\mathrm{d}{\mu }_{j^{\prime }k}\\ -{\displaystyle \sum _{h\ne h^{\prime }}{\Gamma }_{h{h}^{\prime }}\mathrm{d}{\mu }_h}-\left[\left({\Gamma }_{k^{\prime }{h}^{\prime }}/{\nu }_{j^{\prime }{k}^{\prime }}^{-}\right)-\left(\frac{1}{\left|z_{k^{\prime }}\right|{\nu }_{j^{\prime }{k}^{\prime }}^{-}}\right){\displaystyle \sum _{j\ne j^{\prime }}{\Gamma }_{j{h}^{\prime }}{z}_j}\right]\hspace{0.17em}\mathrm{d}{\mu }_{j^{\prime }{k}^{\prime }}\end{array}$$

(3.2)

is commonly called the “electrocapillary equation”. As it can be seen, even in the case of a very simple system the Gibbs adsorption equation can take various forms depending on the selection of the independent components, the indicator electrolyte and the indicator ion.

Nevertheless, Equations (3.1) and (3.2) can sometimes be given in somewhat simpler forms. Too much simplification (or the wrong kind of simplification), however, can lead to highly misleading results [51]. For instance, the Gibbs adsorption equation for an ideally polarizable interface (or “interphase”) as presented in the IUPAC Recommendations “Interphases of systems of conducting phases” [35] could be a source of misinterpretation presumably owing to the effort to give as simple equation as possible.

The relevant section (dealing with the introduction of Gibbs equation for an ideally polarizable interphase) reads as follows (the numbering of the equations in the quotation corresponds to the equation numbering in the original paper):

“Differences from the behaviour of interphases containing only neutral species arise when the interphase may be described as ideally polarizable. This term is used when no charged component is common to both phases adjoining the interphase. This may arise as a result of the equilibrium conditions or from the kinetics of charge transfer and leads to an interphase impermeable to electric charge. In such an interphase it is convenient to divide the interfacial region into two parts: One containing the charged species from one phase (α), the other containing those from the other phase (β). The physical charge on unit area of either side of the interphase may then be defined in terms of the surface excesses of the charged species in the system:

$${\sigma }^{\mathsf{\alpha }}={\displaystyle \sum _i{z}_{i}F{\Gamma }_i^{\mathsf{\alpha }}}$$

(4.3.1)

$${\sigma }^{\mathsf{\beta }}={\displaystyle \sum _i{z}_{i}F{\Gamma }_i^{\mathsf{\beta }}}$$

(4.3.2)

where the sum Equation (4.3.1) is over all charged components in phase α and that in Equation (4.3.2) is over all charged components in β. The interphase as a whole is electrically neutral, i.e.,

$${\sigma }^{\mathsf{\alpha }}+{\sigma }^{\mathsf{\beta }}=0$$

(4.3.3)

The Gibbs adsorption equation for an ideally polarizable interphase must have a term in which the charge σ multiplies the change of a difference of electrochemical potentials between one charged species in each of the adjoining phase:

$${\sigma }^{\mathsf{\alpha }}\mathrm{d}\epsilon$$

(4.3.4)

where

$$F\epsilon =\left({\tilde{\mu }}_{\mathrm{B}}^{\mathsf{\alpha }}/z_{\mathrm{B}}\right)\hspace{0.17em}-\hspace{0.17em}\left({\tilde{\mu }}_{\mathrm{C}}^{\mathsf{\beta }}/z_{\mathrm{C}}\right)$$

(4.3.5)

and B and C are particular charged species in phases α and β respectively.

The electrochemical potential difference in Equation (4.3.5) may be expressed as the sum of chemical potentials of neutral groups of charged species (salts, metals etc.) and an electrical potential difference E between two electrodes e.g., between phase α if it is an electronic conductor and a reference electrode (ref. [8]. {reference [14] in the present work}) When the reference electrode is in equilibrium with a cation (anion) in phase β, E is given the subscript + (−). At constant temperature and pressure:

$$\mathrm{d}\epsilon =\mathrm{d}{E}_{+(-)}$$

(4.3.6)

Thus, the Gibbs adsorption equation takes the form:

$$s\mathrm{d}T-\tau \mathrm{d}p+\mathrm{d}\gamma +{\sigma }^{\alpha }\mathrm{d}\epsilon +{\displaystyle \sum {\Gamma }_j\mathrm{d}{\mu }_j=0}$$

(4.3.7)

where j is an electrically neutral component of one or other of the phases and the sum is over all the components but one in each phase. It is not possible to eliminate the term ${\sigma }^{\mathsf{\alpha }}\mathrm{d}\epsilon$ to obtain an equation like Equation (4.2.1). {$s\mathrm{d}T-\tau \mathrm{d}p+\mathrm{d}\gamma +{\displaystyle \sum {\Gamma }_i\mathrm{d}{\mu }_i=0}$ (4.2.1) in [35]}

Equation (4.3.7) is often called the electrocapillary equation because it includes the expression of the phenomenon of electrocapillarity - the dependence of the interfacial tension on the electrical state of the interphase”.

Quite unfortunately, the text and the last term of the above equation in form ${\displaystyle \sum {\Gamma }_j\mathrm{d}{\mu }_j}$ suggests, that only the surface excess of electrically neutral components (j) can be determined. It is, however, well known that in simple cases where only a single electrolyte is present both the relative surface excess of the cation and anion can be determined depending on the reference electrode chosen. Thus accepting that ${\mu }_j$ designates the chemical potential of a neutral component the corresponding relative surface excess quantity should not be denoted by ${\Gamma }_j$ if we are thinking in terms of ion adsorption. (In accordance with Equations (4.3.1) and (4.3.2) the various ${\Gamma }_i$ quantities should somehow figure in the final form of the equation.)

The following example may serve to illustrate the problem: An often-quoted example for a practically ideal polarizable electrode is mercury in contact with an aqueous KCl solution. At constant T and p one possible form of the electrocapillary equation is

$$\mathrm{d}\gamma +{\sigma }^{\mathsf{\alpha }}\mathrm{d}{E}_{+}+{{\Gamma }^{\prime }}_{{\mathrm{Cl}}^{-}}\mathrm{d}{\mu }_{\mathrm{KCl}}=0$$

(3.3)

Another possible form is

$$\mathrm{d}\gamma +{\sigma }^{\mathsf{\alpha }}\mathrm{d}{E}_{-}+{{\Gamma }^{\prime }}_{{\mathrm{K}}^{+}}\mathrm{d}{\mu }_{\mathrm{KCl}}=0$$

(3.4)

hence

$${{\Gamma }^{\prime }}_{{\mathrm{Cl}}^{-}}=-{\left(\frac{\partial \gamma }{\partial {\mu }_{\mathrm{KCl}}}\right)}_{T,p,E_{+}}$$

(3.5)

and

$${{\Gamma }^{\prime }}_{{\mathrm{K}}^{+}}=-{\left(\frac{\partial \gamma }{\partial {\mu }_{\mathrm{KCl}}}\right)}_{T,p,E_{-}}$$

(3.6)

On the other hand, by following the IUPAC recommendation, we have:

$$\mathrm{d}\gamma +{\sigma }^{\mathsf{\alpha }}\mathrm{d}\epsilon +{{\Gamma }^{\prime }}_{\mathrm{KCl}}\mathrm{d}{\mu }_{\mathrm{KCl}}=0$$

(3.7)

and

$${{\Gamma }^{\prime }}_{\mathrm{KCl}}=-{\left(\frac{\partial \gamma }{\partial {\mu }_{\mathrm{KCl}}}\right)}_{T,p,\epsilon }$$

(3.8)

Since according to Equation (4.3.6) in the IUPAC recommendation $\mathrm{d}\epsilon =\mathrm{d}{E}_{+(-)}$, the relative surface excess is given by

$${{\Gamma }^{\prime }}_{\mathrm{KCl}}=-{\left(\frac{\partial \gamma }{\partial {\mu }_{\mathrm{KCl}}}\right)}_{T,p,E_{+}}$$

(3.9)

and

$${{\Gamma }^{\prime }}_{\mathrm{KCl}}=-{\left(\frac{\partial \gamma }{\partial {\mu }_{\mathrm{KCl}}}\right)}_{T,p,E_{-}}$$

(3.10)

Generally, ${{\Gamma }^{\prime }}_{{\mathrm{K}}^{+}}\ne {{\Gamma }^{\prime }}_{{\mathrm{Cl}}^{-}}$. (The two quantities can be equal at the point of zero charge, as a particular case [15].) Consequently, in Equations (3.9) and (3.10) two different quantities (or functions) are denoted with ${{\Gamma }^{\prime }}_{\mathrm{KCl}}$, which is rather unfortunate.

Of course, the meaning of ${{\Gamma }^{\prime }}_{\mathrm{KCl}}$ in the specific cases can be clarified in some extent by additional explanations (like in reference [14]), but the use of potentially confusing notations should be avoided.

The derivations discussed in this section indicate that even in the case of quite simple systems the Gibbs adsorption equation cannot be given in a simplified form as it was attempted in some previous studies. Nevertheless, as it has been shown above, the equation can take various forms depending on the selection of the set of independent components, the choice of the indicator electrolyte and the indicator ion.

4. Difficulties Related to the Formulation and Interpretation of Charge Transfer Processes Involving Adsorbed Species

At the top of the list, one of the most important topics of electrochemical science is the investigation of the mechanism and consequences of charge transfer at electrodes (electrode interfaces). We may talk about the transfer of electrons or ions from an electronic conductor (or semiconductor) phase (i.e., a solid or liquid phase, e.g., a metal) to an ionic conductor phase (e.g., an electrolyte solution), or vice versa, but this an abstraction at least to the extent that electrochemical systems that can be studied in practice always involve two or more electrodes. In addition, such systems can only be investigated as part of complete electrical circuits involving electronic devices.

In many modern electrochemical textbooks two types of electrode processes are distinguished:

• “Faradaic processes” are processes, in which charges are transferred across the metal/solution interface. Such electrodes are also called charge transfer electrodes.
• There are potential ranges where no charge transfer reactions take place or do not take place to a significant extent at the electrode interface, because such processes are kinetically or thermodynamically unfavorable. On the other hand, surface processes like double layer charging or adsorption and desorption can occur, and the structure of the interface layer can change with the changing electrode potential or solution composition. Such processes are usually called “Nonfaradaic processes”. Even though under such conditions charged species does not cross the interface, current can flow, at least temporarily, in the outer circuit (“transient current”).

On the other hand, a survey of the electrochemical literature, research papers and text books as well, leaves the impression that the occurrence of a charge transfer process between two species adsorbed at an electrode should be regarded as a physical reality, generating current flow in an electric circuit connected to the terminals of an electrochemical cell. This conception was criticized e.g., in references [28,52,53,54]. Two examples will be presented here for the purpose of demonstrating the problems associated with this approach.

The first example is a quotation from reference [55]. In this well-known textbook, the following assumptions were made for the interpretation of the voltammetric responses of certain redox species:

“(ii) …the electrochemical reaction can be represented by:

$${\mathrm{O}}_{\mathrm{ads}}\hspace{0.17em}+\hspace{0.17em}n{\mathrm{e}}^{-}\hspace{0.17em}\leftrightarrow \hspace{0.17em}{\mathrm{R}}_{\mathrm{ads}}$$

and is kinetically fast enough to maintain Nernstian (i.e., reversible) behaviour at each point in the CV or LSV scan such that the concentrations of O and R, near the electrode, obey the Nernst equation.

(iii) … the oxidised and reduced species are both strongly adsorbed and have the same enthalpy of adsorption.

(iv) There is no O or R in solution.”

For the electrode potentials recorded during a sweep the following relationship are considered:

…”Neglecting the activities of the surface species, E can be expressed approximately in terms of the Nernst equation:

$$E=E_0+\left[RT/nF\right]\cdot {\log }_{\mathrm{e}}\left[{\theta }_{\mathrm{ox}}/{\theta }_{\mathrm{red}}\right]$$

where θ_ox and θ_red are the coverages of the oxidized and reduced forms at any time t. θ_red = (1 − θ_ox), thus:

$$E=E_0+\left[RT/nF\right]\cdot {\log }_{\mathrm{e}}\left[{\theta }_{\mathrm{ox}}/\left(1-{\theta }_{\mathrm{ox}}\right)\right]”$$

Finally, for the charge (and current) involved in the transformation the following statements have been made:

“From Faraday’s laws of electrolysis, the charge passed at any time t, Q, is the current in amperes, I, multiplied by the time in seconds, t; in terms of the surface coverage this is:

$$Q=N_{T}n{e}_0\left(1-{\theta }_{\mathrm{ox}}\right)$$

where N_T is the total number of O and R-species present on the surface, e₀ is the electronic charge and we have assumed that E is sufficiently positive of E⁰ for θox to be essentially unity. In addition, since:

$$Q={\displaystyle \underset{0}{\overset{t}{\int }}I\mathrm{d}t}$$

$$\mathrm{d}Q/\mathrm{d}t=I=-N_{T}n{e}_0\left(\mathrm{d}{\theta }_{\mathrm{ox}}/\mathrm{d}t\right),\hspace{0.17em}\hspace{0.17em}$$

or:

$$\mathrm{d}Q=I\mathrm{d}t=-\hspace{0.17em}{N}_{T}n{e}_0\cdot \mathrm{d}{\theta }_{\mathrm{ox}}”$$

Even at first glance, it is clear that the two statements “…There is no O or R in solution…” and “…the concentrations of O and R near the electrode obey the Nernst equation… “ are conflicting and contradictory reflecting the ambiguity of the entire subject.

In electrochemistry, equilibrium potentials, or, more precisely, equilibrium potential differences, refer to equilibriums between two phases.

When there are no redox species in the solution phase (none of the members of the redox pair), then it is questionable to refer to “Nernstian behavior”. On the other hand, Γox(θox) and Γred(θred) are indistinguishable from thermodynamic point of view owing to the existence of the electrochemical/thermodynamic equilibrium. Either O or R can be considered as an independent component, but not both of them simultaneously.

Any current measured at an electrode should involve charge transfer between two phases or between a bulk phase and the interface (“interphase”, see e.g., Section 3). An adsorbed species originating from the solution phase passed this step earlier. Faraday’s law, referred to above, involves that during a current flow simultaneous charge and material transfer takes place between phases (and in the phases). This charge and material transfer should be ascribed to one or more components present in the bulk liquid phase. However, the approach presented above (example 1) ignores the fact that an adsorbed species does not belong to any bulk phase.

Another interesting example is discussed e.g., in references [28,52,53,54,55,56,57]. According to the claims of a great number of authors (see references [57,58,59] and papers cited therein) the “determination of the rate constant for electron transfer between an immobilized redox molecule and the electrode” can be achieved by potential step chronoamperometry or cyclic voltammetry. For the first sight this statement, which is in contrast to the conclusions presented in the preceding section and which is very popular in the literature, seems to be quite acceptable, however, we get into trouble if we look after its precise meaning in the light of the statements made in references [52,53].

In order to clarify the doubts that could arise we should recourse to semantics. The main problem is that what is the meaning of the concept of “electron transfer between an electrode and redox adsorbate”. Whether “electrode” and “redox adsorbate” represent two different phases or not. If we assume that “electrode” in the quoted phrase means an electronic conductor phase (preferably metal) in contact with a liquid phase the redox adsorbate should be present in the interface between the bulk solid and liquid phase. If we consider this picture the electron transfer as formulated above occurs between the solid bulk phase and the interface and not between two bulk phases, therefore this process cannot be considered generally as a step unequivocally and directly connected with a current flow in an electrochemical cell, for instance, under the conditions of voltammetry.

In reality, the current observed during voltammetry is measuring the rate of the electron transfer between two electrodes of a galvanic cell through the external circuit. If there is a flow of electrons in the external circuit charged species should move from and to the electronic conductor/ionic conductor interfaces, existing at both electrodes. Therefore, it is quite improbable that the “voltammetric response of redox adsorbates” without the knowledge of the chemical nature of adsorbed species could furnish explicit information on the rate constant for electron transfer between “electrodes and redox adsorbates”.

Despite this situation, models and procedures are suggested in the literature for the determination of the rate constant of electron transfer to redox adsorbate on the basis of several assumptions. Unfortunately, a number of these assumptions are far from being unambiguous and are even in contradiction with each other. For instance, in reference [57] there are 13 assumptions, however, some of them are incoherent.

Only the most peculiar ones are mentioned here.

(i) and (vi):

“(i)…The redox couple is not present in the bulk phase or is present in such low concentrations that the current from electron-transfer reactions of molecules diffusing to the electrode is negligible…”

This statement is apparently in conflict with:

“(vi) In the case of physical adsorption a Langmuir isotherm is assumed in which the adsorption coefficients and the maximum surface coverage are independent of potential.”

The contradiction is quite obvious, since if the redox couple is not present in the bulk phase what could be the meaning and use of an adsorption isotherm?

The confusion becomes more pronounced when we consider the contradiction between the second statement in point (i) and that in point (iv).

“(i) … Adsorption is considered to be strong that in the time scale of the experiment, desorption is negligible…” while according to “(iv) adsorption and desorption are rapid and therefore do not control the kinetics of the reactions.”

If both the adsorption and desorption are rapid practically an equilibrium situation should be attained between the adsorbed and dissolved species. However, this conclusion (or consequence) is in conflict with the assumption that the role of dissolved redox species could be neglected.

In view of this contradiction, we may have some troubles what to consider adsorbing and desorbing species and what should be the meaning of the equilibria characterized by two reversible peak potentials [57] connected with equations

$$“{\mathrm{O}}^{z_{\mathrm{O}}}+n{e}^{-}\rightleftharpoons \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathrm{O}}^{z_{\mathrm{R}}}\hspace{1em}{E}_{\mathrm{c}}^{\mathrm{r}}$$

(4.1)

and the subsequent oxidation of R on the reverse sweep {(4.1) and (4.2) correspond to (1) and (2) in the original paper; there is a typographic error in (2) in the original paper.}

$${\mathrm{R}}^{z_{\mathrm{R}}}\hspace{0.17em}\hspace{0.17em}-n{e}^{-}\rightleftharpoons \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathrm{O}}^{z_{\mathrm{O}}}\hspace{1em}{E}_a^r$$

(4.2)

$E_{\mathrm{c}}^{\mathrm{r}}$ and $E_{\mathrm{a}}^{\mathrm{r}}$ are the reversible peak potentials. Subscripts c and a refer to cathodic and anodic processes, respectively. The reversible region is defined as the region, bounded on one side by v→0, in which the peak potentials are constant with increasing sweep rates. The point at which the peak potential changes with increasing sweep rate represents the onset of quasireversibility. $E_c^r$ and $E_a^r$ are listed as separate values since it is frequently observed that even under reversible conditions the cathodic and anodic peaks are separated ($\Delta E_{\mathsf{\rho }}\ne 0$).”

The simultaneous use of Equations (4.1) and (4.2) for the description of a reversible process is hardly understandable in terms of usual stoichiometry as the equations represent the same reversible reactions. In the case of reversibility, no separation of the anodic and cathodic peak potentials should be observed. If the potentials of anodic and cathodic potential peaks are not dependent on sweep rate but they are different the situation can be explained only by the assumption that during the cathodic and anodic sweeps different reversible reactions take place. Only by this assumption can be avoided the violation of the relevant laws of thermodynamics.

If we consider the technique of linear sweep voltammetry, we encounter further difficulties. Namely, a sweep rate independent peak potential and “regular shaped” voltammetric curves can be expected only in the case of redox processes with high exchange current densities. This equals to the statement that the rate of charge transfer through the interface in both directions is significantly higher than the net current measured in the external circuit and represented by the voltammograms.

In fact, Equations like (4.1) and (4.2) do not contain any information concerning the species involved in the charge exchange between the solution phase and the interface. Nevertheless, in some cases a closer examination of the system allows us to get a real picture of the processes involving solution species. This is the situation, e.g., in the case of redox transformation of quinones at graphite surfaces [60,61], where instead of the simplified schema given by Equations (4.1) or (4.2), the real chemical transformation can be expressed as Equation (4.3) (or Equation (4.4)) [61]:

$${\mathrm{Q}}_{\mathrm{ads}}+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}\to {\mathrm{H}}_2{\mathrm{Q}}_{\mathrm{ads}}$$

(4.3)

or

$${\mathrm{H}}_2{\mathrm{Q}}_{\mathrm{ads}}-2{\mathrm{e}}^{-}\to {\mathrm{Q}}_{\mathrm{ads}}+2{\mathrm{H}}^{+}$$

(4.4)

In reference [61] Q and H₂Q stand for 9,10-phenantrenequinone and 9,10-phenantrenehydro-quinone, respectively. It is evident that in this case the current is directly related to the transfer of hydrogen ions between the interface (“interphase”) and the bulk electrolyte solution phase and to the simultaneous electron transfer between the interphase and the electron conducting (graphite) phase of the electrode. This conclusion is further supported by the fact the electrochemical behavior of the system can be influenced significantly by changing the pH of the electrolyte solution in which the voltammograms are recorded. In this kind of reaction charged fragments of the adsorbed species (molecules in the particular case outlined above) move from the interphase into the solution, or ions enter the interphase and bond to adsorbed molecules.

Reaction equations like Equations (4.3) or (4.4) may always correspond to the physical reality in view of the facts that all species participating in the reactions are indicated and charge balance is maintained. It is important to note that a simultaneous charge transfer reaction at the counter electrode should also occur.

Considering Equations (4.3) and (4.4) it is quite evident that „well-shaped” cyclic voltammetric curves with sweep rate independent peak potentials can be obtained only in cases where the exchange current density of the overall

$${\mathrm{Q}}_{\mathrm{ads}}+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}\rightleftarrows {\mathrm{H}}_2{\mathrm{Q}}_{\mathrm{ads}}$$

(4.5)

process is high enough. If we consider this reaction only from the side of the solution phase (or the metal phase), one cannot help noticing the complete analogy of Equation (4.5) with the equation describing the electrosorption of protons e.g., on Pt sites:

$$2{\mathrm{H}}^{+}+2{\mathrm{e}}^{-}\rightleftarrows 2{\mathrm{H}}_{\mathrm{ads}}$$

(4.6)

In the case of the validity of Equations (4.5) and (4.6), nobody could claim that the electrochemical measurements furnish a rate constant of electron transfer to species confined to the surface. Obviously, the real process is much more complex, and the kinetic data obtained from electrochemical measurements reflect the overall reaction occurring at the interface.

Generally, one has the impression that the main source of the misunderstandings in this field is connected with ambiguities concerning the concept of electron transfer or charge transfer.

According to the definition in physics [62]: “…electron transfer is the passage of an electron from one atom or molecule to another by collision or other means”. In contrast to this, the definition of electron transfer or more generally the charge transfer is quite different in electrochemistry, e.g., according to [63]: “…the electrode reaction, must always include at least one elementary step in which charge is transferred from one phase to the other, but may also involve purely chemical steps within the interfacial region. The charge transfer step, like the electrode reaction is normally written as if the electrons were the carrier of charge across the interface. Consequently, this step is frequently referred to as an electron transfer step. Since charge can also be transferred by ions, the more general term charge transfer step is preferred.” or according to [64]: „Charge transfer reaction: Any→electrode reaction is an interfacial (heterogeneous) reaction that necessarily involves a charge transfer step … The latter can be a neutralization or formation of ions (ion transfer), or alteration of the ionic charge by the gain or loss electrons from or to the metal (→electron transfer), respectively. This is the actual electrochemical reaction. Charge transfer can occur not only at solid|liquid interface but practically at any variations of interfaces (e.g., liquid|liquid, solid|solid) causing a chemical change. The charge transfer has to be distinguished from the→charge transport.”

Although the Marcus theory [65,66] gives a unified treatment of both heterogeneous electron transfer at electrodes and homogeneous electron transfer in solutions. It follows from the foregoing considerations that electrochemical measurements can be evaluated only in terms of the latter definitions and in principle only the so called observable electrode reaction rate constant, characteristic for the overall reaction, can be determined [63].

5. Conclusions

In the light of the above review of literature and discussion, the following overall conclusions can be drawn:

(i) Although the electrosorption valency as usually defined is an extra-thermodynamic and self-contradictory concept, experimental determined formal partial charge numbers $l_{\mathrm{B}}=\frac{-{\left(\partial q_{\mathrm{m}}/\partial {\Gamma }_{\mathrm{B}}\right)}_{E,{\mu }_{\mathrm{i}}\ne {\mu }_{\mathrm{B}}}}{F}$ can be a useful tool for researchers studying adsorption kinetics, since the observed deviation between the values of $l_{\mathrm{S}}$ (or $\gamma$) and $z_{\mathrm{S}}$ explicitly indicates a complex (or at least “non-simple”) mechanism of the adsorption process, which should be taken into consideration in data evaluation, mathematical modeling, and theoretical interpretation of the experimental results.

(ii) The derivations and equations discussed in Section 3 clearly indicate that even in the case of rather simple systems the Gibbs adsorption equation can take various forms depending on the selection of the set of independent components, the choice of the indicator electrolyte and the indicator ion, and it should not be given in an oversimplified form as it was attempted in some previous studies.

(iii) Generally, one has the impression that the main source of the misunderstandings related to the formulation and interpretation of charge transfer processes involving adsorbed species is connected with ambiguities concerning the concept of electron transfer or charge transfer. It is highly probable that the origin of the concept of charge transfer between species in adsorbed state is based on the misinterpretation of some phenomena observed during voltammetric analysis of thin and ultrathin layers. Thin layer being a “bulk” phase, the material and charge transfer is not separated in the interpretations that can sometimes be found in the electrochemical literature.

In this regard a thin layer is not the equivalent of an adsorbed layer, therefore the equations describing the voltammetric behavior of a thin layer should differ from those of an adsorbed layer. Unfortunately, talking about adsorbed layer (or about interface or interphase) and applying equations derived for thin layers can lead to serious confusions.