Effect of Localized Surface Plasmons on the Nonlinear Optical Properties in the Semi-Parabolic Quantum Well

Abstract

In this paper, the effects of localized surface plasmons on the nonlinear optical properties of a composite system are studied. The system operates by placing a metal nanoparticle next to a semi-parabolic quantum well under a terahertz laser field. Firstly, the energy expression of the semi-parabolic well in the terahertz laser field is derived via a Kramers–Henneberger transformation, and then the new energy levels and wave functions are solved by the finite difference method. Next, optical absorption coefficients and refraction index changes are derived according to quantum theory. Finally, the study shows that localized surface plasmons can cause a redshift in the peak position, while simultaneously weakening the peak value of optical absorption coefficients. The results confirm that the desired performance can be obtained by adjusting the radius of the particle, the distance between the particle and the quantum well, or the natural frequency of the quantum well.

1. Introduction

The nonlinear optical properties of semiconductor materials continue to attract growing research interest [1,2]. Nonlinear optics offers profound insights into how light interacts with matter [3], reveals many basic physical phenomena, and promotes the development of many semiconductor industries and technologies [4] in the fields of opto-electronic devices [5], laser technology [6], sensors, and optical communications [7]. However, due to the material characteristics and electronic structure of some semiconductors, nonlinear optical properties are not ideal and cannot meet the application requirements [8,9]. Therefore, to improve the performance of optical instruments and exhibit new properties, it is necessary to find ways to improve the nonlinear optical properties of semiconductor materials [10,11].

In recent decades, according to different theoretical and experimental studies, experimenters and scientists have proposed various methods and completed different projects to improve nonlinear optical properties in semiconductors. Qiang Ma studied the effect of ZnO nanofilms on vertical Au nanorod arrays and showed that the scattering ability of a vertical gold array would be enhanced by increasing the diameter of the gold array [12]. Ungan demonstrated the effect of the terahertz laser field (TLF) on optical absorption coefficients (OACs) and refraction index changes (RICs) of an asymmetric n-shaped quantum well [13]. Through the analysis of nonlinear optical phenomena in a metal nanoparticle (MNP), Smolyaninov proved that nonlinear optical phenomena are affected by surface plasmons, and new qualitative effects emerge [14]. It is found that the optical absorption coefficients of quantum-sized spherical dome semiconductor nanoshells can be significantly improved by the resonance of surface plasmaons [15].

Semi-parabolic quantum wells are very important in the development of physics. Semi-parabolic quantum wells provide an ideal model to study the quantum confinement effect and help people understand the behavior of electrons in low-dimensional systems [16]. At the same time, semi-parabolic quantum wells are widely used in opto-electronic devices such as lasers, optical modulators, and photo-detectors. Their energy level structure and optical properties make these devices critical in modern communications and information technology [17]. Zhang studied the influence of the electric field on refraction index changes of semi-parabolic wells [18]. The effects of quantum confinement, incident light intensity, and relaxation rate on absorption coefficients in a semi-parabolic well were studied by Yu, XQ [19]. Yu, Y. B. considered the exciton effect and deduced nonlinear optical properties in a semi-parabolic quantum wire [20]. However, the effects of localized surface plasmons on the nonlinear optical effects of semi-parabolic wells have not been sufficiently studied. Therefore, we proposed a model of combining a metal nanosphere with a semi-parabolic quantum well. Based on the quantum effect and the coupling effect between a metal nanosphere and a quantum well, we theoretically derived the Hamiltonian of the composite system, and we finally obtain the changes in optical absorption coefficients and refractive index changes of the composite system under different conditions. The work in this paper supplements the missing constituents in previous works regarding the influence of the nanosphere on semi-parabolic quantum wells. The second section is devoted to the theoretical derivation, and the third section encompasses the results and discussion, concluding with a summary of the findings.

2. Theory

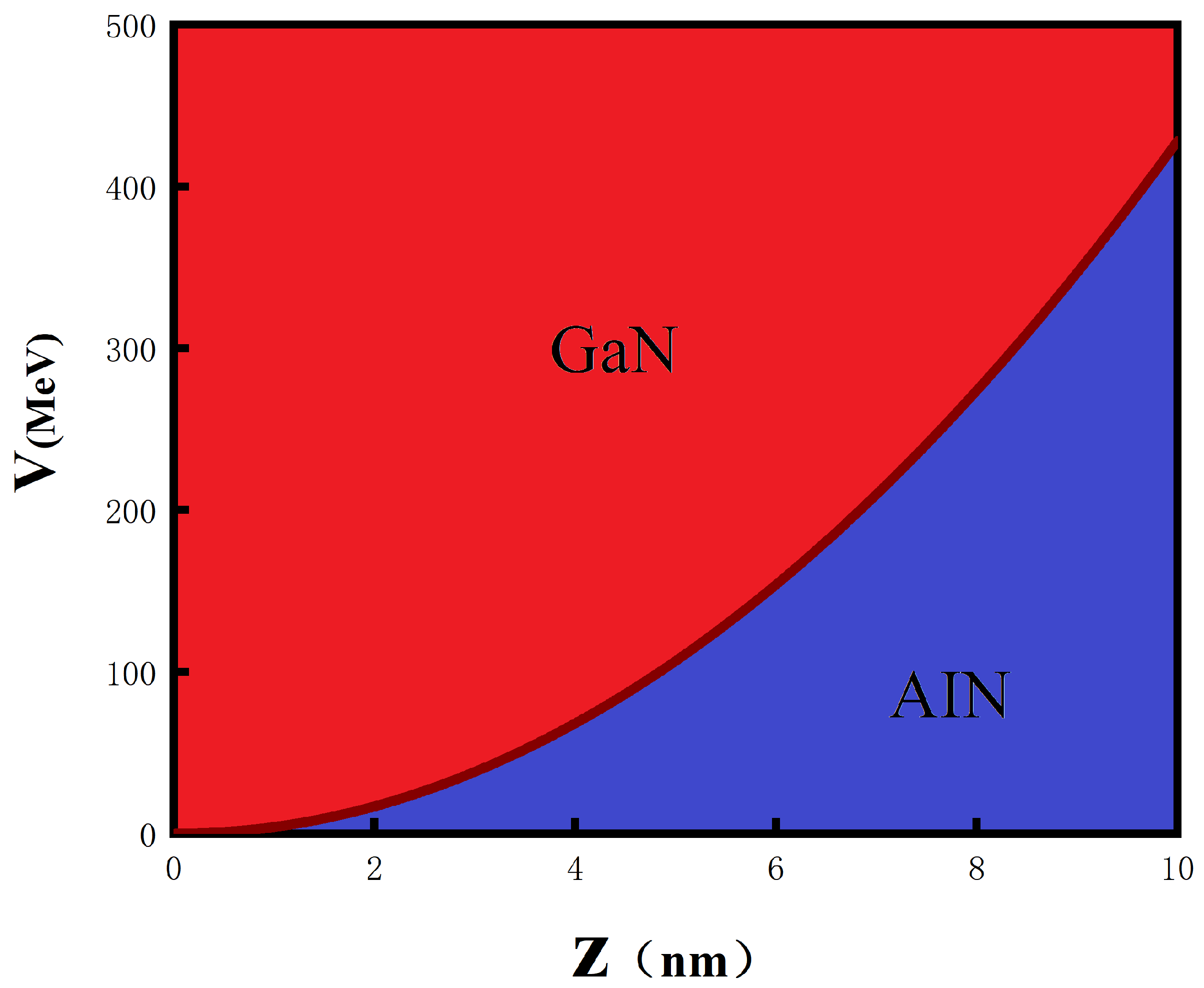
The formation of a semi-parabolic quantum well occurs through embedding a GaN into a larger energy band interval of AlN. The semi-parabolic quantum well structure is shown schematically in Figure 1.

The potential well boundary of the system is at the origin. In the semi-parabolic quantum well with moderate electron densities, the many-body electron interactions can be reduced to an effective single-particle problem through a mean-field treatment, owing to the screening effects and spatial confinement [21]. By adopting single-electron approximation (where electron–electron interactions are treated via a mean-field potential), using the effective mass approximation, the Schrödinger equation of the system is written as

$$-{\displaystyle \frac{{\hslash }^2}{2m^{*}}}{\nabla }^2\psi \left(\mathbf{z}\right)+V\left(\mathbf{z}\right)\psi \left(\mathbf{z}\right)=H\psi \left(\mathbf{z}\right),$$

(1)

where $\psi$(z) is the wave function of the electron obtained by solving the Schrödinger equation, and V(z) is the potential energy function in the z-direction. In order to solve the system accurately, the method of effective mass is adopted. The potential V(z) of the system is defined as follows:

$$V\left(\mathbf{z}\right)=\left\{\begin{array}{cc}\infty \hfill & \mathrm{if}\mathbf{z}<0\hfill \\ {\displaystyle \frac{1}{2}}{m}^{*}{\omega }^{*2}{z}^2\hfill & \mathrm{if}\mathbf{z}\ge 0\hfill \end{array}\right.$$

(2)

where $m^{*}$ is the effective electron mass, and ${\omega }^{*}$ is the natural frequency of the quantum well. We develop a theoretical framework modeling the semi-parabolic quantum well under the influence of an external terahertz laser field. The Schrödinger equation of the system needs to be rewritten due to the addition of terahertz laser field. According to ref. [22], the Schrödinger equation in the terahertz laser field can be rewritten as

$$i\hslash {\displaystyle \frac{\partial }{\partial t}}\psi (\mathbf{z},t)=\left[{\displaystyle \frac{1}{2m^{*}}}{\left(\widehat{p}+{\displaystyle \frac{q}{c}}A\right)}^2+V\left(\mathbf{z}\right)\right]\psi (\mathbf{z},t),$$

(3)

where $\widehat{p}$ signifies electron momentum (as opposed to the second term in the parentheses, which is field momentum) and $A(z,t)$ is the vector potential of the electromagnetic field of the laser. Utilizing the Kramers–Henneberger approach and dipole approximation approach [23,24], the time-dependent Schrödinger equation can be transformed into a time-independent form, where the laser field contribution shifts from the vector potential $A(z,t)$ in the Hamiltonian to the potential energy term $V_T\left(\mathbf{z}\right)$. The specific expression is as follows:

$$-{\displaystyle \frac{{\hslash }^2}{2m^{*}}}{\nabla }^2\psi \left(\mathbf{z}\right)+V_T\left(\mathbf{z}\right)\psi \left(\mathbf{z}\right)=H\psi \left(\mathbf{z}\right),$$

(4)

where $V_T\left(\mathbf{z}\right)$ signifies the formulation of the semi-parabolic quantum well with a laser field, given by

$$V_T\left(\mathbf{z}\right)={\displaystyle \frac{{\omega }_T}{2\pi }}{\int }_0^{{\displaystyle \frac{2\pi }{{\omega }_T}}}V\left[\mathbf{z}+\alpha \left(t\right)\right]dt,$$

(5)

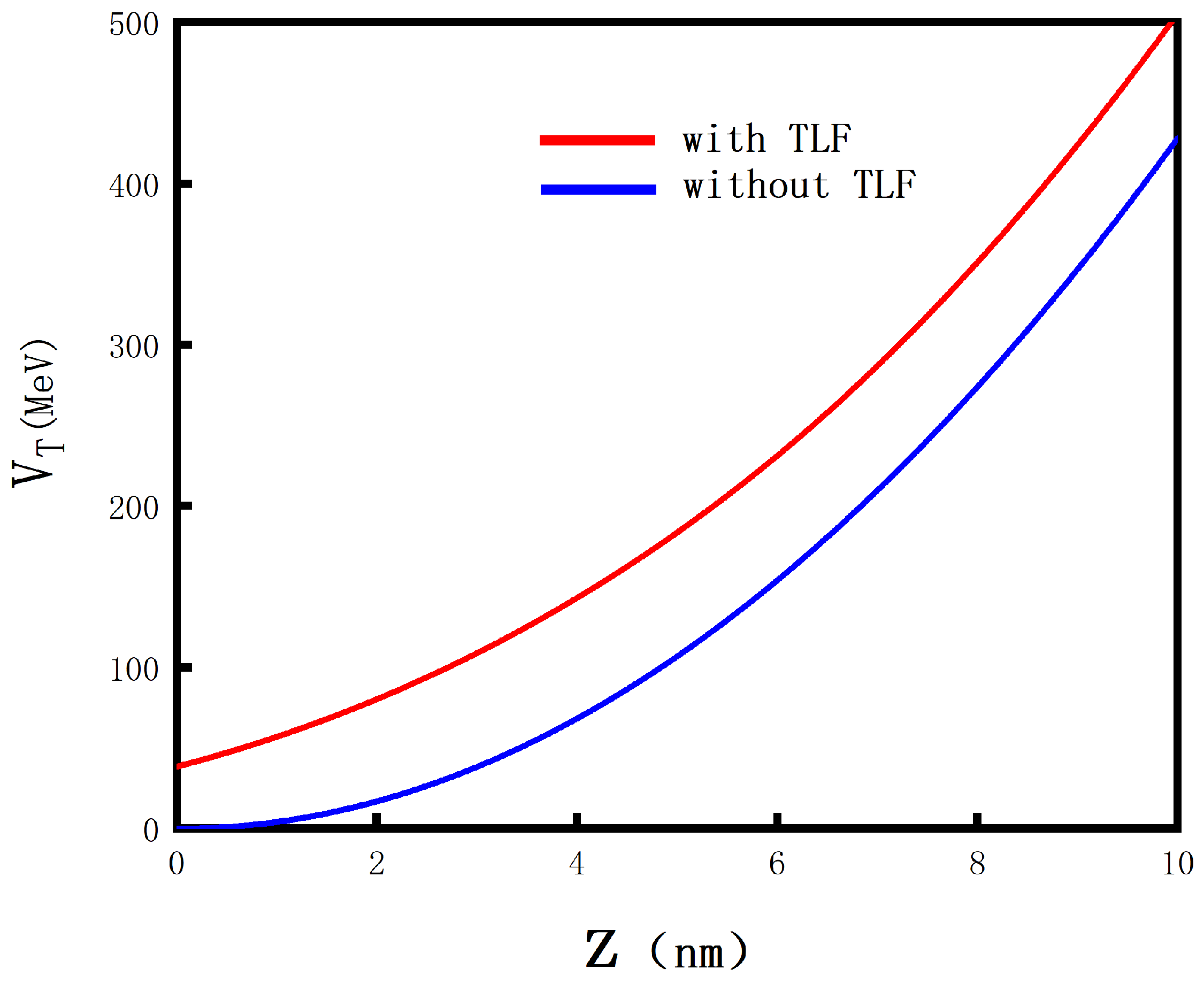
where ${\omega }_T$ signifies the angular frequency associated with a laser field, $\alpha \left(t\right)={\alpha }_{0}sin\left({\omega }_{T}t\right)$. The field-induced modifications of the semi-parabolic quantum well under terahertz laser irradiation, relative to the field-free case, are characterized in Figure 2. The parameter ${\alpha }_0$ signifies the laser-dressing parameter, given by ${\alpha }_0={\displaystyle \frac{e{A}_0}{m^{*}{\omega }_T}}$, where $A_0$ refers to the amplitude of a laser field. We can obtain the energy function after adding a strong laser field. Following this, the finite difference method can be employed to derive the wave function of the Schrödinger equation and its corresponding energy levels [25].

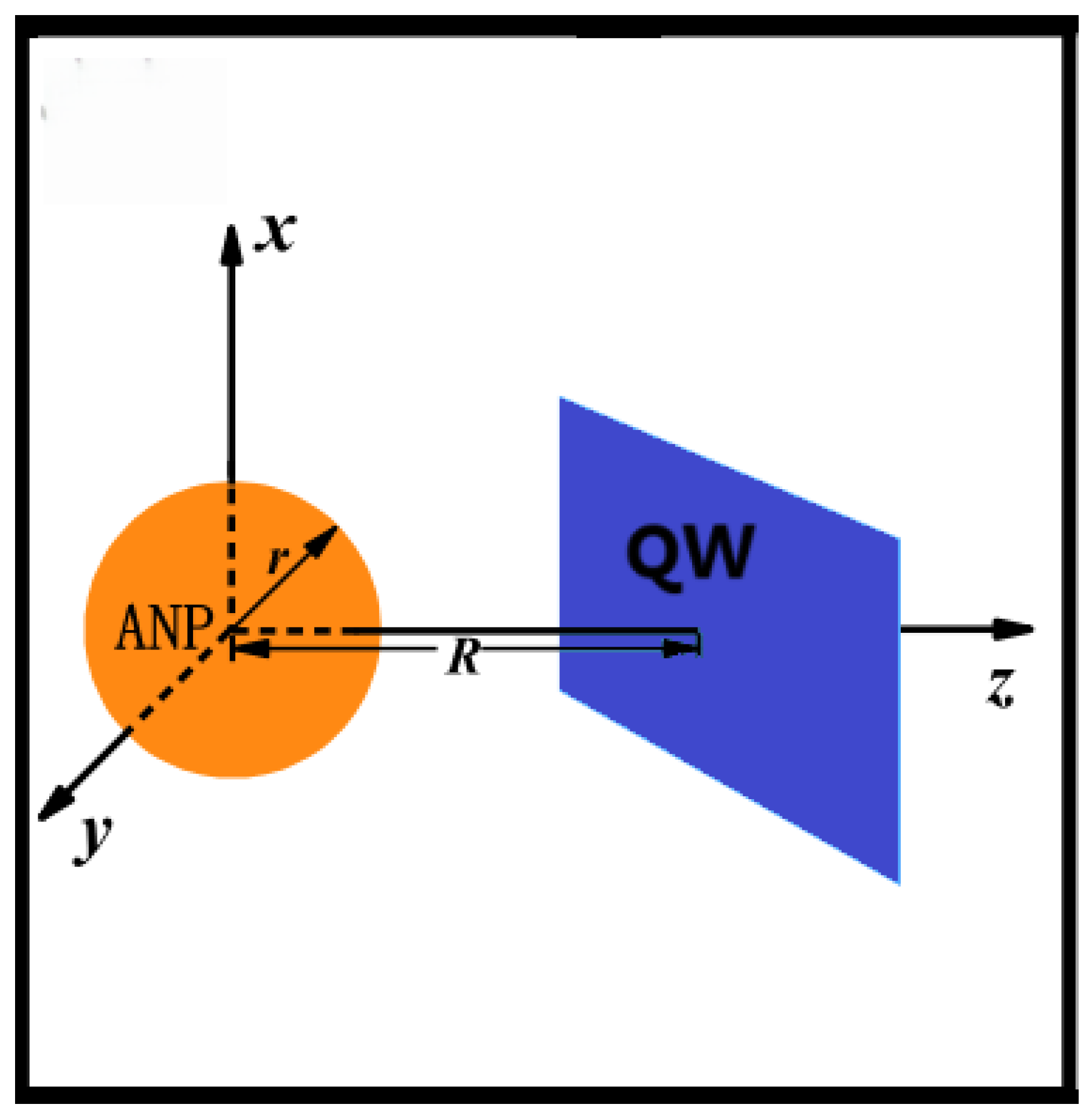
The composite system, embedded within a dielectric medium of permittivity ${ϵ}_B$, integrates the semi-parabolic quantum well under laser illumination and a gold metal nanoparticle. As schematized in Figure 3, the metal nanoparticle is positioned adjacent to the quantum well confinement region to enable strong plasmon–exciton coupling, characterized by bidirectional energy exchange.

When irradiated by the laser field ${\mathbf{E}}_t=E_{0}cos\left({\omega }_{T}t\right)\widehat{\mathbf{z}}$, the gold metal nanoparticle exhibits localized surface plasmons through the resonant excitation of coherent collective oscillations of conduction electrons at the metal–dielectric interface. These plasmonic modes arise when the driving laser frequency ${\omega }_T$ approaches the characteristic surface plasmon resonance frequency ${\omega }_{\mathrm{SPR}}$, determined by the nanoparticle geometry, size, material properties (described by ${ϵ}_{\mathrm{MNP}}$), and surrounding dielectric environment (${ϵ}_B$). At resonance, significant electromagnetic field localization occurs, generating substantial near-field enhancement. The enhanced field concentrates near the nanoparticle surface and diminishes quickly away from it, with its strength dropping sharply over nanometer-scale distances.

This plasmonic near-field directly interacts with the adjacent quantum well confinement region through three primary mechanisms:

• Potential modification : The strong local electric field redistributes charge carriers in the quantum well, effectively modifying the confinement potential landscape.
• Dipole enhancement: The plasmonic field coherently couples to inter-sub-band dipole moments, amplifying the effective dipole transition matrix elements ${\mu }_{ij}$ between quantum states.
• Dissipation pathway: Energy transfer between the quantum well excitations and plasmon oscillations creates additional relaxation channels, altering the carrier scattering dynamics.

Collectively, these interactions induce renormalization of the fundamental quantum parameters: the energy gap between states $|0\rangle$ and $|1\rangle$ shifts from $H_{10}$ to $H_{10}^{\prime }=H_{10}-\hslash G_R$, while the relaxation rate increases from $\Gamma$ to ${\Gamma }^{\prime }=\Gamma +G_I$. This plasmon-mediated modification of quantum properties forms the physical basis for tuning the nonlinear optical coefficients of the hybrid system [26]. This plasmonic response modifies the effective field governing the quantum well (QW) dynamics via three components:

$${\mathbf{E}}_{\mathrm{QW}}={\mathbf{E}}_1+{\mathbf{E}}_2+{\mathbf{E}}_3,$$

where

-

${\mathbf{E}}_1$ denotes the unperturbed laser field;

-

${\mathbf{E}}_2$ represents the plasmon-enhanced field originating from the metal nanoparticle polarization driven by ${\mathbf{E}}_t$;

-

${\mathbf{E}}_3$ corresponds to the feedback field arising from the metal nanoparticle polarization induced by the QW’s dipole moment ${\mathbf{P}}_{\mathrm{QW}}={\mu }_{10}({\widehat{\rho }}_{01}^{*}{e}^{i\omega t}+{\widehat{\rho }}_{01}{e}^{-i\omega t})$.

The self-consistent nature of ${\mathbf{E}}_3$ establishes a feedback loop between the quantum well and the metal nanoparticle, confirming the strong coupling regime. This dual-field mechanism underpins enhanced nonlinear optical responses in the hybrid system [26]. The expressions of $E_1$, $E_2$, and $E_3$ are, respectively [27,28],

$$\begin{array}{cc}\hfill & E_1={\displaystyle \frac{E_0}{{ϵ}_{eff}}},{ϵ}_{eff}={\displaystyle \frac{2{ϵ}_B+{ϵ}_R}{3{ϵ}_B}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & E_2={\displaystyle \frac{S_{\alpha }{P}_{MNP}^{\left(2\right)}}{4\pi {ϵ}_B{ϵ}_{eff}{R}^3}},P_{MNP}^{\left(2\right)}=4\pi {ϵ}_B\gamma r^3{E}_0,\hspace{1em}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & E_3={\displaystyle \frac{S_{\alpha }{P}_{MNP}^{\left(3\right)}}{4\pi {ϵ}_B{ϵ}_{eff}{R}^3}},P_{MNP}^{\left(3\right)}=4\pi {ϵ}_B\gamma r^3{E}_{MNP},\hfill \end{array}$$

$$\begin{array}{cc}\hfill & E_{MNP}={\displaystyle \frac{S_{\alpha }{P}_{QWs}}{4\pi {ϵ}_B{ϵ}_{eff}{R}^3}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hfill \end{array}$$

(8)

where $\gamma ={\displaystyle \frac{{ϵ}_{MNP}-{ϵ}_B}{2{ϵ}_B+{ϵ}_{MNP}}}$, and $S_{\alpha }=2$ when the electric field $E_0$ is parallel to the z-axis. By solving the optical Bloch equations, the $E_{QWs}$ can be expressed as follows:

$$\begin{array}{cc}\hfill & E_{QW}={\displaystyle \frac{\hslash }{{\mu }_{10}}}[(\Omega +G{\widehat{\rho }}_{01})e^{-i\omega t}+({\Omega }^{*}+G^{*}{\widehat{\rho }}_{01}^{*})e^{i\omega t}],\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \Omega ={\displaystyle \frac{E_0{\mu }_{10}}{2\hslash {ϵ}_{eff}}}(1+{\displaystyle \frac{S_{\alpha }\gamma r^3}{R^3}}),\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & G=G_R+i{G}_I={\displaystyle \frac{S_{\alpha }^2\gamma r^3{\mu }_{10}^2}{4\pi {ϵ}_B\hslash {ϵ}_{eff}^2{R}^6}},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hfill \end{array}$$

(11)

where ${\mu }_{10}$ denotes the transition matrix element. $G_I$ is generated when the applied field polarizes the quantum well. The quantum well polarizes the metal nanoparticle, and the generated field then interacts with the quantum well. Therefore, this can be regarded as a self-interaction of the quantum well. The real and imaginary components of G are designated as $G_R$ and $G_I$, respectively. The primary coupling term $\Omega$ directly interacts with the applied field, while the secondary term $\Omega$ arises from the nanoparticle-generated field.

Crucially, the localized surface plasmons modify the quantum system’s fundamental parameters such that the energy gap, which becomes $H_{10}^{\prime }=H_{10}-\hslash G_R$, and the relaxation rate, which becomes ${\Gamma }^{\prime }=\Gamma +G_I$. Metallic nanosphere-induced localized surface plasmons modulate the energy gap and relaxation rates in the quantum well, thereby directly tuning its optical coefficients. This mechanism provides the physical basis for enhanced nonlinear optical responses in hybrid quantum systems.

Subsequently, by utilizing the compact density matrix theory and the iterative method, the linear absorption coefficient ${\alpha }^{\left(1\right)}\left(\omega \right)$ and nonlinear absorption ${\alpha }^{\left(3\right)}\left(\omega \right)$ of the semi-parabolic quantum well are, respectively, expressed as [29,30,31]

$$\begin{array}{cc}\hfill & {\alpha }^{\left(1\right)}\left(\omega \right)=\omega \sqrt{{\displaystyle \frac{{\mu }_0}{{ϵ}_R}}}\left[{\displaystyle \frac{{\sigma }_v\hslash {\Gamma }^{\prime }{\left|{\mu }_{10}\right|}^2}{{(H_{10}^{\prime }-\hslash \omega )}^2+{(\hslash {\Gamma }^{\prime })}^2}}\right],\hfill \\ \hfill & {\alpha }^{\left(3\right)}(\omega ,I)=-\omega \sqrt{{\displaystyle \frac{{\mu }_0}{{ϵ}_R}}}{\displaystyle \frac{\omega I}{2{ϵ}_0{n}_{r}c}}\hfill \\ \hfill & {\displaystyle \frac{{\sigma }_v\hslash {\Gamma }^{\prime }{\left|{\mu }_{10}\right|}^2}{{[{(H_{10}^{\prime }-\hslash \omega )}^2+{(\hslash {\Gamma }^{\prime })}^2]}^2}}\{4{\left|{\mu }_{10}\right|}^2\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & -{\displaystyle \frac{|{\mu }_{11}-{\mu }_{00}{|}^2[H_{10}^{\prime 2}-4H_{10}^{\prime }\hslash \omega +{\hslash }^2({\omega }^2-{\Gamma }^{\prime 2})]}{H_{10}^{\prime 2}+{(\hslash {\Gamma }^{\prime })}^2}}\}\hfill \end{array}$$

(13)

and the total absorption coefficients are expressed by

$$\begin{array}{cc}\hfill \alpha (\omega ,I)& ={\alpha }^{\left(1\right)}\left(\omega \right)+{\alpha }^{\left(3\right)}(\omega ,I),\hfill \end{array}$$

(14)

where ${ϵ}_R=n_r^2{ϵ}_0$ represents the actual dielectric constant; $n_r$ represents the refractive index; I represents the intensity of the incoming probe light; ${\sigma }_v$ represents the electron number density; ${\mu }_0$ represents the permeability property of the system; ${\mu }_{ij}=<{\psi }_i\left|ez\right|{\psi }_j>$ represents the transition matrix; ${\psi }_i$ (i = 0, 1, 2) represents the wave functions of the ground state, first excited state, and second excited state, respectively; and $H_{ij}^{\prime }=\hslash {\omega }_{ij}^{\prime }=\hslash ({\omega }_{ij}-G_R)$ represents the altered energy gap between two distinct electronic states.

The linear refractive index changes ${\displaystyle \frac{\Delta n^{\left(1\right)}\left(\omega \right)}{n_r}}$ and nonlinear refractive index changes ${\displaystyle \frac{\Delta n^{\left(3\right)}\left(\omega \right)}{n_r}}$ of the semi-parabolic quantum well are, respectively, expressed as

$$\begin{array}{cc}\hfill {\displaystyle \frac{\Delta n^{\left(1\right)}\left(\omega \right)}{n_r}}& ={\displaystyle \frac{{\sigma }_v{\left|{\mu }_{10}\right|}^2}{2n_r^2{ϵ}_0}}\left[{\displaystyle \frac{H_{10}^{\prime }-\hslash \omega }{{(H_{10}^{\prime }-\hslash \omega )}^2+{(\hslash {\Gamma }^{\prime })}^2}}\right],\hfill \\ \hfill {\displaystyle \frac{\Delta n^{\left(3\right)}(\omega ,I)}{n_r}}& =-{\displaystyle \frac{|{\mu }_{10}{|}^2}{4n_r^3{ϵ}_0}}{\displaystyle \frac{{\sigma }_v{\mu }_{0}cI}{{[{(H_{10}^{\prime }-\hslash \omega )}^2+{(\hslash {\Gamma }^{\prime })}^2]}^2}}\hfill \\ \hfill & \left[4(H_{10}^{\prime }-\hslash \omega ){\left|{\mu }_{10}\right|}^2-{\displaystyle \frac{{({\mu }_{11}-{\mu }_{00})}^2}{H_{10}^{\prime 2}+{(\hslash {\Gamma }^{\prime })}^2}}\right.\hfill \\ \hfill & \left\{(H_{10}^{\prime }-\hslash \omega )\left[H_{10}^{\prime }(H_{10}^{\prime }-\hslash \omega )-{(\hslash {\Gamma }^{\prime })}^2\right]\right.\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \left.-{(\hslash {\Gamma }^{\prime })}^2(2H_{10}^{\prime }-\hslash \omega )\right\}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$

(16)

and the total refractive index changes are expressed by

$$\begin{array}{cc}\hfill {\displaystyle \frac{\Delta n(\omega ,I)}{n_r}}& ={\displaystyle \frac{\Delta n^{\left(1\right)}\left(\omega \right)}{n_r}}+{\displaystyle \frac{\Delta n^{\left(3\right)}(\omega ,I)}{n_r}}.\hfill \end{array}$$

(17)

We can find that the values of optical absorption coefficients and refraction index changes depend on the energy gap and relaxation rate of the system. Therefore, we can correct the energy range gap and relaxation rate of the system to calculate the influence of a metal nanoparticle on the system.

3. Results and Discussion

This section presents the computational findings of the composite system. All analyses are performed using the following parameters: $m^{*}$ = 0.067 $m_0$, $n_r$ = 3.2, ${\sigma }_v$ = 5.0 × ${10}^{24}{m}^{-3}$, $\Gamma$ = ${\displaystyle \frac{1}{0.11\times {10}^{-12}}}s$, ${ϵ}_B={ϵ}_0=8.85\times {10}^{-12}F/m$ [29].

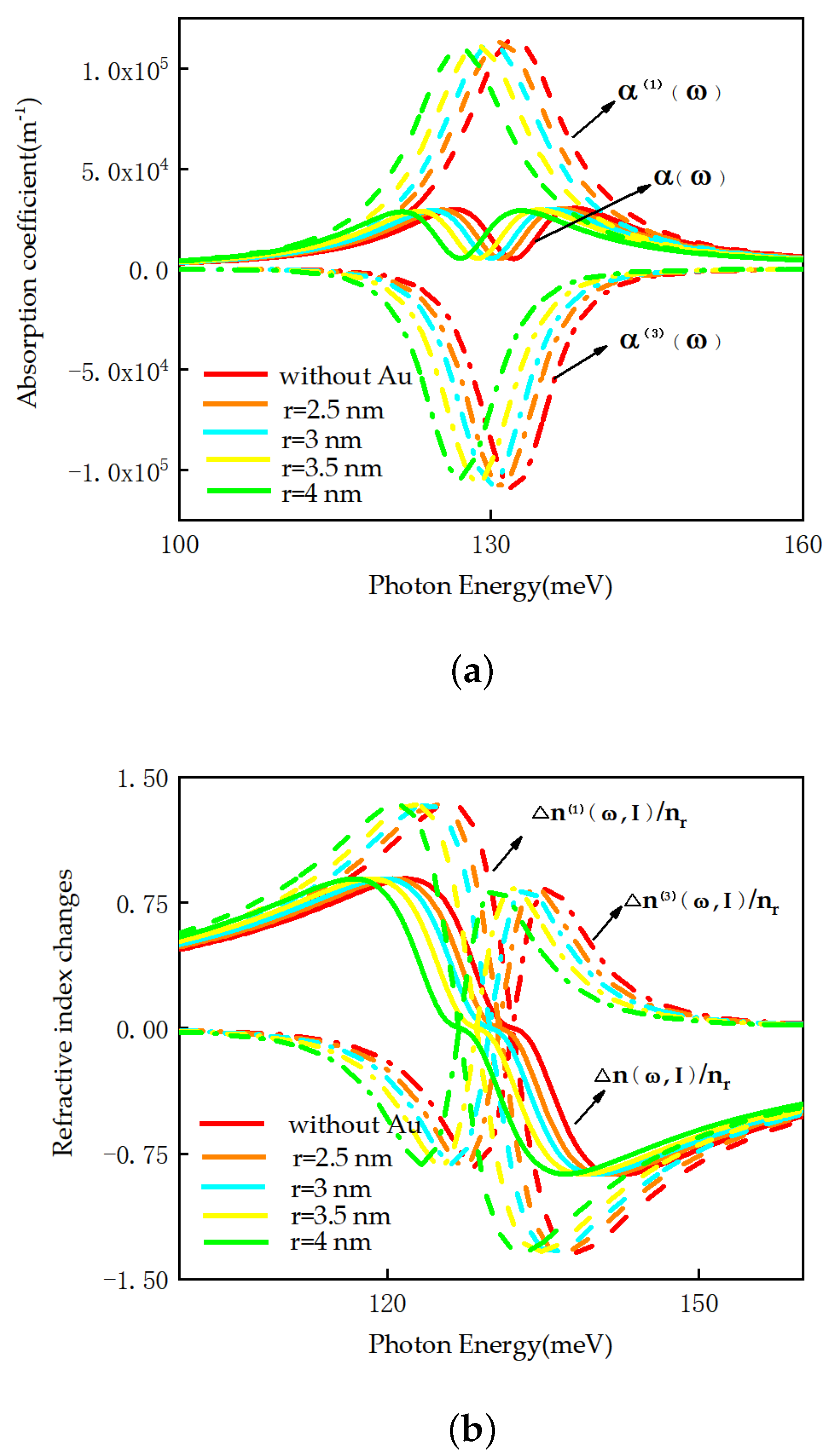
Figure 4 illustrates the optical absorption coefficients and refractive index changes of the semi-parabolic quantum well subjected to a laser field for different particle radii (r), plotted as a function of photon energy ($\hslash \omega$). This analysis considers both scenarios with and without a metal nanoparticle, specifically for $R=5$ nm, $I=0.4$ MW/${\mathrm{cm}}^2$, ${\omega }^{*}=1.0\times {10}^{14}$ ${\mathrm{s}}^{-1}$. As can be seen from Figure 4, the presence of a metal nanoparticle shifts the peak position of absorption coefficients and refraction index changes in the low-frequency direction, as compared to images without the effect of a metal nanoparticle. This phenomenon can be summarized as the metal nanoparticle forms a new local field around it. According to quantum theory, we can infer that the enhancement of the local field makes the electron wave function in the quantum well discrete, reduces the constraint on electron motion, changes the energy level structure of the quantum well, and ultimately leads to the reduction in the energy level gap. Therefore, the presence of a metal nanoparticle causes optical absorption coefficients and refraction index changes to be redshifted. At the same time, it can be found from Figure 4 that the presence of a metal nanoparticle causes the peak value of first-order linear light absorption and third-order nonlinear light absorption to decrease significantly, while the peak value for the refraction index changes remains basically unchanged. The reason is that the amplitudes of optical absorption coefficients and refraction index changes are related to the matrix element, but the optical absorption coefficients are also related to the energy gap, and the energy gap is reduced due to the presence of localized surface plasmons. Therefore, the amplitudes of linear and nonlinear absorption decrease, while the total peak value remains constant because of the counteracting effect between the decrease in linear absorption and the negative contribution of third-order nonlinear absorption.

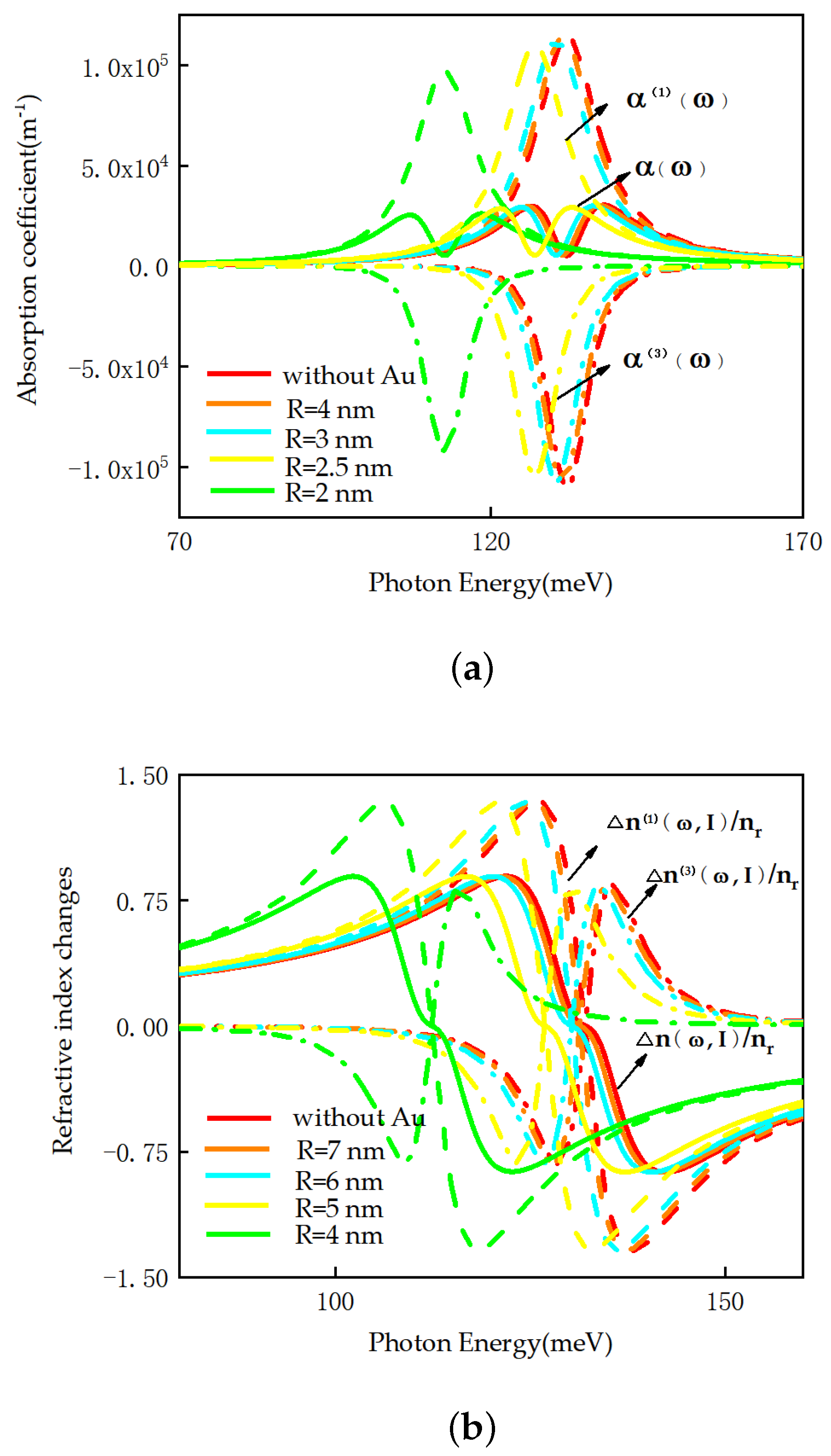
Figure 5 illustrates optical absorption coefficients and refraction index changes of a semi-parabolic quantum well subjected to a laser field at various distances between the particle and quantum well (R), plotted as a function of photon energy ($\hslash \omega$). This analysis considers both scenarios with and without a metal nanoparticle, specifically for $r=1$ nm, $I=0.4$ MW/${\mathrm{cm}}^2$, ${\omega }^{*}=1.0\times {10}^{14}{\mathrm{s}}^{-1}$. It can be found that as distance is reduced, the peak values of optical absorption coefficients show a trend of continuously declining and the peak position being redshifted, while refraction index changes show a redshift of the peak position and the peak value remains relatively unchanged. It can be seen that the characteristics of Figure 5 are similar to those of Figure 4. This case shows that the physical reasons for the appearance of the two figures are the same. Both images show the enhancement of a metal nanoparticle, which leads to a reduction in the energy level gap. At the same time, we find that as R decreases, reducing R further results in a large difference in redshift amplitude. This situation shows that the metal nanoparticle elicits a good regulation effect on the nonlinear optical effects of the semi-parabolic quantum well; moreover, we can set corresponding parameters (R) to effectively adjust the optical effect of the potential well.

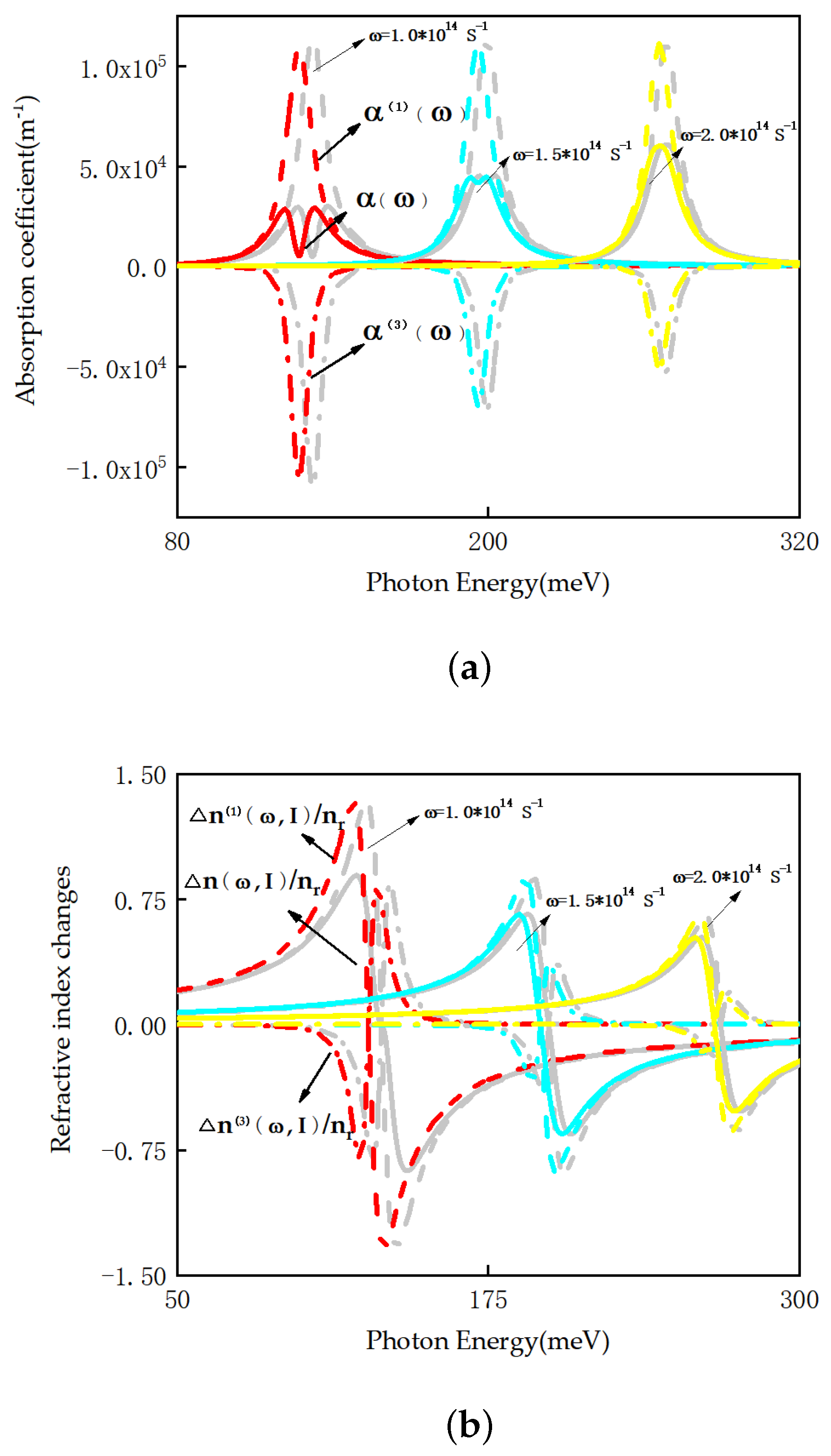
According to Equations (14) and (17), we know that optical absorption coefficients and refraction index changes are related to the energy gap, and the energy gap of the semi-parabolic quantum well depends on the natural frequency. Therefore, we aim to investigate the effect of a metal nanoparticle on a semi-parabolic quantum well with different natural frequencies. Figure 6 illustrates optical absorption coefficients and refraction index changes of a semi-parabolic quantum well subjected to a laser field under various ${\omega }^{*}$ conditions, plotted as a function of photon energy ($\hslash \omega$). This analysis considers both scenarios with and without a metal nanoparticle, specifically for $R=5$ nm, $I=0.4$ MW/${\mathrm{cm}}^2$ and $r=4$ nm. We can find that with an increase in the natural frequency, it can be found that the peak position of optical absorption coefficients and refraction index changes will appear blue-shifted, and the bleaching effect will decrease gradually. This is because with the increase in the natural frequency, the energy level interval and transition frequency increase, which improves the response of the system to light and finally makes the peak position blue-shift. At the same time, with the increase in the natural frequency, the nonlinear response becomes more stable, and the third-order nonlinear polarizabilities of the quantum well are weakened due to the absorption saturation effect; additionally, the bleaching effect is weakened. In Figure 6, we also find that the redshift amplitude of optical absorption coefficients and refraction index changes decrease with the increase in the natural frequency, as the increase in the natural frequency leads to an increase in the energy level gap. It can be found that the nonlinear optical effects can be effectively adjusted by adjusting the natural frequency of the semi-parabolic quantum well.

4. Conclusions

In this paper, the expression of the semi-parabolic quantum well in the terahertz laser field is derived, and the numerical expression and energy level of the semi-parabolic quantum well are given. Following this, the role of localized surface plasmons generated by a metal nanoparticle on a semi-parabolic quantum well in the presence of a laser field is assessed. The effects of localized surface plasmons on optical absorption coefficients and refraction index changes are investigated. It is found that localized surface plasmons can cause a redshift of optical absorption coefficients and refraction index changes while also causing a reduction in the peak values of optical absorption. Finally, it is determined that the peak position can be blue-shifted by altering the natural frequency of a system itself, and the amplitude of the redshift caused by localized surface plasmons can be adjusted, so as to obtain the desired light absorption and refractive index.