Introducing Optical Nonlinearity in PDMS Using Organic Solvent Swelling
Abstract
1. Introduction
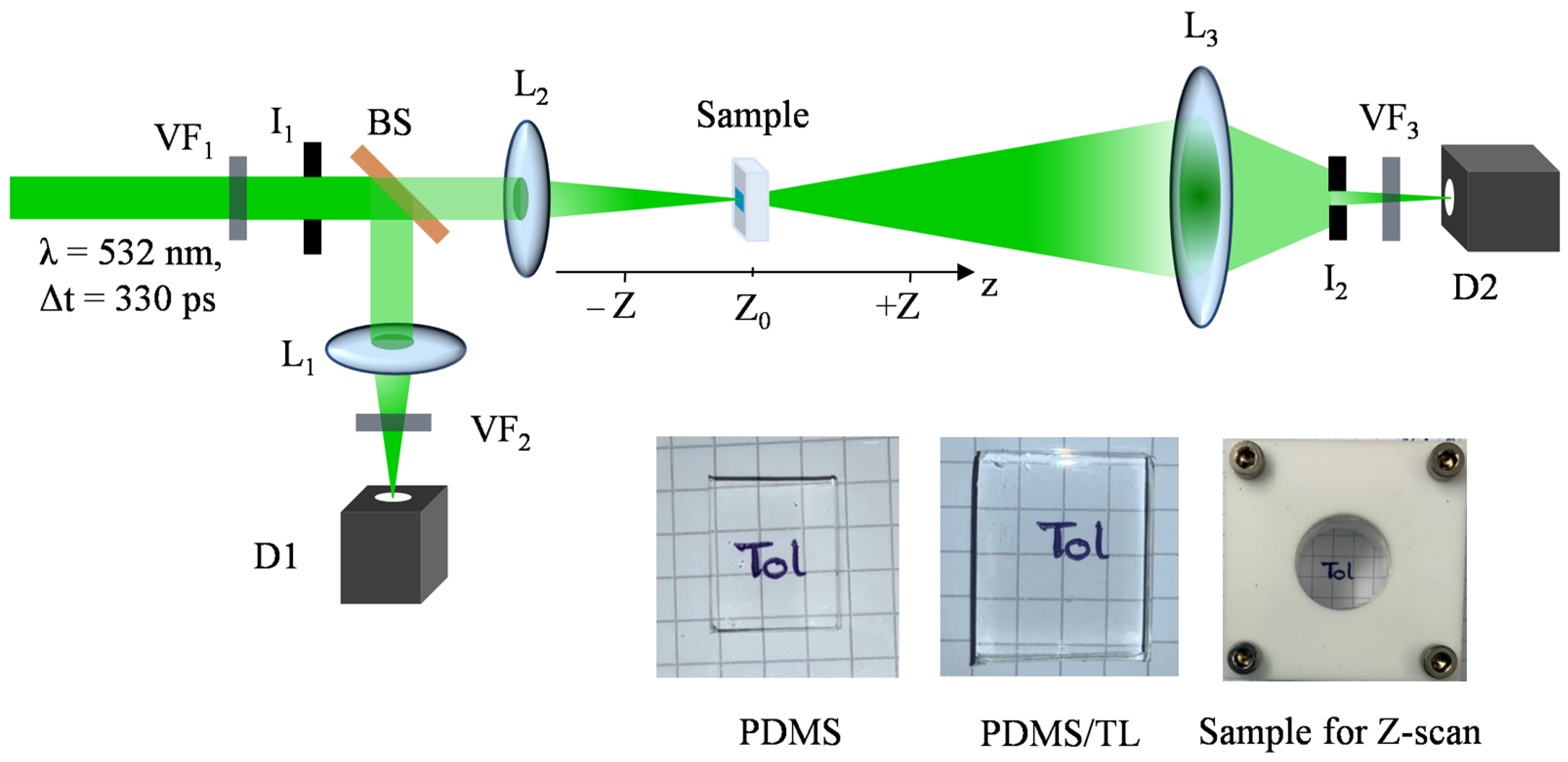
2. Materials and Methods
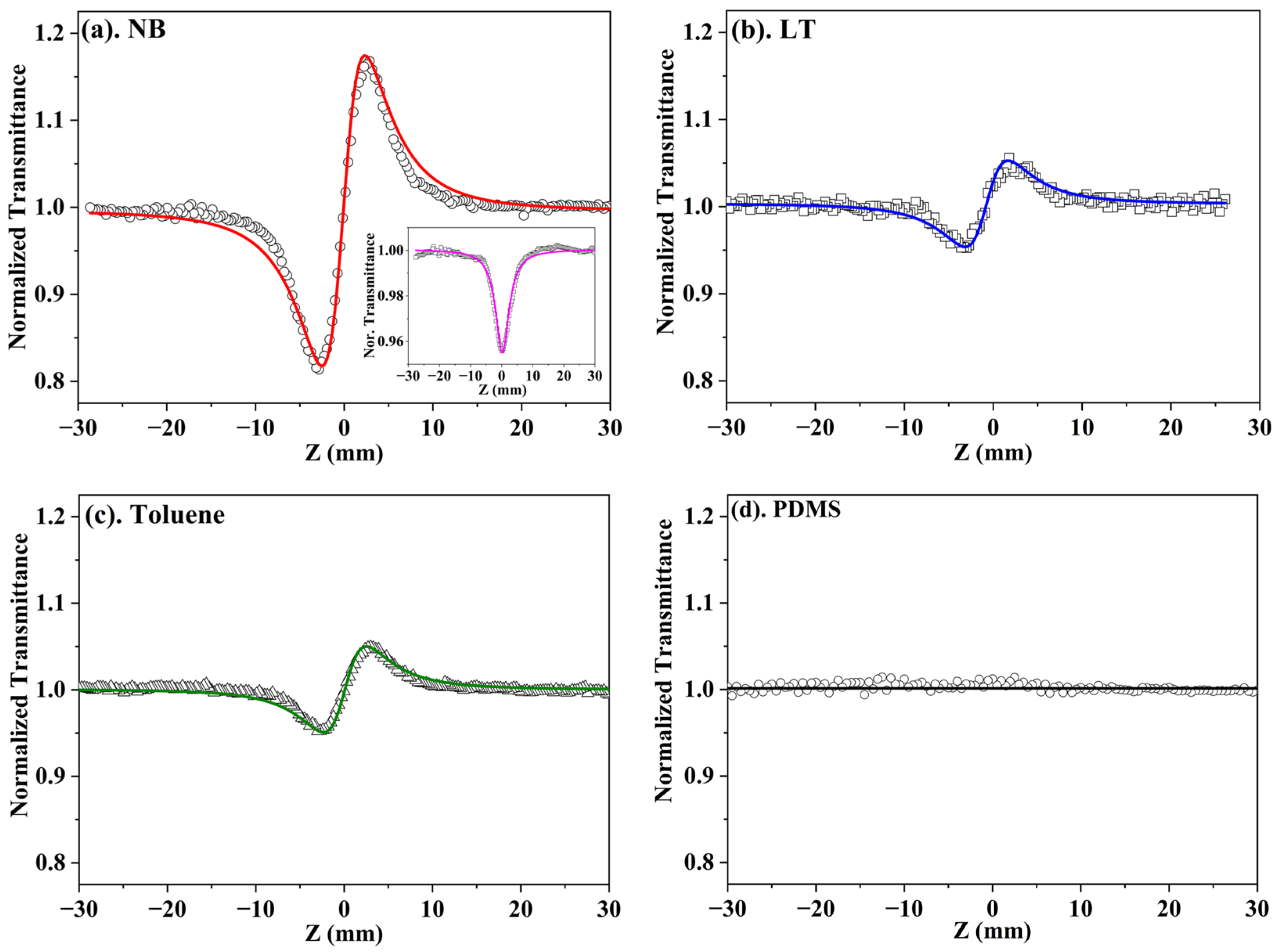
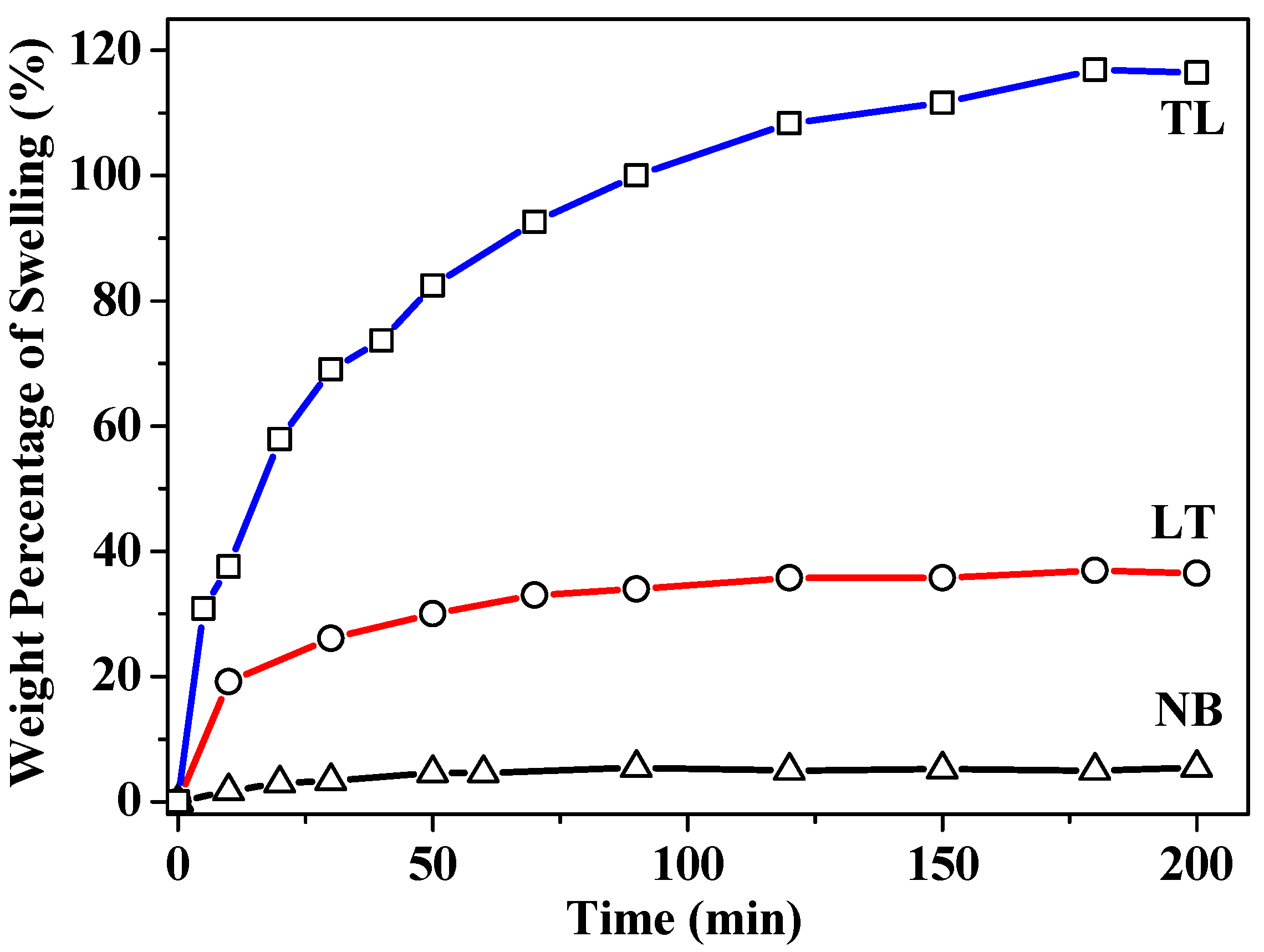
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Lin, C.-Y.; Nikolaenko, A.; Raghunathan, V.; Potma, E.O. Four-wave mixing microscopy of nanostructures. Adv. Opt. Photon. 2011, 3, 1–52. [Google Scholar] [CrossRef]
- Boyd, R.W. Nonlinear Optics; Academic Press, Inc.: Cambridge, MA, USA, 2008. [Google Scholar]
- Zhang, Y.; Lu, D.; Yu, H.; Zhang, H. Low-Dimensional Saturable Absorbers in the Visible Spectral Region. Adv. Opt. Mater. 2019, 7, 1800886. [Google Scholar] [CrossRef]
- Schneider, T. Nonlinear Optics in Telecommunications; Springer Science & Business Media: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Garmire, E. Nonlinear optics in daily life. Opt. Express 2013, 21, 30532. [Google Scholar] [CrossRef]
- Zhang, M.; Buscaino, B.; Wang, C.; Shams-Ansari, A.; Reimer, C.; Zhu, R.; Kahn, J.M.; Lončar, M. Broadband electro-optic frequency comb generation in a lithium niobate microring resonator. Nature 2019, 568, 373–377. [Google Scholar] [CrossRef]
- Li, M.; Chang, L.; Wu, L.; Staffa, J.; Ling, J.; Javid, U.A.; Xue, S.; He, Y.; Lopez-Rios, R.; Morin, T.J.; et al. Integrated Pockels laser. Nat. Commun. 2022, 13, 5344. [Google Scholar] [CrossRef]
- Haag, H.; Hönerlage, B.; Briot, O.; Aulombard, R.L. Influence of defect states on the nonlinear optical properties of GaN. Phys. Rev. B 1999, 60, 11624–11630. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, X.; Yan, H.; Chen, Z.; Liu, Y.; Liu, S. Highly efficient GaN-based high-power flip-chip light-emitting diodes. Opt. Express 2019, 27, A669–A692. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, X.; Yan, H.; Gao, Y.; Xu, H.; Zhao, J.; Liu, S. The effect of nanometre-scale V-pits on electronic and optical properties and efficiency droop of GaN-based green light-emitting diodes. Sci. Rep. 2018, 8, 11053. [Google Scholar] [CrossRef]
- Xia, P.; Kim, C.; Lu, F.; Kanai, T.; Akiyama, H.; Itatani, J.; Ishii, N. Nonlinear propagation effects in high harmonic generation in reflection and transmission from gallium arsenide. Opt. Express 2018, 26, 29393–29400. [Google Scholar] [CrossRef]
- Dalton, L.R.; Günter, P.; Jazbinsek, M. . Organic Electro-Optics and Photonics: Molecules, Polymers, and Crystals; Materials Research Society and Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Xu, J.; Li, X.; Xiong, J.; Yuan, C.; Semin, S.; Rasing, T.; Bu, X.H. Halide Perovskites for Nonlinear Optics. Adv. Mater. 2020, 32, 1806736. [Google Scholar] [CrossRef]
- Guo, B.; Xiao, Q.; Wang, S.; Zhang, H. 2D Layered Materials: Synthesis, Nonlinear Optical Properties, and Device Applications. Laser Photon. Rev. 2019, 13, 1800327. [Google Scholar] [CrossRef]
- You, J.; Bongu, S.; Bao, Q.; Panoiu, N. Nonlinear optical properties and applications of 2D materials: Theoretical and experimental aspects. Nanophotonics 2018, 8, 63–97. [Google Scholar] [CrossRef]
- Mistark, P.A.; Park, S.; Yalcin, S.E.; Lee, D.H.; Yavuzcetin, O.; Tuominen, M.T.; Russell, T.P.; Achermann, M. Block-Copolymer-Based Plasmonic Nanostructures. ACS Nano 2009, 3, 3987–3992. [Google Scholar] [CrossRef]
- Alvarez-Fernandez, A.; Cummins, C.; Saba, M.; Steiner, U.; Fleury, G.; Ponsinet, V.; Guldin, S. Block Copolymer Directed Metamaterials and Metasurfaces for Novel Optical Devices. Adv. Opt. Mater. 2021, 9, 2100175. [Google Scholar] [CrossRef]
- Piechulla, P.M.; Muehlenbein, L.; Wehrspohn, R.B.; Nanz, S.; Abass, A.; Rockstuhl, C.; Sprafke, A. Fabrication of Nearly-Hyperuniform Substrates by Tailored Disorder for Photonic Applications. Adv. Opt. Mater. 2018, 6, 1701272. [Google Scholar] [CrossRef]
- Haynes, C.L.; Van Duyne, R.P. Nanosphere Lithography: A Versatile Nanofabrication Tool for Studies of Size-Dependent Nanoparticle Optics. J. Phys. Chem. B 2001, 105, 5599–5611. [Google Scholar] [CrossRef]
- Shutsko, I.; Buchmüller, M.; Meudt, M.; Görrn, P. Plasmon-Induced Disorder Engineering for Robust Optical Sensors. Adv. Opt. Mater. 2022, 10, 2102783. [Google Scholar] [CrossRef]
- Buchmüller, M.; Shutsko, I.; Schumacher, S.O.; Görrn, P. Harnessing Short-Range Surface Plasmons in Planar Silver Films via Disorder-Engineered Metasurfaces. ACS Appl. Opt. Mater. 2023, 1, 1777–1782. [Google Scholar] [CrossRef]
- Wang, B.; Yu, P.; Wang, W.; Zhang, X.; Kuo, H.C.; Xu, H.; Wang, Z.M. High-Q Plasmonic Resonances: Fundamentals and Applications. Adv. Opt. Mater. 2021, 9, 2001520. [Google Scholar] [CrossRef]
- Wang, B.; Yu, P.; Wang, W.; Zhang, X.; Kuo, H.; Xu, H.; Wang, Z.M. Theoretical Description of Node-Aligned Resonant Waveguide Gratings. Optics 2022, 3, 60–69. [Google Scholar]
- Henkel, A.; Schumacher, S.O.; Meudt, M.; Knoth, C.; Buchmüller, M.; Görrn, P. High-Contrast Switching of Light Enabled by Zero Diffraction. Adv. Photonics Res. 2023, 4, 2300230. [Google Scholar] [CrossRef]
- Nalwa, H.S. Organic Materials for Third-Order Nonlinear Optics. Adv. Mater. 1993, 5, 341–358. [Google Scholar] [CrossRef]
- González-Estefan, J.H.; Gonidec, M.; Vu, T.T.; Daro, N.; Chastanet, G. In Situ Fine-Tuning of Microfluidic Chips by Swelling and Its Application to Droplet Microfluidics. Adv. Mater. Technol. 2019, 4, 1900232. [Google Scholar] [CrossRef]
- Dangla, R.; Gallaire, F.; Baroud, C.N. Microchannel deformations due to solvent-induced PDMS swelling. Lab Chip 2010, 10, 2972–2978. [Google Scholar] [CrossRef]
- Qi, D.; Zhang, K.; Tian, G.; Jiang, B.; Huang, Y. Stretchable Electronics Based on PDMS Substrates. Adv. Mater. 2021, 33, 2003155. [Google Scholar] [CrossRef]
- Polywka, A.; Jakob, T.; Stegers, L.; Riedl, T.; Görrn, P. Facile Preparation of High-Performance Elastically Stretchable Interconnects. Adv. Mater. 2015, 27, 3755–3759. [Google Scholar] [CrossRef]
- Kolaric, B.; Desprez, S.; Brau, F.; Damman, P. Design of curved photonic crystal using swelling induced instabilities. J. Mater. Chem. 2012, 22, 16205–16208. [Google Scholar] [CrossRef]
- Usui, K.; Matsumoto, K.; Katayama, E.; Akamatsu, N.; Shishido, A. A Deformable Low-Threshold Optical Limiter with Oligothiophene-Doped Liquid Crystals. ACS Appl. Mater. Interfaces 2021, 13, 23049–23056. [Google Scholar] [CrossRef] [PubMed]
- Haripadmam, P.C.; Thanuja, T.H.; Varsha, G.S.; Beryl, C.D.; Aji, A. Nonlinear optical absorption in PVA films doped by the novel natural dye extract from C. redflash leaves. Opt. Mater. 2021, 112, 110804. [Google Scholar] [CrossRef]
- Fu, B.; Sun, J.; Cheng, Y.; Ouyang, H.; Compagnini, G.; Yin, P.; Zhang, H. Recent Progress on Metal-Based Nanomaterials: Fabrications, Optical Properties, and Applications in Ultrafast Photonics. Adv. Funct. Mater. 2021, 31, 2107363. [Google Scholar] [CrossRef]
- Kauranen, M.; Zayats, A.V. Nonlinear plasmonics. Nat. Photonics 2012, 6, 737–748. [Google Scholar] [CrossRef]
- Bai, T.; Dong, N.; Cheng, H.; Cheng, Q.; Wang, J.; Chen, Y. CH3NH3PbI3 perovskite:poly(N-vinylcarbazole) blends for broadband optical limiting. RSC Adv. 2017, 7, 1809–1813. [Google Scholar] [CrossRef]
- Johnson, V.; Gandhiraj, V. Enhanced nonlinear characteristics of polymer-perovskite hybrid (PVA/CMC/LaAlO3) fabricated via solution casting process for optical limiting applications. J. Mater. Sci. Mater. Electron. 2023, 34, 2103. [Google Scholar] [CrossRef]
- Guo, J.; Shi, R.; Wang, R.; Wang, Y.; Zhang, F.; Wang, C.; Chen, H.; Ma, C.; Wang, Z.; Ge, Y.; et al. Graphdiyne-Polymer Nanocomposite as a Broadband and Robust Saturable Absorber for Ultrafast Photonics. Laser Photon. Rev. 2020, 14, 1900367. [Google Scholar] [CrossRef]
- Mu, H.; Lin, S.; Wang, Z.; Xiao, S.; Li, P.; Chen, Y.; Zhang, H.; Bao, H.; Lau, S.P.; Pan, C.; et al. Black Phosphorus–Polymer Composites for Pulsed Lasers. Adv. Opt. Mater. 2015, 3, 1447–1453. [Google Scholar] [CrossRef]
- Lee, J.N.; Park, C.; Whitesides, G.M. Solvent Compatibility of Poly(dimethylsiloxane)-Based Microfluidic Devices. Anal. Chem. 2003, 75, 6544–6554. [Google Scholar] [CrossRef] [PubMed]
- Sheik-Bahae, M.; Said, A.A.; Van Stryland, E.W. High-sensitivity, single-beam n_2 measurements. Opt. Lett. 1989, 14, 955. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.; Wei, T.-H.; Hagan, D.; Van Stryland, E. Sensitive Measurement of Optical Nonlinearities Using a Single Beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
- Bongu, S.R.; Buchmüller, M.; Neumaier, D.; Görrn, P. Electric Control of Thermal Contributions to the Nonlinear Optical Properties of Nitrobenzene. Adv. Phys. Res. 2023, 3, 2300053. [Google Scholar] [CrossRef]
- Cabrera, M.H.; Marcano, O.A.; Ojeda, A.J.; Wetter, N.U.; Frejlich, J. Absorption Spectra of Nitrobenzene Measured with Incoherent White-Light Excitation. AIP Conf. Proc. 2008, 992, 1183–1188. [Google Scholar]
- Kedenburg, S.; Vieweg, M.; Gissibl, T.; Giessen, H. Linear refractive index and absorption measurements of nonlinear optical liquids in the visible and near-infrared spectral region. Opt. Mater. Express 2012, 2, 1588–1611. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J., Jr. Statistical mechanics of cross-linked polymer networks II. Swelling. J. Chem. Phys. 1943, 11, 521–526. [Google Scholar] [CrossRef]


| Sample | (×10−15 cm2/W) | (cm/GW) | (×10−16 cm2/V2) |
|---|---|---|---|
| NB | 22.8 | 0.36 | 1.97 |
| LT | 7.1 | - | 0.56 |
| TL | 7.1 | - | 0.57 |
| PDMS/TL | 3.1 | - | 0.26 |
| PDMS/LT | 1.5 | - | 0.11 |
| PDMS/NB | n.a. * | n.a. * | n.a. * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bongu, S.R.; Buchmüller, M.; Neumaier, D.; Görrn, P. Introducing Optical Nonlinearity in PDMS Using Organic Solvent Swelling. Optics 2024, 5, 66-75. https://doi.org/10.3390/opt5010005
Bongu SR, Buchmüller M, Neumaier D, Görrn P. Introducing Optical Nonlinearity in PDMS Using Organic Solvent Swelling. Optics. 2024; 5(1):66-75. https://doi.org/10.3390/opt5010005
Chicago/Turabian StyleBongu, Sudhakara Reddy, Maximilian Buchmüller, Daniel Neumaier, and Patrick Görrn. 2024. "Introducing Optical Nonlinearity in PDMS Using Organic Solvent Swelling" Optics 5, no. 1: 66-75. https://doi.org/10.3390/opt5010005
APA StyleBongu, S. R., Buchmüller, M., Neumaier, D., & Görrn, P. (2024). Introducing Optical Nonlinearity in PDMS Using Organic Solvent Swelling. Optics, 5(1), 66-75. https://doi.org/10.3390/opt5010005







