High Quality Factor Silicon Membrane Metasurface for Intensity-Based Refractive Index Sensing
Abstract
:1. Introduction
2. Results and Discussion
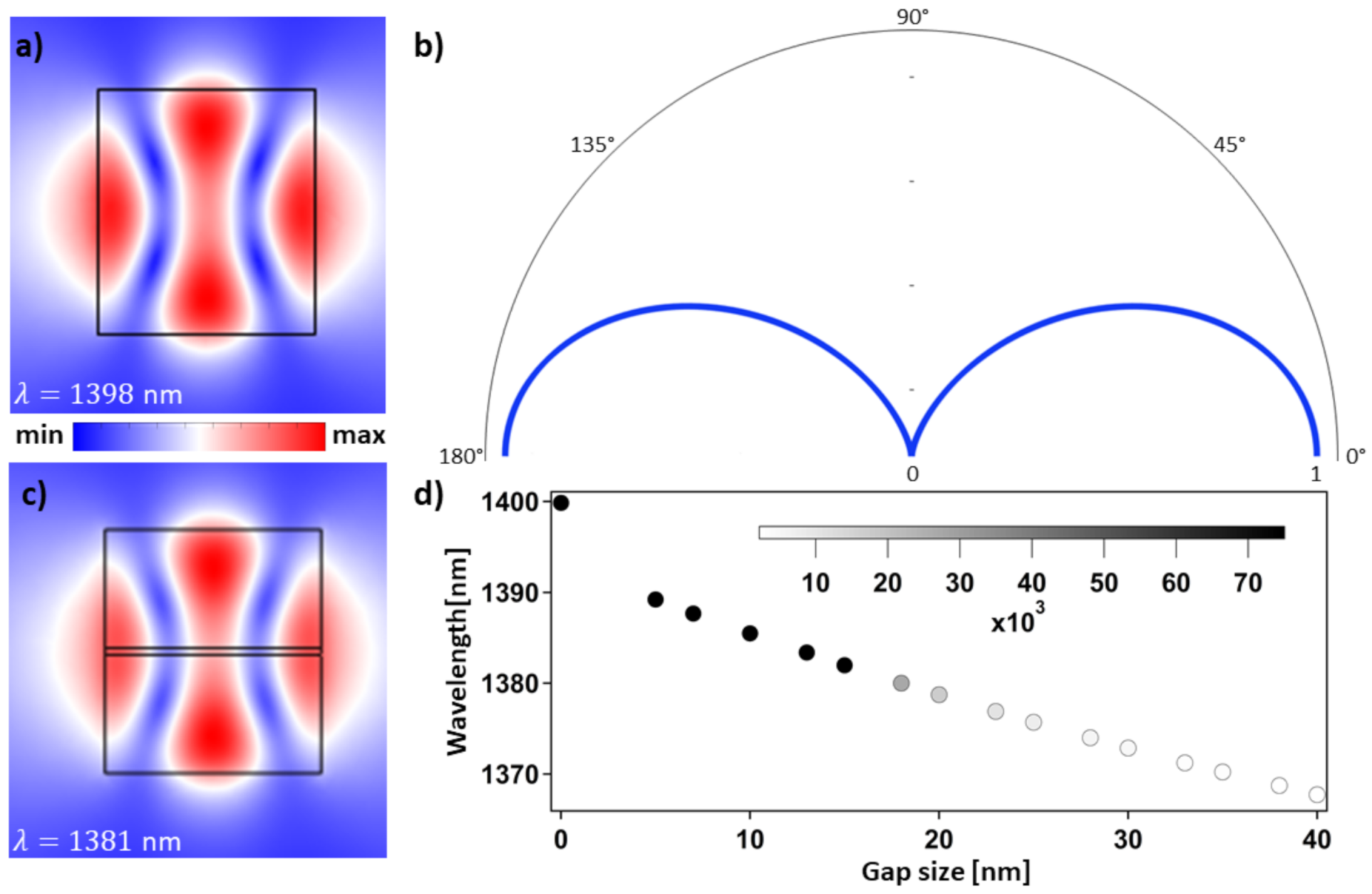
2.1. Metasurface Design
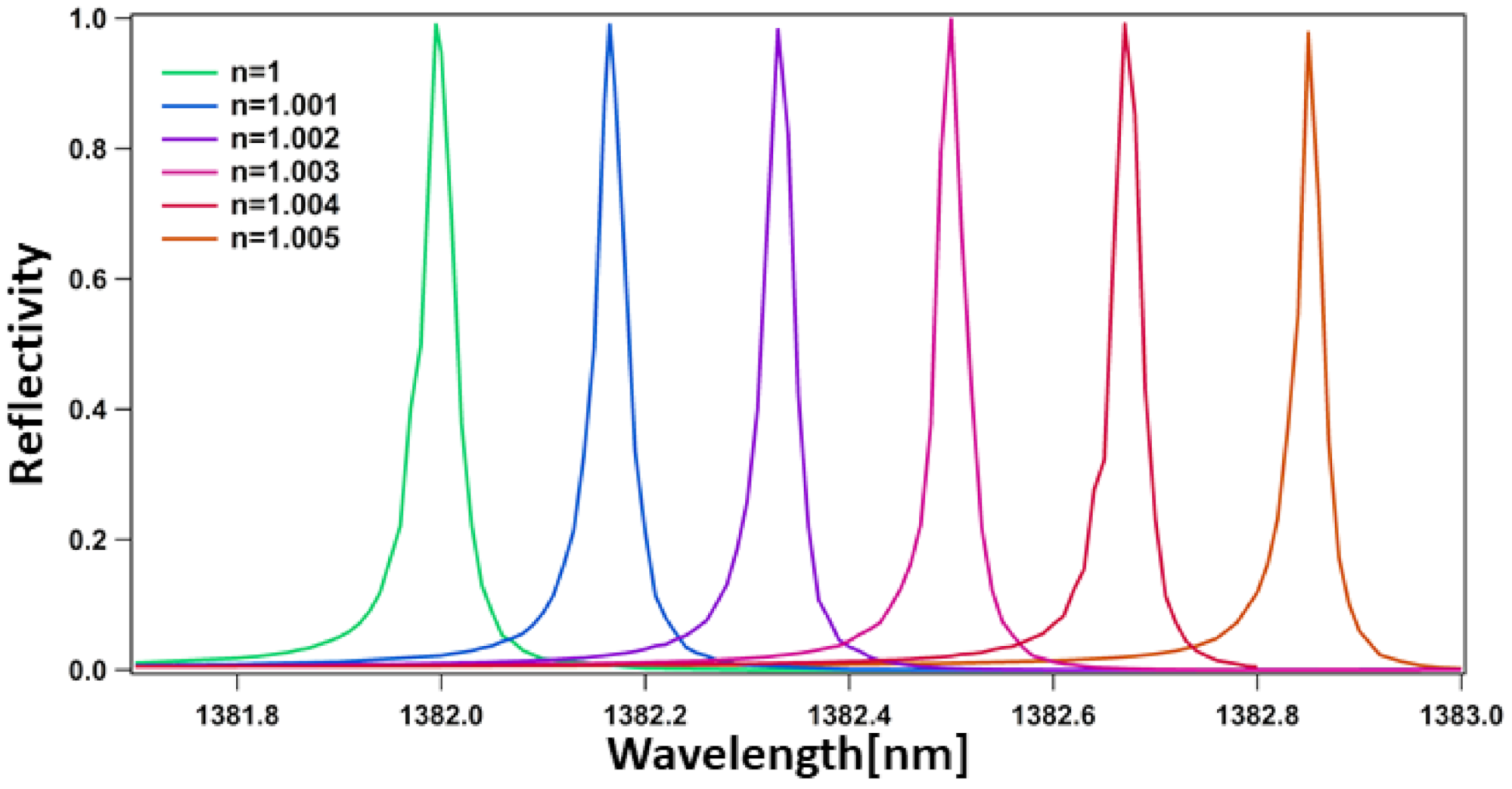
2.2. Sensing Mechanism
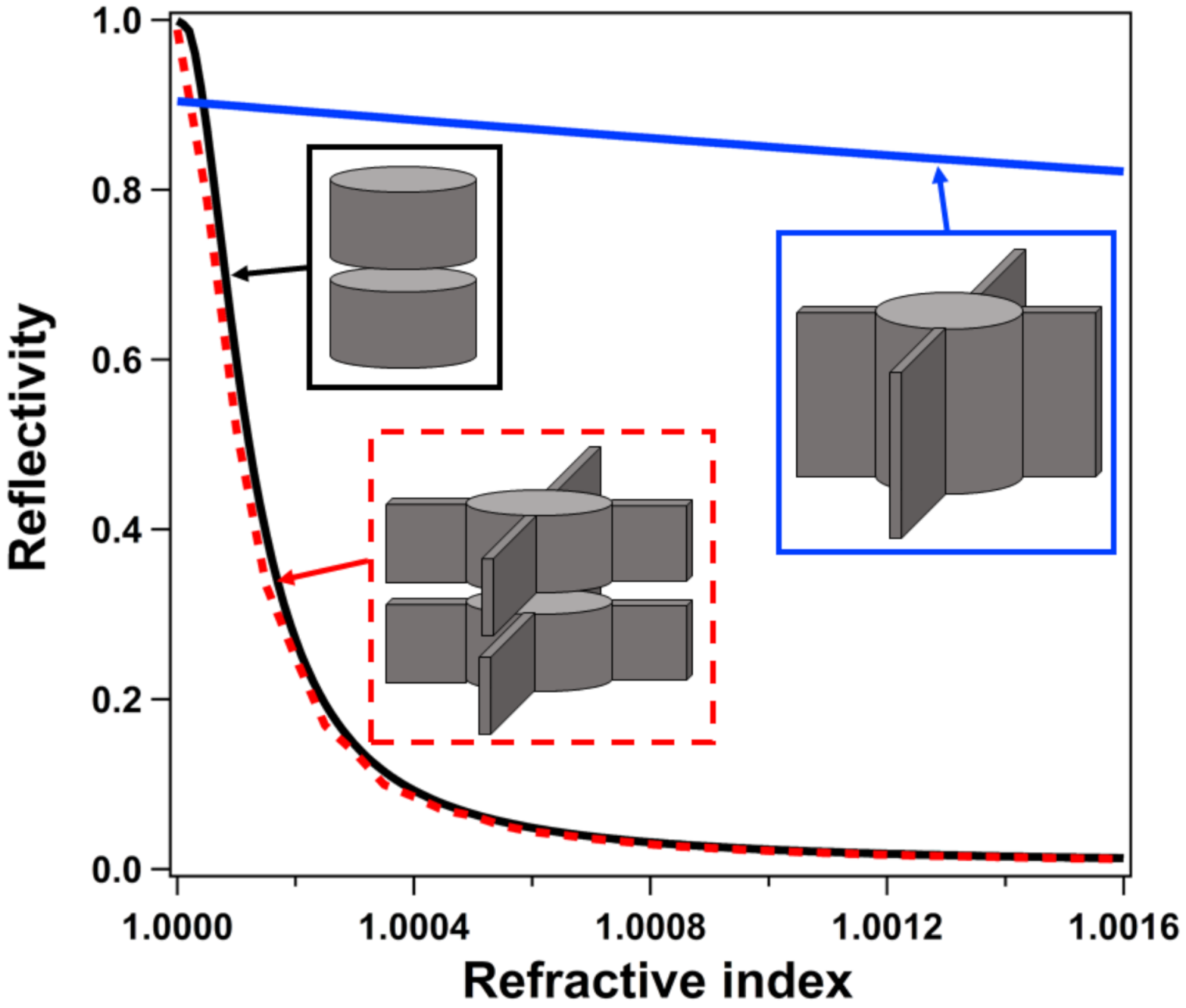
2.3. Practical Structure Design
3. Conclusions
4. Materials and Methods
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Homola, J. Surface Plasmon Resonance Sensors for Detection of Chemical and Biological Species. Chem. Rev. 2008, 108, 462–493. [Google Scholar] [CrossRef]
- Mehta, B.; Benkstein, K.D.; Semancik, S.; Zaghloul, M.E. Gas Sensing with Bare and Graphene-covered Optical Nano-Antenna Structures. Sci. Rep. 2016, 6, 21287. [Google Scholar] [CrossRef] [PubMed]
- Pitruzzello, G.; Krauss, T.F. Photonic crystal resonances for sensing and imaging. J. Opt. 2018, 20, 073004. [Google Scholar] [CrossRef]
- Ruffato, G.; Romanato, F.; Garoli, D.; Cattarin, S. Nanoporous gold plasmonic structures for sensing applications. Opt. Express 2011, 19, 13164. [Google Scholar] [CrossRef] [PubMed]
- Gandolfi, M.; Banfi, F.; Glorieux, C. Optical wavelength dependence of photoacoustic signal of gold nanofluid. Photoacoustics 2020, 20, 100199. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.C.; Chang, Y.J.; Chuang, Y.C.; Huang, B.Z.; Chen, C.C. A plasmonic refractive index sensor with an ultrabroad dynamic sensing range. Sci. Rep. 2019, 9, 5134. [Google Scholar] [CrossRef] [Green Version]
- Rodrigo, D.; Limaj, O.; Janner, D.; Etezadi, D.; de Abajo, F.J.G.; Pruneri, V.; Altug, H. Mid-infrared plasmonic biosensing with graphene. Science 2015, 349, 165–168. [Google Scholar] [CrossRef] [Green Version]
- Cai, S.; Pan, H.; González-Vila, Á.; Guo, T.; Gillan, D.C.; Wattiez, R.; Caucheteur, C. Selective detection of cadmium ions using plasmonic optical fiber gratings functionalized with bacteria. Opt. Express 2020, 28, 19740–19749. [Google Scholar] [CrossRef]
- Kumar, S.; Guo, Z.; Singh, R.; Wang, Q.; Zhang, B.; Cheng, S.; Liu, F.Z.; Marques, C.; Kaushik, B.K.; Jha, R. MoS2 Functionalized Multicore Fiber Probes for Selective Detection of Shigella Bacteria Based on Localized Plasmon. J. Light. Technol. 2021, 39, 4069–4081. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, X.; Guo, T.; Albert, J. Optical detection of the percolation threshold of nanoscale silver coatings with optical fiber gratings. APL Photonics 2020, 5, 076101. [Google Scholar] [CrossRef]
- Baratto, C.; Faglia, G.; Carletti, L.; Angelis, C.D. New Trends in Optical Resonant Bio-Chemical Sensing. IEEE Sens. J. 2021, 21, 12856–12867. [Google Scholar] [CrossRef]
- Chong, K.E.; Orton, H.W.; Staude, I.; Decker, M.; Miroshnichenko, A.E.; Brener, I.; Kivshar, Y.S.; Neshev, D.N. Refractive index sensing with Fano resonances in silicon oligomers. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2017, 375, 20160070. [Google Scholar] [CrossRef] [PubMed]
- Bontempi, N.; Chong, K.E.; Orton, H.W.; Staude, I.; Choi, D.Y.; Alessandri, I.; Kivshar, Y.S.; Neshev, D.N. Highly sensitive biosensors based on all-dielectric nanoresonators. Nanoscale 2017, 9, 4972–4980. [Google Scholar] [CrossRef]
- Muslimov, E.; Hugot, E.; Jahn, W.; Vives, S.; Ferrari, M.; Chambion, B.; Henry, D.; Gaschet, C. Combining freeform optics and curved detectors for wide field imaging: A polynomial approach over squared aperture. Opt. Express 2017, 25, 14598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rocco, D.; Tognazzi, A.; Carletti, L.; Baratto, C.; Angelis, C.D. Sensing through the optical radiation pattern in dielectric metastructures. In Proceedings of the International Conference on Quantum, Nonlinear, and Nanophotonics 2019 (ICQNN 2019); Dreischuh, A.A., Neshev, D.N., Staude, I., Spassov, T., Eds.; SPIE—International Society for Optics and Photonics: Bellingham, WA, USA, 2019. [Google Scholar] [CrossRef]
- Lu, X.; Gautam, V.; Shishmarev, D.; Daria, V.R. Sensing refractive index gradients along dielectric nanopillar metasurfaces. Opt. Express 2020, 28, 31594. [Google Scholar] [CrossRef]
- Tseng, M.L.; Jahani, Y.; Leitis, A.; Altug, H. Dielectric Metasurfaces Enabling Advanced Optical Biosensors. ACS Photonics 2020, 8, 47–60. [Google Scholar] [CrossRef]
- Kodigala, A.; Lepetit, T.; Gu, Q.; Bahari, B.; Fainman, Y.; Kanté, B. Lasing action from photonic bound states in continuum. Nature 2017, 541, 196–199. [Google Scholar] [CrossRef]
- Celiksoy, S.; Ye, W.; Wandner, K.; Kaefer, K.; Sönnichsen, C. Intensity-Based Single Particle Plasmon Sensing. Nano Lett. 2021, 21, 2053–2058. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef] [Green Version]
- von Neumann, J.; Wigner, E. Über merkwürdigediskrete Eigenwerte. Phys. Z. 1929, 30, 465–467. [Google Scholar]
- Koshelev, K.; Favraud, G.; Bogdanov, A.; Kivshar, Y.; Fratalocchi, A. Nonradiating photonics with resonant dielectric nanostructures. Nanophotonics 2019, 8, 725–745. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of trapped light within the radiation continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campione, S.; Liu, S.; Basilio, L.I.; Warne, L.K.; Langston, W.L.; Luk, T.S.; Wendt, J.R.; Reno, J.L.; Keeler, G.A.; Brener, I.; et al. Broken Symmetry Dielectric Resonators for High Quality Factor Fano Metasurfaces. ACS Photonics 2016, 3, 2362–2367. [Google Scholar] [CrossRef]
- Staude, I.; Miroshnichenko, A.E.; Decker, M.; Fofang, N.T.; Liu, S.; Gonzales, E.; Dominguez, J.; Luk, T.S.; Neshev, D.N.; Brener, I.; et al. Tailoring Directional Scattering through Magnetic and Electric Resonances in Subwavelength Silicon Nanodisks. ACS Nano 2013, 7, 7824–7832. [Google Scholar] [CrossRef]
- Camacho-Morales, R.; Rocco, D.; Xu, L.; Gili, V.F.; Dimitrov, N.; Stoyanov, L.; Ma, Z.; Komar, A.; Lysevych, M.; Karouta, F.; et al. Infrared upconversion imaging in nonlinear metasurfaces. Adv. Photonics 2021, 3, 036002. [Google Scholar] [CrossRef]
- Liu, N.; Weiss, T.; Mesch, M.; Langguth, L.; Eigenthaler, U.; Hirscher, M.; Sönnichsen, C.; Giessen, H. Planar Metamaterial Analogue of Electromagnetically Induced Transparency for Plasmonic Sensing. Nano Lett. 2009, 10, 1103–1107. [Google Scholar] [CrossRef]
- Fusco, Z.; Rahmani, M.; Bo, R.; Verre, R.; Motta, N.; Käll, M.; Neshev, D.; Tricoli, A. Nanostructured Dielectric Fractals on Resonant Plasmonic Metasurfaces for Selective and Sensitive Optical Sensing of Volatile Compounds. Adv. Mater. 2018, 30, 1800931. [Google Scholar] [CrossRef] [Green Version]
- Green, M.A. Self-consistent optical parameters of intrinsic silicon at 300 K including temperature coefficients. Sol. Energy Mater. Sol. Cells 2008, 92, 1305–1310. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tognazzi, A.; Rocco, D.; Gandolfi, M.; Locatelli, A.; Carletti, L.; De Angelis, C. High Quality Factor Silicon Membrane Metasurface for Intensity-Based Refractive Index Sensing. Optics 2021, 2, 193-199. https://doi.org/10.3390/opt2030018
Tognazzi A, Rocco D, Gandolfi M, Locatelli A, Carletti L, De Angelis C. High Quality Factor Silicon Membrane Metasurface for Intensity-Based Refractive Index Sensing. Optics. 2021; 2(3):193-199. https://doi.org/10.3390/opt2030018
Chicago/Turabian StyleTognazzi, Andrea, Davide Rocco, Marco Gandolfi, Andrea Locatelli, Luca Carletti, and Costantino De Angelis. 2021. "High Quality Factor Silicon Membrane Metasurface for Intensity-Based Refractive Index Sensing" Optics 2, no. 3: 193-199. https://doi.org/10.3390/opt2030018
APA StyleTognazzi, A., Rocco, D., Gandolfi, M., Locatelli, A., Carletti, L., & De Angelis, C. (2021). High Quality Factor Silicon Membrane Metasurface for Intensity-Based Refractive Index Sensing. Optics, 2(3), 193-199. https://doi.org/10.3390/opt2030018










