Interferometric Ice Particle Imaging in a Wind Tunnel
Abstract
1. Introduction
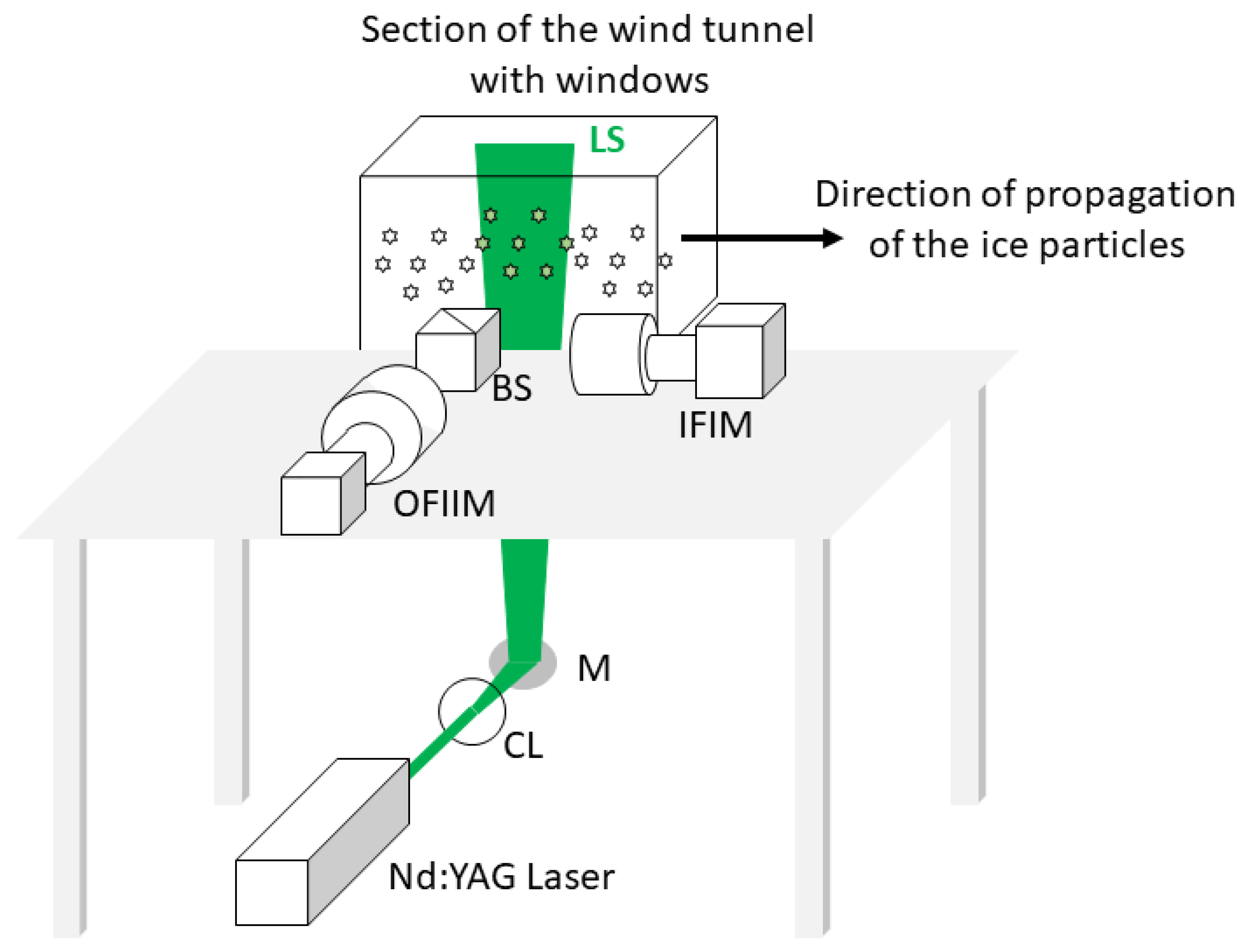
2. Experimental Set-Up
3. Results
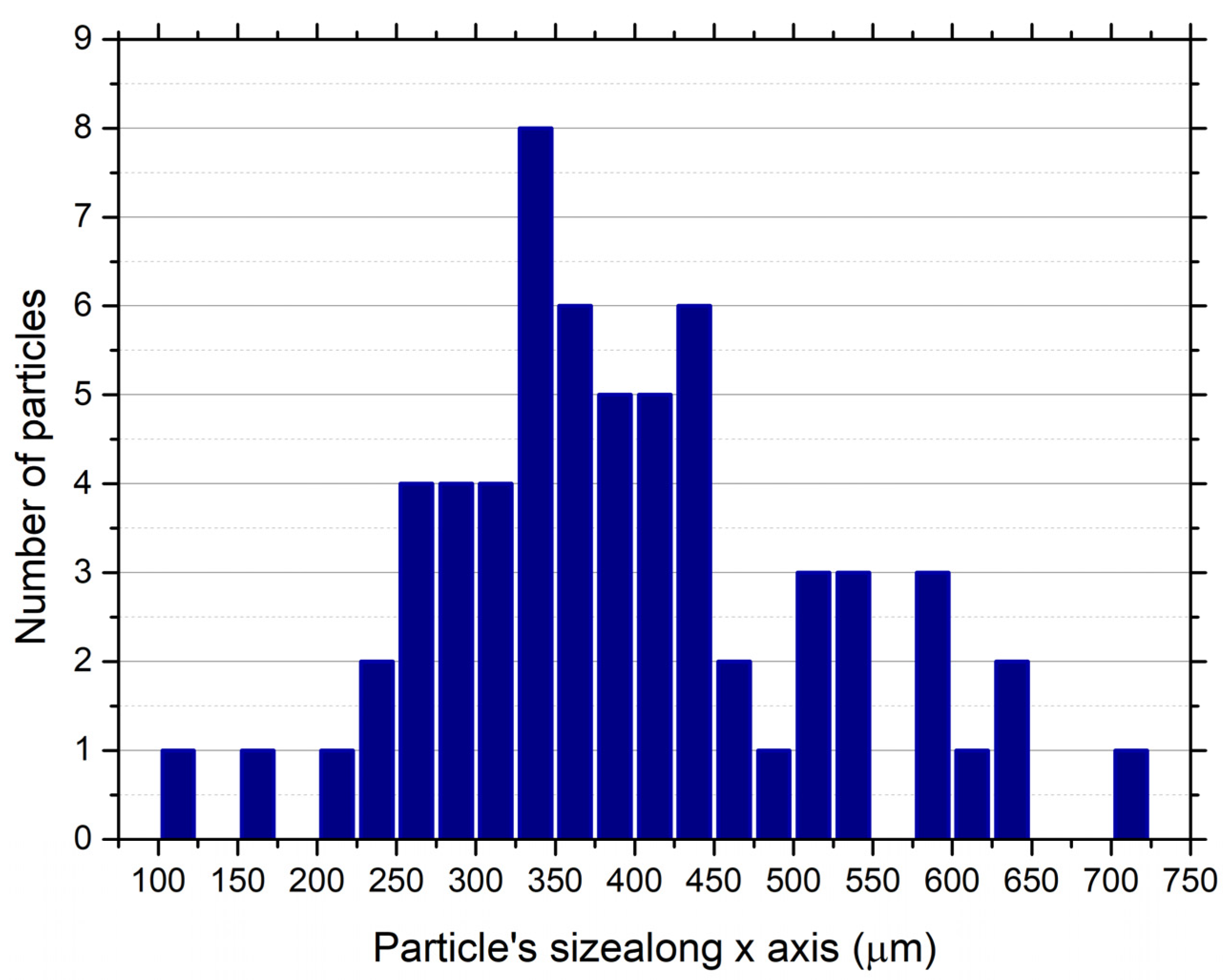
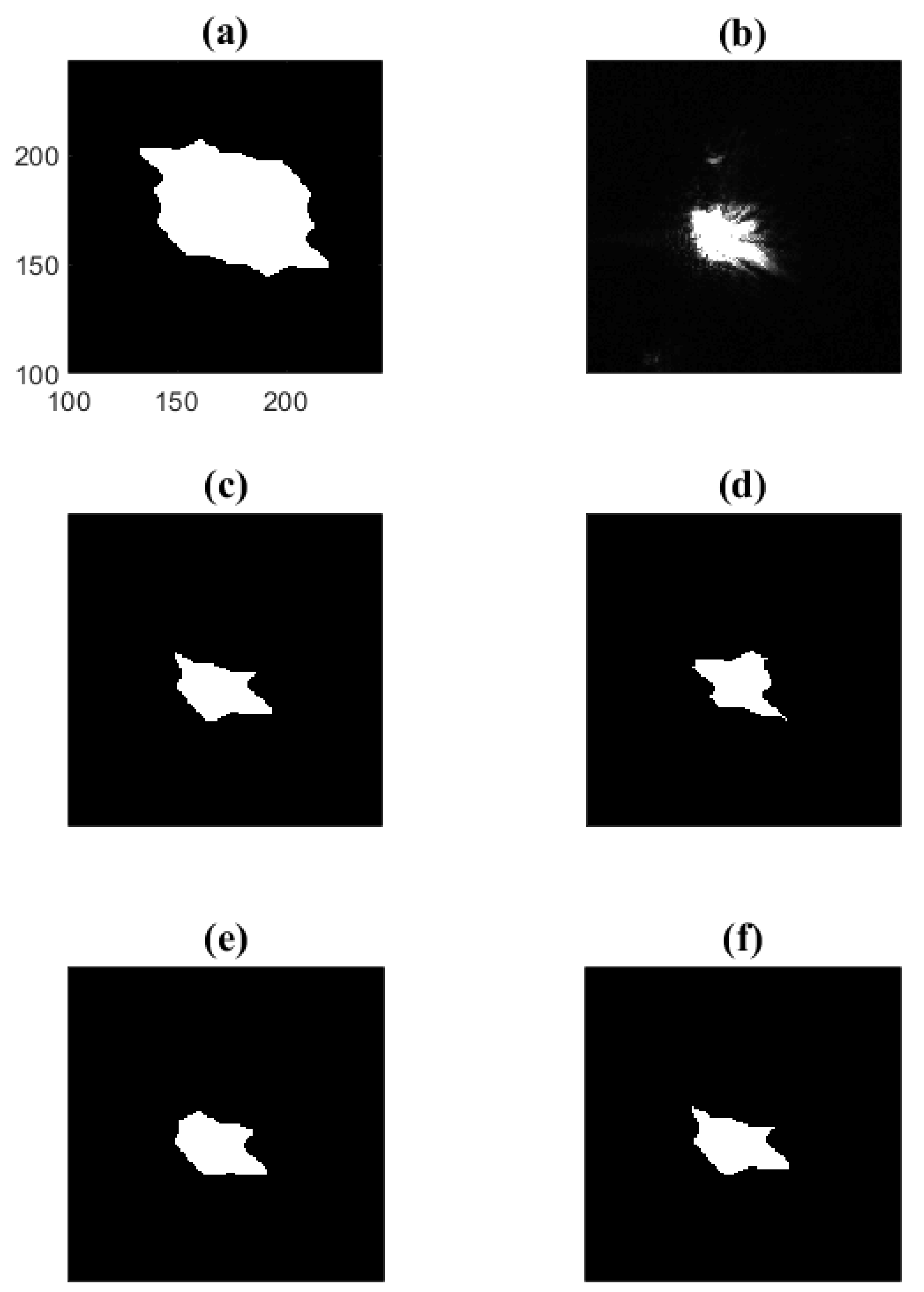
3.1. Size Measurements of Single Ice Particles Using the IPI Technique
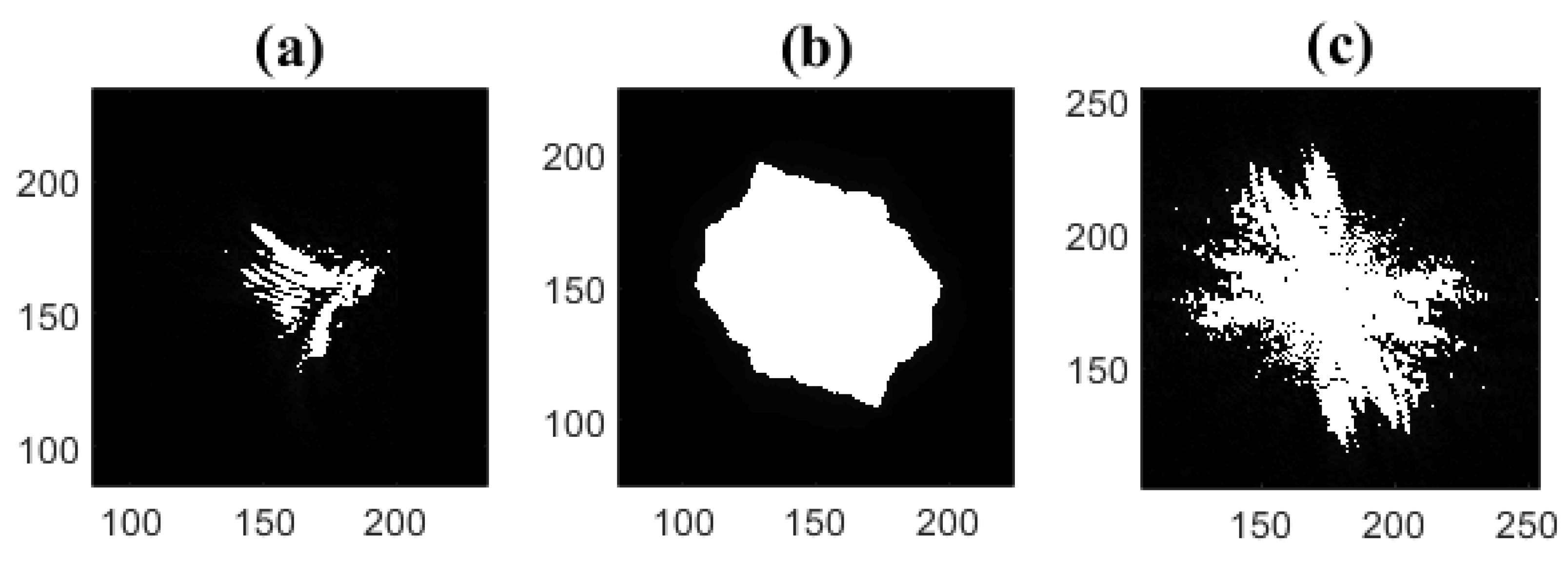
3.2. Size Measurements of Ice Particles When Their IPI Images Overlap
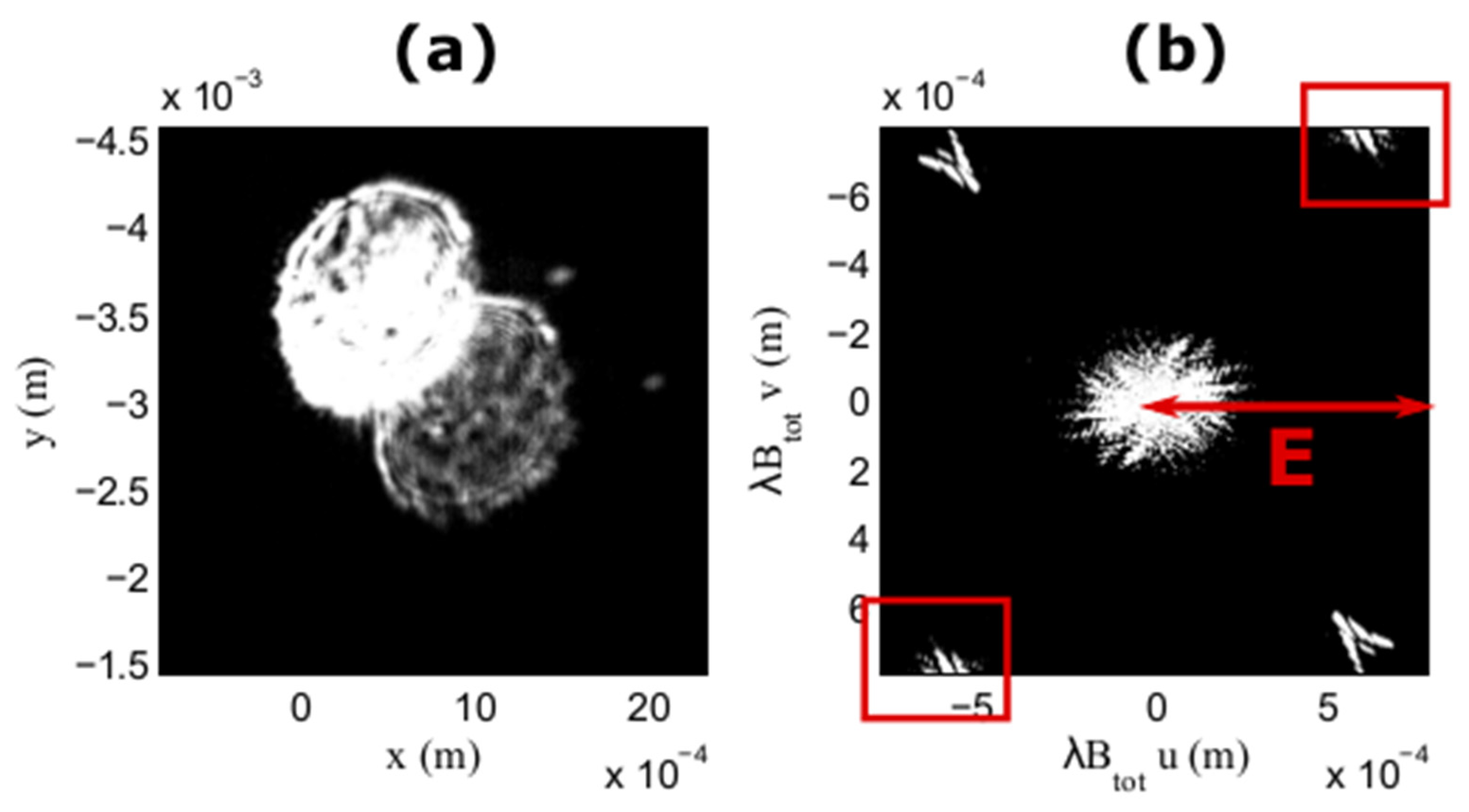
3.3. Noise Sources in Particle Size Measurements Using IPI Technique
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- König, G.; Anders, K.; Frohn, A. A new light-scattering technique to measure the diameter of periodically generated moving droplets of the article. J. Aerosol Sci. 1986, 17, 157–167. [Google Scholar] [CrossRef]
- Glover, A.R.; Skippon, S.M.; Boyle, R.D. Interferometric laser imaging for droplet sizing: A method for droplet-size measurement in sparse spray systems. Appl. Opt. 1995, 34, 8409–8421. [Google Scholar] [CrossRef]
- Kawaguchi, T.; Akasaka, Y.; Maeda, M. Size measurements of droplets and bubbles by advanced interferometric laser imaging technique. Meas. Sci. Technol. 2002, 13, 308. [Google Scholar] [CrossRef]
- Mounaïm-Rousselle, C.; Pajot, O. Droplet sizing by Mie scattering interferometry in a spark ignition engine. Part. Part. Syst. Charact. 1999, 16, 160–168. [Google Scholar] [CrossRef]
- Damaschke, N.; Nobach, H.; Tropea, C. Optical limits of particle concentration for multi-dimensional particle sizing techniques in fluid mechanics. Exp. Fluids 2002, 32, 143–152. [Google Scholar]
- Dehaeck, S.; van Beeck, J.P.A.P. Designing a maximum precision interferometric particle imaging set-up. Exp. Fluids 2007, 42, 767–781. [Google Scholar] [CrossRef]
- Hardalupas, Y.; Sahu, S.; Taylor, A.; Zarogoulidis, K. Simultaneous planar measurement of droplet velocity and size with gas phase velocities in a spray by combined ILIDS and PIV techniques. Exp. Fluids 2010, 49, 417–434. [Google Scholar] [CrossRef]
- Quérel, A.; Lemaitre, P.; Brunel, M.; Porcheron, E.; Gréhan, G. Real time global interferometric laser imaging for droplet sizing (ILIDS) analysis for airbone research. Meas. Sci. Tech. 2010, 21, 015306. [Google Scholar] [CrossRef]
- Lacour, C.; Durox, D.; Ducruix, S.; Massot, M. Interaction of a polydisperse spray with vortices. Exp. Fluids 2011, 51, 295–311. [Google Scholar] [CrossRef]
- Volkov, R.S.; Kuznetsov, G.V.; Strizhak, P.A. Influence of droplet concentration on evaporation in a high-temperature gas. Int. J. Heat Mass Transf. 2016, 96, 20–28. [Google Scholar] [CrossRef]
- Zhang, H.; Zhai, M.; Sun, J.; Zhou, Y.; Jia, D.; Liu, T.; Zhang, Y. Discrimination between spheres and spheroids in a detection system for single particles based on polarization characteristics. J. Quantum Spectrosc. Radiat. Transf. 2017, 187, 62–75. [Google Scholar] [CrossRef]
- Ulanowski, Z.; Hirst, E.; Kaye, P.H.; Greenaway, R.S. Retrieving the size of particles with rough and complex surfaces from two-dimensional scattering patterns. J. Quantum Spectrosc. Radiat. Transf. 2012, 113, 2457–2464. [Google Scholar] [CrossRef]
- Brunel, M.; Shen, H.; Coëtmellec, S.; Gréhan, G.; Delobel, T. Determination of the size of irregular particles using interferometric out-of-focus imaging. Int. J. Opt. 2014, 2014, 143904. [Google Scholar] [CrossRef]
- Brunel, M.; González Ruiz, S.; Jacquot, J.; van Beeck, J. On the morphology of irregular rough particles from the analysis of speckle like interferometric out-of-focus images. Opt. Commun. 2015, 338, 193–198. [Google Scholar] [CrossRef]
- García Carrascal, P.; González Ruiz, S.; van Beeck, J.P.A.J. Irregular particle sizing using speckle pattern for continuous wave laser applications. Exp. Fluids 2014, 55, 1851. [Google Scholar] [CrossRef]
- Jacquot-Kielar, J.; Lemaitre, P.; Gobin, C.; Wu, Y.; Porcheron, E.; Coetmellec, S.; Gréhan, G.; Brunel, M. Simultaneous interferometric in-focus and out-of-focus imaging of ice crystals. Opt. Commun. 2016, 372, 185–195. [Google Scholar] [CrossRef]
- Ruiz, S.G.; van Beeck, J. Sizing of sand and ash particles using their speckle pattern: Influence of particle opacity. Exp. Fluids 2017, 58, 100. [Google Scholar] [CrossRef]
- Wu, Y.; Gong, Y.; Shi, L.; Lin, Z.; Wu, X.; Gong, C.; Zhou, Z.; Zhang, Y. Backward interferometric speckle imaging for evaluating size and morphology of irregular coal particles. Opt. Commun. 2021, 491, 126957. [Google Scholar] [CrossRef]
- Qieni, L.; Kan, H.; Baozhen, G.; Xiang, W. High-accuracy simultaneous measurement of particle size and location using interferometric out-of-focus imaging. Opt. Express 2016, 24, 16530. [Google Scholar] [CrossRef]
- Garcia-Magarino, A.; Sor, S.; Bardera, R.; Munoz-Campillejo, J. Interferometric laser imaging for droplet sizing method for long range measurements. Measurement 2021, 168, 108418. [Google Scholar] [CrossRef]
- Porcheron, E.; Lemaitre, P.; van Beeck, J.; Vetrano, R.; Brunel, M.; Gréhan, G.; Guiraud, L. Development of a spectrometer for the airborne measurement of droplet sizes in clouds. J. Eur. Opt. Soc. 2015, 10, 15030. [Google Scholar] [CrossRef]
- Ouldarbi, L.; Talbi, M.; Coëtmellec, S.; Lebrun, D.; Gréhan, G.; Perret, G.; Brunel, M. 3D-shape recognition and size measurement of irregular rough particles using multi-views interferometric out-of-focus imaging. Appl. Opt. 2016, 55, 9154–9159. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Dlugach, J.M.; Yurkin, M.A.; Bi, L.; Cairns, B.; Liu, L.; Lee Panetta, R.; Travis, L.D.; Yang, P.; Zakharova, N.T. First-principles modeling of electromagnetic scattering by discrete and discretely heterogeneous random medi. Phys. Rep. 2016, 632, 1–75. [Google Scholar] [CrossRef]
- Walters, S.; Zallie, J.; Seymour, G.; Le Pan, Y.; Videen, G.; Aptowicz, K.B. Characterizing the size and absorption of single nonspherical aerosol particles from angularly-resolved elasric light scattering. J. Quantum Spectrosc. Radiat. Transf. 2019, 224, 439–444. [Google Scholar] [CrossRef]
- Piedra, P.; Kalume, A.; Zubko, E.; Mackowski, D.; Le Pan, Y.; Videen, G. Particle-shape classification using light scattering: An exercise in deep learning. J. Quantum Spectrosc. Radiat. Transf. 2019, 231, 140–156. [Google Scholar] [CrossRef]
- Laning, J.C.; Berg, M.J. Orthographic imaging of free-flowing aerosol particles. OSA Contin. 2019, 2, 3514–3520. [Google Scholar] [CrossRef]
- Brunel, M.; Coetmellec, S.; Gréhan, G.; Shen, H. Interferometric out-of-focus imaging simulator for irregular rough particles. J. Eur. Opt. Soc. 2014, 9, 14008. [Google Scholar] [CrossRef]
- Talbi, M.; Gréhan, G.; Brunel, M. Interferometric particle imaging of ice particles using a multi-view optical system. Appl. Opt. 2018, 57, 6188–6197. [Google Scholar] [CrossRef] [PubMed]
- Brunel, M.; Lemaitre, P.; Porcheron, E.; Coëtmellec, S.; Gréhan, G.; Jacquot-Kielar, J. Interferometric out-of-focus imaging of ice particles with overlapping images. Appl. Opt. 2016, 55, 4902–4909. [Google Scholar] [CrossRef] [PubMed]
- Talbi, M.; Brunel, M. Interferometric particle sizing with overlapping images despite Moiré. Opt. Commun. 2017, 400, 61–68. [Google Scholar] [CrossRef]
- Jacquot-Kielar, J.; Wu, Y.; Coëtmellec, S.; Lebrun, D.; Gréhan, G.; Brunel, M. Size determination of mixed liquid and frozen water droplets using interferometric out-of-focus imaging. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 108–116. [Google Scholar] [CrossRef]
- Sun, J.; Li, Z.; Tian, P.; Li, R.; Jia, D.; Liu, T.; Zhang, H. Measurement of cloud particles in a cloud chamber based on interference technology. Appl. Opt. 2019, 58, 8757–8764. [Google Scholar] [CrossRef]
- Jacquot, J.; Talbi, M.; Brunel, M. Third glare point effect in 90° Interferometric Laser Imaging for Droplet Sizing. Opt. Commun. 2020, 462, 125349. [Google Scholar] [CrossRef]
- Fienup, R.; Crimmins, T.R.; Holsztynski, W. Reconstruction of the support of an object fro the support of its autocorrelation. J. Opt. Soc. Am. 1982, 7, 3–13. [Google Scholar]
- Shen, H.; Wu, L.; Li, Y.; Wang, W. Two-dimensional shape retrieval from the interferometric out-of-focus image of a nonspherical particle—Part I: Theory. Appl. Opt. 2018, 57, 4968–4976. [Google Scholar] [CrossRef]
- Brunel, M.; Delestre, B.; Talbi, M. 3D-reconstructions for the estimation of ice particle’s volume using a two-views interferometric out-of-focus imaging set-up. Rev. Sci. Instrum. 2019, 90, 053109. [Google Scholar] [CrossRef] [PubMed]
- Talbi, M.; Gréhan, G.; Coëtmellec, S.; Brunel, M. Self-generated off-axis holography in interferometric out-of-focus imaging of ice particles. J. Electromag. Wav. Appl. 2019, 33, 1–17. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Sun, J.; Fu, Y.; Jia, D.; Liu, T. Characterization of particle size and shape by an IPI system through deep learning. J. Quantum Spectrosc. Radiat. Transf. 2021, 268, 107642. [Google Scholar] [CrossRef]
- Delestre, B.; Abad, A.; Talbi, M.; Fromager, M.; Brunel, M. Experimental particle’s shapes reconstructions from their interferometric images using the Error-Reduction algorithm. Opt. Commun. 2021, 498, 127229. [Google Scholar] [CrossRef]
- Lemaitre, P.; Brunel, M.; Rondeau, A.; Gréhan, G.; Porcheron, E. Quasi real-time analysis of mixed-phase cloud using Interferometric out-of-focus imaging: Application the detection of freezing conditions. Meas. Sci. Technol. 2015, 26, 125403. [Google Scholar] [CrossRef][Green Version]





| From Column (b) | From Column (d) | ||
|---|---|---|---|
| xIPI,size (μm) | yIPI,size (μm) | xIPI,size (μm) | yIPI,size (μm) |
| 221 ± 10 | 151 ± 10 | 181 ± 10 | 164 ± 10 |
| 243 ± 10 | 165 ± 10 | 158 ± 10 | 164 ± 10 |
| 193 ± 10 | 119 ± 10 | 222 ± 10 | 181 ± 10 |
| 141 ± 10 | 155 ± 10 | 104 ± 10 | 104 ± 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talbi, M.; Duperrier, R.; Delestre, B.; Godard, G.; Brunel, M. Interferometric Ice Particle Imaging in a Wind Tunnel. Optics 2021, 2, 216-227. https://doi.org/10.3390/opt2040020
Talbi M, Duperrier R, Delestre B, Godard G, Brunel M. Interferometric Ice Particle Imaging in a Wind Tunnel. Optics. 2021; 2(4):216-227. https://doi.org/10.3390/opt2040020
Chicago/Turabian StyleTalbi, Mohamed, Romain Duperrier, Barbara Delestre, Gilles Godard, and Marc Brunel. 2021. "Interferometric Ice Particle Imaging in a Wind Tunnel" Optics 2, no. 4: 216-227. https://doi.org/10.3390/opt2040020
APA StyleTalbi, M., Duperrier, R., Delestre, B., Godard, G., & Brunel, M. (2021). Interferometric Ice Particle Imaging in a Wind Tunnel. Optics, 2(4), 216-227. https://doi.org/10.3390/opt2040020






