Analytical Homogenization Approach for Double-Wall Corrugated Cardboard Incorporating Constituent Layer Characterization
Abstract
1. Introduction
2. Materials and Methods
2.1. Paper Material
2.2. Characterization of Paper
2.2.1. Density
2.2.2. Scanning Electron Microscopy (SEM) Observation
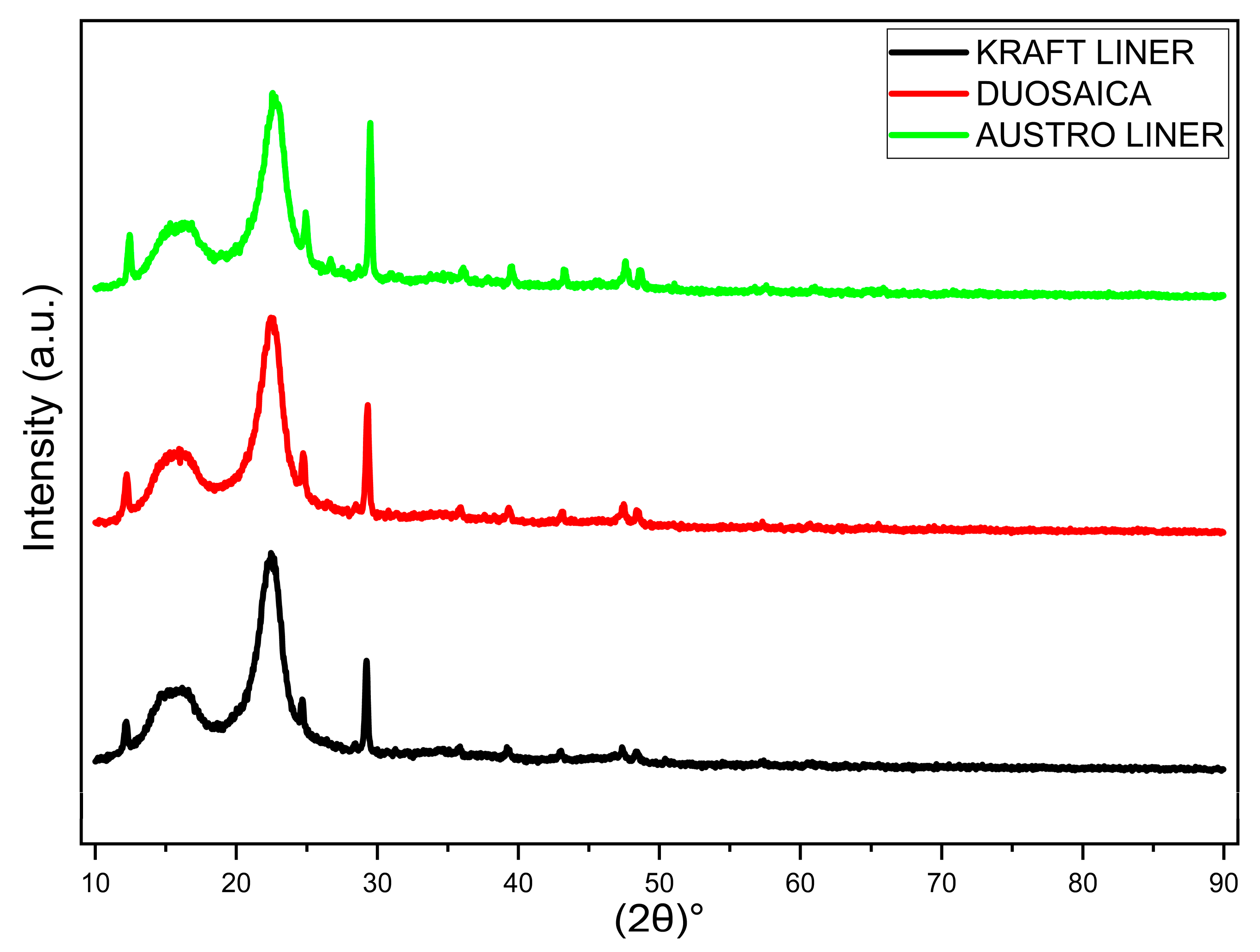
2.2.3. X-Ray Diffraction Analysis (XRD) Results
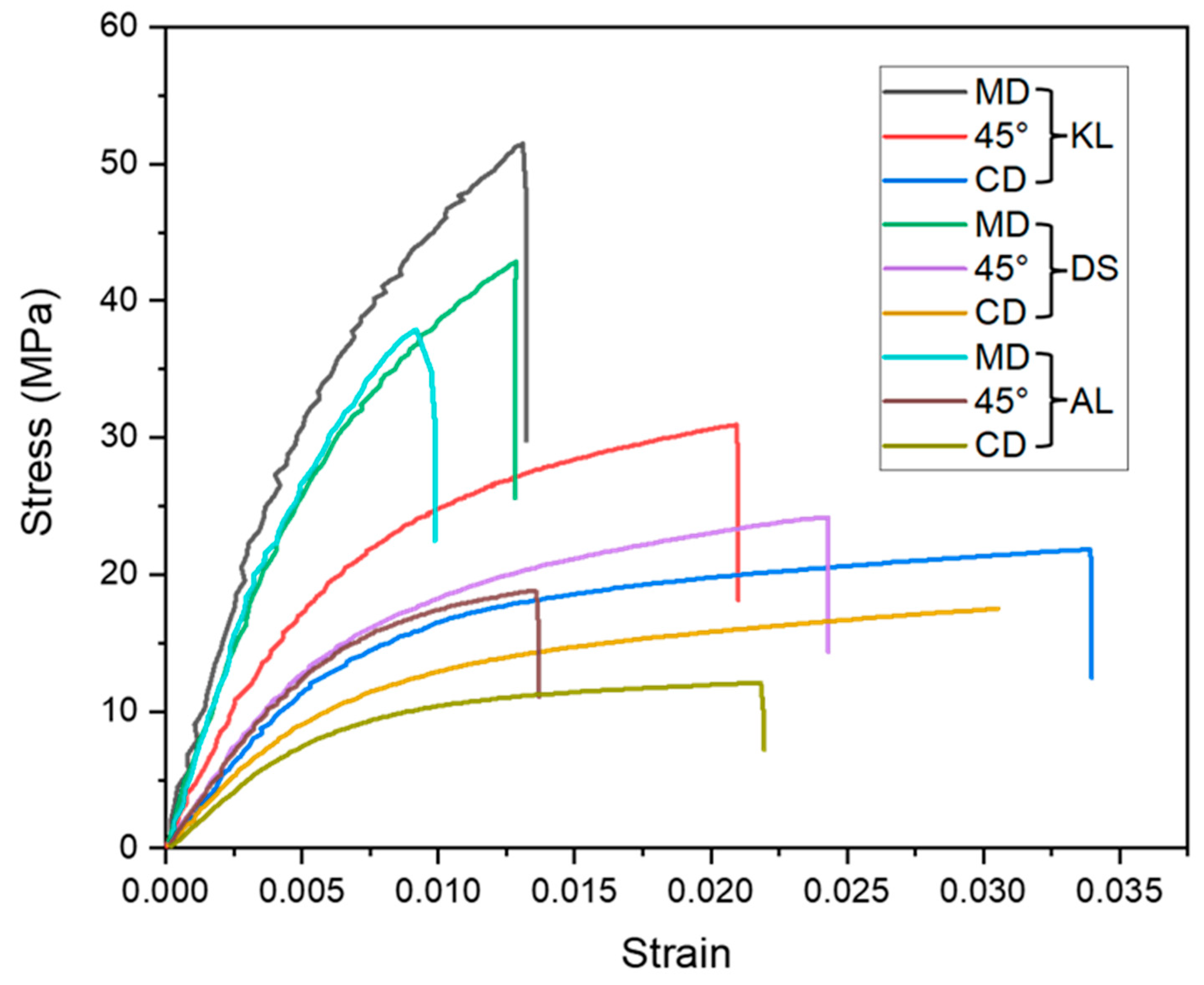
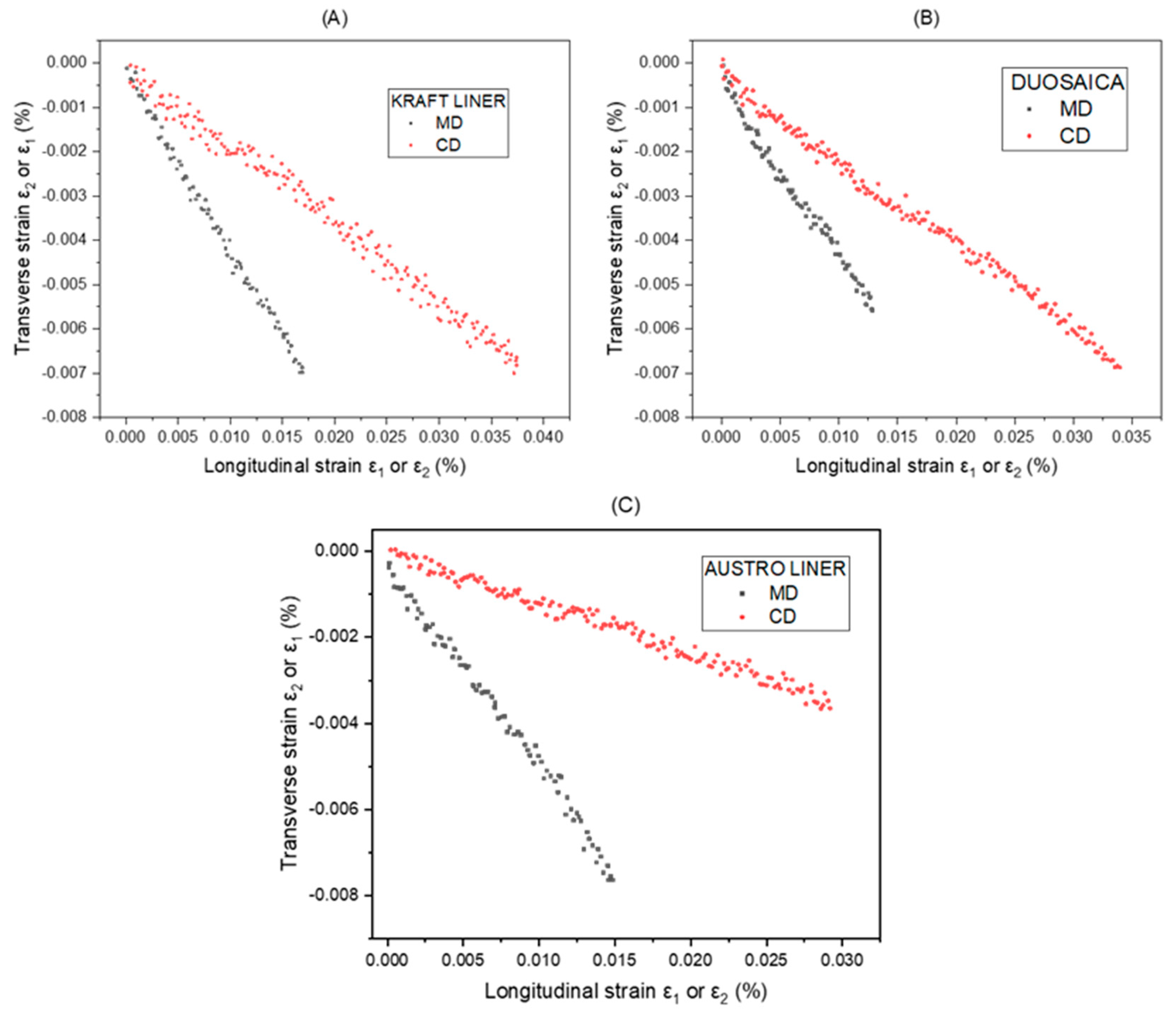
2.2.4. Tensile Test
3. Homogenization Model for Corrugated Board
3.1. Theory of Laminated Plates
3.2. Adapting Laminate Theory to Double-Wall Corrugated Board
3.3. Traction and Bending Stiffnesses
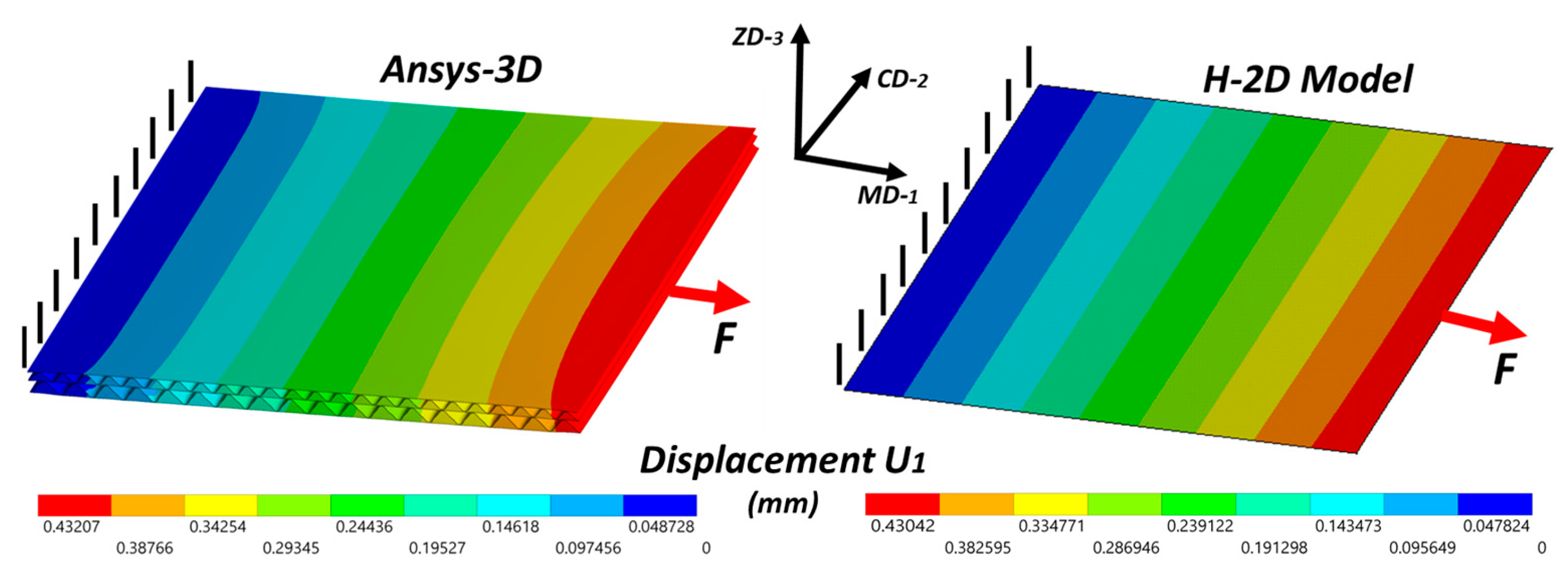
3.4. Implementation of the Homogenized Model in FE Analysis
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Biancolini, M.E.; Brutti, C. Numerical and experimental investigation of the strength of corrugated board packages. Packag. Technol. Sci. 2003, 16, 47–60. [Google Scholar] [CrossRef]
- Rejab, M.R.M.; Rejab, M.R.M.; Cantwell, W.J. The Mechanical Behaviour of Corrugated-Core Sandwich Panels. Compos. Part B-Eng. 2013, 47, 267–277. [Google Scholar] [CrossRef]
- Liu, S.; Xiao, J. Mechanical Properties Analysis of Carbon Fiber Panels Sandwich Structure Containing Aluminum Alloy Corrugated Core. In Proceedings of the DEStech Transactions on Engineering and Technology Research; DEStech Publications, Inc.: Lancaster, PA, USA, 2019. [Google Scholar] [CrossRef]
- Song, Y.-T.; Lee, H.-Y.; Esashi, M. A Corrugated Bridge of Low Residual Stress for RF-MEMS Switch. Sens. Actuators A-Phys. 2007, 135, 818–826. [Google Scholar] [CrossRef]
- Wang, D.-W.; Wen, Z.-H.; Glorieux, C.; Ma, L. Sound Absorption of Face-centered Cubic Sandwich Structure with Micro-perforations. Mater. Des. 2020, 186, 108344. [Google Scholar] [CrossRef]
- Minh, D.P.T.; Khoa, N.N. An analytic homogenization model in traction and bending for orthotropic composite plates with the type of double corrugated cardboard. Vietnam. J. Mech. 2016, 38, 41–50. [Google Scholar] [CrossRef]
- Duong, P.T.M. Analysis and simulation for the double corrugated cardboard plates under bending and in-plane shear force by homogenization method. Int. J. Mech. 2017, 11, 176–181. [Google Scholar]
- Minh, D.P.T.; Tien, D.L.; Hung, N.Q. Experimental and Numerical Characterization of Mechanical Behavior for the Corrugated Cardboard. In Advances in Engineering Research and Application; Sattler, K.-U., Nguyen, D.C., Vu, N.P., Long, B.T., Puta, H., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 425–433. [Google Scholar] [CrossRef]
- Garbowski, T.; Garbowski. Review on Numerical Homogenization of Corrugated Materials. State-of-the-art in Modeling of Corrugated Board. BioResources 2025, 20, 5157. [Google Scholar] [CrossRef]
- Garbowski, T.; Knitter-Pi atkowska, A. Analytical Determination of the Bending Stiffness of a Five-Layer Corrugated Cardboard with Imperfections. Materials 2022, 15, 663. [Google Scholar] [CrossRef] [PubMed]
- Mrówczynski, D.; Knitter-Piatkowska, A.; Garbowski, T. Non-Local Sensitivity Analysis and Numerical Homogenization in Optimal Design of Single-Wall Corrugated Board Packaging. Materials 2022, 15, 720. [Google Scholar] [CrossRef] [PubMed]
- Garbowski, T.; Grabski, J.K.; Marek, A. Full-Field Measurements in the Edge Crush Test of a Corrugated Board Analytical and Numerical Predictive Models. Materials 2021, 14, 2840. [Google Scholar] [CrossRef] [PubMed]
- Mrówczynski, D.; Knitter-Piątkowska, A.; Garbowski, T. Numerical Homogenization of Single-Walled Corrugated Board with Imperfections. Appl. Sci. 2022, 12, 9632. [Google Scholar] [CrossRef]
- Garbowski, T.; Marek, A. Homogenization of corrugated boards through inverse analysis. In Proceedings of the International Conference on Engineering and Applied Sciences Optimization OPT-i, Kos Town, Greece, 4–6 June 2014; Available online: https://api.semanticscholar.org/CorpusID:191602306 (accessed on 7 February 2020).
- Mrówczyński, D.; Garbowski, T. Influence of Imperfections on the Effective Stiffness of Multilayer Corrugated Board. Materials 2023, 16, 1295. [Google Scholar] [CrossRef] [PubMed]
- ISO:2019; Paper and Board—Determination of Grammage. International Organization for Standardization: Geneva, Switzerland, 2019.
- ISO:2011; Paper and Board—Determination of Thickness, Density and Specific Volume. International Organization for Standardization: Geneva, Switzerland, 2011.
- ISO:2022; Paper, Board and Pulps—Standard Atmosphere for Conditioning and Testing and Procedure for Monitoring the Atmosphere and Conditioning of Samples. International Organization for Standardization: Geneva, Switzerland, 2022.
- Nwabor, O.F.; Singh, S.; Chorachoo, J.; Vongkamjan, K. Valorization of Wastepaper Through Antimicrobial Functionalization with Biogenic Silver Nanoparticles, a Sustainable Packaging Composite. Waste Biomass Valorization 2021, 12, 3287–3301. [Google Scholar] [CrossRef]
- Kethiri, M.-A.; Chikhi, M.; Belghar, N.; Chekired, F.; Guerira, B. A thermophysical investigation of the potential for the use of wastepaper for insulation building materials. Int. Wood Prod. J. 2024, 15, 63–71. [Google Scholar] [CrossRef]
- Zwain, H.M.; Chang, S.; Dahlan, I. Physicochemical characteristics of microbial content in a modified anaerobic inclining-baffled reactor (MAI-BR) treating recycled paper mill effluent (RPME). Prep. Biochem. Biotechnol. 2019, 49, 344–351. [Google Scholar] [CrossRef] [PubMed]
- ASTM D828-16; Standard Test Method for Tensile Properties of Paper and Paperboard Using Constant-Rate-of-Elongation Apparatus. ASTM International: West Conshohocken, PA, USA, 2016. [CrossRef]
- Talbi, N.; Batti, A.; Ayad, R.; Guo, Y.Q. An analytical homogenization model for finite element modelling of corrugated cardboard. Compos. Struct. 2009, 88, 280–289. [Google Scholar] [CrossRef]






| Layers | Grammage (g/m2) | ±Standard Deviation (g/m2) | Thickness (mm) | ±Standard Deviation (mm) | Density (kg/m3) | ±Standard Deviation (kg/m3) |
|---|---|---|---|---|---|---|
| KL | 125.0 | 0.7 | 0.175 | 0.005 | 714.3 | 13.9 |
| DS | 130.0 | 0.9 | 0.190 | 0.004 | 684.2 | 11.0 |
| AL | 135.0 | 0.6 | 0.185 | 0.005 | 729.7 | 10.4 |
| KL | ±Standard Deviation | DS | ±Standard Deviation | AL | ±Standard Deviation | |
|---|---|---|---|---|---|---|
| (MPa) | 6200 | 156 | 5738 | 189 | 6567 | 210 |
| (MPa) | 3928 | 120 | 3111 | 141 | 2919 | 132 |
| (MPa) | 2425 | 78 | 2202 | 71 | 1770 | 55 |
| (MPa) | 31 | 0.78 | 28.7 | 0.94 | 32.8 | 1.05 |
| 12 | 0.42 | 0.02 | 0.39 | 0.04 | 0.47 | 0.03 |
| 21 | 0.17 | 0.01 | 0.15 | 0.02 | 0.13 | 0.02 |
| G12 (MPa) | 1716 | 18 | 1266 | 32 | 1243 | 21 |
| G13 (MPa) | 112.7 | 2.8 | 104.3 | 3.4 | 119.4 | 3.8 |
| G23 (MPa) | 177.1 | 4.4 | 164 | 5.4 | 187.6 | 6 |
| Rigidities | (N/mm) | (N/mm) | (N/mm) | (N) | (N) | (N) | (N.mm) | (N.mm) | (N.mm) |
|---|---|---|---|---|---|---|---|---|---|
| Values | 3595.6 | 546.5 | 4055.2 | 710.5 | 90.0 | 466.8 | 23,235.1 | 3802.1 | 12,602.9 |
| Ansys-3D | H-2DModel | Error (%) | |||
|---|---|---|---|---|---|
| Traction F = 1500 N | MD | Displacement U1 (mm) | 0.4321 | 0.4304 | −0.39 |
| CD | Displacement U2 (mm) | 0.3755 | 0.3818 | −1.65 | |
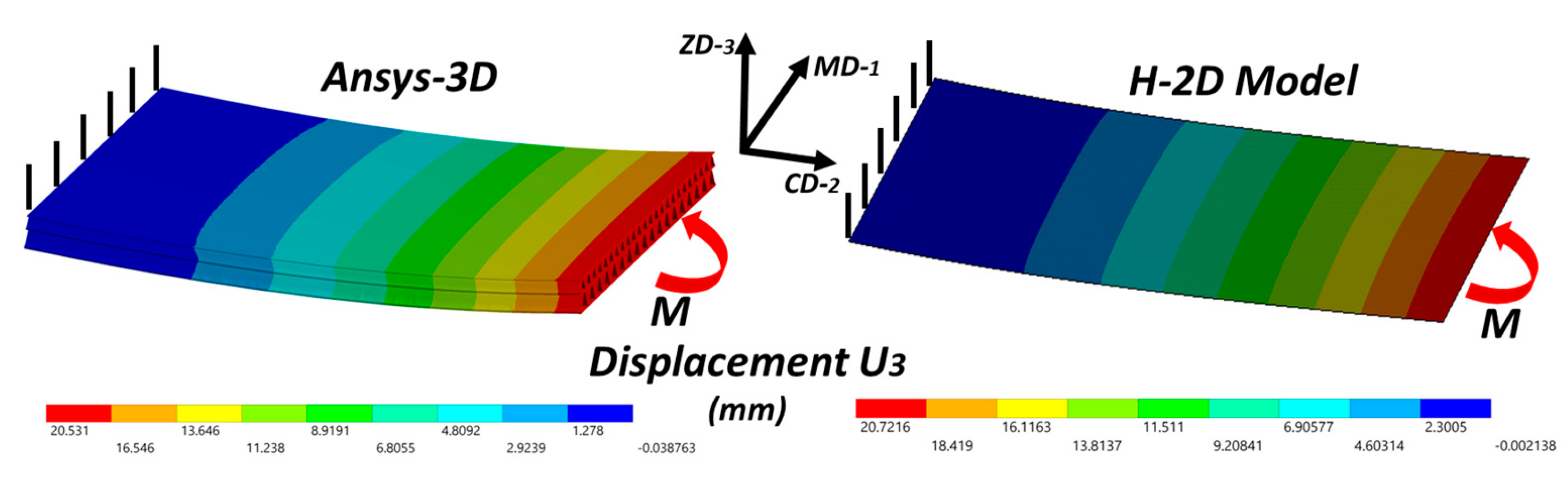
| Bending M = 8 KNmm | MD | Displacement U3 (mm) | 22.8365 | 23.2175 | −1.64 |
| CD | Displacement U3 (mm) | 20.5310 | 20.7216 | +0.91 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Maouche, M.-F.; Hecini, M. Analytical Homogenization Approach for Double-Wall Corrugated Cardboard Incorporating Constituent Layer Characterization. Appl. Mech. 2026, 7, 4. https://doi.org/10.3390/applmech7010004
Maouche M-F, Hecini M. Analytical Homogenization Approach for Double-Wall Corrugated Cardboard Incorporating Constituent Layer Characterization. Applied Mechanics. 2026; 7(1):4. https://doi.org/10.3390/applmech7010004
Chicago/Turabian StyleMaouche, Mohamed-Fouad, and Mabrouk Hecini. 2026. "Analytical Homogenization Approach for Double-Wall Corrugated Cardboard Incorporating Constituent Layer Characterization" Applied Mechanics 7, no. 1: 4. https://doi.org/10.3390/applmech7010004
APA StyleMaouche, M.-F., & Hecini, M. (2026). Analytical Homogenization Approach for Double-Wall Corrugated Cardboard Incorporating Constituent Layer Characterization. Applied Mechanics, 7(1), 4. https://doi.org/10.3390/applmech7010004





