The Role of Domain Size and Boundary Conditions in Mathematical Modeling of Railway Tracks
Abstract
1. Introduction
2. Analytical Methods
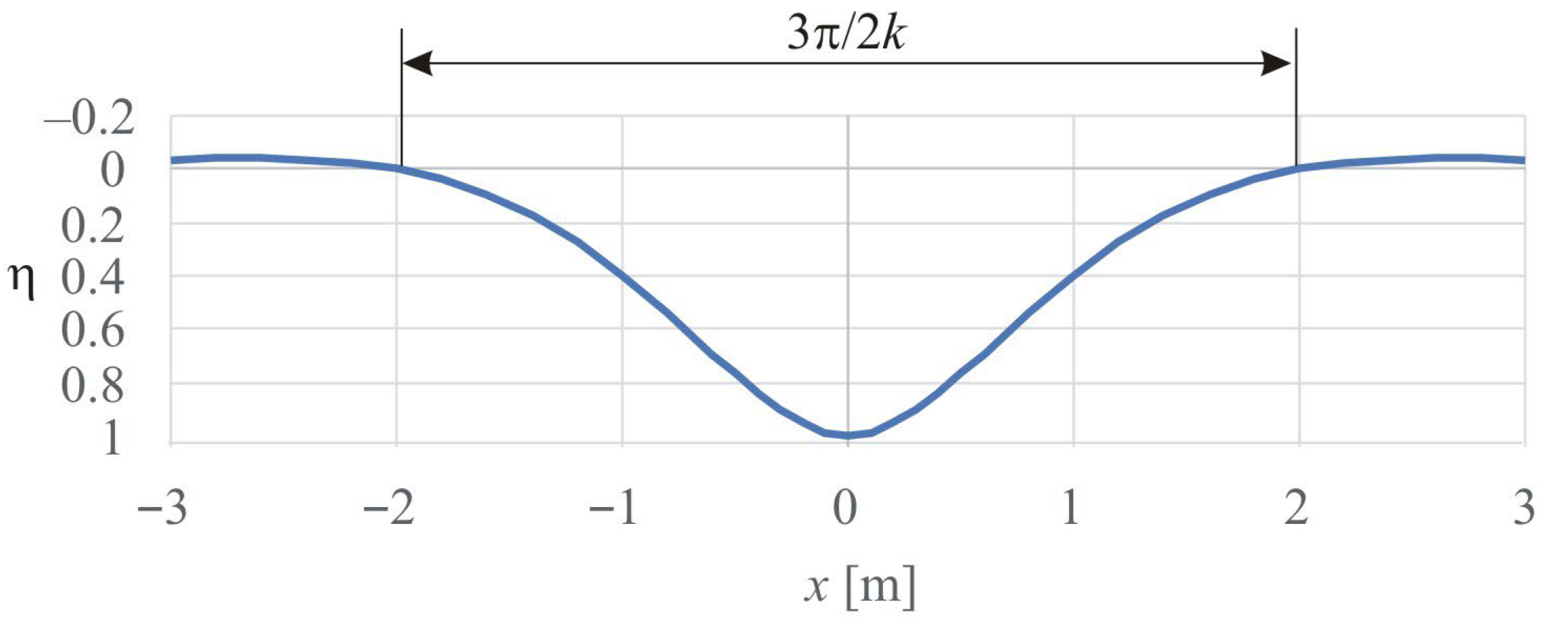
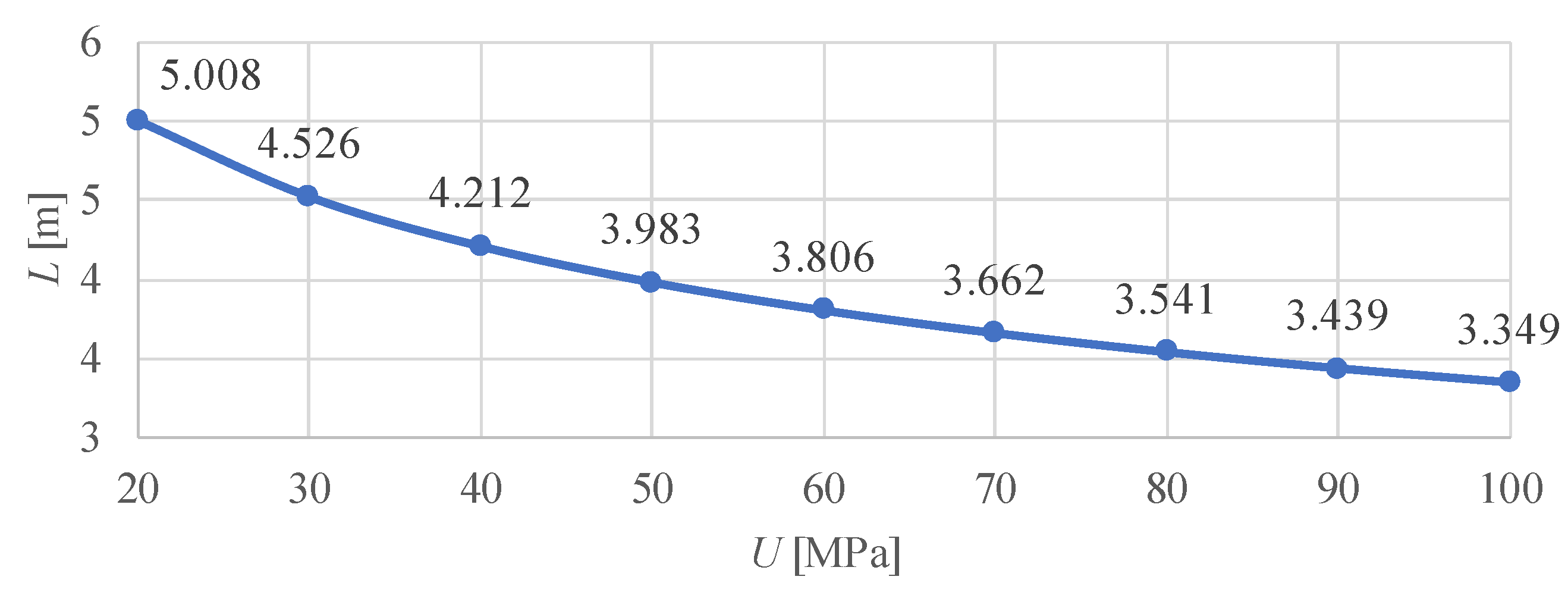
2.1. Rail Deflection Length
2.2. Number of Sleeper Units Along the Modeled Section
- Option (a). The rail bends under the external load, and the deflection profile and amplitude determine the contact forces from the rail to the sleepers. This option most closely corresponds to the physical behavior of the system and, where possible, should be preferred over the others. However, its application has certain requirements. First, the rail length in the mathematical model must be sufficient to reproduce the ”complete” rail deflection with an appropriate profile and amplitude (see Section 2.1). Second, the model must include the necessary physical–mathematical tools to simulate not only compression (tension) but also bending.
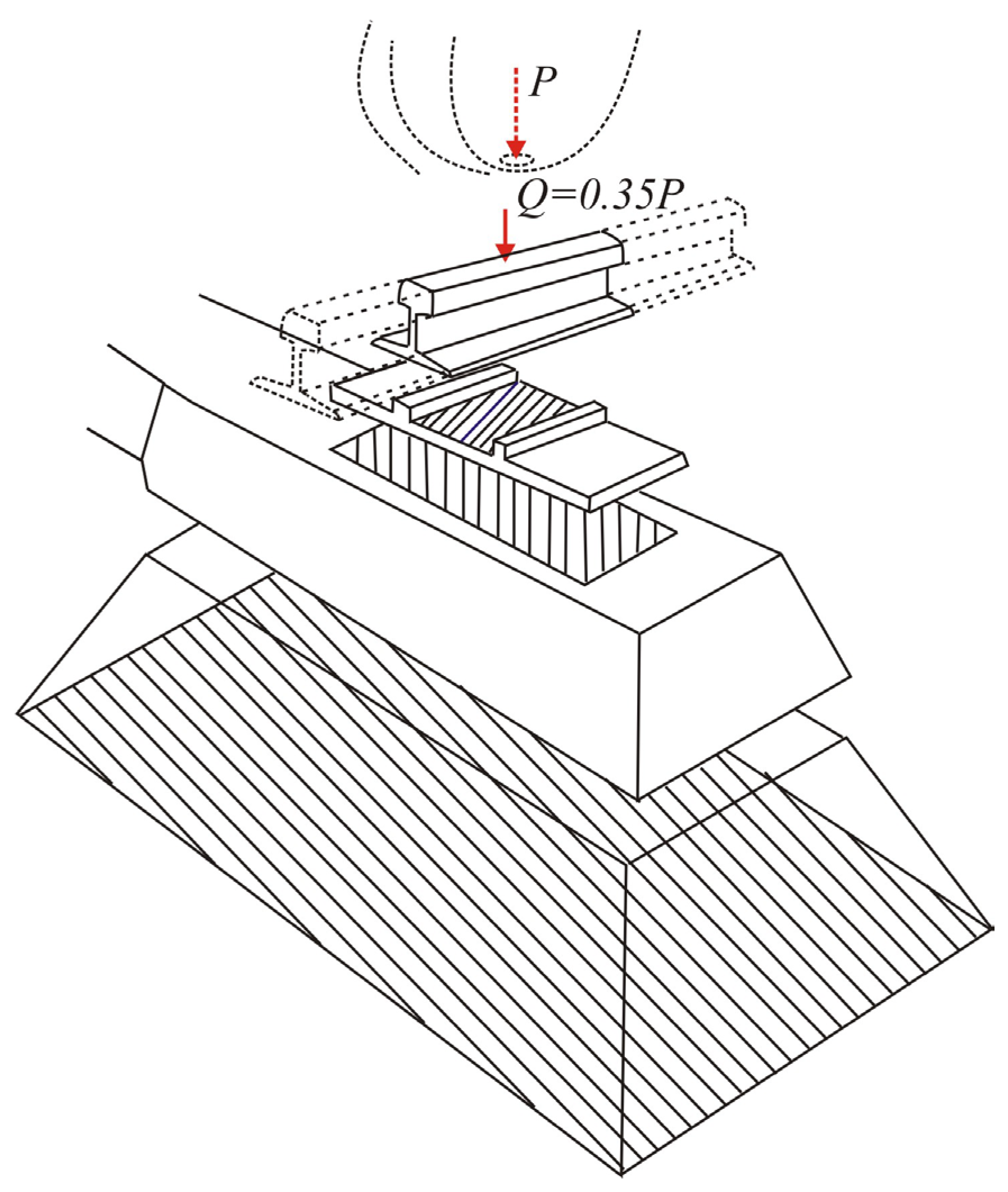
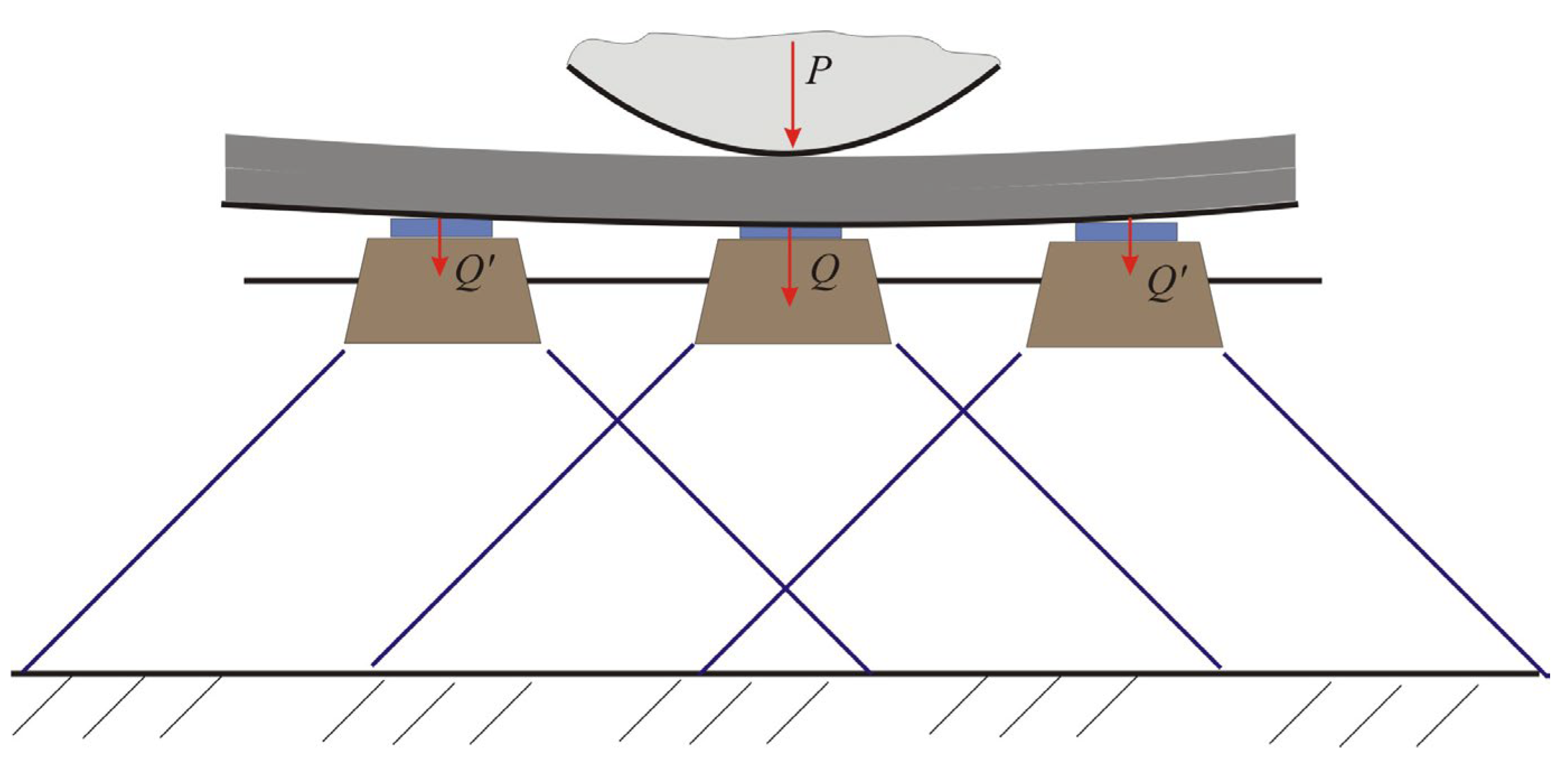
- Option (b). The rail is represented by notional short segments, with the pressure on each corresponding sleeper specified separately. This approach makes sense for models where the length of the railway track section is shorter than the full rail deflection length but long enough to include several sleepers. In this case, the external load can be specified as a distributed pressure on individual sleepers, as shown in Figure 3 and Equation (5).
- Option (c). The rail transmits the load to the central sleeper only, while the loads on adjacent sleepers are neglected. This is reasonable for railway track models where the influence of adjacent sleepers on the stresses in the lower ballast layers and subgrade can be ignored. It should be noted that the use of very short models, whose length covers no more than one sleeper, does not automatically exclude the need to account for the additional pressure at the relevant depths beneath the sleeper foundation.
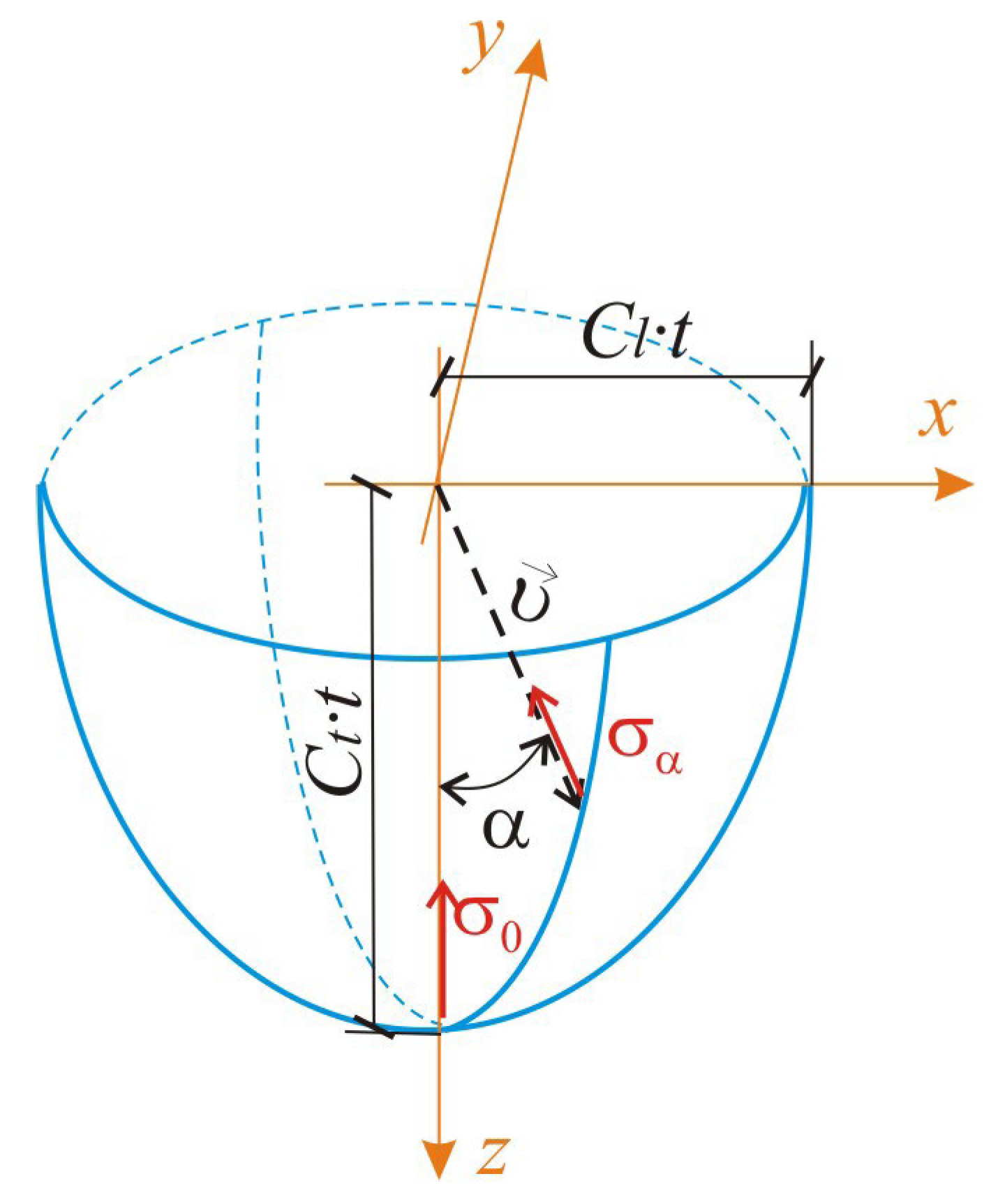
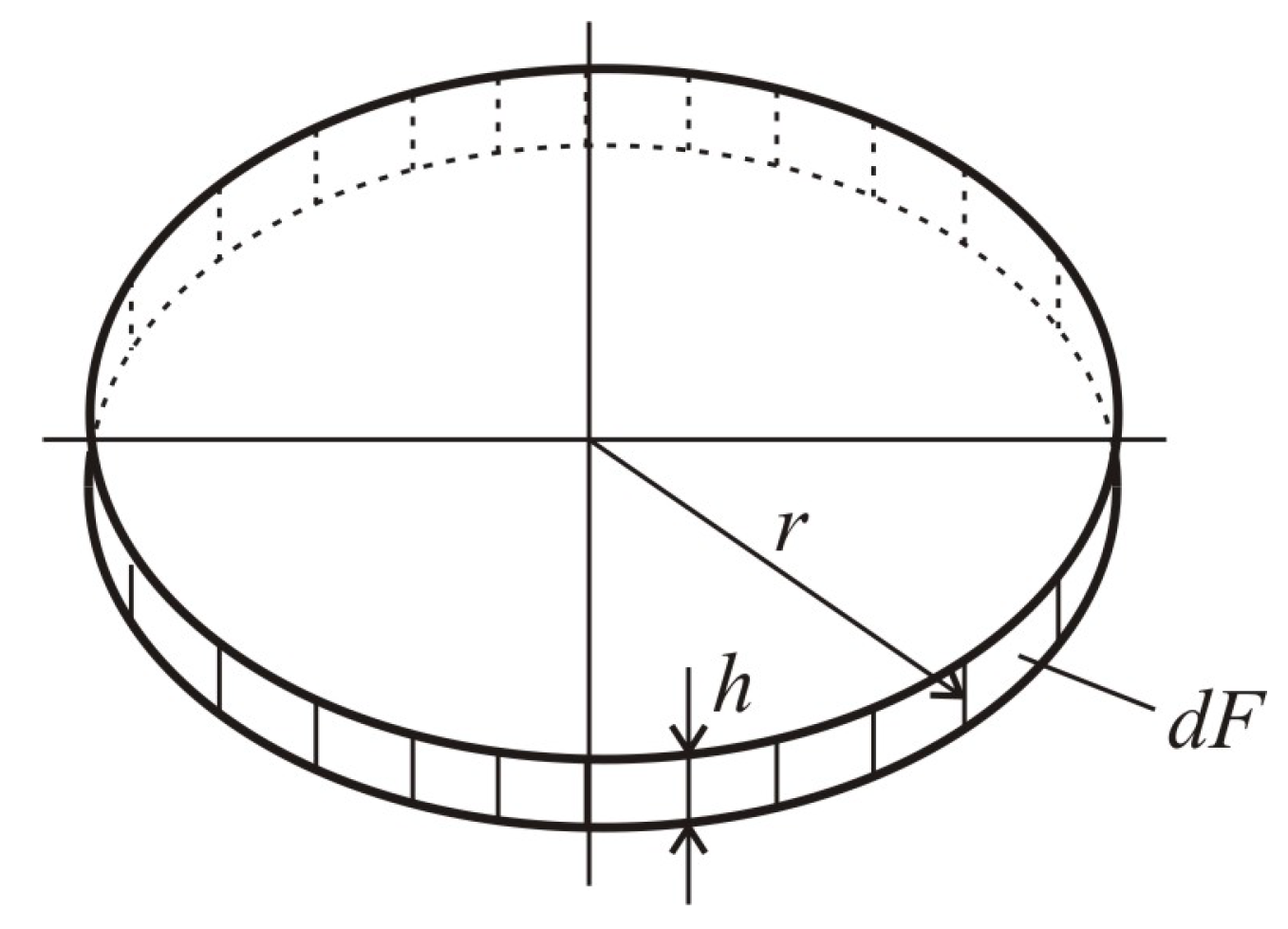
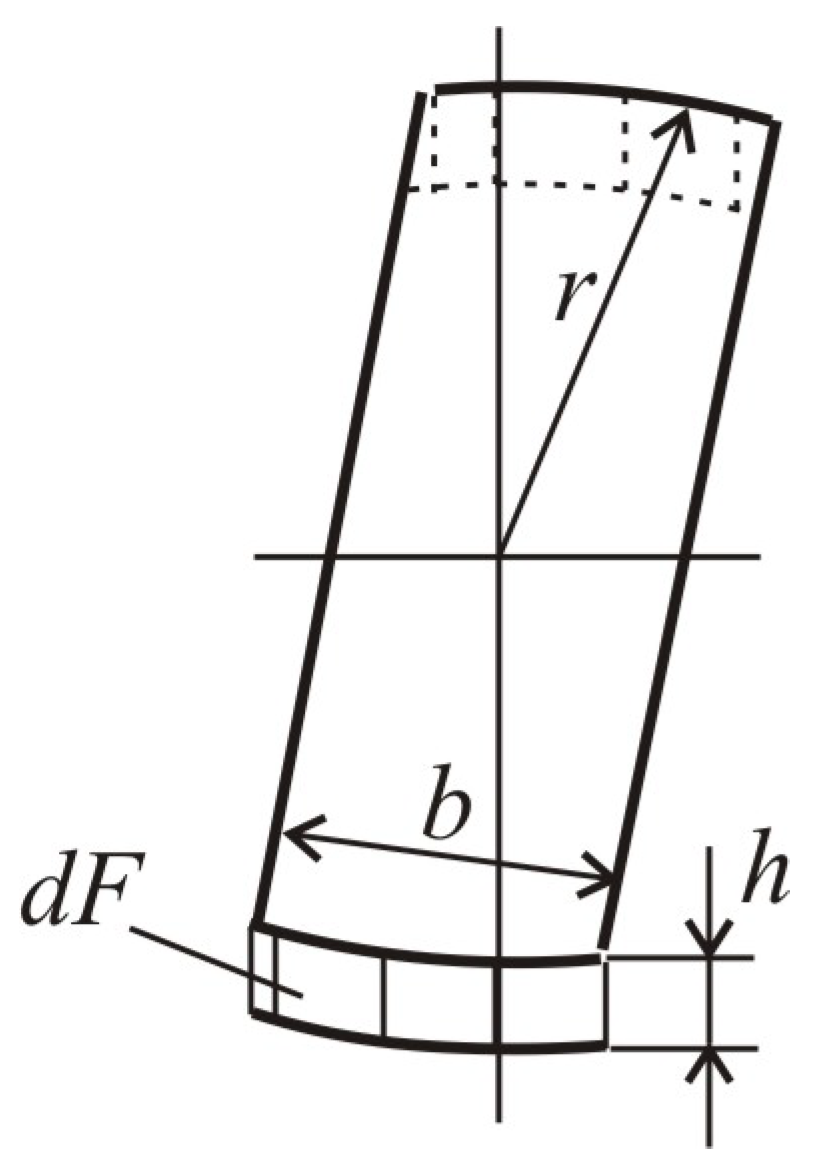
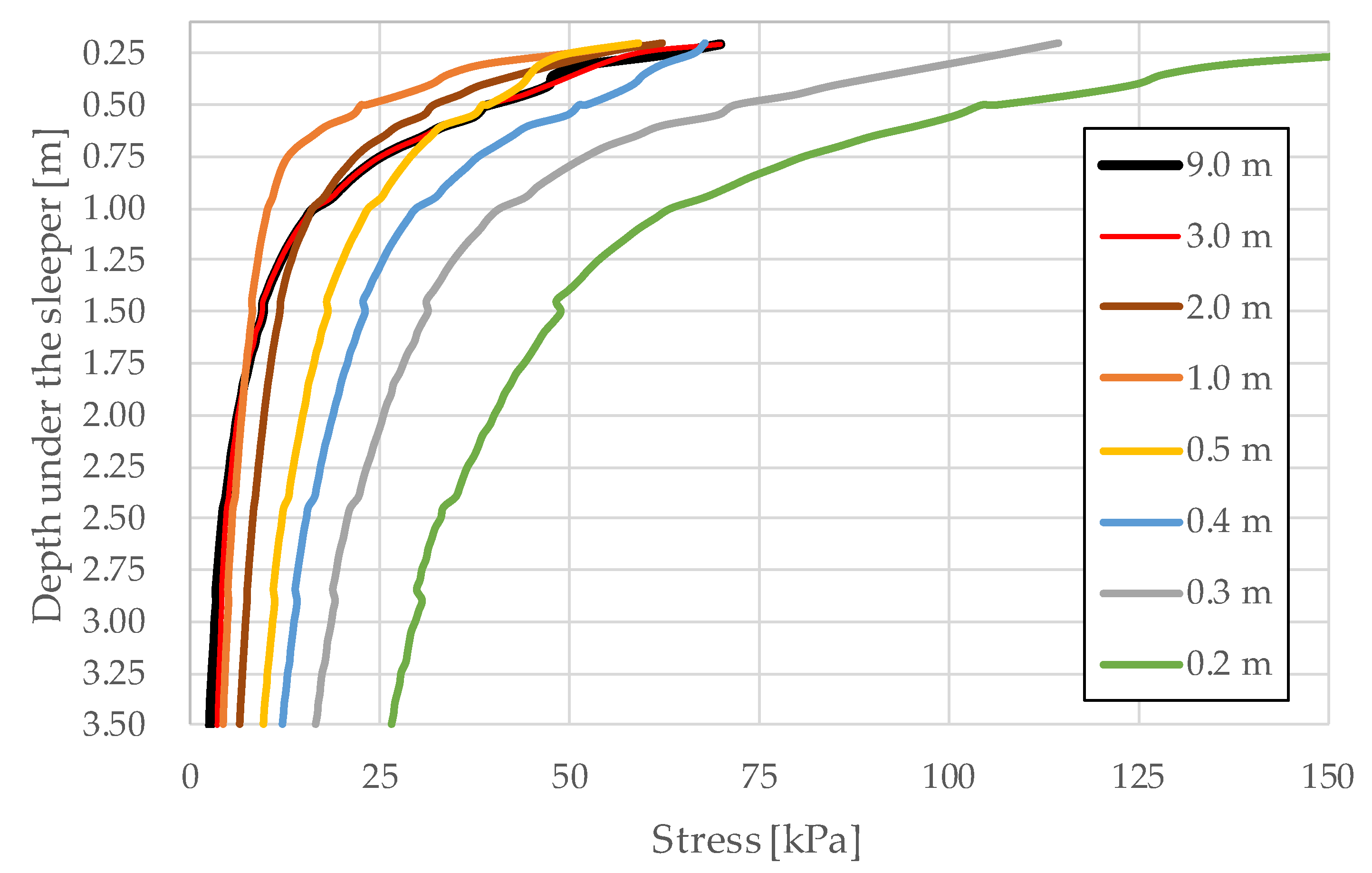
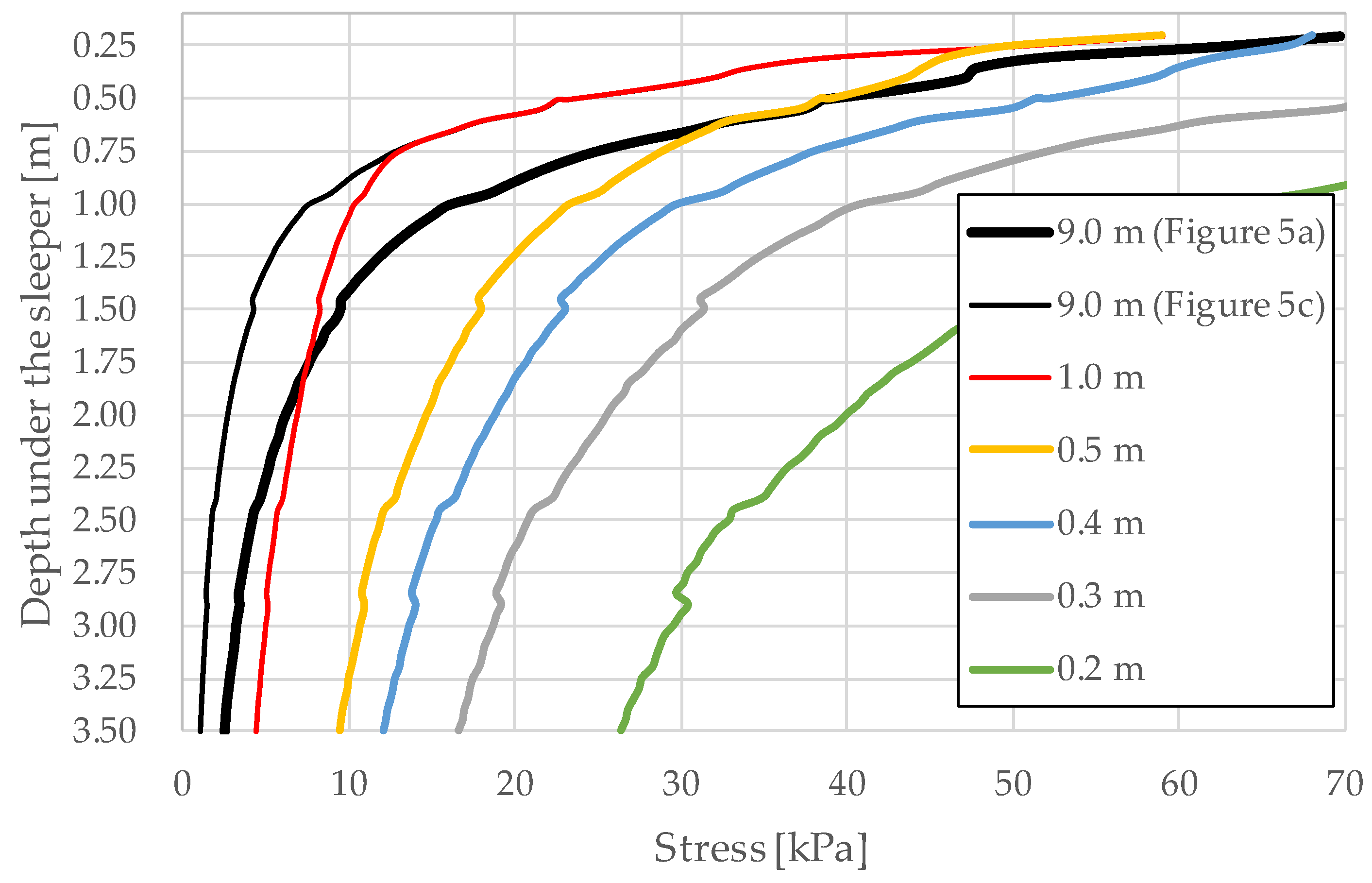
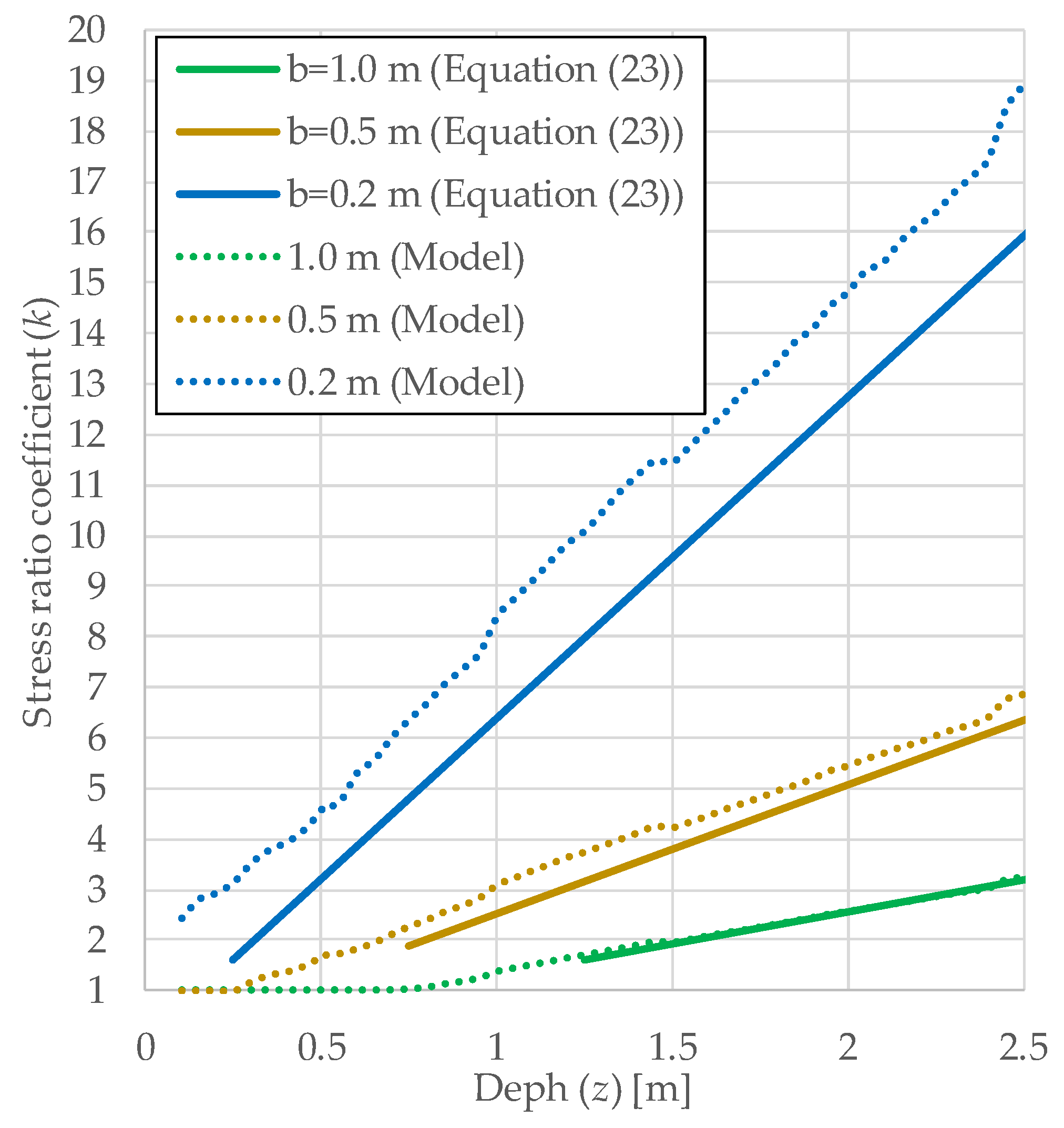
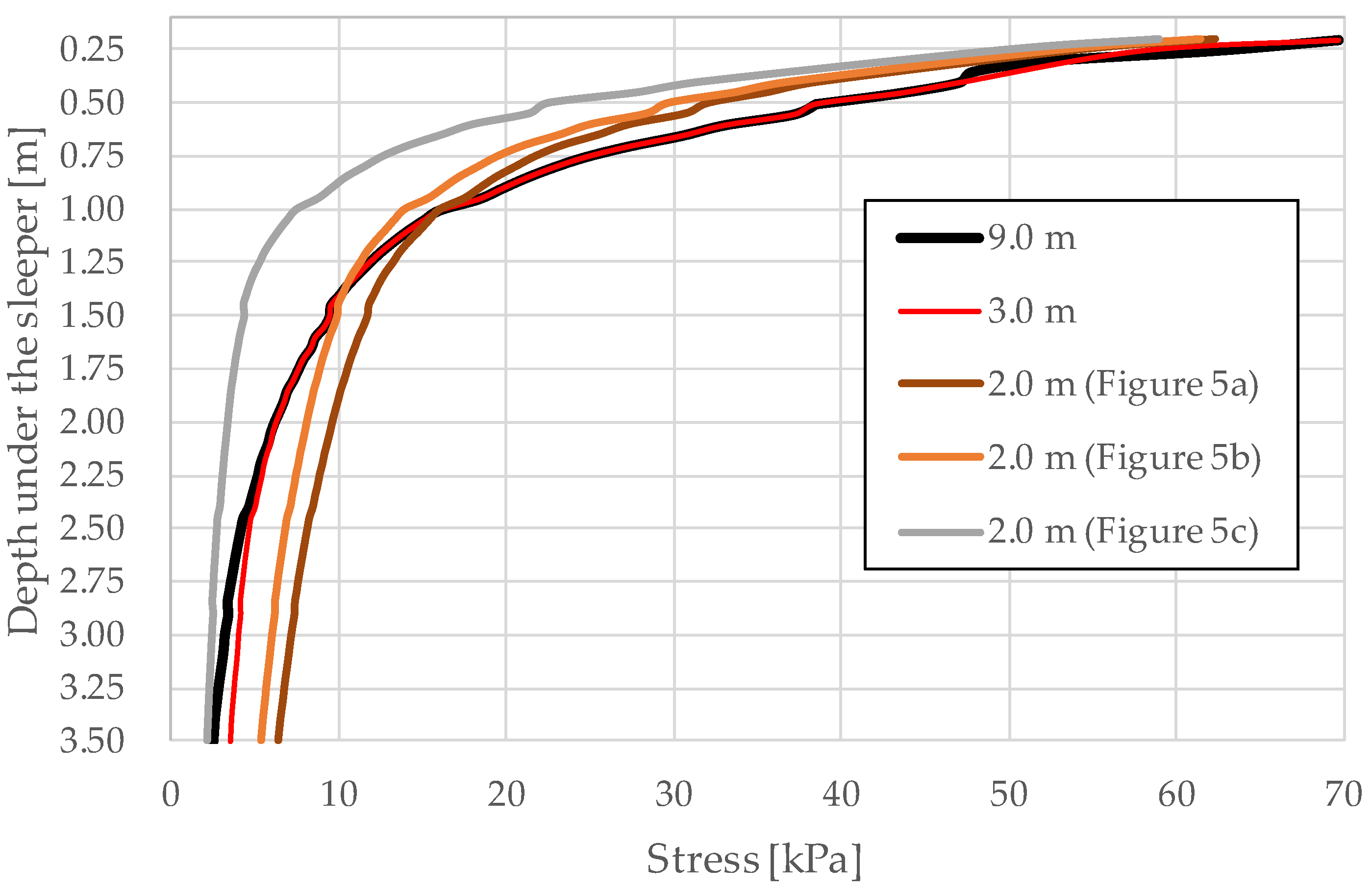
2.3. Shape and Dimensions of the Sub-Rail Domain
3. Results of Mathematical Modeling
3.1. Modeling the Railway Track Through the Propagation of Elastic Waves
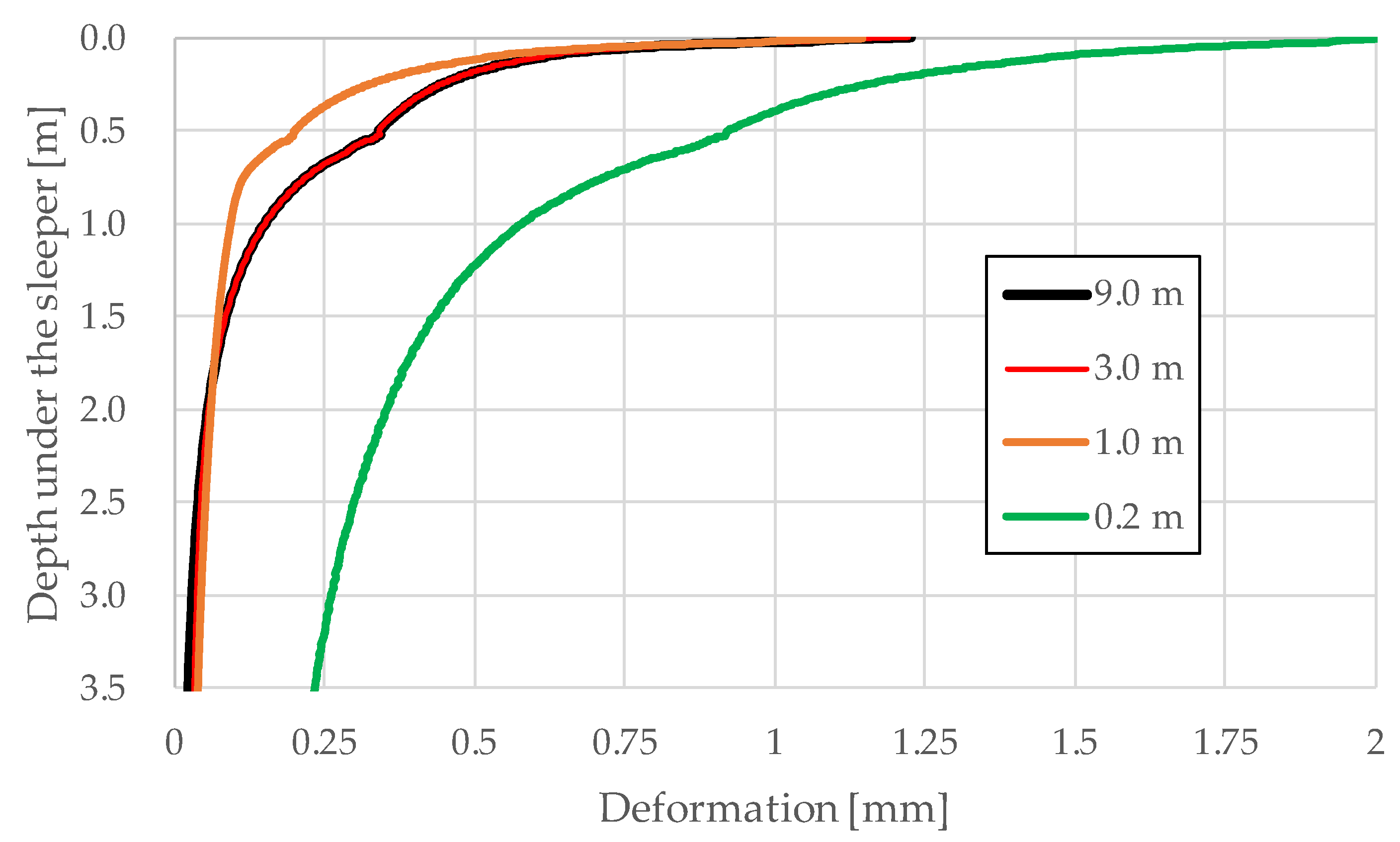
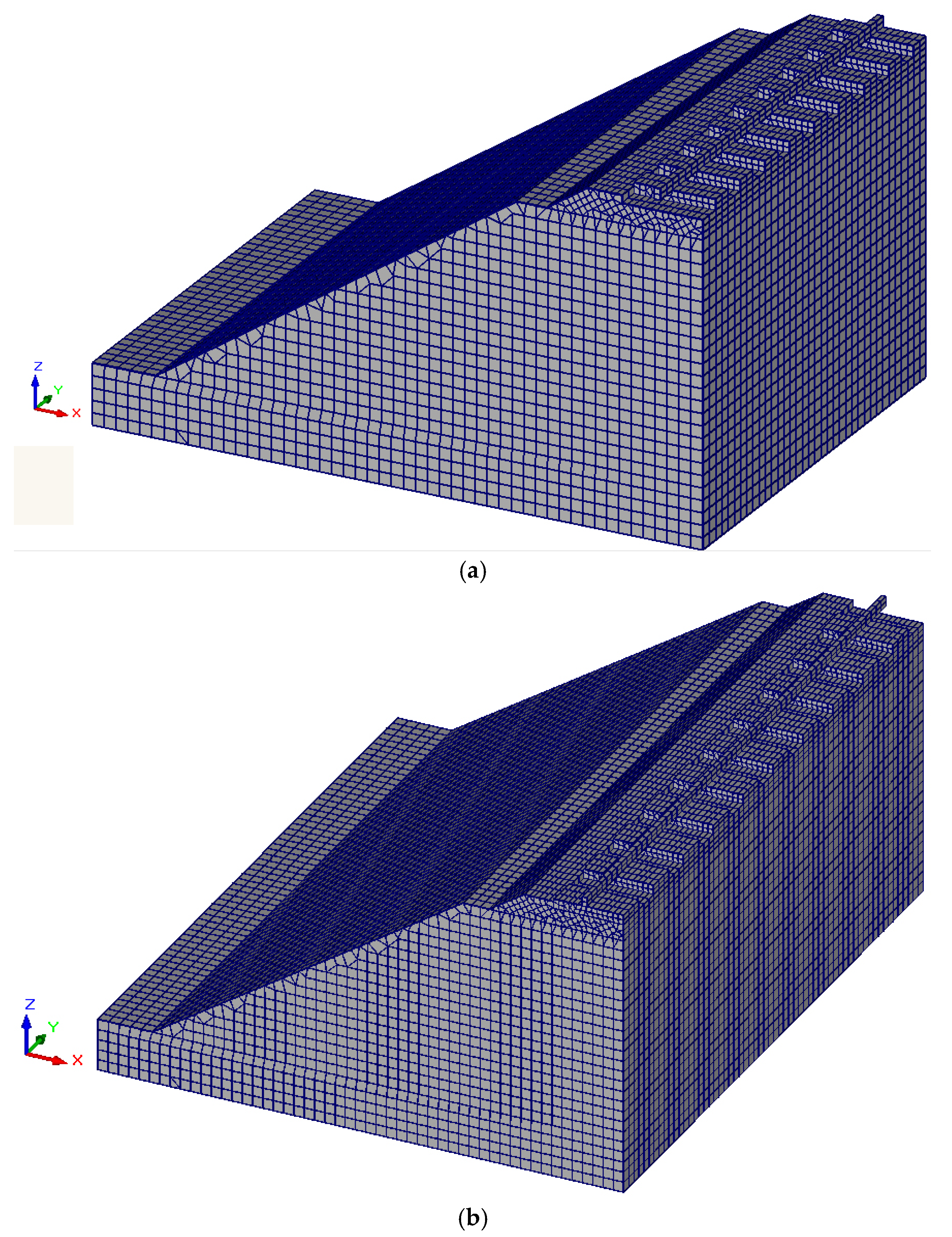
3.2. Finite Element Modeling
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alkhdour, A.; Tiutkin, O.; Fischer, S.; Kurhan, D. An Analytical Method for Determining the Stress–Strain State of a Subgrade with Combined Reinforcement. Infrastructures 2024, 9, 240. [Google Scholar] [CrossRef]
- Petrenko, V.; Bannikov, D.; Kharchenko, V.; Tkach, T. Regularities of the deformed state of the geotechnical system “soil base—Micropile”. IOP Conf. Ser. Earth Environ. Sci. 2022, 970, 12028. [Google Scholar] [CrossRef]
- Jankowski, W.; Sołkowski, J. The modelling of railway subgrade strengthening foundation on weak soils. Open Eng. 2022, 12, 539–554. [Google Scholar] [CrossRef]
- Alsirawan, R.; Koch, E.; Alnmr, A. Proposed Method for the Design of Geosynthetic-Reinforced Pile-Supported (GRPS) Embankments. Sustainability 2023, 15, 6196. [Google Scholar] [CrossRef]
- Alsirawan, R.; Koch, E. The finite element modeling of rigid inclusion-supported embankment. Pollack Period. 2022, 17, 86–91. [Google Scholar] [CrossRef]
- Deng, Y.; Zhao, H.; Li, L.; Yao, Z.; Li, L. Research on static and dynamic loading performance of geosynthetic reinforced and pile-supported embankment. Appl. Sci. 2023, 13, 3152. [Google Scholar] [CrossRef]
- Guo, Q.; Li, B.; Ye, Z.; Xu, J. Finite Element Analysis on the Behavior of Solidified Soil Embankments on Piled Foundations under Dynamic Traffic Loads. Appl. Sci. 2024, 14, 4464. [Google Scholar] [CrossRef]
- Alsirawan, R.; Koch, E. Dynamic analysis of geosynthetic-reinforced pile-supported embankment for a high-speed rail. Acta Polytech. Hung. 2023, 21, 31–50. [Google Scholar] [CrossRef]
- Chango, I.V.L.; Yan, M.; Ling, X.; Liang, T.; Assogba, O.C. Dynamic response analysis of geogrid reinforced embankment supported by CFG pile structure during a high-speed train operation. Lat. Am. J. Solids Struct. 2019, 16, e214. [Google Scholar] [CrossRef]
- Feng, G.; Luo, Q.; Lyu, P.; Connolly, D.P.; Wang, T. An Analysis of Dynamics of Retaining Wall Supported Embankments: Towards More Sustainable Railway Designs. Sustainability 2023, 15, 7984. [Google Scholar] [CrossRef]
- Giner, I.G.; Alvarez, A.R.; Sánchez-Cambronero García-Moreno, S.; Camacho, J.L. Dynamic modelling of high-speed ballasted railway tracks: Analysis of the behaviour. Transp. Res. Procedia 2016, 18, 357–365. [Google Scholar] [CrossRef]
- Kurhan, D.; Fischer, S. Modeling of the Dynamic Rail Deflection using Elastic Wave Propagation. J. Appl. Comput. Mech. 2022, 8, 379–387. [Google Scholar] [CrossRef]
- Xie, H.; Luo, Q.; Wang, T.; Jiang, L.; Connolly, D.P. Stochastic analysis of dynamic stress amplification factors for slab track foundations. Int. J. Rail Transp. 2024, 12, 281–303. [Google Scholar] [CrossRef]
- Xu, F.; Yang, Q.; Liu, W.; Leng, W.; Nie, R.; Mei, H. Dynamic stress of subgrade bed layers subjected to train vehicles with large axle loads. Shock Vib. 2018, 2018, 2916096. [Google Scholar] [CrossRef]
- Fesharakifard, R.; Dequidt, A.; Tison, T.; Coste, O. Dynamics of railway track subjected to distributed and local out-of-round wheels. Mech. Ind. 2013, 14, 347–359. [Google Scholar] [CrossRef]
- Sayeed, M.A.; Shahin, M.A. Dynamic Response Analysis of Ballasted Railway Track–Ground System under Train Moving Loads Using 3D Finite Element Numerical Modelling. Transp. Infrastruct. Geotech. 2023, 10, 639–659. [Google Scholar] [CrossRef]
- Darenskiy, A.N.; Malishevskaya, A.S. Using mathematical models of dynamic systems “crew-track” powers to study the interaction of rolling stock and tracks underground. Inf. Control Syst. Rail Transp. 2017, 1, 43–51. [Google Scholar] [CrossRef][Green Version]
- Kurhan, D.; Kurhan, M. Modeling the Dynamic Response of Railway Track. IOP Conf. Ser. Mater. Sci. Eng. 2019, 708, 12013. [Google Scholar] [CrossRef]
- Auersch, L. Reduction of train-induced vibrations—calculations of different railway lines and mitigation measures in the transmission path. Appl. Sci. 2023, 13, 6706. [Google Scholar] [CrossRef]
- Moreno, A.G.; López, A.A.; Carrasco García, M.G.; Turias, I.J.; Ruiz Aguilar, J.J. A novel application of computational contact tools on nonlinear finite element analysis to predict ground-borne vibrations generated by trains in ballasted tracks. Modelling 2024, 5, 1454–1468. [Google Scholar] [CrossRef]
- Hawksbee, S.; Grossoni, I.; Bezin, Y.; Lee, B.; Watson, G.; Milne, D.; Le Pen, L.; Abadi, T.; Jorge, P. Modelling the Improved Behaviour of a Switch Installed on Ballast-Asphalt Track. Civ.-Comp Conf. 2022, 1, 5.6. [Google Scholar] [CrossRef]
- Hou, B.; Wang, D.; Wang, B.; Chen, X.; Pombo, J. Vibration reduction in ballasted track using ballast mat: Numerical and experimental evaluation by wheelset drop test. Appl. Sci. 2022, 12, 1844. [Google Scholar] [CrossRef]
- Kuchak, A.J.T.; Marinkovic, D.; Zehn, M. Parametric investigation of a rail damper design based on a lab-scaled model. J. Vib. Eng. Technol. 2021, 9, 51–60. [Google Scholar] [CrossRef]
- Nielsen, J.C.O.; Pieringer, A.; Thompson, D.J.; Torstensson, P.T. Wheel–Rail Impact Loads, Noise and Vibration: A Review of Excitation Mechanisms, Prediction Methods and Mitigation Measures. Notes Numer. Fluid Mech. Multidiscip. Des. 2021, 150, 3–40. [Google Scholar] [CrossRef]
- Farooq, M.A.; Meena, N.K.; Punetha, P.; Nimbalkar, S.; Lam, N. Experimental and computational analyses of sustainable approaches in railways. Infrastructures 2024, 9, 53. [Google Scholar] [CrossRef]
- Ngo, T.; Hasan, M. Finite element modelling of geogrids reinforced ballasted tracks. Transp. Infrastruct. Geotech. 2024, 11, 2425–2447. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, J.; Cai, D.; Su, Q.; Yang, G.; Yuan, S.; Jiang, G. Recent advances in subgrade engineering for high-speed railway. ITI J. (Oxf. Univ. Press) 2023, 2, liad001. [Google Scholar] [CrossRef]
- Yahia Alabbasi, M.H. Geomechanical Modelling of Railroad Ballast: A Review. Arch. Comput. Methods Eng. 2019, 26, 327–365. [Google Scholar] [CrossRef]
- Charoenwong, C.; Connolly, D.P.; Colaço, A.; Alves Costa, P.; Woodward, P.K.; Romero, A.; Galvín, P. Railway slab vs ballasted track: A comparison of track geometry degradation. Constr. Build. Mater. 2023, 378, 131121. [Google Scholar] [CrossRef]
- Hua, X.; Zatar, W.; Cheng, X.; Chen, G.S.; She, Y.; Xu, X.; Liao, Z. Modeling and Characterization of Complex Dynamical Properties of Railway Ballast. Appl. Sci. 2024, 14, 11224. [Google Scholar] [CrossRef]
- Zulkifli, M.A.; Basaruddin, K.S.; Abdul Rahim, Y.; Afendi, M.; Gurubaran, P.; Ibrahim, I. Three-dimensional finite element analysis on railway rail. IOP Conf. Ser. Mater. Sci. Eng. 2018, 429, 012010. [Google Scholar] [CrossRef]
- Kukulski, J.; Jacyna, M.; Gołębiowski, P. Finite element method in assessing strength properties of a railway surface and its elements. Symmetry 2019, 11, 1014. [Google Scholar] [CrossRef]
- Charoenwong, C.; Connolly, D.P.; Odolinski, K.; Alves Costa, P.; Galvín, P.; Smith, A. The Effect of Rolling Stock Characteristics on Differential Railway Track Settlement: An Engineering-Economic Model. Transp. Geotech. 2022, 37, 100845. [Google Scholar] [CrossRef]
- Mosleh, A.; Aires Montenegro, P.; Alves Costa, P.; Calçada, R. Railway Vehicle Wheel Flat Detection with Multiple Records Using Spectral Kurtosis Analysis. Appl. Sci. 2021, 11, 4002. [Google Scholar] [CrossRef]
- Kurhan, D.; Fischer, S.; Khmelevskyi, V. Mathematical Modeling of the Rail Track Superstructure—Subgrade System. Geotechnics 2025, 5, 20. [Google Scholar] [CrossRef]
- Moretti, L.; Loprencipe, G.; Di Mascio, P. Competition in rail transport: Methodology to evaluate economic impact of new trains on track. In Proceedings of the Sustainability, Eco-Efficiency and Conservation in Transportation Infrastructure Asset Management, Pisa, Italy, 28 April 2014; pp. 669–675. [Google Scholar]
- Sayeed, M.A.; Shahin Mohamed, A. Three-dimensional numerical modelling of ballasted railway track foundations for high-speed trains with special reference to critical speed. Transp. Geotech. 2016, 6, 55–65. [Google Scholar] [CrossRef]
- Auersch, L. Site-Specific Amplitude-Distance Laws, Wave Velocities, Damping, and Transfer Functions of the Soil from Hammer Impacts and Application to Railway-Induced Ground Vibration: Similarities and Mid-Frequency Differences. J. Vib. Eng. Technol. 2023, 11, 2671–2687. [Google Scholar] [CrossRef]

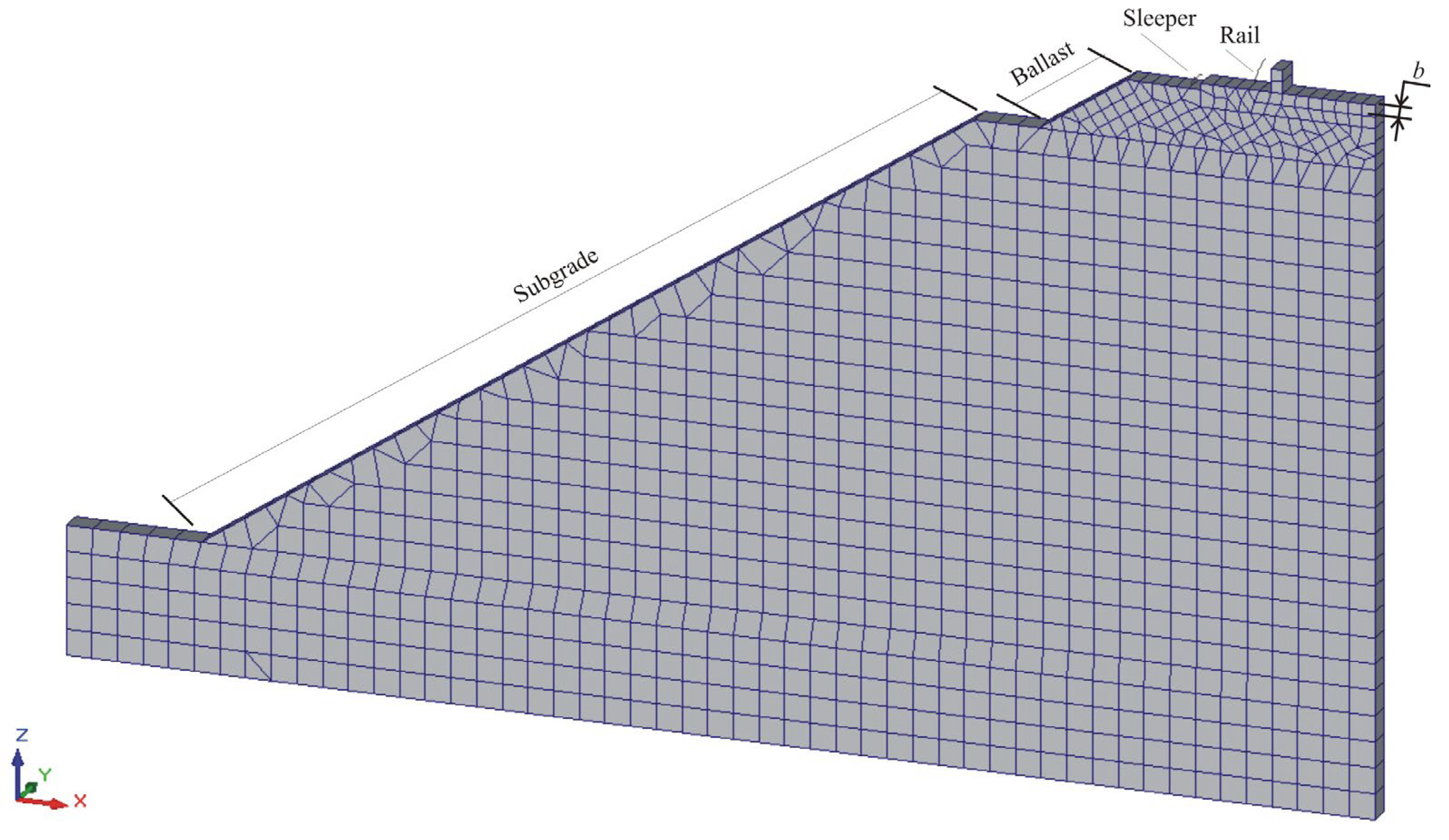

| Element (Layer) | Thickness, m | Elastic Modulus, MPa | Unit Weight, kN/m3 | Poisson’s Ratio |
|---|---|---|---|---|
| Rail | 0.172 | 2.1·105 | 77.0 | 0.3 |
| Sleeper | 0.193 under rail | 3.6·104 | 24.5 | 0.2 |
| Ballast | 0.5 | 100 | 20.0 | 0.2 |
| Subgrade | 4.0 | 35 | 18.5 | 0.3 |
| Foundation | 30 | 18.0 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, S.; Kurhan, D.; Kurhan, M.; Tiutkin, O. The Role of Domain Size and Boundary Conditions in Mathematical Modeling of Railway Tracks. Appl. Mech. 2025, 6, 72. https://doi.org/10.3390/applmech6030072
Fischer S, Kurhan D, Kurhan M, Tiutkin O. The Role of Domain Size and Boundary Conditions in Mathematical Modeling of Railway Tracks. Applied Mechanics. 2025; 6(3):72. https://doi.org/10.3390/applmech6030072
Chicago/Turabian StyleFischer, Szabolcs, Dmytro Kurhan, Mykola Kurhan, and Oleksii Tiutkin. 2025. "The Role of Domain Size and Boundary Conditions in Mathematical Modeling of Railway Tracks" Applied Mechanics 6, no. 3: 72. https://doi.org/10.3390/applmech6030072
APA StyleFischer, S., Kurhan, D., Kurhan, M., & Tiutkin, O. (2025). The Role of Domain Size and Boundary Conditions in Mathematical Modeling of Railway Tracks. Applied Mechanics, 6(3), 72. https://doi.org/10.3390/applmech6030072







