Impact of Far- and Near-Field Records on the Seismic Fragility of Steel Storage Tanks
Abstract
1. Introduction
2. Tank Numerical Models
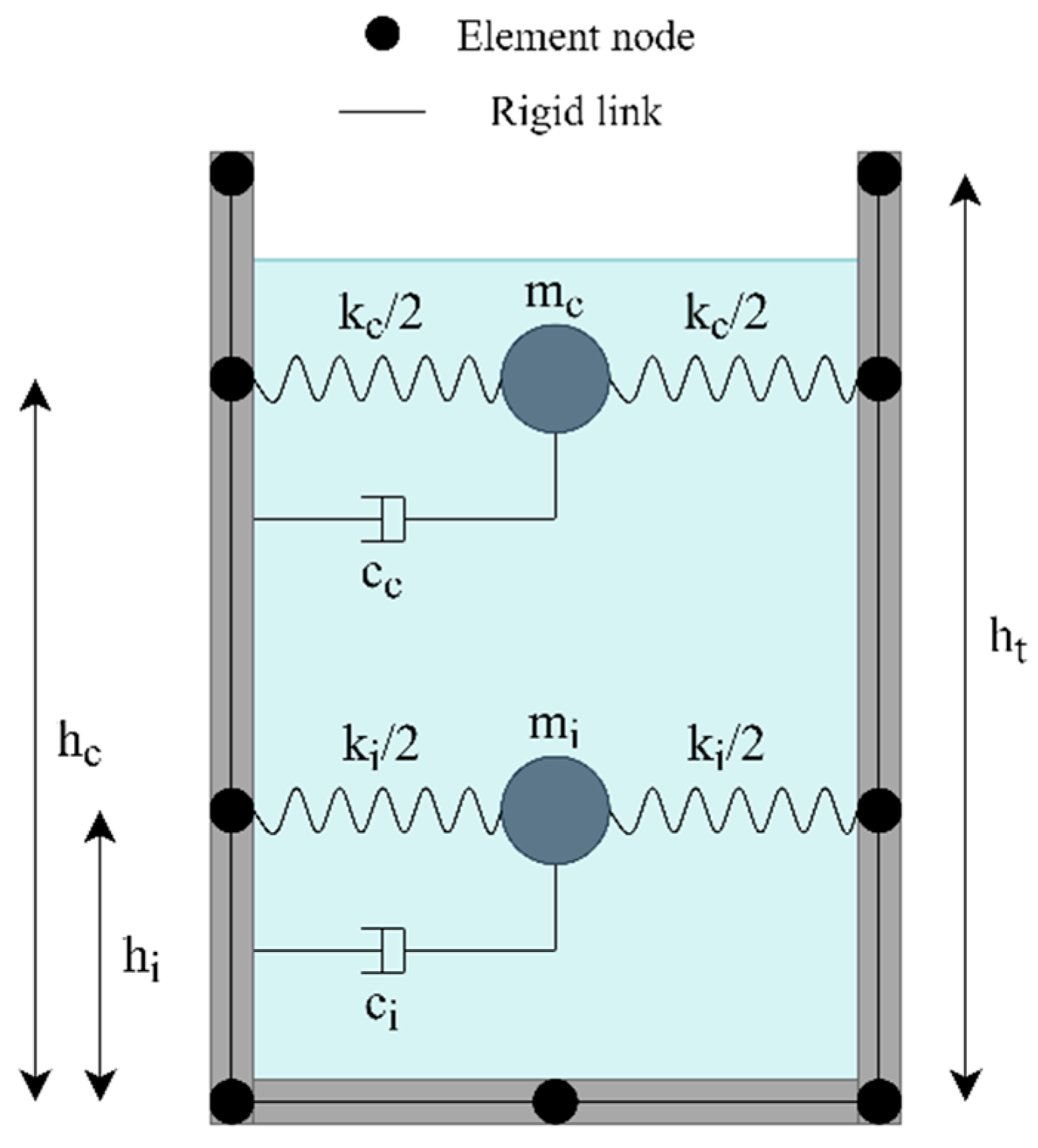
2.1. Anchored Steel Storage Tanks
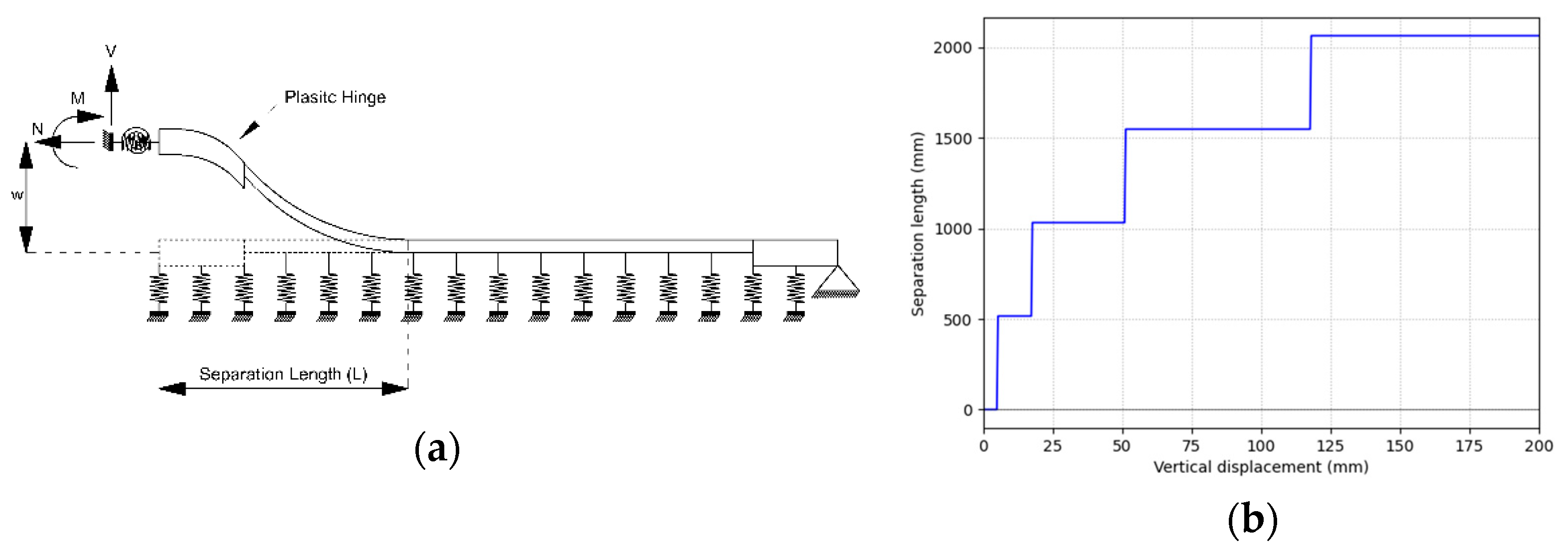
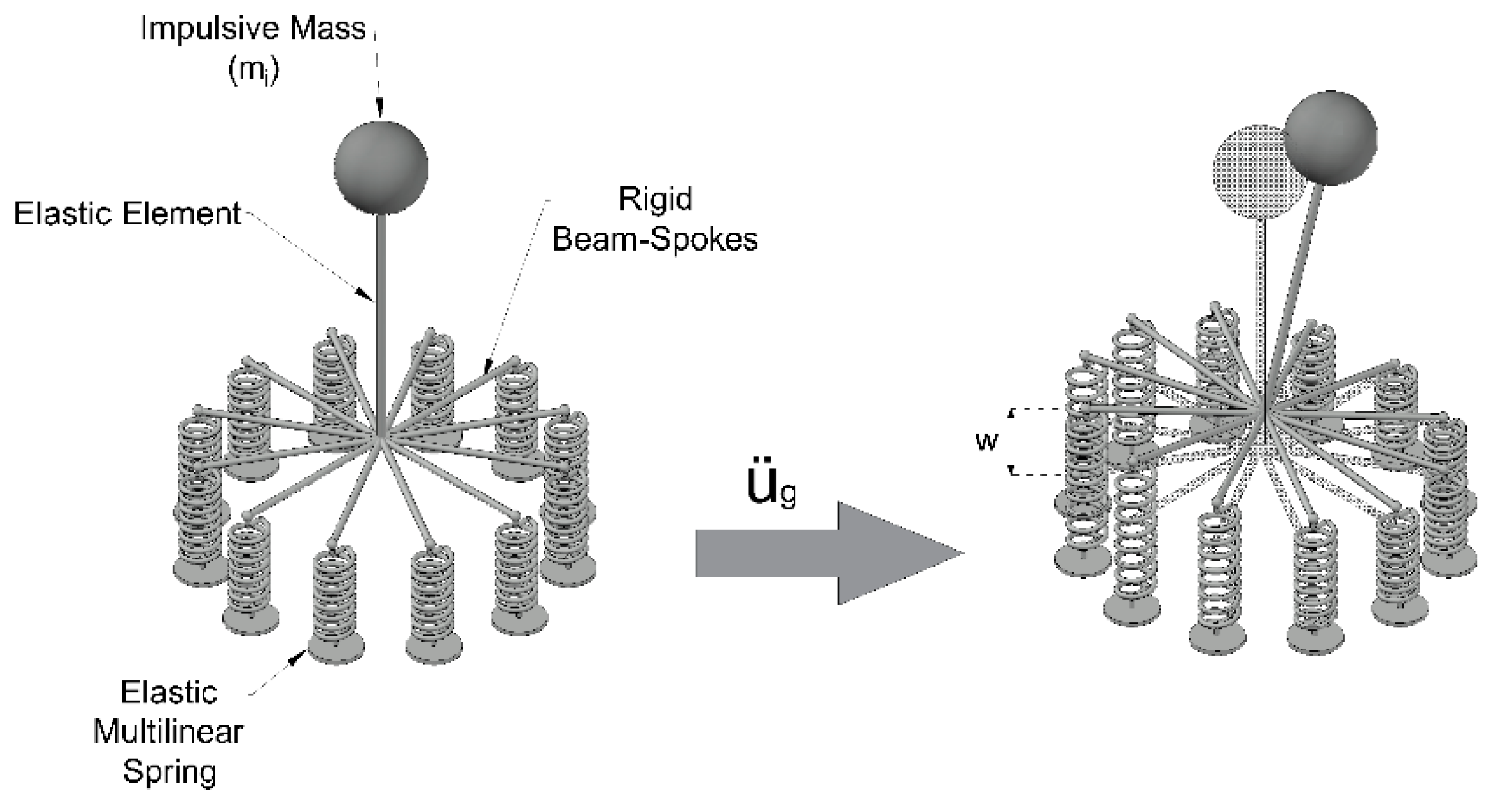
2.2. Unanchored Steel Storage Tanks
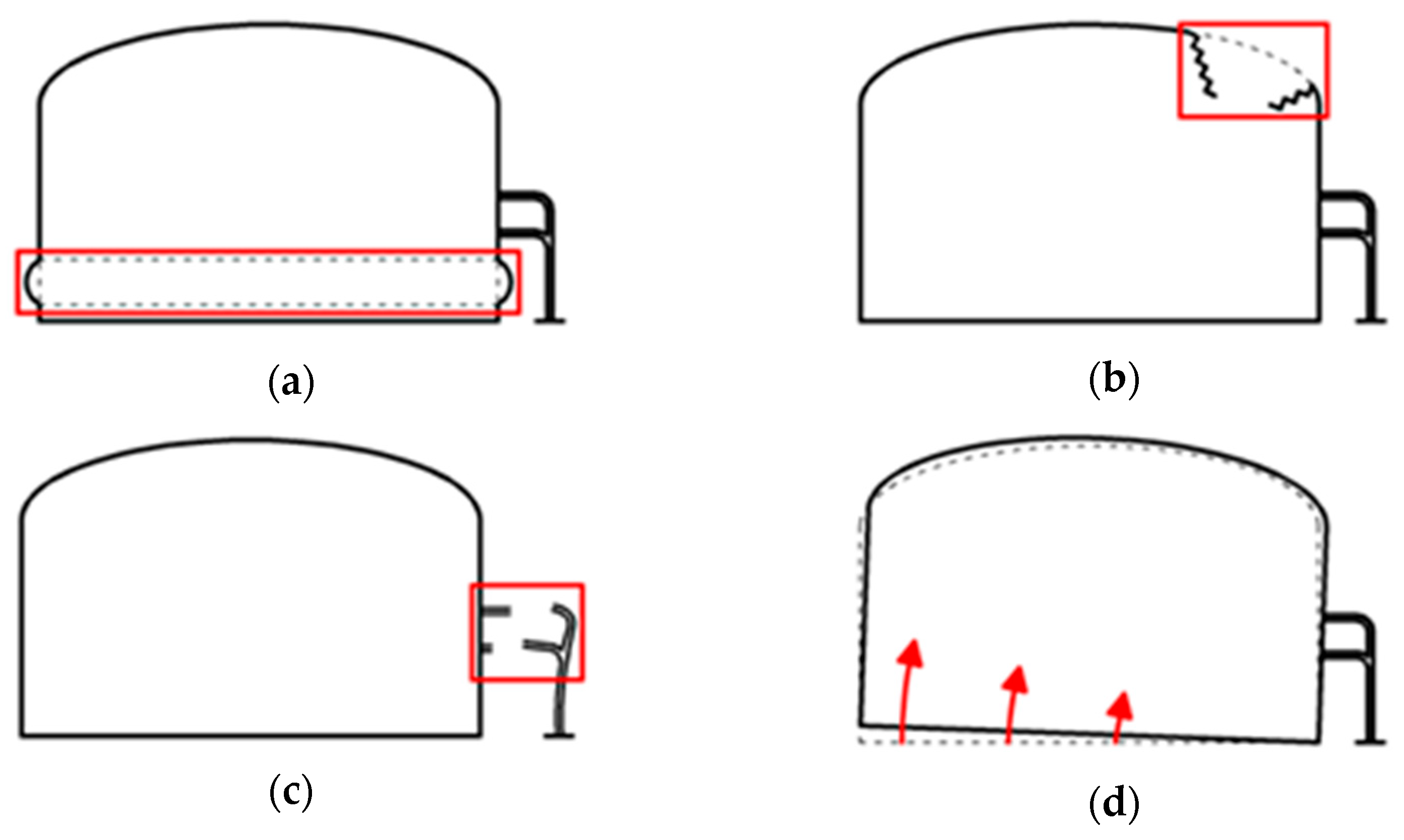
2.3. Damage States Definition
- Convective wave exceeding the freeboard;
- Exceeding 80% of the Elephant Foot Buckling threshold (EFB1);
- Exceeding 100% of the Elephant Foot Buckling threshold (EFB2);
- Exceeding 140% of the Elephant Foot Buckling threshold (EFB3);
- Tank uplift (for the unanchored configuration);
- Tank overturning (for the unanchored configuration).
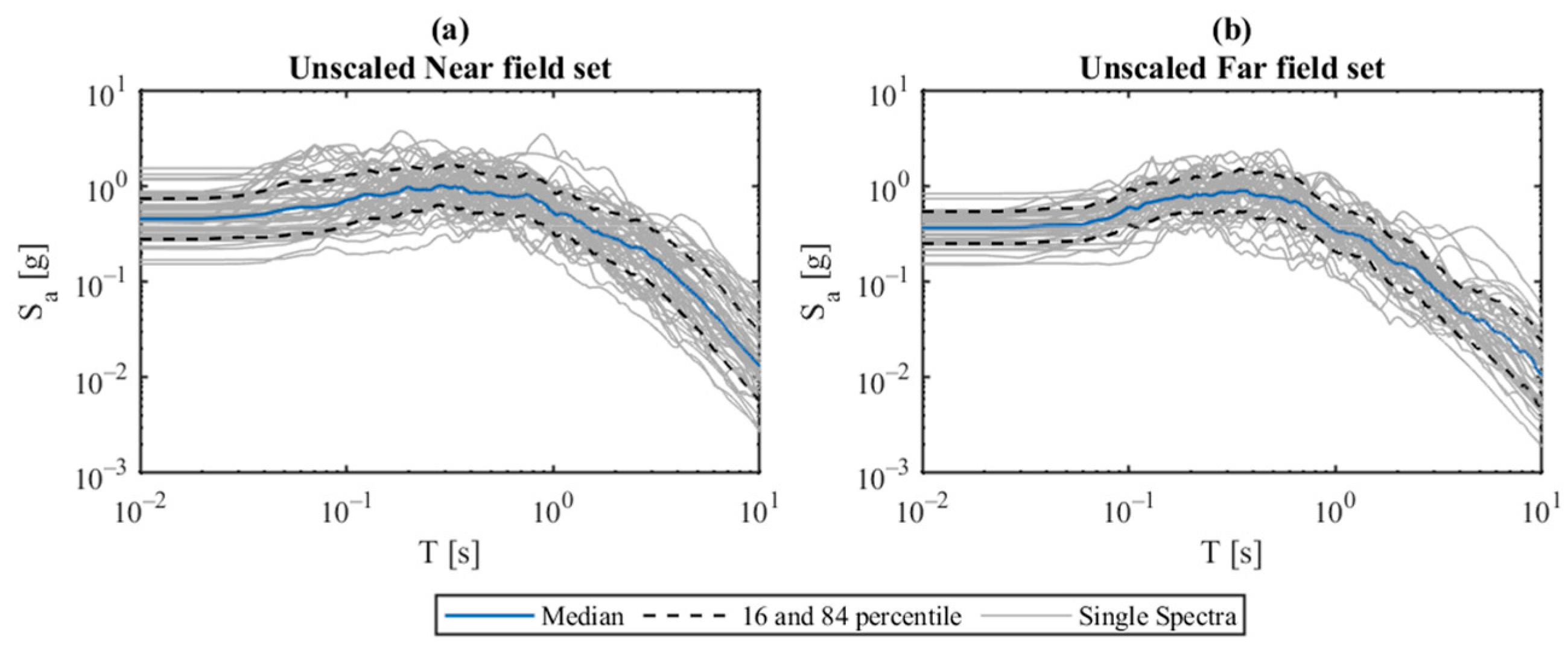
3. Seismic Hazard and Record Selection
4. Results of the Dynamic Analyses
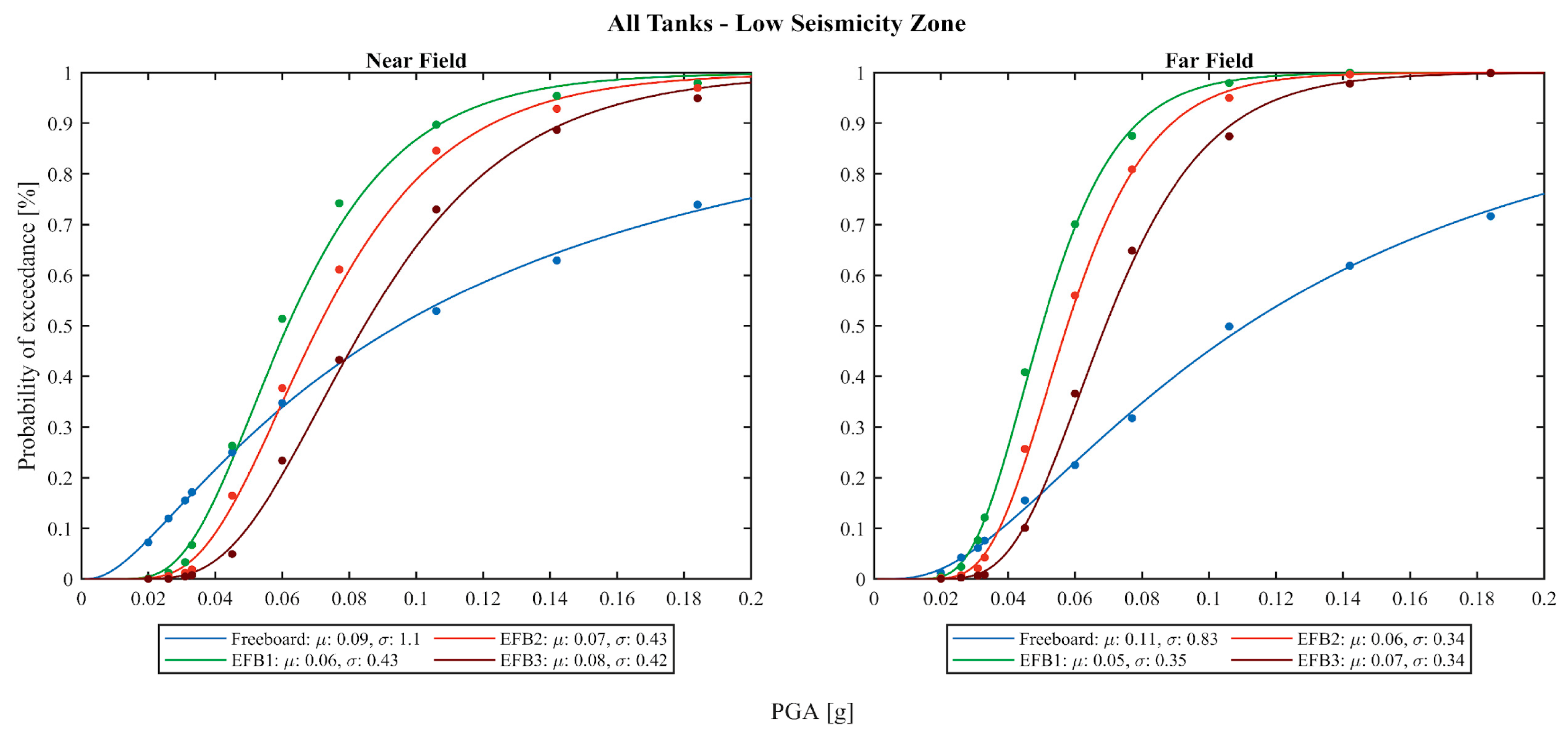
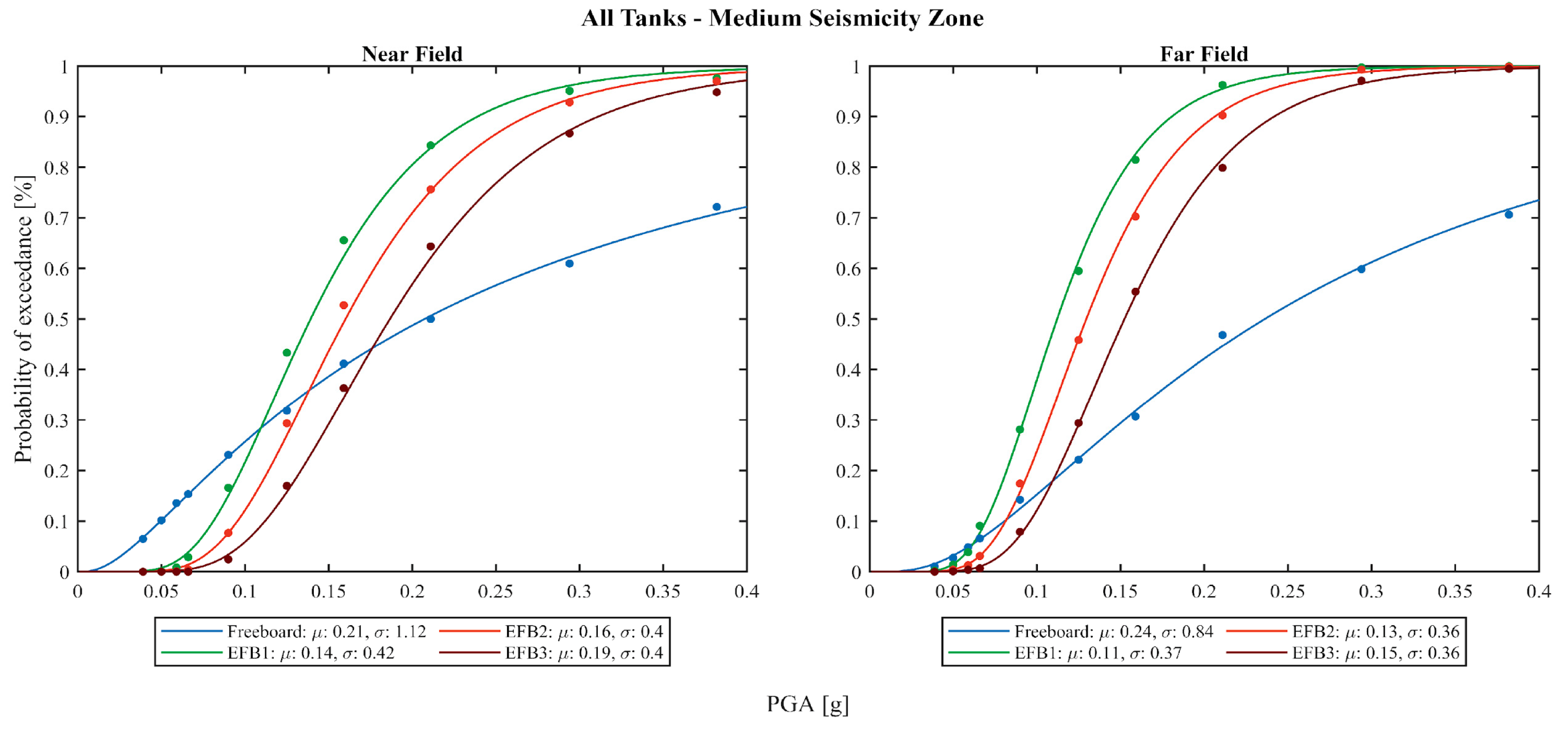
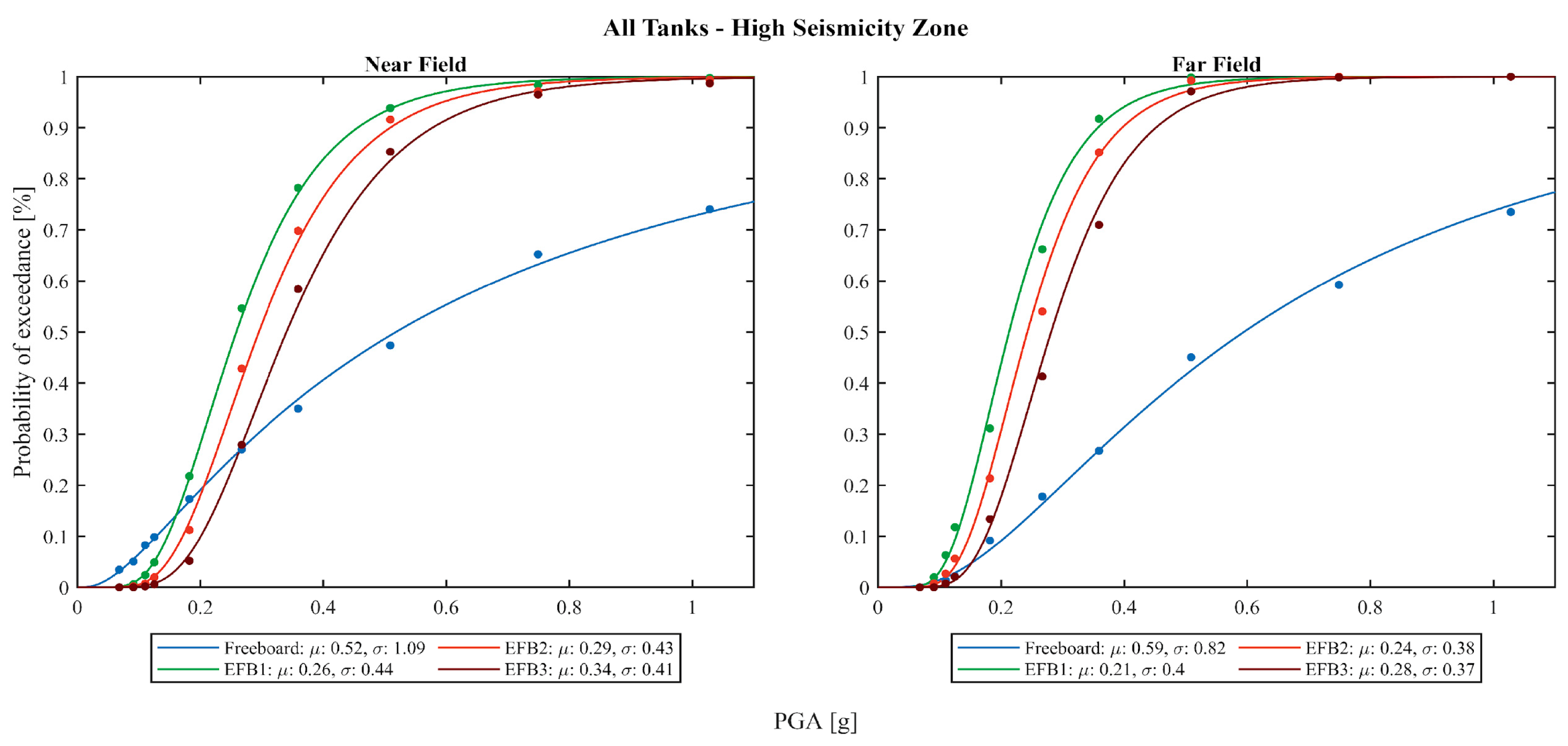
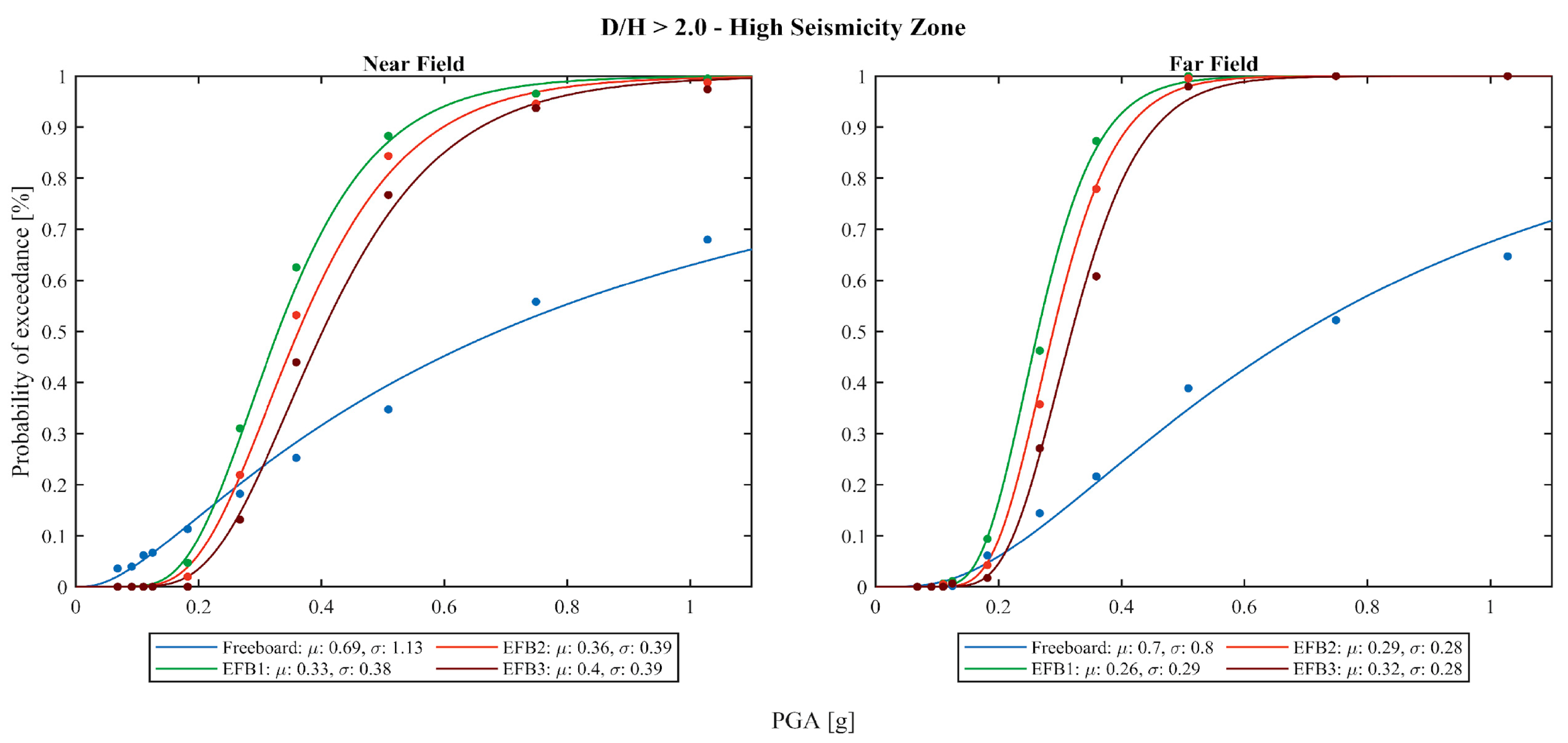
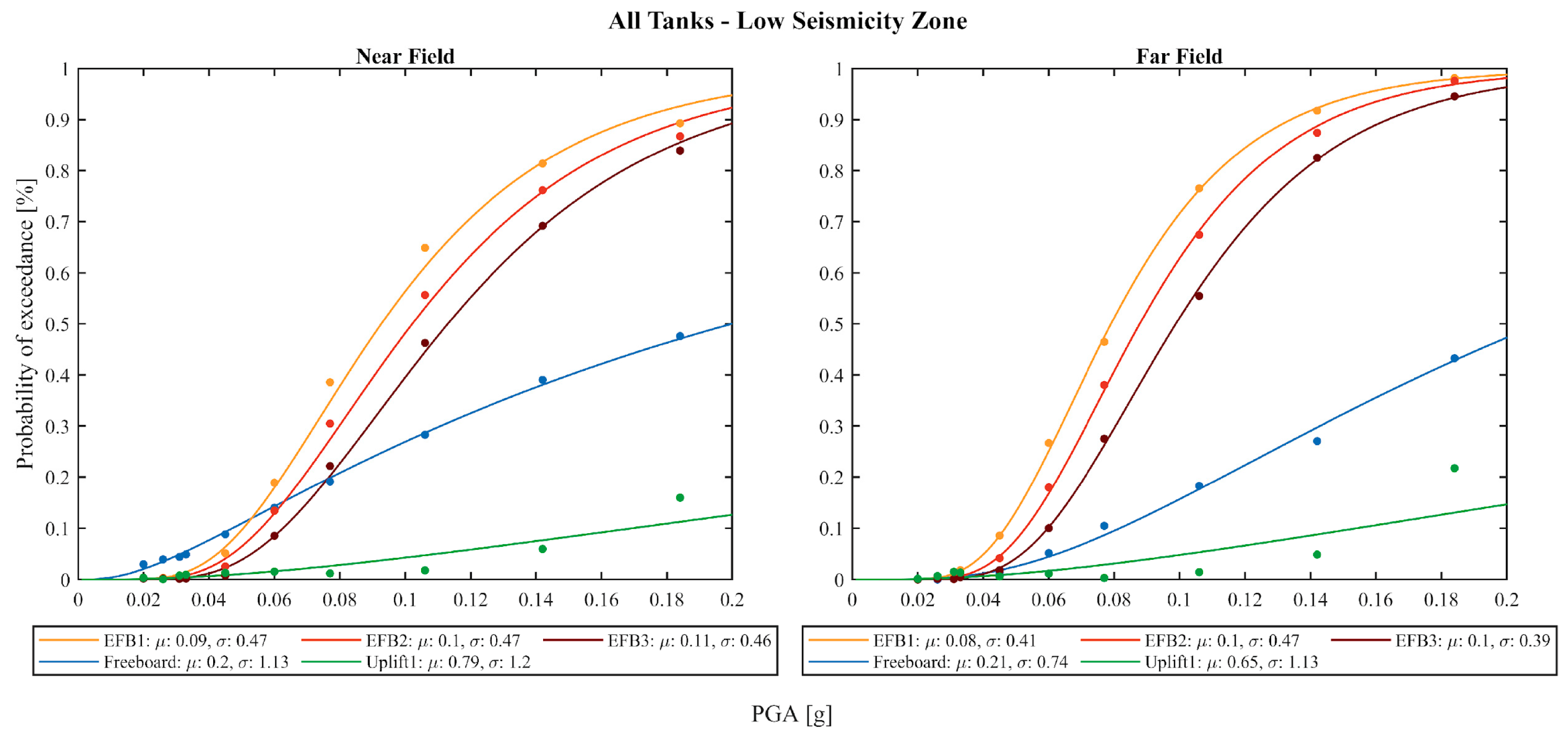
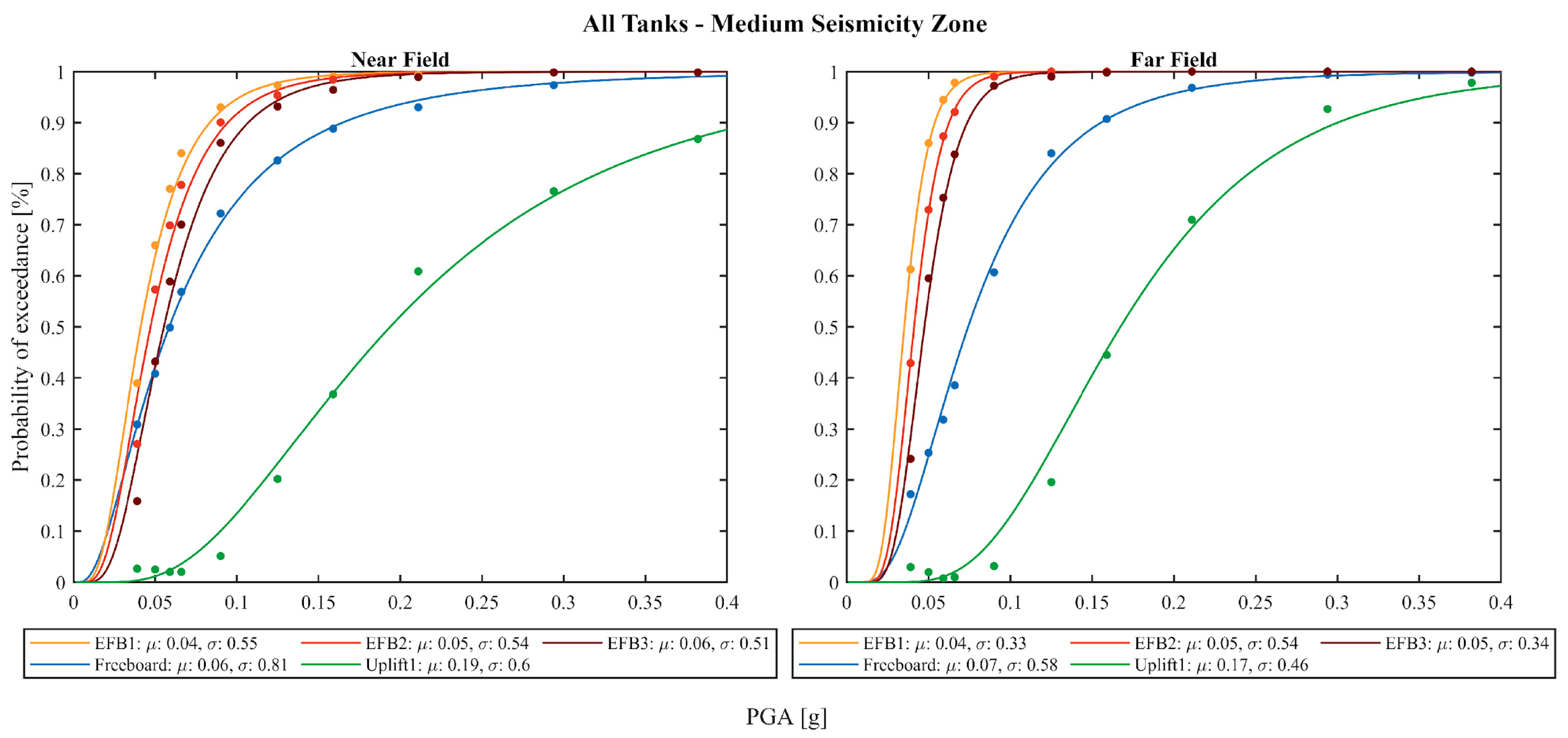
4.1. Anchored Tanks Results
4.2. Unanchored Tanks Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Anchored Tank | Low Seismic Zone | Medium Seismic Zone | High Seismic Zone | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D [m] | H [m] | t [mm] | fy [N/mm2] | D [m] | H [m] | t [mm] | fy [N/mm2] | D [m] | H [m] | t [mm] | fy [N/mm2] | |
| 1 | 5.0 | 5.0 | 2.0 | 235 | 5.0 | 4.8 | 3.0 | 235 | 5.0 | 4.4 | 3.0 | 235 |
| 2 | 6.0 | 6.0 | 3.0 | 235 | 6.0 | 5.8 | 3.0 | 235 | 6.0 | 5.3 | 4.0 | 235 |
| 3 | 7.0 | 7.0 | 3.0 | 235 | 7.0 | 6.8 | 4.0 | 235 | 7.0 | 6.3 | 5.0 | 235 |
| 4 | 8.0 | 8.0 | 4.0 | 235 | 8.0 | 7.8 | 5.0 | 235 | 8.0 | 7.2 | 6.0 | 235 |
| 5 | 9.0 | 9.0 | 5.0 | 235 | 9.0 | 8.8 | 6.0 | 235 | 9.0 | 8.2 | 7.0 | 235 |
| 6 | 10.0 | 10.0 | 5.0 | 235 | 10.0 | 9.8 | 7.0 | 235 | 10.0 | 9.2 | 8.0 | 235 |
| 7 | 11.0 | 11.0 | 6.0 | 235 | 11.0 | 10.8 | 8.0 | 235 | 11.0 | 10.2 | 10.0 | 235 |
| 8 | 12.0 | 12.0 | 7.0 | 235 | 12.0 | 11.8 | 9.0 | 235 | 12.0 | 10.7 | 10.0 | 235 |
| 9 | 13.0 | 13.0 | 8.0 | 235 | 13.0 | 12.8 | 10.0 | 235 | 13.0 | 11.2 | 10.8 | 235 |
| 10 | 14.0 | 14.0 | 9.0 | 235 | 14.0 | 13.8 | 12.0 | 235 | 14.0 | 12.1 | 12.0 | 235 |
| 11 | 15.0 | 15.0 | 10.0 | 235 | 15.0 | 14.8 | 13.0 | 235 | 15.0 | 12.4 | 12.7 | 235 |
| 12 | 16.0 | 16.0 | 11.0 | 235 | 16.0 | 15.8 | 14.0 | 235 | 16.0 | 13.2 | 13.7 | 235 |
| 13 | 17.0 | 17.0 | 12.0 | 235 | 17.0 | 16.8 | 15.0 | 235 | 17.0 | 14.1 | 15.0 | 235 |
| 14 | 18.0 | 18.0 | 13.0 | 235 | 18.0 | 16.2 | 15.0 | 235 | 18.0 | 13.4 | 14.7 | 235 |
| 15 | 19.0 | 19.0 | 14.0 | 235 | 19.0 | 17.1 | 16.0 | 235 | 19.0 | 14.2 | 16.0 | 235 |
| 16 | 20.0 | 20.0 | 15.0 | 235 | 20.0 | 17.1 | 16.7 | 235 | 20.0 | 14.0 | 16.3 | 235 |
| 17 | 21.0 | 21.0 | 16.0 | 235 | 21.0 | 18.0 | 18.0 | 235 | 21.0 | 13.8 | 16.6 | 235 |
| 18 | 22.0 | 22.0 | 17.0 | 235 | 22.0 | 18.8 | 19.0 | 235 | 22.0 | 14.5 | 18.6 | 235 |
| 19 | 23.0 | 23.0 | 18.0 | 235 | 23.0 | 18.6 | 19.6 | 235 | 23.0 | 15.1 | 20.0 | 235 |
| 20 | 24.0 | 24.0 | 19.0 | 235 | 24.0 | 18.3 | 19.6 | 235 | 24.0 | 14.7 | 19.6 | 235 |
| 21 | 25.0 | 24.9 | 21.0 | 235 | 25.0 | 19.1 | 21.0 | 235 | 25.0 | 15.3 | 21.0 | 235 |
| 22 | 26.0 | 25.9 | 22.0 | 235 | 26.0 | 19.8 | 22.0 | 235 | 26.0 | 14.8 | 20.7 | 235 |
| 23 | 27.0 | 25.7 | 22.1 | 235 | 27.0 | 19.3 | 22.1 | 235 | 27.0 | 15.3 | 21.6 | 235 |
| 24 | 28.0 | 26.6 | 23.5 | 235 | 28.0 | 20.0 | 23.5 | 235 | 28.0 | 15.9 | 23.0 | 235 |
| 25 | 29.0 | 27.6 | 25.0 | 235 | 29.0 | 20.7 | 24.5 | 235 | 29.0 | 16.4 | 24.0 | 235 |
| 26 | 30.0 | 27.1 | 25.0 | 235 | 30.0 | 20.0 | 24.0 | 235 | 30.0 | 15.6 | 23.5 | 235 |
| 27 | 31.0 | 26.6 | 25.5 | 235 | 31.0 | 20.7 | 25.5 | 235 | 31.0 | 16.1 | 24.4 | 235 |
| 28 | 32.0 | 27.4 | 26.5 | 235 | 32.0 | 21.3 | 27.0 | 235 | 32.0 | 16.6 | 25.9 | 235 |
| 29 | 33.0 | 28.3 | 28.0 | 235 | 33.0 | 21.9 | 28.0 | 235 | 33.0 | 17.1 | 26.9 | 235 |
| 30 | 34.0 | 27.5 | 27.8 | 235 | 34.0 | 21.0 | 27.3 | 235 | 34.0 | 17.5 | 28.4 | 235 |
| 31 | 35.0 | 28.3 | 29.4 | 235 | 35.0 | 21.6 | 28.8 | 235 | 35.0 | 18.0 | 29.4 | 235 |
| 32 | 36.0 | 27.4 | 28.8 | 235 | 36.0 | 22.2 | 30.0 | 235 | 36.0 | 16.9 | 28.2 | 235 |
| 33 | 37.0 | 28.2 | 30.4 | 235 | 37.0 | 21.0 | 29.1 | 235 | 37.0 | 17.3 | 29.1 | 235 |
| 34 | 38.0 | 28.9 | 32.0 | 235 | 38.0 | 21.6 | 30.1 | 235 | 38.0 | 17.7 | 30.7 | 235 |
| 35 | 39.0 | 27.8 | 31.7 | 235 | 39.0 | 22.1 | 31.7 | 235 | 39.0 | 18.2 | 33.0 | 235 |
| 36 | 40.0 | 28.5 | 32.6 | 235 | 40.0 | 22.7 | 32.6 | 235 | 40.0 | 16.8 | 30.6 | 235 |
| 37 | 41.0 | 29.2 | 34.3 | 235 | 41.0 | 23.2 | 34.3 | 235 | 41.0 | 17.2 | 32.2 | 235 |
| 38 | 42.0 | 27.9 | 33.3 | 235 | 42.0 | 21.8 | 32.2 | 235 | 42.0 | 17.5 | 33.6 | 235 |
| 39 | 43.0 | 28.5 | 34.6 | 235 | 43.0 | 22.3 | 33.8 | 235 | 43.0 | 17.9 | 34.6 | 235 |
| 40 | 44.0 | 29.2 | 36.3 | 235 | 44.0 | 22.8 | 34.8 | 235 | 44.0 | 18.3 | 36.3 | 235 |
| 41 | 45.0 | 29.8 | 38.0 | 235 | 45.0 | 23.3 | 36.5 | 235 | 45.0 | 18.7 | 38.0 | 235 |
| 42 | 46.0 | 30.5 | 39.0 | 235 | 46.0 | 23.8 | 38.2 | 235 | 46.0 | 19.1 | 39.0 | 235 |
| 43 | 47.0 | 28.9 | 37.6 | 235 | 47.0 | 24.2 | 39.2 | 235 | 47.0 | 17.3 | 36.0 | 235 |
| 44 | 48.0 | 29.5 | 39.2 | 235 | 48.0 | 22.5 | 36.8 | 235 | 48.0 | 17.6 | 36.8 | 235 |
| 45 | 49.0 | 30.1 | 41.0 | 235 | 49.0 | 22.9 | 38.5 | 235 | 49.0 | 18.0 | 38.5 | 235 |
| 46 | 50.0 | 28.3 | 39.5 | 235 | 50.0 | 23.4 | 39.5 | 235 | 50.0 | 18.3 | 39.5 | 235 |
| 47 | 51.0 | 28.8 | 40.4 | 235 | 51.0 | 23.8 | 41.3 | 235 | 51.0 | 18.7 | 41.3 | 235 |
| 48 | 52.0 | 29.4 | 42.2 | 235 | 52.0 | 24.2 | 42.2 | 235 | 52.0 | 19.0 | 43.1 | 235 |
| 49 | 53.0 | 29.9 | 44.1 | 235 | 53.0 | 24.7 | 44.1 | 235 | 53.0 | 19.3 | 44.1 | 235 |
| 50 | 54.0 | 30.5 | 45.0 | 235 | 54.0 | 22.6 | 40.5 | 235 | 54.0 | 17.2 | 39.6 | 235 |
| 51 | 55.0 | 28.4 | 43.2 | 235 | 55.0 | 23.0 | 42.3 | 235 | 55.0 | 17.4 | 40.5 | 235 |
| 52 | 56.0 | 28.9 | 44.2 | 235 | 56.0 | 23.3 | 43.2 | 235 | 56.0 | 17.7 | 42.3 | 235 |
| 53 | 57.0 | 29.4 | 46.1 | 235 | 57.0 | 23.7 | 45.1 | 235 | 57.0 | 18.0 | 43.2 | 235 |
| 54 | 58.0 | 29.9 | 47.0 | 235 | 58.0 | 24.1 | 46.1 | 235 | 58.0 | 18.3 | 45.1 | 235 |
| 55 | 59.0 | 30.4 | 49.0 | 235 | 59.0 | 24.5 | 48.0 | 235 | 59.0 | 18.6 | 47.0 | 235 |
| 56 | 60.0 | 30.9 | 50.0 | 235 | 60.0 | 24.9 | 49.0 | 235 | 60.0 | 18.9 | 48.0 | 235 |
| 57 | 61.0 | 28.4 | 46.9 | 235 | 61.0 | 22.4 | 45.0 | 235 | 61.0 | 19.2 | 50.0 | 235 |
| 58 | 62.0 | 28.9 | 48.9 | 235 | 62.0 | 22.8 | 46.8 | 235 | 62.0 | 19.5 | 51.0 | 235 |
| 59 | 63.0 | 29.3 | 49.8 | 235 | 63.0 | 23.1 | 47.7 | 235 | 63.0 | 19.8 | 53.0 | 235 |
| 60 | 64.0 | 29.8 | 51.8 | 235 | 64.0 | 23.4 | 48.6 | 235 | 64.0 | 20.1 | 54.0 | 235 |
| Unanchored Tank | Low Seismic Zone | Medium Seismic Zone | High Seismic Zone | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D [m] | H [m] | t [mm] | fy [N/mm2] | D [m] | H [m] | t [mm] | fy [N/mm2] | D [m] | H [m] | t [mm] | fy [N/mm2] | |
| 1 | 5.0 | 4.8 | 3.0 | 235 | 5.0 | 5.0 | 2.0 | 235 | 5.0 | 4.4 | 3.0 | 235 |
| 2 | 6.0 | 5.8 | 3.0 | 235 | 6.0 | 6.0 | 3.0 | 235 | 6.0 | 5.3 | 4.0 | 235 |
| 3 | 7.0 | 6.8 | 4.0 | 235 | 7.0 | 7.0 | 3.0 | 235 | 7.0 | 6.3 | 5.0 | 235 |
| 4 | 8.0 | 7.8 | 5.0 | 235 | 8.0 | 8.0 | 4.0 | 235 | 8.0 | 7.2 | 6.0 | 235 |
| 5 | 9.0 | 8.8 | 6.0 | 235 | 9.0 | 9.0 | 5.0 | 235 | 9.0 | 8.2 | 7.0 | 235 |
| 6 | 10.0 | 9.8 | 7.0 | 235 | 10.0 | 10.0 | 5.0 | 235 | 10.0 | 9.2 | 8.0 | 235 |
| 7 | 11.0 | 10.8 | 8.0 | 235 | 11.0 | 11.0 | 6.0 | 235 | 11.0 | 10.2 | 10.0 | 235 |
| 8 | 12.0 | 11.8 | 9.0 | 235 | 12.0 | 12.0 | 7.0 | 235 | 12.0 | 10.7 | 10.0 | 235 |
| 9 | 13.0 | 12.8 | 10.0 | 235 | 13.0 | 13.0 | 8.0 | 235 | 13.0 | 11.2 | 10.8 | 235 |
| 10 | 14.0 | 13.8 | 12.0 | 235 | 14.0 | 14.0 | 9.0 | 235 | 14.0 | 12.1 | 12.0 | 235 |
| 11 | 15.0 | 14.8 | 13.0 | 235 | 15.0 | 15.0 | 10.0 | 235 | 15.0 | 12.4 | 12.7 | 235 |
| 12 | 16.0 | 15.8 | 14.0 | 235 | 16.0 | 16.0 | 11.0 | 235 | 16.0 | 13.2 | 13.7 | 235 |
| 13 | 17.0 | 16.8 | 15.0 | 235 | 17.0 | 17.0 | 12.0 | 235 | 17.0 | 14.1 | 15.0 | 235 |
| 14 | 18.0 | 16.2 | 15.0 | 235 | 18.0 | 18.0 | 13.0 | 235 | 18.0 | 13.4 | 14.7 | 235 |
| 15 | 19.0 | 17.1 | 16.0 | 235 | 19.0 | 19.0 | 14.0 | 235 | 19.0 | 14.2 | 16.0 | 235 |
| 16 | 20.0 | 17.1 | 16.7 | 235 | 20.0 | 20.0 | 15.0 | 235 | 20.0 | 14.0 | 16.3 | 235 |
| 17 | 21.0 | 18.0 | 18.0 | 235 | 21.0 | 21.0 | 16.0 | 235 | 21.0 | 13.8 | 16.6 | 235 |
| 18 | 22.0 | 18.8 | 19.0 | 235 | 22.0 | 22.0 | 17.0 | 235 | 22.0 | 14.5 | 18.6 | 235 |
| 19 | 23.0 | 18.6 | 19.6 | 235 | 23.0 | 23.0 | 18.0 | 235 | 23.0 | 15.1 | 20.0 | 235 |
| 20 | 24.0 | 18.3 | 19.6 | 235 | 24.0 | 24.0 | 19.0 | 235 | 24.0 | 14.7 | 19.6 | 235 |
| 21 | 25.0 | 19.1 | 21.0 | 235 | 25.0 | 24.9 | 21.0 | 235 | 25.0 | 15.3 | 21.0 | 235 |
| 22 | 26.0 | 19.8 | 22.0 | 235 | 26.0 | 25.9 | 22.0 | 235 | 26.0 | 14.8 | 20.7 | 235 |
| 23 | 27.0 | 19.3 | 22.1 | 235 | 27.0 | 25.7 | 22.1 | 235 | 27.0 | 15.3 | 21.6 | 235 |
| 24 | 28.0 | 20.0 | 23.5 | 235 | 28.0 | 26.6 | 23.5 | 235 | 28.0 | 15.9 | 23.0 | 235 |
| 25 | 29.0 | 20.7 | 24.5 | 235 | 29.0 | 27.6 | 25.0 | 235 | 29.0 | 16.4 | 24.0 | 235 |
| 26 | 30.0 | 20.0 | 24.0 | 235 | 30.0 | 27.1 | 25.0 | 235 | 30.0 | 15.6 | 23.5 | 235 |
| 27 | 31.0 | 20.7 | 25.5 | 235 | 31.0 | 26.6 | 25.5 | 235 | 31.0 | 16.1 | 24.4 | 235 |
| 28 | 32.0 | 21.3 | 27.0 | 235 | 32.0 | 27.4 | 26.5 | 235 | 32.0 | 16.6 | 25.9 | 235 |
| 29 | 33.0 | 21.9 | 28.0 | 235 | 33.0 | 28.3 | 28.0 | 235 | 33.0 | 17.1 | 26.9 | 235 |
| 30 | 34.0 | 21.0 | 27.3 | 235 | 34.0 | 27.5 | 27.8 | 235 | 34.0 | 17.5 | 28.4 | 235 |
| 31 | 35.0 | 21.6 | 28.8 | 235 | 35.0 | 28.3 | 29.4 | 235 | 35.0 | 18.0 | 29.4 | 235 |
| 32 | 36.0 | 22.2 | 30.0 | 235 | 36.0 | 27.4 | 28.8 | 235 | 36.0 | 16.9 | 28.2 | 235 |
| 33 | 37.0 | 21.0 | 29.1 | 235 | 37.0 | 28.2 | 30.4 | 235 | 37.0 | 17.3 | 29.1 | 235 |
| 34 | 38.0 | 21.6 | 30.1 | 235 | 38.0 | 28.9 | 32.0 | 235 | 38.0 | 17.7 | 30.7 | 235 |
| 35 | 39.0 | 22.1 | 31.7 | 235 | 39.0 | 27.8 | 31.7 | 235 | 39.0 | 18.2 | 33.0 | 235 |
| 36 | 40.0 | 22.7 | 32.6 | 235 | 40.0 | 28.5 | 32.6 | 235 | 40.0 | 16.8 | 30.6 | 235 |
| 37 | 41.0 | 23.2 | 34.3 | 235 | 41.0 | 29.2 | 34.3 | 235 | 41.0 | 17.2 | 32.2 | 235 |
| 38 | 42.0 | 21.8 | 32.2 | 235 | 42.0 | 27.9 | 33.3 | 235 | 42.0 | 17.5 | 33.6 | 235 |
| 39 | 43.0 | 22.3 | 33.8 | 235 | 43.0 | 28.5 | 34.6 | 235 | 43.0 | 17.9 | 34.6 | 235 |
| 40 | 44.0 | 22.8 | 34.8 | 235 | 44.0 | 29.2 | 36.3 | 235 | 44.0 | 18.3 | 36.3 | 235 |
| 41 | 45.0 | 23.3 | 36.5 | 235 | 45.0 | 29.8 | 38.0 | 235 | 45.0 | 18.7 | 38.0 | 235 |
| 42 | 46.0 | 23.8 | 38.2 | 235 | 46.0 | 30.5 | 39.0 | 235 | 46.0 | 19.1 | 39.0 | 235 |
| 43 | 47.0 | 24.2 | 39.2 | 235 | 47.0 | 28.9 | 37.6 | 235 | 47.0 | 17.3 | 36.0 | 235 |
| 44 | 48.0 | 22.5 | 36.8 | 235 | 48.0 | 29.5 | 39.2 | 235 | 48.0 | 17.6 | 36.8 | 235 |
| 45 | 49.0 | 22.9 | 38.5 | 235 | 49.0 | 30.1 | 41.0 | 235 | 49.0 | 18.0 | 38.5 | 235 |
| 46 | 50.0 | 23.4 | 39.5 | 235 | 50.0 | 28.3 | 39.5 | 235 | 50.0 | 18.3 | 39.5 | 235 |
| 47 | 51.0 | 23.8 | 41.3 | 235 | 51.0 | 28.8 | 40.4 | 235 | 51.0 | 18.7 | 41.3 | 235 |
| 48 | 52.0 | 24.2 | 42.2 | 235 | 52.0 | 29.4 | 42.2 | 235 | 52.0 | 19.0 | 43.1 | 235 |
| 49 | 53.0 | 24.7 | 44.1 | 235 | 53.0 | 29.9 | 44.1 | 235 | 53.0 | 19.3 | 44.1 | 235 |
| 50 | 54.0 | 22.6 | 40.5 | 235 | 54.0 | 30.5 | 45.0 | 235 | 54.0 | 17.2 | 39.6 | 235 |
| 51 | 55.0 | 23.0 | 42.3 | 235 | 55.0 | 28.4 | 43.2 | 235 | 55.0 | 17.4 | 40.5 | 235 |
| 52 | 56.0 | 23.3 | 43.2 | 235 | 56.0 | 28.9 | 44.2 | 235 | 56.0 | 17.7 | 42.3 | 235 |
| 53 | 57.0 | 23.7 | 45.1 | 235 | 57.0 | 29.4 | 46.1 | 235 | 57.0 | 18.0 | 43.2 | 235 |
| 54 | 58.0 | 24.1 | 46.1 | 235 | 58.0 | 29.9 | 47.0 | 235 | 58.0 | 18.3 | 45.1 | 235 |
| 55 | 59.0 | 24.5 | 48.0 | 235 | 59.0 | 30.4 | 49.0 | 235 | 59.0 | 18.6 | 47.0 | 235 |
| 56 | 60.0 | 24.9 | 49.0 | 235 | 60.0 | 30.9 | 50.0 | 235 | 60.0 | 18.9 | 48.0 | 235 |
| 57 | 61.0 | 22.4 | 45.0 | 235 | 61.0 | 28.4 | 46.9 | 235 | 61.0 | 19.2 | 50.0 | 235 |
| 58 | 62.0 | 22.8 | 46.8 | 235 | 62.0 | 28.9 | 48.9 | 235 | 62.0 | 19.5 | 51.0 | 235 |
| 59 | 63.0 | 23.1 | 47.7 | 235 | 63.0 | 29.3 | 49.8 | 235 | 63.0 | 19.8 | 53.0 | 235 |
| 60 | 64.0 | 23.4 | 48.6 | 235 | 64.0 | 29.8 | 51.8 | 235 | 64.0 | 20.1 | 54.0 | 235 |
References
- Van Loenhout, J.; Below, R. Human Cost of Disasters: An Overview of the Last 20 Years 2000–2019; Centre of Research on the Epidemiology of Disasters—United Nations Office for Disaster Risk Reduction: Brussels, Belgium, 2021. [Google Scholar]
- Yazdanian, M.; Ingham, J.M.; Lomax, W.; Wood, R.; Dizhur, D. Damage observations and remedial options for approximately 1500 legged and flat-based liquid storage tanks following the 2016 Kaikōura earthquake. Structures 2020, 24, 357–376. [Google Scholar] [CrossRef]
- Grajales-Ortiz, C.; Melissianos, V.E.; Bakalis, K.; Kohrangi, M.; Vamvatsikos, D.; Bazzurro, P. Relationships between earthquake-induced damage and material release for liquid storage tanks. In Proceedings of the 18th World Conference on Earthquake Engineering, Milan, Italy, 30 June–5 July 2024. [Google Scholar]
- Bevere, L.; Ewald, M.; Wunderlich, S. A Decade of Major Earthquakes: Lessons for Business; Swiss Re Institute: Zurich, Switzerland, 2019. [Google Scholar]
- Campedel, M. Analysis of Major Industrial Accidents Triggered by Natural Events Reported in the Principal Available Chemical Accident Databases. JRC Scientific and Technical Reports JRC42281. 2008. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC42281 (accessed on 13 January 2025).
- Gabbianelli, G.; Perrone, D.; Brunesi, E.; Monteiro, R. Seismic acceleration demand and fragility assessment of storage tanks installed in industrial steel moment-resisting frame structures. Soil Dyn. Earthq. Eng. 2022, 152, 107016. [Google Scholar]
- Gabbianelli, G.; Milanesi, R.R.; Gandelli, E.; Dubini, P.; Nascimbene, R. Seismic vulnerability assessment of steel storage tanks protected through sliding isolators. Earthq. Eng. Struct. Dyn. 2023, 52, 2597–2618. [Google Scholar] [CrossRef]
- Malhotra, P.K. Seismic Response of Soil-Supported Unanchored Liquid-Storage Tanks. J. Struct. Eng. 1997, 123, 440–450. [Google Scholar]
- Malhotra, P.K. Practical Nonlinear Seismic Analysis. Earthq. Spectra 2000, 16, 473–492. [Google Scholar]
- Vasquez Munoz, L.; Dolšek, M. A risk-targeted seismic performance assessment of elephant-foot buckling in walls of unanchored steel storage tanks. Earthq. Eng. Struct. Dyn. 2024, 52, 3915–4299. [Google Scholar] [CrossRef]
- Vasquez Munoz, L.; Dolšek, M. Parametric seismic fragility model for elephant-foot buckling in unanchored steel storage tanks. Bull. Earthq. Eng. 2024, 22, 5775–5804. [Google Scholar] [CrossRef]
- Moreno, M.; Colombo, J.; Wilches, J.; Reyes, S.; Almazán, J. Buckling of steel tanks under earthquake loading: Code provisions vs FEM comparison. J. Constr. Steel Res. 2023, 209, 108042. [Google Scholar] [CrossRef]
- Bakalis, K.; Karamanos, S.A. Uplift mechanics of unanchored liquid storage tanks subjected to lateral earthquake loading. Thin-Walled Struct. 2021, 158, 107145. [Google Scholar]
- Kilic, S.; Akbas, B.; Shen, J.; Paolacci, F. Seismic behavior of liquid storage tanks with 2D and 3D base isolation systems. Struct. Eng. Mech. 2022, 83, 627–644. [Google Scholar]
- Tsipianitis, A.; Tsompanakis, Y.; Psarropoulos, P.N. Impact of Dynamic Soil–Structure Interaction on the Response of Liquid-Storage Tanks. Front. Built Environ. 2020, 6, 140. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, B.; Wang, L.; Wei, J.; Wang, W. Dynamic response of polyurea coated thin steel storage tank to long duration blast loadings. Thin-Walled Struct. 2021, 163, 107747. [Google Scholar] [CrossRef]
- Kalemi, B.; Caputo, A.C.; Corritore, D.; Paolacci, F. A probabilistic framework for the estimation of resilience of process plants under Na-Tech seismic events. Bull. Earthq. Eng. 2024, 22, 75–106. [Google Scholar] [CrossRef]
- EN 1998-4; Eurocode 8: Design of Structures for Earthquake Resistance—Part 4: Silos, Tanks and Pipelines. European Committee for Standardisation: Brussels, Belgium, 2006.
- EN 1993-1-6; Eurocode 3: Design of Steel Structures—Part 1–6: Strength and Stability of Shell Structures. European Committee for Standardisation: Brussels, Belgium, 2007.
- Zhu, M.; McKenna, F.; Scott, M.H. OpenSeesPy: Python library for the OpenSees finite element framework. SoftwareX 2018, 7, 6–11. [Google Scholar] [CrossRef]
- Housner, G.W. Dynamic Analysis of Fluids in Containers Subject to Acceleration. In Nuclear Reactors and Earthquakes; Report No. TID 7024; United States Atomic Energy Commission, Division of Reactor Development: Washington, DC, USA, 1963. [Google Scholar]
- Caprinozzi, S.; Paolacci, F.; Dolšek, M. Seismic risk assessment of liquid overtopping in a steel storage tank equipped with a single deck floating roof. J. Loss Prev. Proc. Ind. 2020, 67, 104269. [Google Scholar] [CrossRef]
- Bakalis, K.; Vamvatsikos, D.; Fragiadakis, M. Seismic risk assessment of liquid storage tanks via a nonlinear surrogate model. Earthq. Eng. Struct. Dyn. 2017, 46, 2851–2868. [Google Scholar] [CrossRef]
- Bakalis, K.; Fragiadakis, M.; Vamvatsikos, D. Surrogate modelling of liquid storage tanks for seismic performance design and assessment. In Proceedings of the 5th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015), Athens, Greece, 25–27 May 2015. [Google Scholar]
- Brunesi, E.; Nascimbene, R.; Pagani, M.; Beilic, D. Seismic Performance of Storage Steel Tanks during the May 2012 Emilia, Italy, Earthquakes. J. Perform. Constr. Facil. 2015, 29, 04014137. [Google Scholar] [CrossRef]
- Merino Vela, R.J.; Brunesi, E.; Nascimbene, R. Seismic assessment of an industrial frame-tank system: Development of fragility functions. Bull. Earthq. Eng. 2019, 17, 2569–2602. [Google Scholar] [CrossRef]
- Phan, H.N.; Paolacci, F.; Di Filippo, R.; Bursi, O.S. Seismic vulnerability of above-ground storage tanks with unanchored support conditions for Na-tech risks based on Gaussian process regression. Bull. Earthq. Eng. 2020, 18, 6883–6906. [Google Scholar] [CrossRef]
- Phan, H.N.; Paolacci, F.; Alessandri, S. Enhanced Seismic Fragility Analysis of Unanchored Steel Storage Tanks Accounting for Uncertain Modeling Parameters. J. Press. Vessel Technol. Trans. ASME 2019, 141, 010903. [Google Scholar] [CrossRef]
- Wu, J.Y.; Yu, Q.Q.; Peng, Q.; Gu, X.L. Seismic responses of liquid storage tanks subjected to vertical excitation of near-fault earthquakes. Eng. Struct. 2023, 289, 116284. [Google Scholar]
- Luo, D.; Liu, C.; Sun, J.; Cui, L.; Wang, Z. Sloshing effect analysis of liquid storage tank under seismic excitation. Structures 2022, 43, 40–58. [Google Scholar]
- Merino Vela, R.J.; Brunesi, E.; Nascimbene, R. Derivation of floor acceleration spectra for an industrial liquid tank supporting structure with braced frame systems. Eng. Struct. 2018, 171, 105–122. [Google Scholar]
- Quinci, G.; Nardin, C.; Paolacci, F.; Bursi, O.S. Modelling of non-structural components of an industrial multi-storey frame for seismic risk assessment. Bull. Earthq. Eng. 2023, 21, 6065–6089. [Google Scholar]
- Rotter, J.M. Local Collapse of Axially Compressed Pressurized Thin Steel Cylinders. J. Struct. Eng. 1990, 116, 1955–1970. [Google Scholar]
- Chen, J.F.; Rotter, J.M.; Teng, J.G. A simple remedy for elephant’s foot buckling in cylindrical silos and tanks. Adv. Struct. Eng. 2006, 9, 409–420. [Google Scholar]
- API650; API Standard 650, Welded Tanks for Oil Storage, American Petroleum Institute, 13th ed. American Petroleum Institute: Washington, DC, USA, 2021.
- EN 1998-1; Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardisation: Brussels, Belgium, 2011.
- Italian Ministry of Infrastructure and Transport. Norme Tecniche per Le Costruzioni (NTC18), Ministerial Decree on 17/1/2018; Gazzetta Ufficiale della Repubblica Italiana: Rome, Italy, 2018. [Google Scholar]
- Federal Emergency Management Agency (FEMA). Quantification of Building Seismic Performance Factors (FEMA P695); Federal Emergency Management Agency: Washington, DC, USA, 2009.

| Anchorage Ratio J | Criteria |
|---|---|
| No calculated uplift was detected during the analysis; the tank is self-anchored tanks to its own weight. | |
| Partial uplift of the bottom base, but the tank is still considered stable. | |
| Tank is not stable and overturns; it is necessary to mitigate this risk by introducing anchoring systems or increasing the dimension of the annular ring. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabbianelli, G.; Rapone, A.; Milanesi, R.R.; Nascimbene, R. Impact of Far- and Near-Field Records on the Seismic Fragility of Steel Storage Tanks. Appl. Mech. 2025, 6, 24. https://doi.org/10.3390/applmech6020024
Gabbianelli G, Rapone A, Milanesi RR, Nascimbene R. Impact of Far- and Near-Field Records on the Seismic Fragility of Steel Storage Tanks. Applied Mechanics. 2025; 6(2):24. https://doi.org/10.3390/applmech6020024
Chicago/Turabian StyleGabbianelli, Giammaria, Aldo Rapone, Riccardo R. Milanesi, and Roberto Nascimbene. 2025. "Impact of Far- and Near-Field Records on the Seismic Fragility of Steel Storage Tanks" Applied Mechanics 6, no. 2: 24. https://doi.org/10.3390/applmech6020024
APA StyleGabbianelli, G., Rapone, A., Milanesi, R. R., & Nascimbene, R. (2025). Impact of Far- and Near-Field Records on the Seismic Fragility of Steel Storage Tanks. Applied Mechanics, 6(2), 24. https://doi.org/10.3390/applmech6020024







