The Influence of Reverse Yielding on the Plastic Conditioning of Interference Fits in Power Transmission Engineering
Abstract
1. Introduction
2. Interference Fits under Plastic Stress Conditions
2.1. Consideration of Stresses in Interference Fits
- d (mm): Diameter coordinate (control variable);
- DaA (mm): Outer diameter of the outer part;
- DiA (mm): Inner diameter of the outer part;
- pi (MPa): Internal pressure of the hub;
- QA: Diameter ratio of the outer part;
- σrA(d) (MPa): Radial stress at d of outer part;
- σtA(d) (MPa): Tangential stress at d of outer part.
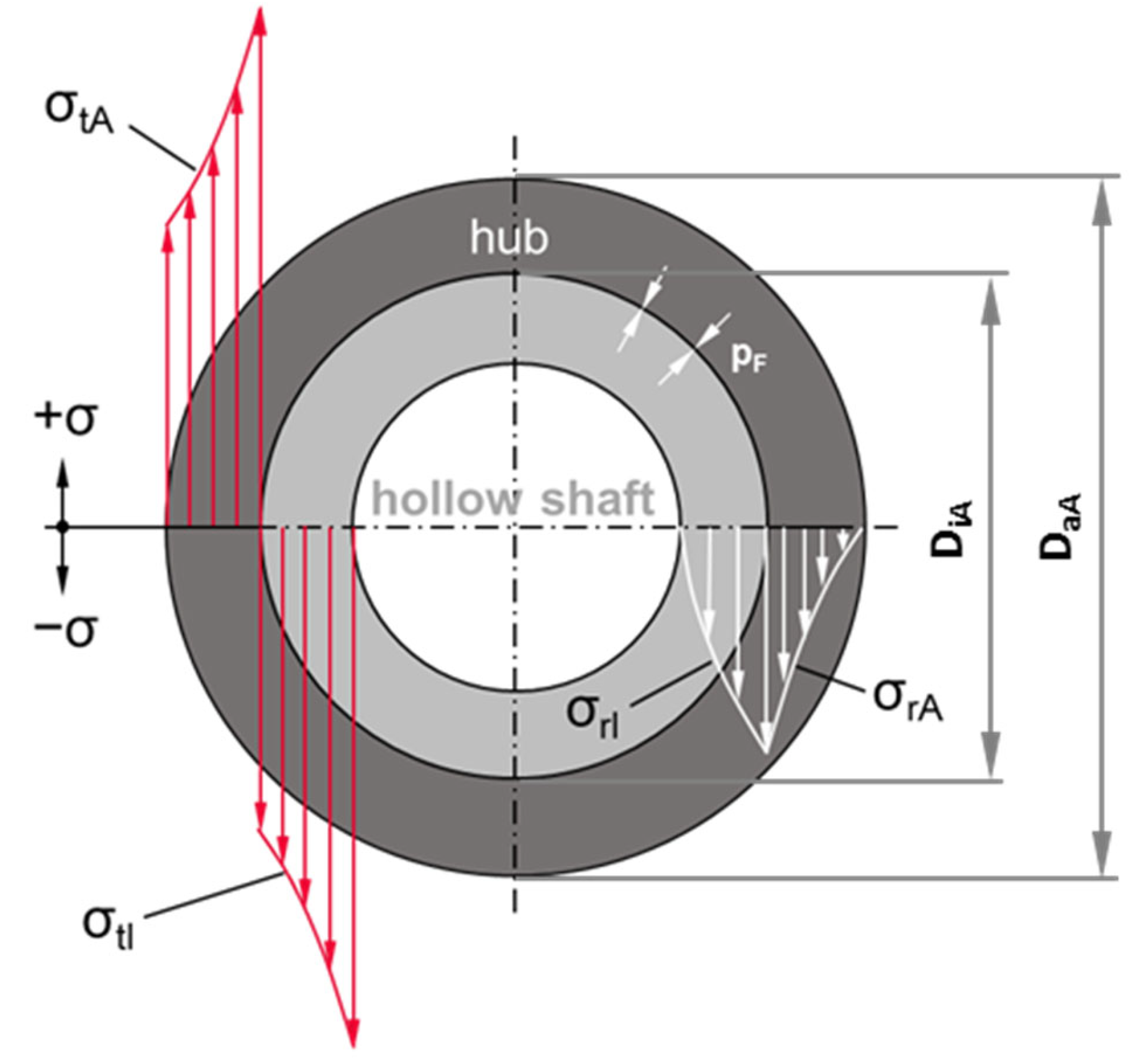
- DaA (mm): Outer diameter of the outer part;
- DiA (mm): Inner diameter of the outer part;
- m: Factor for determining the angle of inclination;
- QA: Diameter ratio of the outer part;
- a (°): Inclination angle for load line and relief straight line;
- σr (MPa): Radial stress;
- σt (MPa): Tangential stress.
2.2. Plastic Conditioning of Interference Fits, Stress–Mechanical Principles
- σr (MPa): Radial stress;
- σt (MPa): Tangential stress;
- σv (MPa): Equivalent stress.
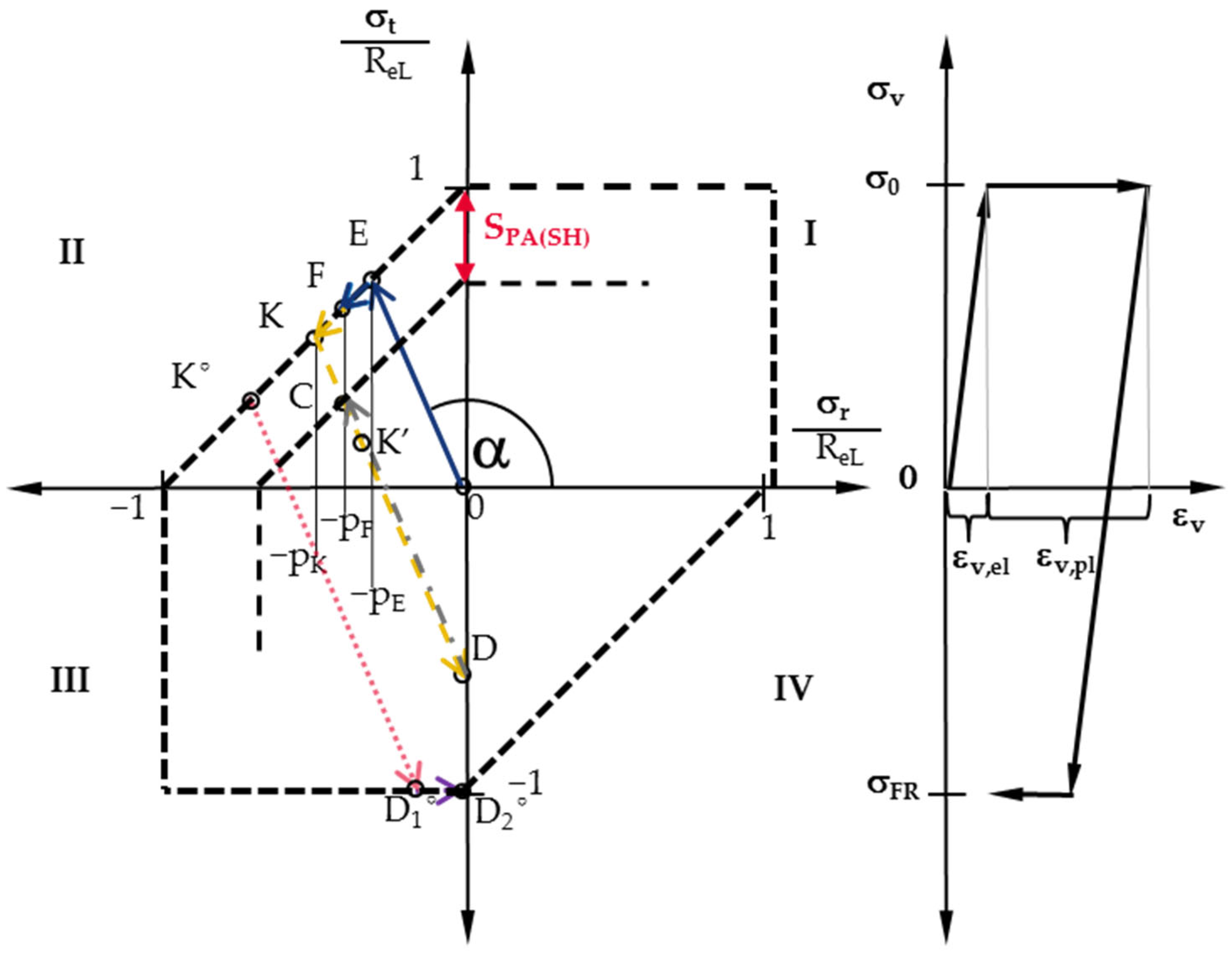
- Dσr(SH) (MPa): Radial Stress Value at Point D (SH);
- Dσt(SH) (MPa): Tangential Stress Value at Point D (SH);
- pE (MPa): Elastic joint pressure at yield strength;
- pK (MPa): Conditioning pressure.
- ReL,A (MPa): Lower yield strength of the outer part;
- SPA(SH): Safety against plastic deformation of the outer part achieved by conditioning;
- pF (MPa): Joint pressure;
- ΔpK (MPa): pressure difference between pK and pF.
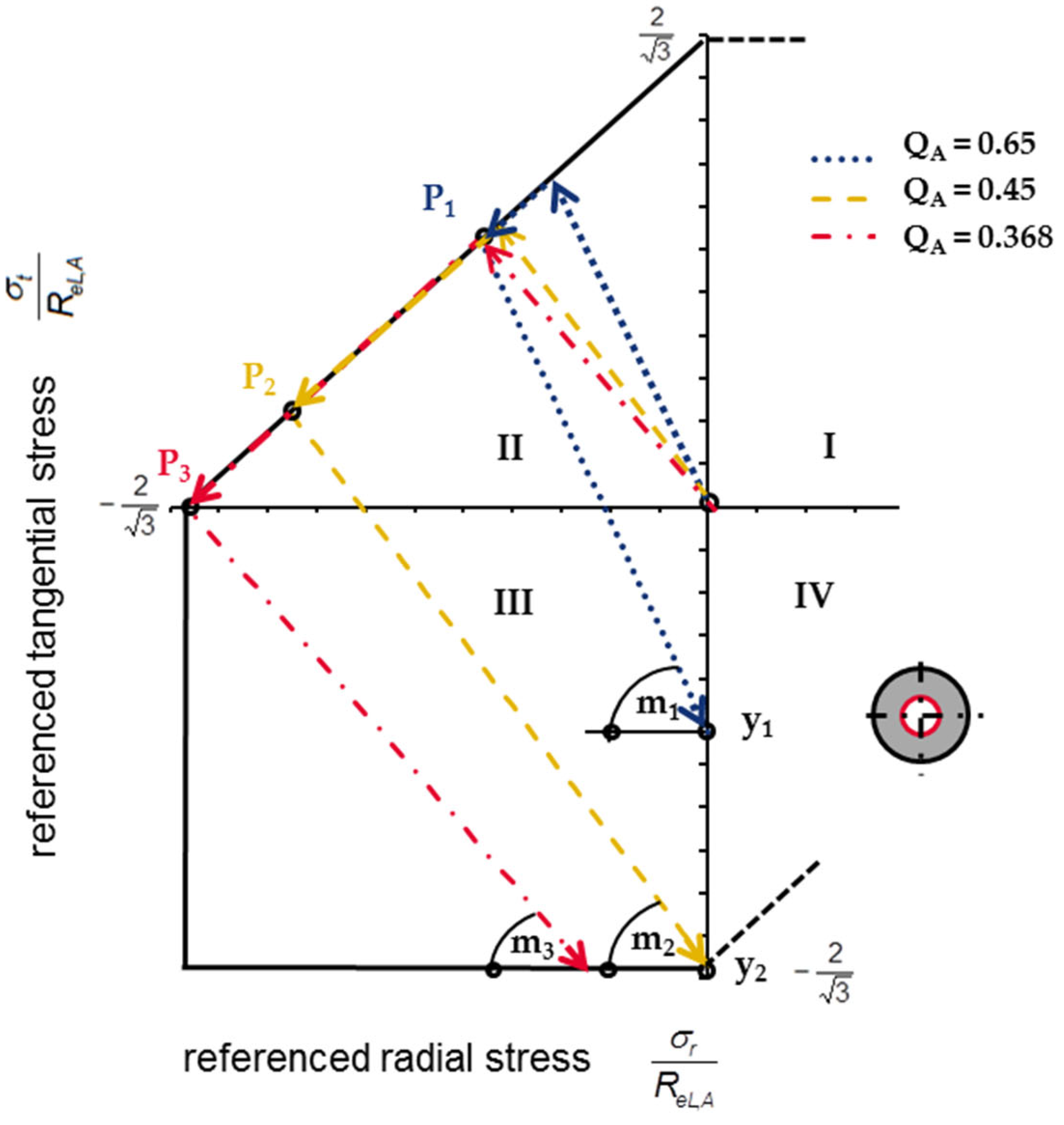
3. Reverse Yielding
3.1. Occurrence of Reverse Yielding in Plastic Conditioning
3.2. Influencing Parameters for Reverse Yielding
- pkrit,SH (MPa): Critical pressure for Reverse Yielding (SH).
- pmax,SH (MPa): Maximum possible pressure before the fully plastic state of the hub for ideal plastic material (SH).
- pmax,MSH (MPa): Maximum possible pressure before the fully plastic state of the hub for ideal plastic material (MSH).
- pkrit,MSH (MPa): Critical pressure for Reverse Yielding (MSH).
- y (MPa): Intersection of the relief straight line with the ordinate (tangential residual stress after complete relief).
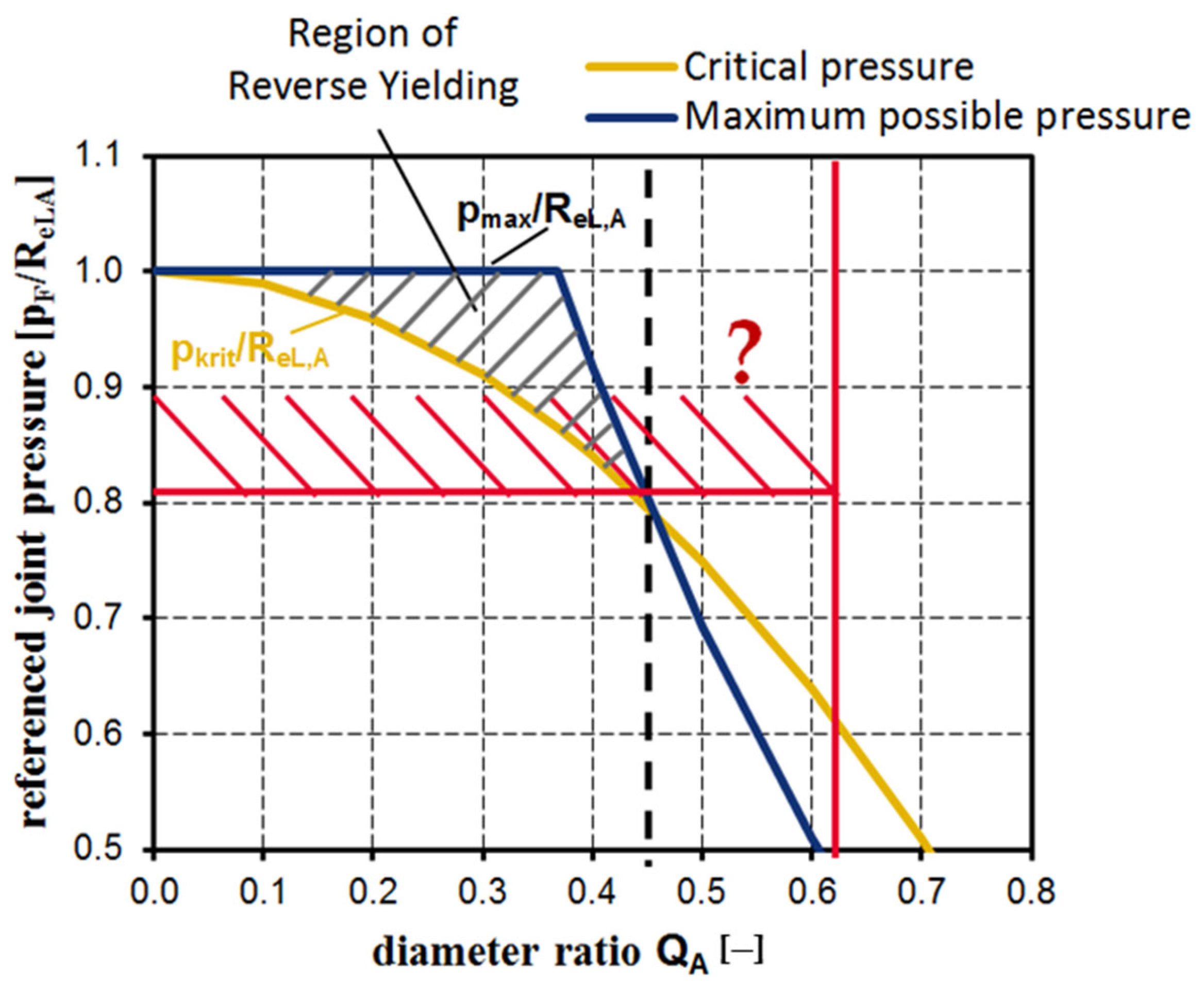
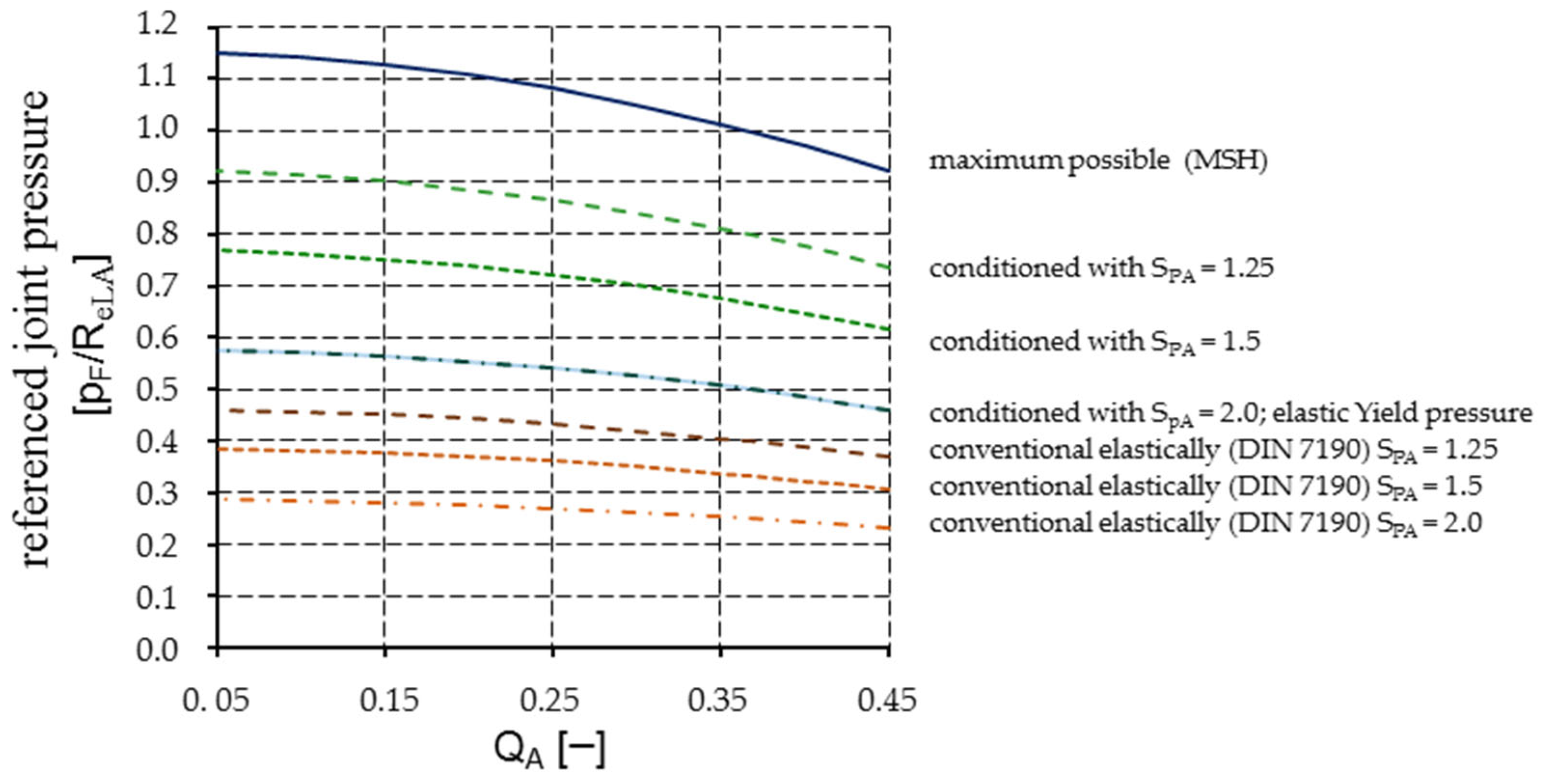
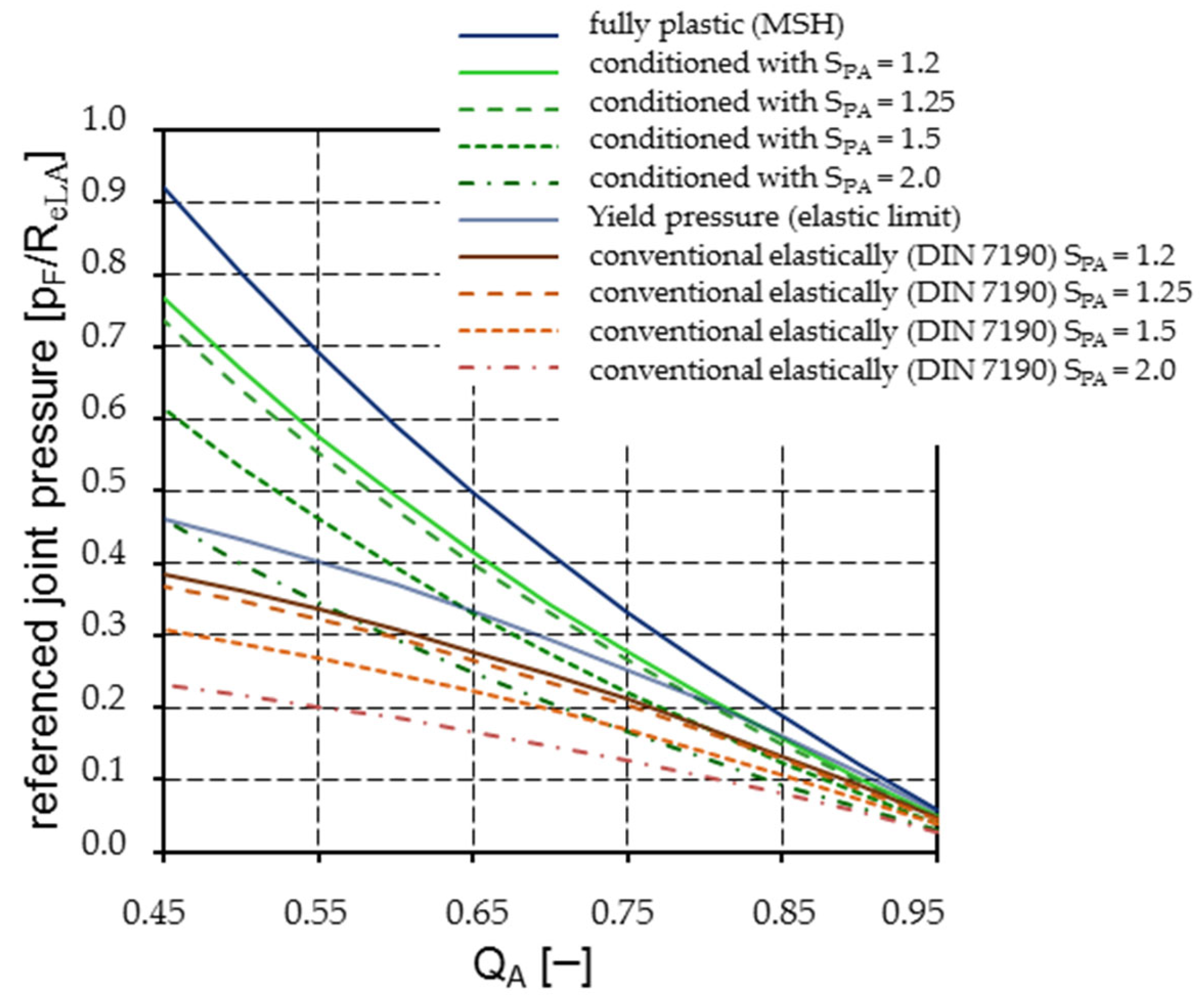
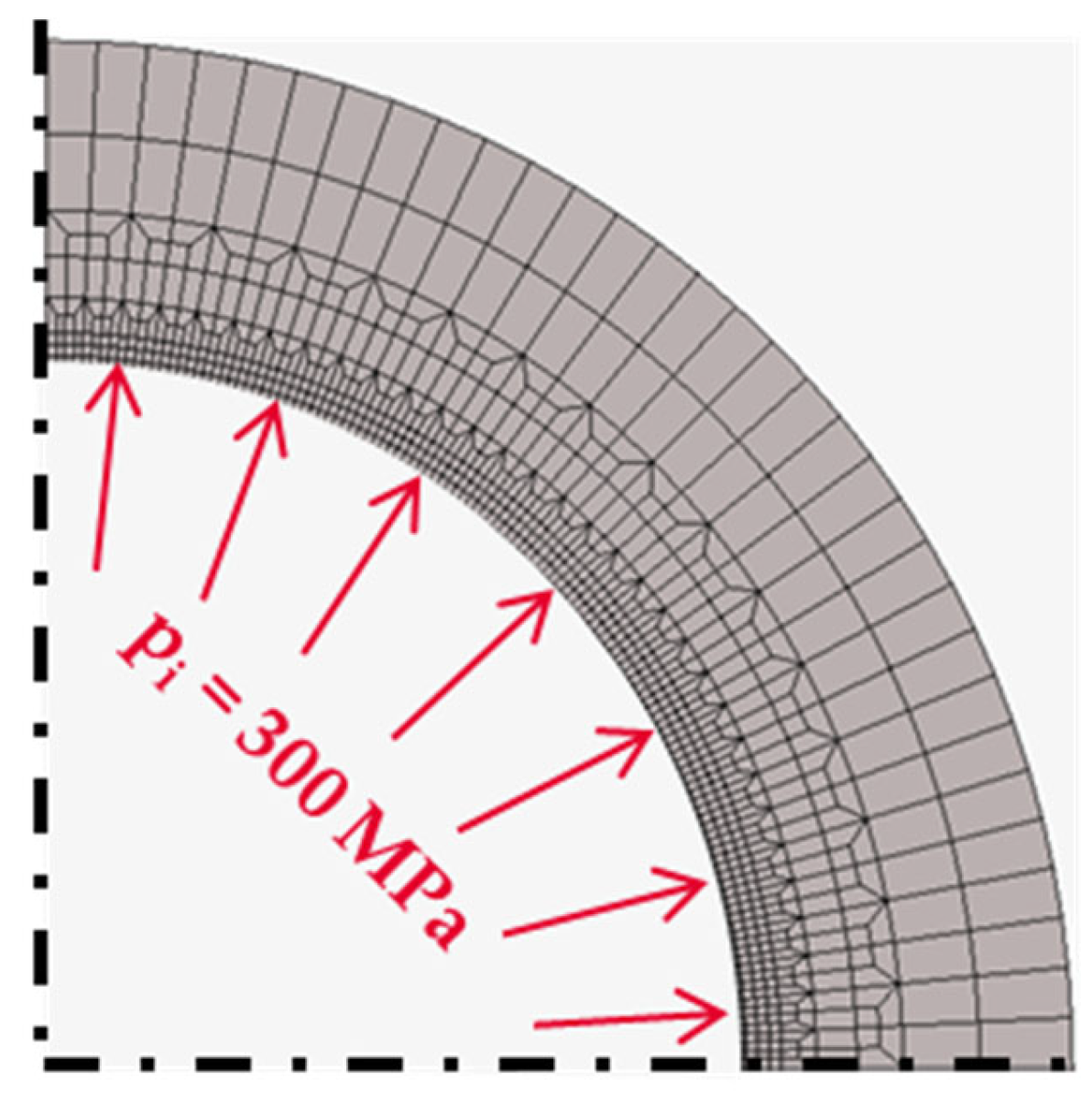
4. Calculation Results
4.1. Results under MSH and Ideal Plastic Material Behavior Assumptions
4.2. Results Regarding VMYC and Hardening Material Behavior
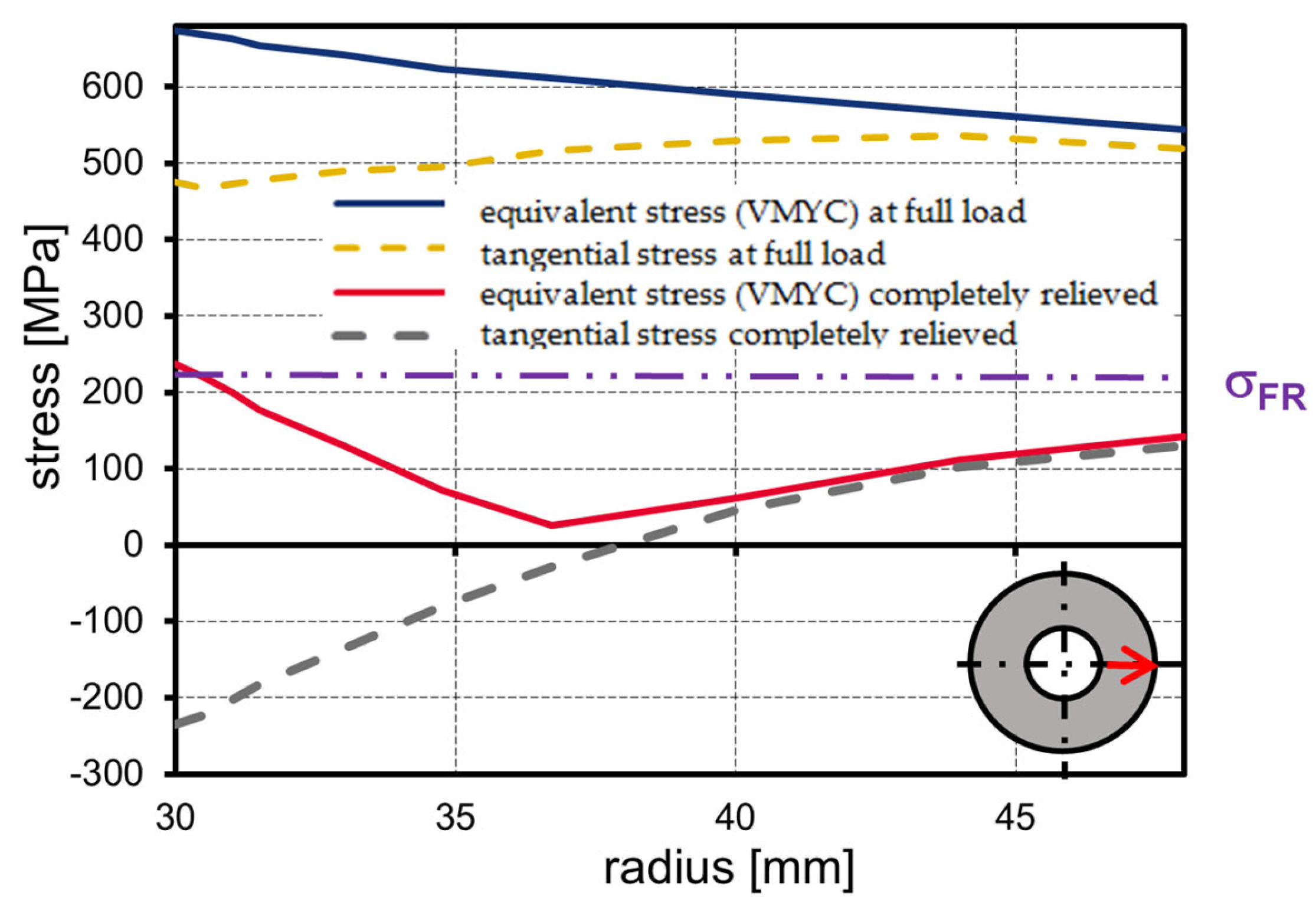
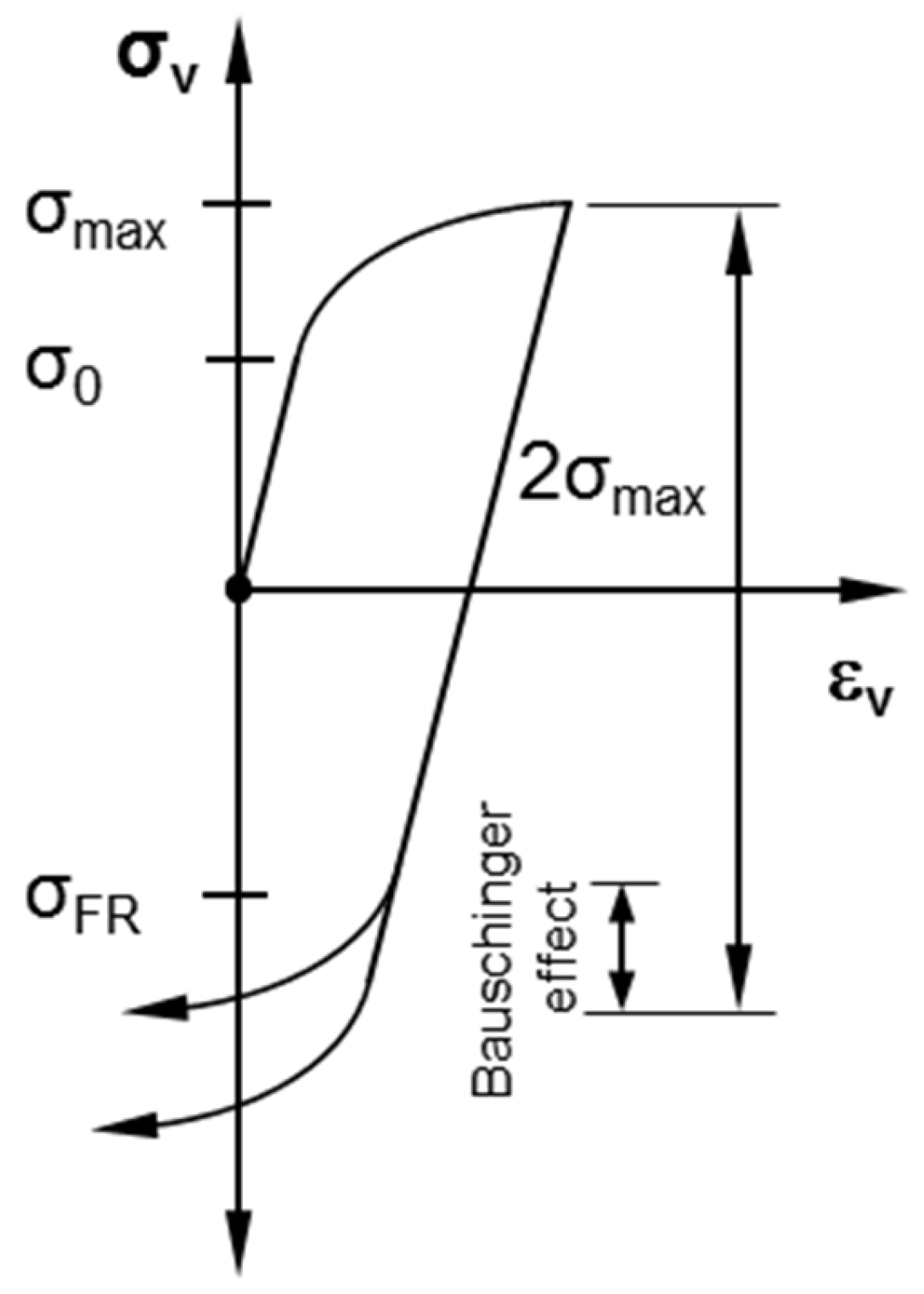
4.3. Results with Respect to the Bauschinger Effect
- βBS: Bauschinger Stress Parameter;
- σFR (MPa): Yield strength that is reached when the material is subsequently subjected to stress in the opposite direction;
- σmax (MPa): Maximum stress achieved by plastic deformation as a result of hardening.
4.4. Technological Avoidance of Reverse Yielding
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Unit | Meaning |
| d | mm | Diameter coordinate (control variable) |
| DaA | mm | Outer diameter of the outer part |
| DF | mm | Joint diameter (nominal) |
| DiA | mm | Inner diameter of the outer part |
| DPA | mm | Plasticity diameter of the outer part |
| Dσr(SH), Dσt(SH) | MPa | Stress values at point D in the principal stress plane for Shear Stress Hypothesis (SH) |
| m | - | Factor for determining the angle of inclination |
| pi | MPa | Internal pressure of the hub |
| pE | MPa | Elastic joint pressure at the yield strength |
| pF | MPa | Joint pressure |
| pK | MPa | Conditioning pressure |
| pKond,max | MPa | Maximum joint pressure when conditioning |
| pkrit,SH | MPa | Critical pressure for Reverse Yielding according to Shear Stress Hypothesis (SH) |
| pkrit,MSH | MPa | Critical pressure for Reverse Yielding according to Modified Shear Stress Hypothesis (MSH) |
| pmax,SH | MPa | Maximum possible pressure before the fully plastic state of the hub for ideal plastic material according to Shear Stress Hypothesis (SH) |
| pmax,MSH | MPa | Maximum possible pressure before the fully plastic state of the hub for ideal plastic material according to Modified Shear Stress Hypothesis (MSH) |
| QA | - | Diameter ratio of the outer part |
| ReL,A | MPa | Lower yield strength of the outer part |
| SPA | - | Safety against plastic deformation of the outer part |
| SPA(SH) | - | Safety against plastic deformation of the outer part achieved by conditioning |
| y | MPa | Intersection of the relief straight line with the ordinate (tangential residual stress after complete relief) |
| α | ° | Inclination angle for load line and relief straight line |
| βBS | - | Bauschinger Stress Parameter |
| εv | - | Equivalent strain |
| εv,el | - | Equivalent elastic strain |
| εv,pl | - | Equivalent plastic strain |
| σ0 | MPa | Yield strength |
| σFR | MPa | Yield strength that is reached when the material is subsequently subjected to stress in the opposite direction |
| σmax | MPa | Maximum stress achieved by plastic deformation as a result of hardening |
| σr | MPa | Radial stress |
| σrA(d) | MPa | Radial stress at d of outer part |
| σt | MPa | Tangential stress |
| σtA(d) | MPa | Tangential stress at d of outer part |
| σv | MPa | Equivalent stress |
| AT | Outer part of the Interference fit | |
| PSS | Plane Stress State | |
| FE | Finite elements | |
| FEM | Finite element method | |
| MSH | Modified Shear Stress Hypothesis according to Kollmann | |
| VMYC | Von Mises Yield Criterion | |
| SH | Shear Stress Hypothesis according to Tresca | |
| IKAT | Institute of Construction and Drive Technology (TU Chemnitz) | |
References
- Rees, D.W.A. Elastic-Plastic Stresses in Rotating Discs by von Mises and Tresca. ZAMM·Z. Angew. Math. Mech. 1999, 79, 281–288. [Google Scholar] [CrossRef]
- Jiang, J.F.; Bi, Y.B. An Elastic-Plastic Analysis of Interference Fit Connection. IOP Conf. Ser. Mater. Sci. Eng. 2019, 504, 012071. [Google Scholar] [CrossRef]
- Laghzale, N.; Bouzid, A. Analytical Modelling of Elastic-Plastic Interference Fit Joints. Int. Rev. Model. Simul. 2016, 9, 191–199. [Google Scholar] [CrossRef]
- Lätzer, M.; Leidich, E. FVA-Nr. 566 I-Heft 993-Übertragungsfähigkeit von Klemmverbindungen unter Besonderer Berücksichtigung Plastischer Verformungen; Abschlussbericht, Forschungsvereinigung Antriebstechnik e.V: Frankfurt, Germany, 2011. [Google Scholar]
- Zhang, P.; Hu, X.; Bui, T.Q.; Yao, W. Phase field modeling of fracture in fiber reinforced composite laminate. Int. J. Mech. Sci. 2019, 161–162, 105008. [Google Scholar] [CrossRef]
- Hu, X.; Tan, S.; Xia, D.; Min, L.; Xu, H.; Yao, W.; Sun, Z.; Zhang, P.; Bui, T.Q.; Zhuang, X.; et al. An overview of implicit and explicit phase field models for quasi-static failure processes, implementation and computational efficiency. Theor. Appl. Fract. Mech. 2023, 124, 103779. [Google Scholar] [CrossRef]
- Chen, P.C.T. The bauschinger and hardening effect on residual stresses in an autofrettaged thick-walled cylinder. J. Press. Vessel Technol. 1985, 108, 108–112. [Google Scholar] [CrossRef]
- Parker, A.P.; Underwood, J.H.; Kendall, D.P. Bauschinger Effect Design Procedures for Autofrettaged Tubes Including Material Removal and Sachs’ Method. ASME J. Press. Vessel Technol. 1999, 121, 430–437. [Google Scholar] [CrossRef]
- Ghorbanpour, A.; Loghman, A.; Khademizadeh, H.; Moradi, M. The Bauschinger and hardening effect on residual stresses in thick-walled cylinders of SUS 304. Trans. Can. Soc. Mech. Eng. 2003, 26, 361–372. [Google Scholar] [CrossRef]
- Jahed, H.; Dubey, R.N. An Axisymmetric Method of Elastic-Plastic Analysis Capable of Predicting Residual Stress Field. ASME J. Press. Vessel Technol. 1997, 119, 264–273. [Google Scholar] [CrossRef]
- Kollmann, F.G.; Önöz, E. Die Eigenspannungen in den Ringen eines elastisch-plastisch beanspruchten Querpreßverbandes nach der Entlastung. Forsch. Ingenieurwesen A 1979, 45, 169–177. [Google Scholar] [CrossRef]
- Koiter, T.W. Progress in Solid Mechanics, Vol. I. In General Theorems for Elastic-Plastic Solids; North Holland Publishing Comp: Amsterdam, The Netherlands, 1960. [Google Scholar]
- Gamer, U. Die Spannungen im elastisch-plastischen Preßverband nach Rotation. Forsch. Ingenieurwesen A 1987, 53, 97–100. [Google Scholar] [CrossRef]
- Mack, W. Entlastung und sekundares Fließen in rotierenden elastisch-plastischen Hohlzylindern. ZAMM·Z. Angew. Math. Mech. 1992, 72, 65–68. [Google Scholar] [CrossRef]
- Schierz, M. Steigerung des Elastischen Potenzials von Pressverbindungen Durch Plastische Konditionierung der Fügepartner. Ph.D. Thesis, Technische Universität Chemnitz, Chemnitz, Germany, 2018. [Google Scholar]
- Schierz, M.; Leidich, E.; Ziaei, M. Plastisch konditionierte Pressverbindungen. In Welle-Nabe-Verbindungen; VDI-Berichte Nr. 2337; VDI Wissensforum GmbH: Karlsruhe, Germany, 2018. [Google Scholar]
- Schierz, M. Increase in Elastic Stress Limits by Plastic Conditioning: Influence of Strain Hardening on Interference Fits. Appl. Mech. 2022, 3, 375–389. [Google Scholar] [CrossRef]
- DIN 7190-1:2017; Pressverbände—Teil 1: Berechnungsgrundlagen und Gestaltungsregeln. Deutsches Institut für Normung e.V.: Berlin, Germany, 2017.
- Buciumeanu, M.; Palaghian, L.; Miranda, A.; Silva, F. Fatigue life predictions including the Bauschinger effect. Int. J. Fatigue 2011, 33, 145–152. [Google Scholar] [CrossRef]
- Parker, A.P. Bauschinger Effect Design Procedures for Compound Tubes Containing an Autofrettaged Layer. J. Press. Vessel Technol. 2001, 123, 203–206. [Google Scholar] [CrossRef]
- Loffredo, M. Measurement and modelling of Bauschinger effect for low-level plastic strains on AISI 4140 steel. Procedia Struct. Integr. 2018, 8, 265–275. [Google Scholar] [CrossRef]
- Jahed, H.; Faritus, M.R.; Jahed, Z. Residual Stress Measurements in an Autofrettage Tube Using Hole Drilling Method. J. Press. Vessel Technol. 2012, 134, 051501. [Google Scholar] [CrossRef]
- Huang, X.P.; Cui, W.C. Effect of Bauschinger Effect and Yield Criterion on Residual Stress Distribution of Autofrettaged Tube. J. Press. Vessel Technol. 2005, 128, 212–216. [Google Scholar] [CrossRef]
- Hu, X.; Xu, H.; Xi, X.; Zhang, P.; Yang, S. Meso-scale phase field modelling of reinforced concrete structures subjected to corrosion of multiple reinforcements. Constr. Build. Mater. 2022, 321, 126376. [Google Scholar] [CrossRef]
- DIN 7190-2:2017; Pressverbände—Teil 2: Berechnungsgrundlagen und Gestaltungsregeln für Kegelige, Selbsthemmende Pressverbände. Deutsches Institut für Normung e.V.: Berlin, Germany, 2017.

| σv (MPa) | εv (−) |
|---|---|
| 370.00 | 0.00171 |
| 390.00 | 0.00182 |
| 400.00 | 0.00189 |
| 410.00 | 0.01303 |
| 420.00 | 0.01417 |
| 430.00 | 0.01549 |
| 440.00 | 0.01665 |
| 470.00 | 0.02075 |
| 500.00 | 0.02543 |
| 530.00 | 0.03097 |
| 560.00 | 0.03775 |
| 590.00 | 0.04612 |
| 620.00 | 0.05967 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schierz, M.; Hasse, A. The Influence of Reverse Yielding on the Plastic Conditioning of Interference Fits in Power Transmission Engineering. Appl. Mech. 2024, 5, 73-90. https://doi.org/10.3390/applmech5010005
Schierz M, Hasse A. The Influence of Reverse Yielding on the Plastic Conditioning of Interference Fits in Power Transmission Engineering. Applied Mechanics. 2024; 5(1):73-90. https://doi.org/10.3390/applmech5010005
Chicago/Turabian StyleSchierz, Mario, and Alexander Hasse. 2024. "The Influence of Reverse Yielding on the Plastic Conditioning of Interference Fits in Power Transmission Engineering" Applied Mechanics 5, no. 1: 73-90. https://doi.org/10.3390/applmech5010005
APA StyleSchierz, M., & Hasse, A. (2024). The Influence of Reverse Yielding on the Plastic Conditioning of Interference Fits in Power Transmission Engineering. Applied Mechanics, 5(1), 73-90. https://doi.org/10.3390/applmech5010005





