Analysis and Design of Lateral Framing Systems for Multi-Story Steel Buildings
Abstract
1. Introduction
1.1. Research Background
1.2. Literature Review
1.3. Motivation of Research
1.4. Objective of Research
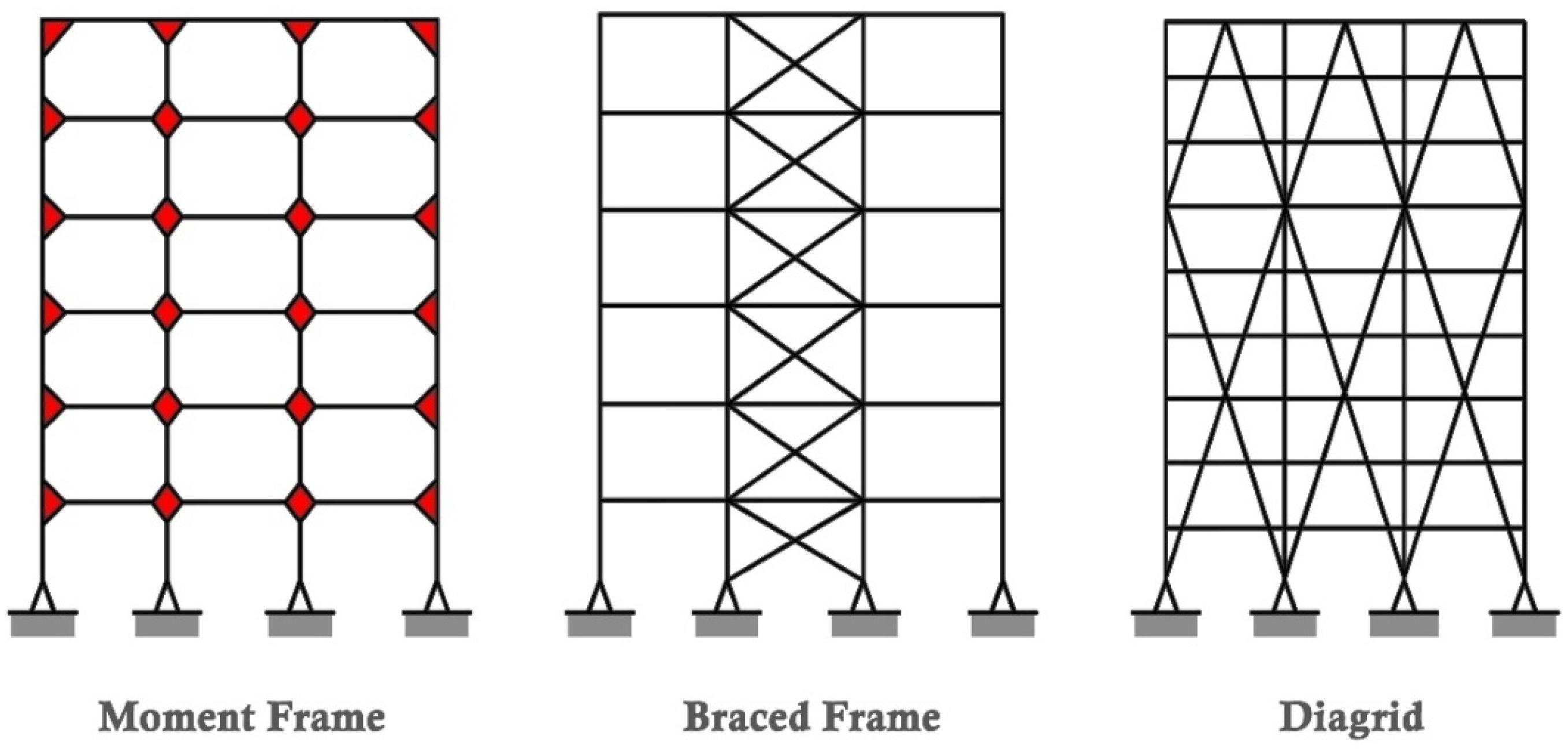
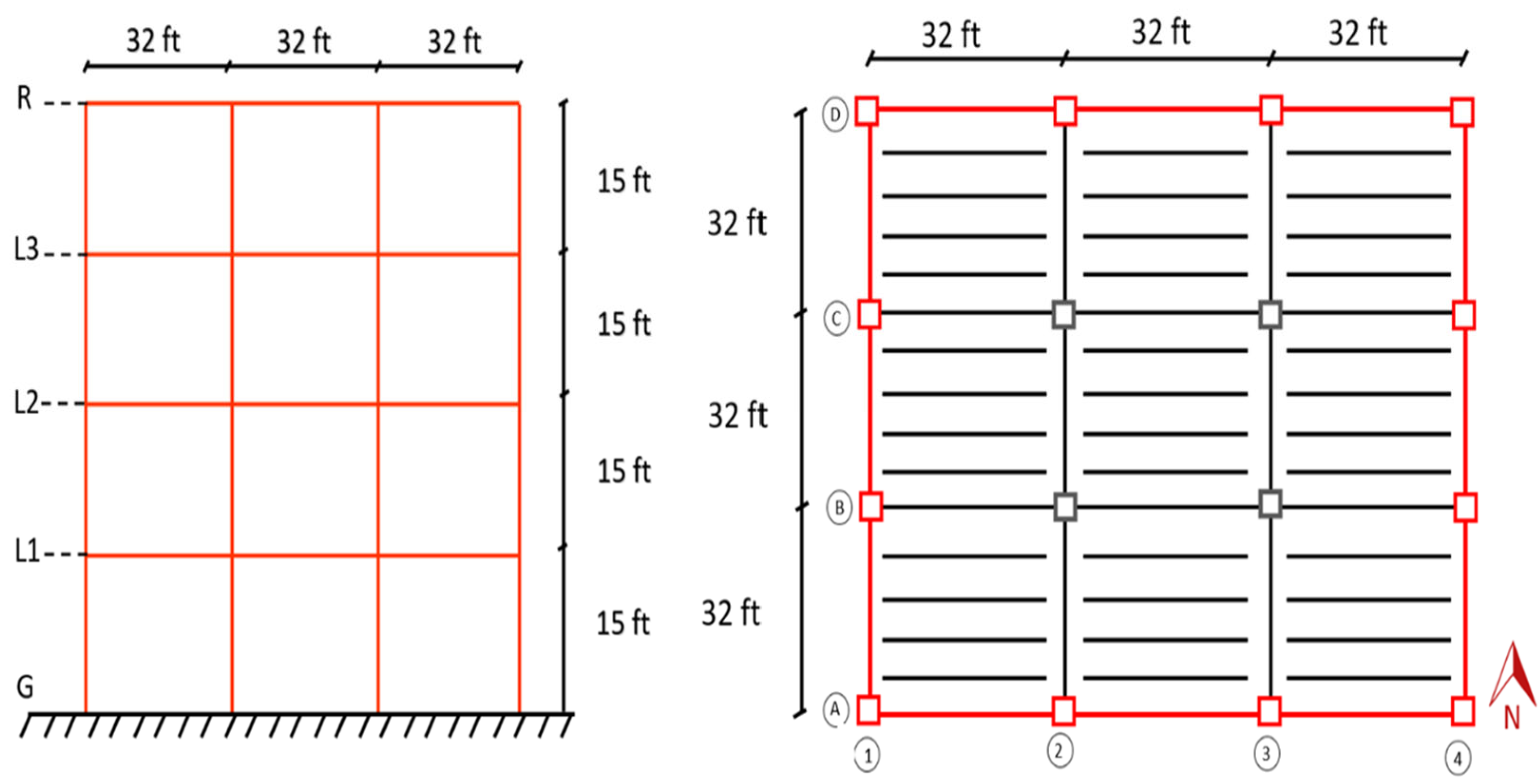
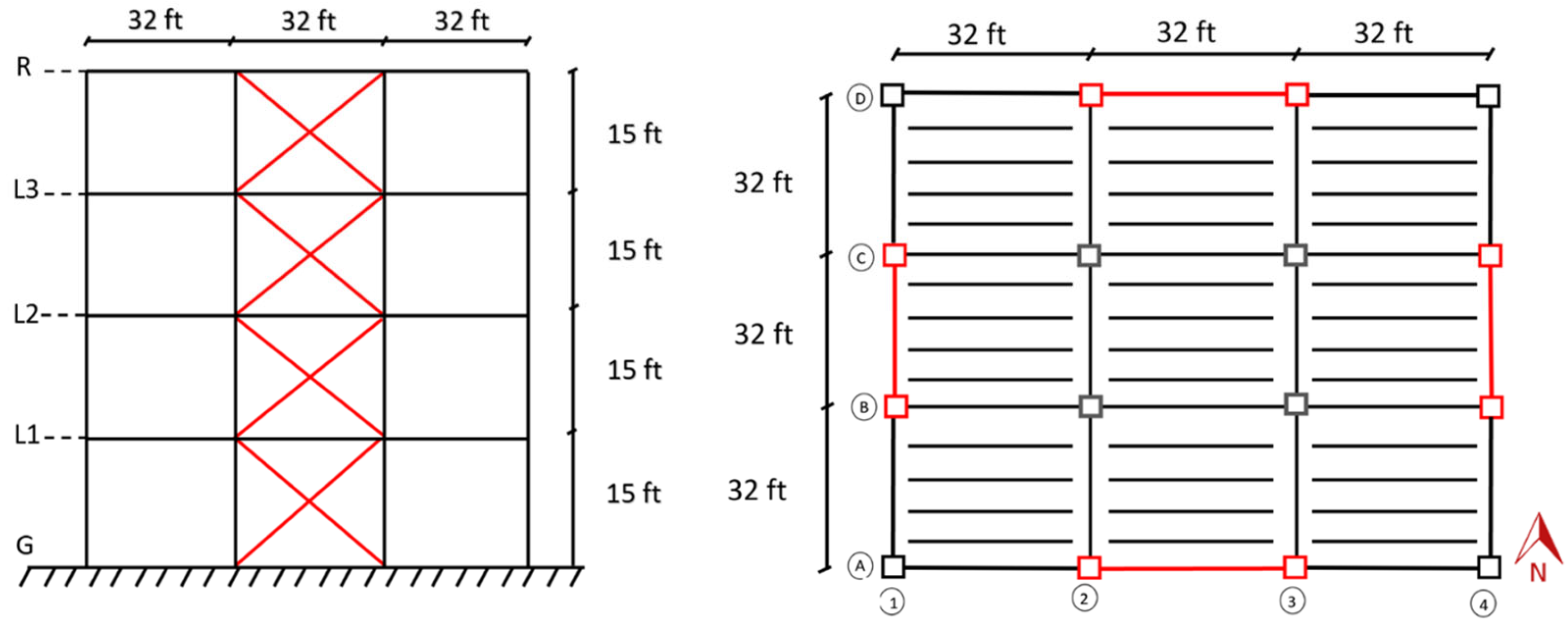
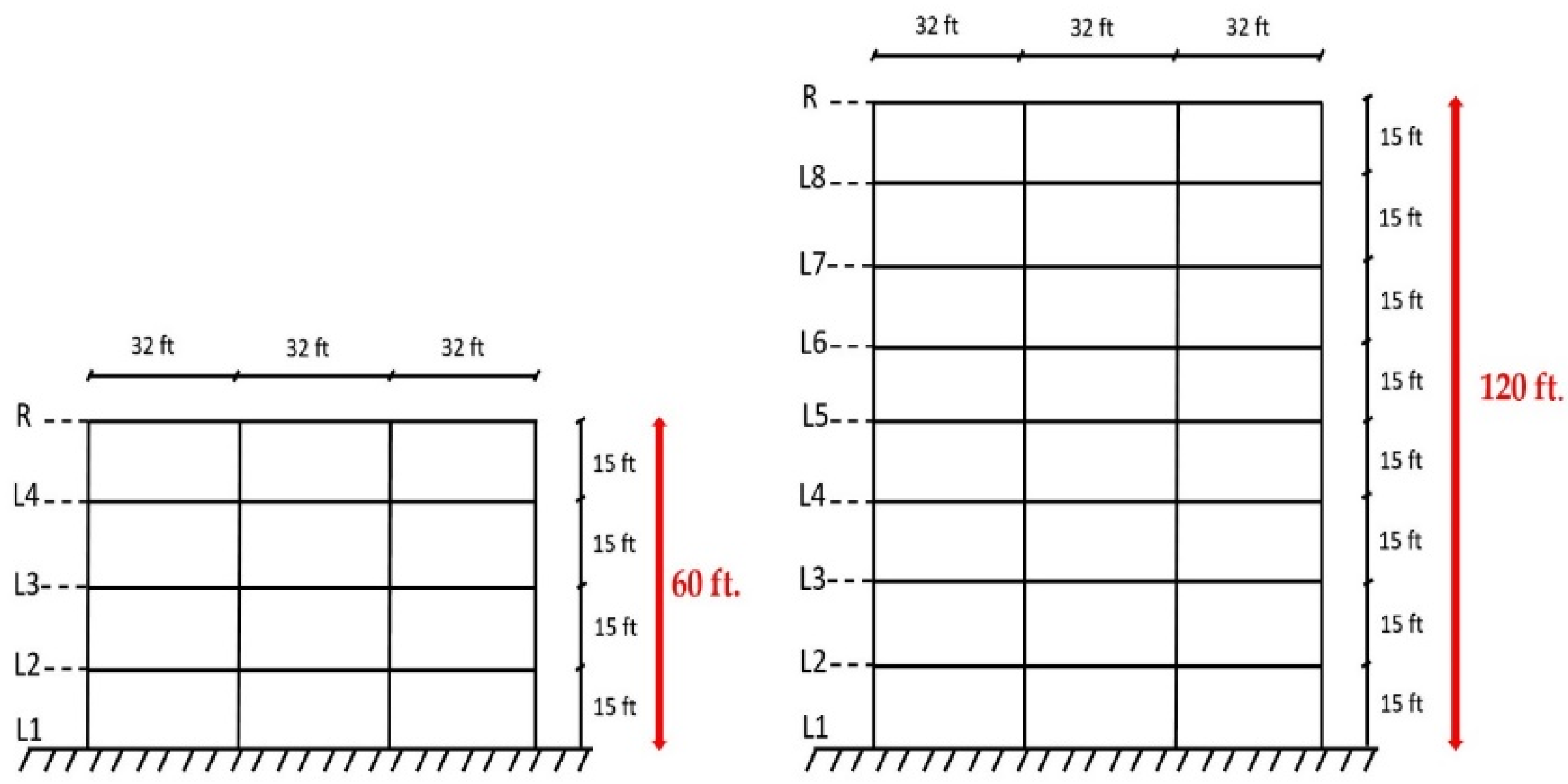
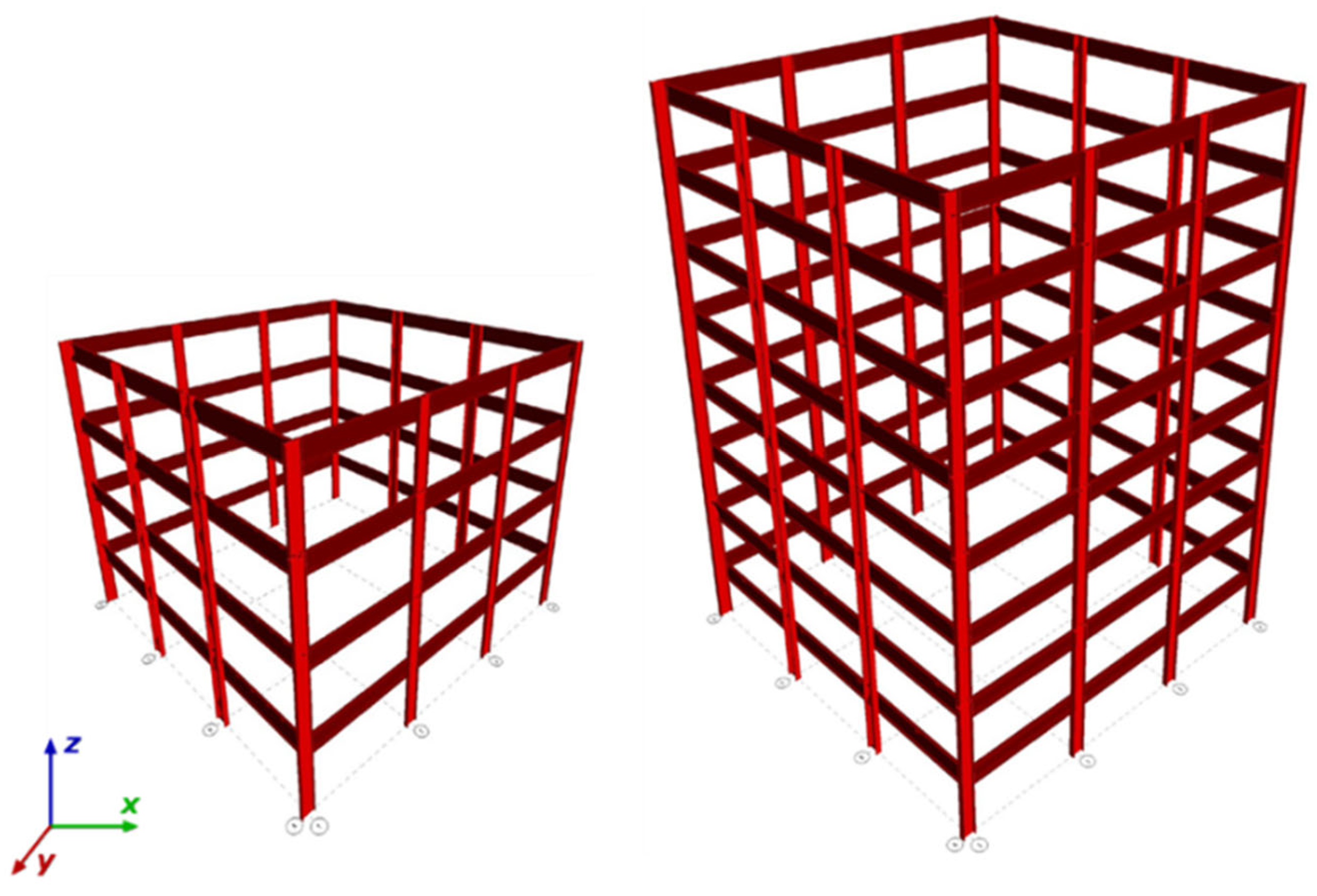
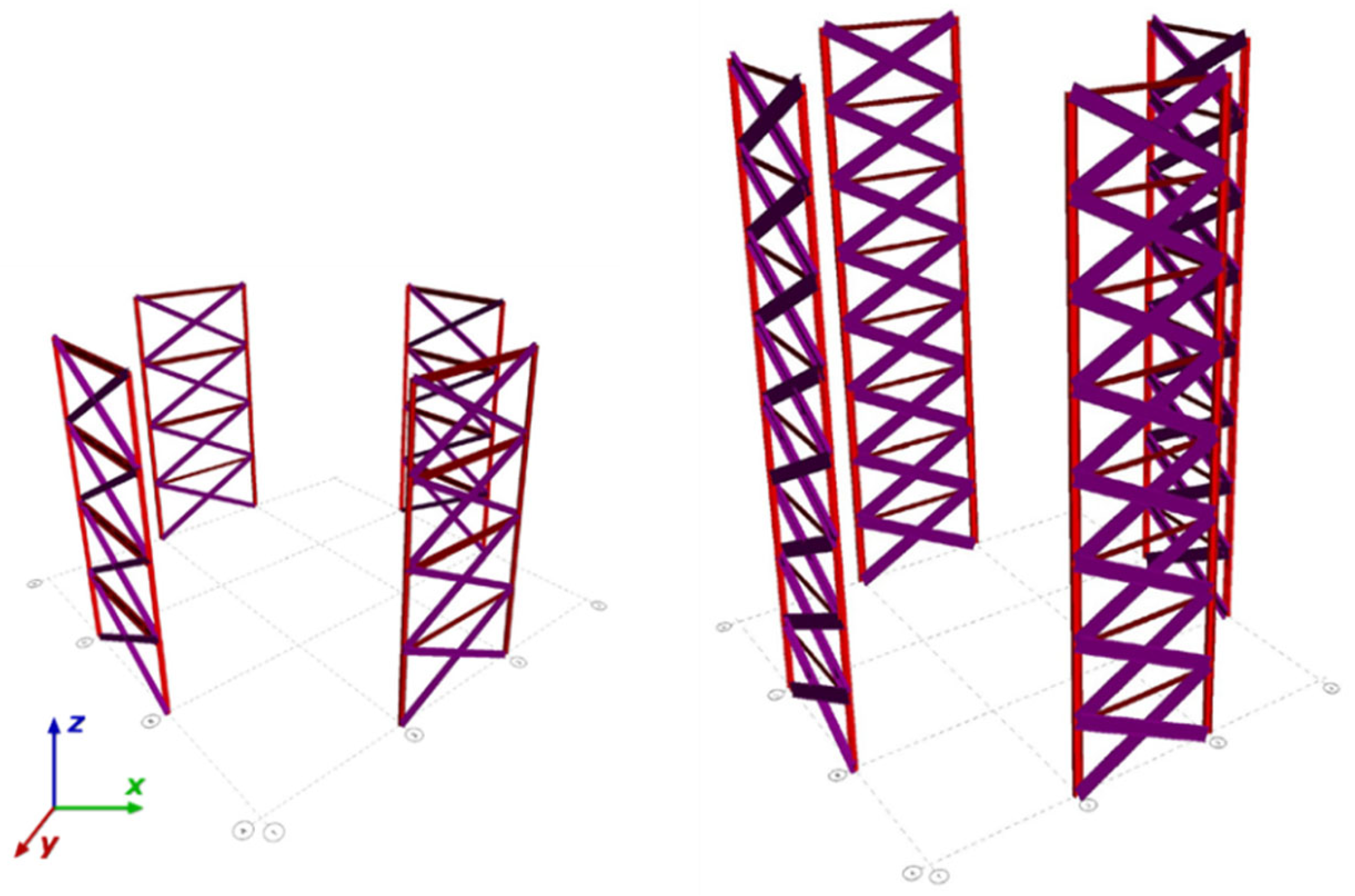
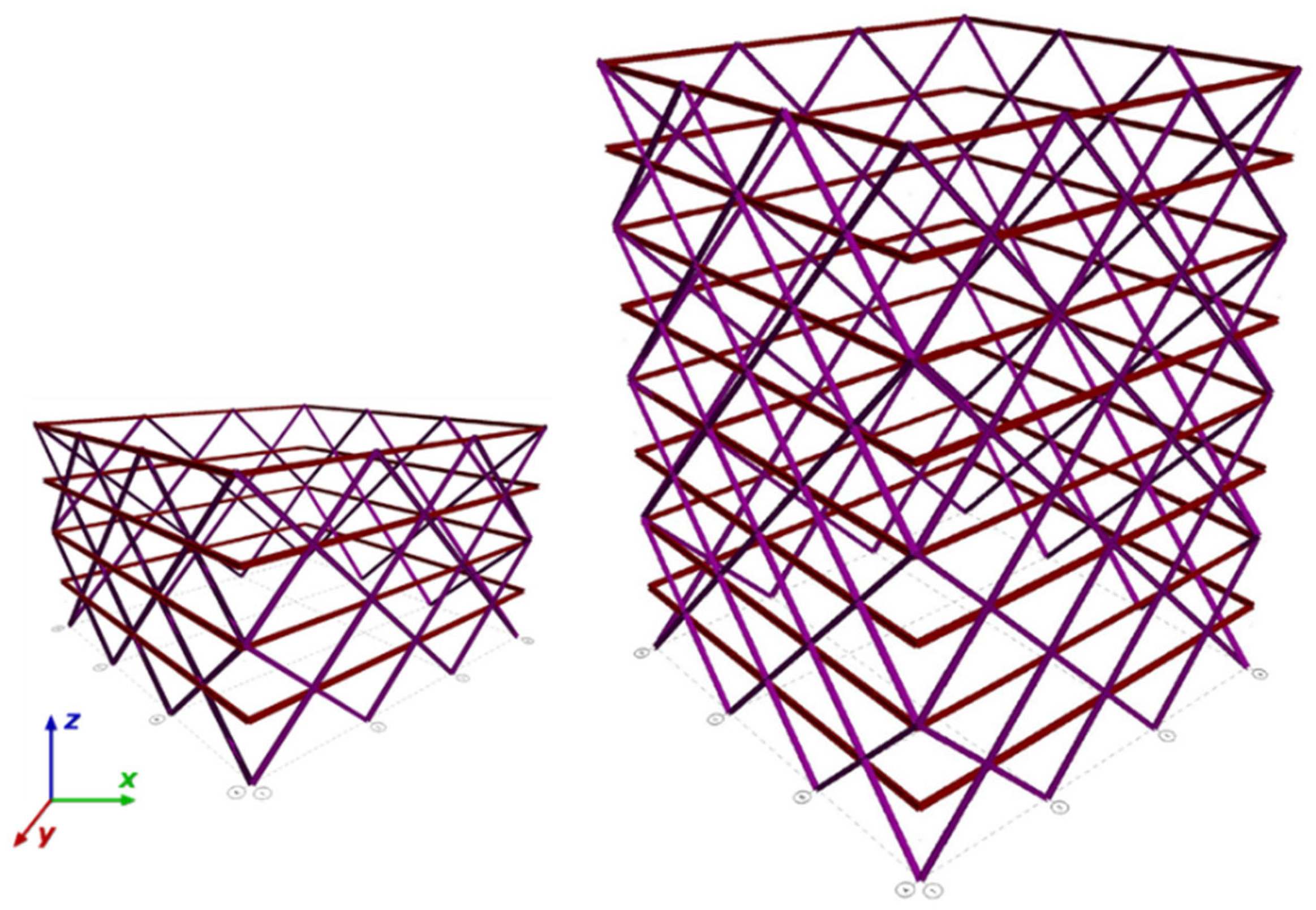
2. Procedure of Work
2.1. Data of Structural Loads
2.1.1. Gravity Loads
2.1.2. Lateral Loads
2.2. Design Verifications
2.2.1. Composite Steel Beam Verification
2.2.2. Steel Column Verification
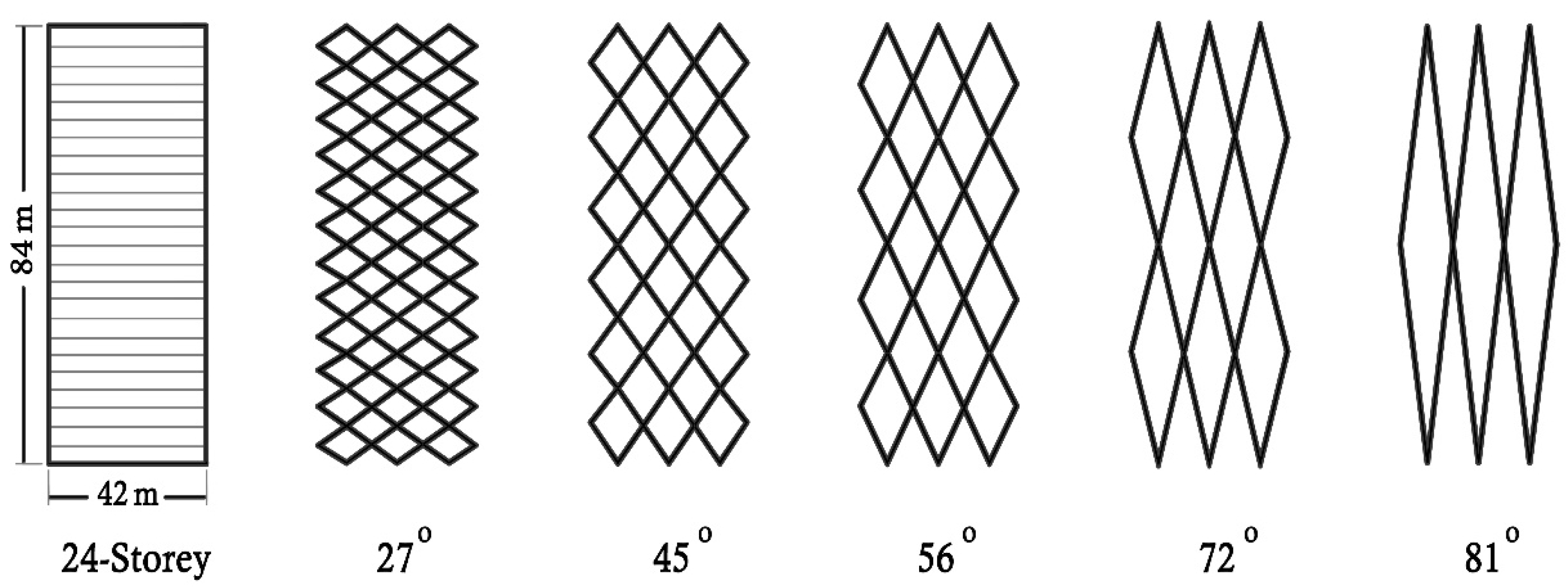
2.3. Response Modification Coefficient (R-Value)
3. Results and Analysis
3.1. Seismic Loads
3.2. Inter-story Drift
3.3. Building Displacement
3.4. Story Stiffness
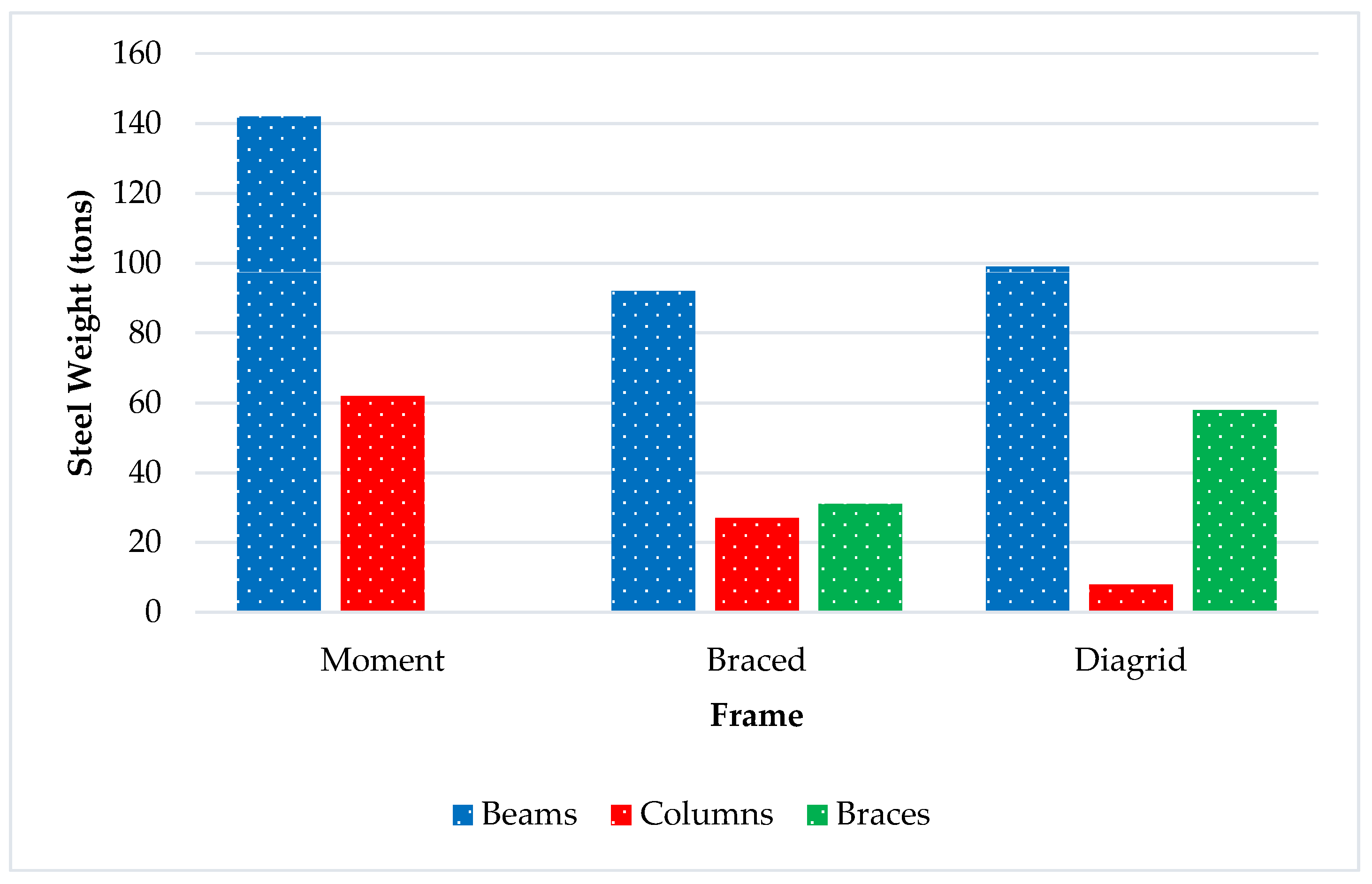
3.5. Steel Weights
3.6. Member Sizes
3.7. Four-Story vs. Eight-Story Models
4. Discussion
5. Conclusions
- Better lateral load resistance system when compared to braced and moment frames.
- The diagonal members on the periphery of the structure resist both the lateral and gravity loads, which makes the system more effective.
- Stiffer system than braced and moment frame.
- Stiffer system even with high-rise building when compared to moment and braced frame.
- Diagrid without corner columns is not very different from the ones with corner columns, but it can save 6% more of the required steel.
- The number of structural elements required (exterior vertical columns eliminated) in the building is reduced, which gives the building a more aesthetic look, especially in the interior space.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boake, T.M. Diagrid Structures: Systems, Connections, Details; Birkhauser Verlag: Basil, Switzerland, 2014. [Google Scholar]
- Elsanadedy, H.; Khawaji, M.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Numerical modeling for assessing progressive collapse risk of RC buildings exposed to blast loads. Structures 2023, 48, 1190–1208. [Google Scholar] [CrossRef]
- Kato, T.; Sakino, Y.; Sano, Y. Effect of Laser Peening with a Microchip Laser on Fatigue Life in Butt-Welded High-Strength Steel. Appl. Mech. 2021, 2, 878–890. [Google Scholar] [CrossRef]
- Tavakoli, H.R.; Alashti, A.R. Evaluation of progressive collapse potential of multi-story moment resisting steel frame buildings under lateral loading. Sci. Iran. 2013, 20, 77–86. [Google Scholar] [CrossRef]
- Labò, S.; Passoni, C.; Marini, A.; Belleri, A.; Camata, G.; Riva, P.; Spacone, E. Prefabricated responsive diagrids for holistic renovation of existing MID-RISE RC buildings. In Proceedings of the COMPDYN 2017—6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017; Volume 2, pp. 4234–4244. [Google Scholar]
- Moon, K. Sustainable Design of Diagrid Structural Systems for Tall Buildings. Int. J. Sustain. Build. Technol. Urban Dev. 2011, 2, 37–42. [Google Scholar] [CrossRef]
- Elhegazy, H.; Ebid, A.M.; Mahdi, I.M.; Haggag, S.A.; Rashid, I.A. Selecting optimum structural system for RC multi-story buildings considering direct cost. Structures 2020, 24, 296–303. [Google Scholar] [CrossRef]
- Taranath, B.S. Tall Building Design: Steel, Concrete, and Composite Systems; CRC Press: New York, NY, USA, 2016. [Google Scholar]
- Veljkovic, M.; Johansson, B. Light steel framing for residential buildings. Thin-Walled Struct. 2007, 44, 1272–1279. [Google Scholar] [CrossRef]
- Shan, S.; Pan, W. Progressive collapse mechanisms of multi-story steel-framed modular structures under module removal scenarios. Structures 2022, 46, 1119–1133. [Google Scholar] [CrossRef]
- Ilgın, H.E. Interrelations of Slenderness Ratio and Main Design Criteria in Supertall Buildings. Int. J. Build. Pathol. Adapt. 2022; in press. [Google Scholar]
- Al-Kodmany, K. Understanding Tall Buildings: A Theory of Placemaking; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Jones, J.; Telionis, D. Aeroform: Designing for Wind and Air Movement; Taylor & Francis: Abingdon, UK, 2022. [Google Scholar]
- Al-Kodmany, K. Eco-Towers: Sustainable Cities in the Sky; WIT Press: Southampton, UK, 2015. [Google Scholar]
- Li, W.; Li, Q.-N.; Jiang, W.-S.; Jiang, L. Seismic performance of composite reinforced concrete and steel moment frame structures—State-of-the-art. Compos. Part B Eng. 2011, 42, 190–206. [Google Scholar] [CrossRef]
- Ali, M.M.G.; Moon, K.S. Structural developments in tall buildings: Current trends and future prospects. Archit. Sci. Rev. 2007, 50, 205–223. [Google Scholar] [CrossRef]
- Moon, K.S. Developments of Structural Systems toward Mile-High Towers. Int. J. High-Rise Build. 2018, 7, 197–214. [Google Scholar]
- Mansouri, E.; Manfredi, M.; Hu, J.-W. Environmentally Friendly Concrete Compressive Strength Prediction Using Hybrid Machine Learning. Sustainability 2022, 14, 12990. [Google Scholar] [CrossRef]
- Seo, J.; Dueñas-Osorio, L.; Craig, J.I.; Goodno, B.J. Metamodel-based regional vulnerability estimate of irregular steel moment-frame structures subjected to earthquake events. Eng. Struct. 2012, 45, 585–597. [Google Scholar] [CrossRef]
- Lew, H.S.; Main, J.A.; Robert, S.D.; Sadek, F.; Chiarito, V.P. Performance of Steel Moment Connections under a Column Removal Scenario. I: Experiments. J. Struct. Eng. 2013, 139, 98–107. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, G.Q. Testing of semi-rigid steel-concrete composite frames subjected to vertical loads. Eng. Struct. 2007, 29, 1903–1916. [Google Scholar] [CrossRef]
- Torres-Rodas, P.; Zareian, F.; Kanvinde, A. Seismic Demands in Column Base Connections of Steel Moment Frames. Earthq. Spectra 2018, 34, 1383–1403. [Google Scholar] [CrossRef]
- Baghi, H.; Oliveira, A.; Valença, J.; Cavaco, E.; Neves, L.; Júlio, E. Behavior of reinforced concrete frame with masonry infill wall subjected to vertical load. Eng. Struct. 2018, 171, 476–487. [Google Scholar] [CrossRef]
- Karavasilis, T.L.; Bazeos, N.; Beskos, D.E. Estimation of seismic drift and ductility demands in planar regular X-braced steel frames. Earthq. Eng. Struct. Dyn. 2007, 36, 2273–2289. [Google Scholar] [CrossRef]
- Di Sarno, L.; Elnashai, A. Seismic Retrofitting of Steel and Composite Building Structures. In Report of the Mid-America Earthquake Center of Civl and Environmental Engineering Department at the University of Illinois at Urbana-Champaign; University of Illinois Press: Champaign, IL, USA, 2002; pp. 1–200. [Google Scholar]
- Tena-Colunga, A.; Vergara, A. Comparative study on the seismic retrofit of a mid-rise steel building: Steel bracing vs. energy dissipation. Earthq. Eng. Struct. Dyn. 1997, 26, 637–655. [Google Scholar] [CrossRef]
- Iwata, M.; Kato, T.; Wada, A. Buckling-restrained braces as hysteretic dampers. In Behaviour of Steel Structures in Seismic Areas; CRC Press: Boca Raton, FL, USA, 2021; pp. 33–38. [Google Scholar]
- Varkey, D.; George, M. Dynamic Analysis of Diagrid System with Complex Shape. Int. J. Innov. Sci. Eng. Technol. 2016, 3, 484–488. [Google Scholar]
- Boake, T.M. Diagrids, The New Stability System: Combining Architecture with Engineering; School of Architecture, University of Waterloo: Cambridge, ON, Canada, 2013. [Google Scholar]
- Chatzikonstantinou, I.; Ekici, B.; Sariyildiz, I.S.; Koyunbaba, B.K. Multi-Objective Diagrid Façade Optimization Using Differential Evolution. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 2311–2318. [Google Scholar]
- Moon, K.S.; Connor, J.J.; John, E.F. Diagrid structural systems for tall buildings: Characteristics and methodology for preliminary design. Struct. Des. Tall Spec. Build. 2007, 16, 205–230. [Google Scholar] [CrossRef]
- Asadi, E.; Adeli, H. Diagrid: An innovative, sustainable, and efficient structural system. Struct. Des. Tall Spec. Build. 2017, 26, e1358. [Google Scholar] [CrossRef]
- Kassegne, S.K.; Donnadieu, A. Seismic Analysis of Building Structures Using the RAM Structural System. In Proceedings of the Mexican Society of Seismic Engineering Meeting, Mexico City, Mexico, 22 April 1998. [Google Scholar]
- Simiu, E. Design of Buildings for Wind: A Guide for ASCE 7–10 Standard Users and Designers of Special Structures; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Griffis, L.G. Serviceability limit states under wind load. Eng. J. 1993, 30, 1–16. [Google Scholar]
- AISC. Specification for structural steel buildings. In AISC 360-10; AISC: Chicago, IL, USA, 2010. [Google Scholar]
- Sun, M. A Comparative Study on the Seismic Performance of Concrete and Steel Diagrid Structures. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, June 2015. [Google Scholar]
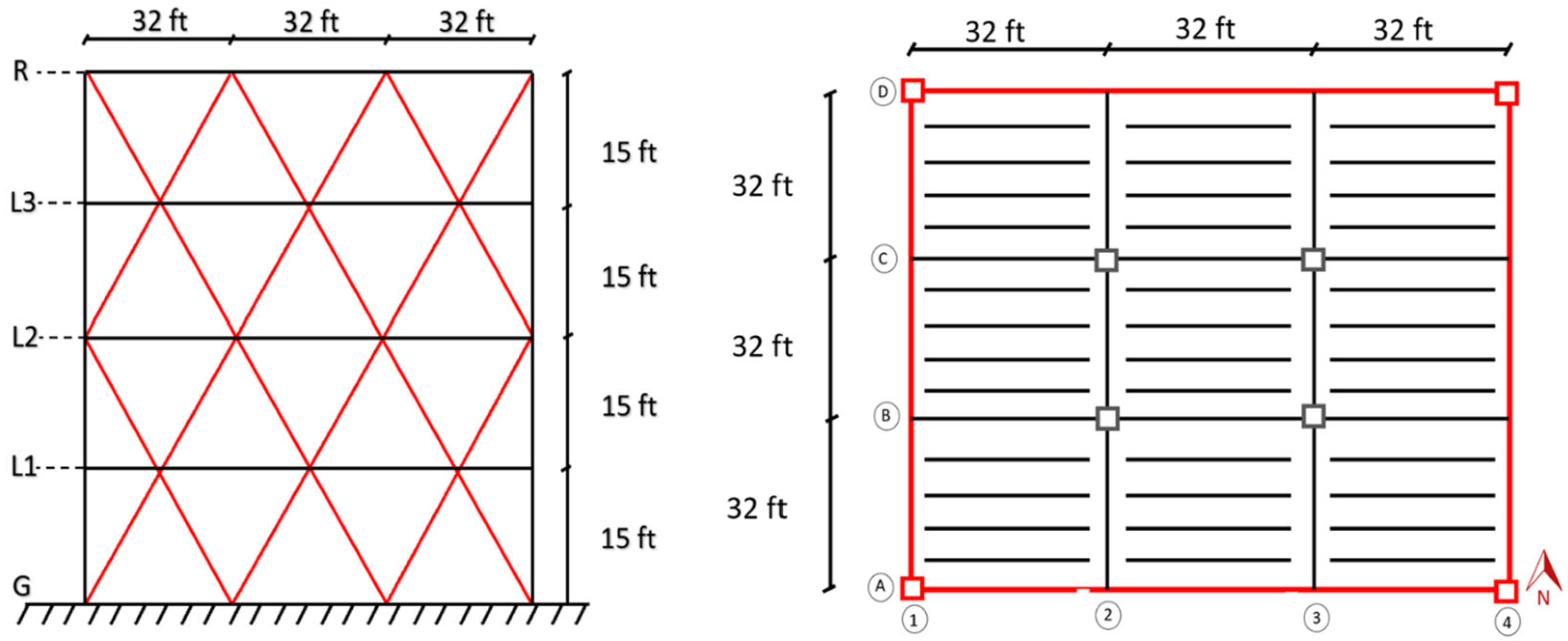


| Gravity Dead Loads | Snow Loads | ||
|---|---|---|---|
| Component | Load (psf) | Description | Input |
| Mechanical/Electrical/Plumbing | 10 | Building Classification | II |
| Structure self-weight | As calculated | Exposure Factor, Ce | 0.9 |
| Ponding | 5 | Thermal Factor, Ct | 1 |
| Allowance for roofing system | 7 | Importance Factor, I_s | 1 |
| Exterior walls (window curtain wall) | 8 | Ground Snow Load, Pg | 25 psf |
| Partitions | 10 | Flat Roof Snow Load, pf | 15.75 psf |
| Wind Loads | |
|---|---|
| Wind Code | ASCE 7–10 |
| Risk Category | II |
| V, Basic Wind Speed | 120 mph |
| Kd, Wind Directionality Factor | 0.85 |
| Exposure Category | C |
| Building Height, h | 60 ft. |
| Kz, Velocity Pressure Coefficient | (ASCE 7–10) |
| Kzt, Topographic Factor | 1 |
| G, Gust Effect Factor | 0.85 |
| Enclosure Classification | Enclosed |
| GCpi, Internal Pressure Coefficient | 0.18 |
| Cp, External Pressure Coefficient | (ASCE 7–10) |
| Windward | 0.8 |
| Leeward | −0.5 |
| Side Wall | −0.7 |
| Seismic Loads | |
|---|---|
| Design Parameters | Value |
| Ss, mapped MCE response acceleration at short periods | 0.095 g |
| S1, mapped MCE response acceleration at 1 s period | 0.045 g |
| Fa, short-period site coefficient | 1.6 |
| Fv, long-period site coefficient | 2.4 |
| SMS, response acceleration at short periods | 0.152 g |
| SM1, response acceleration at 1 s period | 0.108 g |
| SDS, design response acceleration at short periods | 0.101 g |
| SD1, design response acceleration at 1 s period | 0.072 g |
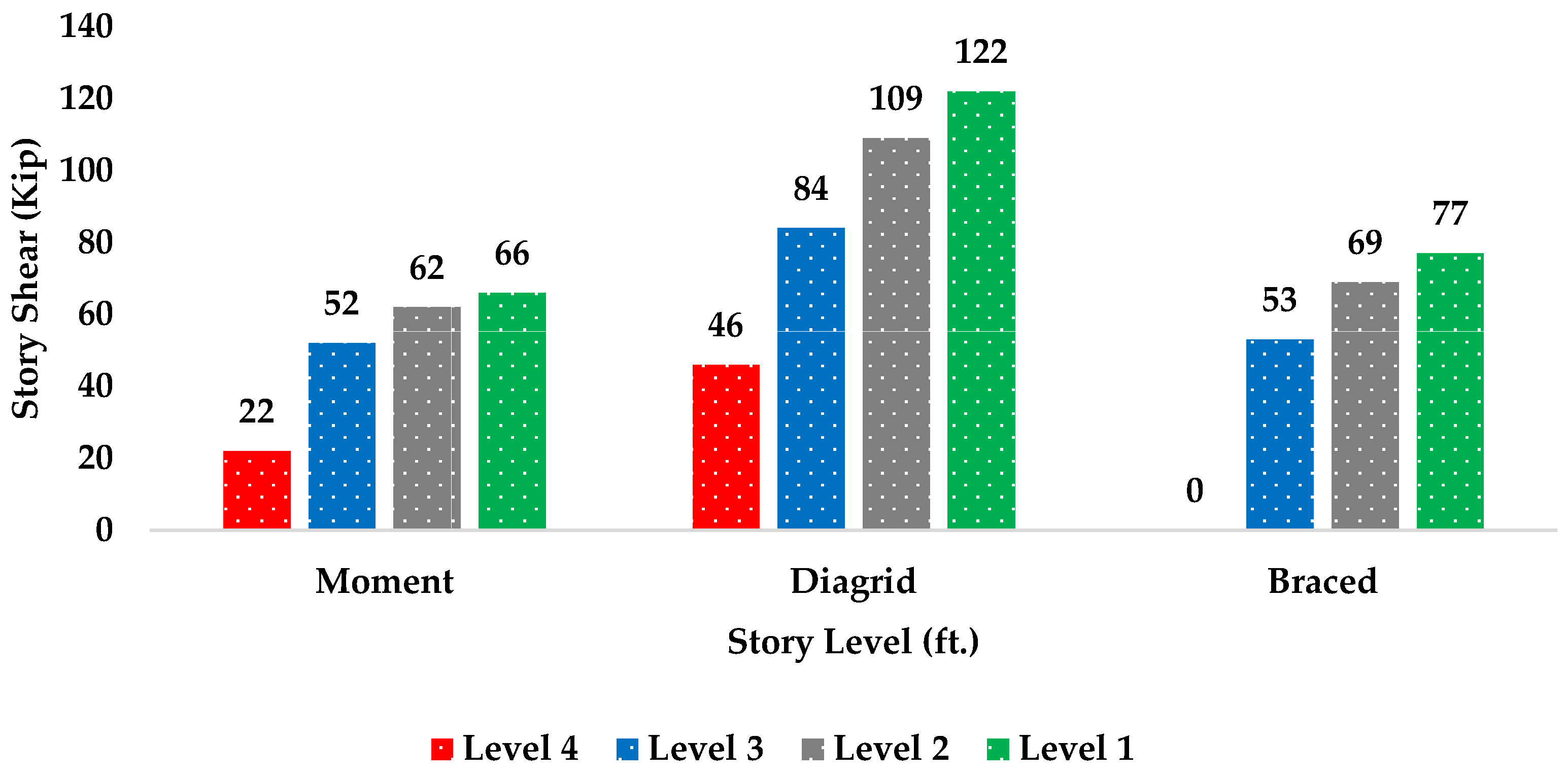
| Story Level | Story Height (ft) | Height hx (ft) | Weight Wx (kip) | Cvx | Story Force Fx (kip) | Story Shear (Calculated) (kip) | Story Shear (RAM) (kip) |
|---|---|---|---|---|---|---|---|
| Roof | 15 | 60 | 1083 | 0.41 | 23 | 0 | 0 |
| Level 3 | 15 | 45 | 1187 | 0.32 | 28 | 23 | 22 |
| Level 2 | 15 | 30 | 1187 | 0.19 | 11 | 51 | 52 |
| Level 1 | 15 | 15 | 1187 | 0.08 | 4 | 62 | 62 |
| Ground | 0 | 0 | 4644 | 0 | 0 | 66 | 66 |
| Story Level | Story Height (ft) | Height hx (ft) | Weight Wx (kip) | Cvx | Story Force Fx (kip) | Story Shear (Calculated) (kip) | Story Shear (RAM) (kip) |
|---|---|---|---|---|---|---|---|
| Roof | 15 | 60 | 1016 | 0.38 | 47 | 0 | 0 |
| Level 3 | 15 | 45 | 1120 | 0.31 | 38 | 47 | 46 |
| Level 2 | 15 | 30 | 1120 | 0.21 | 26 | 85 | 84 |
| Level 1 | 15 | 15 | 1120 | 0.10 | 12 | 111 | 109 |
| Ground | 0 | 0 | 4376 | 0 | 0 | 123 | 122 |
| Story Level | Story Height (ft) | Height hx (ft) | Weight Wx (kip) | Cvx | Story Force Fx (kip) | Story Shear (Calculated) (kip) | Story Shear (RAM) (kip) |
|---|---|---|---|---|---|---|---|
| Roof | 15 | 60 | 1055 | 0.38 | 29 | 0 | 0 |
| Level 3 | 15 | 45 | 1158 | 0.31 | 24 | 29 | 29 |
| Level 2 | 15 | 30 | 1158 | 0.21 | 16 | 53 | 53 |
| Level 1 | 15 | 15 | 1158 | 0.10 | 8 | 69 | 69 |
| Ground | 0 | 0 | 4529 | 0 | 0 | 77 | 77 |
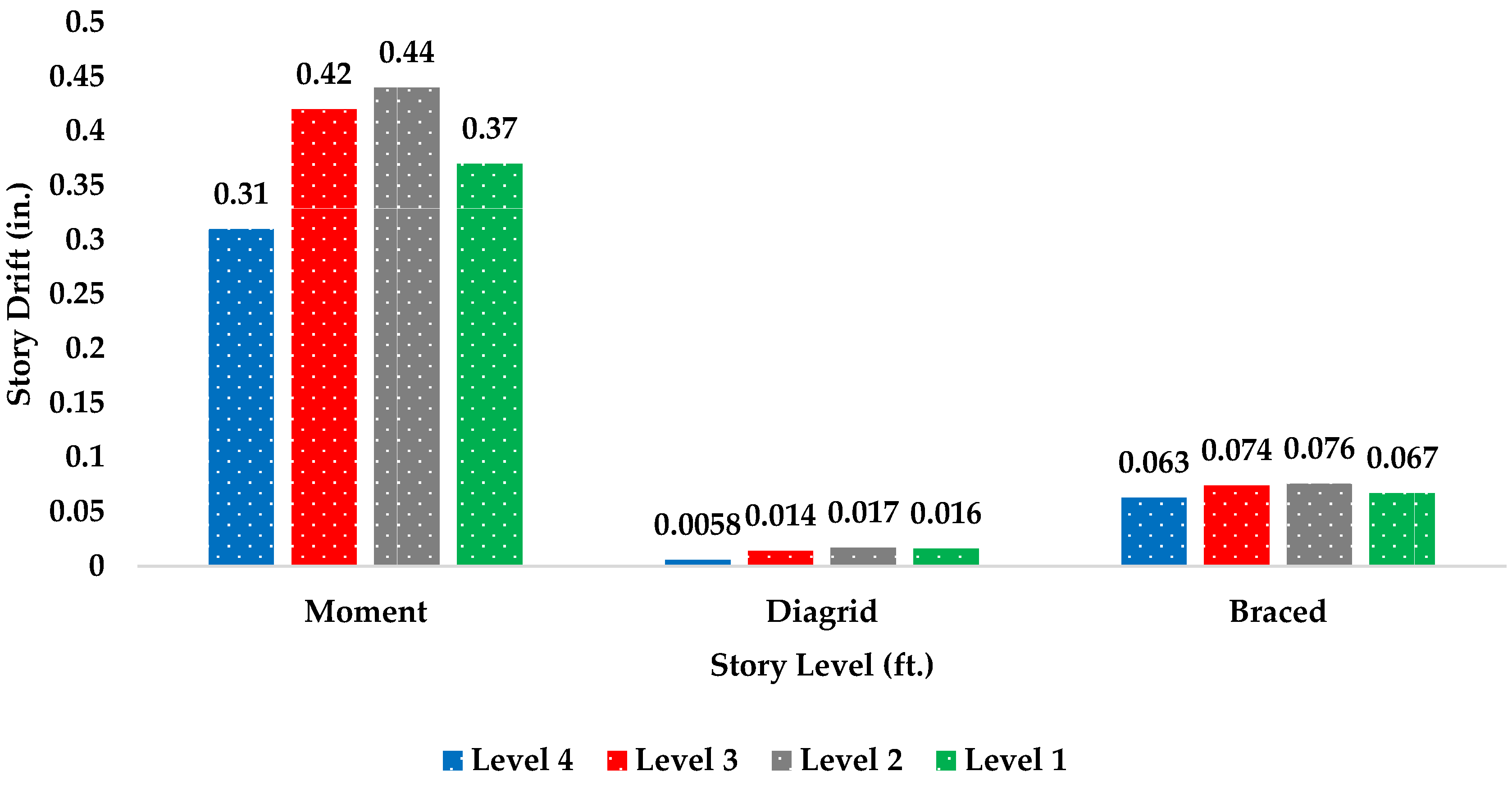
| Story Level | Inter-Story Drift (in) | Limit δ ≤ h/400 (in) | Load Case | OK? | ||
|---|---|---|---|---|---|---|
| Moment | Diagrid | Braced | ||||
| Level 4 | 0.31 | 0.0058 | 0.063 | 0.45 | Wind | ok |
| Level 3 | 0.42 | 0.014 | 0.074 | 0.45 | Wind | ok |
| Level 2 | 0.44 | 0.017 | 0.076 | 0.45 | Wind | ok |
| Level 1 | 0.37 | 0.016 | 0.067 | 0.45 | Wind | ok |
| Story Level | Building Displacement (in) | Limit ∆ ≤ H/400 (in) | Load Case | OK? | ||
|---|---|---|---|---|---|---|
| Moment | Diagrid | Braced | ||||
| Level 4 | 1.53 | 0.045 | 0.28 | 1.8 | Wind | ok |
| Level 3 | 1.22 | 0.040 | 0.22 | 1.35 | Wind | ok |
| Level 2 | 0.81 | 0.031 | 0.14 | 0.90 | Wind | ok |
| Level 1 | 0.37 | 0.016 | 0.067 | 0.45 | Wind | ok |
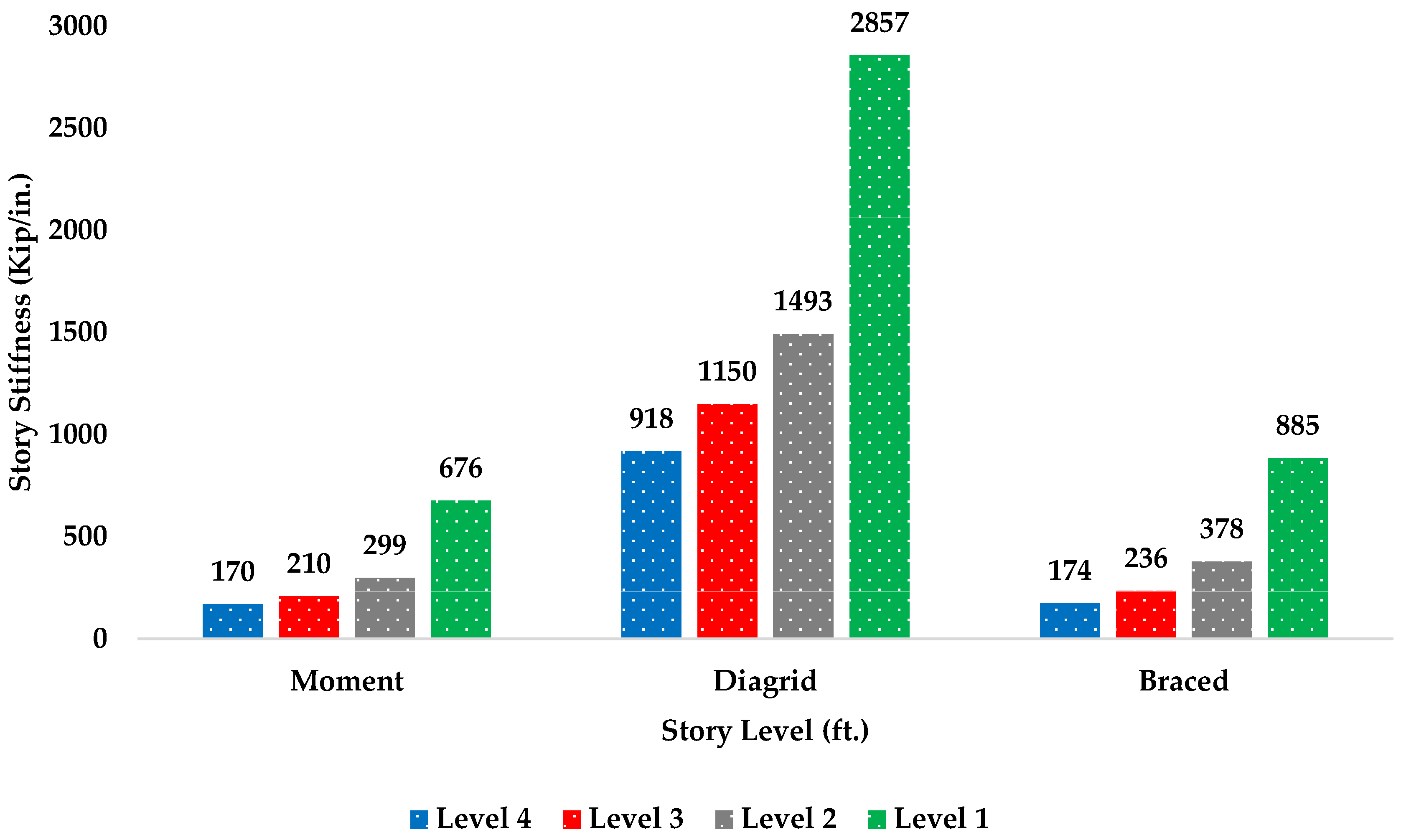
| Story Level | Story Stiffness | ||
|---|---|---|---|
| X-Direction (kip/in) | |||
| Moment | Diagrid | Braced | |
| Story 4 | 170 | 918 | 174 |
| Story 3 | 210 | 1150 | 236 |
| Story 2 | 299 | 1493 | 378 |
| Story 1 | 676 | 2857 | 885 |
| Braced Frame | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Story Level | Gravity | Lateral | ||||||||
| Beams | # | Columns | # | Beams | # | Columns | # | Braces | # | |
| Story 4 | W8X10 W16X26 W21X44 W24X62 | 33 4 4 6 | W10X33 | 8 | W12X106 | 4 | W10X33 W10X49 | 4 4 | W10X54 | 8 |
| Story 3 | W8X10 W16X26 W21X44 W24X62 | 33 4 4 6 | W10X39 W10X49 | 4 4 | W12X106 | 4 | W10X39 W10X49 W10X54 | 4 2 2 | W10X54 | 8 |
| Story 2 | W8X10 W16X26 W21X44 W24X62 | 33 4 4 6 | W12X50 W12X58 | 4 4 | W12X106 | 4 | W10X49 W10X53 W12X53 | 3 4 1 | W10X54 | 8 |
| Story 1 | W8X10 W16X28 W21X44 W24X62 | 33 4 4 6 | W12X72 W12X67 | 4 4 | W12X106 | 6 6 | W10X54 W10X60 W12X68 | 2 2 4 | W10X54 | 8 |
| Moment Frame | ||||||||
|---|---|---|---|---|---|---|---|---|
| Story Level | Gravity | Lateral | ||||||
| Beams | # | Columns | # | Beams | # | Columns | # | |
| Story 4 | W8X10 W24X62 | 33 6 | W12X50 | 4 | W18X35 W21X93 | 6 6 | W18X46 W18X86 | 6 6 |
| Story 3 | W8X10 W24X62 | 33 6 | W12X58 | 4 | W24X94 W24X104 | 6 6 | W18X65 W24X117 | 4 8 |
| Story 2 | W8X10 W24X62 | 33 6 | W12X72 | 4 | W24X117 W24X131 | 6 6 | W21X111 W24X131 | 4 8 |
| Story 1 | W8X10 W24X62 | 33 6 | W12X87 | 4 | W24X117 W24X146 | 6 6 | W24X146 W24X162 | 4 6 |
| Diagrid System | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Story Level | Gravity | Lateral | ||||||||
| Beams | # | Columns | # | Beams | # | Columns | # | Braces | # | |
| Story 4 | W8X10 W24X62 | 33 6 | W12X50 | 4 | W10X33 W12X72 | 2 2 | __ | 0 | W12X40 W12X53 | 12 12 |
| Story 3 | W8X10 W24X62 | 33 6 | W12X58 | 4 | W12X72 W14X99 | 2 2 | __ | 0 | W12X40 W12X53 | 12 12 |
| Story 2 | W8X10 W24X62 | 33 6 | W12X72 | 4 | W12X40 W12X72 | 2 2 | __ | 0 | W12X53 W12X65 | 12 12 |
| Story 1 | W8X10 W24X62 | 33 6 | W12X87 | 4 | W12X72 W12X89 W24X68 | 2 1 1 | __ | 0 | W12X65 W12X72 | 12 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Dughaishi, H.; Al Lawati, J.; Alosta, M.; Mahmood, S.; Al-Kazee, M.F.; Yusoff, N.I.M.; Milad, A. Analysis and Design of Lateral Framing Systems for Multi-Story Steel Buildings. Appl. Mech. 2023, 4, 389-406. https://doi.org/10.3390/applmech4020022
Al Dughaishi H, Al Lawati J, Alosta M, Mahmood S, Al-Kazee MF, Yusoff NIM, Milad A. Analysis and Design of Lateral Framing Systems for Multi-Story Steel Buildings. Applied Mechanics. 2023; 4(2):389-406. https://doi.org/10.3390/applmech4020022
Chicago/Turabian StyleAl Dughaishi, Husam, Jawad Al Lawati, Moad Alosta, Shaker Mahmood, Mohamed Faisal Al-Kazee, Nur Izzi Md Yusoff, and Abdalrhman Milad. 2023. "Analysis and Design of Lateral Framing Systems for Multi-Story Steel Buildings" Applied Mechanics 4, no. 2: 389-406. https://doi.org/10.3390/applmech4020022
APA StyleAl Dughaishi, H., Al Lawati, J., Alosta, M., Mahmood, S., Al-Kazee, M. F., Yusoff, N. I. M., & Milad, A. (2023). Analysis and Design of Lateral Framing Systems for Multi-Story Steel Buildings. Applied Mechanics, 4(2), 389-406. https://doi.org/10.3390/applmech4020022








