Prediction of Effective Elastic and Thermal Properties of Heterogeneous Materials Using Convolutional Neural Networks
Abstract
:1. Introduction
2. Dataset Collection
2.1. Generation of Virtual Microstructure
- -
- Fix the volume fraction by fixing the dimensions of the matrix and the inclusion.
- -
- Define the random position of the inclusion by using the random function of the Numpy library.
- -
- Define the shape of the inclusion by changing the plotting function (Circle, Ellipse, Rectangle…)
- -
- Binarize the image using the THRESH_BINARY function.
- -
- Save the drawn figure.
2.2. Finite Element Calculations
- -
- convert the binary images generated by the first code into “.ras”.
- -
- create the multi-phase mesh.
- -
- launch the calculation to obtain the “.post” file
3. Convolutional Neural Network
3.1. Loading and Pre-Processing Data
3.2. CNN Model
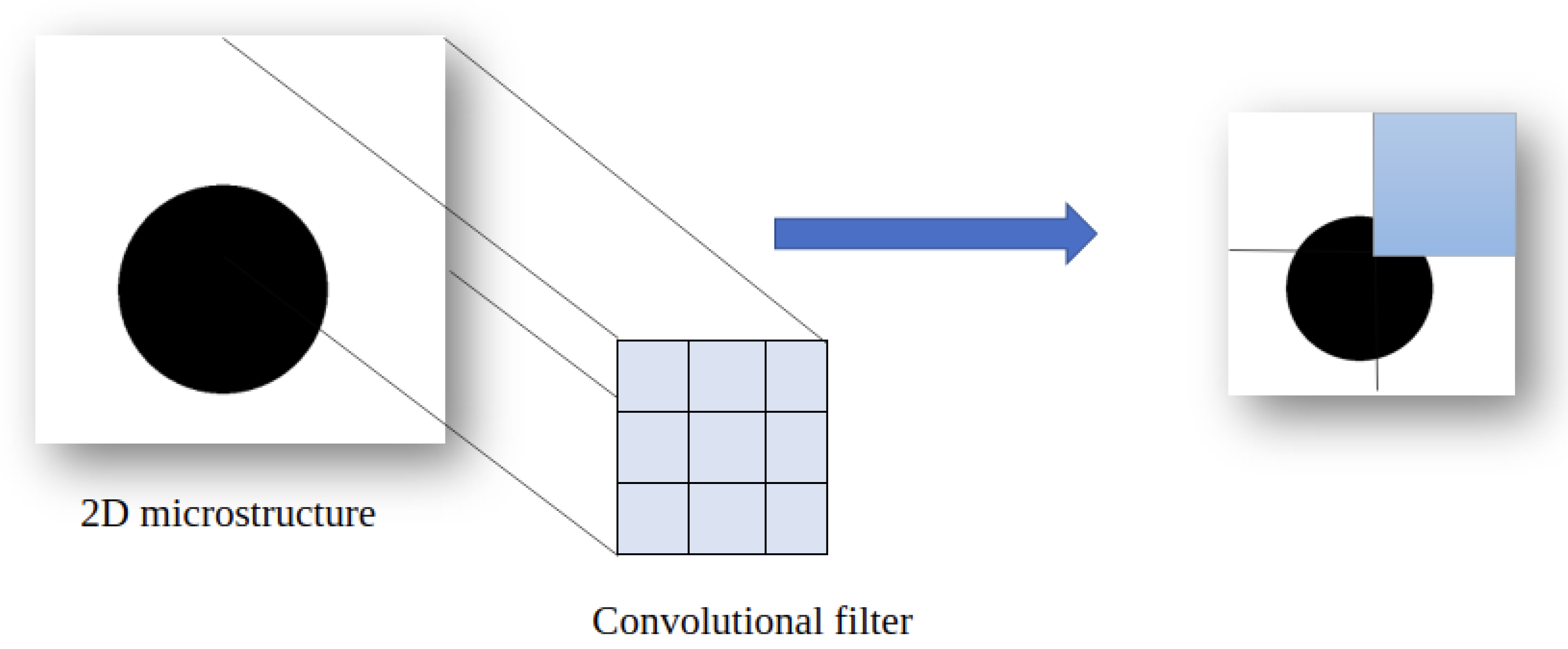
3.2.1. Convolutional Layer
- Less error in learning because the model does not learn from images but from features.
- More accuracy in detection, because the model must recognize features and patterns.
3.2.2. Maxpolling Layer
- -
- gain in accuracy by keeping only relevant data.
- -
- gain in speed: the learning of the model is done much faster because the data is getting progressively smaller.
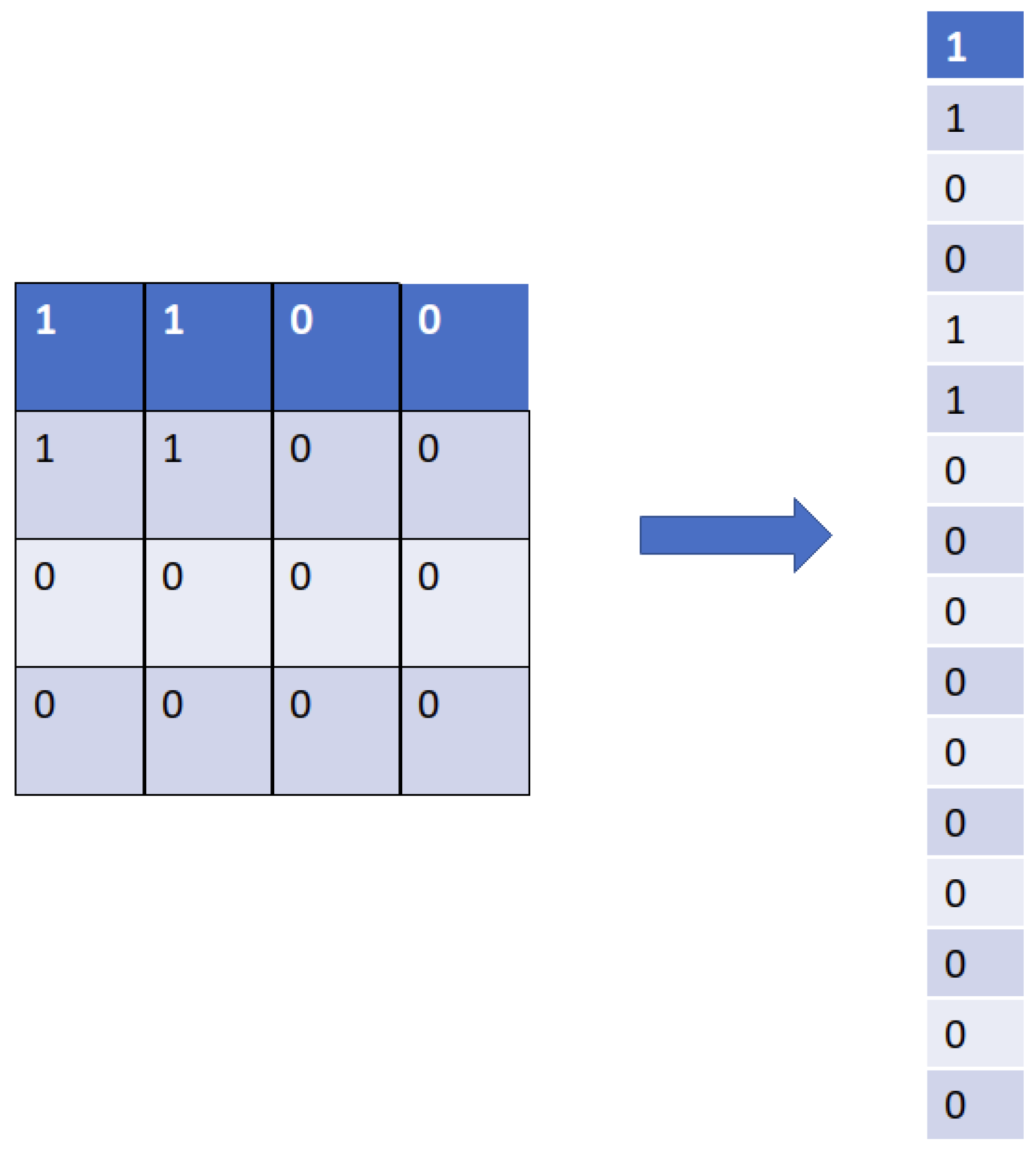
3.2.3. Flatten Layer
3.2.4. Activation Layer
- The ReLU Function
- The Linear Function
3.3. Compiling and Training
- mt: aggregate of gradients at time t [current] (initially, mt = 0)
- mt − 1: aggregate of gradients at time t − 1 [previous]
- wt: weights at time t
- wt + 1: weights at time + 1
- t: learning rate at time t
- δL: derivative of Loss Function
- δwt: derivative of weights at time t
- : Moving average parameter (const, 0.9).
- : weights at time t
- : weights at time
- : learning rate at time t
- δL: derivative of Loss Function
- δ: derivative of weights at time t
- : sum of square of past gradients. [i.e., sum (δL/δ)] (initially, v = 0)
- : Moving average parameter (const, 0.9)
- : A small positive constant ().
- n is the number of fitted points.
- is the actual value.
- is the predicted value.
- n is the number of fitted points.
- is the actual value.
- is the predicted value.
- -
- The training data (train_X), the target data (train_y).
- -
- The validation data.
- -
- Epochs: the number of times the model will run the data. The more epochs we run, the more the model will improve up to a certain point. After this point, the model will stop improving at each epoch.
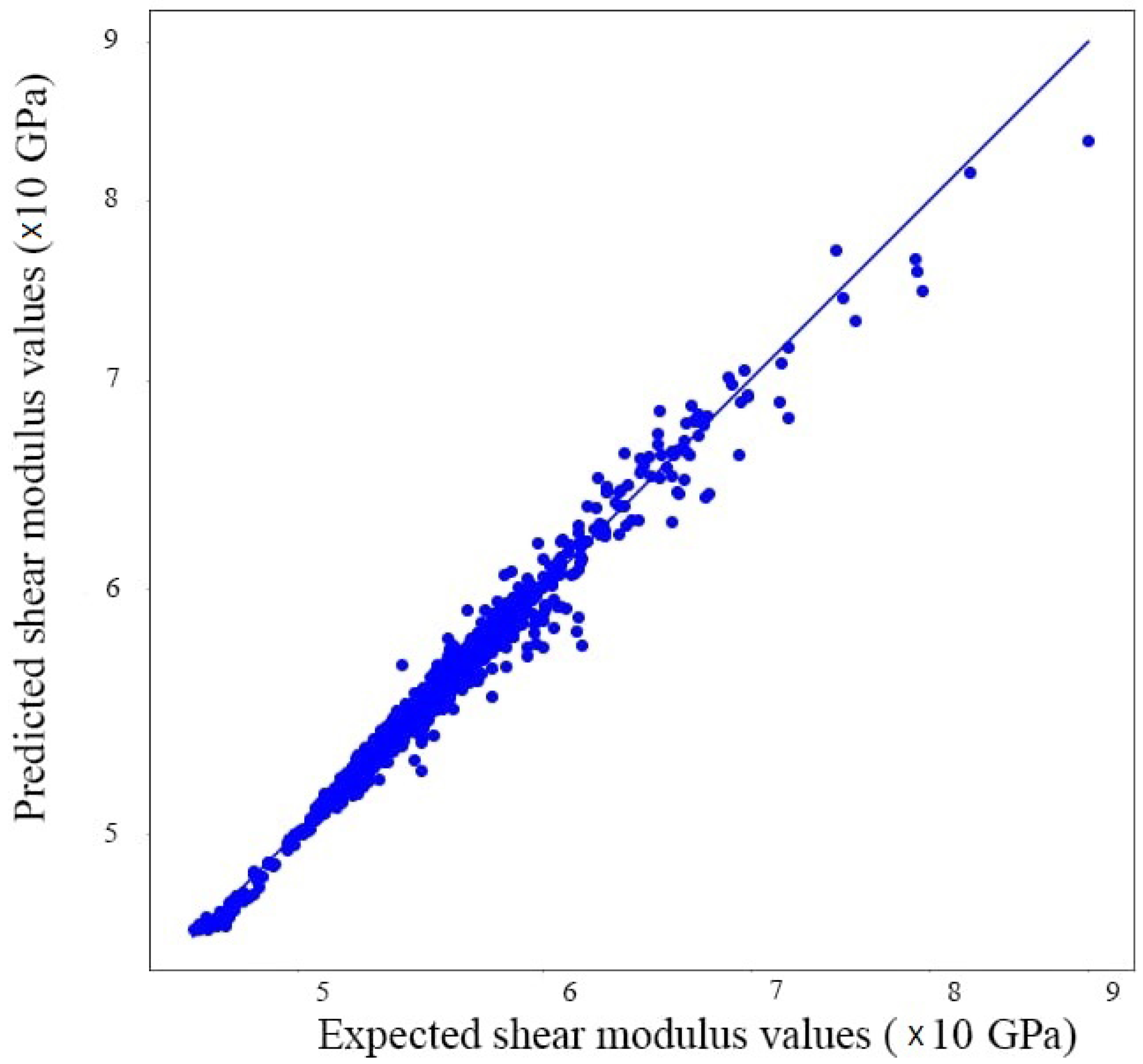
3.4. Evaluation and Prediction
- is the actual value.
- is the predicted value.
- -
- Outliers*: a data which does not ”fit in” with the rest of the data that we are analysing.
- -
- IQR*: the interquartile range, it’s the measure of statistical dispersion equal to the difference between 25% and 75% percentile.
- -
- Z-score*: a tool capable of re-scaling data, its value is between and 3 in the most cases.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moumen, A.E. Prévision du Comportement des Matériaux Hétérogènes Basée sur l’Homogénéisation Numérique: Modélisation, Visualisation et Étude Morphologique. Ph.D. Thesis, IBN Zohr University, Agadir, Marocco, 2014. [Google Scholar]
- Kováčik, J.; Simančík, F. Aluminium foam—Modulus of elasticity and electrical conductivity according to percolation theory. Scr. Mater. 1998, 39, 239–246. [Google Scholar] [CrossRef]
- Ding, Y. Analyse Morphologique de la Microstructure 3D de Réfractaires Électrofondus à Très Haute Teneur en Zircone: Relations Avec les Propriétés Mécaniques, Chimiques et le Comportement Pendant la Transformation Quadratique-Monoclinique. Ph.D. Thesis, Ecole Nationale Supérieure des Mines de Paris, Paris, France, 2012. [Google Scholar]
- Zhou, Q.; Zhang, H.W.; Zheng, Y.G. A homogenization technique for heat transfer in periodic granular materials. Adv. Powder Technol. 2012, 23, 104–114. [Google Scholar] [CrossRef]
- Chaboche, J. Le Concept de Contrainte Effective Appliqué à l’Élasticité et à la Viscoplasticité en Présence d’un Endommagement Anisotrope. In Mechanical Behavior of Aniotropic Solids; Springer: Dordrecht, The Netherlands, 1982. [Google Scholar] [CrossRef]
- Wu, T.; Temizer, I.; Wriggers, P. Computational thermal homogenization of concrete. Cem. Concr. Compos. 2013, 35, 59–70. [Google Scholar] [CrossRef]
- Kanit, T.; N’guyen, F.; Forest, S.; Jeulin, D.; Reed, M.; Singleton, S. Apparent and effective physical properties of heterogeneous materials: Representativity of samples of two materials from food industry. Comput. Methods Appl. Mech. Eng. 2006, 195, 3960–3982. [Google Scholar] [CrossRef]
- González, C.; Segurado, J.; Llorca, J. Numerical simulation of elasto-plastic deformation of composites: Evolution of stress microfields and implications for homogenization models. J. Mech. Phys. Solids 2004, 52, 1573–1593. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. Part B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Mentges, N.; Dashtbozorg, B.; Mirkhalaf, S.M. A micromechanics-based artificial neural networks model for elastic properties of short fiber composites. Compos. Part B Eng. 2021, 213, 108736. [Google Scholar] [CrossRef]
- Li, B.; Zhuang, X. Multiscale computation on feedforward neural network and recurrent neural network. Front. Struct. Civ. Eng. 2020, 14, 1285–1298. [Google Scholar] [CrossRef]
- Ford, E.; Maneparambil, K.; Rajan, S.; Neithalath, N. Machine learning-based accelerated property prediction of two-phase materials using microstructural descriptors and finite element analysis. Comput. Mater. Sci. 2021, 191, 110328. [Google Scholar] [CrossRef]
- Minfei, L.; Yidong, G.; Ze, C.; Zhi, W.; Erik, S.; Branko, Š. Microstructure-informed deep convolutional neural network for predicting short-term creep modulus of cement paste. Cem. Concr. Res. 2022, 152, 106681. [Google Scholar] [CrossRef]
- Sun, Z.; Lei, Z.; Zou, J.; Bai, R.; Jiang, H.; Yan, C. Prediction of failure behavior of composite hat-stiffened panels under in-plane shear using artificial neural network. Compos. Struct. 2021, 272, 114238. [Google Scholar] [CrossRef]
- Barbosa, A.; Upadhyaya, P.; Iype, E. Neural network for mechanical property estimation of multilayered laminate composite. Mater. Today Proc. 2020, 28, 982–985. [Google Scholar] [CrossRef]
- Kim, D.W.; Lim, J.H.; Lee, S. Prediction and validation of the transverse mechanical behavior of unidirectional composites considering interfacial debonding through convolutional neural networks. Compos. Part B Eng. 2021, 225, 109314. [Google Scholar] [CrossRef]
- Venkatesan, N. An Introduction to Making Scientific Publication Plots with Python. Available online: https://towardsdatascience.com/an-introduction-to-making-scientific-publication-plots-with-python-ea19dfa7f51e (accessed on 2 February 2023).
- Gregori, E. Introduction To Computer Vision Using OpenCV. Presented at the 2012 Embedded Systems Conference, San Jose, CA, USA, 26–29 March 2011. [Google Scholar]
- Tanner, G. Introduction to Deep Learning with Keras. 2019. Available online: https://gilberttanner.com/blog/introduction-to-deep-learning-withkeras/ (accessed on 2 February 2023).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI ‘16), Savannah, GA, USA, 2–4 November 2016. Section: GBlog. [Google Scholar]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Rogala, T.; Przystałka, P.; Katunin, A. Damage classification in composite structures based on X-ray computed tomography scans using features evaluation and deep neural networks. Procedia Struct. Integr. 2022, 37, 187–194. [Google Scholar] [CrossRef]










| Scenarios | Contrast | Volume Fraction |
|---|---|---|
| Scenario 1 | 20% | |
| Scenario 2 | 10 | 25% |
| Scenario 3 | 30% | |
| Scenario 4 | 20% | |
| Scenario 5 | 100 | 25% |
| Scenario 6 | 30% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Béji, H.; Kanit, T.; Messager, T. Prediction of Effective Elastic and Thermal Properties of Heterogeneous Materials Using Convolutional Neural Networks. Appl. Mech. 2023, 4, 287-303. https://doi.org/10.3390/applmech4010016
Béji H, Kanit T, Messager T. Prediction of Effective Elastic and Thermal Properties of Heterogeneous Materials Using Convolutional Neural Networks. Applied Mechanics. 2023; 4(1):287-303. https://doi.org/10.3390/applmech4010016
Chicago/Turabian StyleBéji, Hamdi, Toufik Kanit, and Tanguy Messager. 2023. "Prediction of Effective Elastic and Thermal Properties of Heterogeneous Materials Using Convolutional Neural Networks" Applied Mechanics 4, no. 1: 287-303. https://doi.org/10.3390/applmech4010016
APA StyleBéji, H., Kanit, T., & Messager, T. (2023). Prediction of Effective Elastic and Thermal Properties of Heterogeneous Materials Using Convolutional Neural Networks. Applied Mechanics, 4(1), 287-303. https://doi.org/10.3390/applmech4010016





