1. Introduction
The components of engineering structures, which are subject to the highest stresses and which are therefore most prone to mechanical failure (in terms of yield or cracking), often are the mechanical contacts between different parts of the structure. While the solution of a given contact mechanical problem—may it be in a closed analytical form [
1] or based on the Boundary Element Method (BEM) [
2]—is in many cases only concerned with the stresses in the contact interface, an analysis of possible mechanical failure requires the knowledge about the stress state due to the contact loading in the whole subsurface material.
For elastic bodies obeying the restrictions of the half-space approximation, the subsurface stress state can, in theory, be determined from the contact tractions via superposition of the respective fundamental solutions for point loading by Boussinesq [
3] and Cerruti [
4] or via methods of potential theory [
5]. However, for general contact problems, both procedures are mathematically and numerically quite cumbersome, and plane contact problems allow for a straight-forward determination of subsurface stresses based on the complex stress potential by Muskhelishvili [
6]. Several comprehensive analytical solutions for elastically decoupled single plane contacts have been derived with this method, most notably for the contact with a rounded flat punch, which has been analyzed in a series of publications by various authors [
7,
8,
9] due to its importance in the context of fretting fatigue [
10] (“fretting” is the damaging of contact interfaces by small-amplitude oscillations).
In fretting, there are often two competing damage phenomena, depending on the fretting regime [
11], fatigue, and wear: in the partial slip regime, the nucleation and propagation of fatigue cracks in the vicinity of the contact is the dominating damage mechanism, while, in the sliding regime, the dominant phenomenon seems to be wear [
11]. This leads to the dilemma that inhibiting one of the two phenomena often facilitates the other one. For example, it is long-known that fretting wear can be hindered by introducing sharp edges in the contact profiles to suppress local slipping of the contacting surfaces. However, if the sharp edge constitutes the contact boundary, the resulting oscillating stress singularity will result in fatigue. A possible solution strategy for this dilemma on the level of the profile geometry was recently suggested by the author [
12]: If the sharp edge is “soft” enough, so that contact is still established behind the edge—e.g., by truncating an originally smooth profile, like a cylinder—it can be possible to avoid (positive) tensile stresses in the vicinity of the weak stress singularity at the sharp edge, and thus avoid the formation of fatigue cracks.
On the other hand, although the truncated cylinder and truncated wedge are standard profile geometries in plane contact mechanics, exact closed-form solutions for the corresponding subsurface stress fields are still missing in the literature. Hence, these shall be provided in the present manuscript, and applied to a very simple fretting contact problem. Moreover, a numerically extremely fast and very robust semi-analytical method is proposed for the determination of the subsurface stress fields in plane contacts with more complex profile geometries, which defy an exact, closed-form solution, and compared with the analytical solution for the truncated geometries of interest.
The remaining parts of the manuscript are structured as follows: first, the research problem of interest will be stated rigorously. After that, the complex Muskhelishvili potential (which provides the subsurface stresses via elementary linear filtering of its real and imaginary parts) will be calculated in closed form for normal loading—based on the appropriate superposition of flat punch solutions, as first suggested by Jäger [
13]—and for tangential loading—based on the reduction of the tangential contact problem to the respective normal contact via the principle of Jäger [
14] and Ciavarella [
15]. In the last section of the methodological part of the manuscript, an alternative procedure for the determination of the subsurface stress field via the direct superposition of stress fields for the flat punch and parabolic contact, thus avoiding the statement of any complex potentials, is laid out and proven numerically to give exactly the same results as the potential solution. After that, as a numerical example, periodic tangential loading of a truncated cylinder is considered in detail and some conclusive remarks finish the manuscript.
2. Problem Formulation
Let us examine the single contact of two infinite-length truncated bodies made of linearly elastic, isotropic, and homogeneous materials, with Young’s moduli
,
and Poisson’s ratios
,
, under plane strain conditions. The normal axis to the contact plane shall be
y, the tangential axis
x, and the lateral axis
z, i.e., for the strains
,
. As always, the plane stress solution can be retrieved from the plane strain solution via the substitutions
where the hat denotes the respective material constants for the plane stress problem.
The contacting bodies shall obey the restrictions of the half-plane approximation, i.e., their surface gradients in the vicinity of the contact and the characteristic contact width compared to the macroscopic dimensions of the bodies are supposed to be small. The bodies’ materials are assumed to be elastically similar, so that the normal and tangential contact problems are elastically decoupled, i.e., Dundur’s second constant [
16],
with the effective Young’s modulus
shall be zero. In the contact, there shall be friction according to a local Amontons–Coulomb law with a constant coefficient of friction
. Effects of adhesion or surface tension are neglected. The contact is subject to a normal line load
P and an in-plane tangential line load
Q. The form of the gap between the two contacting surfaces
,
in the moment of first contact constitutes the profile function
f,
Within the framework of these assumptions, the contact is equivalent to the one between a rigid indentor with the profile
and an elastic half-plane with the effective Young’s modulus
. As profile functions, let us consider the truncated shallow wedge,
with the small inclination angle
, the half-width of the flat end face
b, and Heaviside’s step function
, as well as the truncated cylinder,
with the radius
R of the cylinder. Note that the profile function for the truncated cylinder can be written as a superposition of the function for a flat punch with rounded corners,
where
R denotes the radius of curvature for the rounded corners, with an appropriate truncated wedge profile,
A sketch of the considered contact problems is shown in
Figure 1.
We aim to determine explicit analytic expressions for the subsurface stress field under normal and tangential loading.
6. Periodic Tangential Loading of a Truncated Cylinder
As is known, for tangential contacts, the solution to the contact problem—and therefore naturally also the subsurface stress state—generally depends on the history of the loading procedure. This is in contrast to, for example, the frictionless normal contact problem, whose solution only depends on the instantaneous contact configuration—in plane, symmetric problems expressed by either the line load
P, or the contact half-width
a. The tangential contact solutions presented above are, as has been stated before, only valid for the simplest loading history of a constant normal load and a subsequently applied, monotonously increasing tangential load. The shown solutions can, however, serve as a basis for the analysis of more complex loading histories, as it has been shown, how the solution for general loading histories can often be constructed by appropriately superposing these basic solutions for the simplest loading history [
5,
13].
To illustrate this idea, in the following, the problem of periodic tangential loading with a constant amplitude, which is relevant in fretting contacts, is considered for the truncated cylinder. The time-dependence of the tangential loading is shown schematically in
Figure 4. Note that the precise temporal function (sinusoidal, “saw-tooth”, etc.) is not relevant (as long, as it is periodic) because the contact configuration during unloading or reloading only depends on the instantaneous value of
Q and its maximum value, i.e., the amplitude. The normal load is supposed to be constant.
For the determination of the subsurface stress state, we only require the general structure of the tangential contact solution for the considered type of loading. To obtain that, we will use yet another superposition idea, which was first used by Jäger [
21] for the tangential contact of elastic spheres under arbitrary 2D oblique loading. Up to point A in the loading diagram, the tangential load is increasing monotonously and the tangential contact solution is therefore given by the classical Ciavarella–Jäger result in Equations (
22) and (
23),
where the star denotes that this is the basic solution for the elementary loading history. Accordingly, the contributions of the tangential load to the subsurface stress state are given by Equation (
27) or (
35).
Then, the sign of the change in
Q is reversed. At the “reversal point” A, there is a spontaneous state of complete sticking of the contact area, since every point of the sliding area is—according to the law of friction—in the “limit state” of sticking,
. After that, a new slip area propagates from the edge of the contact. Since in the slip area the direction of the frictional stresses has been reversed, but their value is still determined by the law of friction, a simple Ciavarella–Jäger solution can be linearly superposed. The distribution of the frictional stresses on the “path” from A to E is therefore due to the Ciavarella–Jäger principle given by
where the minimum half-width of the stick area,
, follows from the maximum tangential load,
and the current value of the half-width of the stick area,
c, can be determined from the superposition relation for the tangential load,
Due to the linearity of all governing equations, the same superposition can be applied for the determination of the tangential loading contributions to the subsurface stress state, based on the basic solutions given in Equation (
27) or (
35).
During reloading, i.e., after point E in the loading diagram, the same happens with the tangential loading directions reversed. Hence, the superpositions in Equations (
37) and (
39) can be used, with all signs reversed on the right-hand side of the equations.
If all stresses are normalized for the average contact pressure , the resulting non-dimensional stresses will only depend on the non-dimensional half-width of the flat face , the friction coefficient , the loading ratio , and the Poisson ratio .
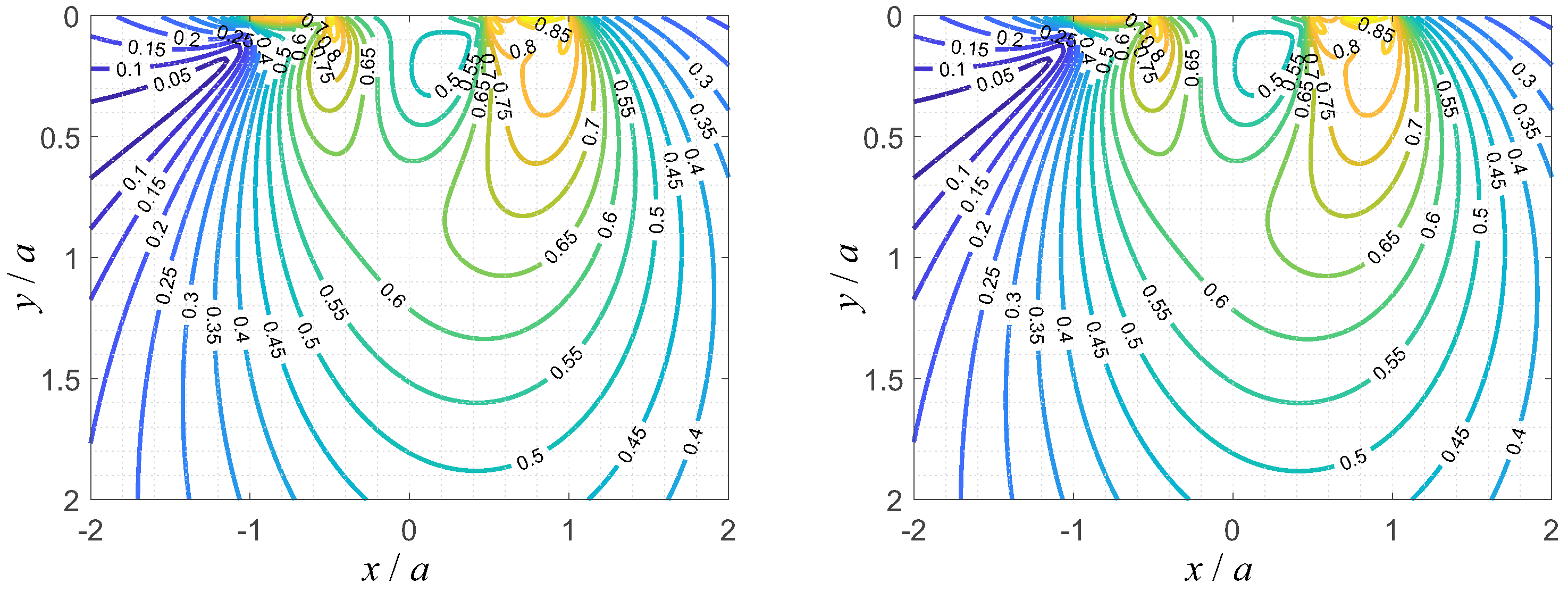
Figure 5 shows the distribution of the equivalent von-Mises stress in the loading plane in normalized variables, for
,
,
and
, at the points A, B, C, and D of the loading diagram; the respective plot in the point E will be just the plot for the point A with the direction of the
x-axis reversed, and is therefore not shown.
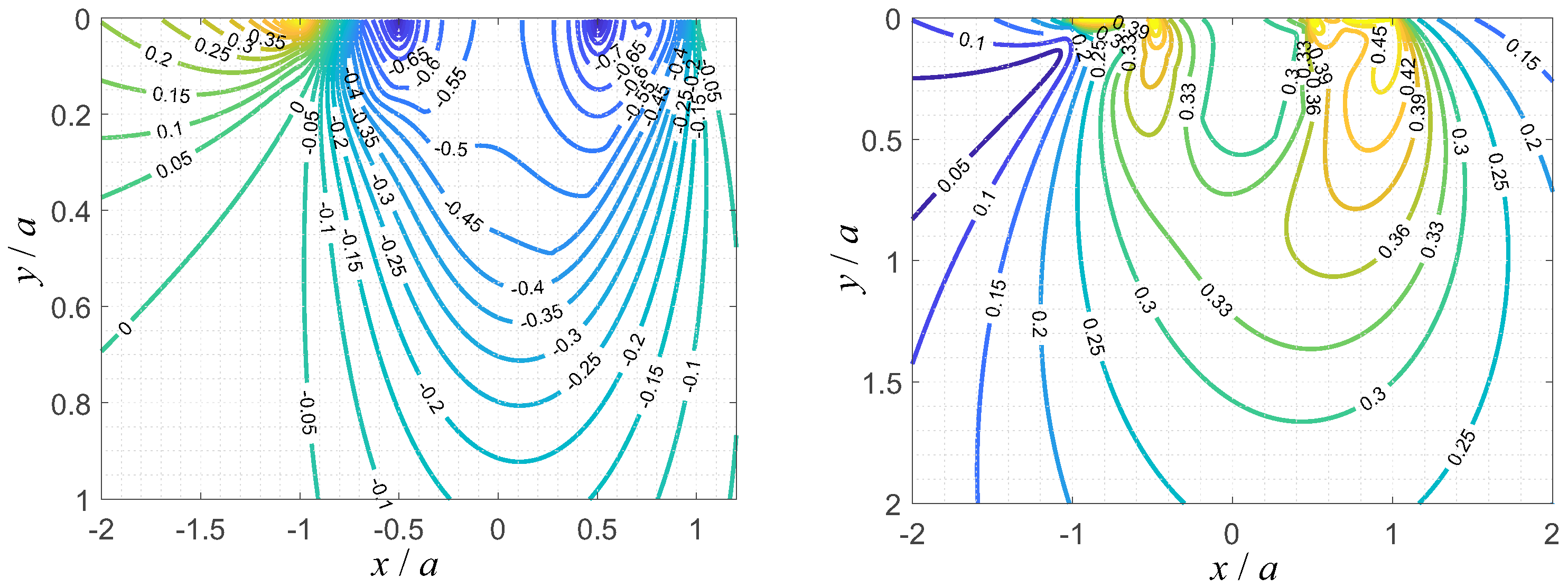
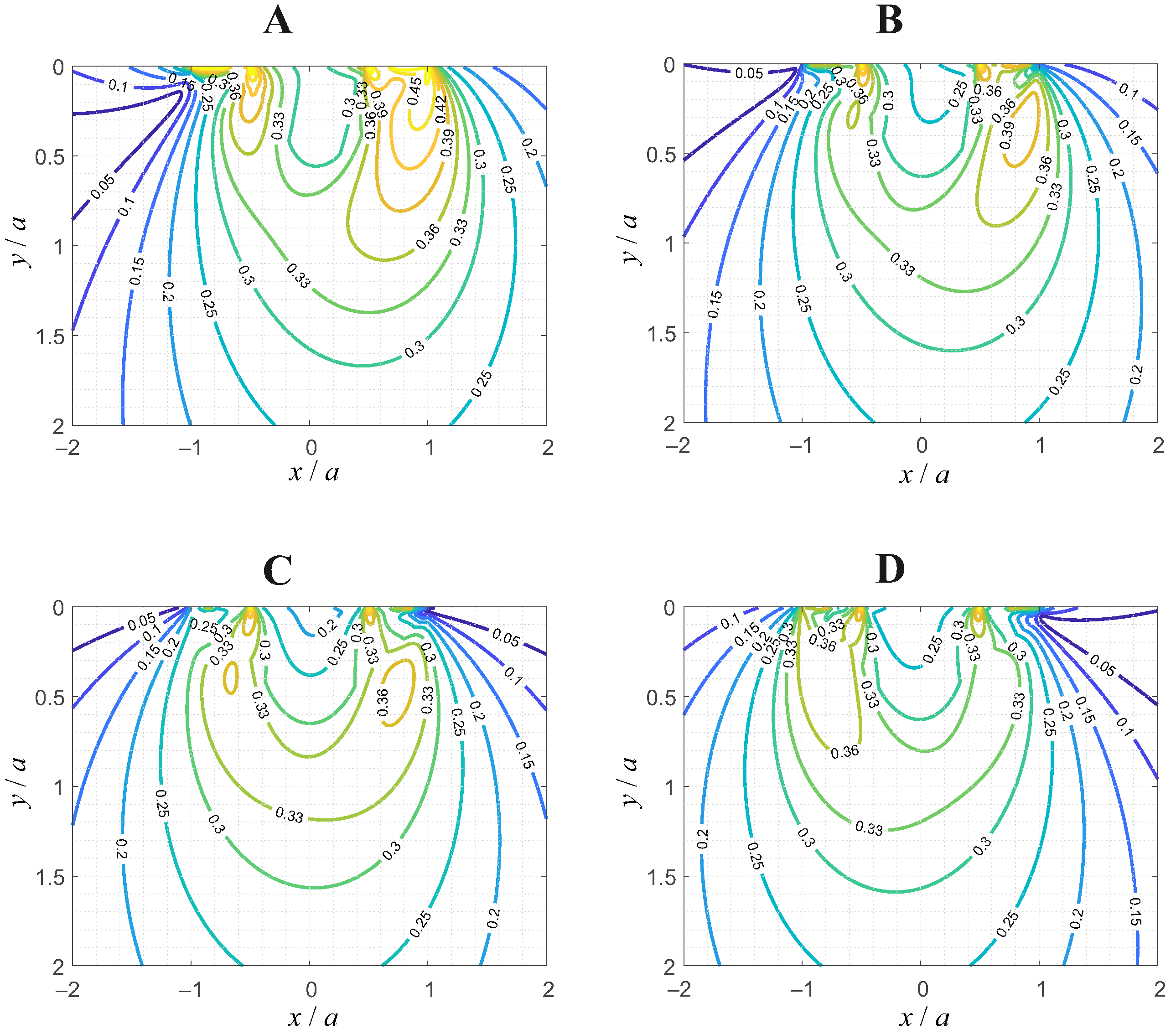
In
Figure 6 and
Figure 7, the corresponding subsurface distributions of the maximum shear stress and largest principal stress in the loading plane are shown in normalized variables, at the points A, B, C, and D of the loading diagram. The maximum shear stress distributions correlate well with the ones for the von-Mises equivalent stress given in
Figure 5; as expected, positive (i.e., tensile) principal stresses only exist in the vicinity of the contact edge, away from the pressure singularity at the edge of the profile, and away from the maxima of the von-Mises equivalent stress, or the maximum shear stress. Therefore, the fretting contact should not be prone to fatigue crack initiation.
7. Discussion
Analytic solutions for the subsurface stress fields in tangential contacts of elastically similar truncated wedges and cylinders have been provided. Two solution methods have been utilized: the determination of Muskhelishvili’s complex stress potential and the direct superposition of stress fields under a rigid flat punch or in the plane Hertzian contact. Both methods have been proven numerically to give exactly the same results (they are, in fact, mathematically equivalent for the contact problems studied in the present manuscript). The determination of the subsurface stress state via an appropriate superposition of the respective known exact solutions for parabolic contact is an extremely fast, easily implemented, and very robust method, which can also be used for more complicated profile geometries, for example arising from the effects of wear.
While Muskhelishvili’s potential corresponds to a specific integral equation, and therefore to a specific class of problems (namely, plane contacts of homogeneous materials), the superposition of incremental flat punch contacts (or parabolic contacts, if one wishes to avoid the edge singularity of the flat punch problem) is a more general idea, whose applicability has been discussed before [
20].
As for most analytical contact solutions, the underlying assumptions may pose more or less severe restrictions that have to be kept in mind when applying the obtained results to real engineering contacts. In the present case, the severest limitations stem from the assumptions of linear elasticity and of a local Amontons–Coulomb friction law with a constant coefficient of friction. In real engineering contacts, the contacting materials, depending on their “class”, will exhibit different degrees of, e.g., viscoelasticity, hyperelasticity, or plasticity. In addition, the Amontons law is, of course, a rather blunt simplification of frictional interaction. Both of these shortcomings of the present study could be tackled in future work without severe methodological alterations, if the problem retains constitutive linearity, e.g., incorporating linear viscoelasticity [
22] or slip-weakening laws [
23].
On the other hand, the advantage of analytic solutions lies in their exactness; they are not bound to discretization or other numerical approximations, and can thus serve as benchmark solutions for numerical solvers—e.g., based on the Finite-Elements (FE) or Boundary Elements Methods—which, in turn, are far more flexible with respect to the physical modelling.
In that regard, one should also note that recently very powerful numerical methods have been developed for the determination of subsurface stress fields in complex two- and three-dimensional problems, namely the differential quadrature finite element method—which proved to require significantly less degrees of freedom than a “regular” FE-based model in the simulation of free vibrations of laminated beams and plates [
24]—and the 2D Bézier method, which is able to solve two-dimensional problems for arbitrary complexity of geometry [
25].
In addition, note that, for elastically dissimilar bodies, there is elastic coupling between the normal and tangential contact problems, i.e., the presence of tangential tractions alters the normal contact problem, and vice versa. This severely complicates the rigorous problem treatment; in fact, closed-form analytical contact solutions for dissimilar materials are only possible for few special cases. Correspondingly, the manuscript’s analysis is only valid for similar materials.
The concept of introducing “soft” sharp edges to avoid wear and fatigue is similar to the already widely used idea of using rounded flat punches in fretting: the flat face shall reduce local slipping and thus wear, and the rounded corners aspire to soften the stress singularity at the edge of the punch. However, a detailed contact mechanical comparison of both types of profile geometries in fretting configurations still remains for future work.
Finally, in the future, the fretting behaviour of truncated contact profiles shall be investigated experimentally, with respect to energy dissipation, wear, and fatigue.