Abstract
When a finger actively slides over a surface, contact conditions including the contact area, sliding speed, and finger moisture naturally fluctuate. These random fluctuations lead to an apparent change of frictional properties and influence tactile pleasantness. Nonetheless, this probabilistic behavior has not been explicitly analyzed in previous studies on human fingertips. This study investigates the dependence of the coefficients of kinetic friction on the normal force produced by sliding a bare finger over different artificial skins with seven levels of hardness. The coefficient of friction was modeled as a power function of the normal force. An experimental study that involved sliding a finger over artificial skin surfaces was carried out under two conditions: the fingertip being wiped by a dry cloth or a cloth soaked in ethanol. Although the exponential term was assumed to be nearly constant for identical tribological conditions, we observed that the exponent varied randomly and could be negative, zero, or positive. This can be attributed to the variation of gross finger deformation that was not controlled during the observation. The probability density function of the exponent depended on the moisture content of the finger and object hardness. The variability of the exponent was higher for a soft material than it was for a harder material. In other words, for the softer materials, the exponent appears more random. Furthermore, the exponent tended to be positive and the coefficient of friction increased with the normal force when the finger was wiped with ethanol. These findings play an important role in understanding the frictional forces produced during skin–skin contact in terms of determining the root cause of random variations in the dependence of the coefficient of friction on the normal force.
1. Introduction
Humans use their fingers to touch their skin in day-to-day activities. To develop skincare products, artificial skins, or human-friendly surfaces, it is important to study the friction generated while rubbing the skin with fingers because friction is a major determinant of pleasantness in touch [1,2,3]. During active tactile exploration in our daily lives, contact conditions naturally fluctuate. Understanding the effects of this random fluctuation on frictional properties would be helpful to control the pleasantness of touch. This study focuses on the relationship between the coefficient of friction (COF) and the normal force produced when a human finger slides on artificial skin surfaces.
The frictional force acting on elastic bodies such as the skin deviates from the Amontons–Coulomb friction laws because the coefficient of kinetic friction depends on the normal force and sliding speed [4,5,6]. The frictional force on the skin surface is considered a combination of two mechanisms, namely adhesion and deformation frictions [7,8,9]. In adhesion friction, the adhesive force acting on the real contact area between two elastic bodies is overcome by the interfacial shear strength [7]. If a sphere, imitating a finger pad, applies a load on an elastic plane and the apparent contact area A, derived from the Hertzian contact theory, and real contact area are identical, the coefficient of adhesion friction is proportional to the function of the negative exponent of the normal force, as shown below.
In contrast, deformation friction is produced due to the restoring force of the deformed material. The deformation friction force is proportional to the exponent of the normal force [7,10], as shown below.
Thus, the coefficient of deformation friction, , is proportional to the positive exponent of the normal force.
Hence, the coefficient of friction, , is generally expressed as an exponential function of the normal force, as shown below.
According to Equations (1) and (3), is negative if the adhesion friction is dominant and positive if the deformation friction is dominant, respectively, as in Figure 1. Various studies investigating the frictional forces acting on human skin focus on their dependence on the normal force, i.e., the exponent in (4) [4,11,12,13,14,15,16,17]. Because adhesion friction is a dominant force acting on dry human skin [7,18,19,20], the real contact area responsible for the adhesion friction and its dependence on the normal force are two important factors as well [21]. The values reported in these studies do not necessarily follow the range shown in Figure 1 partly because the Hertzian contact theory is not accurately applicable to human finger contact.

Figure 1.
Relationship between the exponent and the frictional mechanisms.
Several studies have analyzed the COF between the skin and a rigid probe and the COF between a finger and a rigid plane. Most studies have reported that the COF decreased with increasing normal force. The exponent of the normal force, , in (4) was approximately equal to [4,13,16,18]. Mahdi et al. investigated the friction between a skin model and a rigid probe and observed that the ratio of the adhesion friction to deformation friction was approximately 8:2 [20]. Adhesion friction was dominant under dry conditions, i.e., for the friction between the skin and rigid bodies was negative under dry conditions.
Several studies have calculated the frictional force for different surface roughness values, lubrication conditions of the contact surfaces, and contact states. Derler et al. measured the friction between the human skin and glass plates for different surface roughness values and lubrication conditions. They observed that ranged from approximately to when adhesion friction was dominant, and from to when deformation friction was prominent [11]. Ules et al. studied the variation of the frictional force when a finger slid over a glass surface with varying roughness values. The value of was approximately 0 for a rough surface and approximately for a smooth surface [17]. Han et al. measured the maximum coefficient of static friction between an acrylic plate and a finger while varying the angle of contact of the finger. They observed that ranged from to and was dependent on the finger angle and the participants [14]. These values were less than the value of calculated from the Hertzian contact theory, which was equal to . According to these studies, the dependence of the COF on the normal force differs for different surfaces and conditions, such as roughness and lubrication. Nevertheless, in part, because of the random variation of the gross finger deformation, actually varies under the identical surface conditions and its probabilistic variation has not been thoroughly discussed.
Although previous studies have analyzed the friction between the skin and rigid bodies, very few studies have focused on the frictional force when a finger or finger-like probes slide over the skin [22,23,24]. For example, Nonomura et al. investigated the frictional phenomena between the skin and soft materials under non-stationary sliding conditions [22,24]. Experiments were performed in the present study on artificial skin samples that replicated the hardness and texture of the human skin and studied the dependence of the COF on the normal force. We studied the dependence of the COF on the normal force by applying (4), which has been used in previous studies to calculate the friction between the skin and rigid bodies. We observed in our previous study [25] that randomly assumed positive and negative values while calculating the friction between a finger and artificial skin, even across identical tribological conditions. For example, can attain a positive value during a single active sliding motion of the finger over artificial skin; however, if a similar motion is replicated, the value of could be positive, zero, or negative. This variation was completely random. The random variation of while calculating human skin friction has not been discussed in previous studies. The objective of this study is to investigate the apparent randomness of in the coefficient of kinetic friction that changes for each active finger slide.
This study builds upon our previous one [25], where random fluctuation of was observed by investigating the dependence of the randomness of on the hardness of the artificial skin. The friction acting on the surface of the skin changes with varying moisture contents at the contact interface [7,11,12,26,27]. The random values of can be attributed to the transient nature of skin sweat. Hence, we experimented on two differently treated skin surfaces and compared the results obtained under both conditions. In the first case, the fingertip was wiped with a dry cloth before each trial. The second case involved wiping the fingertip with a cloth soaked in ethanol and drying it before each trial to moderately control the moisture content on the finger surface. Notably, some of the data presented in this study were acquired in our previous study [28].
2. Methods
2.1. Measurement of the Two-Axial Forces and Sliding Speed
The normal and shear forces generated by rubbing artificial skin with a finger were measured in self-assembled axial force sensing units (Figure 2) [29]. The normal force was measured by using two uniaxial force sensors (9313AA2, Kistler, Winterthur, Switzerland) installed in the lower part of the device, and the shear force was measured using a uniaxial high-sensitivity force sensor (9217A, Kistler, Switzerland) centrally attached to two metal pieces of the device. The signals from both normal and shear force sensors were amplified by two charge amplifiers (5073A2 and 5015, Kistler, Switzerland; nominal drifts were 0.005 N/s and 0.0003 N/s, respectively). Finger movement was measured using two wired encoders (MTL-12, MTL. Co., Yokohama, Japan) by winding a wire, attached to the encoders, around the finger. The resolution of this device was nominally 0.01 mm. The sampling frequency was set to 2 kHz.
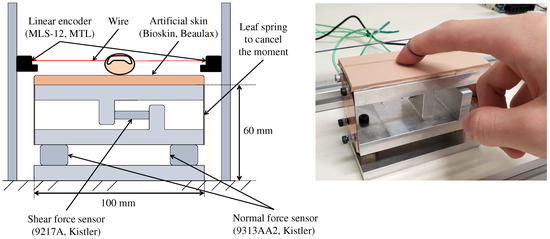
Figure 2.
Measurement setup. The normal force was measured using two uniaxial force sensors installed in the lower part of the device, and the shear force was measured using a uniaxial force sensor fixed in the upper part of the device. The finger movement was measured through two wire encoders by winding a wire attached to the encoders around a finger.
2.2. Artificial Skins Used in the Experiment
Commercially available artificial skins (Bioskin, Beaulax Ltd., Saitama, Japan), with seven levels of hardness, were used in the experiment. The softest level of hardness was represented by 1, whereas the hardest was represented by 7. Their thicknesses were 5 mm, and their surfaces were covered with a thin film of thermoplastic polyurethane. The surface asperity of this film is similar to that of human skin. The average roughness value, , of the artificial skin was m [30]. Table 1 summarizes the shore AO hardness and Young’s moduli of artificial skins and finger pads. For the measurements, we used a durometer (GS-721N, Teclock, Japan) following the ISO 7619–1 guideline and an indentation tester (Yawasa, Tech Gihan Co. Ltd., Kyoto, Japan). The finger pad values account for the average and standard error among all the participants (11 participants). As listed in Table 1, we tested artificial skins softer than, close to, and harder than the finger pads.

Table 1.
Young’s moduli (E) and Shore AO hardness of artificial skin models and human fingers. For the finger, the mean and standard error are shown.
2.3. Task
The participants rubbed the surface of the artificial skin attached to the top of the measurement instrument using the index finger of their right hand. They were asked to rub the surface in a manner identical to that of an individual examining the quality of the material of the surface. The participants were instructed to lay down their fingers and rub the surface of the artificial skin with their finger pad while maintaining the same posture as much as possible (see discussion about the potential effects of contact angle). There were no instructions regarding the finger speed and force to be applied. The experiments were conducted under two conditions: (1) where participants wiped the finger and artificial skin using a dry cloth after each trial and (2) where participants wiped the finger using a cloth soaked in ethanol and then dried to lower the moisture content. The results for case 1 were sourced from our previous study [28]. The measurement periods for cases 1 and 2 were 10 s and 5 s, respectively. The measurement time for case 2 was less than that of case 1, to minimize the effect of sweat on the fingertips during measurement. Three trials were performed for case 1 and 10 trials were performed for case 2 using each skin model. This increased the amount of data collected for case 2, thereby improving the experimental accuracy. The experiments for the two cases were conducted on the same day for each participant in an air-conditioned room at 20 °C. We did not control and record the humidity. The participants rubbed the artificial skin surface on multiple occasions during the measurement process. Seven types of skin models were tested randomly.
2.4. Participants
Eleven university students participated in the experiment. All of them participated in case 1. However, one of them did not participate in case 2. The participants were all males and in their early 20s. The participants provided written informed consent and were unaware of the objectives of the study before the experiment was performed.
2.5. Analysis
Before data analysis, we removed the linear drift component that was defined by the zero force levels before and after a slide. The measured normal and shear forces were subjected to zero-phase filtering using a low-pass FIR filter with a passband frequency of 20 Hz. Only the data extracted from the trials that involved clear sliding of the finger on the artificial skins were used to analyze the kinetic friction. This ensured that the instantaneous normal force and shear force were at least 0.05 N, and the sliding velocity v was at least 20 mm/s. Evident stick-slip phenomena that could be visually detected by checking the shear force profiles were not observed in our setup. The value of the COF was calculated as a ratio of to for each moment. We plotted the instant values of and for each finger slide as in Figure 3 and approximated their relationship according to Equation (4) using the Curve Fitting Toolbox of MATLAB 2019a (Mathworks Inc., Natic, MA, USA). Only the valid slides, i.e., slides in which N, N, and mm/s during a single sliding motion, were used for the subsequent analysis. We analyzed 1130 and 725 slides for cases 1 and 2, respectively. The minimum and maximum values in each valid slide were N and N (mean and standard deviation), respectively. This range covers that reported for rubbing fine abrasive papers [31]. The number of slides obtained within the stipulated time for each case varied from individual to individual. In general, the sliding velocity affects the COF [26,32], but its effect is small for the artificial skins used in this study. For example, for the softest and the hardest artificial skins (hardness levels 1 and 7) in case 1, the COF only changed by 0.04 and 0.01, respectively, when the sliding velocity changed by 10 mm/s [28], and we did not consider its effects.
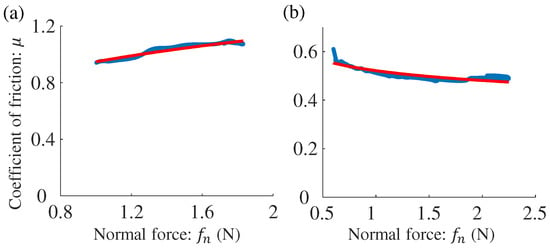
Figure 3.
Data plots and fitting results of the relationship between and . Red curves represent the fitting curves, and the blue dots correspond to the observed coefficients of friction. (a) is positive (). (b) is negative ().
The exponent was classified into three categories, namely, significantly positive, significantly negative, and not significantly different from zero. The proportions of these categories in the results were then calculated. The values were classified according to a significance level of 5% and the effect size, i.e., Cohen’s d [33]. The values that did not meet the conditions for either the significance level or effect size were assumed to be equal to 0. The two criteria for the effect size were set as and to ensure that the results were not dependent on the criterion of the chosen effect size. In addition, a chi-square test was conducted to compare the proportions of the values between the two cases for each of the seven artificial skins. If the chi-square test indicated a significant difference, a residual analysis was performed to analyze the category which differed significantly between the two cases. The significance level was set to 5%, and the Bonferroni correction was applied in these tests.
The average values of curve fitting for an effect size of are listed below. For the slides with in case 1, the maximum average value was for a hardness level of 1. The minimum value of in case 1 was for a hardness level of 4. In the case of slides with in case 1, the maximum average value of was for a hardness level of 3 whereas the minimum value was for a hardness level of 5. The slides with in case 2 reported a maximum value of for a hardness level of 6 and a minimum value of for a hardness level of 3. The slides with in case 2 reported maximum and minimum values of for a hardness level of 2 and for a hardness level of 7, respectively. The value is the square value of correlation coefficient for which empirically 0.7–0.9 are considered a strong correlation (e.g., [34]). We consider that values greater than 0.49 are acceptable.
The probability density function of was calculated via kernel density estimation because the sample distribution of did not appear to be popular among the distribution functions. The kernel function was a normal distribution, and the bandwidth was defined by Silverman’s method. For this purpose, we used all the participants’ trials to compute the density function for each hardness level because each density function needs to be drawn based on a satisfactory number of samples.
3. Results
3.1. Probability Density Functions of
The probability density functions of for each hardness value in cases 1 and 2 are shown in Figure 4 and Figure 5, respectively. The horizontal axis indicates the value of , and the vertical axis indicates the estimated probability density of . The solid lines represent the probability density functions calculated from the slides by artificial skin hardness. The red, blue, and black dotted lines represent the probability density functions of the positive, negative, and insignificant categories, respectively. The effect size was used to categorize the values. It is evident from Figure 4 and Figure 5 that despite sliding a finger over the artificial skin under identical friction conditions, regardless of the material hardness and conditions, the value of was not constant and varied probabilistically.
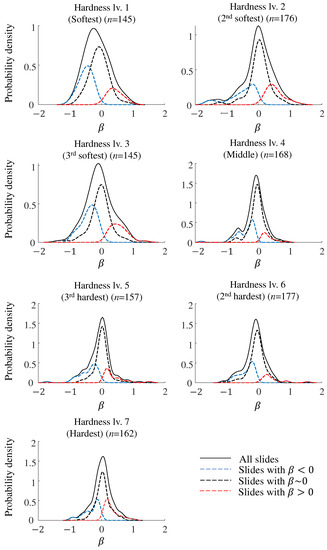
Figure 4.
Probability density functions of under case 1, in which the finger pad was wiped by a dry cloth. Solid lines include all the slides, and red, blue, and black dotted lines are the distributions of positive, negative, and insignificant (), respectively. for categorizing the sign of .
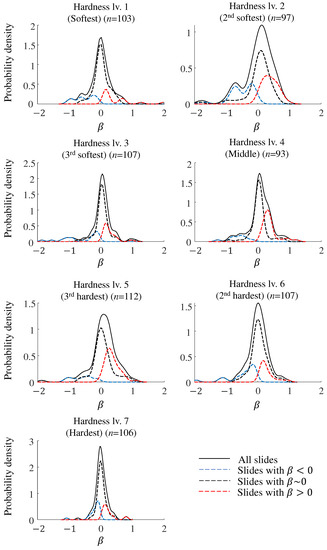
Figure 5.
Probability density functions of under case 2 (ethanol condition). Solid lines include all the slides, and red, blue, and black dotted lines are the distributions of positive, negative, and insignificant (), respectively. for categorizing the sign of .
3.2. Second Moments and Interquartile Range of
The second moments and the interquartile ranges of the probability distributions of for all artificial skins are shown in Table 2 and Figure 6 based on the AO hardness scores of the artificial skins. Negative correlations were observed between the second moments and the AO hardness scores at and for cases 1 and 2, respectively. The correlation was significant in case 2 (). Negative correlations were also observed between the interquartile ranges and AO hardness scores at and for cases 1 and 2, respectively. The correlation was significant in case 1 (). We observed that the magnitude of the random variation of tended to decrease with the increasing hardness of the artificial skin. However, this finding is inconclusive because the degree of negative correlation changes depending on the type of the variability index.

Table 2.
Second moment (and interquartile range) of under cases 1 (dry cloth) and 2 (ethanol cloth). A higher AO hardness value corresponds to a harder material, while higher values of the second moment and the interquartile range indicate greater variability of values.
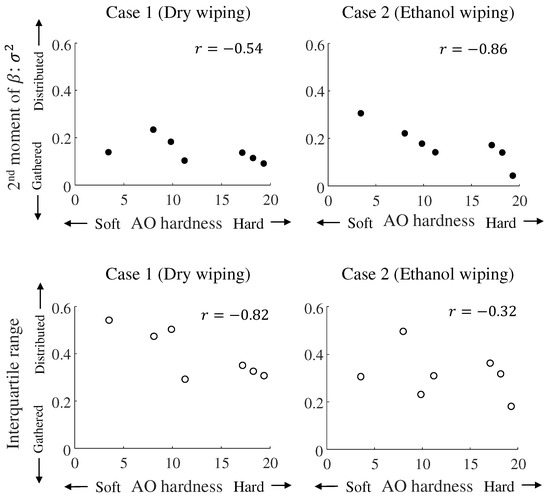
Figure 6.
Scatter plots between the second moments (dots) and the interquartile ranges (circles), and AO hardness values of artificial skins. The left and right section represent the results of case 1 (dry-wipe condition) and case 2 (ethanol-wipe condition), respectively. The vertical axis indicates the second moments and the interquartile ranges, with greater values indicating greater variability in .
3.3. Proportions of Positive, Negative, and Insignificant Values
The proportions of the positive, negative, and insignificant values for effect sizes of and are shown in Figure 7 and Figure 8, respectively. The bars represent the proportions of the positive, negative, and insignificant values from left to right. The upper and lower figures indicate the classification results for cases 1 and 2 (ethanol condition), respectively. The colors of the bars correspond to different participants. randomly assumed positive, negative, and insignificant values for all artificial skins, regardless of the experimental conditions and the effect size criteria, as shown in Figure 7 and Figure 8.
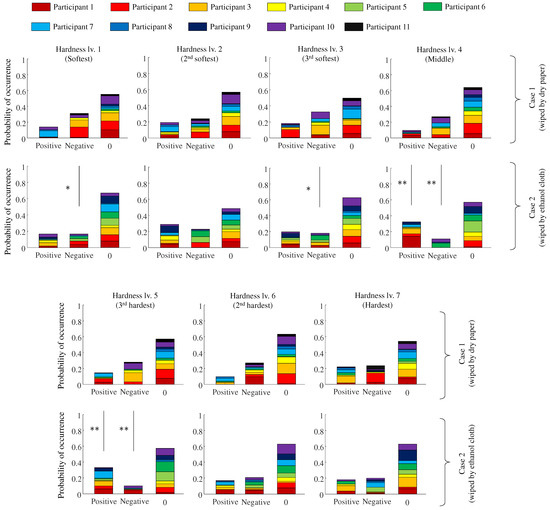
Figure 7.
Probability of occurrence of positive, negative, and insignificant values. The upper and lower sections represent the results under case 1 (wiped by a dry cloth) and case 2 (wiped by ethanol), respectively. Cohen’s . Asterisks * and ** indicate statistical differences in the proportions between cases at and , respectively. The sum of the proportions for all individuals is 1. Note that the number of slides differs from participant to participant.
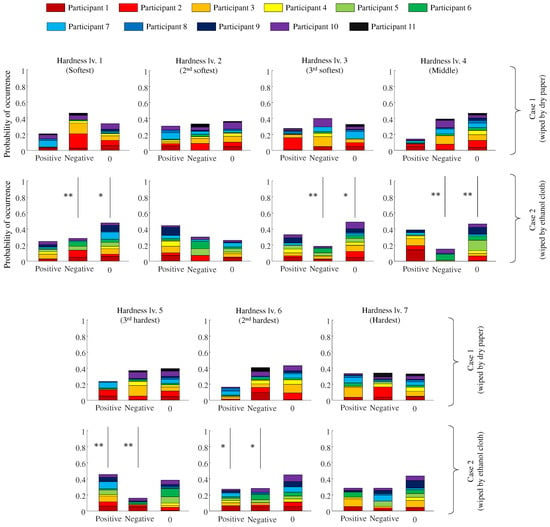
Figure 8.
Probability of occurrence of positive, negative, and insignificant values. The upper and lower sections represent the results under case 1 (wiped by a dry cloth) and case 2 (wiped by ethanol), respectively. Cohen’s . Asterisks * and ** indicate statistical differences in the proportions between cases at and , respectively. The sum of the proportions for all individuals is 1. Note that the number of slides differs from participant to participant.
The proportion of negative values in case 2 was less than that of case 1 for several hardness levels. This trend was consistent for the two arbitrarily selected criteria of effect size. In particular, there was a significant reduction in the proportion of the negative values for hardness levels of 1, 3, 4, and 5 when the criterion for the effect size was .
4. Discussion
It was observed that the exponential component of the normal force , which was obtained from (4), was not constant and varied randomly, despite the same finger rubbing the same artificial skin surface under identical lubrication conditions. One of the reasons for this random variation can be a change in the real contact area due to transient changes in the amount of moisture on the fingertips. Because the fingertips were wiped with ethanol and dried in case 2, we expected a reduction in the value of the variability of the probability density function of , thereby indicating that the variability of was smaller in case 2 than in case 1. However, a comparison between the variability of in both the cases, as shown in Table 2 and Figure 6, proved that there was no reduction in the variability of in case 2. This implies that the transient variation of the moisture content on the fingertips was not responsible for the random variation of . Nonetheless, it is noted that wiping with an ethanol-soaked cloth only moderately dried the fingertip.
However, the fingertip moisture influences the dependence of the COF on the normal force. The application of alcohol reduced the average proportion of the negative values for all artificial skins from in case 1 (wiped by a dry cloth) to in case 2 (wiped by ethanol). The fingertips were considered to be naturally moisturized in case 1. Under such conditions, the COF is proportional to the negative exponent of the normal force [8,27], as shown in (1). In case 2, the contribution of adhesion friction to the total frictional force was decreased, whereas the contribution of deformation friction was increased. The value of the deformation friction was proportional to the positive exponent of the normal force, as shown in (3). Thus, the proportion of negative values is reduced, whereas the proportions of and are increased when the moisture on the fingertips is moderately controlled in case 2.
One reason for the randomness of could be the differences in the manner of rubbing. Although participants were instructed not to change their rubbing mannerisms during the experiment, minor variations were unavoidable. Han et al. demonstrated that varied within a small range of approximately – for a variation of 30 degrees in the contact angle between a finger and an object [14]; however, they did not report that assumed positive and negative values. In addition, the real contact area , which is a major determinant of friction [35], can vary randomly even for the same normal force [21,36]. Such random variations of might have affected the random variation of . Further, the present experiment did not control the rate of normal force and finger velocity. In other words, the frictional phenomena were not steady-state, and the variation of might have been caused by the viscoelastic properties of finger pads. There is no evidence that the fingers were constantly sliding on the artificial skins and they might have rolled or twisted partially. Tribological phenomena during rolling or twisting are not represented by (4), based on which our analysis was. These aforementioned factors could have collectively caused the random variation .
There were negative correlations between the variability, i.e., second moment and interquartile range, and AO hardness for both cases, as shown in Table 2 and Figure 6. When rubbing soft objects, a slight variation in the normal force led to a change in the contact status i.e., the contact state was mutable, and was likely to assume a different value for each finger slide. Rubbing a hard, artificial skin resulted in minimal deformation of the artificial skin with a less mutable contact status, irrespective of any variation in the normal force. As a result, the likelihood of assuming random values is reduced. The variation in contact stability due to the different hardness values of the artificial skin is reflected in the relationship between the variability of the normal force dependence of the COF and the hardness. Note that we did not find any singular phenomenon when the finger slid over the artificial skins of levels 2 or 3, of which hardness were close to those of the participants’ finger pads.
We tested several types of artificial skins manufactured by the same company. Hence, we are not sure whether similar findings can be found for other artificial skins or objects. However, there is no special reason to deny potentially similar observations for other objects as long as the major cause of the random variation of is the variation of the contact status between the fingertip and object surfaces.
5. Conclusions
The current study investigated how the dependence of the COF on the normal force fluctuates while rubbing an artificial skin sample with a finger. Participants were made to actively slide their fingers on different kinds of artificial skin under two different conditions, namely, wiping the finger with a dry cloth and wiping the finger with a cloth soaked in ethanol to control the moisture content on the finger. The dependence of the COF on the normal force varied randomly with each finger slide, despite maintaining identical tribological conditions. The randomness was more prominent for the softer artificial skins. The moisture content of the fingertips influenced the dependence of the COF on the normal force. The COF either increased or remained constant with increasing normal force when the finger pad was wiped using ethanol. Although the dependence of the COF on the normal force may be influenced by the variation of the contact state between the artificial skin and a finger and transient changes in the moisture content of the fingertip, there are additional factors that are responsible for the random variation of the dependence of the COF on the normal force. These findings help in designing surfaces, such as artificial skins and cosmetic products with stably low friction, which leads to pleasant and preferred textures [1,2,3].
Author Contributions
Conceptualization, K.I. and S.O.; methodology, K.I. and S.O.; software, K.I.; validation, K.I. and S.O.; formal analysis, K.I. and S.O.; investigation, K.I. and S.O.; resources, K.I.; data curation, K.I.; writing—original draft preparation, K.I. and S.O.; writing—review and editing, K.I., S.O., Y.A. and Y.Y.; supervision, S.O., Y.A. and Y.Y.; project administration, S.O.; funding acquisition, S.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MEXT Kakenhi (20H04263 and 21H05819).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of the School of Engineering, Nagoya University (#15-12).
Informed Consent Statement
Written informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data are accessible by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klöcker, A.; Oddo, C.M.; Camboni, D.; Penta, M.; Thonnard, J.L. Physical factors influencing pleasant touch during passive fingertip stimulation. PLoS ONE 2014, 9, e101361. [Google Scholar] [CrossRef] [PubMed]
- Klöcker, A.; Wiertlewski, M.; Théate, V.; Hayward, V.; Thonnard, J.L. Physical factors influencing pleasant touch during tactile exploration. PLoS ONE 2013, 8, e79085. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skedung, L.; Harris, K.; Collier, E.S.; Arvidsson, M.; Wäckerlin, A.; Haag, W.; Bieri, M.; Romanyuk, A.; Rutland, M.W. Feeling Smooth: Psychotribological Probing of Molecular Composition. Tribol. Lett. 2018, 66, 138. [Google Scholar] [CrossRef] [Green Version]
- Koudine, A.A.; Barquins, M.; Anthoine, P.; Aubert, L.; Leveque, J.L. Frictional properties of skin: Proposal of a new approach. Int. J. Cosmet. Sci. 2000, 22, 11–20. [Google Scholar] [CrossRef]
- Schallamach, A. The Load Dependence of Rubber Friction. Proc. Phys. Soc. Sect. B 1952, 65, 657–661. [Google Scholar] [CrossRef]
- Zhang, M.; Mak, A. In vivo friction properties of human skin. Prosthetics Orthot. Int. 1999, 23, 135–141. [Google Scholar] [CrossRef] [Green Version]
- Adams, M.J.; Briscoe, B.J.; Johnson, S.A. Friction and lubrication of human skin. Tribol. Lett. 2007, 26, 239–253. [Google Scholar] [CrossRef]
- Derler, S.; Gerhardt, L.C. Tribology of skin: Review and analysis of experimental results for the friction coefficient of human skin. Tribol. Lett. 2012, 45, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Dowson, D. Tribology and the skin surface. In Bioengineering of the Skin: Skin Imaging and Analysis, 2nd ed.; Wilhelm, K.P., Elsner, P., Berardesca, E., Maivadh, H.I., Eds.; CRC Press: Boca Raton, FL, USA, 1997; pp. 159–179. [Google Scholar]
- Greenwood, J.A.; Tabor, D. The friction of hard sliders on lubricated rubber: The importance of deformation losses. Proc. Phys. Soc. 1958, 71, 989–1001. [Google Scholar] [CrossRef]
- Derler, S.; Gerhardt, L.C.; Lenz, A.; Bertaux, E.; Hadad, M. Friction of human skin against smooth and rough glass as a function of the contact pressure. Tribol. Int. 2009, 42, 1565–1574. [Google Scholar] [CrossRef]
- Dzidek, B.; Adams, M.; Zhang, Z.; Johnson, S.; Bochereau, S.; Hayward, V. Role of occlusion in non-Coulombic slip of the finger pad. In Haptics: Neuroscience, Devices, Modeling, and Applications; Springer: Berlin/Heidelberg, Germany, 2014; pp. 109–116. [Google Scholar]
- Fagiani, R.; Massi, F.; Chatelet, E.; Costes, J.P.; Berthier, Y. Contact of a finger on rigid surfaces and textiles: Friction coefficient and induced vibrations. Tribol. Lett. 2012, 48, 145–158. [Google Scholar] [CrossRef]
- Han, H.Y.; Shimada, A.; Kawamura, S. Analysis of friction on human fingers and design of artificial fingers. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 3061–3066. [Google Scholar]
- van Kuilenburg, J.; Masen, M.A.; van der Heide, E. A review of fingerpad contact mechanics and friction and how this affects tactile perception. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 243–258. [Google Scholar] [CrossRef]
- Sivamani, R.K.; Goodman, J.; Gitis, N.V.; Maibach, H.I. Friction coefficient of skin in real-time. Skin Res. Technol. 2003, 9, 235–239. [Google Scholar] [CrossRef]
- Ules, T.; Hausberger, A.; Grießer, M.; Schlögl, S.; Gruber, D.P. Introduction of a new in-situ measurement system for the study of touch-feel relevant surface properties. Polymers 2020, 12, 1380. [Google Scholar] [CrossRef] [PubMed]
- Duvefelt, K.; Olofsson, U.; Johannesson, C.M.; Skedung, L. Model for contact between finger and sinusoidal plane to evaluate adhesion and deformation component of friction. Tribol. Int. 2016, 96, 389–394. [Google Scholar] [CrossRef]
- Fujii, Y.; Okamoto, S.; Yamada, Y. Friction model of fingertip sliding over wavy surface for friction-variable tactile feedback panel. Adv. Robot. 2016, 30, 1–13. [Google Scholar] [CrossRef]
- Mahdi, D.; Riches, A.; Gester, M.; Yeomans, J.; Smith, P. Rolling and sliding: Separation of adhesion and deformation friction and their relative contribution to total friction. Tribol. Int. 2015, 89, 128–134. [Google Scholar] [CrossRef]
- Liu, X.; Carré, M.; Zhang, Q.; Lu, Z.; Matcher, S.; Lewis, R. Measuring Contact Area in a Sliding Human Finger-Pad Contact. Skin Res. Technol. 2018, 24, 31–44. [Google Scholar] [CrossRef]
- Nonomura, Y.; Ouchi, H. Friction Dynamics on Human Skin Surfaces. J. Oleo Sci. 2020, 69, 461–465. [Google Scholar] [CrossRef] [Green Version]
- Tang, W.; Zhang, J.; Chen, S.; Chen, N.; Zhu, H.; Ge, S.; Zhang, S. Tactile perception of skin and skin cream. Tribol. Lett. 2015, 59, 24. [Google Scholar] [CrossRef]
- Sakata, Y.; Mayama, H.; Nonomura, Y. Friction dynamics of moisturized human skin under non-linear motion. Int. J. Cosmet. Sci. 2021, 44, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Inoue, K.; Okamoto, S.; Akiyama, Y.; Yamada, Y. Random switch of adhesion and deformation friction depending on material hardness. In Proceedings of the IEEE 2nd Global Conference on Life Sciences and Technologies, Kyoto, Japan, 10–12 March 2020; pp. 204–206. [Google Scholar]
- Pasumarty, S.M.; Johnson, S.A.; Watson, S.A.; Adams, M.J. Friction of the Human Finger Pad: Influence of Moisture, Occlusion and Velocity. Tribol. Lett. 2011, 44, 117–137. [Google Scholar] [CrossRef]
- Tomlinson, S.E.; Lewis, R.; Liu, X.; Texier, C.; Carré, M. Understanding the Friction Mechanisms between the Human Finger and Flat Contacting Surfaces in Moist Conditions. Tribol. Lett. 2011, 41, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Inoue, K.; Okamoto, S.; Akiyama, Y.; Yamada, Y. Effect of Material Hardness on Friction between a Bare Finger and Dry and Lubricated Artificial Skin. IEEE Trans. Haptics 2020, 13, 123–129. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, H.; Okamoto, S.; Yamada, Y. Phase difference between normal and shear forces during tactile exploration represents textural features. IEEE Trans. Haptics 2020, 13, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, R.; Nonomura, Y. Preparation of artificial skin that mimics human skin surface and mechanical properties. J. Oleo Sci. 2018, 67, 47–54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tanaka, Y.; Bergmann Tiest, W.M.; Kappers, A.M.L.; Sano, A. Contact force and scanning velocity during active roughness perception. PLoS One 2014, 9, e93363. [Google Scholar] [CrossRef]
- Adams, M.J.; Johnson, S.A.; Lefèvre, P.; Lévesque, V.; Hayward, V.; André, T.; Thonnard, J.L. Finger pad friction and its role in grip and touch. J. R. Soc. Interface 2013, 10, 20120467. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1988. [Google Scholar]
- Mukaka, M.M. Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Persson, B.N.J.; Kovalev, A.; Gorb, S.N. Contact mechanics and friction on dry and wet human skin. Tribol. Lett. 2013, 50, 17–30. [Google Scholar] [CrossRef]
- Dzidek, B.M.; Adams, M.J.; Andrews, J.W.; Zhang, Z.; Johnson, S.A. Contact mechanics of the human finger pad under compressive loads. J. R. Soc. Interface 2017, 14, 20160935. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).