Abstract
This paper presents a finite element implementation of plates and shells for the analysis of flexible multibody systems. The developments are set within the framework of the motion formalism that (1) uses configuration and motion to describe the kinematics of flexible multibody systems, (2) couples their displacement and rotation components by recognizing that configuration and motion are members of the Special Euclidean group, and (3) resolves all tensors components in local frames. The formulation based on the motion formalism (1) provides a theoretical framework that streamlines the formulation of shell elements, (2) leads to governing equations of motion that are objective, intrinsic, and present a reduced order of nonlinearity, (3) improves the efficiency of the solution process, (4) circumvents the shear locking phenomenon that plagues shell formulations based on classical kinematic descriptions, and (5) prevents the occurrence of singularities in the treatment of finite rotation. Numerical examples are presented to illustrate the advantageous features of the proposed formulation.
1. Introduction
Plates are defined as structures possessing one dimension far smaller than the other two. The mid-plane of the plate lies along the two long dimensions of the plate, whereas the normal to the plate extends along the shorter dimension. The term “plate” is reserved for flat structures, whereas the term “shell” refers to curved plates.
Solid mechanics theories describing plates and shells, commonly referred to as plate or shell theories, play an important role in structural mechanics because they provide tools for the analysis of these structures that are in common use. Although more sophisticated tools, such as three-dimensional finite element methods, are widely available for the analysis of complex structures, plate and shell models are often preferred because they provide valuable insight into the behavior of these structures at a much reduced computational cost.
Classical plate theories are based on kinematic assumptions about the behavior of the normal material line, i.e., a set of material particles initially aligned in a direction normal to the mid-plane of the plate. For instance, Kirchhoff plate theory [1] assumes that the normal material line remains (1) straight and (2) normal to the deformed mid-plane of the plate. In Reissner–Mindlin plate theory [2,3,4], the same normal material line is assumed to remain rigid but does not remain normal to the deformed mid-plane of the plate, enabling shearing deformation.
In many applications, however, plates are complex built-up structures. In aeronautical constructions, for instance, the increased use of laminated composite materials leads to heterogeneous, highly anisotropic structures. Layers of anisotropic material are stacked through the thickness of the plate. This new type of structural component prompted the development of new plate theories [5,6,7], often based on classical lamination theory [8,9]. The comprehensive review of the many shell theories that have been developed is beyond the scope of this paper but can be found in several publications [10,11]. While many of the more advanced theories relax the assumption of the rigid normal material line by allowing an arbitrary, superimposed warping displacement field, plate deformation measures are defined based on a rigid, average configuration of this normal.
This thought process also applies to beam theories. Classical theories, such as the Euler–Bernoulli [1] or Timoshenko [12] beam theories, are based on the assumption of a rigid-cross section. More advanced theories [13,14,15] have been developed that relax this assumption, but here again, beam deformation measures are defined based on a rigid, average configuration of this cross-section.
The configuration of a frame is described by the position of its origin and the orientation of three mutually orthogonal unit vectors. Under the rigid cross-section assumption, a frame can be attached at any point along the axis of a beam, and the resulting one-dimensional field of frames defines the beam’s configuration unequivocally. Under the rigid normal material line assumption, a frame can be attached at any point over the mid-surface of a plate and the resulting two-dimensional field of frames defines the shell’s configuration. Note that a material line does not define a frame unequivocally because it can rotate freely about this material line; this rotation, often called the “drilling degree of freedom” has to be treated carefully.
The relative motion of two neighboring cross-sections of a beam that are infinitesimally close is infinitesimal, giving rise to a finite curvature. This situation is treated through the tools of calculus: The curvature field is the spatial derivative of the frame field. Because frames are functions of time, their temporal derivatives give rise to the velocity field. Similarly, the spatial and temporal derivatives of the two-dimensional field of frames defining the configuration of shells give rise to its curvature and velocity fields, respectively.
Clearly, frames and their relative configuration play a fundamental role in the analysis of shells: They describe the system but also embody the fundamental assumption on which the analysis is based. Rigid bodies, beams, plates, and shells are examples of Cosserat solids, also called “directed continua”. The brothers Cosserat [16] were the first to develop a mechanics theory of such media. Later, Naghdi [17] developed a theory of plates and shells based on these concepts.
The manipulation of frames involves the treatment of displacement components that form a linear space but also that of rotation components, sometimes referred to as orientation or attitude variables. Rotations form a nonlinear manifold called , the Special Orthogonal group, and hence must be treated with care. Indeed, all parameterizations of rotation involve singularities [18,19], and furthermore, the careless manipulation of rotation can lead to the loss of objectivity of the formulation.
The equations of motion of a system are the equilibrium equations expressed in terms of the components of the strain and curvature vectors, linear and angular velocity vectors, etc, and the kinematic relationships that relate these quantities to the position and orientation of the bodies. The analyst is then faced with a choice: Which frame should these tensor components be resolved in? Because the equations of motion are invariant under a change of frame, physics does not provide an answer to this question. Rather, this choice of the frame is dictated by convenience and numerical efficiency.
The sectional forces in a shell are naturally expressed in a frame attached to the shell’s normal material line. When resolved in this frame, the force components can be interpreted as the in-plane and transverse shear force components. If the same force vectors were resolved in the inertial frame, its components could not be interpreted easily because the shell’s section is at an arbitrary orientation with respect to the inertial frame. The same observation applies to the components of deformation measures and velocity vectors.
These local frame coordinates are obtained naturally through the consistent use of frame kinematics: Frames are elements of , the Special Euclidean group. This rigorous framework, sometimes called screw theory [20], has become the lingua franca in the theoretical kinematics [21,22] and robotics communities [23,24,25].
Within the mathematical structure provided by the Special Euclidean group, the position and rotation coordinates are coupled rather than being treated as independent entities. Although most commonly used in structural mechanics, the latter approach can lead to inconsistent formulations that lack objectivity and to numerical problems, such as the locking phenomenon in finite element implementations. By placing frame transformations at the heart of the formulation, the resulting governing equations exhibit a reduced level of non linearity because they are invariant under rigid-body motions, which are, de facto, “filtered out”.
This paper refers to “motion formalism” as a formalism that (1) uses configuration and motion to describe the kinematics of flexible multibody systems, (2) couples their displacement and rotation components by recognizing that configuration and motion are members of the Special Euclidean group, and (3) resolves all tensors components in local frames. The approach has been embraced by Müller et al. [26,27,28] for the modeling of rigid multibody systems, by Borri and Bottasso [29] and Sonneville et al. [30] for beams, and by Merlini and Morandini [31] for finite deformation elasticity. Yet, it remains largely ignored by the mechanics and structural mechanics communities, although it opens the door to the development of geometrically consistent and efficient solution procedures.
In his doctoral thesis, Sonneville [32] presented a shell element based on the concept of local frames, but key elements of his development differ from those presented here. First, this paper treats kinematics via dual orthogonal rather than homogeneous transformation matrices. Second, the present paper derives a closed-form solution of the implicit interpolation scheme for motion, leading to a closed-form expression for the interpolated strain field that simplifies the formulation considerably. In contrast, the thesis relies on an implicit interpolation scheme that has to be solved numerically at each Gauss point. Third, the thesis developed a consistent interpolation formula for the velocity field that satisfies the space-time Lie bracket identically; the simpler interpolation scheme developed in this paper proves to be effective. Fourth, the present paper treats body attached frames and change of frame operations in a consistent, streamlined manner; in contrast, the thesis uses different approaches for the representation of the two kinematic entities. Finally, the present paper presents realistic multibody applications, whereas the doctoral thesis tackled benchmark examples only.
The goal of this paper is to develop a finite element formulation for shell elements within the framework of the motion formalism, which is summarized in Section 2. The kinematics of shell problems and the resulting governing equations are presented in Section 3 and Section 4, respectively. Finally, the finite element implementation of the proposed formulation appears in Section 5, followed by numerical examples in Section 6.
2. The Motion Formalism
Rigid-body motion can be represented by motion tensor , where denotes the rotation tensor, the position vector of a reference point of the rigid body, and parameter is such that for . The rotation tensor , where is the special Orthogonal group, is the primal part of the motion tensor, and the matrix is its dual part. In the sequel, the following short-hand notation is used: , where operator computes the motion tensor from the corresponding rotation tensor and position vector. The principle of transference [33,34] implies that all mathematical formulæ for rotation can be extended to rigid-body motion by replacing all real variables by their dual counterparts [35].
Given motion field , where t denotes time, the components of the dual velocity vector are:
where notation indicates a derivative with respect to time. The components of the angular and linear velocity vectors are denoted as and , respectively. In this paper, notation indicates tensor components resolved in the inertial frame. For instance, in Equation (1), the components of the motion tensor are resolved in the inertial frame, whereas the components of the velocity vector are resolved in the material frame.
The definitions of the dual virtual and incremental motion vectors are similar to that of the dual velocity vector, Equation (1):
where and denote the virtual displacement and rotation vectors, respectively; and denote the incremental displacement and rotation vectors, respectively.
The motion tensor is a continuous function of its spatial and temporal variables, and hence, second derivatives commute . Elementary vector identities then yield:
These equations are called “compatibility equations”.
2.1. Parameterization of Motion
The vectorial parameterization of motion [35,36] is defined as:
where is a dual function of dual scalar , called the “generating dual function”, or “generating function” for short, and is the unit dual vector representing Chasles’ line [19,37,38]. The primal part of the generating dual function is the generating function for the vectorial parameterization of rotation [19,39], . The following dual scalar functions play an important role in the vectorial parameterization of motion:
Let , , and with associated dual parameters , , and , respectively, be the motion parameter vectors of three motion tensors such that . The relationship between the various parameters is then [35,36]:
The first equation is used to compute and hence, . The second equation then yields the components of the motion parameter vector.
The motion tensor can be expressed in terms of dual motion parameter vector . The following notation is introduced:
Operator extracts motion parameter vector from motion tensor , whereas operator computes motion tensor from the corresponding motion parameter vector. The derivative and increments of the motion parameter vector are related to the dual velocity and incremental motion by:
where is the tangent operator, which enjoys the following remarkable properties:
For the Euler–Rodrigues parameterization [19,35,36], the tangent operator and its inverse are:
where:
2.2. The Interpolation of Motion
The classical interpolation schemes [40,41] used in the finite element method were developed to interpolate displacement fields, which form a linear space. These schemes cannot be used for the interpolation of rotation or motion that form nonlinear manifolds.
Figure 1 illustrates the typical interpolation problem for shell elements: The components of the motion tensors at the nodes of the shell and the components of the interpolated motion tensor are denoted , and , respectively, all resolved in the inertial frame. Non-dimensional coordinates and are defined over the mid-surface of the shell.
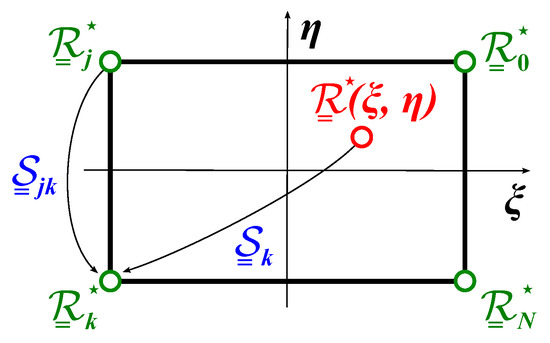
Figure 1.
Interpolation of motion in a two-dimensional space.
Numerous authors [31,42,43] have developed schemes for the interpolation of motion that can be written in the following form:
where shape functions are two-dimensional Lagrangian polynomials, and is a motion parameter vector associated with relative motion tensor , which defines the relative motion of motion tensor with respect to its counterpart , resolved in frame , see Figure 1. Any vectorial parameterization of motion can be used in Equation (18), but because of its simplicity, the Euler–Rodrigues parameterization is preferred, .
Because the components of motion parameter vectors are resolved in the unknown interpolated frame, Equation (18) is an implicit, nonlinear interpolation scheme, in contrast with its explicit, linear counterpart used in classical finite element formulations. Nevertheless, for the Euler–Rodrigues parameterization of motion, a closed-form solution of the interpolation scheme can be found. First, given the motion tensors at the nodes, , the relative motion tensors at the nodes are evaluated as , see Figure 1. Next, the corresponding Euler–Rodrigues motion parameters vectors, are computed together with the associated parameters using Equation (17). The relative motion parameter vector is then:
where dual scalar is defined as:
For clarity of the exposé, these results are derived in Appendices Appendix A.1 and Appendix A.2. Finally, the interpolated motion is obtained as . Any node k can be used for the interpolation process.
Expression (20) involves a double summation, but a single summation extending over the independent relative motions at the nodes suffices:
where:
The following notation was introduced , where the summation extends for . Indices correspond to , and the subsequent pairs are , defining a unique correspondence between index and the associated values of indices j and k.
The above closed-form solution relies on the parameterization of the relative motion tensors at the nodes; while the motions at each node might be large, the relative motions at the nodes remain small if the interpolation operation makes sense. In finite element applications involving structures undergoing small deformations, the relative motions at the nodes remain very small, and the present approach provides a closed-form solution of the problem that is free of singularities. Because it is expressed in terms relative motions only, the interpolation scheme is objective [44], i.e., the interpolated motion remains unchanged if a rigid-body motion is added to all nodal motions.
2.3. The Interpolation and Linearization of Curvature
Finite element applications require the interpolation of the curvature field. The spatial derivative of the motion field gives rise to the components of the curvature tensor resolved in the material frame, , where notation indicates a derivative with respect to . Because , it follows that and Equation (13) now yields:
Taking a spatial derivative of Equation (18) yields and introducing Equation (23) leads to:
where matrix . Curvature vector can be defined in a similar manner.
For the Euler–Rodrigues parameterization, an explicit expression for matrix can be obtained as , where the second equality results from interpolation scheme (18). Clearly, matrix reduces to a dual scalar, and its inverse is simply . Equation (24) now yields the interpolated curvature field:
where the second equality follows from the use of Equation (19), the last uses the compact notation introduced earlier, and
Equation (7) shows that for and Equation (21) now implies under the same condition. Clearly, as the magnitudes of the relative motions at the nodes decrease, and quadratically within the element, because shape functions are of the order of unity. Furthermore, those shape functions vanish at the nodes, and hence, at the nodes. As the element size decreases, the magnitudes of the relative motions at the nodes decrease: . Because quadratically within the element, the error incurred by setting is smaller that that incurred by the interpolation itself. Consequently, it is valid to assume , and Equation (25) reduces to:
which expresses the curvature field as a linear combination of the relative motions at the nodes; shape functions describe the distribution of the curvature field over the element for a unit relative motion at the nodes, .
Curvature interpolation (27) is expressed in terms the relative motions at the nodes, but the unknowns of the problem are the motion tensors at the nodes. The relationship between the two sets of quantity is nonlinear, but it can be linearized as follows: . Recasting this relationship is matrix form yields:
where array stores the incremental motion vectors at the nodes and matrix , of size , and contains two non-vanishing entries only: If , these entries are and in columns j and k, respectively. Matrix depends on the relative motions at the nodes only.
2.4. The Interpolation of the Velocity Field
Finite element applications require the interpolation of the velocity field. The time derivative of the motion field gives rise to the components of the velocity tensor resolved in the material frame, . It is easily verified that , where the components of the nodal velocity vectors, resolved in the material frame, are . It now follows that:
where the second equality follows from Equation (13). Taking a time derivative of interpolation scheme (18) yields , and introducing Equation (29) leads to:
where matrix .
For the Euler–Rodrigues parameterization, and the interpolated velocity field reduces to:
where matrix is defined as , and
To be consistent with the discussion presented in the previous paragraph, factor in Equation (31) can be ignored.
2.5. The Extended Notation
The inner product operation in the dual number domain does not yield the expected virtual work. Following the advice of Dimentberg [45], the “extended notation” is introduced, which recasts dual vectors and matrices in to entities in , i.e.,
In the dual notation, the velocity vector, virtual motion vector, incremental motion vector, motion tensor, and tangent tensor, denoted as , , , , and , respectively, become , , , , and , in the extended notation, respectively.
3. Kinematics of the Problem
Figure 2 shows a shell of mid-surface with a normal material line . The volume of the shell is generated by sliding the normal material line over the mid-surface. The curvilinear coordinates and define a parameterization of this mid-surface. Point B is located at the intersection of the mid-surface the normal material line.
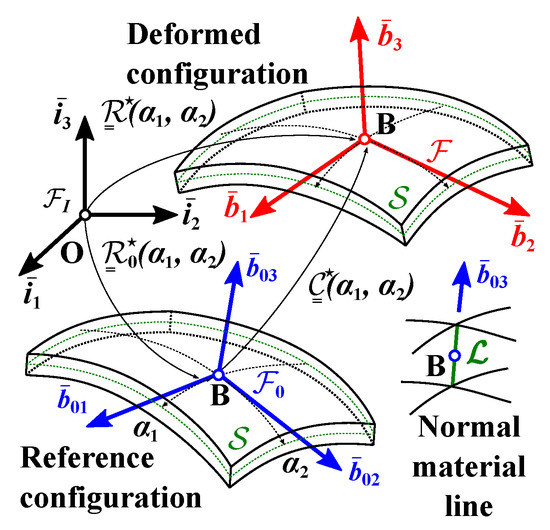
Figure 2.
Configuration of the shell in the reference and deformed configurations.
3.1. The Reference Configuration
Frame defines the normal material line in the reference configuration. Unit vector defines the orientation of the normal material line. Unit vectors , tangent to coordinate line and , and tangent to coordinate line define the plane tangent to the shell’s mid-surface at point B. A set of material coordinates that represent the configuration of the beam naturally is selected as follows: , , and , where the last coordinate measures length along the direction of normal material line .
The location of reference point B and the orientation of the normal material line change as they slide along mid-surface , and hence, frame is a function of coordinates and . The motion tensor that brings frame to is denoted as , where is the position vector of material point B with respect to point O, and rotation tensor brings basis to basis . The components of the shell’s curvature vectors resolved in the material frame in its initial configuration are defined as and , where notation , i = 1 or 2 indicates a derivative with respect to coordinate or , respectively. Curvature vector includes the curvature vector and tangent vectors defined as and , respectively, both resolved in the material basis. A similar notation can be introduced for curvature vector .
3.2. The Rigid-Normal Motion
Figure 2 also shows the configuration of the shell in its deformed state. The plate’s displacement field is now decomposed into two parts: (1) a rigid normal-material-line motion and (2) an additional warping field. Because expression “rigid normal-material-line motion” is wordy, it will be abbreviated as “rigid-normal motion” in the sequel. The rigid-normal motion of the shell is defined as one that allows arbitrary deformation of its mid-surface and independent rotation of each normal material line, i.e., each normal material line undergoes a rigid-body motion. This motion is, in fact, the only motion allowed by the Reissner–Mindlin assumptions [2,3,4]. The rigid-normal motion generates strains because it is not a rigid-body motion of the entire plate. It is characterized by five degrees of freedom only, three displacements and two rotations, because the rotation of the normal line about its own axis, called “drilling rotation”, is immaterial. After the rigid-normal motion, the normal material line is defined by frame . The shell’s mid-surface describes a new surface in space denoted as .
The motion tensor that bring frame to is defined as , where matrix stores the components of the rotation tensor that brings basis to basis , and array stores the components of the position vector of material point B after deformation with respect to point O, both resolved in the inertial frame. The components of the shell’s curvature vectors after deformation, resolved in the material frame, are defined as and . Curvature vector includes the curvature and tangent vectors, and , respectively, both defined in the material frame. A similar notation can be introduced for curvature vector .
Finally, motion tensor describes the change in configuration from frame to frame . Composition of motion yields , where are the components of the change in configuration tensor resolved in the inertial frame.
3.3. Velocities, Deformation Measures, and Stress Resultants
The components of the velocity vector resolved in the material frame are:
The deformation measures of the shell are defined as the differences between the curvature vectors in the deformed and reference configurations:
The array of sectional deformation measures now becomes:
where the second equality follows from Equations (35) and (36). The array of sectional deformation measures is , where and are the in-plane strain along unit vectors and , respectively; is the in-plane shear strain; and are the transverse shear strains; and are the curvatures about unit vectors and , respectively; and is the twisting curvature; all components are resolved in the material frame. Boolean matrices and are defined as:
The components of the stress resultant vector and of the deformation measures, both resolved in the material frame, are related through the following constitutive law:
Stiffness matrix , of size , is computed with point B as the reference point, see Figure 2, and stores the components of the shell’s stiffness tensor resolved in the material frame. For homogeneous plates, this stiffness matrix is computed easily, see Timoshenko et al. [46]; for laminated plates, classical lamination theory [8] provides a simple approach to the computation of this stiffness matrix that can also be obtained from three-dimensional models, see Hodges et al. [47,48,49,50], Carrera et al. [10,51], or Han and Bauchau [11].
The array of stress resultants is , where and are the in-plane forces along unit vectors and , respectively; is the in-plane shear force; and are the transverse shear forces acting on faces normal to unit vectors and , respectively; and are the bending moments about unit vectors and , respectively; and is the twisting moment; all components are resolved in the material frame.
In the present formulation, the deformed configuration of the shell is described by motion tensor , which features six independent degrees of freedom. The drilling rotation does not strain the shell and hence, frame is free to rotate about unit vector , see Figure 2, without straining the shell, resulting in zero-energy modes. The drilling rotation of frame , denoted as , can be expressed as:
where and .
4. Governing Equations
The governing equations of the problem will be derived from Hamilton’s principle. After integration over the normal material line of the shell, mass matrix , of size , becomes:
where the following mass constants were defined: , , and . In these expressions, is the mass density of the material per unit volume of the reference configuration, m is the mass of the shell per unit area, is the location of the center of mass of the normal material line with respect to point B, see Figure 2, and is the mass moment of inertia per unit area computed with respect to point B, all resolved in the material frame. Finally, the position vector of the center of mass with respect to point B is denoted as , and the mass moment of inertia tensor is denoted as . The inertial effects due to normal material line warping can be ignored for shells undergoing low-frequency motion, i.e., frequencies whose associated wave lengths are much longer than the thickness of the shell.
The kinetic energy of the shell is written as:
where the mass matrix adjusted for the initial configuration of the shell is . Taking a variation of the kinetic energy gives , where array stores the components of the momentum vector resolved in the material frame. Using compatibility relationships (4) then leads to:
For the problem at hand, the externally applied loading consists of moments and forces per unit area acting over the shell’s mid-surface and their components, resolved in the material frame, denoted and , respectively; moment components are computed with respect to reference point B. These distributed loading components are stored in array . The virtual work performed by the externally applied loading is:
where .
The strain energy, denoted A, stored in the shell is written as a quadratic form of the deformation measures given by Equation (37):
where the stiffness matrix adjusted for the initial configuration of the shell is defined as:
The following strain and force arrays were defined:
Variation in the strain energy is now evaluated easily:
where compatibility Equation (5) have been used.
The governing equations of the system are now obtained from Hamilton’s principle, which states that . Introducing Equations (43), (44), and (48) leads to:
Integration by parts then yields:
Hence, the dynamic equilibrium equations of the shell are:
The last of these six equations vanishes identically because it is the equation associated with the drilling degree of freedom.
5. Finite Element Implementation
The kinematic description of shells, as presented in Section 3, is expressed in terms of a motion field defined over the mid-surface of the shell, see Figure 2. When applying the finite element method, it becomes necessary to interpolate this motion field based on its nodal values; similarly, the curvature and velocity fields must be interpolated.
5.1. Kinematics of the Finite Element
Equation (25) provides the interpolated curvature field as:
where shape functions are defined by Equation (26), and shape functions are defined similarly.
The interpolation process took place in the computational domain defined by variables . To compute the correct strain components, the Jacobian of the transformation from coordinates over the shell’s mid-surface to coordinates must be taken into account. Figure 2 shows that coordinates and are aligned with unit vectors and , respectively, and hence, form an orthogonal coordinate system. Because coordinates and also form an orthogonal system, the Jacobian of the coordinate transformation reduces to a diagonal matrix, , where and .
Curvature vector includes the curvature vector and tangent vectors defined as and , respectively. It now follows that , and hence, .
With the help of this Jacobian matrix, the deformation measures defined Equation (51) are transformed to their counterparts in coordinates system to find:
where array stores the relative motion parameter vectors at the nodes. Matrix is defined as , where , , and is defined by Equation (26). A similar notation is introduced to define matrix . Because the interpolated curvature field depends on relative motions at the nodes only, the interpolation is objective: any rigid-body motion superimposed to the configuration of the element leaves relative motions at the nodes unchanged.
Variations of the curvature field are easily obtained as:
Equation (37) now provides the interpolated curvature field and its increments as:
where matrix is defined as:
5.2. Inertial Forces and Their Linearization
The velocity field within the shell element will be interpolated using the scheme developed in Section 2.4, leading to:
where is the nodal velocity at node k, matrix , velocity interpolation matrix is given by Equation (32), and is the configuration tensor at node k. Array stores the nodal velocity vectors.
Variation in the kinetic energy defined by Equation (42) now becomes:
where the interpolation of the velocity field, Equation (59), was introduced to obtain the second equality. The constant mass matrix of the element is:
For simplicity of the formulation, matrix is evaluated in the reference configuration of the element, leading to .
Compatibility Equation (4) provides the variation of the velocity vector at node k as , which implies , where array stores the virtual nodal motion vectors. Introducing this result into Equation (60) then yields:
where the second equality follows from integration by parts and array stores the nodal momentum vectors. The nodal inertial forces for the shell element are:
The increments of these inertial forces are found easily as , where the gyroscopic matrix is , and the notation is defined implicitly by identity .
Inertial forces (63) depend on velocity and acceleration components, as expected, but remain independent of the position and orientation variables that define the configuration of the shell with respect to the inertial frame. Such formulations are referred to as intrinsic [52,53]. The same observations carry over to the linearization.
5.3. Elastic Forces and Their Linearization
The virtual work performed by the elastic forces is:
where the last equality is found by introducing Equations (56) and (57). The vector of nodal elastic forces, , is defined as:
Matrix is defined by Equation (28), where the constant stiffness matrix of the element is:
and the elastic stiffness matrix of the shell, adjusted for its initial configuration, , is defined by Equation (46).
The linearization of the elastic forces yields , where the effective stiffness matrix of the element is:
Matrix is implicitly defined by identity .
Elastic forces (65) depend on the relative motions at the nodes, as expected, but remain independent of the position and orientation variables that define the configuration of the shell with respect to the inertial frame. Such formulations are referred to as intrinsic [52,53]. The same observations carry over to the linearization.
5.4. Treatment of the Drilling Degree of Freedom
As mentioned in Section 3.3, the drilling rotation does not strain the shell, resulting in zero-energy modes. To overcome this problem, the vanishing of the drilling rotation is enforced via the penalty method by adding the following term to the strain energy:
where is the drilling rotation defined by Equation (40), and p is the penalty coefficient. In this effort, the penalty coefficient was selected as , where is the in-plane shearing stiffness of the plate, i.e., . The analysis was found to be very insensitive to the selection of the penalty coefficients: Selecting any yields nearly identical predictions.
6. Numerical Examples
In this study, the quadratic, nine-node shell element was implemented based on the formulation described above. The mass and stiffness matrices were obtained based on a full integration scheme featuring Gauss points. For all simulations, the penalty coefficient was selected as .
6.1. Clamped Plate under Uniform Loading
A square plate of side a = 0.8 is subjected to a static, uniform transverse pressure = 1 . Three plate thicknesses were investigated, h = 1.5, 15, and 50 , corresponding to aspect ratios = 533, 53.3, and 16, respectively. A convergence study was conducted to understand the behavior of the proposed formulation; 10 grid sizes, , , , , , , , , , and quadratic shell elements, were used to model the square plate.
To monitor the convergence of the process, predictions obtained with the finest mesh () were taken as the exact solution, and error measures were computed, where is the predicted value with one of the first nine grid sizes, and is the corresponding prediction obtained with the finest grid size.
Figure 3a shows the error measures for the transverse displacement at the middle of the plate as a function of the number of degrees of freedom of the model. The logarithmic plot shows the behavior of the plate for the three aspect ratios. The convergence rate of the element was established by fairing a straight line through the error measures obtained for the five finest mesh sizes, see Figure 3a. The convergence rate is 2 for aspect ratios = 53.3 and 16 but reduces to 1 for = 533. Figure 3b shows the corresponding results for the bending moment at the middle of the plate. A convergence rate 1.3 is observed for aspect ratios = 53.3 and 16, but reduces to 0.7 for = 533. Finally, the corresponding results for the shear force at the middle of the edge of the plate are depicted in Figure 4. A convergence rate 1 is observed for all three aspect ratios.
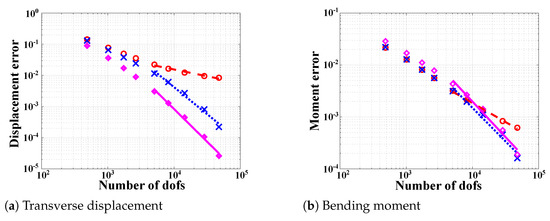
Figure 3.
Convergence of the error measures at the middle of the plate versus number of degrees of freedom. = 533: dashed line (∘); = 53.3: dotted line (×); = 16: solid line (⋄).
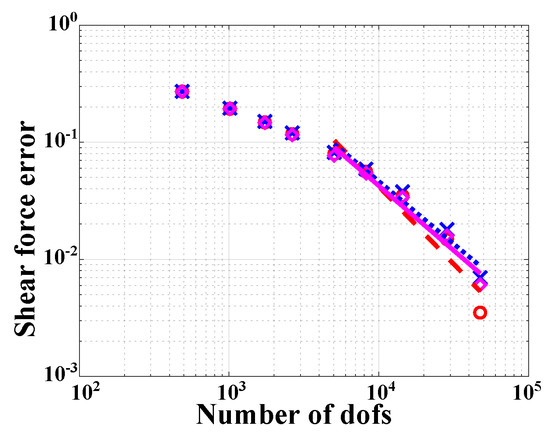
Figure 4.
Convergence of the shear force at the side of the plate versus number of degrees of freedom. = 533: dashed line (∘); = 53.3: dotted line (×); = 16: solid line (⋄).
The behavior observed above can be explained based on the physical nature of the governing equations. As the thickness of the plate decreases, , the ratio of the sectional shearing stiffness, S, to the sectional bending stiffness, D, increases rapidly, . For high aspect ratios, the governing equations of the problem become increasingly ill-conditioned and difficult to solve.
Note that aspect ratio = 533 is unrealistic: Such a thin plate would collapse under its own weight. In high-performance structures such as ultra-light-weight space structures, sandwich constructions are selected to increase the bending stiffness dramatically without incurring a heavy weight penalty, effectively increasing the thickness of the plate and decreasing its aspect ratio. For realistic aspect ratios, the proposed element yields accurate predictions, and the expected convergence rates for quadratic elements are observed.
Bucalem and Bathe [54] present an extensive review of the literature concerning the shear and membrane locking phenomena that plague shell elements based on classical kinematic descriptions, together with the numerous numerical techniques that have been proposed to remedy the problem. This first example reveals an important property of the proposed shell element: although no particular numerical technique was used to alleviate locking, the element appears to be locking free. This important property stems from the manner in which strain components are evaluated. For classical kinematics formulations, transverse shear strain components are the difference between the slope of the plate and the rotation of the normal material line. Because these two quantities are interpolated to different orders, the shear strain component cannot vanish over the element, as expected for thin plates, leading to locking. In the present formulation, all strain components are interpolated simultaneously using Equation (51), which does not involve differences between quantities interpolated to different orders, thereby relieving the locking phenomenon. While the proposed element does not lock, its rate of convergence decreases when dealing with very thin plates.
6.2. The Crank-Plate Mechanism
The crank-plate mechanism shown in Figure 5 consists of a square plate a side a = 1 connected to reinforcing beam BeamCD along edge CD; at points C and D, BeamCD is connected to the ground by means of two revolute joints that allow rotation about unit vector . At point B, a spherical joint connects the plate to the push-rod of length = 0.5 . Next, the push-rod is connected to a crank of length = 0.2 by means of a universal joint at point F. Finally, a revolute joint connects the crank to the ground at point E, and the relative rotation at this joint is denoted . The mechanism is initially at rest and the rotation of the crank is prescribed as for and, for ; period T = 2 .
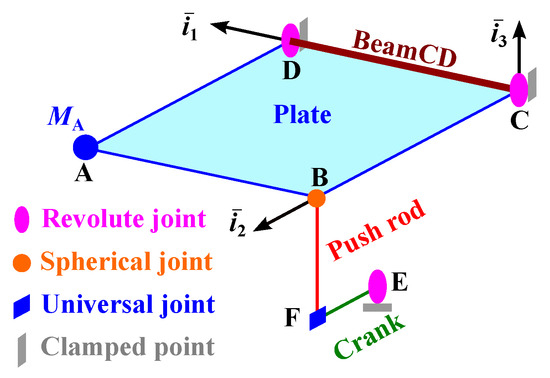
Figure 5.
Configuration of the crank-plate mechanism.
The plate is of thickness , corresponding in an aspect ratio = 100. Beam BeamCD has a square cross-section of . The crank and push-rod present circular cross-sections of radii = 24 and = 12 , respectively. The mechanism is made of aluminum: Young’s modulus E = 73 , Poisson’s ratio = 0.3, and density = 2700 . A rigid body of mass = 2 is connected to the plate at point A.
The plate was modeled with a square grid of quadratic shell elements. The crank and push-rod were modeled with two and three cubic beam elements, respectively. The simulation was run with a constant time step size = 0.5 .
Figure 6a shows the components of the velocity vectors at points A and B along unit vectors and , denoted and , respectively, while Figure 6b show the components of the angular velocity vectors at same points about unit vectors and , denoted as and , respectively. At point B, the plate follows the input of the crank-push rod mechanism closely, resulting in rather smooth velocity histories. In contrast, the dynamic response at point A is affected by the flexibility of the plate. A single-frequency vibration is present in the linear velocity components and multi-frequency vibrations are observed in the angular velocity components.
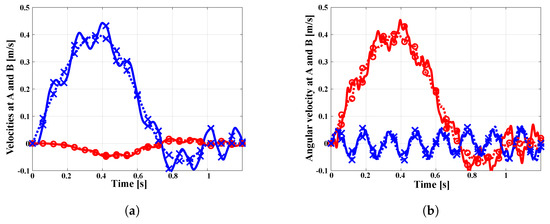
Figure 6.
Vertical and horizontal components of velocity at points A (solid line) and B (dashed line). (a) Linear velocities at points A and B; (∘), (×). (b) Angular velocities at points A and B (∘), (×).
Figure 7a,b show the bending moment and shear force components at the center of the plate, respectively. Several elastic vibration modes of the plate are excited and affect its dynamic response. Bending moment component shows the effect of the lowest vibration mode only, whereas the other components are affected by higher-frequency modes as well. The shear forces components show higher amplitudes of vibration for the higher-frequency modes.
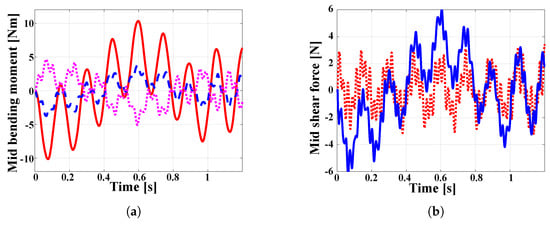
Figure 7.
Stress resultant histories at the center of the plate. (a) Bending moments: , solid line; , dotted line; , dashed line. (b) Shear forces: , dotted line; , solid line.
Figure 8 shows the phase plot of velocity component versus displacement component , both oriented along unit vector . Due to the stiffness of the crank-push rod mechanism, the phase plot of point B is prescribed precisely. In contrast, the phase plot of point A is affected by vibrations of significant amplitude.
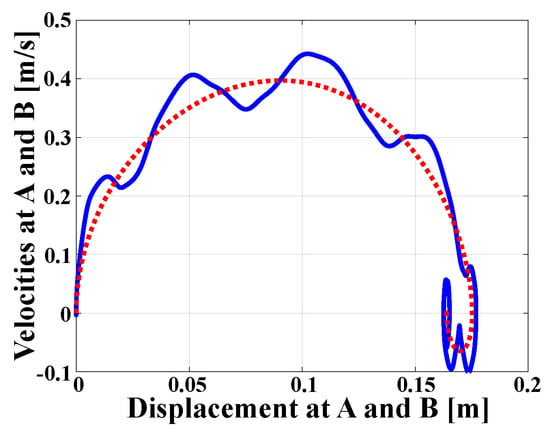
Figure 8.
Phase plot at points A (solid line) and B (dashed line).
The crank-push rod mechanism is stiff enough to prescribe the motion of point B, see Figure 8, but this does not imply that the crank remains unaffected by plate vibrations. Figure 9 shows the axial and transverse forces at the mid-span of the crank. During the first half of the simulation, the transverse shear force generated by the bending moment in the crank dominates, whereas during the second half of the simulation, the crank and push-rod are nearly aligned and the axial force dominates. Both force components show large amplitude vibrations resulting from the oscillations of the plate.
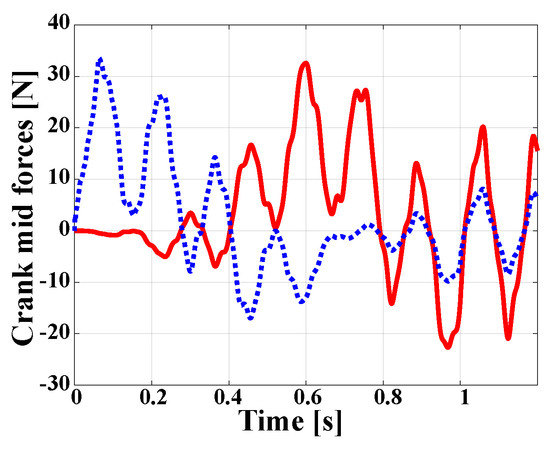
Figure 9.
Mid-point crank forces: axial force (solid line), shear force (dotted line).
This example shows the versatility of the proposed approach. Rigid bodies, beams, and plates, which are all Cosserat solids, are treated in a unified manner using the motion formalism; furthermore, the constraint conditions at the kinematic joints are treated with the same formalism. Consequently, complex systems can be described easily. In this example, the plate shares its degrees of freedom along edge CD with BeamCD, shares its degrees of freedom at point A with rigid mass , and shares its degrees of freedom at point B with the spherical joint at that point. The standard assembly procedure of the finite element method is sufficient to connect the various structural components of the system.
6.3. The Half-Cylinder Mechanism
The half-cylinder mechanism shown in Figure 10 consists of a semi-circular shell of radius R = 1 and length L = 1.2 connected to reinforcing beams, BeamAB and BeamCD, along its two opposite edges, AB and CD, respectively. At point A, BeamAB is connected to the ground by means of a clamped revolute joint that allows rotation about unit vector . At point B, BeamAB is connected to the ground by means of a revolute joint that allows rotation about unit vector . This revolute is connected to a clamped prismatic joint, which allows point B to translate freely along unit vector . The mechanism is initially at rest and is subjected to two concentrated forces, and , applied at point C and acting along unit vectors, and , respectively. for and, for ; period T = 2 and = 100 . The magnitude and schedule of force are identical to those of force .
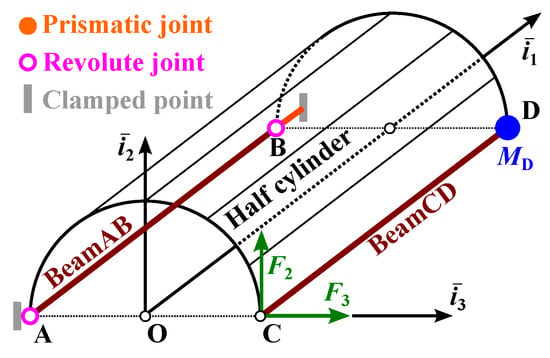
Figure 10.
Configuration of the half-cylinder mechanism.
The shell is of thickness . Beams BeamAB and BeamCD have a square cross-section of and , respectively. The mechanism is made of aluminum: Young’s modulus E = 73 , Poisson’s ratio = 0.3, and density = 2700 . A rigid body of mass = 15 is connected to the plate at point D.
The shell was modeled with a grid of nine and five quadratic elements along the circumferential and length directions, respectively. The simulation was run with a constant time step size = 2 .
Under the effect of the applied forces, the half-cylinder undergoes a large rigid-body rotation. Figure 11 shows that the relative rotations at the revolute joints located at points A and B are large, with a magnitude of about 90. For times 4 , the applied forces vanish, and the half cylinder continues to rotate at a nearly uniform angular speed about line AB. The prismatic joint allows the translation of point B along unit vector , the magnitude of which is shown in Figure 12. This joint relieves the axial force in BeamAB.
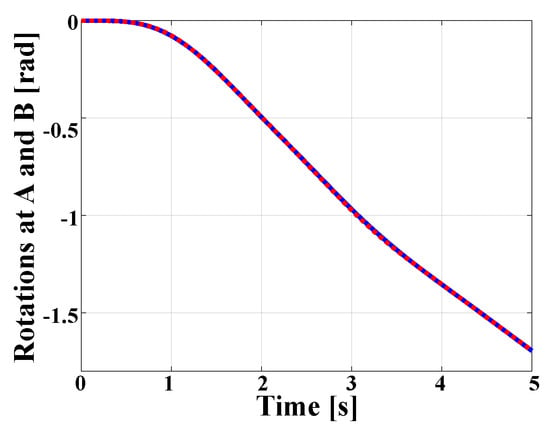
Figure 11.
Rotations for the revolute joints at points A (solid line) and B (dashed line).
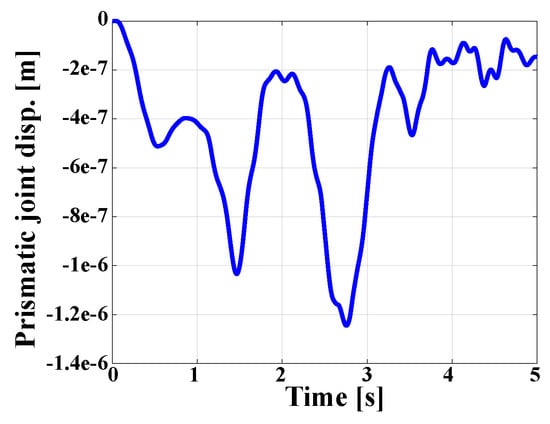
Figure 12.
Displacement for the prismatic joint at point B.
While the overall motion of the shell can be described as a rigid-body motion, the impulsive forces applied at point C, redistributed within the half-cylinder through BeamCD, generate time-dependent stress resultants in the shell. Figure 13a,b show the bending moment and transverse shear force components, respectively, at the center point of the half-cylinder. For time = 4 , large peaks are observed in the sectional stress resultants; for 4 , the half cylinder continues its rigid-body rotation with superimposed, small-amplitude vibrations. Figure 14a,b show the forces and moments, respectively, at the mid-points of BeamAB and BeamCD. Because these beams share degrees of freedom with the shell, forces and moments are transferred seamlessly between the two structural components.
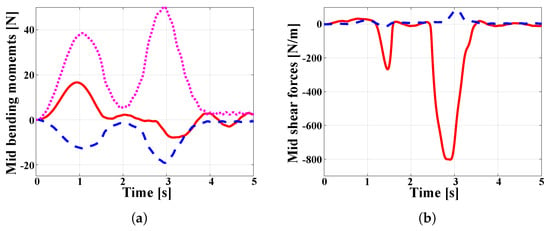
Figure 13.
Stress resultants at the center point of the half cylinder. (a) Bending moments: (dotted line), (dashed line), and (solid line). (b) Transverse shear forces: (solid line), and (line dashed).
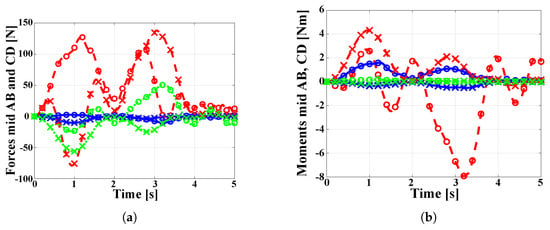
Figure 14.
Mid-point stress resultants for BeamAB (∘) and BeamCD (×). (a) Axial force (dashed line), shear forces and (solid and dotted lines, respectively). (b) Torque (dashed line), bending moments and (solid and dotted lines, respectively).
This example shows that the proposed formulation handles plates and shallow shells equally well. The curvature of the element is encoded directly into the material properties: Equation (46) shows that the sectional stiffness properties are adjusted for the initial configuration of the element represented by motion tensor . A similar adjustment takes place for the sectional mass properties, see Equation (61). Except for the adjustment of the section properties, the formulation remains independent of the curvature of the element.
6.4. Lateral Buckling of a Thin Plate
A plate of length L = 1 , height h = 100 , and thickness t = 10 is clamped along edge AB, as shown in Figure 15. Along edge CD, the plate is reinforced by a beam with a square cross-section of side a = 20 , not shown on the figure for clarity. The plate is modeled by a rectangular grid of quadratic elements. At point T, located in the middle of edge CD, the plate attaches to a spherical joint at point F through a rigid connection. The link connects this spherical joint to the revolute joint at point E, and finally, the crank is connected to the ground via a revolute joint at point G.
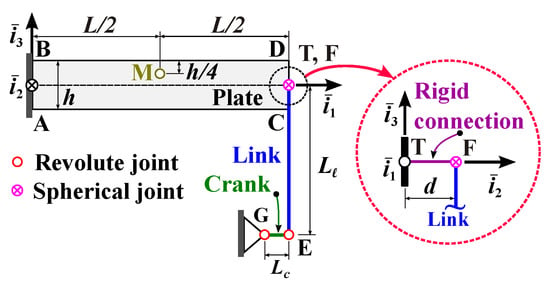
Figure 15.
Configuration of the thin plate.
The crank and link are of lengths = 50 and = 250 , respectively; have circular cross-sections of radii = 24 and = 12 , respectively; and are modeled by one and two cubic beam elements, respectively. The plate (points A, B, C, D, and T) is contained in plane . To simulate an initial imperfection of the system, the crank-link mechanism (points G, E, and F) is located in a plane parallel to plane with an offset d = 0.1 .
To validate the predictions of the proposed shell element, a second model was developed, where the plate replaced by a beam with a rectangular cross-section of 10 by 100 located along the axis of the plate; the geometrically exact beam was modeled with four cubic elements. The mechanism is made of aluminum: Young’s modulus E = 73 , Poisson’s ratio = 0.3, and density = 2700 .
The rotation of the crank is prescribed a , where T = 2 and pushes point T up. When the buckling load is reached, the plate snaps laterally and becomes significantly softer in bending due to the pronounced twisting deformation. The simulation was run for a total of 0.75 using a constant time step size = 0.25 .
The plate center-point displacement and rotation components are shown in Figure 16a,b, respectively. Good qualitative agreement is observed between the predictions obtained with the plate and beam models. Lateral buckling occurs at about 0.32 into the simulation. The buckling load predicted by the plate model is slightly higher than that predicted by the beam model, probably because the clamping of the plate along edge AB provides a stiffer boundary condition than the clamping of the beam at its root. In the post-buckling regime, elastic vibrations are superimposed onto the overall motion imparted by the crank. The plate becomes significantly softer in bending due to its large twisting allowed by the spherical joint: Figure 16b shows the sudden appearance of rotation component about unit vector at buckling.
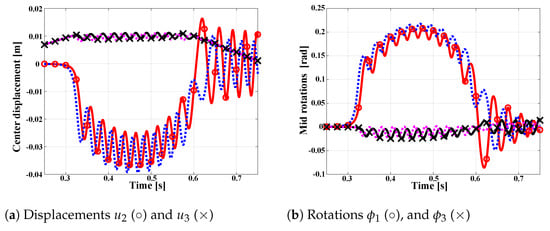
Figure 16.
Center-point displacement and rotation: plate model (solid line); beam model (dashed line).
Prior to buckling, the plate resists the loads applied by the crank-link mechanism with very small in-plane deformations and stresses. When buckling occurs, twisting of the plate renders it much softer in the vertical direction, offering little resistance to further crank rotation. Figure 17 shows the driving moment applied to the crank at point G versus crank rotation angle . Note the linear increase in this moment up to 210 , followed by an abrupt drop at buckling. Excellent quantitative agreement is observed between the plate and beam models.
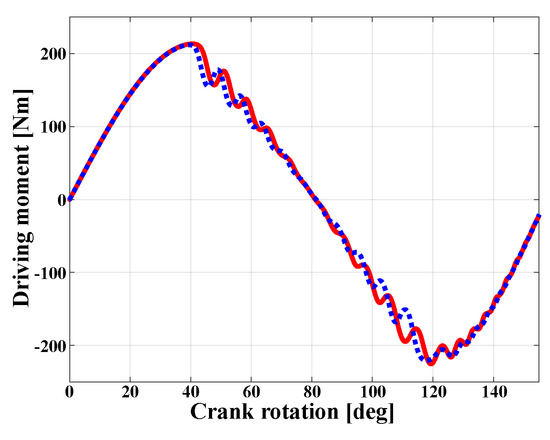
Figure 17.
Driving moment for the revolute joint at point G: plate model (solid line); beam model (dashed line).
Figure 18 shows the bending and twisting moments at point M, see Figure 15. Prior to buckling, these moments vanish because the plate is loaded in its own plane only. At buckling, the plate bends out of plane and twists, generating large bending moment and twisting moment components. These plate quantities cannot be related to their beam counterparts directly. The abrupt onset of out-of-plane deformation at buckling results in lateral oscillations of the plate.
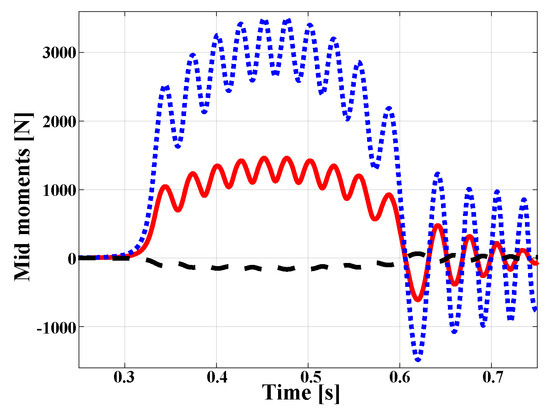
Figure 18.
Bending moment (dashed line), (dotted line), and (solid line) at point M.
The tip of the plate, point T, is connected to the spherical joint at point F through a very short rigid connection (d = 0.1 ), see Figure 15. Due to the high lateral stiffness of the crank-link mechanism, point T experiences a small displacement in the direction of unit vector , denoted , and the corresponding velocity components is denoted . Figure 19 shows the phase plot of velocity component versus displacement component . Because this graph reflects the overall, integrated response of the structure, good correlation is observed between the plate and beam models. Finally, rotation components and about unit vectors and , respectively, for the spherical joint are shown in Figure 20.
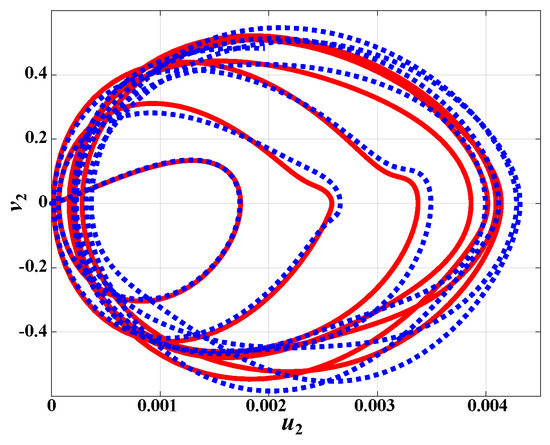
Figure 19.
Phase plot at point T: plate model (solid line); beam model (dashed line).
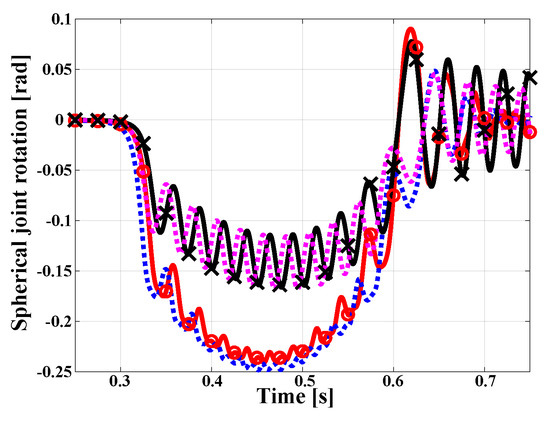
Figure 20.
Rotation components for the spherical joint: (∘), and (×): plate model, solid line; beam model, dashed line.
7. Conclusions
A finite element approach for the analysis of plate and shell structures was presented. It is based on the motion formalism that (1) uses configuration and motion to describe the kinematics of flexible multibody systems, (2) recognizes that these are members of the Special Euclidean group, thereby coupling their displacement and rotation components, and (3) resolves all tensors components in local frames.
The following advantages result. (1) The proposed shell element interfaces easily with other finite elements to provide a comprehensive solution to the modeling of flexible multibody systems. (2) Large amplitude motions are handled properly, eliminating the potential occurrence of singularities. (3) The formulation is intrinsic: Position and rotation variables describing the configuration of structural components with respect to an inertial system are eliminated from the governing equations. (4) Deformation measures resulting from the systematic use of the formalism are objective and tensorial. (5) The mass and stiffness matrices of the shell elements remain constant throughout the simulation, resulting in improved computational efficiency. (6) Parameterizations are used for local transformations only. (7) Because the formulation is objective, equilibrium equations remain invariant under superimposed rigid-body motions, leading to a reduced order of nonlinearity. (8) The element appear to be locking free.
Author Contributions
Conceptualization, V.S. and O.B.; software, O.B.; validation, O.B. and V.S.; writing and editing, O.B. and V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
Valentin Sonneville acknowledges support from the Technical University of Munich—Institute for Advanced Study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Solution of the Implicit Interpolation Scheme
Appendix A.1. The Case of the Vectorial Parameterization of Motion
Generic interpolation scheme (18) involves motion parameter vectors , which are nonlinear functions of the interpolated motion tensor . It is helpful to express motion parameter vectors in terms of the motion parameter vectors associated with the relative motions at the nodes. Consider two nodes, denoted nodes j and k, and the associated relative motion tensors and , respectively. Next, the relative motion tensor that brings the motion at node j to that at node k is defined as:
Although motion tensors and are spatially dependent, motion tensor is not.
The motion parameter vectors associated with the relative motions at the nodes are and present the following properties:
which imply for . A total of independent relative motions at the nodes remain.
Because , motion composition Formulas (8) and (9) yields:
where parameters , , and are associated with motion parameter vectors , , and , respectively, see Equation (7). The relationship between relative motions and their counterparts at the nodes is nonlinear due to the last terms on the right-hand sides of Equations (A3) and (A4). A generic interpolation Formula (18) will be used to eliminate these nonlinear terms.
Generic interpolation Formula (18) implies the vanishing of the second term on the right-hand side of the first equation and of the first and third terms on the right-hand side of the second, leading to:
where . These equations show that spatially dependent relative motion vectors that appear in the generic interpolation scheme can be expressed as linear combinations of the spatially independent relative motions at the nodes .
Multiplying Equations (A5) and (A6) by and summing over all nodes yields:
where the left-hand side of the second equation vanishes due to generic interpolation Formula (18). Properties (A2) imply for and , leading to the vanishing of the right-hand side of the second equation, which, hence, is then satisfied identically. This is not unexpected because the generic interpolation formula was used in the derivation of these equations. In view of properties (A2), Equation (A7) reduces to:
The property of partition of unity was used in the derivation of this last expression. Equation (A6) can be recast as:
This expression shows that relative motion vector is closely related to the relative motion vectors at the nodes, . This relationship is further explored below.
Appendix A.2. The Case of the Euler-Rodrigues Parameterization
For the Euler–Rodrigues parameterization of motion, , and hence, . With these simplifications, Equation (A10) reduces to:
where dual scalar , defined by Equation (A9), becomes:
Equation (A11) expresses relative motion vector as a weighted average of the relative motions at the nodes; the weighting factors are the classical shape functions of the finite element method. Dual scalar , defined by Equation (A12), acts as a normalization factor that is a function of the relative motions at the nodes only. Note that while relative motion vectors are spatially dependent, the relative motions at the nodes are not.
References
- Bauchau, O.A.; Craig, J.I. Structural Analysis with Applications to Aerospace Structures; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Reissner, E. The Effect of Transverse Shear Deformation on the Bending of Elastic Plates. Z. Angew. Math. Phys. 1945, 12, A.69–A.77. [Google Scholar] [CrossRef]
- Reissner, E. On Bending of Elastic Plates. Q. Appl. Math. 1947, 5, 55–68. [Google Scholar] [CrossRef] [Green Version]
- Mindlin, R.D. Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic Elastic Plates. J. Appl. Mech. 1951, 18, 31–38. [Google Scholar] [CrossRef]
- Librescu, L. Elastostatics and Kinetics of Anisotropic and Heterogeneous Shell-Type Structures; Noordhoff International Publishing: Leyden, The Netherlands, 1975. [Google Scholar]
- Whitney, J.M. Structural Analysis of Laminated Anisotropic Plates; Technomic Publishing Company: Lancaster, UK, 1987. [Google Scholar]
- Reddy, J.N. Mechanics of Laminated Composite Plates; CRC Press: Boca Raton, MA, USA, 1996. [Google Scholar]
- Christensen, R.M. Mechanics of Composite Materials; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Tsai, S.W.; Hahn, H.T. Introduction to Composite Materials; Technomic Publishing Co., Inc.: Westport, CT, USA, 1980. [Google Scholar]
- Carrera, E. Developments, Ideas, and Evaluations Based upon Reissner’s Mixed Variational Theorem in The Modeling of Multilayered Plates and Shells. Appl. Mech. Rev. 2001, 54, 301–329. [Google Scholar] [CrossRef]
- Han, S.L.; Bauchau, O.A. A Novel, Single-Layer Model for Composite Plates Using Local-Global Approach. Eur. J. Mech. A/Solids 2016, 60, 1–16. [Google Scholar] [CrossRef]
- Timoshenko, S.P. On the Transverse Vibrations of Bars of Uniform Cross-Section. Philos. Mag. 1921, 43, 125–131. [Google Scholar] [CrossRef] [Green Version]
- Giavotto, V.; Borri, M.; Mantegazza, P.; Ghiringhelli, G.; Carmaschi, V.; Maffioli, G.C.; Mussi, F. Anisotropic Beam Theory and Applications. Comput. Struct. 1983, 16, 403–413. [Google Scholar] [CrossRef]
- Hodges, D.H. Nonlinear Composite Beam Theory; AIAA: Reston, VA, USA, 2006. [Google Scholar]
- Bauchau, O.A.; Han, S.L. Three-Dimensional Beam Theory for Flexible Multibody Dynamics. J. Comput. Nonlinear Dyn. 2014, 9, 041011. [Google Scholar] [CrossRef]
- Cosserat, E.; Cosserat, F. Théorie des Corps Déformables, 2nd ed.; A. Hermann et Fils: Paris, France, 1909. [Google Scholar]
- Naghdi, P.M. The Theory of Plates and Shells. In Handbuch der Physik; Flügge, S., Ed.; Springer: Berlin, Germany, 1972; Volume 2, pp. 425–640. [Google Scholar]
- Stuelpnagel, J. On the Parameterization of the Three-Dimensional Rotation Group. SIAM Rev. 1964, 6, 422–430. [Google Scholar] [CrossRef] [Green Version]
- Bauchau, O.A. Flexible Multibody Dynamics. In Solid Mechanics and Its Applications; Springer: Dordrecht, The Netherlands, 2011; Volume 176. [Google Scholar]
- Ball, R.S. A Treatise on the Theory of Screws; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Bottema, O.; Roth, B. Theoretical Kinematics; Dover Publications, Inc.: New York, NY, USA, 1979. [Google Scholar]
- McCarthy, J.M. An Introduction to Theoretical Kinematics; The MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Murray, R.M.; Li, Z.; Sastry, S.S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Selig, J.M. Geometric Fundamentals of Robotics; Monographs in Computer Science; Springer: New York, NY, USA, 2005. [Google Scholar]
- Angeles, J. Fundamentals of Robotic Mechanical Systems. Theory, Methods, and Algorithms; Mechanical Engineering Series; Springer International Publishing: New York, NY, USA, 2014; Volume 124. [Google Scholar] [CrossRef]
- Müller, A.; Terze, Z. The Significance of the Configuration Space Lie Group for the Constraint Satisfaction in Numerical Time Integration of Multibody Systems. Mech. Mach. Theory 2014, 82, 173–202. [Google Scholar] [CrossRef] [Green Version]
- Müller, A. A Note on the Motion Representation and Configuration Update in Time Stepping Schemes for the Constrained Rigid Body. BIT Numer. Math. 2016, 56, 995–1015. [Google Scholar] [CrossRef]
- Müller, A. Screw and Lie Group Theory in Multibody Kinematics. Multibody Syst. Dyn. 2018, 43, 37–70. [Google Scholar] [CrossRef] [Green Version]
- Borri, M.; Bottasso, C.L. An Intrinsic Beam Model Based on a Helicoidal Approximation. Part I: Formulation. Int. J. Numer. Methods Eng. 1994, 37, 2267–2289. [Google Scholar] [CrossRef]
- Sonneville, V.; Cardona, A.; Brüls, O. Geometrically Exact Beam Finite Element Formulated on the Special Euclidean Group SE(3). Comput. Methods Appl. Mech. Eng. 2014, 268, 451–474. [Google Scholar] [CrossRef]
- Merlini, T.; Morandini, M. The Helicoidal Modeling in Computational Finite Elasticity. Part I: Variational Formulation. Int. J. Solids Struct. 2004, 41, 5351–5381. [Google Scholar] [CrossRef]
- Sonneville, V. A Geometric Local Frame Approach for Flexible Multibody Systems. Ph.D. Thesis, Université de Liège, Liège, Germany, 2015. [Google Scholar]
- Study, E. Geometrie der Dynamen; Teubner: Leipzig, Germany, 1903. [Google Scholar]
- Martinez, J.M.R.; Duffy, J. The Principle of Transference: History, Statement And Proof. Mech. Mach. Theory 1993, 28, 165–177. [Google Scholar] [CrossRef]
- Han, S.L.; Bauchau, O.A. Manipulation of Motion via Dual Entities. Nonlinear Dyn. 2016, 85, 509–524. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Choi, J.Y. The Vector Parameterization of Motion. Nonlinear Dyn. 2003, 33, 165–188. [Google Scholar] [CrossRef]
- Chasles, M. Note sur les Propriétés Générales du Système de deux Corps Semblables entre eux et Placés d’une Manière Quelconque dans l’Espace; et sur le Déplacement Fini, ou Infiniment Petit d’un Corps Solide Libre. Bulletin des Sciences Mathématiques Férussac 1830, 14, 321–326. [Google Scholar]
- Angeles, J. The Application of Dual Algebra to Kinematic Analysis. In Computational Methods in Mechanical Systems; Angeles, J., Zakhariev, E., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 161, pp. 3–31. [Google Scholar]
- Bauchau, O.A.; Trainelli, L. The Vectorial Parameterization of Rotation. Nonlinear Dyn. 2003, 32, 71–92. [Google Scholar] [CrossRef]
- Hughes, T.J.R. The Finite Element Method; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Sonneville, V.; Brüls, O.; Bauchau, O.A. Interpolation Schemes for Geometrically Exact Beams: A Motion Approach. Int. J. Numer. Methods Eng. 2017, 112, 1129–1153. [Google Scholar] [CrossRef]
- Han, S.L.; Bauchau, O.A. On the Global Interpolation of Motion. Comput. Methods Appl. Mech. Eng. 2018, 337, 352–386. [Google Scholar] [CrossRef]
- Malvern, L.E. Introduction to the Mechanics of a Continuous Medium; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1969. [Google Scholar]
- Dimentberg, F.M. The Screw Calculus and Its Applications; Technical Report AD 680993, Clearinghouse for Federal and Scientific Technical Information; Foreign Technology Division: Springfield, VA, USA, 1968. [Google Scholar]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill Book Company: New York, NY, USA, 1959. [Google Scholar]
- Sutyrin, V.G.; Hodges, D.H. On Asymptotically Correct Linear Laminated Plate Theory. Int. J. Solids Struct. 1996, 33, 3649–3671. [Google Scholar] [CrossRef]
- Sutyrin, V.G. Derivation of Plate Theory Accounting Asymptotically Correct Shear Deformation. J. Appl. Mech. 1997, 64, 905–915. [Google Scholar] [CrossRef]
- Yu, W.B.; Hodges, D.H.; Volovoi, V.V. Asymptotic Generalization of Reissner-Mindlin theory: Accurate Three-Dimensional Recovery for Composite Shells. Comput. Methods Appl. Mech. Eng. 2002, 191, 5087–5109. [Google Scholar] [CrossRef]
- Yu, W.B.; Hodges, D.H. A Geometrically Nonlinear Shear Deformation Theory for Composite Shells. J. Appl. Mech. 2004, 71, 1–9. [Google Scholar] [CrossRef]
- Carrera, E.; Demasi, L. Classical and Advanced Multilayered Plate Elements Based upon PVD and RMVT. Part 1: Derivation of Finite Element Matrices. Int. J. Numer. Methods Eng. 2002, 55, 191–231. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on The Mathematical Theory of Elasticity, 4th ed.; Dover: New York, NY, USA, 1944. [Google Scholar]
- Hodges, D.H. Geometrically Exact, Intrinsic Theory for Dynamics of Curved and Twisted Anisotropic Beams. AIAA J. 2003, 41, 1131–1137. [Google Scholar] [CrossRef]
- Bucalem, M.L.; Bathe, K.J. Finite Element Analysis of Shell Structures. Arch. Comput. Methods Eng. 1997, 4, 3–61. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).