A Practice-Oriented Procedure for Seismic Reliability Assessment of RC Structures Affected by Carbonation-Induced Degradation
Abstract
:1. Introduction
2. Outline of Theoretical Models for Carbonation-Induced Degradation Phenomena
2.1. Carbonation and Corrosion Models
- -
- ke is environmental function (-);
- -
- kc is execution transfer parameter (-);
- -
- kt is regression parameter (-);
- -
- RACC,0−1 is inverse effective carbonation resistance of concrete ((mm2/years)/(kg/m3));
- -
- εt is error term;
- -
- Cs is the CO2 concentration (kg/m3);
- -
- Wt is the weather function, intended at simulating the effects of driving rains on carbonation of the member under consideration (-).
- -
- β is a parameter controlling propagation (-);
- -
- p (t − td) is a measure of the propagation phenomenon (mm), which can be equalled to the loss of radius in steel bars xcorr(t).
- -
- (d’ − ϕ/2)/ϕ is the ratio between the initial concrete cover and the initial bar diameter (mm);
- -
- ft,sp is the splitting strength of concrete;
- -
- a1, a2, and a3 are calibration parameters.
2.2. Influence of Rebar Corrosion on the Chord Rotation
3. Outline of the Bases of Reliability Analysis
3.1. Risk Evaluation Methods
3.1.1. The “2000 SAC/FEMA” Method
- the pseudo-acceleration value Sa(Tf) corresponding to a period T close to the fundamental period of the structure Tf is often assumed as the intensity measure (IM) for seismic signals which can be scaled for covering the entire relevant integration domain;
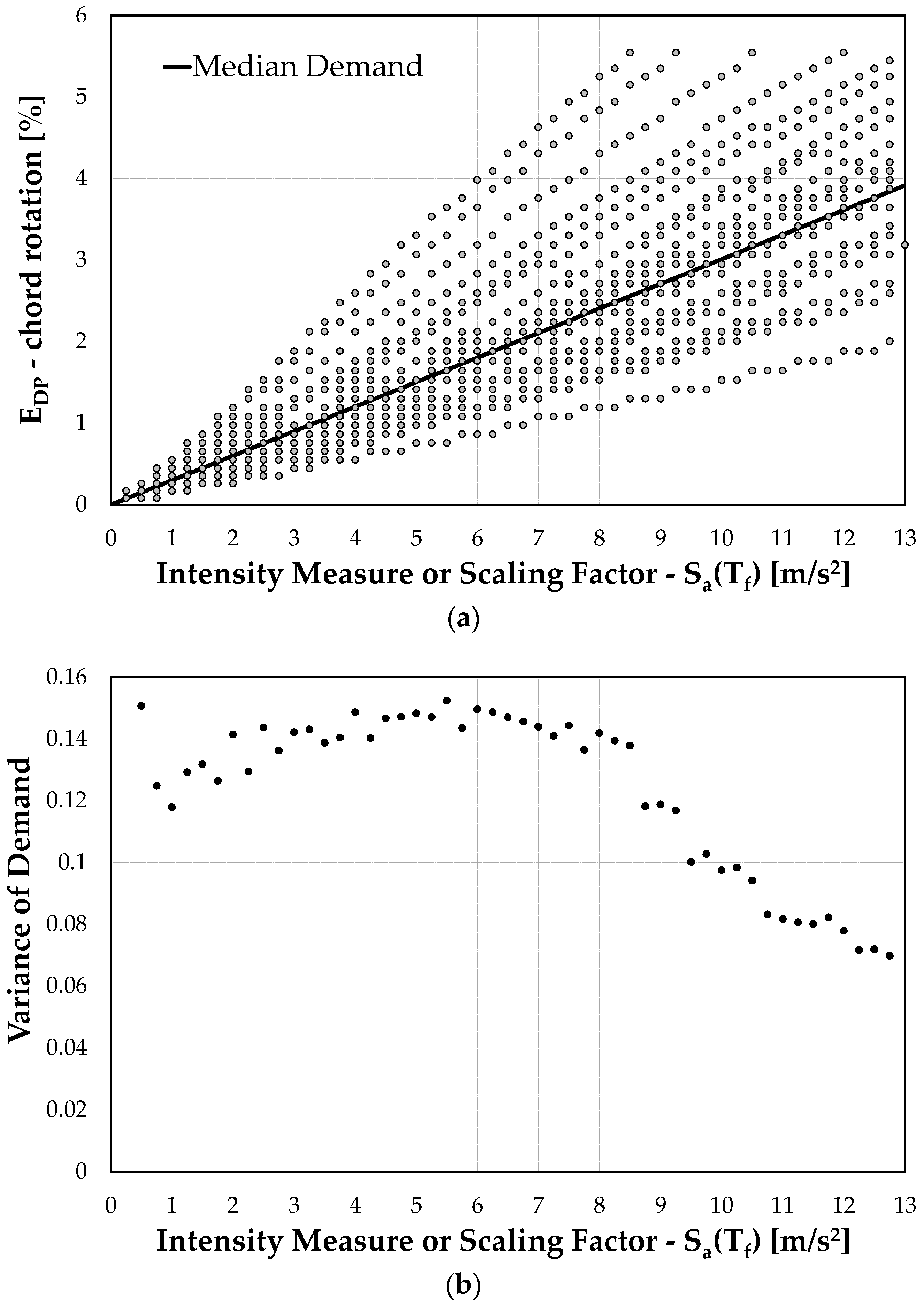
- to quantify seismic response of structures, a consistent engineering demand parameter (EDP) is defined. While a comparative analysis of those parameters can be found in [29], in the present paper, chord rotation is considered as the demand measure, as usually adopted in similar applications;
- demand “D” is a log-normal random variable, characterized by the median value . The relationship between the intensity measure sa and the median demand is assumed to be a power law, as follows:
- is the annual probability of occurrence of an earthquake whose intensity Sa is larger than the value sa, which corresponds to a median demand equal to median capacity for a given Limit State (. Hence, this term represents the probability for the structure to achieve the LS of interest considering both capacity and demand as deterministic variables: the former one is defined as a function of the geometric and mechanical model of the structure members and the latter one is basically defined as a function of the seismic intensity measure;
- represents a magnification factor (MF) accounting for the probabilistic nature of seismic demand (the “record-to-record” variability, related to the accelerograms chosen for the analyses) and structural capacity. In particular and represent the variances of demand and capacity (associated with a certain LS), both regarded as random variables log-normally distributed.
3.1.2. The Equivalent Constant Rate (ECR)
- -
- PLS(t) expresses the time-evolution of PLS and, according to the authors, could be approximately derived from the regression parameters that describe the evolution of seismic demand and its dispersion during time;
- -
- α is the societal discount rate, which can be fixed for instance at 0.1%. In this case, the ECR will be approximately equal to the average rate, defined in the following lines.
3.2. Analysis Procedure
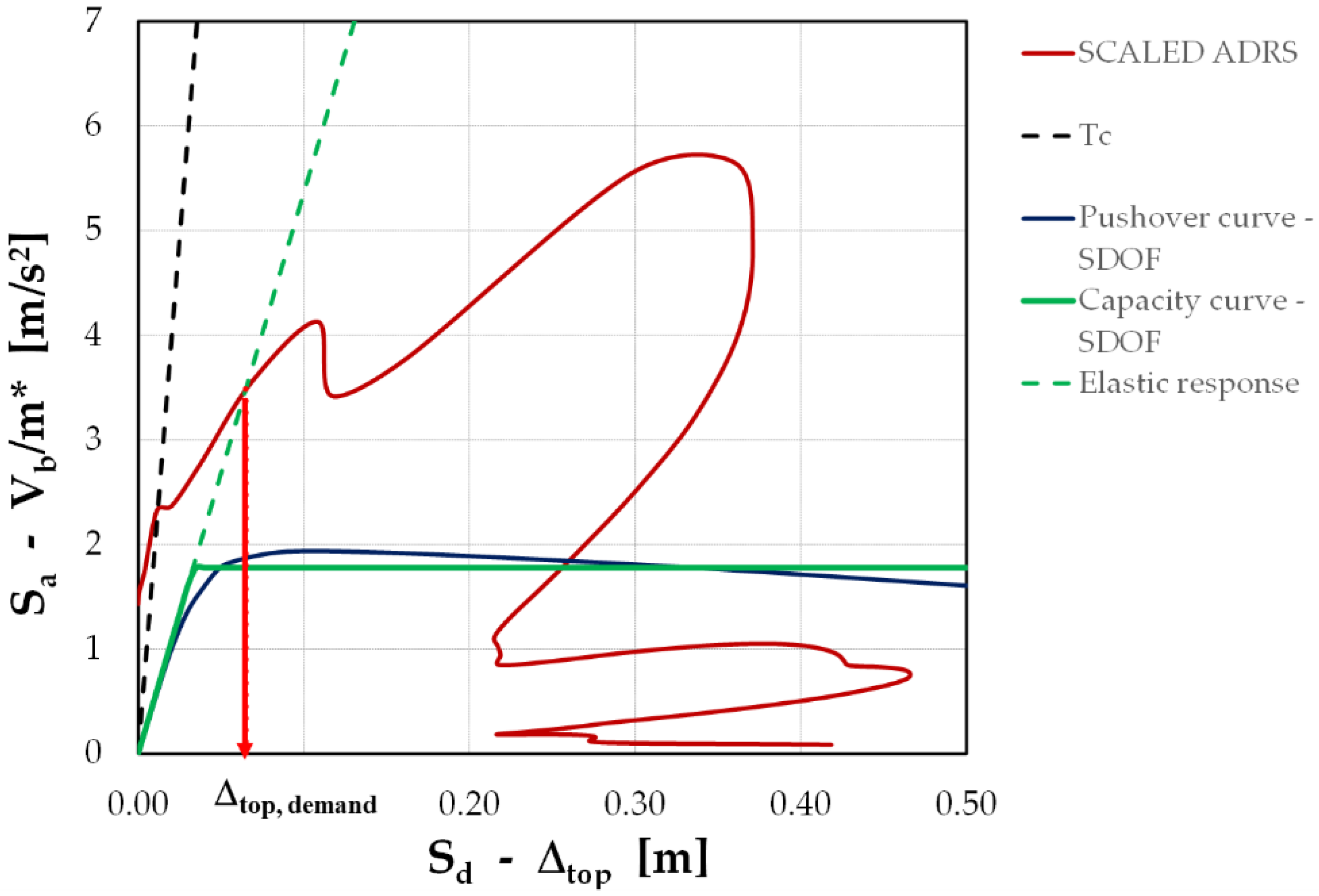
3.2.1. Use of Nonlinear Static (Pushover) Analysis
3.2.2. Seismic Demand Determination
- -
- μ is the ductility factor, defined as the ratio between the maximum displacement and the yield displacement;
- -
- Rμ is the reduction factor due to ductility (i.e., due to hysteretic energy dissipation of ductile structures);
- -
- T0 is the transition period, which is assumed to be equal to the characteristic period TC, which represents the intersection between the constant pseudo-acceleration branch and the constant pseudo-velocity one according to the Newmark and Hall idealization of seismic spectra [32].
3.2.3. Evaluation of the PLS and Extension to the Case of Ageing Structures
4. Parametric Analysis
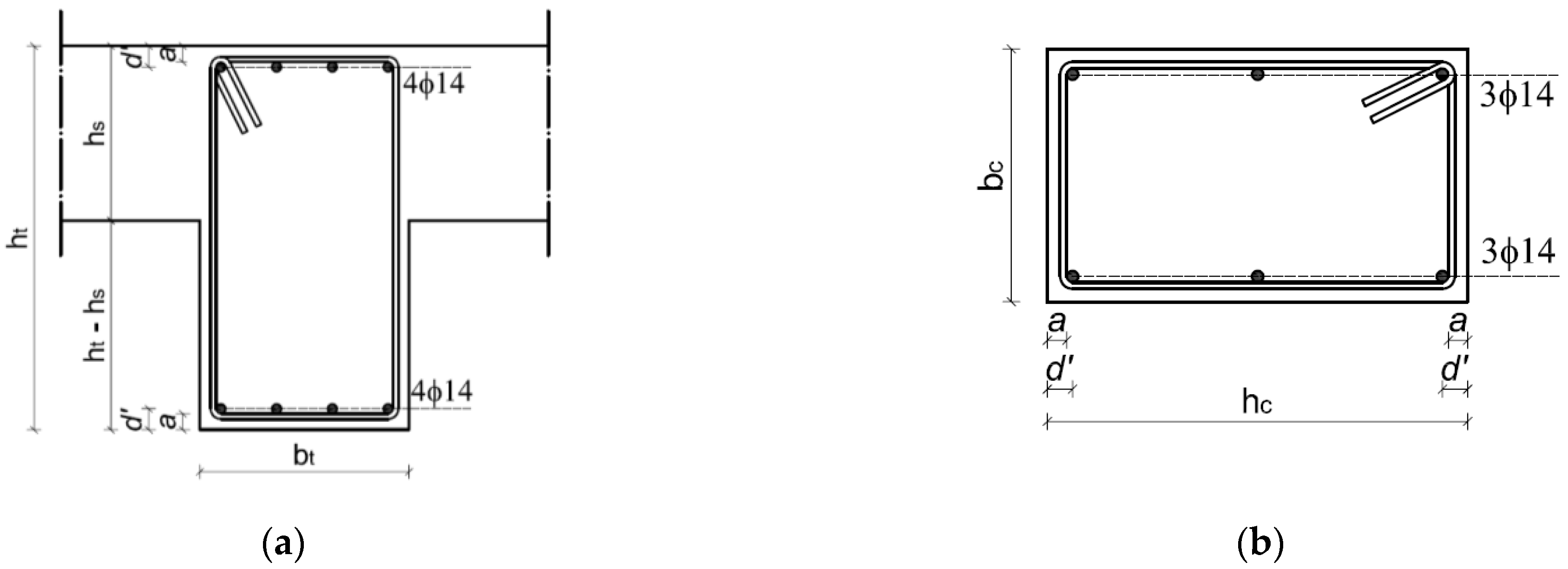
4.1. Structure Presentation
4.2. Material Degradation Modelling
- Scenario 1: median (50%) fractiles are used to evaluate RACC,0−1 and Vcorr;
- Scenario 2: 95% fractiles are used to evaluate RACC,0−1 and Vcorr.
4.3. Parametric Field
4.4. Application
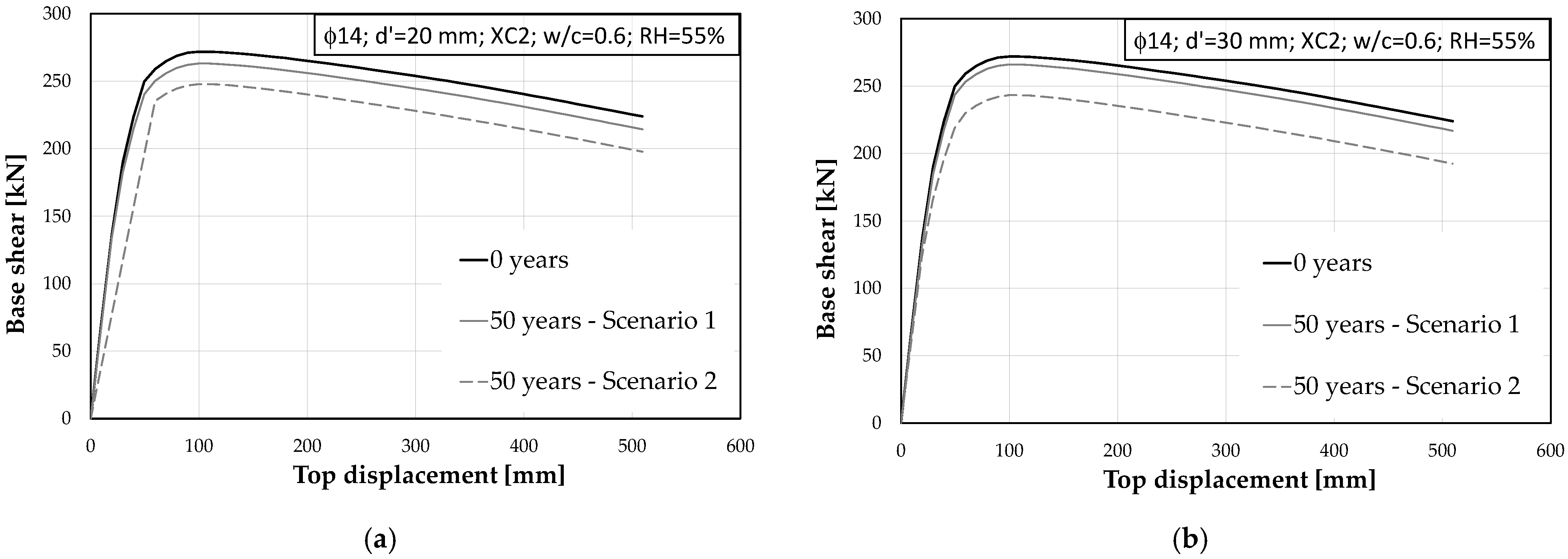
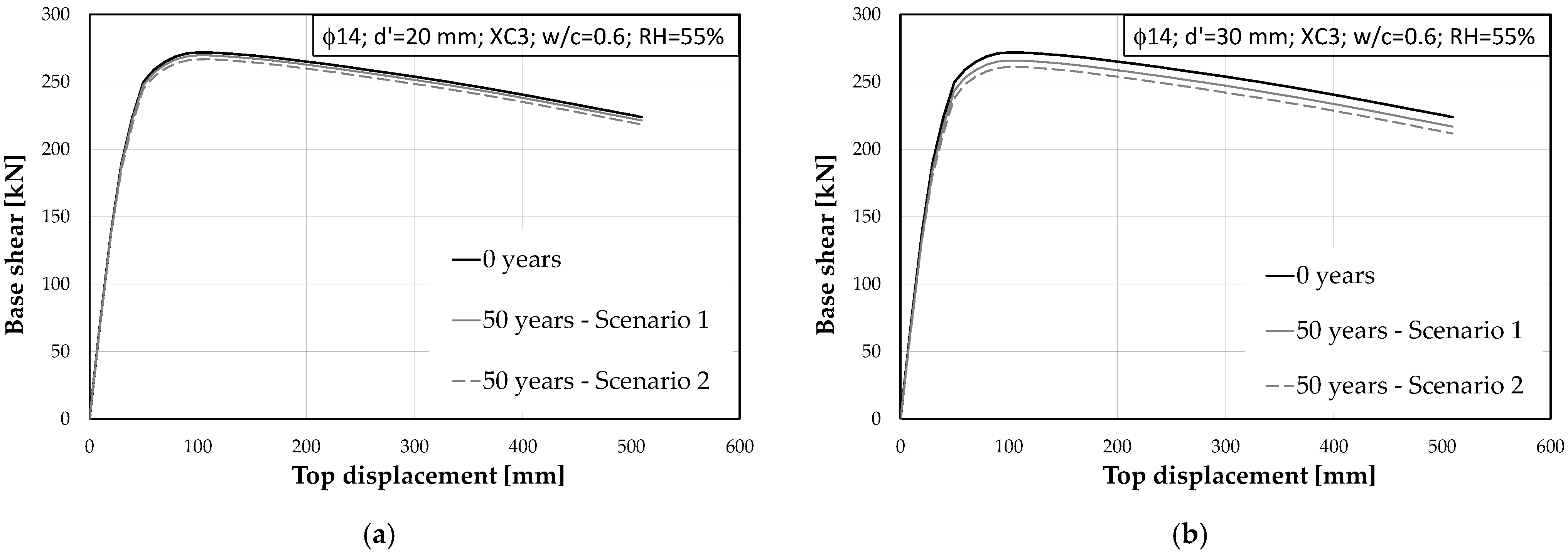
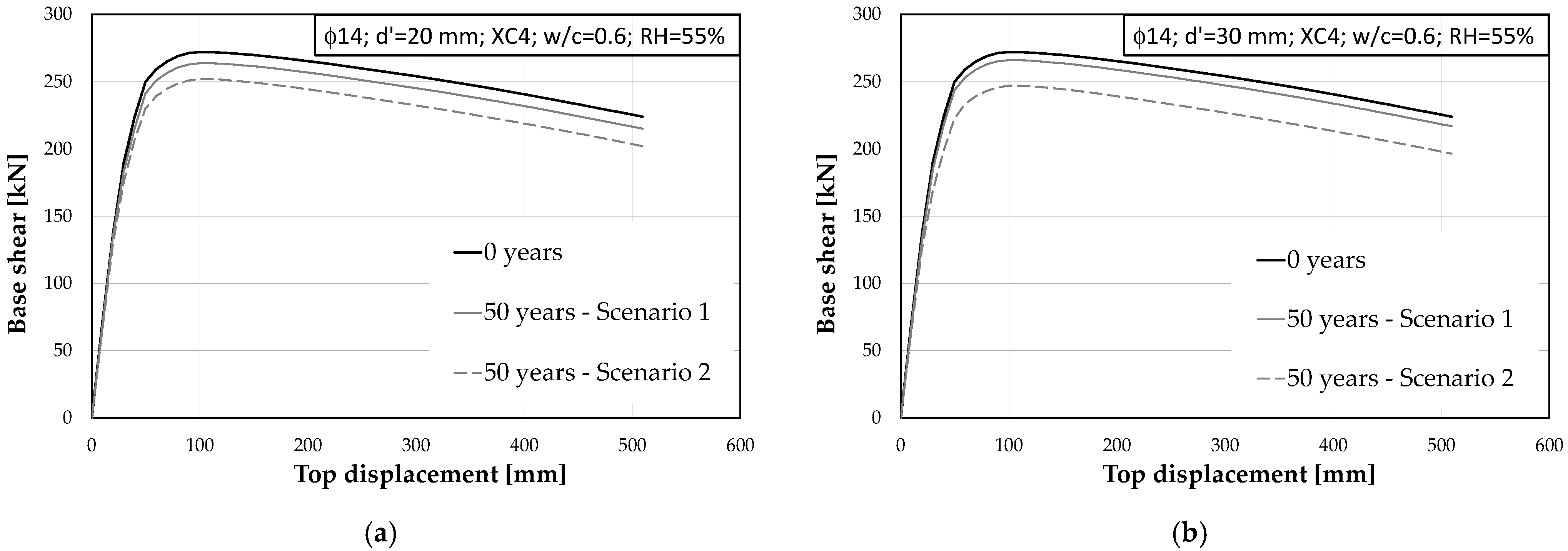
4.4.1. Time-Evolution of Pushover Curves
4.4.2. Evaluation of Median Demand and Its Dispersion
4.4.3. Evaluation of PLS
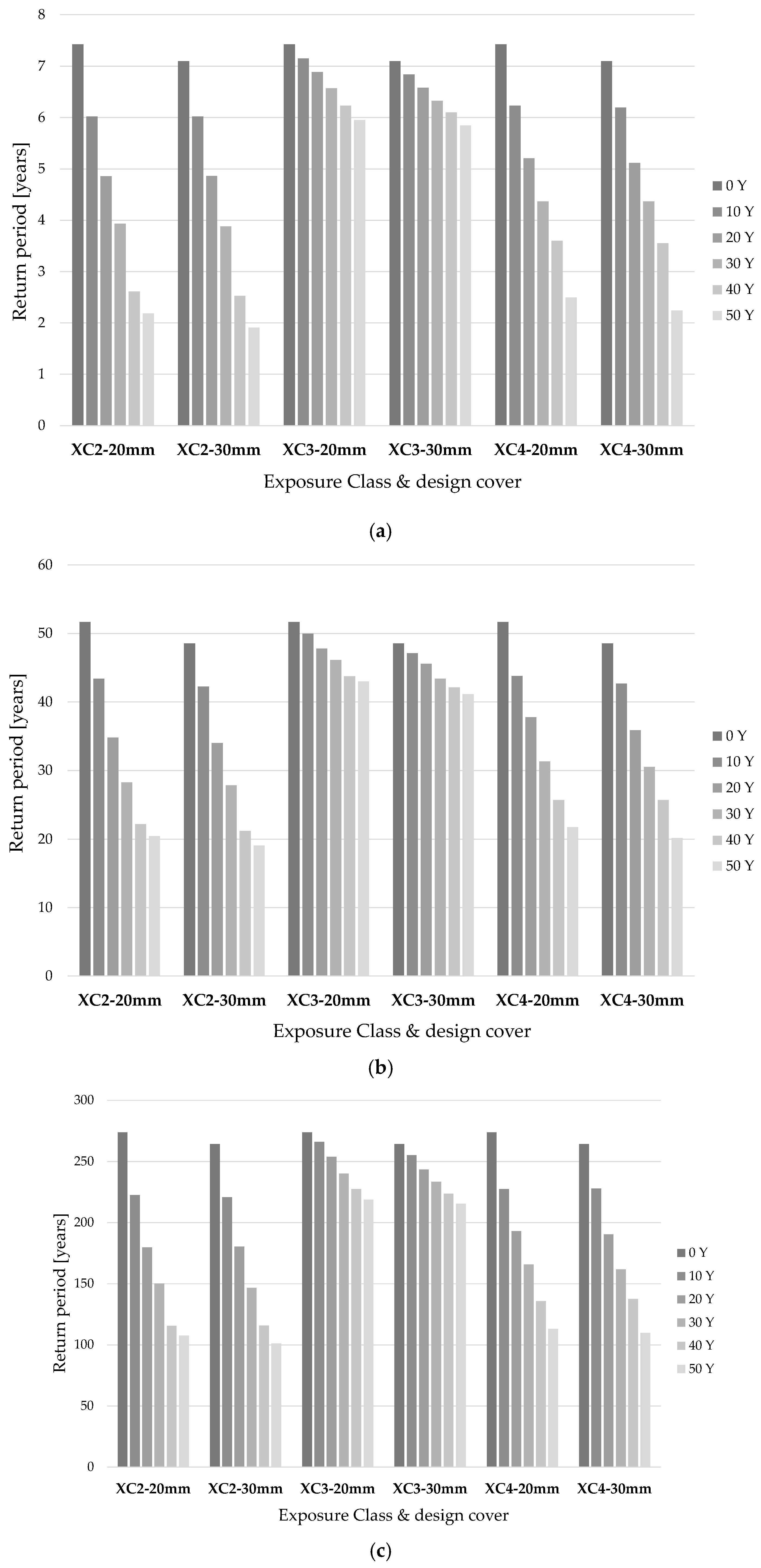
4.4.4. Results of the 1st Scenario: 50% Fractiles for Evaluation of RACC,0−1 and Vcorr
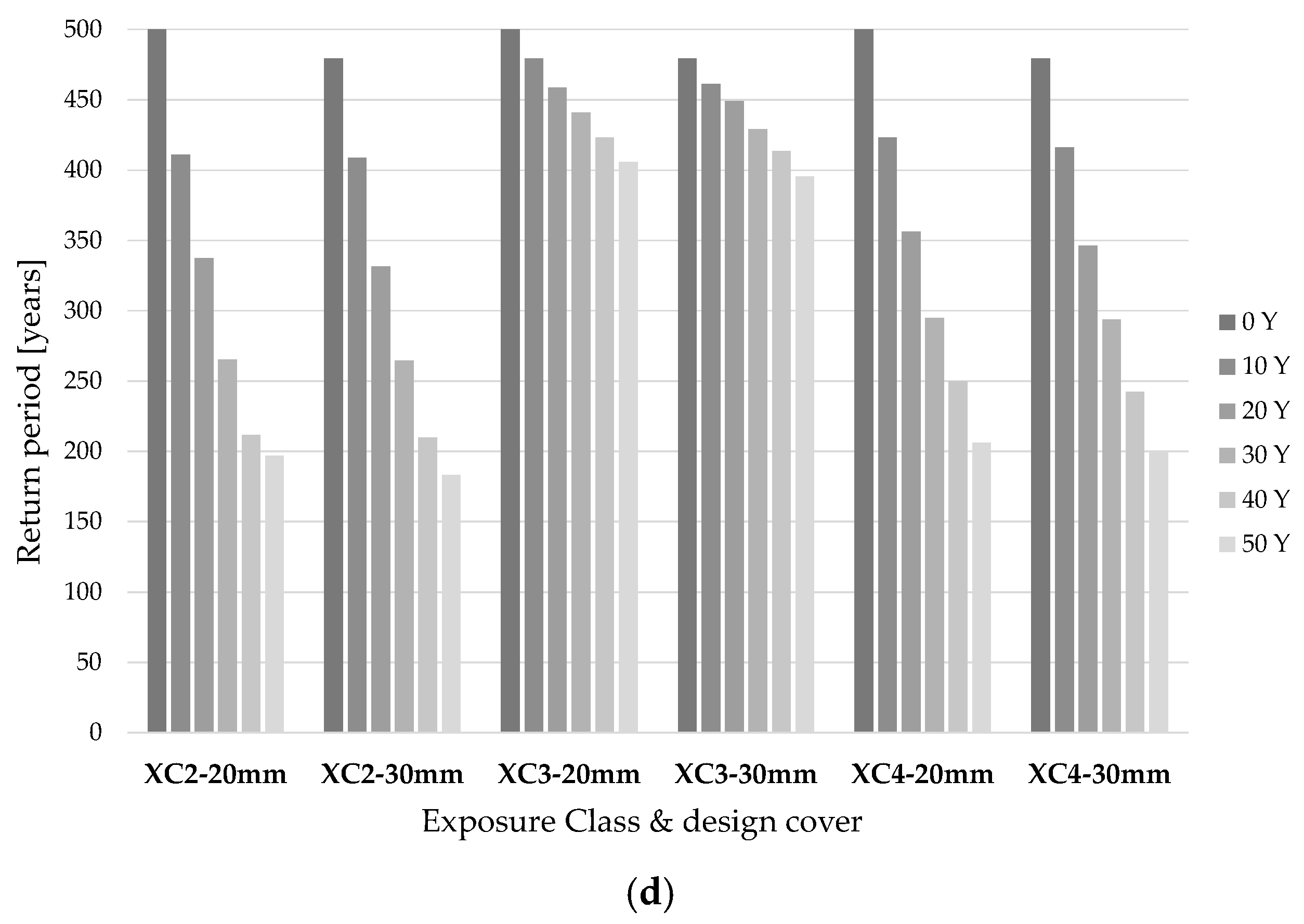
4.4.5. Results of the 2nd Scenario: 95% Fractiles for Evaluation of RACC,0−1 and Vcorr
4.4.6. Results in Terms of Equivalent Constant Rate (ECR)
4.5. Discussion
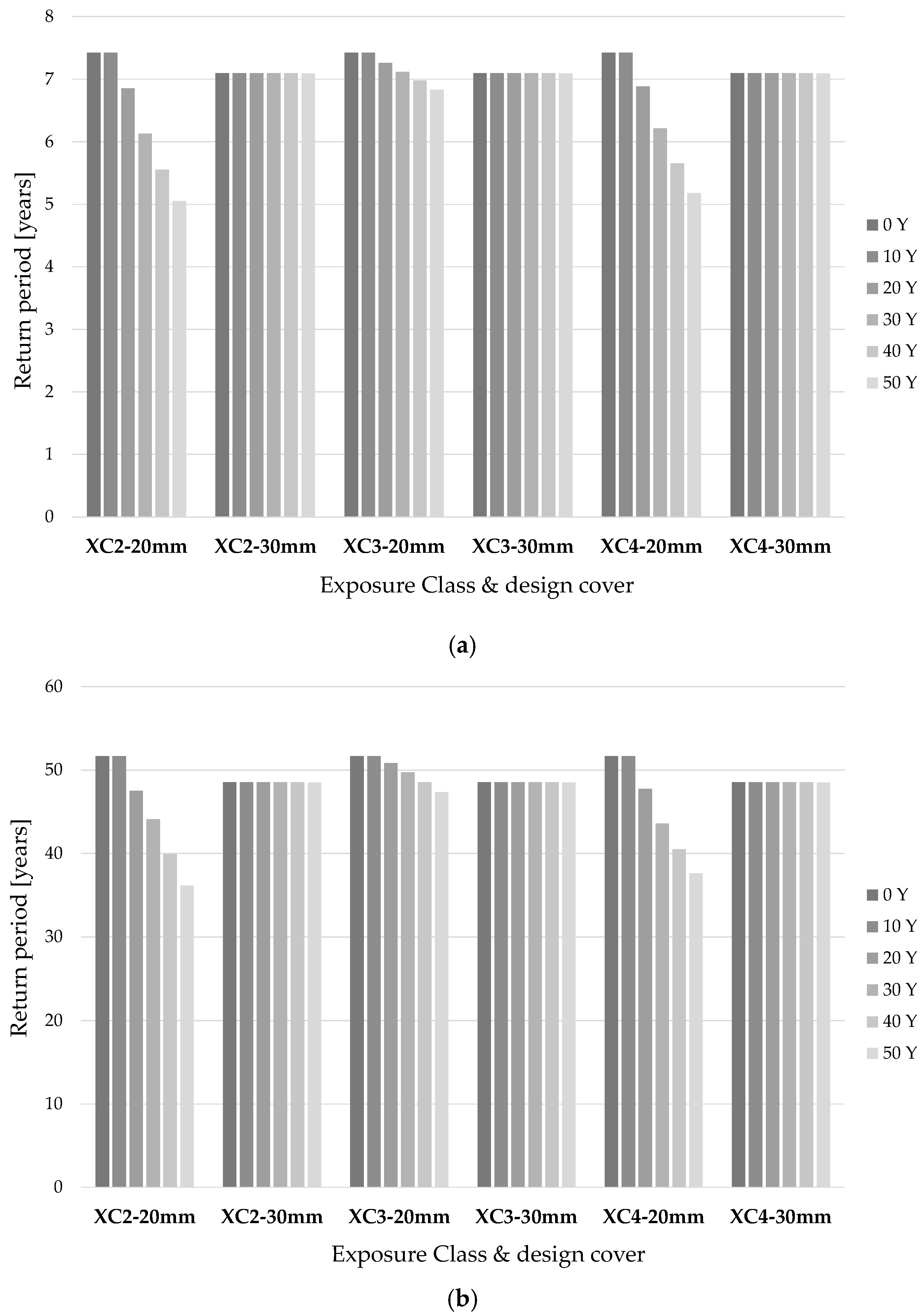
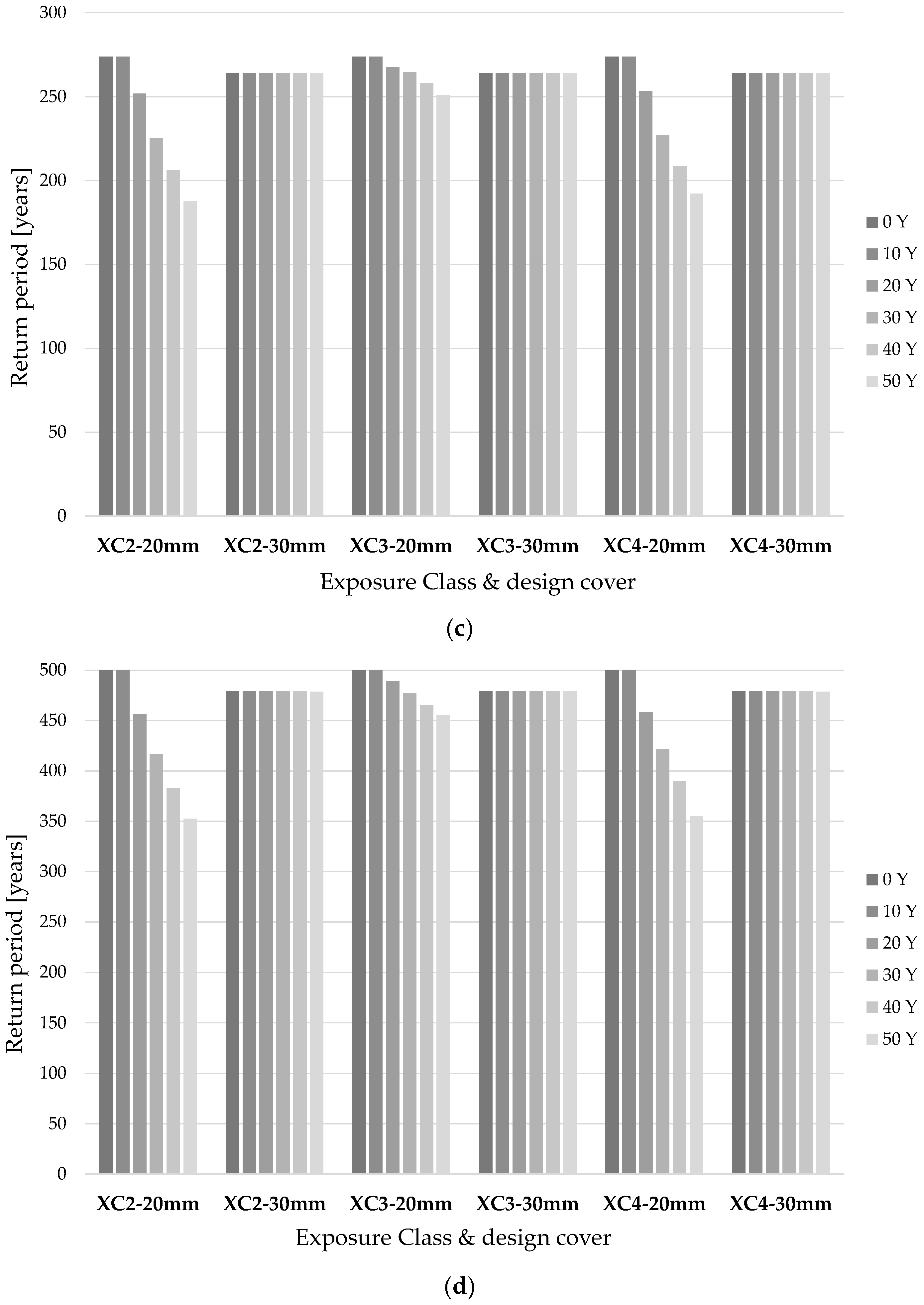
- the effects of corrosion due to carbonation-induced degradation on RC members cannot be generally neglected, especially when the design cover is up to 20 mm. In these cases, a non-negligible loss in terms of the return period is observed on the structure fully exposed to XC2 and XC4 environmental actions;
- if the parameters RACC,0−1 and Vcorr are described by their median value (Scenario 1), concrete cover thickness plays a vital role in controlling the time evolution of RC sections. It can significantly delay the development of degradation, increasing the depassivation time (td) from 10 years (with a 20 mm cover) to approximately 50 years (with a 30 mm cover);
- if the parameters RACC,0−1 and Vcorr are described by their median value (Scenario 1), the usage of a design cover of 30 mm avoids significant reductions in the return period, while a design cover of up to 20 mm leads to premature degradation. This result is explained by the fact that in this condition, the depassivation time (td) is approximately equal to the theoretical service life Td; consequently, material degradation effects arise if the time span is expanded;
- the preliminary approach presented in this paper can also be employed in order to confirm the code provisions concerning the minimum values of design cover for different structural classes and exposure classes, reported in EC2 [7] confirm that in ordinary conditions (structural class S4), a design cover of 30 mm can grant a highly durable performance (in the case of carbonation induced corrosion);
- if the parameters RACC,0−1 and Vcorr are described by their median value (Scenario 1), the effect of the reduction in columns’ chord rotation capacity is still noticeable on the structure for exposure classes XC2 and XC4, when the design cover is up to 20 mm;
- if the parameters RACC,0−1 and Vcorr tend to be much higher than their median value (Scenario 2), no significant differences arise between the effect in the usage of the two values of design cover considered in this work;
- if the parameters RACC,0−1 and Vcorr tend to be much higher than their median value (Scenario 2), the effects of material degradation phenomena are still not really relevant for exposure class XC3, while they highly threaten the structural reliability for XC2 and XC4 exposure classes; indeed, in the former case, the difference between “TR, 0 y” and “TR, 50 y” is less than 20%, while in the latter cases, this difference reaches 60%;
- the variable “TRECR” is a good indicator of structural ageing. As shown in Table 7 and Table 8 (4.4.6.), if the difference between “TR, 0 y” and “TRECR” is up to 10%, the effect of ageing may be neglected, while higher values of this difference certainly imply a safety decrease (in terms of return period) higher than 25% (after 50 years);
- the decay observed in the return period is more pronounced for exposure classes XC2 and XC4 rather than for XC3, which is indeed referred to a “sheltered condition”; this is consistent with the parameters describing the degradation models reported in Section 2;
- the comparison between the two considered scenarios outlines the importance of probabilistic representation of parameters controlling Equations (1)–(4), with particular regard to RACC,0−1 and Vcorr; in the present work, they are employed in a deterministic way, although their randomness can lead to local capacity reduction that may affect the global structural response;
- since RACC,0−1 and Vcorr are defined in statistical terms, it seems evident that a more conservative approach (e.g., the usage of 95% fractiles) can lead to an excessive increase in the minimum value of design cover required to achieve a sufficiently durable performance;
- the considerations written above appear to be valid for each limit state studied.
5. Conclusions
- the effects of material degradation phenomena should be generally taken into account in the seismic reliability assessment of RC structures, if maintenance is not properly realized;
- although the work deals with the common carbonation-induced degradation phenomena that are relevant for all RC structures, the proposed procedure can be applied to any degradation phenomena, with minor specifications about material modelling and structural analysis; it is clear that carbonation-induced degradation induces a “mild” effect in terms of degradation, although it affects the entire member length, while other degradation phenomena (such as chloride ions attack) usually result in a local cross sectional strength reduction;
- the expected reduction in terms of displacement capacity induced by material degradation plays a major role in reducing the seismic reliability of the structure under consideration. As a matter of fact, the combined effect of the concrete cover loss, rebar corrosion and EDP, lim reduction can threaten the structural reliability;
- making use of simple models available in the literature for material degradation phenomena, it is possible to derive a simple expression of the time variation of the structural reliability in terms of return periods TR in a linear way; this approach may be less rigorous than the one presented in [17], but it could lead to more comprehensible results and can be more cost-effective;
- pushover analyses can be implemented for seismic reliability assessment, utilizing natural spectra (directly derived by accelerograms) in order to reproduce the record-to-record variability, as well, since the results of pushover analyses (in terms of risk) are almost equal to typical results of IDAs given in the scientific literature [16];
- the simplified procedure presented herein allows us to also explicitly predict the durability performance granted by a certain structure: for a chosen environment (in terms of exposure class), it is possible to compare the results of this analyses with the EC 8 provision for structural durability [7];
- a significant variability can be expected in the resulting structural response based on the actual rate of propagation and diffusion of the material degradation phenomena, also within the limits foreseen by the predictive models currently available in the literature and mentioned in the present paper.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Commission. EU Buildings Factsheets 2013. Available online: https://ec.europa.eu/energy/eu-buildings-factsheets_en (accessed on 1 August 2021).
- Berto, L.; Vitaliani, R.; Saetta, A.; Simioni, P. Seismic assessment of existing RC structures affected by degradation phenomena. Struct. Saf. 2009, 31, 284–297. [Google Scholar] [CrossRef]
- De Schutter, G. Damage to Concrete Structures, 1st ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Lu, C.; Jin, W.; Liu, R. Reinforcement corrosion-induced cover cracking and its time prediction for reinforced concrete structures. Corros. Sci. 2011, 53, 1337–1347. [Google Scholar] [CrossRef]
- Lay, S.; Schieβl, P. Lifecon Deliverable D 3.2, Service Life Models, “Instructions on Methodology and Application of Models for the Prediction of the Residual Service Life for Classified Environmental Loads and Types of Structures in Europe”. 2003. Available online: https://docplayer.net/49899904-Lifecon-deliverable-d-3-2-service-life-models.html (accessed on 1 September 2021).
- DuraCrete. Probabilistic Performance Based Durability Design of Concrete Structures: Statistical Quantification of the Variables in the Limit State Functions; Report No.: BE 95-1347; CUR: Amsterdam, The Netherlands, 2000. [Google Scholar]
- CEN. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; EN 1992-1-1:2004; Comité Européen de Normalisation: Brussels, Belgium, 2004. [Google Scholar]
- François, R.; Laurens, S.; Deby, F. Steel Corrosion in reinforced concrete. In Corrosion and its Consequences for Reinforced Concrete Structures, 1st ed.; ISTE Press Ltd.: London, UK; Elsevier Ltd.: New York, NY, USA, 2018; pp. 1–41. [Google Scholar]
- Berto, L.; Saetta, A.; Simioni, P. Structural risk assessment of corroding RC structures under seismic excitation. Constr. Build. Mater. 2012, 30, 803–813. [Google Scholar] [CrossRef]
- Kashani, M.M.; Lowes, L.N.; Crewe, A.J.; Alexander, N.A. Phenomenological hysteretic model for corroded reinforcing bars including inelastic buckling and low-cycle fatigue degradation. Comput. Struct. 2015, 156, 58–71. [Google Scholar] [CrossRef] [Green Version]
- Vecchi, F.; Belletti, B. Capacity Assessment of Existing RC Columns. Buildings 2021, 11, 161. [Google Scholar] [CrossRef]
- Erduran, E.; Martinelli, E. Some remarks on the seismic assessment of RC frames affected by carbonation-induced corrosion of steel bars. In Proceedings of the fib CACRCS DAYS 2020: Capacity Assessment of Corroded Reinforced Concrete Structures, on-line event, 1–4 December 2020. [Google Scholar]
- Sohail, M.G.; Kahraman, R.; Ozerkan, N.G.; Alnuaimi, N.A.; Gencturk, B.; Dawood, M.; Belarbi, A. Reinforced Concrete Degradation in the Harsh Climates of the Arabian Gulf: Field Study on 30-to-50-Year-Old Structures. J. Perform. Constr. Fac. 2018, 32, 04018059. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. Open System for Earthquake Engineering Simulation User Command-Language Manual. 2009. Available online: https://OpenSEES.berkeley.edu/OpenSEES/manuals/usermanual/index.html (accessed on 1 September 2021).
- Pinto, P.E.; Giannini, R.; Franchin, P. Specialized methods for seismic problems. In Seismic Reliability Analysis of Structures, 1st ed.; IUSS Press: Pavia, Italy, 2004; pp. 215–218. [Google Scholar]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 SAC Federal Emergency Management Agency Steel Moment Frame Guidelines. ASCE J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef] [Green Version]
- Vamvatsikos, D.; Dolšek, M. Equivalent constant rates for performance-based seismic assessment of ageing structures. Struct. Saf. 2011, 33, 8–18. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, A.C. Incremental Dynamic Analysis. Earthq. Eng. Struct. D 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Fajfar, P. Capacity Spectrum Method Based on Inelastic Demand Spectra. Earthq. Eng. Struct. D 1999, 28, 979–993. [Google Scholar] [CrossRef]
- Dolsek, M.; Fajfar, P. IN2—A Simple Alternative for IDA. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. Paper No. 3353. [Google Scholar]
- Faella, C.; Lima, C.; Martinelli, E. Non-linear static methods for seismic fragility analysis and reliability evaluation of existing structures. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- CNR-DT 212/2013. Recommendations for the Probabilistic Seismic Assessment of Existing Buildings; Consiglio Nazionale delle Ricerche: Rome, Italy, 2013; Available online: http://www.cnr.it/sitocnr/IlCNR/Attivita/NormazioneeCertificazione/DT212.html (accessed on 1 September 2021). (In Italian)
- Lima, C.; Martinelli, E. OpenSEES procedure for implementing reliability analysis of RC frames. In Proceedings of the OpenSEES Days, 2nd Italian Conference, Salerno, Italy, 10–11 June 2015. [Google Scholar]
- FIB. Model Code for Service Life Design; Fédération Internationale du Béton: Lausanne, Switzerland, 2006. [Google Scholar]
- FIB. Model Code for Concrete Structures 2010; Fédération Internationale du Béton: Lausanne, Switzerland, 2013. [Google Scholar]
- Tuutti, K. Corrosion of Steel in Concrete; Swedish Cement and Concrete Research Institute: Stockholm, Sweden, 1982. [Google Scholar]
- DARTS. Durable and Reliable Tunnel Structures: Data, European Commission, Growths 2000, Contract G1RD-CT-2000-00467; Project GrD1-25633; Comité Européen de Normalisation: Brussels, Belgium, 2004. [Google Scholar]
- Siemes, T.; Edvardsen, C. DURACRETE: Service Life Design for Concrete Structures. 1999, pp. 1343–1356. Available online: https://www.irbnet.de/daten/iconda/CIB2068.pdf (accessed on 1 September 2021).
- Faella, C.; Lima, C.; Martinelli, E.; Nigro, E. Comparative Application of Capacity Models for Seismic Vulnerability Evaluation of Existing RC Structures. In Proceedings of the MERCEA’08 Conference, Reggio Calabria, Italy, 8–11 July 2008; pp. 1187–1194. [Google Scholar]
- Kunnath, S.K.; Reinhorn, A.M.; Park, Y.J. Analytical modeling of inelastic seismic response of R/C structures. J. Struct. Eng. 1990, 116, 996–1017. [Google Scholar] [CrossRef]
- Spacone, E.; Filippou, F.C.; Taucer, F.F. Fiber beam-column model for nonlinear analysis of R/C frames. 1: Formulation. Earthq. Eng. Struct. D 1996, 25, 711–725. [Google Scholar] [CrossRef]
- Newmark, N.M.; Hall, W.J. Earthquake Spectra and Design; Earthquake Engineering Research Institute: Berkeley, CA, USA, 1982. [Google Scholar]
- Verderame, G.M.; Ricci, P.; Esposito, M.; Sansiviero, F.C. Le caratteristiche meccaniche degli acciai impiegati nelle strutture in c.a. realizzate dal 1950 al 1980. In Proceedings of the XXVI Convegno Nazionale AICAP “Le Prospettive di Sviluppo delle Opere in Calcestruzzo Strutturale nel Terzo Millennio”, Padova, Italy, 19–21 May 2011. Paper No. 54. [Google Scholar]
- DM 17/01/2018. Italian Technical Code of Constructions; Ministerial Decree: Rome, Italy, 2018. [Google Scholar]
- Federal Emergency Management Agency (FEMA). Quantification of Building Seismic Performance Factors; CreateSpace Independent Publishing Platform: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Pacific Earthquake Engineering Research Center (PEER NGA DATABASE). Available online: http://peer.berkeley.edu/nga (accessed on 1 September 2021).
| TR | ag | F0 | TC | CC | SS |
|---|---|---|---|---|---|
| [years] | [g] | [-] | [s] | [-] | [-] |
| 30 | 0.053 | 2.342 | 0.282 | 1.417 | 1.200 |
| 50 | 0.070 | 2.316 | 0.311 | 1.389 | 1.200 |
| 72 | 0.084 | 2.332 | 0.326 | 1.377 | 1.200 |
| 101 | 0.099 | 2.344 | 0.335 | 1.369 | 1.200 |
| 140 | 0.116 | 2.351 | 0.342 | 1.363 | 1.200 |
| 201 | 0.137 | 2.354 | 0.351 | 1.356 | 1.200 |
| 475 | 0.196 | 2.371 | 0.367 | 1.344 | 1.200 |
| 975 | 0.253 | 2.430 | 0.379 | 1.336 | 1.154 |
| 2475 | 0.336 | 2.497 | 0.403 | 1.319 | 1.065 |
| Exposure Class | Design Cover [mm] | Time [years] | Fractiles for Degradation Parameters RACC,0−1 and Vcorr |
|---|---|---|---|
| XC2 | 20 | From 0 to 50 (steps of 10) | 50% (Scenario 1); 95% (Scenario 2) |
| XC2 | 30 | From 0 to 50 (steps of 10) | 50% (Scenario 1); 95% (Scenario 2) |
| XC3 | 20 | From 0 to 50 (steps of 10) | 50% (Scenario 1); 95% (Scenario 2) |
| XC3 | 30 | From 0 to 50 (steps of 10) | 50% (Scenario 1); 95% (Scenario 2) |
| XC4 | 20 | From 0 to 50 (steps of 10) | 50% (Scenario 1); 95% (Scenario 2) |
| XC4 | 30 | From 0 to 50 (steps of 10) | 50% (Scenario 1); 95% (Scenario 2) |
| a 1 | b 1 | k 2 | k0 2 |
|---|---|---|---|
| 0.0029 | 0.9820 | −2.0958 | 0.0491 |
| Limit State | EDP,lim 1 - | SF 2 m/s2 | PLS,det 3 - | β2D - | Magnif. Factor - | PLS,tot - | TR 4 years |
|---|---|---|---|---|---|---|---|
| IO | 0.002 | 0.70 | 0.1047 | 0.11 | 1.29 | 0.1347 | 7 |
| DL | 0.005 | 1.77 | 0.0148 | 0.12 | 1.31 | 0.0194 | 52 |
| LS | 0.011 | 4.04 | 0.0026 | 0.15 | 1.39 | 0.0037 | 274 |
| IC | 0.015 | 5.42 | 0.0014 | 0.15 | 1.40 | 0.0020 | 502 |
| a 1 | b 1 | k 2 | k0 2 |
|---|---|---|---|
| 0.0030 | 1.0015 | −2.0958 | 0.0491 |
| Limit State | EDP,lim 1 - | SF 2 m/s2 | PLS,det 3 - | β2D - | Magnif. Factor - | PLS,tot - | TR 4 years |
|---|---|---|---|---|---|---|---|
| IO | 0.001 | 0.46 | 0.2534 | 0.27 | 1.81 | 0.4583 | 2 |
| DL | 0.003 | 1.14 | 0.0372 | 0.12 | 1.31 | 0.0489 | 20 |
| LS | 0.008 | 2.56 | 0.0068 | 0.14 | 1.36 | 0.0093 | 107 |
| IC | 0.010 | 3.42 | 0.0037 | 0.14 | 1.36 | 0.0051 | 197 |
| Damage Limitation Limit State | Life Safety Limit State | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TR, 0 y | TR ECR | TR ECR − TR, 0 y | TR, 0 y − TR, 50 y | TR, 0 y | TR ECR | TR ECR − TR, 0 y | TR, 0 y − TR, 50 y | |||||
| [years] | [years] | [years] | [%] 1 | [years] | [%] 1 | [years] | [years] | [years] | [%] 1 | [years] | [%] 1 | |
| XC2—20 mm | 52 | 45 | 6 | 12% | 16 | 30% | 274 | 237 | 37 | 14% | 86 | 31% |
| XC2—30 mm | 49 | 49 | 0 | 0% | 0 | 0% | 264 | 264 | 0 | 0% | 0 | 0% |
| XC3—20 mm | 52 | 50 | 2 | 3% | 4 | 8% | 274 | 265 | 9 | 3% | 23 | 8% |
| XC3—30 mm | 49 | 49 | 0 | 0% | 0 | 0% | 264 | 264 | 0 | 0% | 0 | 0% |
| XC4—20 mm | 52 | 46 | 6 | 12% | 14 | 27% | 274 | 238 | 35 | 13% | 82 | 30% |
| XC4—30 mm | 49 | 49 | 0 | 0% | 0 | 0% | 264 | 264 | 0 | 0% | 0 | 0% |
| Damage Limitation Limit State | Life Safety Limit State | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TR, 0 y | TR ECR | TR ECR − TR, 0 y | TR, 0 y − TR, 50 y | TR, 0 y | TR ECR | TR ECR − TR, 0 y | TR, 0 y − TR, 50 y | |||||
| [years] | [years] | [years] | [%] 1 | [years] | [%] 1 | [years] | [years] | [years] | [%] 1 | [years] | [%] 1 | |
| XC2—20 mm | 52 | 34 | 18 | 35% | 31 | 60% | 274 | 176 | 98 | 36% | 166 | 61% |
| XC2—30 mm | 49 | 32 | 16 | 33% | 29 | 61% | 264 | 172 | 92 | 35% | 163 | 62% |
| XC3—20 mm | 52 | 47 | 5 | 9% | 9 | 17% | 274 | 247 | 27 | 10% | 55 | 20% |
| XC3—30 mm | 49 | 45 | 4 | 8% | 7 | 15% | 264 | 239 | 25 | 9% | 49 | 19% |
| XC4—20 mm | 52 | 35 | 16 | 31% | 30 | 58% | 274 | 185 | 88 | 32% | 161 | 59% |
| XC4—30 mm | 49 | 34 | 14 | 30% | 28 | 58% | 264 | 183 | 82 | 31% | 154 | 58% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nigro, F.; Zinco, A.; Martinelli, E. A Practice-Oriented Procedure for Seismic Reliability Assessment of RC Structures Affected by Carbonation-Induced Degradation. Appl. Mech. 2021, 2, 820-840. https://doi.org/10.3390/applmech2040047
Nigro F, Zinco A, Martinelli E. A Practice-Oriented Procedure for Seismic Reliability Assessment of RC Structures Affected by Carbonation-Induced Degradation. Applied Mechanics. 2021; 2(4):820-840. https://doi.org/10.3390/applmech2040047
Chicago/Turabian StyleNigro, Francesco, Adamo Zinco, and Enzo Martinelli. 2021. "A Practice-Oriented Procedure for Seismic Reliability Assessment of RC Structures Affected by Carbonation-Induced Degradation" Applied Mechanics 2, no. 4: 820-840. https://doi.org/10.3390/applmech2040047
APA StyleNigro, F., Zinco, A., & Martinelli, E. (2021). A Practice-Oriented Procedure for Seismic Reliability Assessment of RC Structures Affected by Carbonation-Induced Degradation. Applied Mechanics, 2(4), 820-840. https://doi.org/10.3390/applmech2040047







