Prediction of Load-Bearing Capacity of Composite Parts with Low-Velocity Impact Damage: Identification of Intra- and Inter-Ply Constitutive Models
Abstract
1. Introduction
2. Materials and Manufacturing
3. Experimental Methods
3.1. Material Characterization
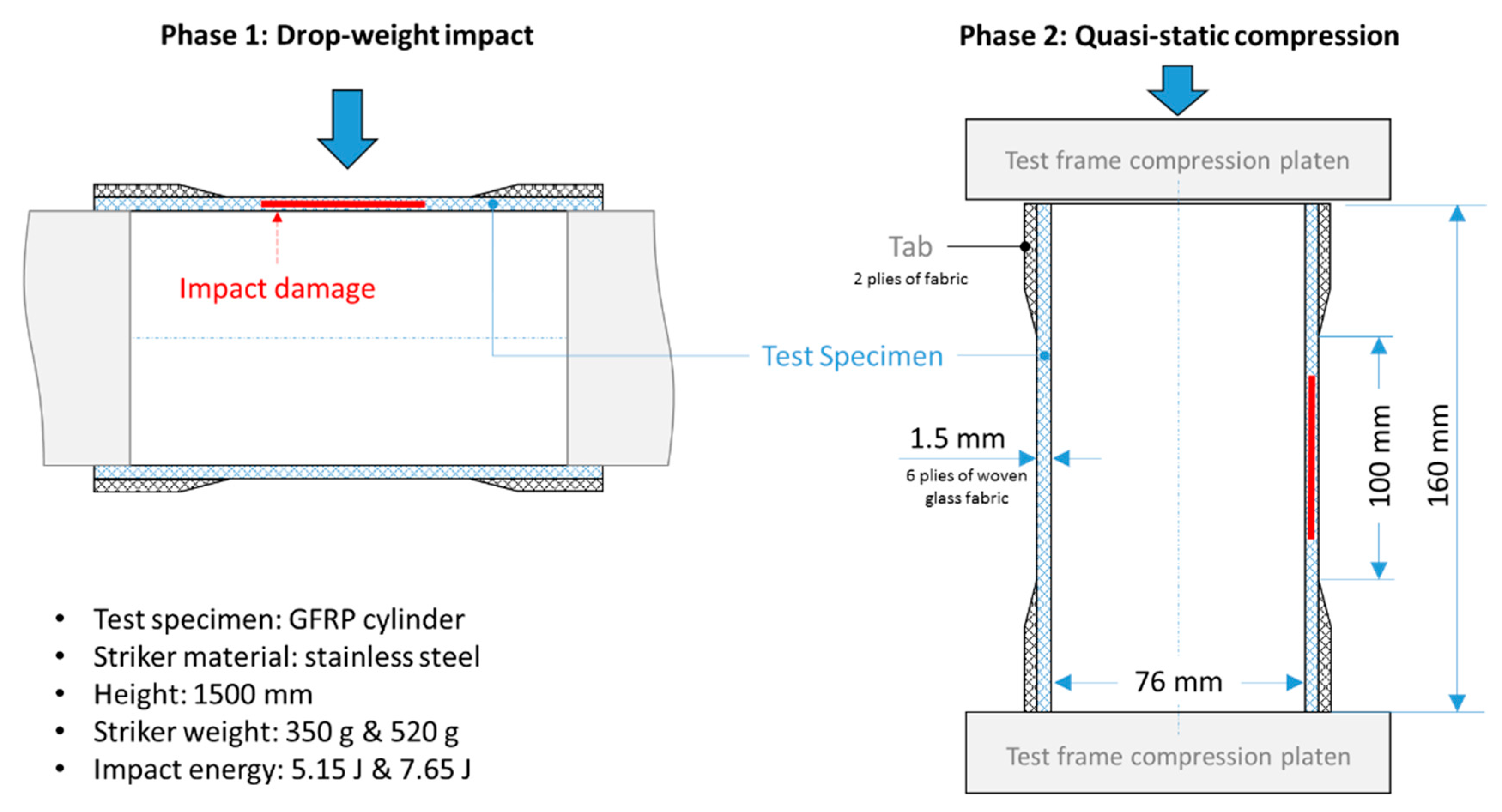
3.2. Testing of Composite Cylinders
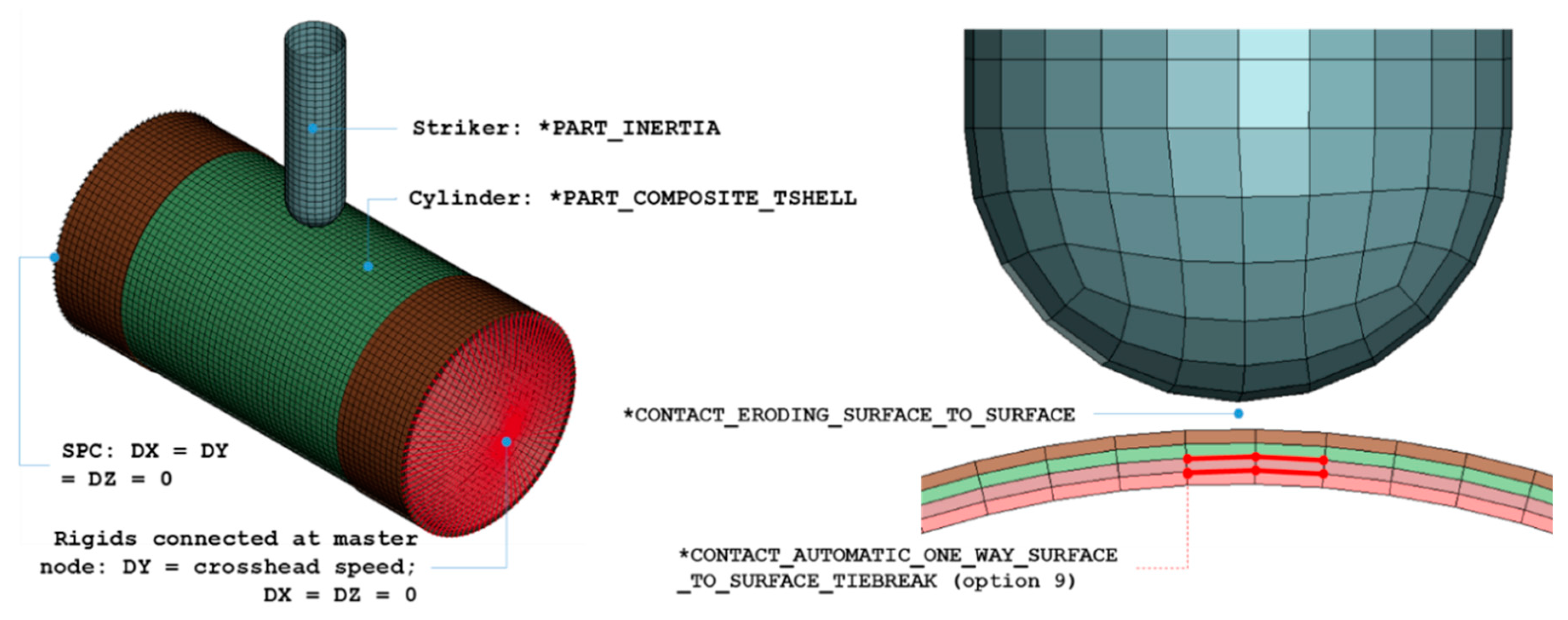
4. Modeling Techniques
5. Results and Discussion
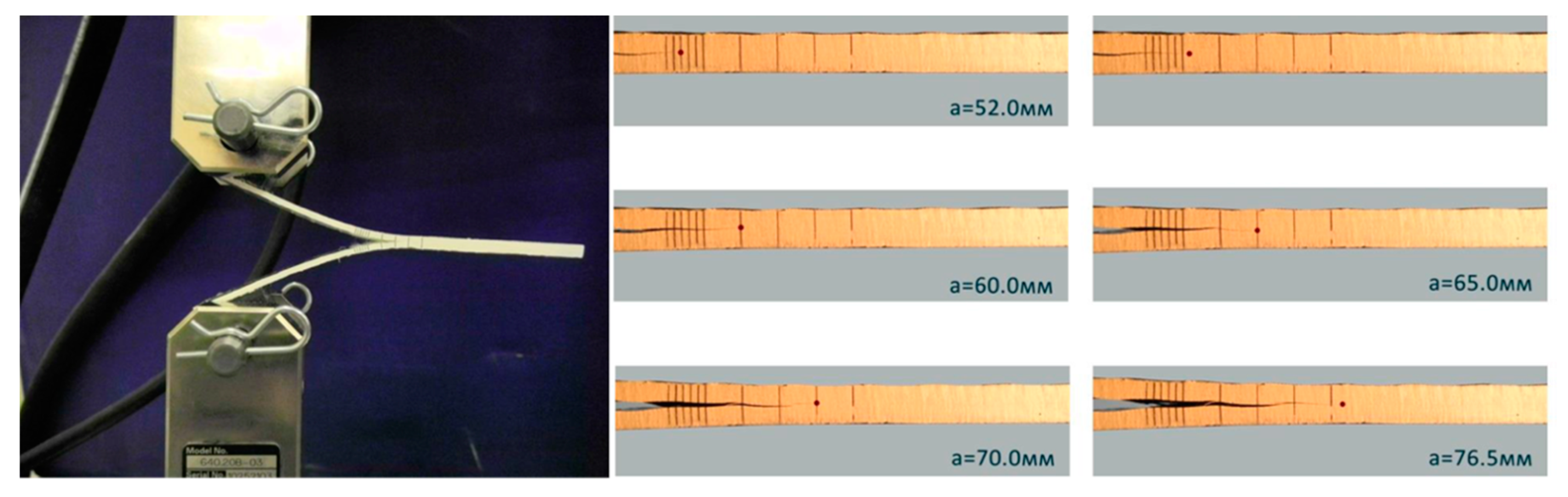
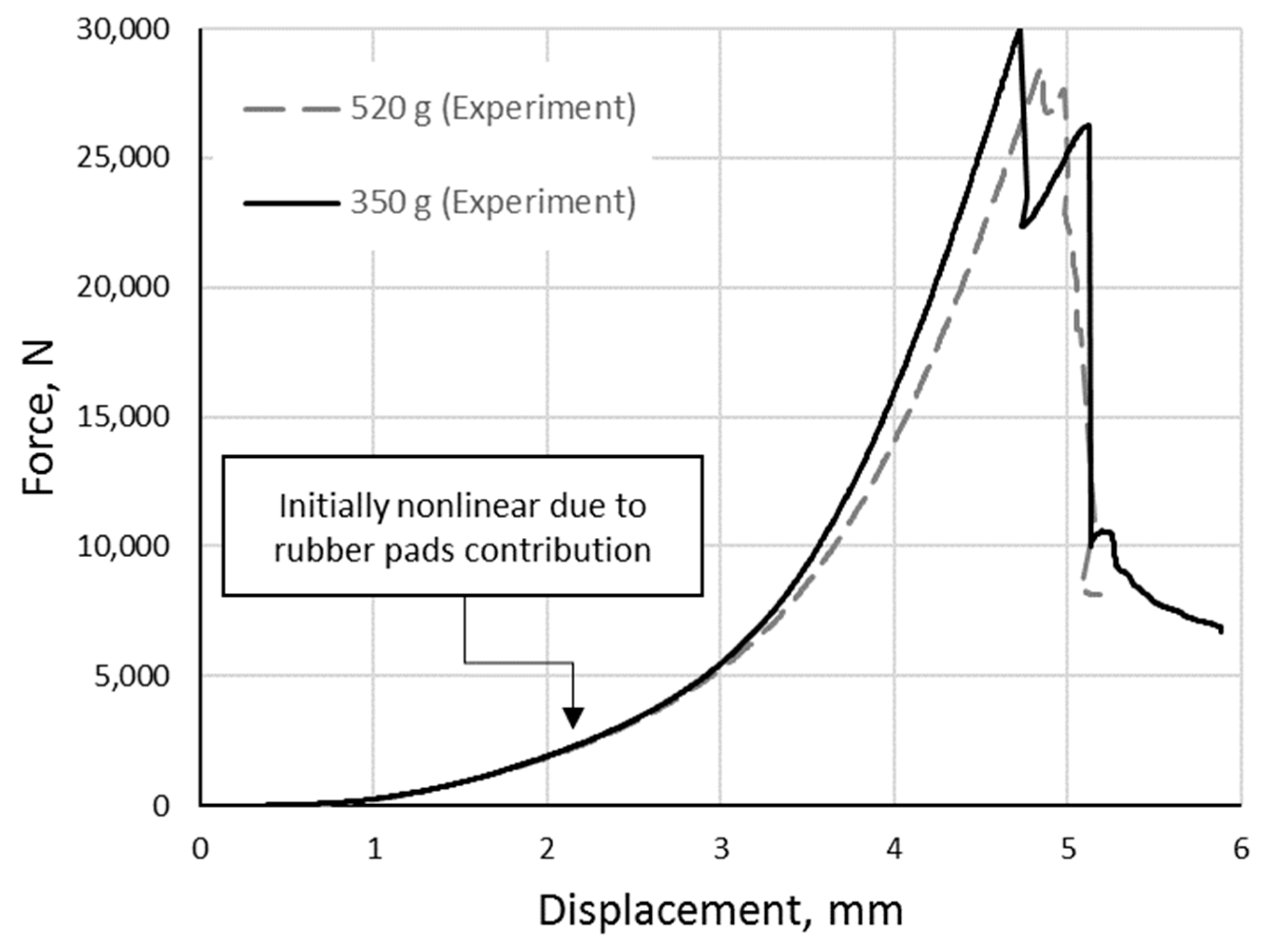
5.1. Experimental Results
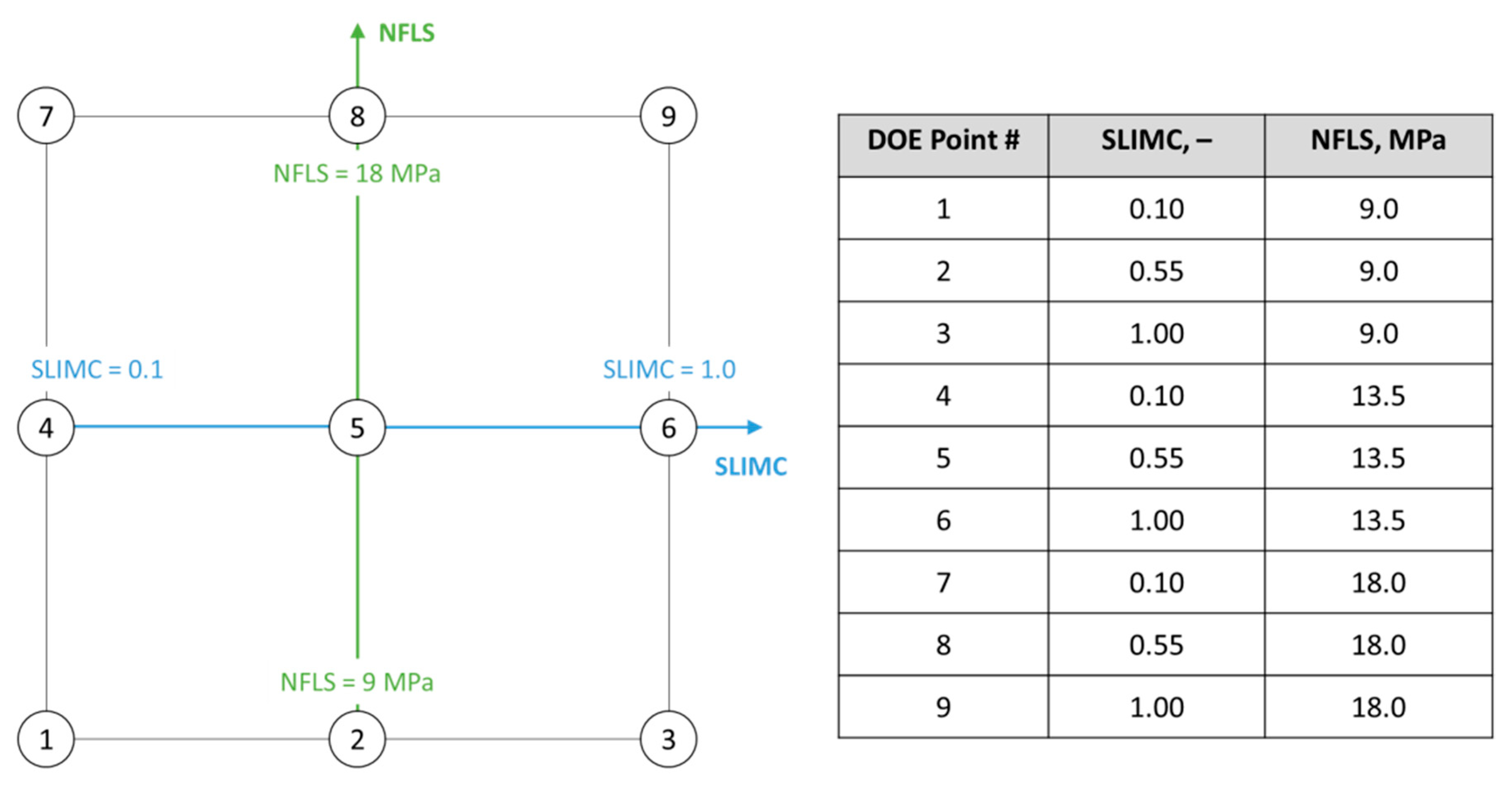
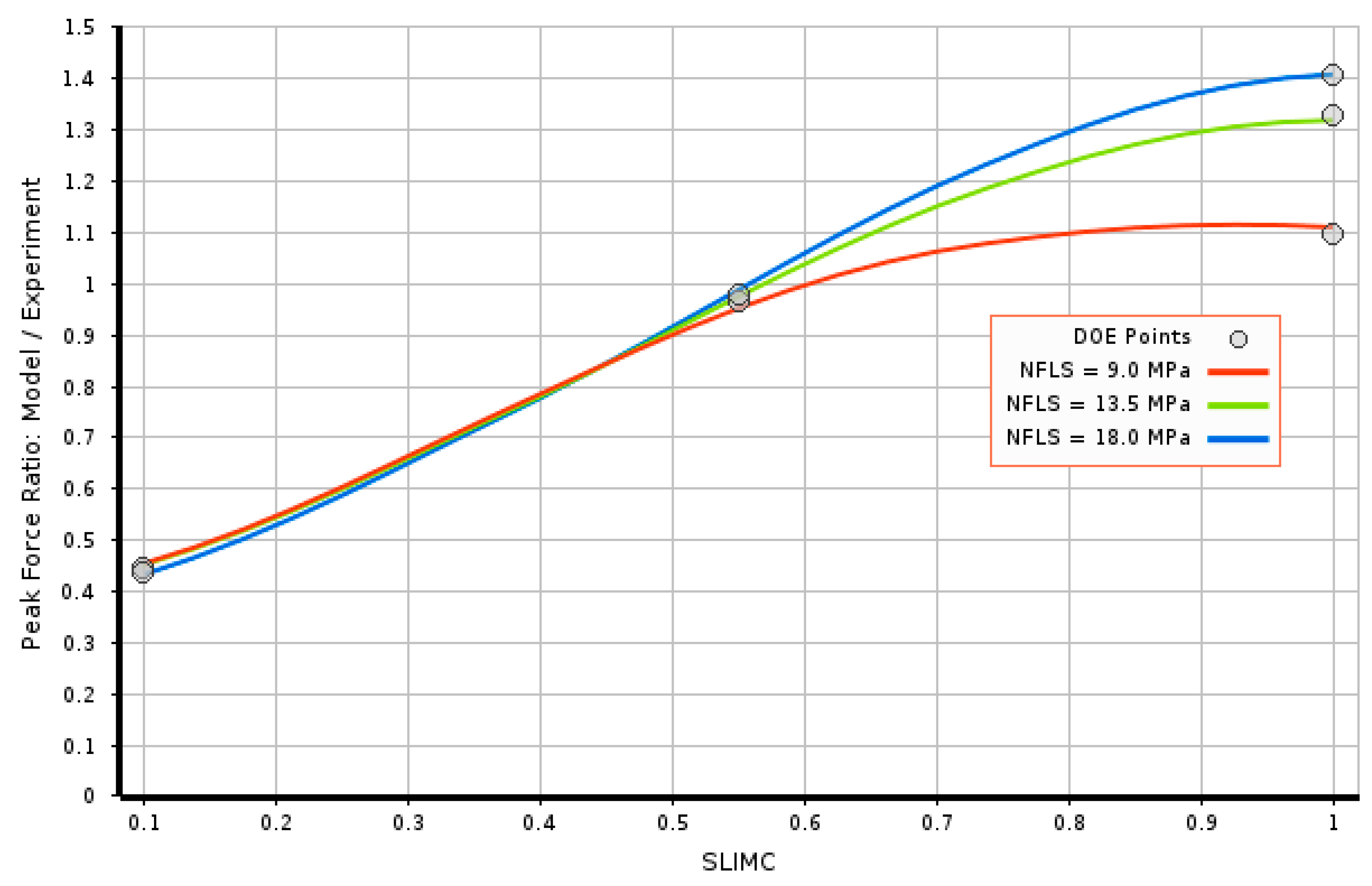
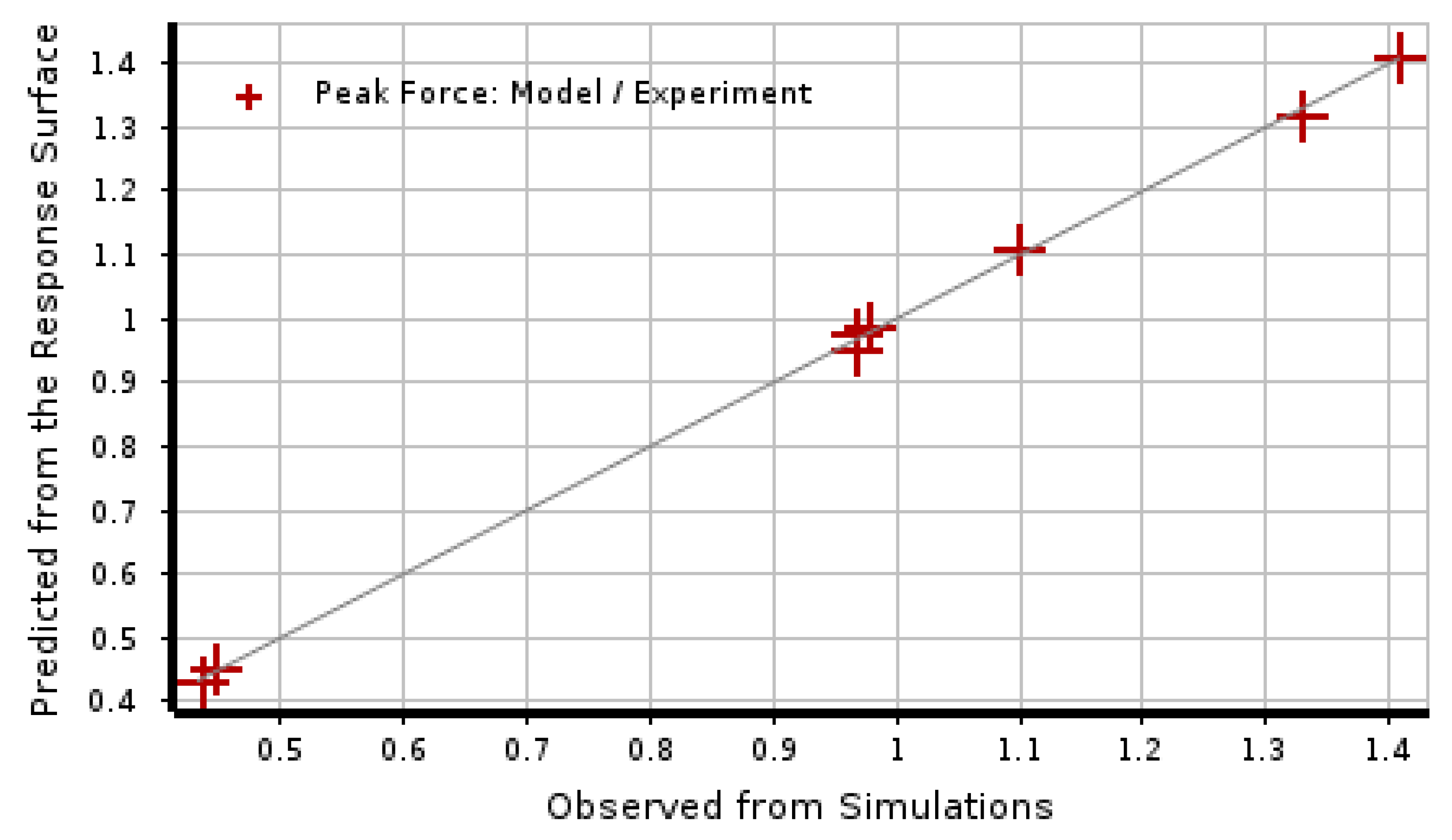
5.2. Load-Bearing Capacity: Calibration of SLIMC and NFLS Parameters
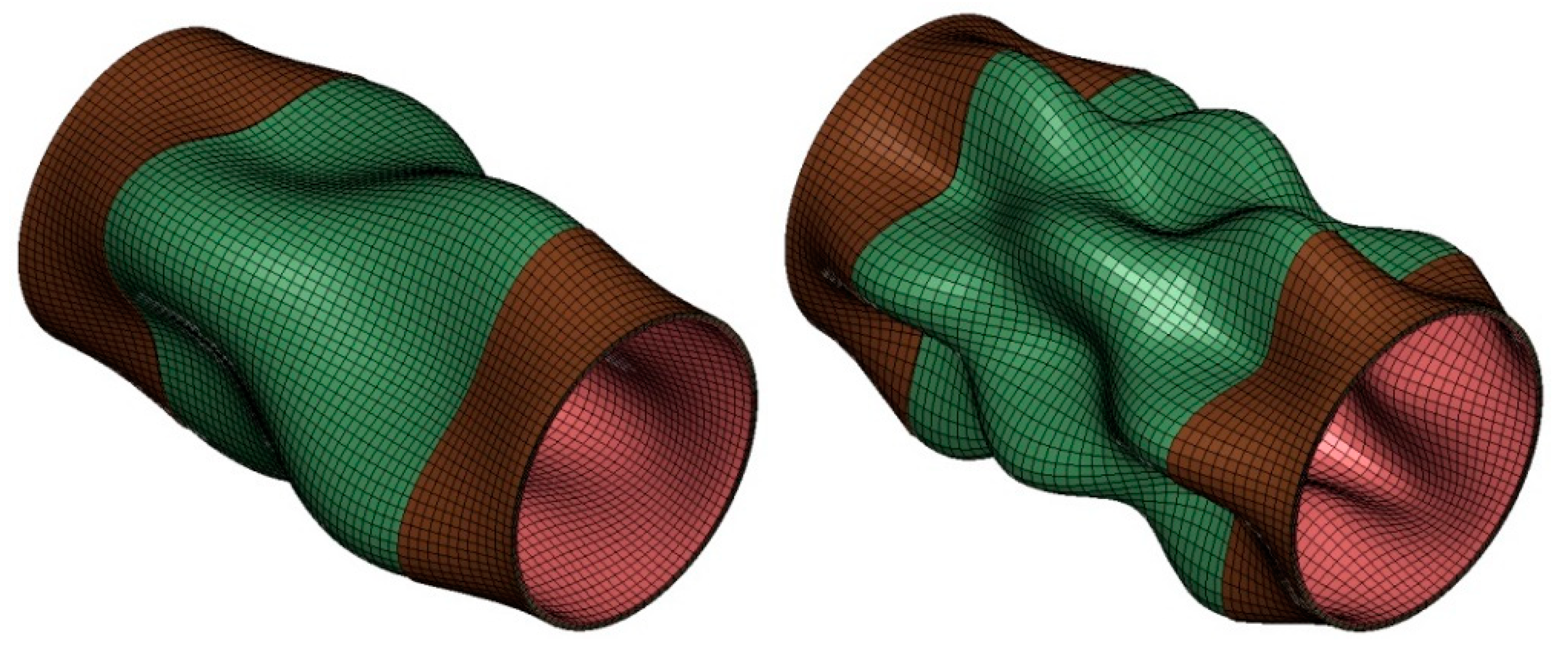
5.3. Predicted and Experimentally Observed Damage
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mouli, Y.S.C.; Upadhyay, C.S.; Mohite, P.M. Intra-ply Damage Modeling of Low-Velocity Impact on Composite Laminates. In International Conference on Emerging Trends in Engineering (ICETE); Springer: Berlin/Heidelberg, Germany, 2020; pp. 731–738. [Google Scholar]
- Moncayo, E.D.; Wagner, H.; Drechsler, K. Benchmarks for composite delamination using LS-DYNA: Low velocity impact. In Proceedings of the 6th LS-DYNA Anwenderforum, Frankenthal, Germany, 12–13 October 2007. [Google Scholar]
- Aymerich, F.; Dore, F.; Priolo, P. Prediction of impact-induced delamination in cross-ply composite laminates using cohesive interface elements. Compos. Sci. Technol. 2008, 68, 2383–2390. [Google Scholar] [CrossRef]
- Di Caprio, F.; Langella, A.; Lopresto, V.; Caprino, G. Numerical, Experimental and analytical correlation for predicting the structural behavior of composite structures under impact. Procedia Eng. 2016, 167, 80–87. [Google Scholar] [CrossRef]
- Long, S.; Yao, X.; Zhang, X. Delamination prediction in composite laminates under low-velocity impact. Compos. Struct. 2015, 132, 290–298. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Z.; Zhang, Q.; Huili, Y. Study of fiber modulus effect on impact energy absorption characteristics of composite laminates at normal and oblique impacts. Mater. Res. Express 2019, 6, 085610. [Google Scholar] [CrossRef]
- Cherniaev, A.; Butcher, C.; Montesano, J. Predicting the axial crush response of CFRP tubes using three damage-based constitutive models. Thin-Walled Struct. 2018, 129, 349–364. [Google Scholar] [CrossRef]
- De Luca, A.; Caputo, F. A review on analytical failure criteria for composite materials. AIMS Mater. Sci. 2017, 4, 1165–1185. [Google Scholar] [CrossRef]
- Lin, S.; Waas, A.M. Experimental and high-fidelity computational investigations on the low velocity impact damage of laminated composite materials. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 724. [Google Scholar]
- Borkowski, L.; Kumar, R.S.; Palliyaguru, U.R. Mechanics-based modeling approach for rapid prediction of low velocity impact damage in composite laminates. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 726. [Google Scholar]
- James, R.; Mei, H.; Haider, M.F.; Giurgiutiu, V. Challenges of generating controlled one-inch impact damage in thick CFRP composites. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 723. [Google Scholar]
- Heimbs, S.; Heller, S.; Middendorf, P. Simulation of low velocity impact on composite plates with compressive preload. In Proceedings of the 7th LS-DYNA Anwenderforum, Frankenthal, Germany, 10–12 October 2008. [Google Scholar]
- Dang, T.D.; Hallet, S.R.; Kim, B.C.; Cahain, Y.L.; Butler, R.; Liu, W. Modelling of as manufactured geometry for prediction of impact and compression after impact behaviour of variable angle tow laminates. J. Compos. Mater. 2014, 49, 1423–1438. [Google Scholar] [CrossRef]
- McQuigg, T.D. Compression after Impact Experiments and Analysis on Honeycomb Core Sandwich Panels with Thin Facesheets. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2011. [Google Scholar]
- James, C.T.; Watson, A.; Cunningham, P.R. Numerical modelling of the compression-after-impact performance of a composite sandwich panel. J. Sandw. Struct. Mater. 2015, 17, 376–398. [Google Scholar] [CrossRef]
- ASTM Test Method D3039/D3039M-17, Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM Test Method D3518/D3518M-13, Standard Test Method for In-Plane Shear Response of Polymer Matrix Composite Materials by Tensile Test of a ±45° Laminate; ASTM International: West Conshohocken, PA, USA, 2013.
- ASTM Test Method D3410/D3410M-16, Standard Test Method for Compressive Properties of Polymer Matrix Composite Materials with Unsupported Gage Section by Shear Loading; ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM Test Method D5528-13, Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2013.
- Carlsson, L.A.; Adams, D.F.; Pipes, R.B. Experimental Characterization of Advanced Composite Materials, 4th ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Ls-Dyna, Keyword User’s Manual, Volume II: Material Models; Livermore Software Technology Corporation: Livermore, CA, USA, 2013.
- Schweizerhof, K.; Weimar, K.; Münz, T.; Rottner, T. Crashworthiness analysis with enhanced composite material models in LS-DYNA—Merits and limits. In Proceedings of the LS-DYNA Conference, Detroit, MI, USA, 21–22 September 1998. [Google Scholar]
- de Moura, M.F.S.F.; Gongalves, J.P.M.; Marques, A.T.; Castro, P.M.S.T. Prediction of compressive strength of carbon-epoxy laminates containing delamination by using a mixed-mode damage model. Compos. Struct. 2000, 50, 151–161. [Google Scholar] [CrossRef]
- Davila, C.G.; Camanho, P.P. Decohesion elements using two and three-parameter mixed-mode criteria. In Proceedings of the American Helicopter Society Conference, Williamsburg, VA, USA, 29 October–1 November 2001. [Google Scholar]
- Graf, T.; Haufe, A.; Andrade, F. Adhesives modeling with LS-DYNA: Recent developments and future work. In Proceedings of the Nordic LS-DYNA Forum, Stuttgart, Germany, 12–13 October 2014. [Google Scholar]



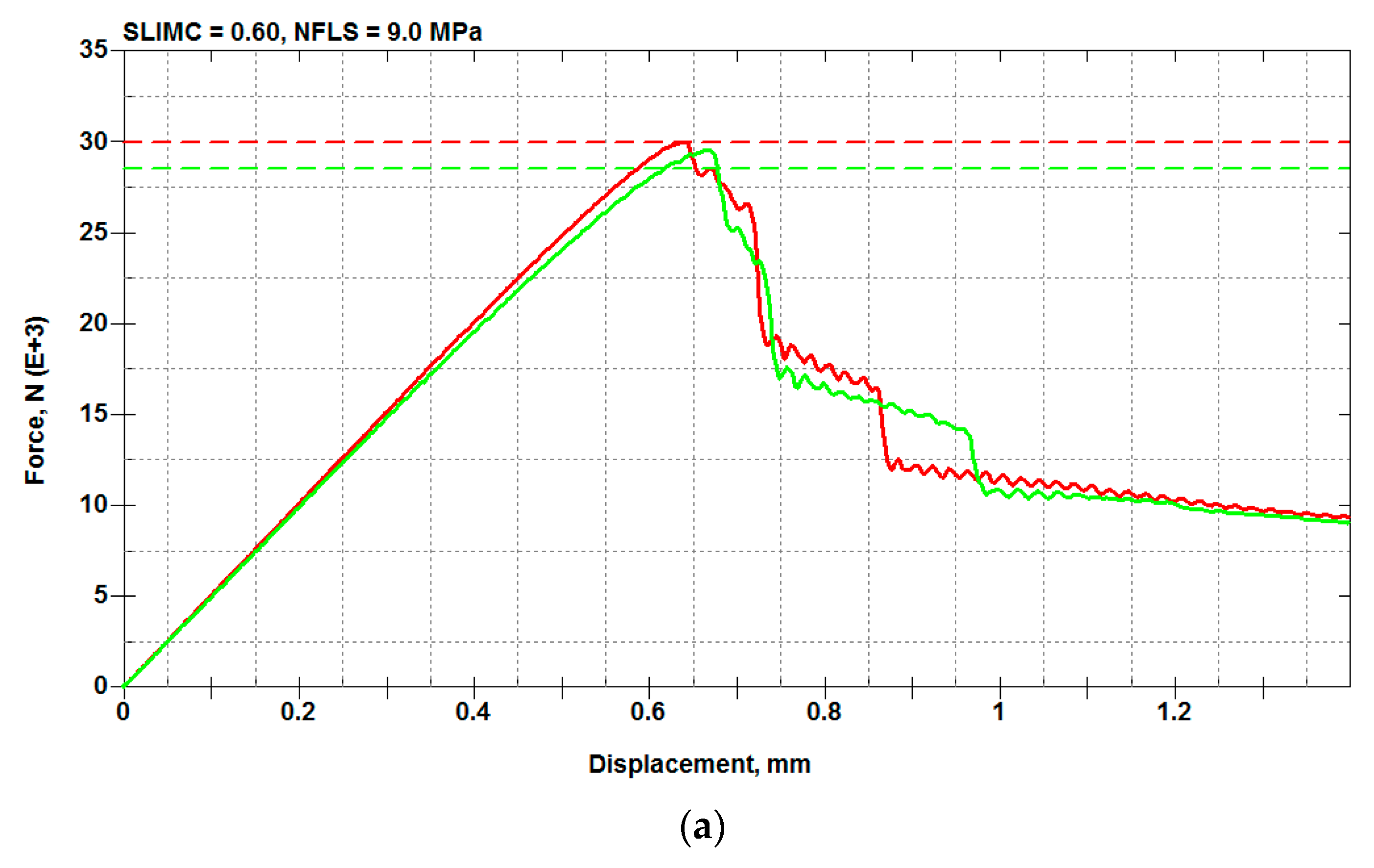
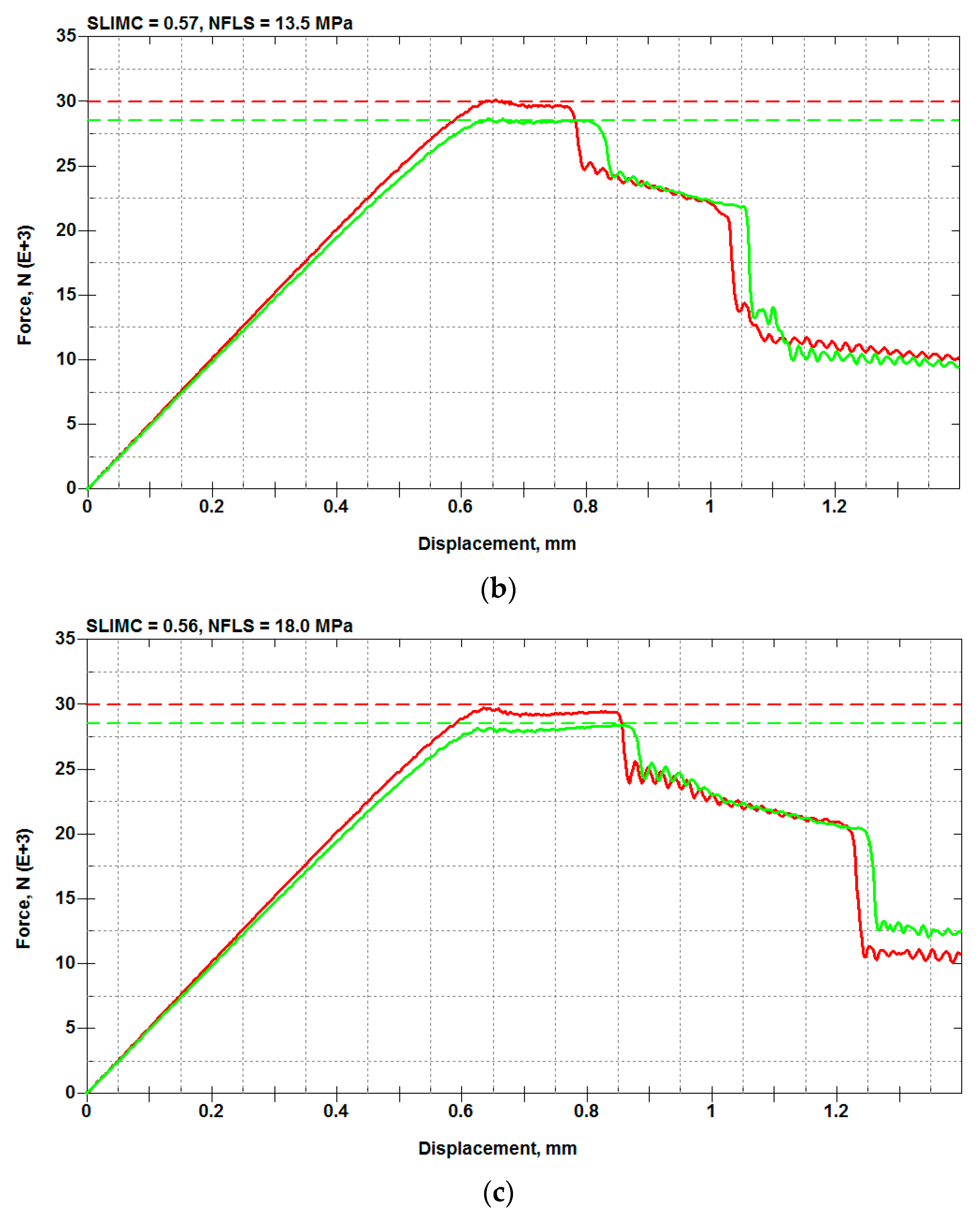
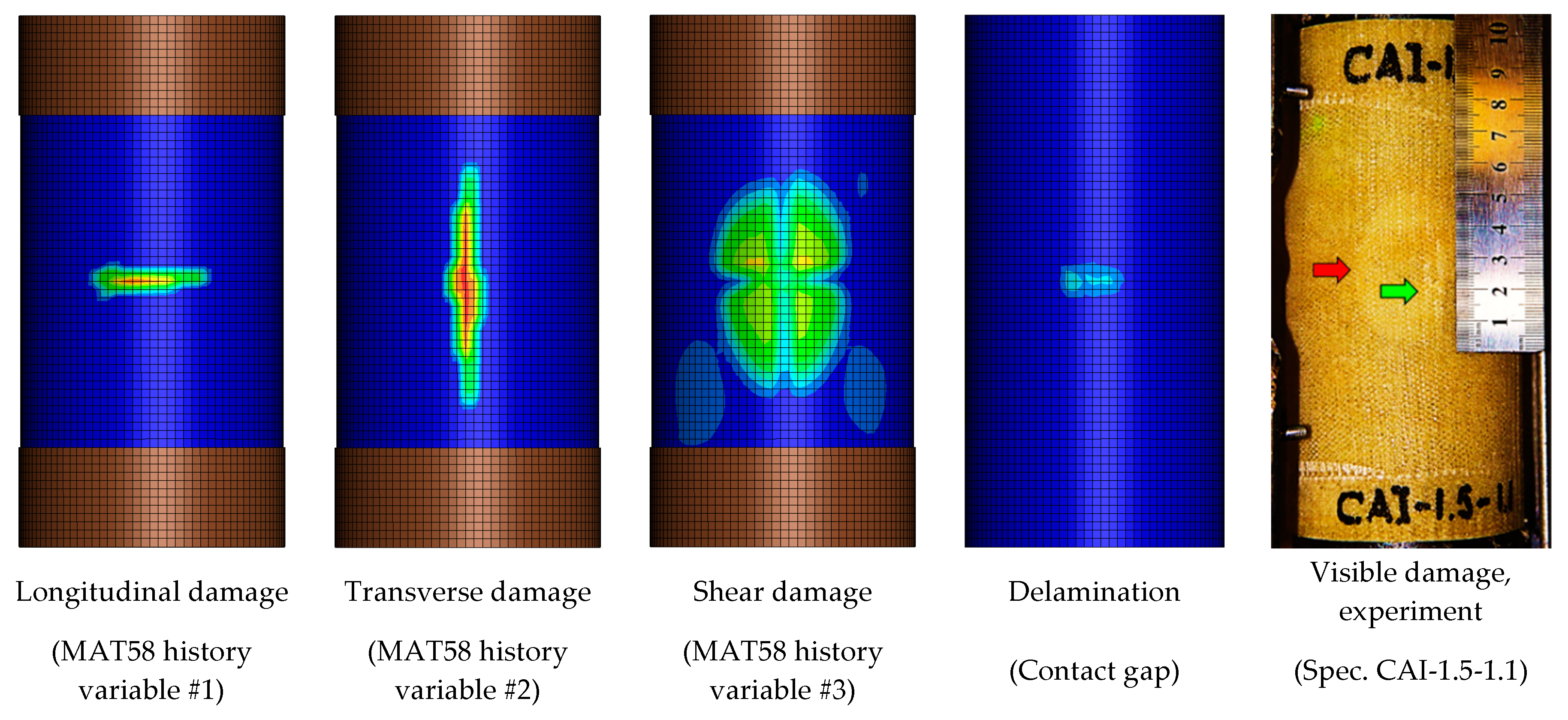
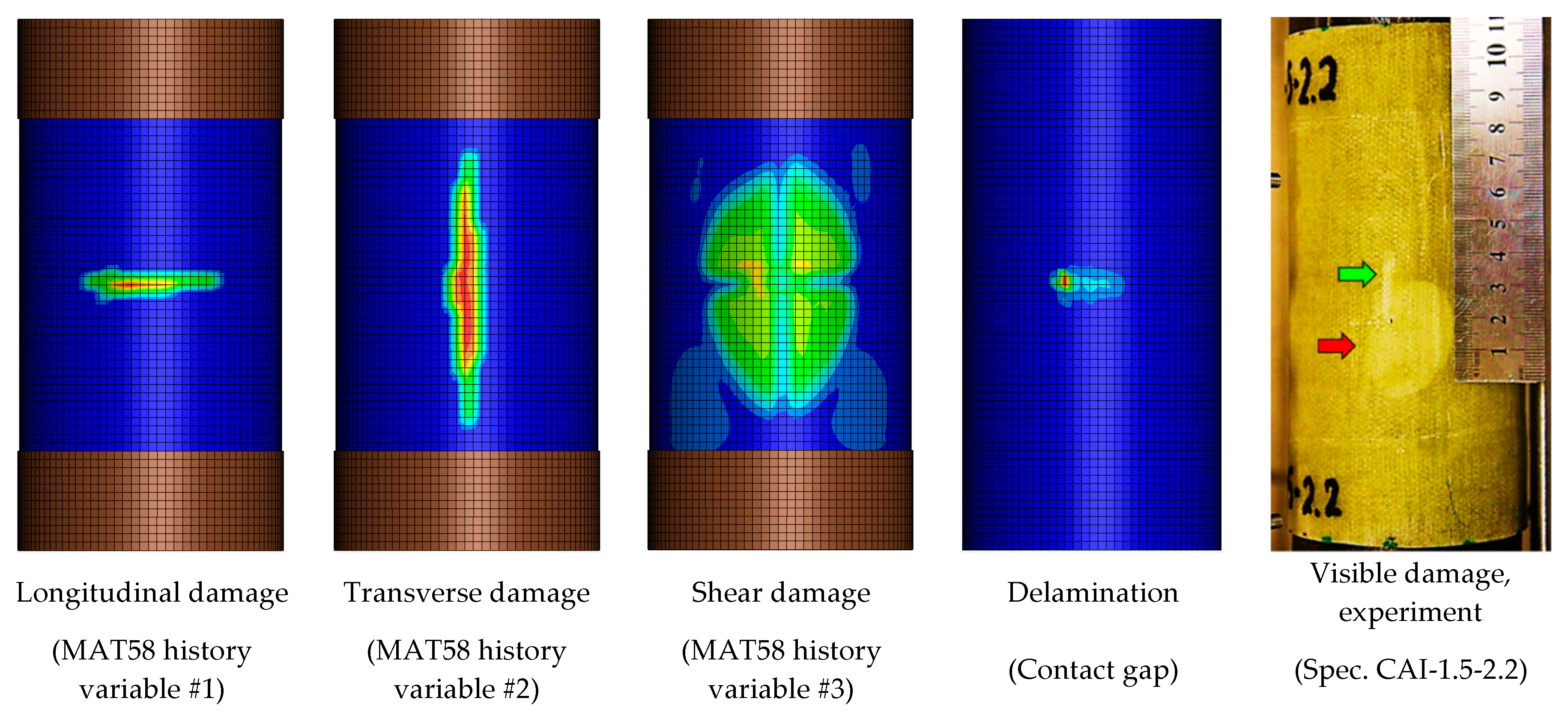


| Parameter | Meaning | Units | Value or Range | Comment for the Chosen Initial Value |
|---|---|---|---|---|
| TSIZE | Time step for automatic element deletion. | s | 1E-10 | Disabled by choosing a very small time step value for element deletion. |
| ERODS | Maximum effective strain for element failure. If lower than zero, the element fails when effective strain calculated from the full strain tensor exceeds ERODS. | mm/mm | −2.00 | Chosen to be significantly higher than any directional strain at failure initiation. |
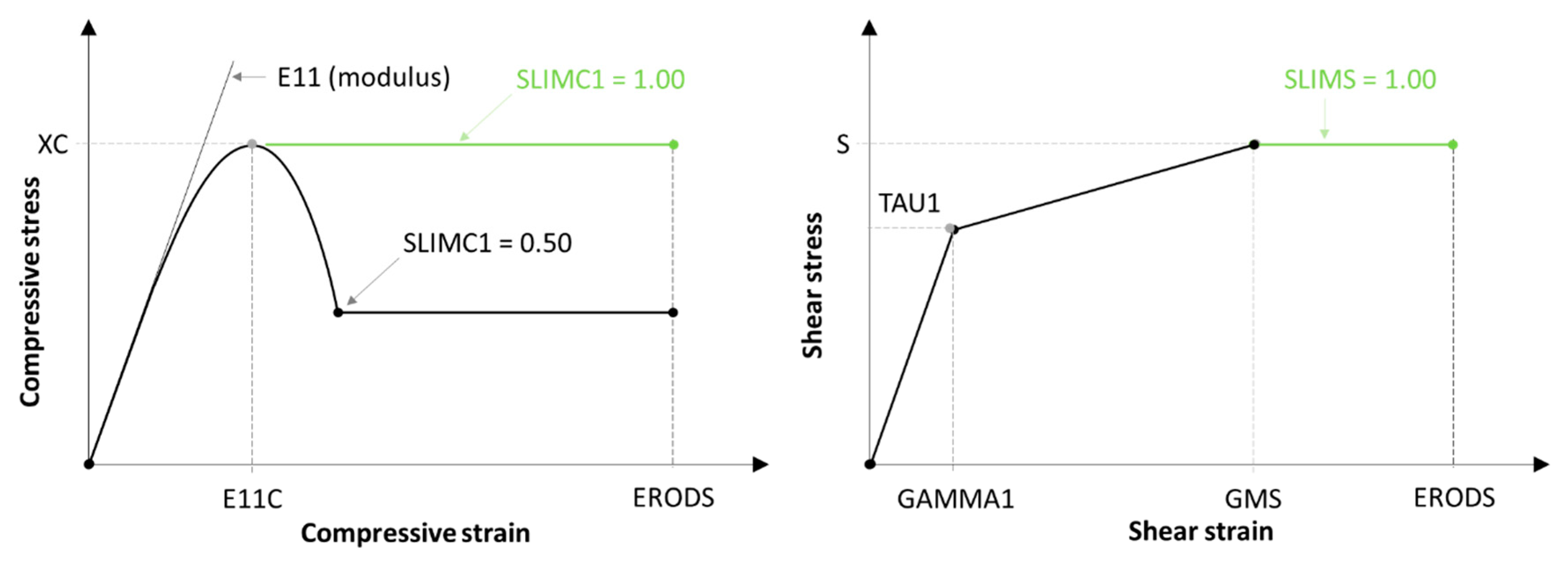
| SLIMT1 | Factor to determine the minimum stress limit after stress maximum (fiber tension). | - | 0.10 | A recommended value [21] |
| SLIMC1 | Factor to determine the minimum stress limit after stress maximum (fiber compression). | - | 0.1–1.0 | See discussion in Section 4. |
| SLIMT2 | Factor to determine the minimum stress limit after stress maximum (matrix tension). | - | 0.10 | A recommended value [21] |
| SLIMC2 | Factor to determine the minimum stress limit after stress maximum (matrix compression). | - | 0.1–1.0 | See discussion in Section 4. |
| SLIMS | Factor to determine the minimum stress limit after stress maximum (shear). | - | 1.00 | A recommended value [21] |
| Property | Value or Range | Rationale |
|---|---|---|
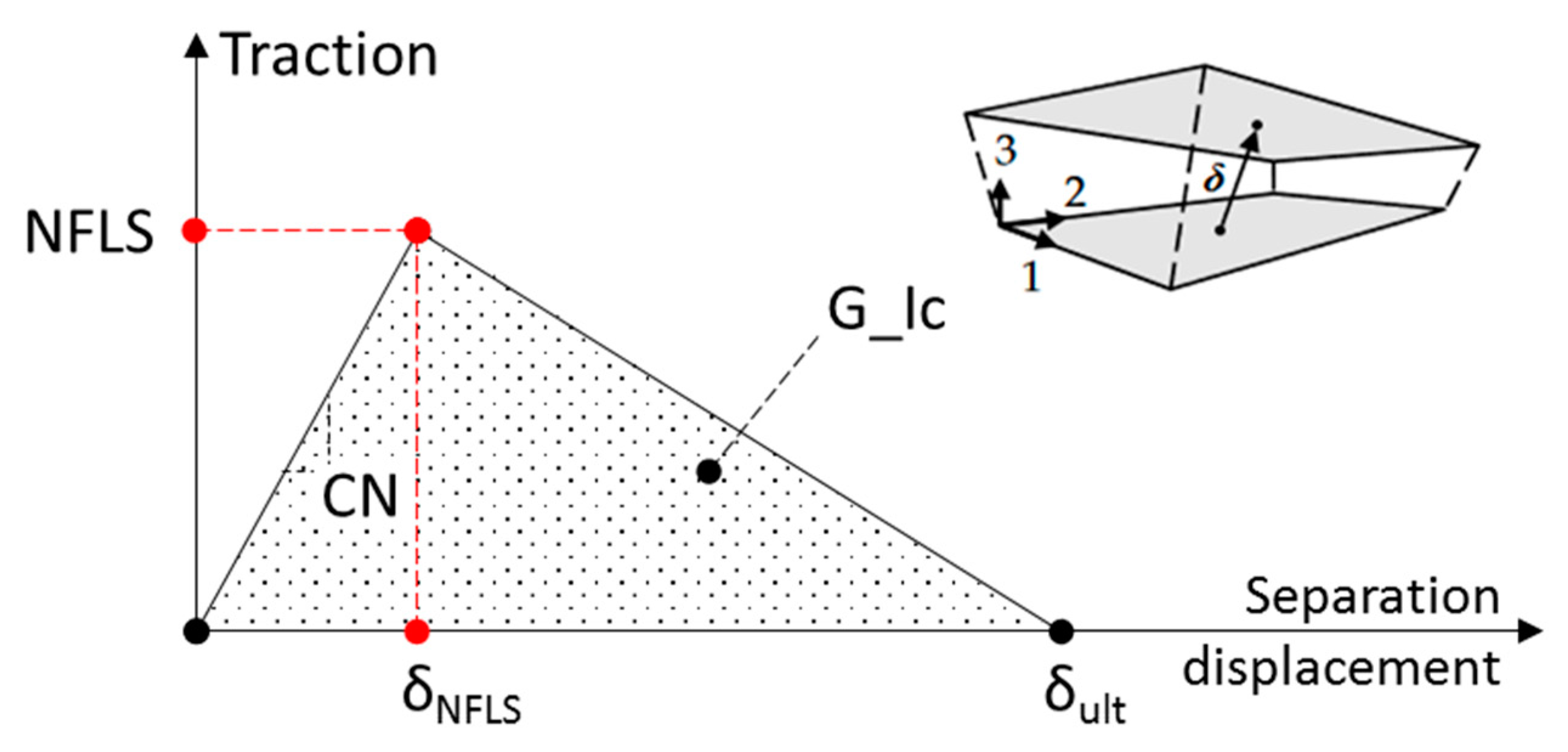
| NFLS, MPa | 9.00–18.00 | NFLS can be bound by the following values: lower bound—the transverse strength of a typical unidirectional GFRP (~30 MPa), which would be a reasonable estimate in the case of interlaminar failure by adhesive mechanism (cracks formed at the interface between the epoxy in the interlaminar resin-rich region and fibers in the layer adjacent to it). upper bound—the ultimate strength of bulk epoxy resin (~60 MPa), which would be a reasonable estimate in the case of interlaminar failure by cohesive mechanism. In addition, a scaling factor of 0.30 was used to account for the mesh dependency observed for this delamination model (see the recommendation provided in [25] for meshes with element sizes between 2 and 3 mm). A particular value from the specified range was chosen via calibration with experimental data, as will be discussed in Section 5.2. |
| SFLS/NFLS, - | 0.58 | Assumed as SFLS = NFLS/ (von Mises criterion) |
| G_Ic, kJ/m2 | 0.24 | Measured experimentally, see Table 3 in Section 5.1 |
| G_IIc, kJ/m2 | 1.96 | Measured experimentally, see Table 3 in Section 5.1 |
| CN, MPa/mm | 200,000.00 | CN = Eepoxy/δRRR, where Eepoxy is the Young’s modulus of epoxy matrix (~3650 MPa) and δRRR is the thickness of the interlaminar resin-rich region (typically within 0.01 and 0.10 mm). Thus, the lower and upper bounds for CN correspond to 36,500 MPa/mm and 365,000 MPa/mm, accordingly. This averages to 200,000 MPa/mm as an estimate for the CN parameter. In addition, the condition for CN > CNmin must be ensured (see [15]), where CNmin = (1/2) × (NFLS2)/(G_Ic). This condition is satisfied for the listed set of parameters of the delamination model. |
| CT2CN, - | 0.37 | CT2CN = CT/CN = Gepoxy/Eepoxy = 1/2 × (1 + νepoxy), where Gepoxy and νepoxy are the shear modulus and the Poisson’s ratio (~0.35) of epoxy resin, correspondingly. |
| Property | Value | Standard Deviation | Test Method |
|---|---|---|---|
| Longitudinal Young’s modulus (E1), MPa | 20,800 | 1600 | ASTM D 3039 |
| Transverse Young’s modulus (E2), MPa | 12,200 | 740 | ASTM D 3039 |
| Poisson’s ratio (nu21) | 0.079 | n/a | ASTM D 3039 |
| Shear modulus (G12), MPa | 2950 | 53.12 | ASTM D 3518 |
| Tensile strength in warp direction (Xt), MPa | 397 | 22.64 | ASTM D 3039 |
| Compressive strength in warp direction (Xc), MPa | 153 | 5.76 | ASTM D 3410 |
| Tensile strength in fill direction (Yt), MPa | 240 | 14.59 | ASTM D 3039 |
| Compressive strength in fill direction (Yc), MPa | 101 | 5.32 | ASTM D 3410 |
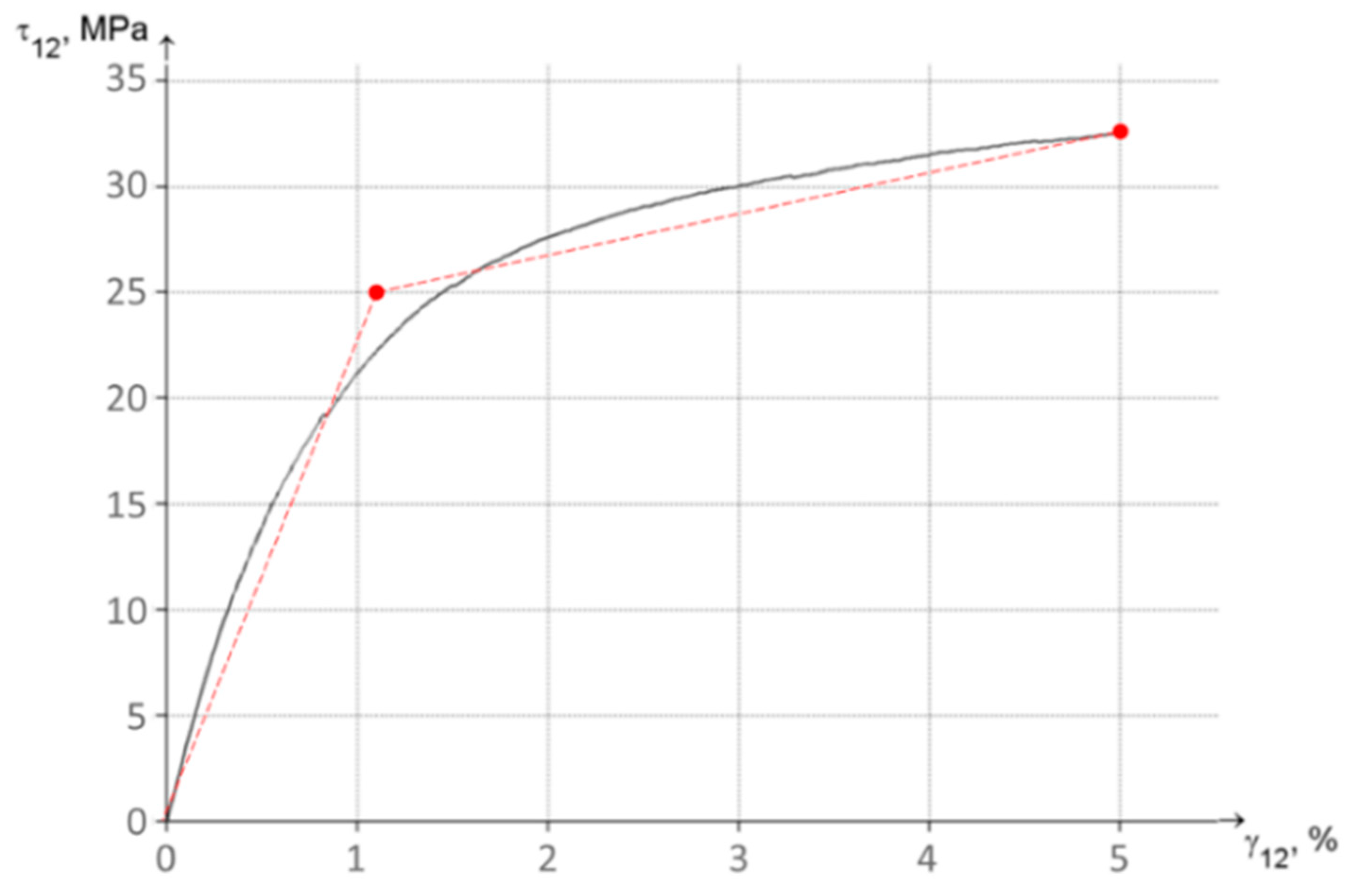
| Shear stress at onset of nonlinearity, MPa | 25 (see Figure 11) | n/a | ASTM D 3518 |
| Shear stress at 5% shear strain, MPa | 33 | 1.87 | ASTM D 3518 |
| Mode I critical strain energy release rate (G_Ic), kJ/m2 | 0.24 | 0.02 | ASTM D 5528-01 |
| Mode II critical strain energy release rate (G_IIc), kJ/m2 | 1.96 | 0.50 | End-notched flexure |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherniaev, A.; Pavlova, S.; Pavlov, A.; Komarov, V. Prediction of Load-Bearing Capacity of Composite Parts with Low-Velocity Impact Damage: Identification of Intra- and Inter-Ply Constitutive Models. Appl. Mech. 2020, 1, 59-78. https://doi.org/10.3390/applmech1010005
Cherniaev A, Pavlova S, Pavlov A, Komarov V. Prediction of Load-Bearing Capacity of Composite Parts with Low-Velocity Impact Damage: Identification of Intra- and Inter-Ply Constitutive Models. Applied Mechanics. 2020; 1(1):59-78. https://doi.org/10.3390/applmech1010005
Chicago/Turabian StyleCherniaev, Aleksandr, Svetlana Pavlova, Aleksandr Pavlov, and Valeriy Komarov. 2020. "Prediction of Load-Bearing Capacity of Composite Parts with Low-Velocity Impact Damage: Identification of Intra- and Inter-Ply Constitutive Models" Applied Mechanics 1, no. 1: 59-78. https://doi.org/10.3390/applmech1010005
APA StyleCherniaev, A., Pavlova, S., Pavlov, A., & Komarov, V. (2020). Prediction of Load-Bearing Capacity of Composite Parts with Low-Velocity Impact Damage: Identification of Intra- and Inter-Ply Constitutive Models. Applied Mechanics, 1(1), 59-78. https://doi.org/10.3390/applmech1010005





