Automated Pruning Framework for Large Language Models Using Combinatorial Optimization
Abstract
1. Introduction
2. Related Work
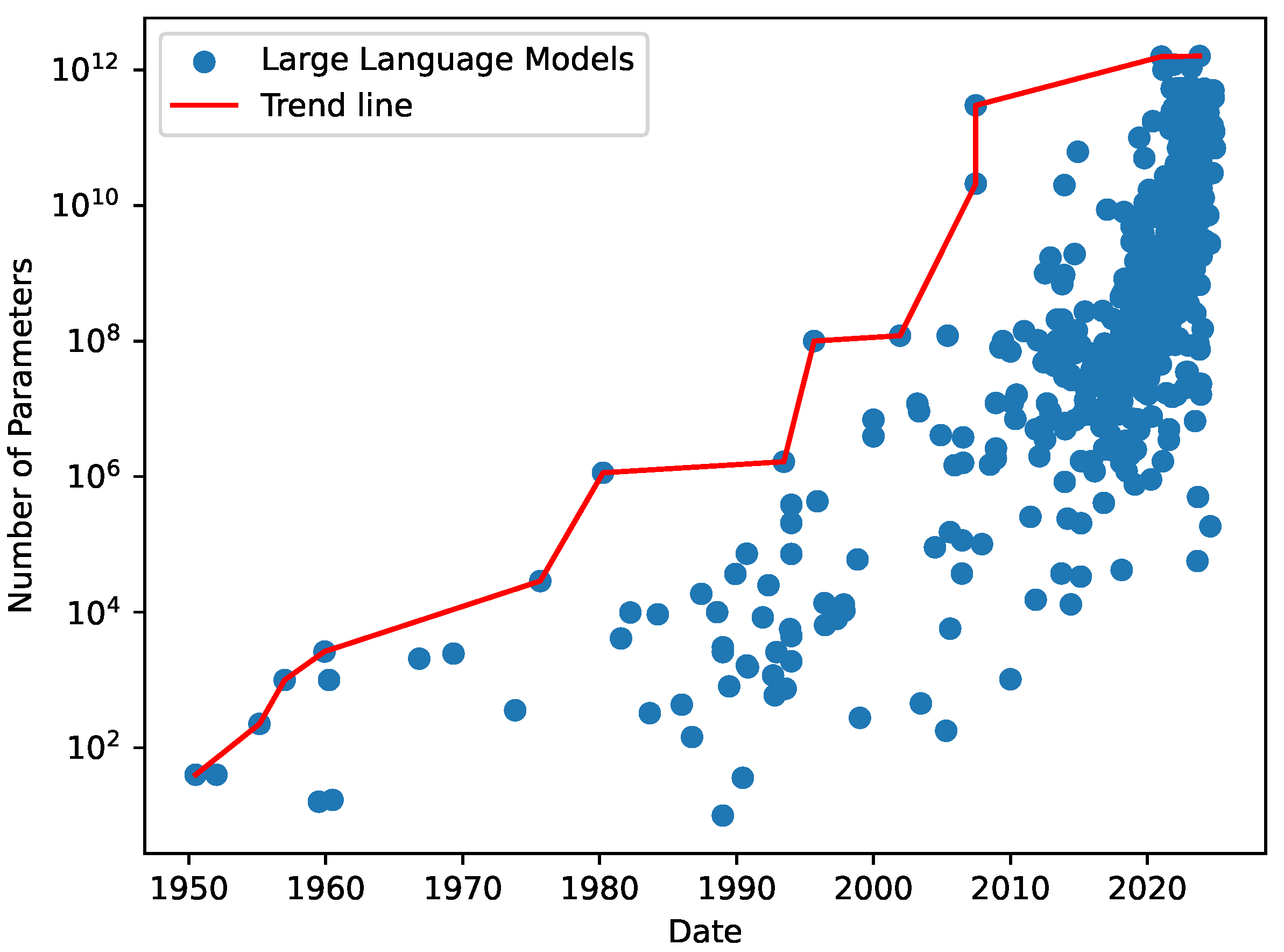
2.1. Large Language Models
2.2. Model Compression Techniques
2.3. Pruning Methods
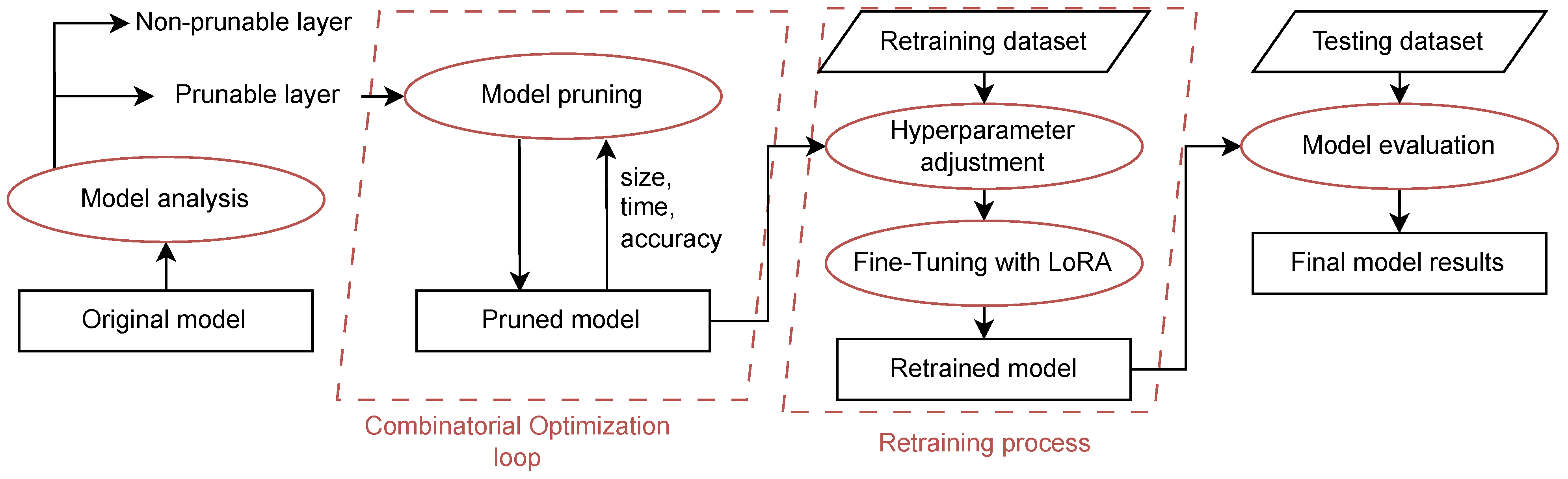
3. Materials and Methods
3.1. Model Analysis
- Multi-Head Self-Attention Mechanism: Enables the model to capture a wide range of contextual relationships by projecting inputs into multiple attention subspaces;
- Feedforward Neural Networks: Position-wise feedforward layers in each transformer block boost the model to learn complex representations;
- Rotary Positional Embeddings (RoPE): Enables the model to process long sequences by including relative positional information directly into the attention.
3.2. Model Pruning
3.3. Combinatorial Optimization Algorithms
3.4. Model Retraining
- Hyperparameter Adjustment: To improve convergence and stability after pruning, key hyperparameters, such as learning rate, batch size, and number of epochs, are carefully tuned.
- Fine-Tuning with LoRA: The pruned model is fine-tuned using a general-domain dataset, enhanced by incorporating low-rank adaptation (LoRA) [39]. Unlike conventional fine-tuning that updates all model parameters, LoRA introduces lightweight and efficient parameter updates by injecting trainable low-rank matrices into the model, allowing effective adaptation with a smaller number of parameters. This approach requires less computational overhead and prevents overfitting by focusing on a smaller set of parameters. This method helps the pruned model to adjust its remaining parameters effectively while maintaining versatility and generalization across a wide range of downstream tasks.
3.5. Model Evaluation
4. Experimental Results
4.1. Experimental Setup
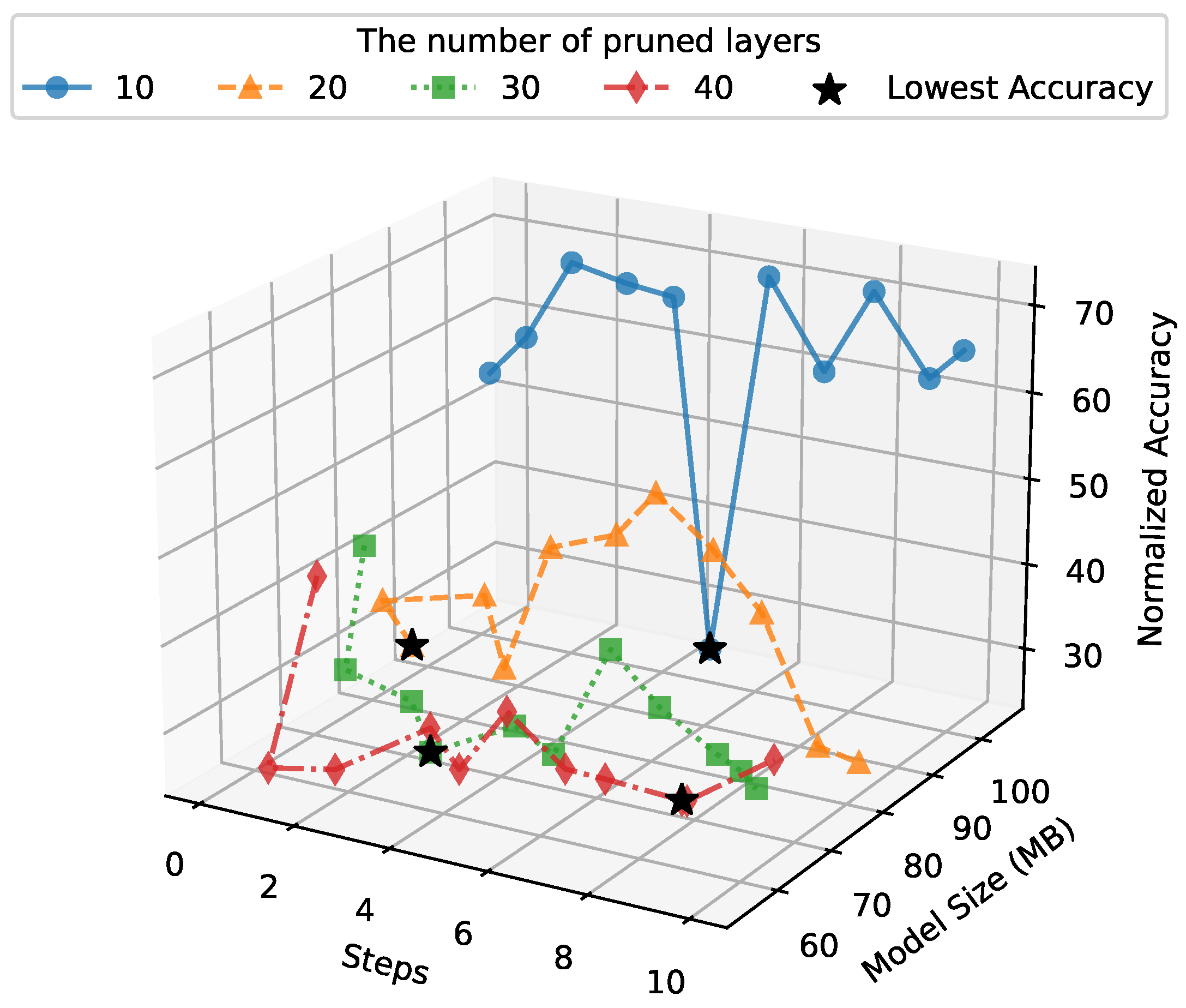
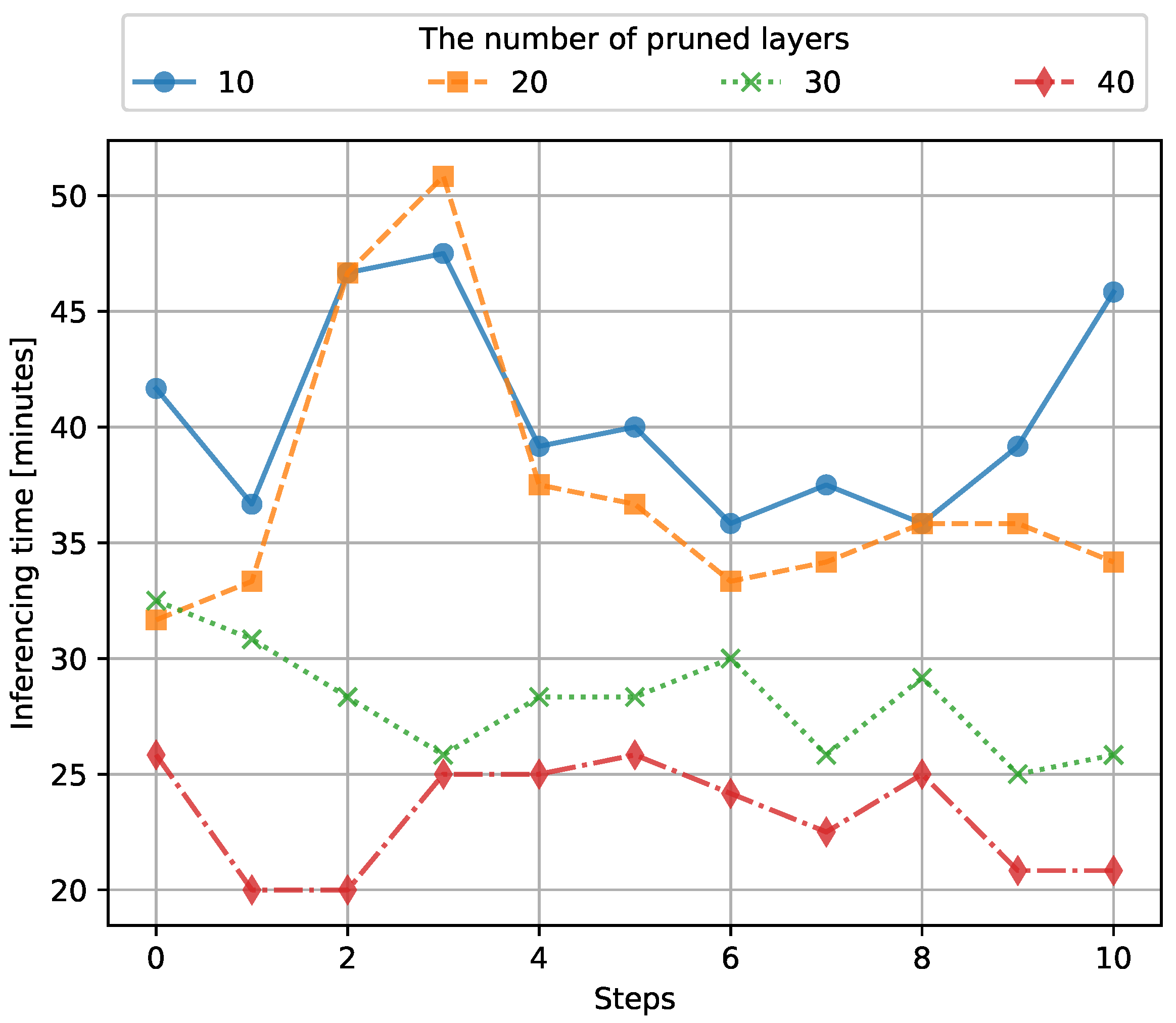
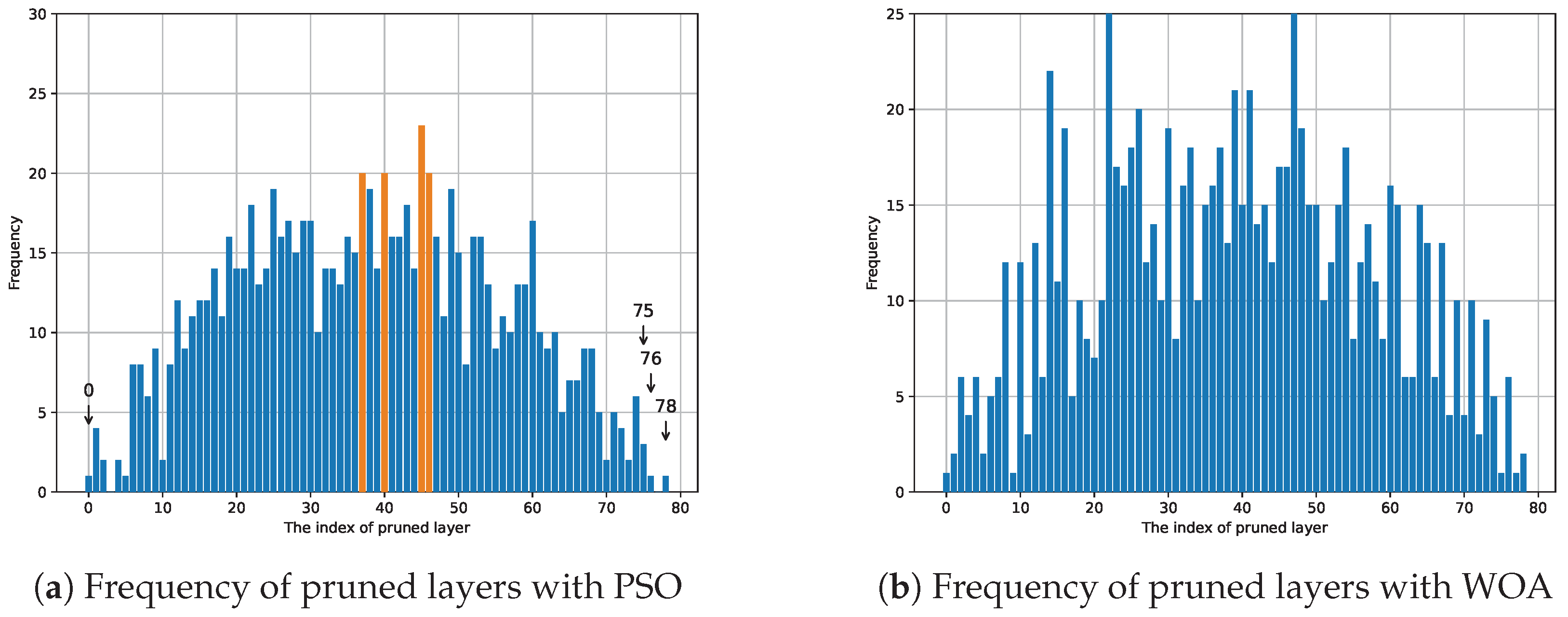
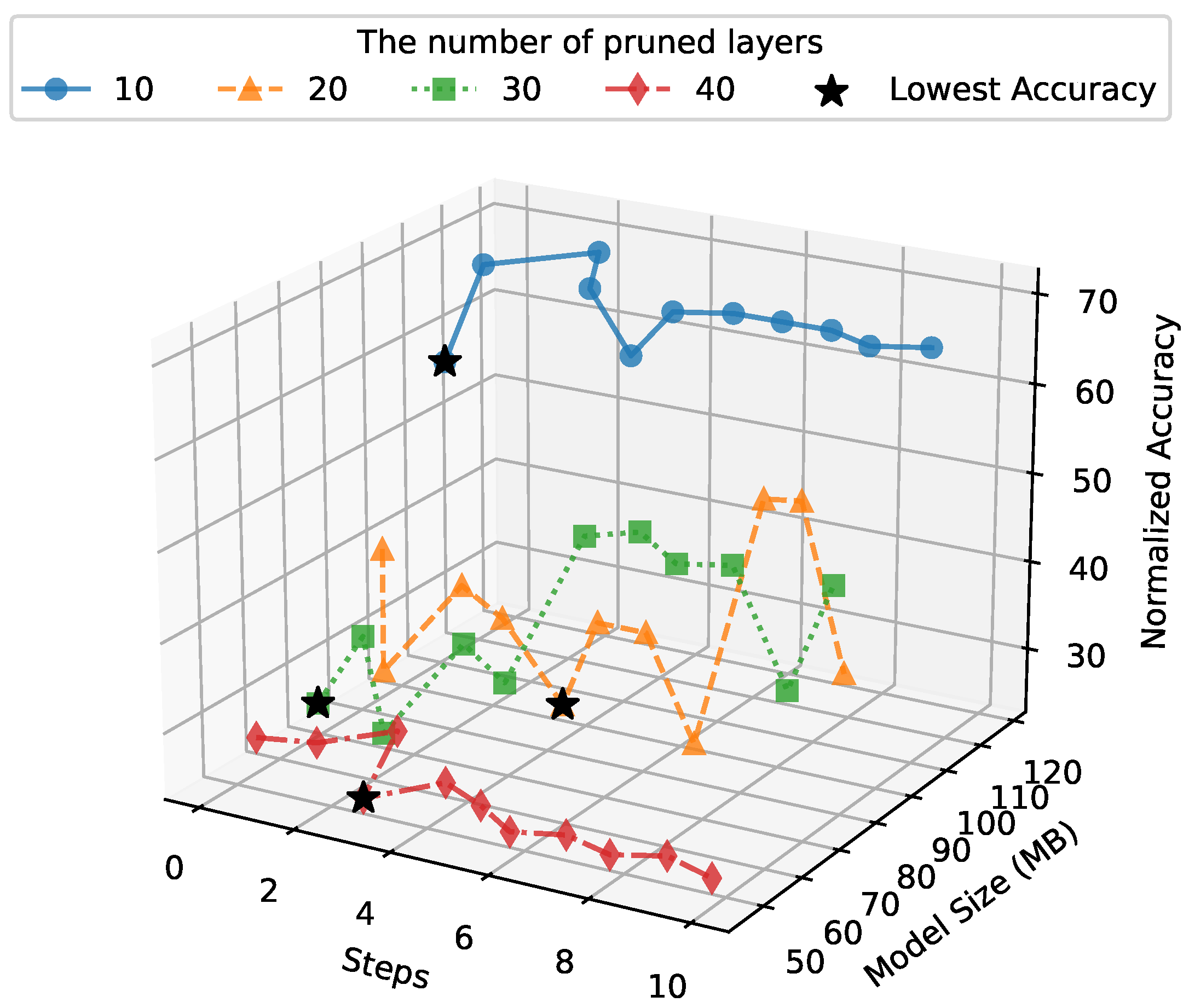
4.2. PSO Results
4.3. Results for Pruning with WOA
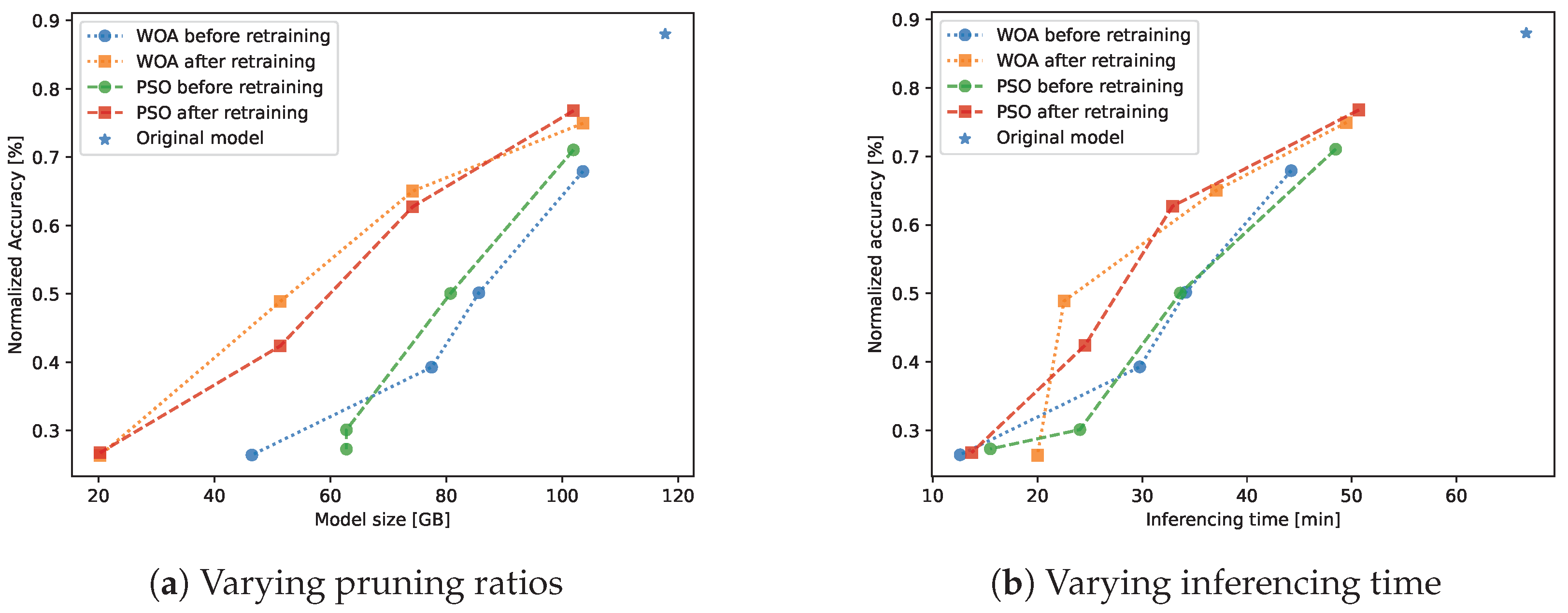
4.4. Comparison Between PSO and WOA
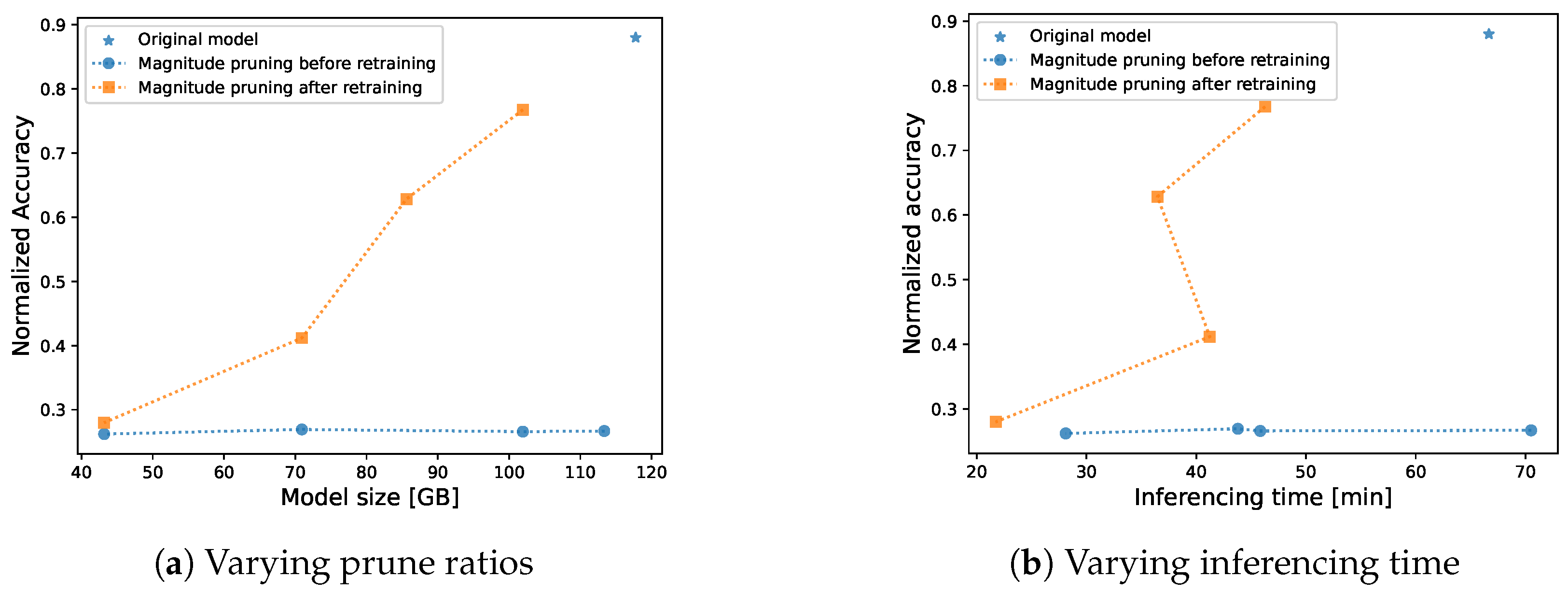
4.5. Compared to Original Model
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Prentzas, J.; Sidiropoulou, M. Assessing the Use of Open AI Chat-GPT in a University Department of Education. In Proceedings of the International Conference on Information, Intelligence, Systems & Applications, Volos, Greece, 10–12 July 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Islam, R.; Ahmed, I. Gemini-the most powerful LLM: Myth or Truth. In Proceedings of the 2024 5th Information Communication Technologies Conference (ICTC), Nanjing, China, 10–12 May 2024; pp. 303–308. [Google Scholar] [CrossRef]
- Huang, D.; Hu, Z.; Wang, Z. Performance Analysis of Llama 2 Among Other LLMs. In Proceedings of the 2024 IEEE Conference on Artificial Intelligence (CAI), Singapore, 25–27 June 2024; pp. 1081–1085. [Google Scholar] [CrossRef]
- Kok, C.L.; Ho, C.K.; Aung, T.H.; Koh, Y.Y.; Teo, T.H. Transfer Learning and Deep Neural Networks for Robust Intersubject Hand Movement Detection from EEG Signals. Appl. Sci. 2024, 14, 8091. [Google Scholar] [CrossRef]
- Reddy, G.P.; Pavan Kumar, Y.V.; Prakash, K.P. Hallucinations in Large Language Models (LLMs). In Proceedings of the 2024 IEEE Open Conference of Electrical, Electronic and Information Sciences, Vilnius, Lithuania, 25 April 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Raiaan, M.A.K.; Mukta, M.S.H.; Fatema, K.; Fahad, N.M.; Sakib, S.; Mim, M.M.J.; Ahmad, J.; Ali, M.E.; Azam, S. A Review on Large Language Models: Architectures, Applications, Taxonomies, Open Issues and Challenges. IEEE Access 2024, 12, 26839–26874. [Google Scholar] [CrossRef]
- Vakayil, S.; Juliet, D.S.; Anitha, J.; Vakayil, S. RAG-Based LLM Chatbot Using Llama-2. In Proceedings of the 2024 7th International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 19–20 April 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Epoch AI. Data on Notable AI Models. 2024. Available online: https://epoch.ai/data/notable-ai-models (accessed on 29 March 2025).
- Thonglek, K.; Takahashi, K.; Ichikawa, K.; Nakasan, C.; Nakada, H.; Takano, R.; Iida, H. Retraining Quantized Neural Network Models with Unlabeled Data. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Stirapongsasuti, S.; Thonglek, K.; Misaki, S.; Usawalertkamol, B.; Nakamura, Y.; Yasumoto, K. A nudge-based smart system for hand hygiene promotion in private organizations. In Proceedings of the Conference on Embedded Networked Sensor Systems. Association for Computing Machinery, Virtual Event, 16–19 November 2020; pp. 743–744. [Google Scholar] [CrossRef]
- Achiam, J.; Adler, S.; Agarwal, S.; Ahmad, L.; Akkaya, I.; Aleman, F.L.; Almeida, D.; Altenschmidt, J.; Altman, S.; Gu, S.; et al. GPT-4 Technical Report. arXiv 2024, arXiv:2303.08774. [Google Scholar]
- Team, G.; Georgiev, P.; Lei, V.I.; Burnell, R.; Bai, L.; Gulati, A.; Tanzer, G.; Vincent, D.; Pan, Z.; Teplyashin, D.; et al. Gemini 1.5: Unlocking multimodal understanding across millions of tokens of context. arXiv 2024, arXiv:2403.05530. [Google Scholar]
- Anthropic. Claude: A Large Language Model by Anthropic. 2024. Available online: https://www.anthropic.com (accessed on 23 January 2025).
- Mistral AI. Models Overview—Mistral Documentation. 2024. Available online: https://docs.mistral.ai/getting-started/models/models_overview/ (accessed on 21 February 2025).
- Grattafiori, A.; Dubey, A.; Jauhri, A.; Pandey, A.; Kadian, A.; Al-Dahle, A.; Letman, A.; Mathur, A.; Schelten, A.; Vaughan, A.; et al. The Llama 3 Herd of Models. arXiv 2024, arXiv:2407.21783. [Google Scholar]
- Kok, C.L.; Heng, J.B.; Koh, Y.Y.; Teo, T.H. Energy-, Cost-, and Resource-Efficient IoT Hazard Detection System with Adaptive Monitoring. Sensors 2025, 25, 1761. [Google Scholar] [CrossRef] [PubMed]
- Shui, H.; Zhu, Y.; Zhuo, F.; Sun, Y.; Li, D. An Emotion Text Classification Model Based on Llama3-8b Using Lora Technique. In Proceedings of the 2024 7th International Conference on Computer Information Science and Application Technology (CISAT), Hangzhou, China, 12–14 July 2024; pp. 380–383. [Google Scholar]
- Hossain, M.B.; Gong, N.; Shaban, M. Computational Complexity Reduction Techniques for Deep Neural Networks: A Survey. In Proceedings of the 2023 IEEE International Conference on Artificial Intelligence, Blockchain, and Internet of Things (AIBThings), Mount Pleasant, MI, USA, 16–17 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Gao, S.; Huang, F.; Cai, W.; Huang, H. Network Pruning via Performance Maximization. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–21 June 2021; pp. 9266–9276. [Google Scholar] [CrossRef]
- Ben Letaifa, L.; Rouas, J.L. Fine-grained analysis of the transformer model for efficient pruning. In Proceedings of the 2022 21st IEEE International Conference on Machine Learning and Applications (ICMLA), Nassau, Bahamas, 12–14 December 2022; pp. 897–902. [Google Scholar] [CrossRef]
- Chen, P.Y.; Lin, H.C.; Guo, J.I. Multi-Scale Dynamic Fixed-Point Quantization and Training for Deep Neural Networks. In Proceedings of the 2023 IEEE International Symposium on Circuits and Systems, Monterey, CA, USA, 29–31 May 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Bao, Z.; Tong, T.; Du, D.; Wang, S. Image Classification Network Compression Technique Based on Learning Temperature-Knowledge Distillation. In Proceedings of the 2024 20th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Harbin, China, 29–31 July 2024; pp. 1–7. [Google Scholar] [CrossRef]
- Liao, S.; Xie, Y.; Lin, X.; Wang, Y.; Zhang, M.; Yuan, B. Reduced-Complexity Deep Neural Networks Design Using Multi-Level Compression. Trans. Sustain. Comput. 2019, 4, 245–251. [Google Scholar] [CrossRef]
- Abdolali, M.; Rahmati, M. Multiscale Decomposition in Low-Rank Approximation. IEEE Signal Process. Lett. 2017, 24, 1015–1019. [Google Scholar] [CrossRef]
- Yu, Z.; Bouganis, C.S. SVD-NAS: Coupling Low-Rank Approximation and Neural Architecture Search. In Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 2–7 January 2023; pp. 1503–1512. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, G. Layer Pruning for Obtaining Shallower ResNets. IEEE Signal Process. Lett. 2022, 29, 1172–1176. [Google Scholar] [CrossRef]
- Elkerdawy, S.; Elhoushi, M.; Singh, A.; Zhang, H.; Ray, N. One-Shot Layer-Wise Accuracy Approximation For Layer Pruning. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Virtual, 25–28 October 2020; pp. 2940–2944. [Google Scholar] [CrossRef]
- Tang, H.; Lu, Y.; Xuan, Q. SR-init: An Interpretable Layer Pruning Method. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Ma, X.; Fang, G.; Wang, X. LLM-Pruner: On the Structural Pruning of Large Language Models. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; Oh, A., Naumann, T., Globerson, A., Saenko, K., Hardt, M., Levine, S., Eds.; Curran Associates, Inc.: Nice, France, 2023; Volume 36, pp. 21702–21720. [Google Scholar]
- Liang, J.J.; Qu, B.Y. Large-scale portfolio optimization using multiobjective dynamic mutli-swarm particle swarm optimizer. In Proceedings of the 2013 IEEE Symposium on Swarm Intelligence (SIS), Singapore, 16–19 April 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Chu, Z.; Guo, Q.; Wang, C. The PID Control Algorithm based on Whale Optimization Algorithm Optimized BP Neural Network. In Proceedings of the 2023 IEEE 7th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 15–17 September 2023; Volume 7, pp. 2450–2453. [Google Scholar] [CrossRef]
- Wong, L.P.; Choong, S.S. A Bee Colony Optimization algorithm with Frequent-closed-pattern-based Pruning Strategy for Traveling Salesman Problem. In Proceedings of the 2015 Conference on Technologies and Applications of Artificial Intelligence (TAAI), Tainan, China, 20–22 November 2015; pp. 308–314. [Google Scholar] [CrossRef]
- Sukma Putra, A.; Firman, S.; Srigutomo, W.; Hidayat, Y.; Lesmana, E. A Comparative Study of Simulated Annealing and Genetic Algorithm Method in Bayesian Framework to the 2D-Gravity Data Inversion. J. Phys. Conf. Ser. 2019, 1204, 012079. [Google Scholar] [CrossRef]
- Sun, G.; Shang, Y.; Yuan, K.; Gao, H. An Improved Whale Optimization Algorithm Based on Nonlinear Parameters and Feedback Mechanism. Int. J. Comput. Intell. Syst. 2022, 15, 38. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November 27–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Brodzicki, A.; Piekarski, M.; Jaworek-Korjakowska, J. The Whale Optimization Algorithm Approach for Deep Neural Networks. Sensors 2021, 21, 8003. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Shi, J.; Zhou, D.; Lei, Y.; Gong, M. A Multi-objective Particle Swarm Optimization for Neural Networks Pruning. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 570–577. [Google Scholar] [CrossRef]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. LoRA: Low-Rank Adaptation of Large Language Models. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]
- EleutherAI. lm-Evaluation-Harness: A Framework for Evaluating Large Language Models. 2021. Available online: https://github.com/EleutherAI/lm-evaluation-harness (accessed on 27 April 2025).
- Zellers, R.; Holtzman, A.; Bisk, Y.; Farhadi, A.; Choi, Y. HellaSwag: Can a Machine Really Finish Your Sentence? In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 4791–4800. [Google Scholar] [CrossRef]
- AI, M. Llama 3.1 70B Instruct Model. 2024. Available online: https://huggingface.co/meta-llama/Llama-3.1-70B-Instruct (accessed on 20 February 2025).
- Le, V. Mealpy: A Python Metaheuristic Optimization Librar. 2024. Available online: https://mealpy.readthedocs.io/en/latest/ (accessed on 3 November 2024).


| Model | Author | Performance | Use Case | Params | Variant |
|---|---|---|---|---|---|
| GPT | OpenAI [11] | High accuracy, low perplexity | Creative writing, chatbots, coding | 1.8 T | GPT-4o |
| N/A | GPT-03-mini | ||||
| Gemini | Google [12] | Strong reasoning | Creative Applications | >200 B | Gemini 1.5 pro |
| Claude | Anthropic [13] | Extended thinking, strong safety | Safety-critical applications | N/A | Claude 3.7 Sonnet |
| N/A | Claude 3.5 Haiku | ||||
| N/A | Claude 3 OPUS | ||||
| Mistral | Mistral AI [14] | Efficient, Low params | Real-time apps, programming | 8 B | Ministral 8 B |
| 24 B | Mistral Saba | ||||
| LlamA | Meta [15] | Competitive scores | Research, academia, open source | 1 B, 3 B, 11 B, 90 B | Llama 3.2 |
| 70 B, 8 B, 405 B | Llama 3.1 |
| Pruning Method | Advantages | Disadvantages |
|---|---|---|
| Magnitude-based Pruning | Removes least important weights | Requires retraining to recover accuracy, may remove the important parameters |
| Structured Pruning | Optimizes hardware efficiency, improves inference speed | Requires retraining |
| Unstructured Pruning | Leads to sparse models, can greatly reduce parameter count | Requires specialized hardware for efficient execution |
| Iterative Pruning | Helps maintain accuracy by gradual pruning | Increases training time due to multiple pruning cycles |
| Global Pruning | More effective in removing unimportant weights across the model | Computationally expensive and difficult to tune |
| Local Pruning | Easier to implement with per-layer thresholds | Less optimal than global pruning for overall efficiency |
| Layer Pruning | Reduces model complexity significantly, improves execution speed | Requires retraining |
| Hardware | Specification |
|---|---|
| CPU | Xeon Gold 62.30R 26 core ×2 |
| Main Memory | 256 GiB |
| GPU | NVIDIA A100 ×2 |
| GPU Memory | 40 GiB ×2 |
| Models | Avg Search Time (Min) | Red. Model Size (GB) | Infer. Time (Min) | Normalized acc. |
|---|---|---|---|---|
| PSO(10) | 40.5303 | 101.9299 | 50.6833 | 0.7680 |
| WOA(10) | 36.9697 | 103.5619 | 49.4834 | 0.7495 |
| PSO(20) | 37.2727 | 74.1854 | 32.9 | 0.6274 |
| WOA(20) | 36.5151 | 74.1854 | 37.0667 | 0.2676 |
| PSO(30) | 28.1818 | 51.3369 | 24.5166 | 0.4239 |
| WOA(30) | 28.5606 | 51.3369 | 22.5333 | 0.4888 |
| PSO(40) | 23.1818 | 20.2383 | 13.7167 | 0.2676 |
| WOA(40) | 19.9242 | 20.2383 | 20.0 | 0.2637 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratsapa, P.; Thonglek, K.; Chantrapornchai, C.; Ichikawa, K. Automated Pruning Framework for Large Language Models Using Combinatorial Optimization. AI 2025, 6, 96. https://doi.org/10.3390/ai6050096
Ratsapa P, Thonglek K, Chantrapornchai C, Ichikawa K. Automated Pruning Framework for Large Language Models Using Combinatorial Optimization. AI. 2025; 6(5):96. https://doi.org/10.3390/ai6050096
Chicago/Turabian StyleRatsapa, Patcharapol, Kundjanasith Thonglek, Chantana Chantrapornchai, and Kohei Ichikawa. 2025. "Automated Pruning Framework for Large Language Models Using Combinatorial Optimization" AI 6, no. 5: 96. https://doi.org/10.3390/ai6050096
APA StyleRatsapa, P., Thonglek, K., Chantrapornchai, C., & Ichikawa, K. (2025). Automated Pruning Framework for Large Language Models Using Combinatorial Optimization. AI, 6(5), 96. https://doi.org/10.3390/ai6050096