Robust Single-Cell RNA-Seq Analysis Using Hyperdimensional Computing: Enhanced Clustering and Classification Methods
Abstract
1. Introduction
2. Methods
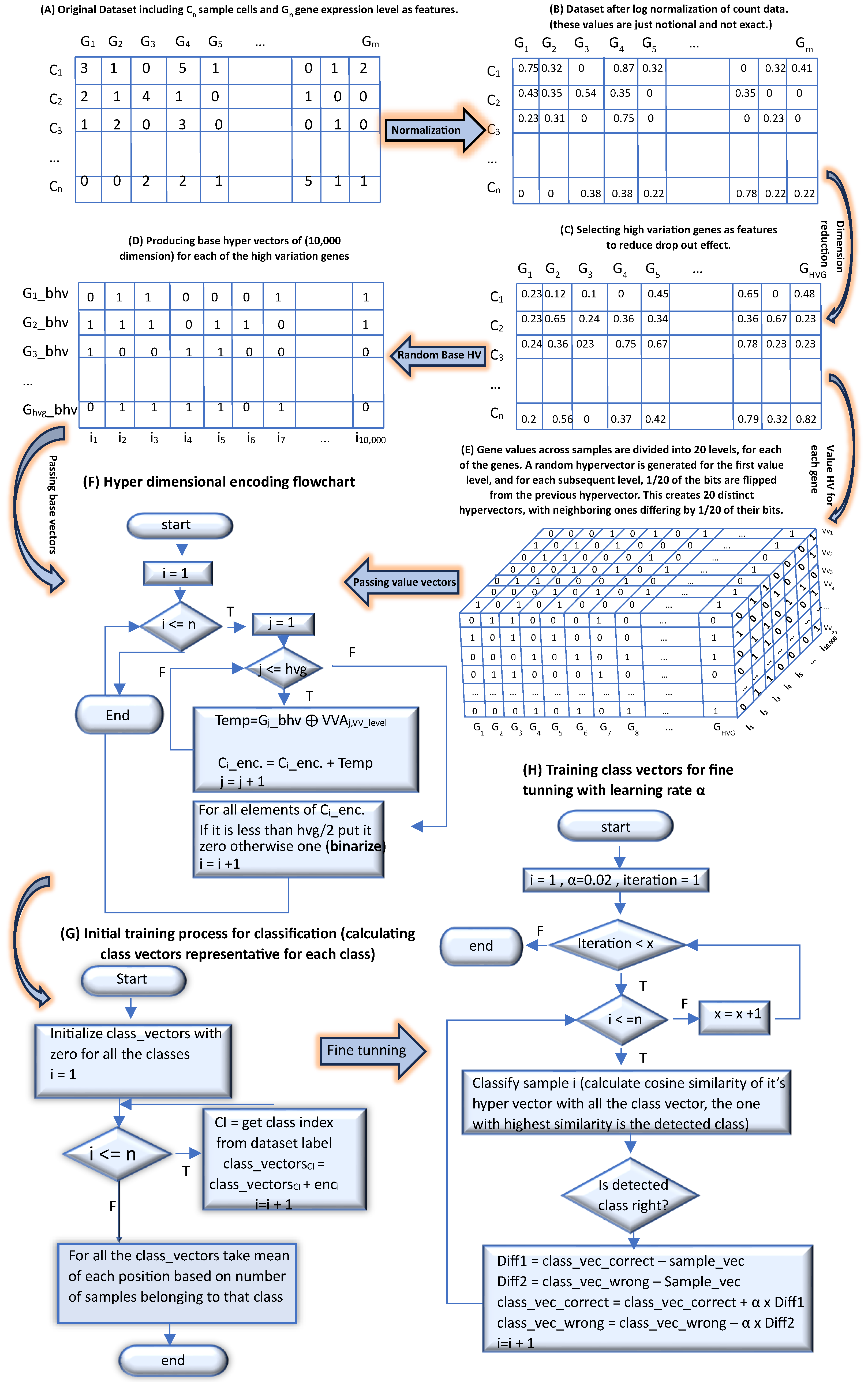
2.1. Preprocessing and Encoding
2.1.1. Preprocessing of scRNA-Seq Data
2.1.2. Hyperdimensional Encoding
2.2. Clustering Methodology
2.2.1. Feature Engineering
2.2.2. Hybrid Clustering
2.3. Classification Methodology
2.3.1. HD Encoding
2.3.2. Classification Process
3. Experiments
3.1. Clustering Experiments
3.1.1. Datasets
3.1.2. Evaluation Metrics
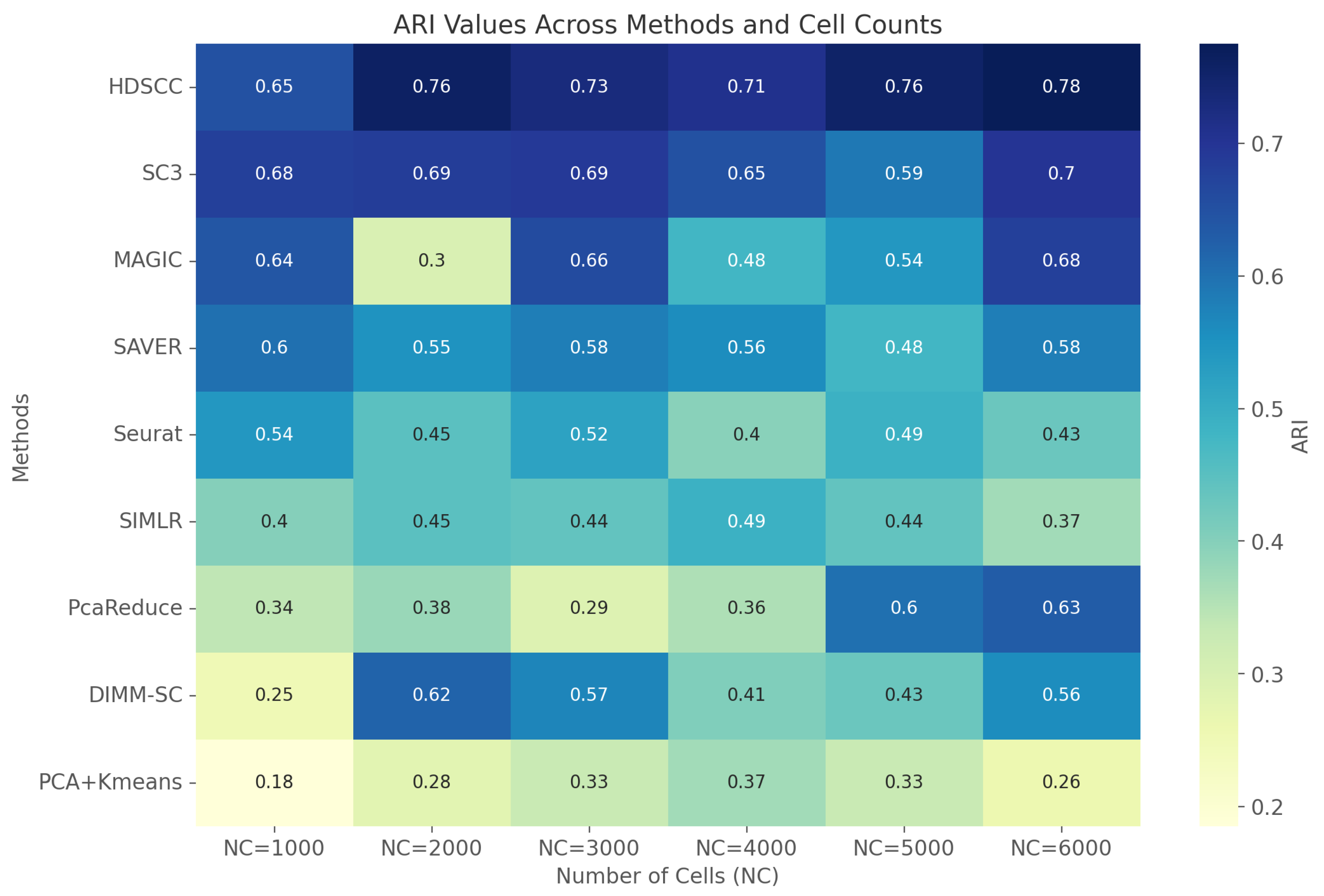
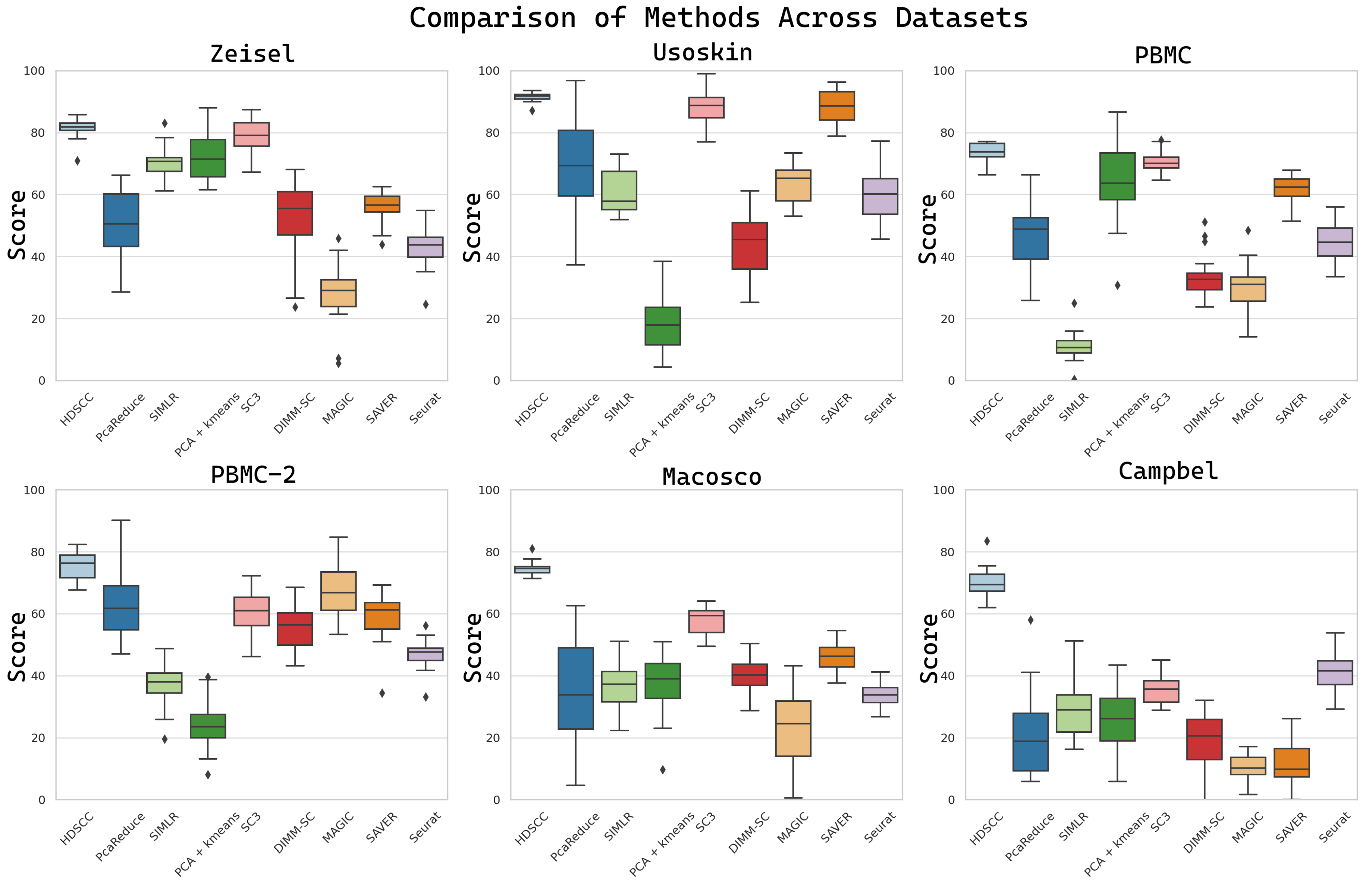
3.1.3. Clustering Performance
3.1.4. Clustering Performance and Data Size
3.1.5. Robustness to Noise
3.1.6. Runtime Comparison
3.2. Classification Experiments
3.2.1. Datasets
3.2.2. Experimental Settings
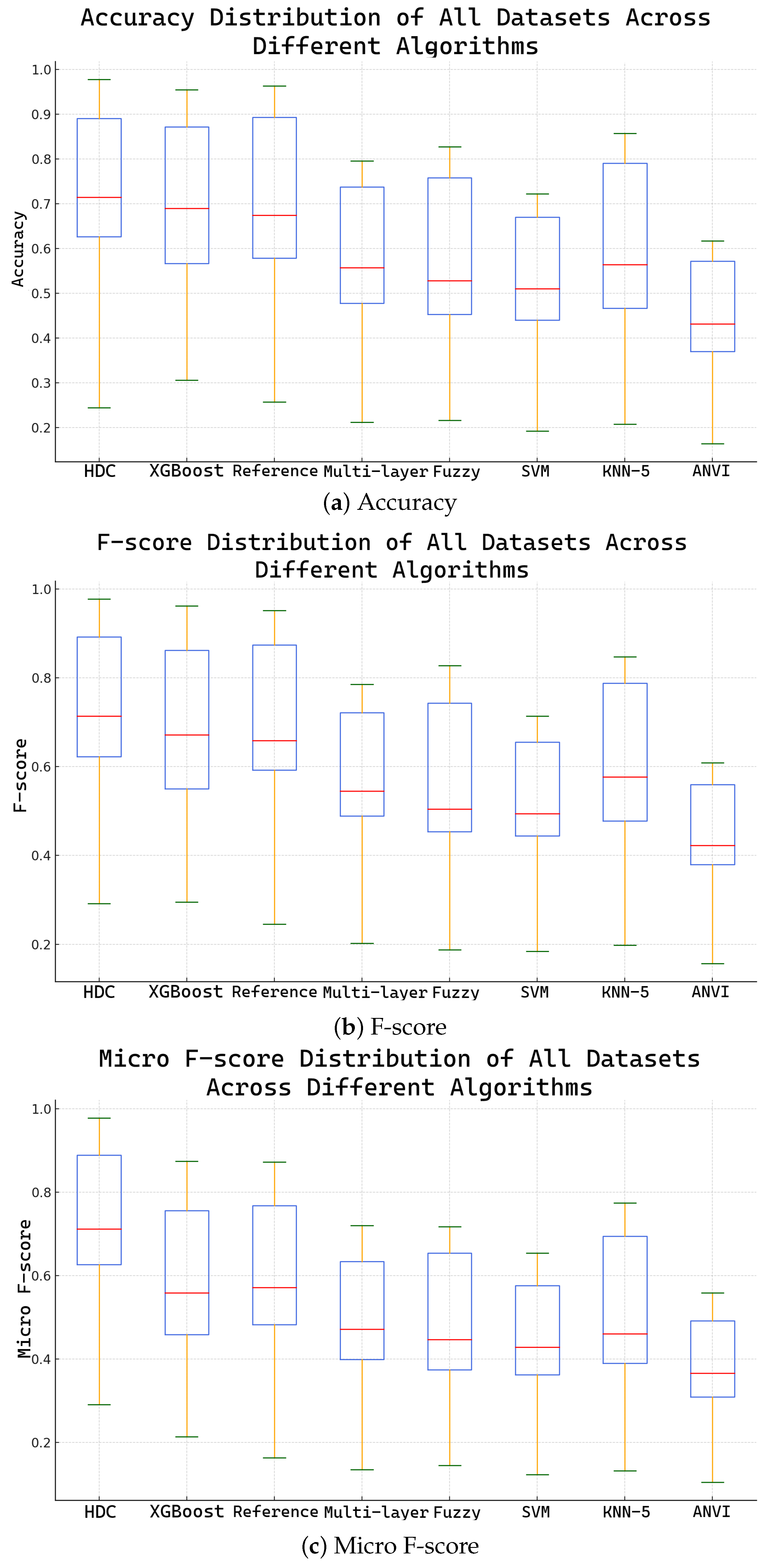
3.2.3. Comparison with Other Models
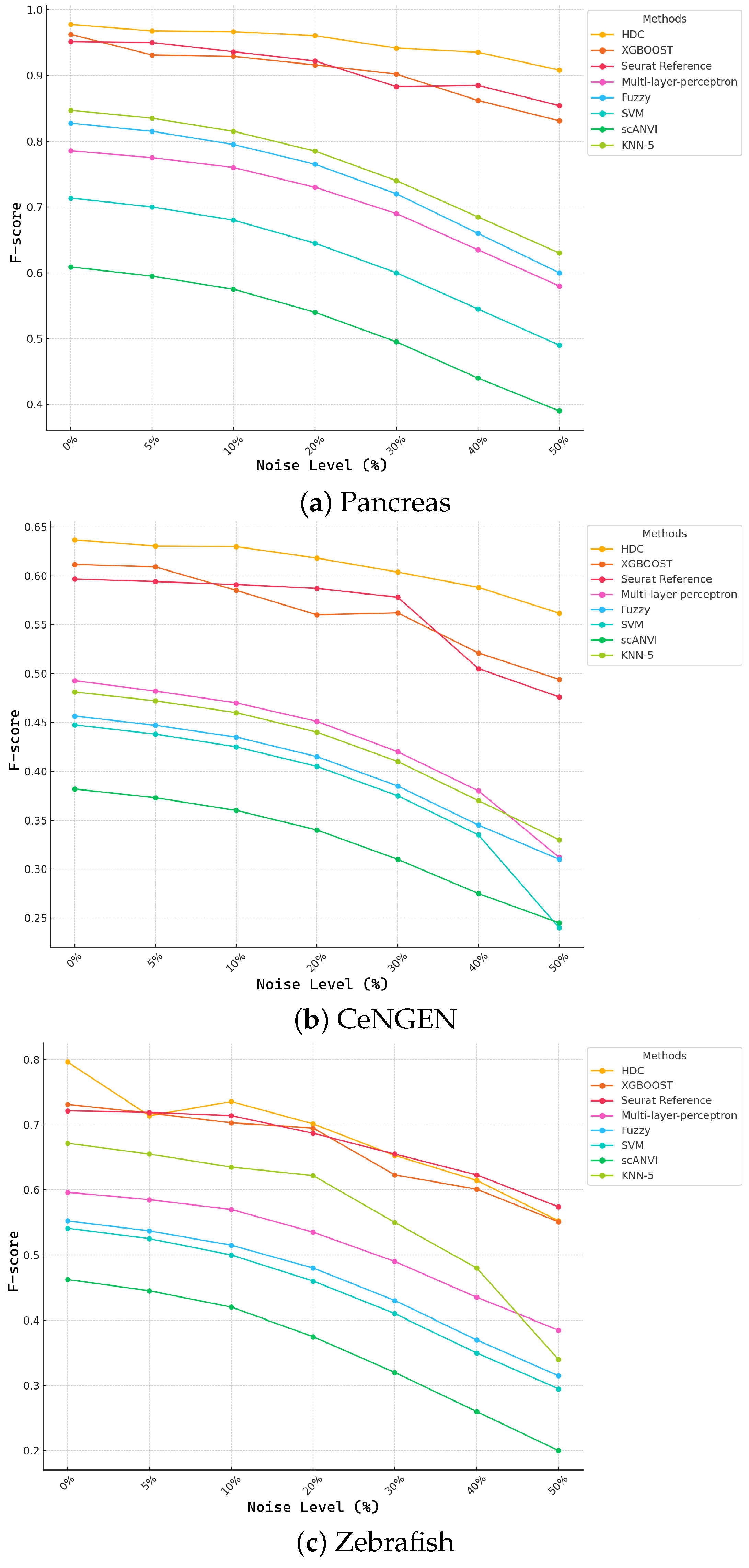
3.3. Noise Robustness Experiments on Classification
3.3.1. Stability Analysis
3.3.2. Robustness to Noise in Data
3.3.3. Proposed Method for Improved Base Hypervector Selection
4. Discussion
4.1. Comparative Analysis of Clustering Methods
4.2. Effectiveness of Hyperdimensional Encoding in Classification
4.3. Noise Robustness in Clustering and Classification
4.4. Computational Efficiency
4.5. Implications for Biomedical Research
4.6. Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stuart, T.; Butler, A.; Hoffman, P.; Hafemeister, C.; Papalexi, E.; Mauck, W.M.; Hao, Y.; Stoeckius, M.; Smibert, P.; Satija, R. Comprehensive integration of single-cell data. Cell 2019, 177, 1888–1902. [Google Scholar] [CrossRef] [PubMed]
- Butler, A.; Hoffman, P.; Smibert, P.; Papalexi, E.; Satija, R. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 2018, 36, 411–420. [Google Scholar] [CrossRef] [PubMed]
- Aldridge, P.L.; Metzner, H.; Morgan, J.P. High-throughput data integration and analysis for single-cell RNA-sequencing. Nat. Methods 2020, 17, 875–882. [Google Scholar]
- Tanay, E.; Regev, A. Scaling single-cell genomics from tissue organization to cell-type atlases. Genes 2019, 10, 10. [Google Scholar]
- Lun, E.; McCarthy, F.; Marioni, M. A Computational Workflow to Enhance Single-Cell RNA-seq Analysis. Nucleic Acids Res. 2021, 49, 705–721. [Google Scholar]
- Li, H.; Courtois, R.; Sengupta, M.; Prahalad, K. A Scalable Computational Framework for Large-Scale Single-Cell RNA-Seq Data. Nat. Biotechnol. 2018, 36, 411–420. [Google Scholar]
- Imani, M.; Rahimi, A.; Ly, D.R.; Rosing, T. HDCluster: An Efficient Clustering Algorithm for Hyperdimensional Computing. IEEE Trans. Comput. 2021, 70, 340–352. [Google Scholar]
- Rahimi, A.; Imani, M.; Lee, J.C.; Rosing, T. Hyperdimensional Computing for Nonlinear Classification of EEG Error-Related Potentials. In Proceedings of the IEEE International Conference on Rebooting Computing (ICRC), Washington, DC, USA, 8–9 November 2017; pp. 1–8. [Google Scholar]
- Neubert, P.; Protzel, P. Hyperdimensional Computing: A New Way of Representing Signals in Robotics. IEEE Robot. Autom. Mag. 2019, 26, 17–22. [Google Scholar]
- Hersche, M.; Stadelmann, R.; Benini, L. Fast and Accurate Multivariate Pattern Recognition of EEG Signals with Hyperdimensional Computing. IEEE Access 2020, 8, 190720–190734. [Google Scholar]
- Kanerva, P. Hyperdimensional computing: An introduction to computing in distributed representation with high-dimensional random vectors. Cogn. Comput. 2012, 1, 139–159. [Google Scholar] [CrossRef]
- Burrello, A.; Marchesoni, S.; Fornaciari, A.; Tagliavini, M. HDNN: Hyperdimensional Computing for Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4049–4063. [Google Scholar]
- Booeshaghi, A.; Pachter, L. Normalization of single-cell RNA-seq counts by log (x + 1) or log (1 + x). Bioinformatics 2021, 37, 2223–2224. [Google Scholar] [PubMed]
- Lun, A. Overcoming systematic errors caused by log-transformation of normalized single-cell RNA sequencing data. bioRxiv 2018, 404962. [Google Scholar] [CrossRef]
- Peng, M.; Lin, B.; Zhang, J.; Zhou, Y.; Lin, B. scFSNN: A feature selection method based on neural network for single-cell RNA-seq data. BMC Genom. 2024, 25, 264. [Google Scholar] [CrossRef]
- Cho, J.; Baik, B.; Nguyen, H.; Park, D.; Nam, D. Characterizing efficient feature selection for single-cell expression analysis. Briefings Bioinform. 2024, 25, bbae317. [Google Scholar]
- Baranpouyan, M.; Mohammadi, H.; Goudarzi, H.T.; Thirunarayan, K.; Chen, L. Enhancing Rare Cell Type Identification in Single-Cell Data: An Innovative Gene Filtering Approach using Bipartite Cell-Gene Relation Graph. In Proceedings of the 2023 IEEE EMBS International Conference on Biomedical and Health Informatics (BHI), Pittsburgh, PA, USA, 15–18 October 2023; pp. 1–5. [Google Scholar]
- Baranpouyan, M.; Mohammadi, H. HDSCC: A robust clustering approach for Single Cell RNA-seq data using Hyperdimensional Encoding. In Proceedings of the 2023 45th Annual International Conference of the IEEE Engineering in Medicine &Biology Society (EMBC), Sydney, Australia, 24–27 July 2023; pp. 1–5. [Google Scholar]
- Imani, M.; Bosch, S.; Datta, S.; Ramakrishna, S.; Salamat, S.; Rabaey, J.; Rosing, T. Quanthd: A quantization framework for hyperdimensional computing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2019, 39, 2268–2278. [Google Scholar] [CrossRef]
- Mohammadi, H.; Baranpouyan, M.; Thirunarayan, K.; Chen, L. HyperCell: Advancing Cell Type Classification with Hyperdimensional Computing. In Proceedings of the 2024 46th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 15–19 July 2024; pp. 1–4. [Google Scholar]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Usoskin, D.; Furlan, A.; Islam, S.; Abdo, H.; Lönnerberg, P.; Lou, D.; Hjerling-Leffler, J.; Haeggström, J.; Kharchenko, O.; Kharchenko, P.V.; et al. Unbiased Classification of Sensory Neuron Types by Large-Scale Single-Cell RNA Sequencing. Nat. Neurosci. 2015, 18, 145–153. [Google Scholar] [CrossRef]
- Zeisel, A.; Muñoz-Manchado, A.B.; Codeluppi, S.; Lönnerberg, P.; La Manno, G.; Juréus, A.; Marques, S.; Munguba, H.; He, L.; Betsholtz, C.; et al. Brain Structure: Cell Types in the Mouse Cortex and Hippocampus Revealed by Single-Cell RNA-seq. Science 2015, 347, 1138–1142. [Google Scholar]
- Macosko, E.Z.; Basu, A.; Satija, R.; Nemesh, J.; Shekhar, K.; Goldman, M.; Tirosh, I.; Bialas, A.R.; Kamitaki, N.; Martersteck, E.M.; et al. Highly Parallel Genome-Wide Expression Profiling of Individual Cells Using Nanoliter Droplets. Cell 2016, 161, 1202–1214. [Google Scholar]
- Campbell, J.N.; Macosko, E.Z.; Fenselau, H.; Pers, T.H.; Lyubetskaya, A.; Tenen, D.; Goldman, M.; Verstegen, A.M.J.; Resch, J.M.; McCarroll, S.A.; et al. A Molecular Census of Arcuate Hypothalamus and Median Eminence Cell Types. Nat. Neurosci. 2017, 20, 484–496. [Google Scholar] [CrossRef] [PubMed]
- 10x Genomics. 1k PBMCs from a Healthy Donor (v3 Chemistry); 10x Genomics: Pleasanton, CA, USA, 2018. [Google Scholar]
- 10x Genomics. 5k Peripheral Blood Mononuclear Cells (PBMCs) from a Healthy Donor with a Panel of TotalSeq™-B Antibodies (v3 Chemistry); 10x Genomics: Pleasanton, CA, USA, 2019. [Google Scholar]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Kiselev, V.Y.; Kirschner, K.; Schaub, M.T.; Andrews, T.; Yiu, A.; Chandra, T.; Natarajan, K.N.; Reik, W.; Barahona, M.; Green, A.R.; et al. SC3: Consensus clustering of single-cell RNA-seq data. Nat. Methods 2017, 14, 483–486. [Google Scholar]
- Wang, B.; Zhu, H.; Zhang, Z.; Gillis, S.P. SIMLR: A Tool for Large-Scale Single-Cell RNA-Seq Data Analysis by Multi-Kernel Learning. BioRxiv 2017, 18, 118901. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, T.; Deng, K.; Wang, X.F.; Lafyatis, R.; Ding, Y.; Hu, M.; Chen, W. DIMM-SC: A Dirichlet mixture model for clustering droplet-based single cell transcriptomic data. Bioinformatics 2018, 34, 139–146. [Google Scholar]
- Žurauskienė, J.; Yau, C. pcaReduce: Hierarchical clustering of single cell transcriptional profiles. BMC Bioinform. 2016, 17, 140. [Google Scholar]
- Huang, M.; Wang, J.; Torre, E.; Dueck, H.; Shaffer, S.; Bonasio, R.; Murray, J.I.; Raj, A.; Li, M.; Zhang, N.R. SAVER: Gene expression recovery for single-cell RNA sequencing. Nat. Methods 2018, 15, 539–542. [Google Scholar]
- Van Dijk, D.; Nainys, J.; Sharma, R.; Kaithail, P.; Carr, A.J.; Moon, K.R.; Mazutis, L.; Wolf, G.; Krishnaswamy, S.; Pe’er, D. Recovering Gene Interactions from Single-Cell Data Using Data Diffusion. Cell 2018, 174, 716–729.e27. [Google Scholar]
- Hafemeister, C.; Satija, R. Normalization and variance stabilization of single-cell RNA-seq data using regularized negative binomial regression. Genome Biol. 2019, 20, 296. [Google Scholar]
- Cao, C.; Zheng, S.; Cox, D.K.; Zhang, Y.; Wang, L.; Li, M.; Chen, H.; Liu, J.; Yang, X.; Huang, Q.; et al. Comprehensive single-cell transcriptome lineages of a multicellular organism. Science 2020, 370, 1234–1240. [Google Scholar]
- Baron, M.; Veres, A.; Wolock, S.L.; Faust, A.L.; Gaujoux, R.; Vetere, A.; Ryu, J.H.; Wagner, B.K.; Shen-Orr, S.S.; Klein, A.M.; et al. A single-cell transcriptomic map of the human and mouse pancreas reveals inter-and intra-cell population structure. Cell Syst. 2016, 3, 346–360. [Google Scholar] [CrossRef] [PubMed]
- Wagner, D.E.; Weinreb, C.; Collins, Z.M.; Briggs, J.A.; Megason, S.G.; Klein, A.M. Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science 2018, 360, 981–987. [Google Scholar]
- Chen, H.; Ryu, J.; Vinyard, M.; Lerer, A.; Pinello, L. SIMBA: Single-cell embedding along with features. Nat. Methods 2024, 21, 1003–1013. [Google Scholar] [CrossRef]
- Indyk, P.; Motwani, R. Approximate nearest neighbors: Towards removing the curse of dimensionality. In Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing (STOC), Dallas, TX, USA, 24–26 May 1998; ACM: New York, NY, USA, 1998; pp. 604–613. [Google Scholar]


| Dataset | Cells | Genes | Cell Types | Sparsity% |
|---|---|---|---|---|
| Usoskin [22] | 622 | 25,334 | 4 | 85 |
| Zeisel [23] | 3005 | 19,972 | 9 | 81 |
| Macosko [24] | 10,559 | 23,288 | 39 | 90 |
| Campbell [25] | 20,921 | 26,774 | 20 | 93 |
| PBMC [26] | 76,899 | 32,738 | 7 | 98 |
| PBMC-2 [27] | 6000 | 32,738 | 3 | 98 |
| Method | Usoskin | Zeisel | Macosko | Campbell | PBMC | PBMC-2 |
|---|---|---|---|---|---|---|
| ARI/NMI | ARI/NMI | ARI/NMI | ARI/NMI | ARI/NMI | ARI/NMI | |
| HDSCC | 91.5/85.1 | 81.5/76.2 | 74.5/79.6 | 70.1/79.2 | 73.4/73.2 | 75.3/74.8 |
| PcaReduce | 71.0/66.6 | 50.4/65.5 | 34.2/68.2 | 15.2/55.4 | 46.4/63.0 | 62.1/63.3 |
| SIMLR | 30.5/34.6 | 70.2/75.6 | 37.1/56.1 | 28.2/53.0 | 10.2/24.6 | 36.8/41.0 |
| PCA + k-means | 18.5/24.9 | 72.0/74.8 | 37.2/69.0 | 23.4/59.9 | 64.1/73.0 | 23.7/31.0 |
| SC3 | 88.5/87.3 | 78.7/71.7 | 58.0/78.8 | 35.2/65.1 | 70.3/74.5 | 60.2/55.2 |
| DIMM-SC | 43.5/52.4 | 52.3/63.7 | 40.1/67.0 | 19.0/56.1 | 33.2/37.4 | 54.0/60.1 |
| MAGIC | 63.6/72.7 | 27.9/50.9 | 22.5/61.3 | 8.2/26.2 | 30.0/32.3 | 67.4/67.3 |
| SAVER | 88.4/85.5 | 56.2/69.8 | 45.7/73.8 | 10.2/18.9 | 60.4/70.8 | 58.3/57.5 |
| Seurat | 61.0/73.2 | 42.8/63.6 | 33.9/37.8 | 40.2/44.2 | 43.7/51.8 | 44.5/46.1 |
| Method/Data | Usoskin | Zeisel | Macosko | Campbell | PBMC |
|---|---|---|---|---|---|
| HDSCC | 10.1 | 11.7 | 19.3 | 71.5 | 97.8 |
| PcaReduce | 20.8 | 45.3 | 343.3 | 439.2 | 402.2 |
| SIMLR | 4.3 | 7.3 | 33.1 | 53.2 | 72.2 |
| PCA + k-means | 7.2 | 8.1 | 18.2 | 63.4 | 92.4 |
| SC3 | 4.3 | 7.4 | 33.4 | 125.3 | 341.1 |
| DIMM-SC | 12.1 | 23.2 | 39.2 | 57.3 | 98.2 |
| MAGIC | 5.1 | 6.5 | 22.3 | 56.3 | 73.2 |
| SAVER | 7.3 | 15.4 | 53.4 | 91.2 | 211.3 |
| Seurat | 7.2 | 9.4 | 28.2 | 40.5 | 110.2 |
| Dataset | Cells | Genes | Experiments | Cell Types |
|---|---|---|---|---|
| CeNGEN | 100,955 | 22,469 | 17 | 169 |
| Pancreas | 16,382 | 18,771 | 6 | 14 |
| Zebrafish | 26,022 | 25,258 | 2 | 24 |
| Dataset | Previous F-Score | Proposed F-Score |
|---|---|---|
| Pancreas | 0.971 | 0.977 |
| CenGEN | 0.64 | 0.67 |
| Zebrafish | 0.78 | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, H.; Baranpouyan, M.; Thirunarayan, K.; Chen, L. Robust Single-Cell RNA-Seq Analysis Using Hyperdimensional Computing: Enhanced Clustering and Classification Methods. AI 2025, 6, 94. https://doi.org/10.3390/ai6050094
Mohammadi H, Baranpouyan M, Thirunarayan K, Chen L. Robust Single-Cell RNA-Seq Analysis Using Hyperdimensional Computing: Enhanced Clustering and Classification Methods. AI. 2025; 6(5):94. https://doi.org/10.3390/ai6050094
Chicago/Turabian StyleMohammadi, Hossein, Maziyar Baranpouyan, Krishnaprasad Thirunarayan, and Lingwei Chen. 2025. "Robust Single-Cell RNA-Seq Analysis Using Hyperdimensional Computing: Enhanced Clustering and Classification Methods" AI 6, no. 5: 94. https://doi.org/10.3390/ai6050094
APA StyleMohammadi, H., Baranpouyan, M., Thirunarayan, K., & Chen, L. (2025). Robust Single-Cell RNA-Seq Analysis Using Hyperdimensional Computing: Enhanced Clustering and Classification Methods. AI, 6(5), 94. https://doi.org/10.3390/ai6050094






