XNODE: A XAI Suite to Understand Neural Ordinary Differential Equations

Abstract

Neural Ordinary Differential Equations (Neural ODEs) have emerged as a promising approach for learning the continuous-time behaviour of dynamical systems from data. However, Neural ODEs are black-box models, posing challenges in interpreting and understanding their decision-making processes. This raises concerns about their application in critical domains such as healthcare and autonomous systems. To address this challenge and provide insight into the decision-making process of Neural ODEs, we introduce the eXplainable Neural ODE (XNODE) framework, a suite of eXplainable Artificial Intelligence (XAI) techniques specifically designed for Neural ODEs. Drawing inspiration from classical visualisation methods for differential equations, including time series, state space, and vector field plots, XNODE aims to offer intuitive insights into model behaviour. Although relatively simple, these techniques are intended to furnish researchers with a deeper understanding of the underlying mathematical tools, thereby serving as a practical guide for interpreting results obtained with Neural ODEs. The effectiveness of XNODE is verified through case studies involving a Resistor–Capacitor (RC) circuit, the Lotka–Volterra predator-prey dynamics, and a chemical reaction. The proposed XNODE suite offers a more nuanced perspective for cases where low Mean Squared Error values are obtained, which initially suggests successful learning of the data dynamics. This reveals that a low training error does not necessarily equate to comprehensive understanding or accurate modelling of the underlying data dynamics.

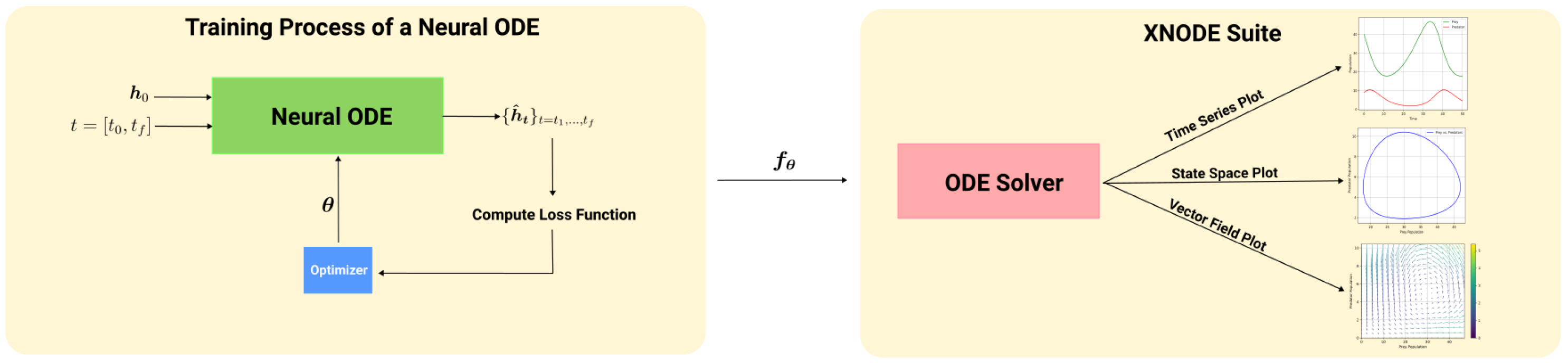
1. Introduction

Real-world systems such as those in the domains of physics, chemistry, biology, and mechanics are present in our daily lives and influence the world in which we live in; therefore, it is imperative to gain a comprehensive understanding of the evolution of these systems.

Traditionally, mathematical modelling relies on Differential Equations (DEs) to describe these systems and to establish relationships between the system variables and their rates of change. However, this process requires understanding the intricate interdependencies among variables, and often entails a laborious trial-and-error time-consuming approach for parameter estimation. Real-world systems often exhibit time-dependent behaviour as variables evolve over time, influenced by interactions among themselves and/or external forces.

Neural Networks (NNs) have emerged as a promising approach to describe the behaviour of these systems by learning from given data [1,2]. However, despite being universal approximators capable of modelling any data dynamics [3], NNs inherently model data using discrete-time functions, which is not ideal for capturing the natural time dependence of real systems. Additionally, due to their inability to perceive time, NNs face challenges with irregularly sampled data, as they cannot perceive the different time distances between data points. This only allows for predictions with a predetermined step size provided by the data.

Neural ODEs [4] were introduced as a promising solution to these challenges. They consist of NN architectures that fit an ODE to the data dynamics, allowing for prediction of the system states $\mathit{h}\left(t_n\right)={\mathit{h}}_n$ with $t_n=t_0,\dots ,t_N$ at arbitrary instants. This introduces time dependence into NNs, making them suitable for modelling real systems by capturing the continuous system dynamics.

For clarity, suppose that we have a collection of $N+1$ ordered observations

$$\mathit{x}=\{{\mathit{x}}_0,{\mathit{x}}_1,\dots ,{\mathit{x}}_N\},$$

which represent the state of a dynamical system at discrete time instants $t_i$ over the interval $[t_0,T]$ (with $t_N=T$). Each observation is given by

$${\mathit{x}}_i=(x_i^1,x_i^2,\dots ,x_i^d)\in {\mathbb{R}}^d,\hspace{1em}i=0,1,\dots ,N,$$

and associated with the corresponding time $t_i$.

We assume that these data can be modelled by the Initial Value Problem (IVP)

$$\left\{\begin{array}{c}{\displaystyle \frac{d\mathit{x}\left(t\right)}{dt}}=\mathit{f}(t,\mathit{x}\left(t\right)),\hfill \\ \mathit{x}\left(t_0\right)={\mathit{x}}_0,\hspace{1em}t\in [t_0,T],\hfill \end{array}\right.$$

(1)

which characterises the evolution of the dynamical system over the interval $[t_0,T]$. Note that neither the solution $\mathit{x}\left(t\right)\in {\mathbb{R}}^d$ nor the function $\mathit{f}(t,\mathit{x}\left(t\right)):\mathbb{R}\times {\mathbb{R}}^d\to {\mathbb{R}}^d$ is known a priori.

Neural ODEs offer a viable approach to approximate the IVP in (1) solely from the observations $\mathit{x}$. Let $\mathit{h}\left(t\right)$ be an approximation of $\mathit{x}\left(t\right)$. In the Neural ODE framework, the differential equation is written as

$$\left\{\begin{array}{c}{\displaystyle \frac{d\mathit{h}\left(t\right)}{dt}}={\mathit{f}}_{\mathit{\theta }}(t,\mathit{h}\left(t\right)),\hfill \\ \mathit{h}\left(t_0\right)={\mathit{x}}_0,\hspace{1em}t\in [t_0,T],\hfill \end{array}\right.$$

(2)

where the analytical function $\mathit{f}(t,\mathit{x}(t\left)\right)$ is replaced by a neural network ${\mathit{f}}_{\mathit{\theta }}(t,\mathit{h}\left(t\right))$. Here, $\mathit{\theta }$ represents the parameters (weights and biases) of the network, which are trained using only the observed data $\mathit{x}$.

The Neural ODE model comprises two main components:

• A numerical ODE solver that computes the approximate solution of (2).
• The neural network ${\mathit{f}}_{\mathit{\theta }}(t,\mathit{h}\left(t\right))$, which is evaluated at each time step within the solver.

Because the output of the Neural ODE model at time t is a numerical approximation, we denote this approximate solution by $\widehat{\mathit{h}}\left(t\right)$. Specifically, we can express the solution at the grid points as

$${\widehat{\mathit{h}}}_i=\mathit{ODESolve}\left({\mathit{f}}_{\theta }, {\mathit{h}}_0, [t_0,t_f]\right),\hspace{1em}i=1,\dots ,N.$$

(3)

Neural ODEs are trained in the same way as traditional NNs, that is, by minimising the error of the fit to the data. Thus, the goal is to optimise the parameters $\mathit{\theta }$ of the NN ${\mathit{f}}_{\mathit{\theta }}$ such that the solution curve $\mathit{h}\left(t\right)$ closely matches the training data. The end result of training a Neural ODE is an ODE like the one in Equation (2), that can be solved numerically and used to make predictions across the entire time domain with arbitrary time steps [4]. Due to these advantages over traditional NNs, Neural ODEs have been extensively used to model real systems (see [5,6] and the references therein).

A common problem across both traditional NNs and Neural ODEs is their black-box approach. While these models excel at capturing complex patterns and making predictions, the opacity of their internal mechanisms raises concerns about their application in critical domains.

In the context of interpreting Neural ODEs, there has been a growing interest in using well-known XAI techniques to unravel the inner workings of these complex models; however, the number of works on this subject is limited. In [7], the authors introduced the Tumour Dynamic Neural ODE framework. They demonstrated that the contribution of tumour dynamics to overall survival can be explained using SHapley Additive exPlanations (SHAP). Furthermore, [8] proposed the use of SHAP values to interpret Neural ODE prediction decisions, further illustrating the growing interest in post hoc explanation methods for these models. In [9], the authors introduced the Explainable Tensorized Neural ODE. This model incorporates an attention mechanism, which provides feature importance analysis to offer explainability about how the network uses the data to make predictions. While these approaches provide valuable insights, they overlook the potential of exploiting the resulting models as DEs to provide explainability.

Therefore, in this study we introduce a set of post hoc XAI techniques that are based on the properties of DEs and tailored specifically for Neural ODEs. These techniques draw inspiration from classical mathematical visualisation methods for DEs. In addition, we propose employing phase and vector plots as powerful tools to comprehend the ODEs generated by Neural ODEs. These plots allow us to depict trajectories, pinpoint equilibrium points, analyse bifurcations, and identify anomalies, thereby offering comprehensive insight into the model’s internal mechanisms and system dynamics. These methods not only enhance model transparency but also the model’s performance and reliability. Furthermore, the proposed XNODE framework is designed to deliver both local and global explanations, enabling users to interpret model behaviour for specific initial conditions and to gain a comprehensive understanding of the overall dynamical structure learned by the Neural ODE. These techniques complement those by [7,9], and we anticipate their adoption by researchers in future studies. Although this work employs simple mathematical tools, it should also serve as a guideline for researchers using Neural ODEs by providing a framework to effectively interpret and infer results.

The rest of this paper is organised as follows: Section 2 presents mathematical background on the existence and uniqueness of solutions and on the stability of the system of differential equations; Section 3 presents a brief review on Neural ODEs and XAI techniques together with the proposed eXplainable Neural ODE suite (XNODE) consisting of a collection of post hoc XAI techniques for Neural ODEs; Section 4 presents three case studies in which we train Neural ODEs to model real systems and show how the proposed techniques can be used to provide explainability to the models; finally, the paper ends with a summary and conclusions in Section 5.

2. Background on Systems of Differential Equations

A general system of first-order Ordinary Differential Equations (ODEs) involving n interrelated unknown functions with respect to a single independent variable (t) is provided by

$$\left\{\begin{array}{c}{\displaystyle \frac{d{x}_1}{dt}}=f_1(t,x_1,x_2,\dots ,x_n)\hfill \\ {\displaystyle \frac{d{x}_2}{dt}}=f_2(t,x_1,x_2,\dots ,x_n)\hfill \\ ⋮\hfill \\ {\displaystyle \frac{d{x}_n}{dt}}=f_n(t,x_1,x_2,\dots ,x_n)\hfill \end{array}\right.\hspace{1em}\mathrm{or}, \mathrm{more} \mathrm{compactly}:\hspace{1em}{\displaystyle \frac{d\mathit{x}}{dt}}=\mathit{f}(t,\mathit{x}),$$

where $\mathit{x}\left(t\right)\in {\mathbb{R}}^n$ and $\mathit{f}(t,\mathit{x}):\mathbb{R}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$.

The Picard–Lindelöf theorem (also known as the Cauchy–Lipschitz theorem) provides sufficient conditions for the existence and uniqueness of a local solution to an initial value problem.

Suppose that $\mathit{f}(t,\mathit{x})$ is continuous in t and $\mathit{x}$ in the neighbourhood of $(t_0,{\mathit{x}}_0)$ and is Lipschitz continuous in $\mathit{x}$, i.e., there exists $L>0$ such that

$$\parallel \mathit{f}(t,{\mathit{x}}_1)-\mathit{f}(t,{\mathit{x}}_2)\parallel \le L\parallel {\mathit{x}}_1-{\mathit{x}}_2\parallel .$$

Then, there exists a unique vector function $\mathit{x}\left(t\right)$ solving

$${\displaystyle \frac{d\mathit{x}}{dt}}=\mathit{f}(t,\mathit{x}),\hspace{1em}\mathit{x}\left(t_0\right)={\mathit{x}}_0$$

on some open interval $t\in (t_0-\epsilon ,t_0+\epsilon )$.

When solving (2), the right hand side function is a neural network; therefore, the Lipschitz-continuous condition can work as a restriction on the optimization problem.

Note that these conditions guarantee local existence. For global existence, it is necessary to ensure that the solution does not blow up in finite time, which usually requires further bounds on $\mathit{f}$, leading to more restrictions on the neural network representing the function $\mathit{f}$.

Lyapunov Stability and Attractors, Repellers, and Saddle Points

Stability is also very important when dealing with these systems. The main goal is to determine whether the system will return to equilibrium or move further away from it under slight perturbations away from equilibrium. Consider the following system:

$${\displaystyle \frac{d\mathit{x}\left(t\right)}{dt}}=\mathit{f}(t,\mathit{x}\left(t\right))$$

where $\mathit{x}\left(t\right)\in {\mathbb{R}}^n$ is the state vector and $\mathit{f}(t,\mathit{x}(t\left)\right)$ is the vector field that depends on both the state $\mathit{x}\left(t\right)$ and time t (non-autonomous system). The Lyapunov stability criterion applies to such systems, but with some additional challenges when compared to autonomous systems. The equilibrium point $\mathit{x}*\left(t\right)$ satisfies ${\displaystyle \frac{d\mathit{x}\left(t\right)}{dt}}=\mathit{f}(t,\mathit{x}*\left(t\right))=0$; for non-autonomous systems, the Lyapunov function $V(\mathit{x},t)$ is used to analyze stability.

A continuously differentiable function $V(\mathbf{x},t):{\mathbb{R}}^n\times \mathbb{R}\to \mathbb{R}$ is called a Lyapunov function around the equilibrium point $\mathbf{x}*$ if there exists a neighborhood $\mathcal{D}\subset {\mathbb{R}}^n$ of $\mathbf{x}*$ such that:

• $V(\mathbf{x},t)>0$ for all $\mathbf{x}\in \mathcal{D}\setminus \{\mathbf{x}*\}$ and all t,
• $V(\mathbf{x}*,t)=0$ for all t,
• The total derivative satisfies

  $$\dot{V}(\mathbf{x},t)={\displaystyle \frac{\partial V}{\partial t}}+{\nabla }_{\mathbf{x}}V(\mathbf{x},t)·\mathbf{f}(t,\mathbf{x})<0\hspace{1em}\mathrm{for} \mathrm{all} \mathbf{x}\ne \mathbf{x}*.$$

If these conditions hold, the equilibrium point $\mathbf{x}*$ is said to be uniformly asymptotically stable.

In XNODE, we take a simplified approach by focusing exclusively on attractors, repellers, and saddle points, intentionally bypassing the more intricate Lyapunov stability analysis. This Lyapunov analysis, which is inherently connected to the study of attractors, repellers, and saddle points, is further explained below.

An attractor is a set of states to which the system evolves as time progresses. In the presence of an attractor, solutions of the system tend to “attract” nearby trajectories. An attractor $\mathcal{A}$ is a set for which there exists a region $U\supseteq \mathcal{A}$ within which solutions of the system starting in U converge to $\mathcal{A}$ as $t\to \infty$:

$$\underset{t\to \infty }{\lim }\mathit{x}\left(t\right)=\mathcal{A}.$$

In Lyapunov stability terms, a system is asymptotically stable if its equilibrium point or attractor is a stable set.

A repeller is the opposite of an attractor, representing a set that pushes away trajectories. A repeller $\mathcal{R}$ is a set that, for any initial condition $\mathit{x}\left(0\right)$ in the neighborhood of $\mathcal{R}$, the trajectory moves away from $\mathcal{R}$ as time progresses:

$$\underset{t\to \infty }{\lim }\mathit{x}\left(t\right)\notin \mathcal{R}.$$

Repellers are typically associated with unstable equilibrium points. The Lyapunov function for a repeller shows that $\dot{V}\left(\mathit{x}\right)>0$ near $\mathcal{R}$.

Let ${\mathbf{x}}_s$ be a critical point or an equilibrium point. To determine the local stability around ${\mathbf{x}}_s$, we can linearize the system around ${\mathbf{x}}_s$ by considering the Jacobian matrix $\mathbf{J}(t,{\mathbf{x}}_s)$ of the function $\mathbf{f}(t,\mathbf{x})$,

$$\mathbf{J}(t,{\mathbf{x}}_s)={\displaystyle \frac{\partial \mathbf{f}(t,\mathbf{x})}{\partial \mathbf{x}}}{|}_{\mathbf{x}={\mathbf{x}}_s}.$$

If the matrix $\mathbf{J}(t,{\mathbf{x}}_s)$ has eigenvalues with both positive and negative real parts, then ${\mathbf{x}}_s$ is a saddle point. Thus, a saddle point is an equilibrium point at which the system has both stable and unstable directions. Saddle points attract trajectories along certain directions (stable manifolds) and repel trajectories along others (unstable manifolds). Saddle points are unstable in the Lyapunov sense, as perturbations along the unstable direction grow, while those along the stable direction decay.

Note that the stability of the system can change dynamically when the right-hand side function $\mathbf{f}(t,\mathbf{x})$ depends on the time t. This means that different behaviours are observed over time, making it more difficult to understand the system’s behaviour.

3. Explainability and Neural ODEs

XAI includes a wide variety of techniques that aim to make the processes by which black-box models arrive at decisions more transparent and interpretable to humans. These techniques can be broadly categorised into three classifications: pre-modelling explainability (pre hoc), post-modelling explainability (post hoc), and interpretable models [10]. Pre-modelling explainability techniques applied before training involve data analysis, summarising, and transformation to uncover patterns and mitigate biases in data [11]. Post-modelling explainability methods employed after training aim to elucidate the internal decision-making of black-box models through local explanations that provide sample-specific insights [7] and global explanations that reveal overall feature contributions [12]. Additionally, interpretable models further enhance understanding of model predictions, either through inherently transparent models or through hybrid combinations that merge black-box performance with interpretability [10].

XAI in Neural ODEs is a largely unexplored research topic; therefore, in this section we introduce three novel post hoc XAI techniques (referred to as the XNODE suite) that take advantage of overlooked traditional mathematical techniques for DEs. Furthermore, we explain how these techniques can be used beyond enhancing Neural ODE explainability by aiding in data anomaly detection, model debugging, and performance enhancement.

3.1. The XNODE Suite

The XNODE suite comprises time series, state space, and vector field plots that provide insights into the dynamics of Neural ODEs, enabling the uncovering of hidden patterns and behaviours in continuous-time models and elucidating the mechanisms governing their evolution and decision-making processes. Applied after model training (see Figure 1), our techniques are both model-agnostic and architecture-agnostic, though they are applicable only when the function adjusted by the neural network is time-dependent. Additionally, the XNODE suite offers global explanations, which addresses SHAP’s limitation of focusing only on sample-by-sample analysis [7].

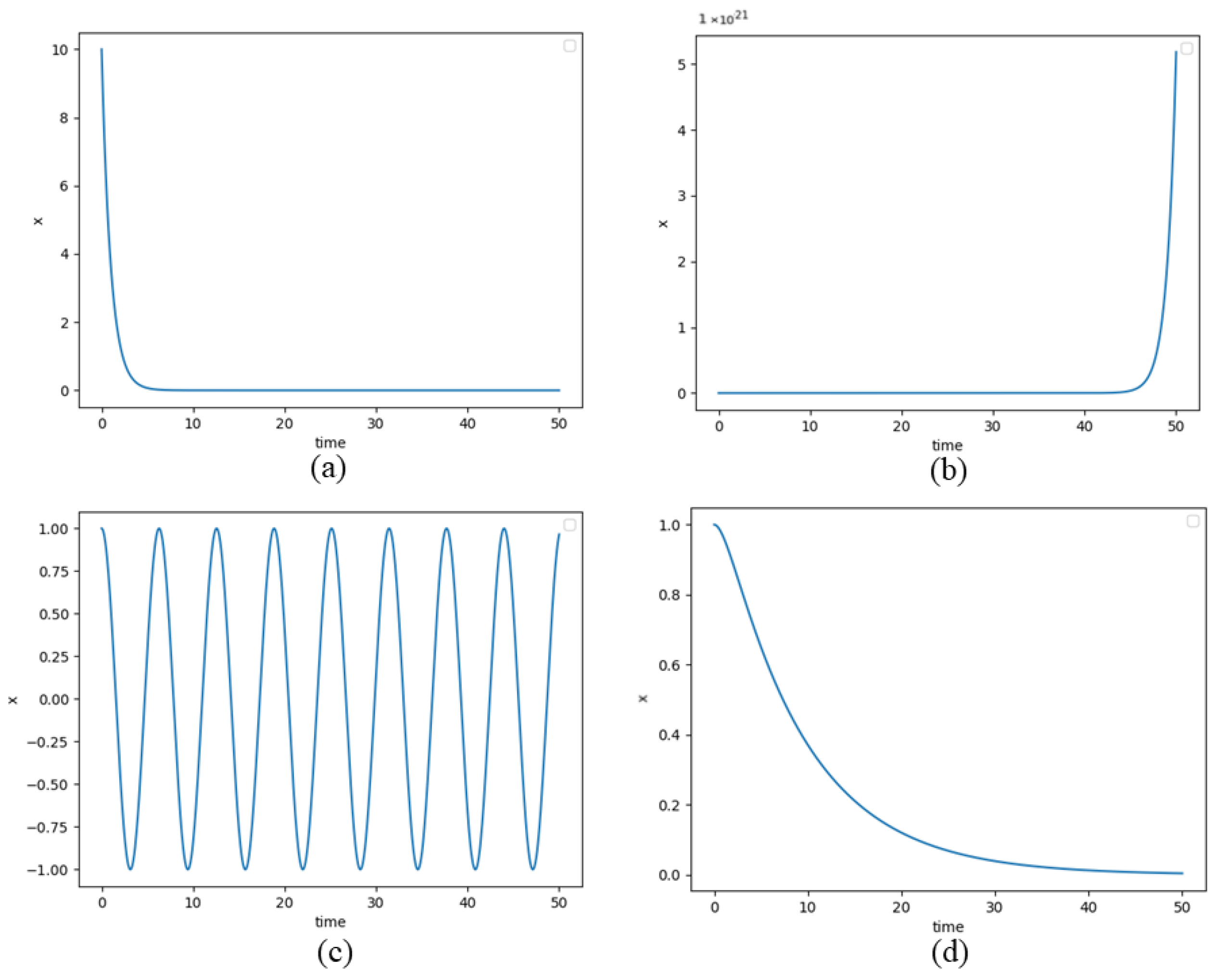
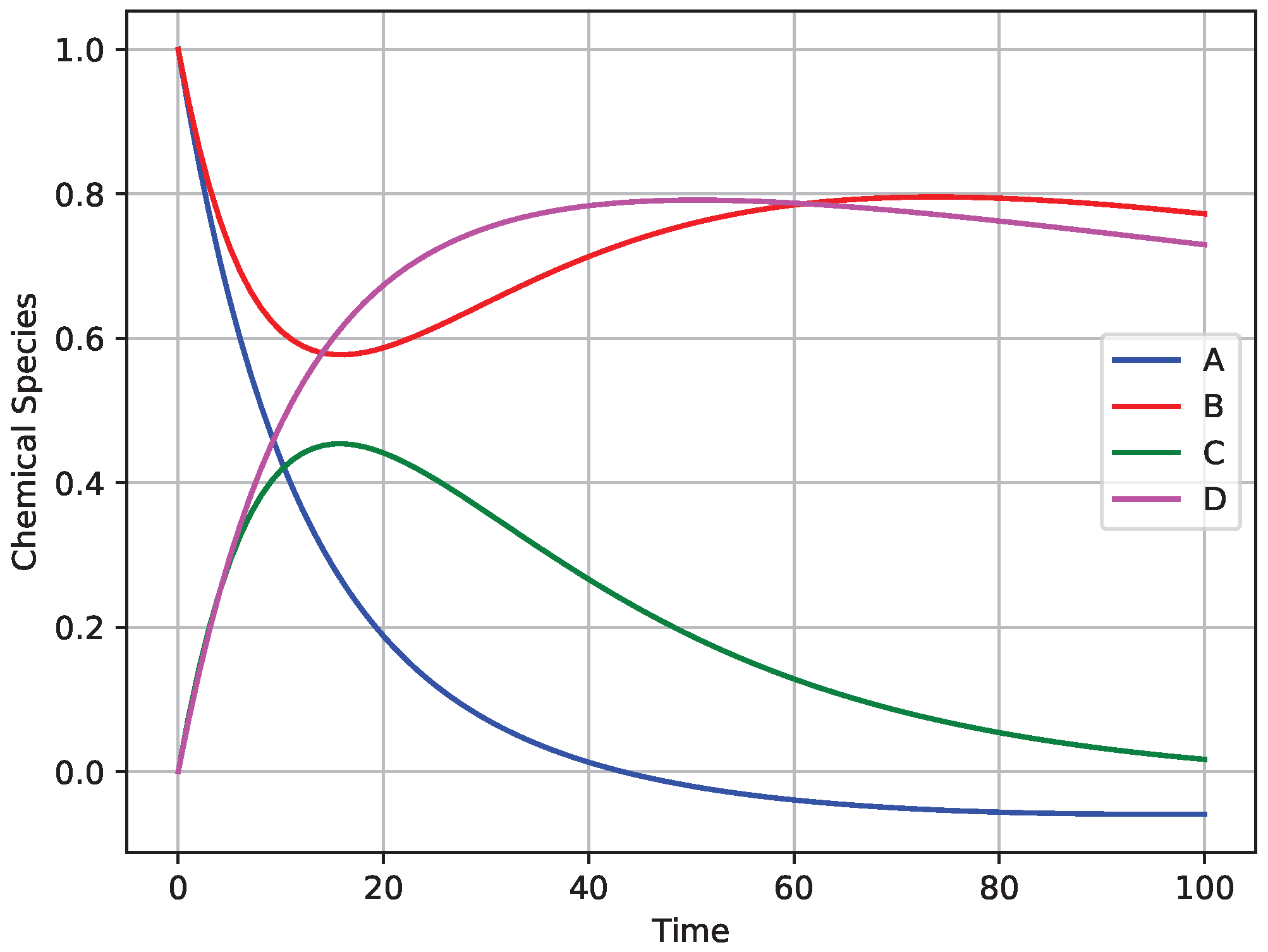
3.1.1. Time Series Plots

Time series plots represent solution trajectories of a system over time, capturing the temporal evolution of variables and enabling the identification of several features:

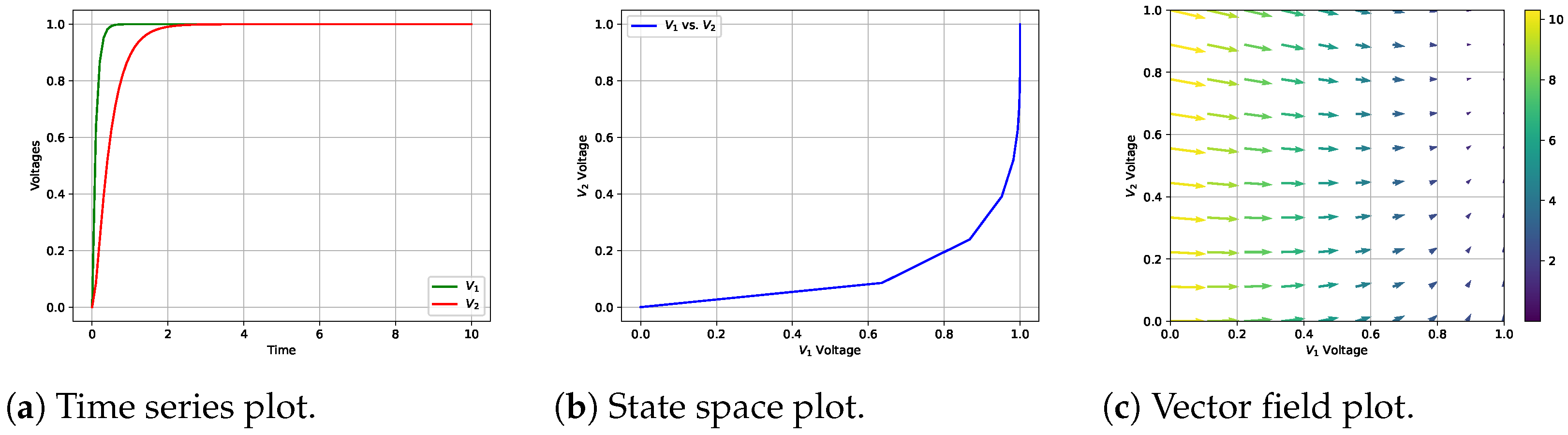
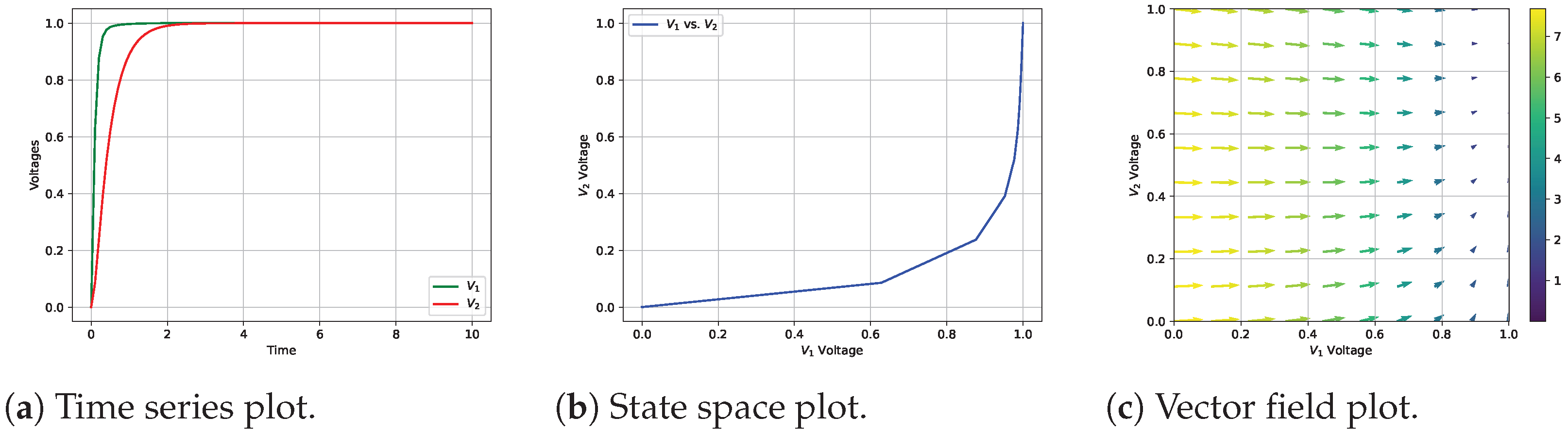
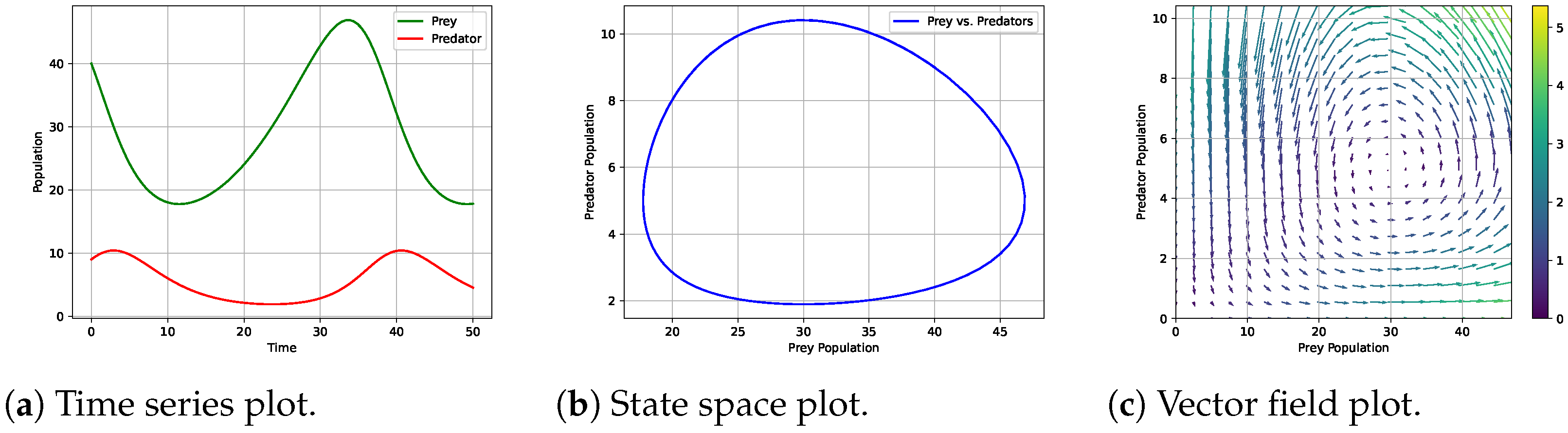
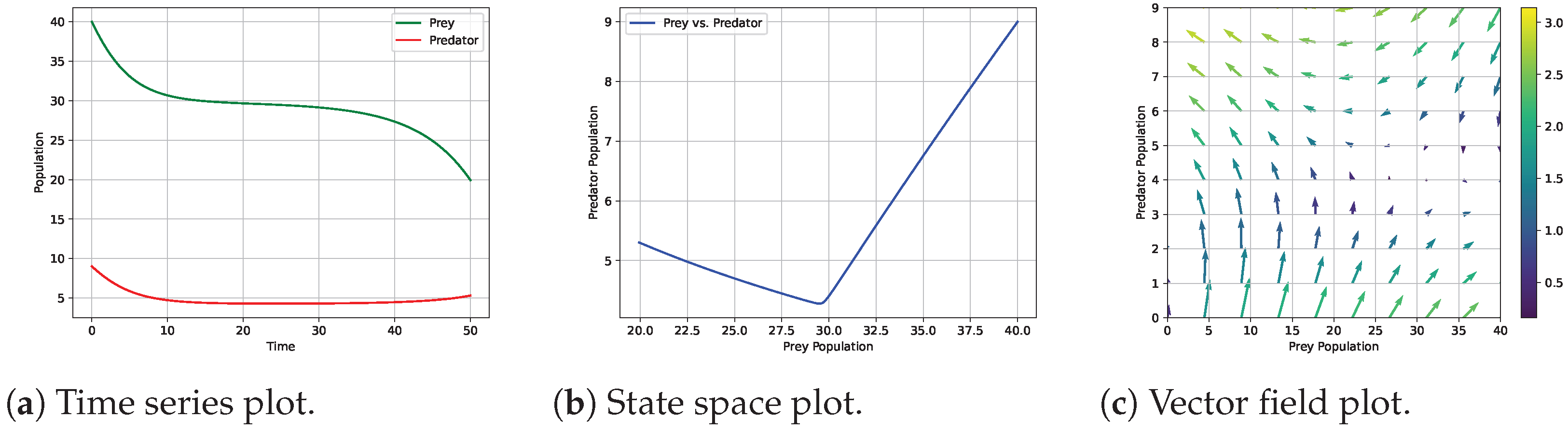
• Stability: This involves identifying stable and unstable regions within the solution space. Stable equilibria feature trajectories that converge towards fixed points, whereas unstable equilibria exhibit divergence. These plots help to detect critical points and bifurcations, making stability analysis more intuitive (Figure 2a,b).
• Periodicity: Repetitive patterns reveal the frequency, amplitude, and period of oscillations, aiding in the interpretation of rhythmic dynamics (Figure 2c).
• Transience: Transient behaviours capture a system’s evolution from the initial conditions to a steady state. These plots highlight relaxation to equilibrium and responses to perturbations, making transient phenomena more cleare (Figure 2d).

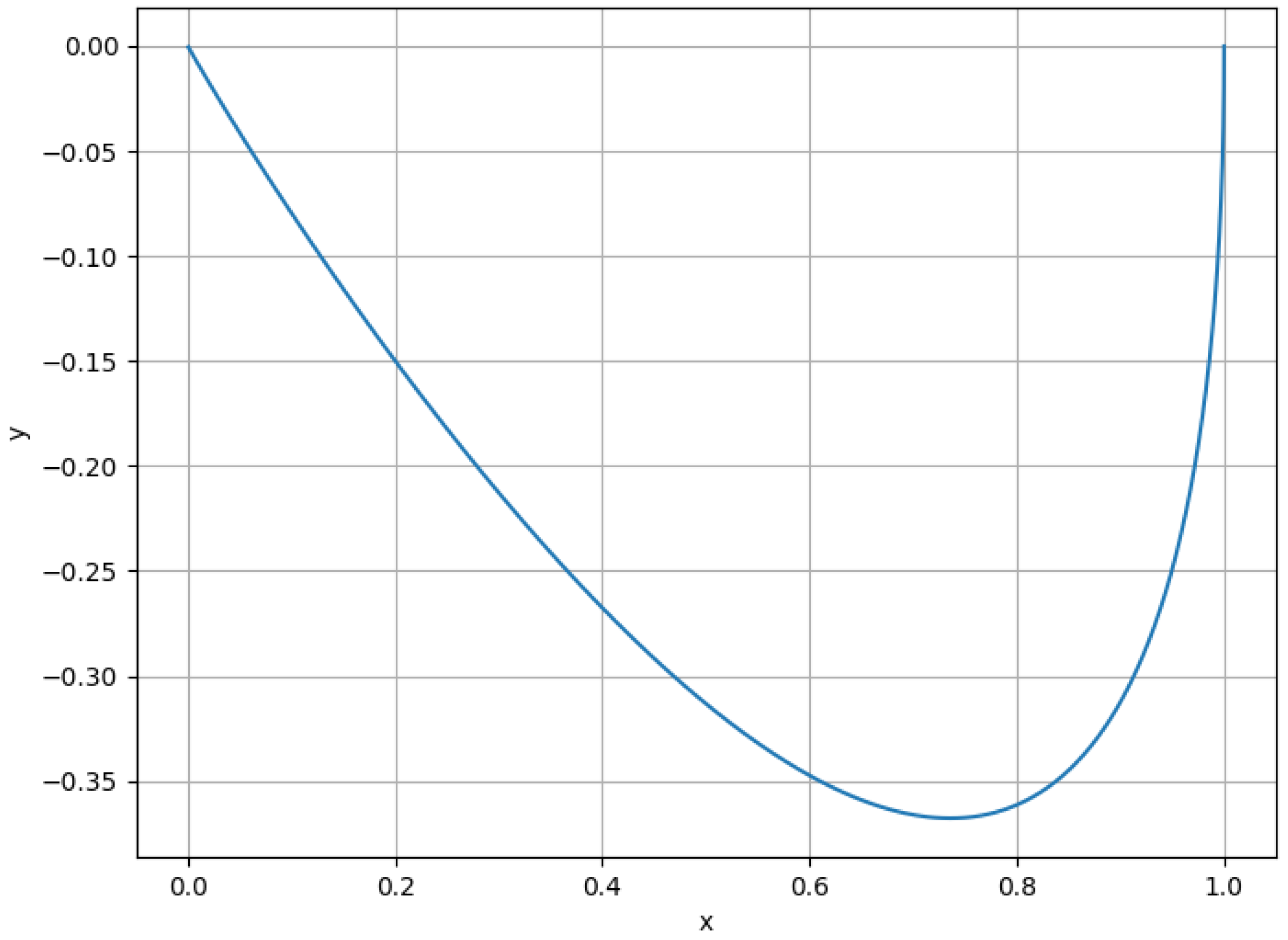
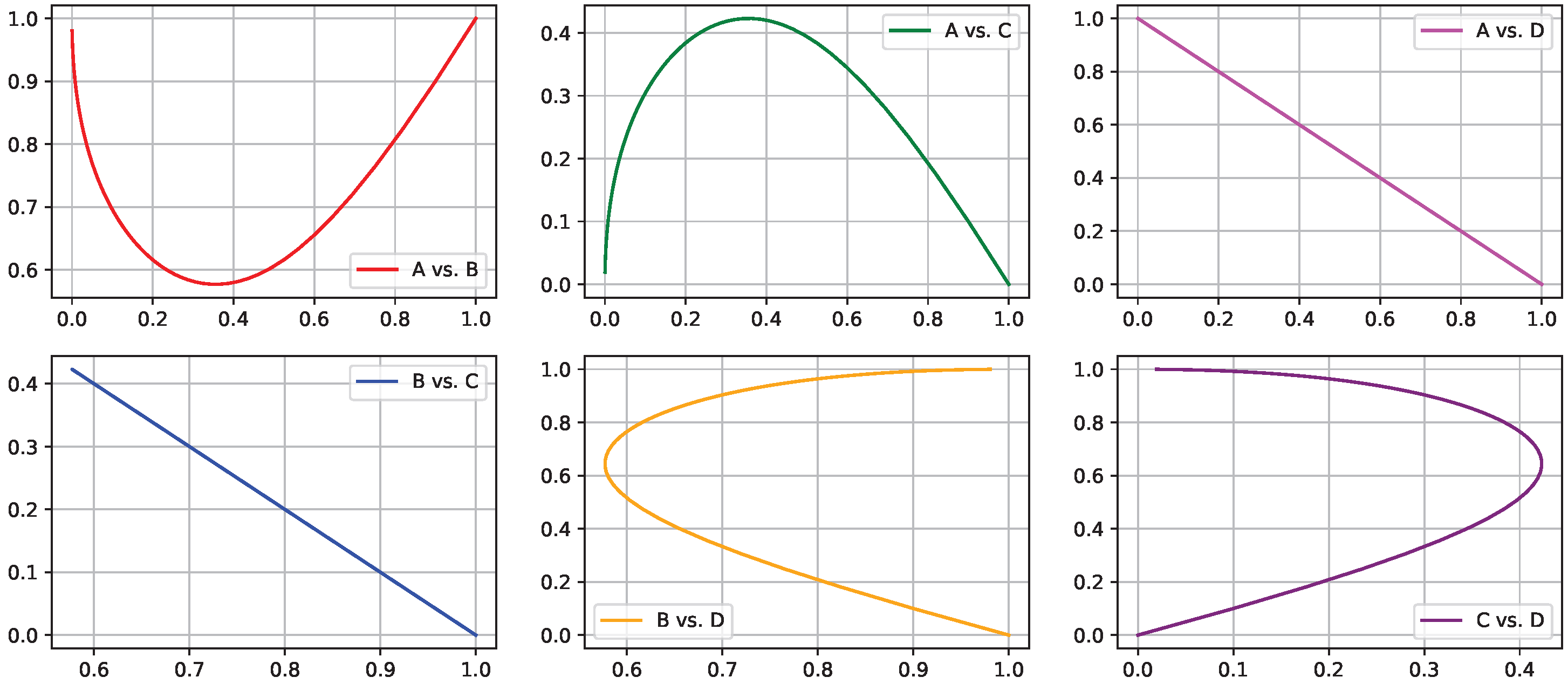
3.1.2. State Space Plots

State space plots graphically represent a system’s variables on distinct axes, showing the system’s evolution over time (Algorithm 1). These plots help to identify stability, periodicity, and transience while also providing insights into other system characteristics.

• Variable Dynamics: This visualization helps to identify relationships and patterns, enhancing the explanation of the system’s behavior (Figure 3).

The ability of state space plots to visualise variables not only helps in understanding the behaviour of individual variables but also aids in discovering intricate relationships and patterns among them. As a result, state space plots serve as a powerful tool to explain the complex dynamics of models such as Neural ODEs, making them more accessible and explainable in the broader context of XAI.

Algorithm 1 Construction of state space plots.

1: Input: ODE ${\mathit{f}}_{\mathit{\theta }}$, initial condition ${\mathit{h}}_0$, time interval $[t_0,t_f]$; 2: Step 1: Solve the ODE; 3: ${\left\{{\mathit{h}}_n\right\}}_{t_n=t_1,\dots ,t_f}\leftarrow$$ODESolve({\mathit{f}}_{\mathit{\theta }},{\mathit{h}}_0,[t_0,t_f])$; 4: Step 2: Plot for each pair or triple of variables; 5: for $x,y$ in $\mathit{h}$ do 6:       Plot: $y_n$ versus $x_n$, $t_n\in [t_0,f_f]$; 7: end for 8: Output: One state space plot per pair or triple of variables in $\mathit{h}$;

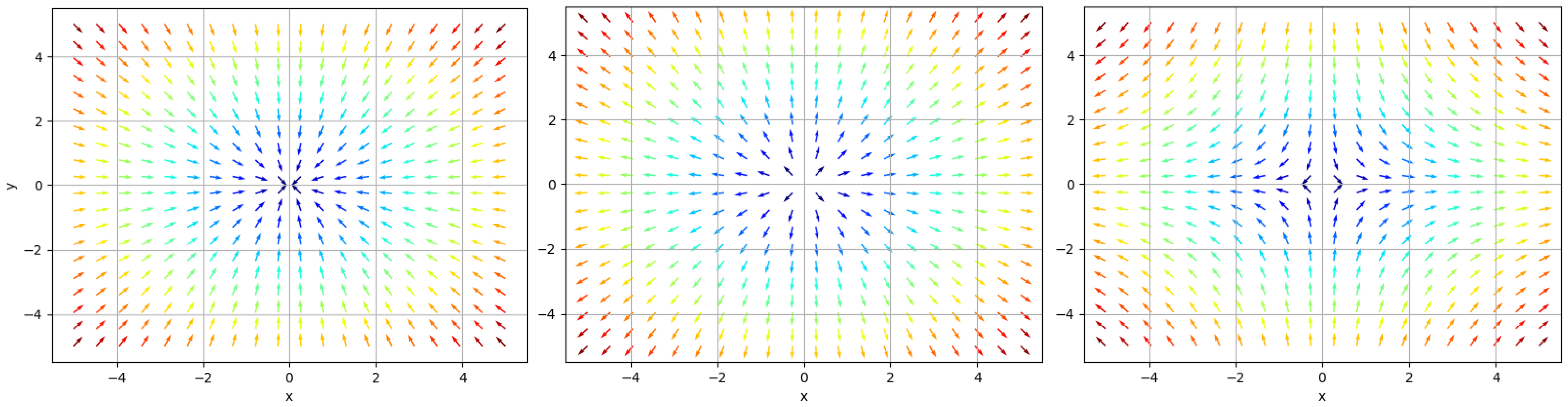
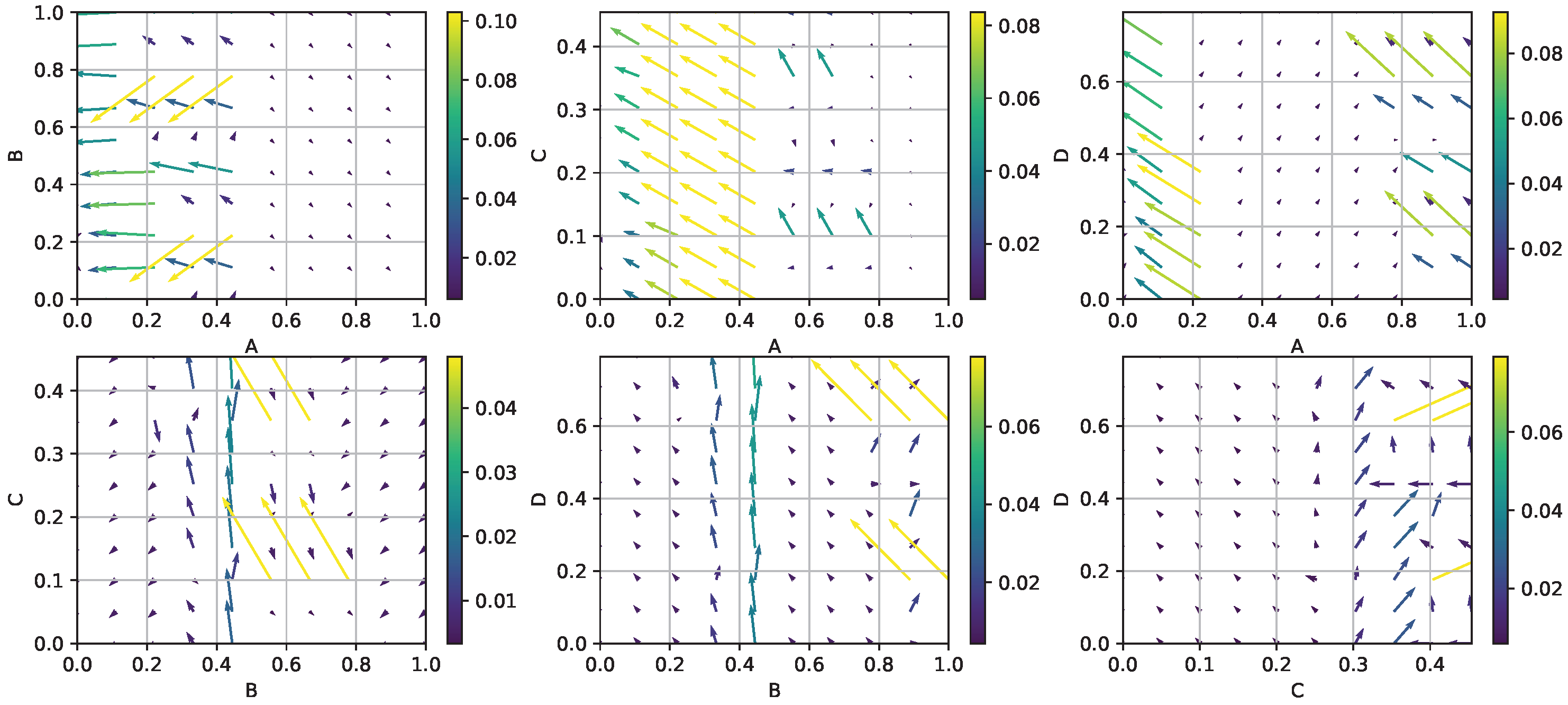
3.1.3. Vector Field Plots

Vector field plots capture solution evolution over time, displaying direction and magnitude at each point (Algorithm 2). Phase portraits help to identify critical points, stability, and periodic behavior.

Vector field plots are a powerful tool for enhancing the explainability of Neural ODE models by providing visually insights into the system’s dynamic behaviour. Identification of attractors, repellers, and saddle points contributes to a more transparent and comprehensive understanding, which promotes the goals of XAI to make complex models more transparent and explainable, Figure 4.

Algorithm 2 Construction of two-dimensional vector field plots.

1: Input: ODE ${\mathit{f}}_{\mathit{\theta }}$, initial condition ${\mathit{h}}_0$, time interval $[t_0,t_f]$;   2: Step 1: Define a grid;   3: for $x,y$ in $\mathit{h}$ do   4:       Define $x_f$ grid points: $x_0,\dots ,x_n,t_n\in [t_0,t_f]$;   5:       Define $y_f$ grid points: $y_0,\dots ,y_n,t_n\in [t_0,t_f]$;   6: end for   7: Step 2: Evaluate the vector field;   8: for $i,j=1:f$do   9:       ${\displaystyle \frac{d{x}_{ij}\left(t\right)}{dt}},{\displaystyle \frac{d{y}_{ij}\left(t\right)}{dt}}\leftarrow {\mathit{f}}_{\mathit{\theta }}(x\left[i\right],y\left[j\right])$; 10: end for 11: Step 3: Plot the vectors whose direction correspond to the direction of change and whose magnitude represents the magnitude of that change; 12: for $i,j=1:f$do 13:      Plot at $\left(x\right[i],y[j\left]\right)$ the tangent vector $\left({\displaystyle \frac{d{x}_{ij}\left(t\right)}{dt}},{\displaystyle \frac{d{y}_{ij}\left(t\right)}{dt}}\right)$; 14: end for 15: Output: 2-dimensional vector field plots;

3.2. Beyond Improving Explainability

While the XNODE suite techniques are simple, they wield considerable power in enhancing the explainability of Neural ODE models. In addition to their impact on model explainability, these techniques provide effective means to address several intrinsic challenges associated with Neural ODEs. Notably, they offer valuable insights into detecting issues related to data anomalies, model inconsistencies, and optimising overall model performance.

• Data Anomaly Detection. The XNODE suite techniques allow for the visualisation of the model dynamics through time, enabling detection of unusual or unexpected behaviours. Anomalies such as sudden deviations, irregular patterns, and unexpected behaviour when subjected to scrutiny by domain experts may serve as indicators warranting attention. Such occurrences may indicate possible poor data quality, which can emerge as anomalies, errors, or outliers. The identification of possible data anomalies is essential for ensuring the reliability of the resulting models.
• Debugging. In the process of modelling real-world systems based on data, large amounts of high-quality data are indispensable for Neural ODEs to effectively capture the intrinsic dynamics of a system and yield robust models. Unfortunately, the scarcity of such large amounts of high-quality data is a prevalent challenge that compromises the output quality of the generated models. In addition, the black-box nature of NNs makes the identification of such problems more difficult. This issue becomes particularly problematic when the systems under consideration are governed by well-defined physical principles that are known a priori; in such cases, the failure of NN models to successfully extract these governing rules from the available data results in non-meaningful predictions, causing field experts to distrust the use of NNs. The proposed XNODE suite techniques can mitigate this issue by providing field experts with insights into the level at which Neural ODE models satisfy physical constraints, i.e., their success (or lack thereof) in extracting the underlying rules from the data. These techniques assist in identifying potential problems by pointing out regions of instability or non-conformance to the expected dynamics. By offering a nuanced understanding of model performance, the XNODE suite can represent a valuable tool for mitigating the challenges posed by data scarcity and ensuring the reliability of the models in scenarios where adherence to known physical principles is crucial.
• Performance Optimisation. The visualisation of Neural ODE model dynamics is a valuable tool for enhancing model performance by providing insights into the optimisation of training hyperparameters. This visual examination enables field experts to determine necessary adjustments, especially concerning the choice of integration schemes employed within the Neural ODE solver. Through application of the XNODE suite techniques, field experts can systematically compare the dynamics produced by different integration schemes showing which scheme aligns more closely with the anticipated behaviour of the modelled systems.

4. Experiments

In this section, to showcase the capability of the XNODE suite in enhancing the explainability of Neural ODE models, three distinct case studies are considered: a Resistor–Capacitor (RC) circuit with two capacitors; the Lotka–Volterra predator–prey system; and a synthetic chemical reaction system. For each case study, a Neural ODE is employed to capture and learn the underlying dynamics of the system, the XNODE suite techniques are systematically applied to analyse and interpret the resulting Neural ODE models, and the outcomes are discussed. Additionally, to provide a comprehensive understanding of the learned dynamics, the XNODE suite techniques are used to visualise the training datasets. These visual representations are a reference for comparing and evaluating the accuracy of the dynamics learned by the Neural ODE models.

All computations were performed in a machine of type C2-standard-16 with an Intel Cascade Lake 16 vCPU and 64GB RAM. All implementations were in Python with Pytorch as the deep learning library. The code to replicate the case studies can be found at https://github.com/CeciliaCoelho/XNODE, accessed on 13 May 2025.

Note that while comparisons with other XAI methodologies serve as valuable benchmarks for validation, it is paramount to recognise that our suite presents a distinct array of capabilities (post hoc, global, and model-agnostic) tailored to address broader interpretability challenges in Neural ODEs, which renders direct comparisons inappropriate.

4.1. RC Circuit System

RC circuits find widespread application in various electronic systems and signal processing devices due to their ability to filter and shape electrical signals.

In this work, we consider a RC circuit with two capacitors connected in series, each coupled with a resistor ($R_1$ and $R_2$, respectively). The evolution of this system through time can be mathematically formulated as two ODEs expressing the rate of change in the voltage with respect to the time for each capacitor, accounting for the flow of current through the resistors and the charging and discharging dynamics of the capacitors:

$$\left\{\begin{array}{c}{\displaystyle \frac{d{V}_1\left(t\right)}{dt}}={\displaystyle \frac{V_{\mathrm{in}}-V_1\left(t\right)}{R_1\times C_1}}\hfill \\ {\displaystyle \frac{d{V}_2\left(t\right)}{dt}}={\displaystyle \frac{V_1\left(t\right)-V_2\left(t\right)}{R_2\times C_2}}\hfill \end{array}\right.$$

(4)

where $V_1\left(t\right)$ and $V_2\left(t\right)$ are the respective voltages of the two capacitors, $V_{\mathrm{in}}$ is the input voltage, $R_1$ and $R_2$ are the respective resistances of the two resistors, and $C_1$ and $C_2$ are the respective capacitances of the two capacitors.

The system in (4) was solved numerically using an ODE solver over a time interval $t=[0,10]$ discretized in 1000 time steps with initial conditions $V_1\left(0\right)=0$ and $V_2\left(0\right)=0$. We set $R_1=1.0$, $R_2=2.0$, $C_1=0.1$, and $C_2=0.2$.

The solutions resulting from solving (4) were then used to train a Neural ODE with the goal of learning the dynamics of the RC circuit system ${\mathit{f}}_{\mathit{\theta }}$. We used a neural network with an input layer consisting of two neurons and a hyperbolic tangent (tanh) activation function, a hidden layer with 50 neurons and an Exponential Linear Unit (ELU) activation function, a hidden layer with 108 neurons and the tanh activation function, and an output layer with two neurons. The Adam optimiser was used with a $1\times {10}^{-4}$ learning rate over 10,000 iterations.

To perform a comparative analysis, XNODE suite plots were generated for both the ground-truth solutions (Figure 5) and the Neural ODE model predictions (Figure 6a).

First, we examine the plots generated using the Neural ODE models. Figure 6a illustrates the temporal evolution of the capacitor voltages $V_1\left(t\right)$ and $V_2\left(t\right)$, which exhibit similar patterns until equilibrium is achieved. Moreover, the rate of increase in $V_2\left(t\right)$ is observed to be comparatively slower than that of $V_1\left(t\right)$. In Figure 6b, an initial linear relationship can be seen between $V_1\left(t\right)$ and $V_2\left(t\right)$, indicating a simultaneous increase. This linear correlation persists until the maximum voltage is reached by $V_1\left(t\right)$, while $V_2\left(t\right)$ continues its ascent until that point. The vector field plot in Figure 6c accentuates the ascending trend of the respective voltages, which slows down until a voltage magnitude of $1.0$ is reached.

As demonstrated through the plots generated by the XNODE suite, these visualisations offer clear insight into the reasoning and conclusions drawn by the Neural ODE model based on the training data. The information provided by these plots facilitates a comprehensive understanding of the decision-making process employed by the model, enhancing its explainability while contributing to a more transparent and comprehensible representation of the learned dynamics.

Furthermore, the plots in Figure 6 can be compared with the expected plots in Figure 5 to assess the quality of the dynamics learned by the Neural ODE. This comparative analysis reveals that the Neural ODE was able to successfully extract the intrinsic dynamics of the system with a high degree of fidelity. Such close alignment underscores the robustness of the learned model, demonstrating that it was able to comprehensively capture the inter-variable relationships within the system. This also corroborates the loss function value, as provided by the Mean Squared Error (MSE), for ending the training at $3.2\times {10}^{-4}$.

4.2. Lotka–Volterra Predator–Prey System

The Lotka–Volterra predator–prey differential equations are a mathematical framework that enables modelling of nonlinear interactions within ecological systems. These equations describe the interplay between predator and prey populations in a biological community. Formulated as two ODEs, the equations translate the temporal evolution of changes in the populations of both predators and prey:

$$\left\{\begin{array}{c}{\displaystyle \frac{dN\left(t\right)}{dt}}=r\times N\left(t\right)-a\times N\left(t\right)\times P\left(t\right)\hfill \\ {\displaystyle \frac{dP\left(t\right)}{dt}}=-s\times P\left(t\right)+b\times N\left(t\right)\times P\left(t\right)\hfill \end{array}\right.$$

(5)

where $N\left(t\right)$ and $P\left(t\right)$ denote the quantities of prey and predator individuals, respectively, r is the growth rate of the prey species, $A\left(t\right)$ is the predation rate that affects the prey species, s is the mortality rate of the predator species in the absence of prey, and $B\left(t\right)$ is the growth rate of the predator species in the presence of prey species [13].

In this work, we set $r=0.1$, $a=0.02$, $s=0.3$, and $b=0.01$. Equation (5) was numerically solved over a time interval of $t=[0,50]$ comprising 100 regular time steps. An ODE solver was employed with initial conditions set at $N\left(0\right)=40$ and $P\left(0\right)=9$. The solutions obtained from solving the system in (5) were then used as a training dataset for a Neural ODE. The goal was for the Neural ODE to learn the predator–prey population dynamics from the training data ${\mathit{f}}_{\mathit{\theta }}$. We used a neural network with an input layer consisting of two neurons and a tanh activation function, one hidden layer with 50 neurons and an ELU activation function, and an output layer with two neurons. The Adam optimiser was used with a $1\times {10}^{-5}$ learning rate over 20,000 iterations.

The ground truth solutions were used to generate the three expected plots that comprise the XNODE suite (Figure 7).

To analyse the relationships learned by the Neural ODE and how its decisions were made, the three plots of the XNODE suite (Figure 8) were constructed as well. In Figure 8a, the time plot illustrates the dynamics of predator and prey populations over time. Upon analysis, it becomes apparent that the Neural ODE model exhibits a learning pattern in which the predator population undergoes minimal changes while the prey population experiences varying rates of decline as time progresses. In Figure 8b, the state space plot presents the direct relationship between predator and prey populations. The Neural ODE model has learned from the data that an increase in the prey population is associated with a decrease in the predator population until a critical turning point is reached, typically around a prey population of 30; beyond this threshold, the model indicates a linear increase in the predator population with the concurrent rise in the prey population. Analysing the vector field plot in Figure 8c reveals that the Neural ODE model has learned that at lower prey population, the predator population increases while the prey population decreases. For higher prey populations, the predator population increases; when the number of predators is larger, there is an increase in the prey population and a slight decrease in the predator population.

Furthermore, when comparing the plots obtained from the Neural ODE model in Figure 8 with the expected plots in Figure 7, it becomes evident that the Neural ODE model was not able to successfully capture the dynamics of the system. This discrepancy suggests potential issues related to the architecture of the NN and the selection of the hyperparameters. The observed divergence between the model’s predictions and the expected behaviour underscores the need for a careful re-evaluation and optimisation of the model’s design and parameter choices in order to improve its performance in capturing the underlying system dynamics.

This example demonstrates that the XNODE suite can contribute to enhancing the explainability of models and aid in the detection of architectural and training issues. In this case, the MSE value when training ended was $5.40\times {10}^1$ after 20,000 iterations, hinting at the need to improve the ODE model.

4.3. Chemical Reaction System

In a chemical reaction, the participating species interact with each other, which can lead to the creation of new chemical species. In this example, we consider a synthetic chemical reaction involving four species: $A\left(t\right)$, $B\left(t\right)$, $C\left(t\right)$, and $D\left(t\right)$. At the initial time, only species $A\left(t\right)$ and $B\left(t\right)$ are present. As time evolves, these two species undergo a chemical reaction, resulting in the formation of species $C\left(t\right)$ and $D\left(t\right)$. The reaction can be mathematically formulated as a system of four ODEs [14,15]:

$$\left\{\begin{array}{c}{\displaystyle \frac{dA\left(t\right)}{dt}}=-k_1\times A\left(t\right)\times B\left(t\right)\hfill \\ {\displaystyle \frac{dB\left(t\right)}{dt}}=-k_1\times A\left(t\right)\times B\left(t\right)+k_2\times C\left(t\right)\hfill \\ {\displaystyle \frac{dC\left(t\right)}{dt}}=k_1\times A\left(t\right)\times B\left(t\right)-k_2\times C\left(t\right)\hfill \\ {\displaystyle \frac{dD\left(t\right)}{dt}}=k_1\times A\left(t\right)\times B\left(t\right)\hfill \end{array}\right.$$

(6)

where $k_1$ and $k_2$ are the respectively rates of the reactions and $A\left(t\right)$, $B\left(t\right)$, $C\left(t\right)$, and $D\left(t\right)$ are the respective masses of each species.

In this work, we set $k_1=0.1$ and $k_2=0.05$. The system in (6) was numerically solved over a time interval of $t=[0,100]$ discretized in 100 time steps with initial conditions $A\left(0\right)=1$, $B\left(0\right)=1$, $C\left(0\right)=0$, $D\left(0\right)=0$.

The solutions obtained from solving the system in (6) were then used as the training dataset for a Neural ODE. The goal was for the Neural ODE to learn the chemical species reaction dynamics from the data. We used a neural network with an input layer consisting of four neurons and a tanh activation function, three hidden layers with 50, 64, and 50 neurons and tanh, ELU, and tanh as the activation functions, respectively, and an output layer with four neurons. The Adam optimiser was used with a $1\times {10}^{-5}$ learning rate over 10,000 iterations.

The solutions from (6) were used to generate the expected plots of the system dynamics, as shown in Figure 9, Figure 10 and Figure 11.

To study the dynamics learned by the Neural ODE and investigate its decision-making process, the XNODE suite plots in Figure 12, Figure 13 and Figure 14 were generated. Figure 12 reveals a pattern in which the decrease in species $A\left(t\right)$ and $B\left(t\right)$ corresponds to an increase in species $C\left(t\right)$ and $D\left(t\right)$. Subsequently, a decline in species $C\left(t\right)$ and $D\left(t\right)$ contributes to an increase in species $B\left(t\right)$. The six state-space plots in Figure 13 provide insights into the decision-making process of the Neural ODE model within the high-dimensional space. The observations can be summarised as follows: an increase in $A\left(t\right)$ initially leads to a decrease in $B\left(t\right)$ until a turning point is reached, after which both increase simultaneously (Figure 13, top left); an increase in $A\left(t\right)$ results in a rapid increase in $C\left(t\right)$ until a turning point is reached, beyond which further increases in $A\left(t\right)$ lead to a decrease in $C\left(t\right)$ (Figure 13, top middle); generally, an increase in $A\left(t\right)$ correlates with a decrease in $B\left(t\right)$ in an almost linear fashion (Figure 13, top right); a decrease in $B\left(t\right)$ leads to a linear increase in $C\left(t\right)$ until a turning point, after which $C\left(t\right)$ starts decreasing when $B\left(t\right)$ increases again (Figure 13, bottom left); initially, a decrease in $B\left(t\right)$ results in an increase in $D\left(t\right)$ until $B\left(t\right)$ starts increasing again while $D\left(t\right)$ continues to increase (Figure 13, bottom middle); and an increase in $C\left(t\right)$ corresponds to an increase in $D\left(t\right)$ until a turning point is reached, after which a decrease in $C\left(t\right)$ leads to a relatively constant value of $D\left(t\right)$ (Figure 13, bottom right).

The six vector field plots in Figure 14 provide additional insights into the workings of the Neural ODE model. Moving from the upper left to the lower right quadrant, when $C\left(t\right),D\left(t\right)=0$ and $A\left(t\right)<0.4$, there is a discernible trend of decreasing $B\left(t\right)$ with varying magnitudes of velocity, including regions of slower and faster flow. At higher values of $A\left(t\right)$, $B\left(t\right)$ generally decreases (Figure 14, top left); under condition $B=1$ and $D=0$, there is an observed increase in $C\left(t\right)$ as $A\left(t\right)$ decreases (Figure 14, top middle); in scenarios where $B\left(t\right)=1$ and $C\left(t\right)=0$, $D\left(t\right)$ tends to increase within the range $0.2<A\left(t\right)<1.0$ (Figure 14, top right); outside of this range, $D\left(t\right)$ demonstrates a decreasing trend (Figure 14, bottom left); with $A\left(t\right)=1$ and $D\left(t\right)=0$, there is a general decrease in $B\left(t\right)$ with respect to $C\left(t\right)$ except when $B\approx 0.4$, where $C\left(t\right)$ exhibits an increasing pattern (Figure 14, bottom middle); when $A\left(t\right)=1$ and $C\left(t\right)=0$, the dynamics resemble those of the $B\left(t\right)$ vs. $C\left(t\right)$ relationship, with the exception that $D\left(t\right)$ consistently exhibits an increasing trend. Under the conditions $A\left(t\right),B\left(t\right)=1$, when $C\left(t\right)<0.3$, $D\left(t\right)$ displays an increase as $C\left(t\right)$ decreases; beyond this range, both $C\left(t\right)$ and $D\left(t\right)$ show an upward trajectory (Figure 14, bottom right).

We note that in order to generate the vector field plots in Figure 11 and Figure 14, the remaining variables were set to the initial values, namely, $A\left(t\right)=1$, $B\left(t\right)=1$, $C\left(t\right)=0$, and $D\left(t\right)=0$. In this case, a comparative analysis cannot be performed between the vector field plots and the state space plots dynamics (Figure 10 and Figure 13, respectively).

The visualisations in Figure 12, Figure 13 and Figure 14 provided by the the XNODE suite techniques provide insights into the workings and relations learned by the Neural ODE model. From these plots, we can easily understand how changing the input values results in changes to the output, thereby enhancing model explainability.

Furthermore, when comparing the plots obtained from the Neural ODE model (Figure 12, Figure 13 and Figure 14) with the expected plots (Figure 9, Figure 10 and Figure 11), it is apparent that the time series plots in Figure 9 and Figure 12 are similar. However, the state space plots in Figure 10 and Figure 13 reveal distinctions between the expected and predicted dynamics, with particular emphasis on the $B\left(t\right)$ vs. $C\left(t\right)$ plot, where the relationship deviates significantly. Although minor inconsistencies are observed in the other state space plots, the discrepancies in the $B\left(t\right)$ vs. $C\left(t\right)$ plot stand out, indicating that the Neural ODE model did not fully capture the expected interdependencies between species. These deviations are not merely numerical inaccuracies but can correspond to fundamentally incorrect qualitative behaviours such as misplaced attractors or misrepresented stability properties. Such differences may significantly alter the system’s long-term predictions.

Furthermore, a closer inspection of the vector field plots in Figure 11 and Figure 14 exposes how these subtle differences impact the dynamics learned by the Neural ODE. The vector field plots highlight a pronounced disparity between the expected dynamics and those captured by the model, further evidencing the importance of employing the XNODE suite techniques. This shows how the XNODE suite techniques complement each other in enhancing explainability and detecting erroneous dynamics in NN models. Interestingly, the MSE value when training ended was $2.8\times {10}^{-5}$ after 10,000 iterations. At first glance, this might suggest successful learning of the data dynamics; however, use of the proposed XNODE suite techniques reveals a more nuanced perspective, indicating that this low training error does not necessarily equate to a comprehensive understanding or accurate modelling of the underlying data dynamics.

5. Conclusions

In this paper, we have proposed a suite of post hoc XAI techniques tailored specifically for Neural ODEs, drawing inspiration from traditional mathematical visualisation techniques for DEs such as time series, state space, and vector field plots. Choosing traditional mathematical visualisation techniques for DEs over general XAI methods offers a more rigorous, intuitive, and mathematically grounded approach to comprehending Neural ODE models, ultimately enhancing the quality of our insights and enabling more precise model understanding and development. We note that the proposed XNODE suite techniques can also be applied to any NN architecture that adjusts continuous-time functions, provided that the state variables reside in a space that is interpretable or projectable into lower dimensions.

To showcase the effectiveness of our proposed XNODE suite, we applied it to three case studies. For each case study, the XNODE techniques were applied to the resulting Neural ODE models and the generated plots were analysed and discussed. The results show how our XNODE suite provides a detailed understanding of the model’s learned dynamics and decision-making process. Furthermore, the case studies provide valuable insights into the limitations of relying solely on the final value of the training losses as a direct performance measure for assessing model efficacy. Although a low training loss value might suggest successful learning of data dynamics on the part of the model, our comprehensive analyses conducted using the XNODE suite techniques offer a more transparent perspective. The results of the case studies underscore the importance of our proposed XNODE suite in guiding more informed and refined assessments of model dynamics. The role of the XNODE suite techniques extends beyond traditional metrics, providing the means to uncover hidden complexities, identify areas for improvement, and ultimately refine models for more robust and accurate representations of real-world data dynamics.

Although the case studies presented in this paper focus on systems with two to four variables in order to facilitate direct visualisation, the XNODE suite is designed to remain applicable as the dimensionality of the Neural ODE increases. In higher-dimensional settings where full vector field or state space plots become impractical, the suite can be adapted to visualise projections onto relevant two- or three-dimensional subspaces. These can be selected based on domain knowledge, variable importance, or statistical techniques such as principal component analysis. This modular approach allows researchers to isolate and interpret meaningful dynamics within complex models. Additionally, the XNODE suite can be integrated with complementary explainability tools such as saliency maps and attention mechanisms, further supporting its application in more complex real-world systems.

The overarching goal of the XNODE suite is to demystify the inherent complexity of Neural ODEs, making their output models more transparent and explainable. Through the identification of stable and unstable regions, periodicity, and transient dynamics, the XNODE suite aims to create a visual narrative that not only helps to anticipate long-term behaviours but also fosters trust in the predictions of the model. In this way, the XNODE suite can serve as a valuable tool for unravelling the intricacies of Neural ODEs, in turn helping to promote transparency and reliability in a variety of applications.