Abstract
Convolutional Neural Networks (CNNs) have exhibited remarkable potential in effectively tackling the intricate task of classifying MRI images, specifically in Alzheimer’s disease detection and brain tumor identification. While CNNs optimize their parameters automatically through training processes, finding the optimal values for these parameters can still be a challenging task due to the complexity of the search space and the potential for suboptimal results. Consequently, researchers often encounter difficulties determining the ideal parameter settings for CNNs. This challenge necessitates using trial-and-error methods or expert judgment, as the search for the best combination of parameters involves exploring a vast space of possibilities. Despite the automatic optimization during training, the process does not guarantee finding the globally-optimal parameter values. Hence, researchers often rely on iterative experimentation and expert knowledge to fine-tune these parameters and maximize CNN performance. This poses a significant obstacle in developing real-world applications that leverage CNNs for MRI image analysis. This paper presents a new hybrid model that combines the Particle Swarm Optimization (PSO) algorithm with CNNs to enhance detection and classification capabilities. Our method utilizes the PSO algorithm to determine the optimal configuration of CNN hyper-parameters. Subsequently, these optimized parameters are applied to the CNN architectures for classification. As a result, our hybrid model exhibits improved prediction accuracy for brain diseases while reducing the loss of function value. To evaluate the performance of our proposed model, we conducted experiments using three benchmark datasets. Two datasets were utilized for Alzheimer’s disease: the Alzheimer’s Disease Neuroimaging Initiative (ADNI) and an international dataset from Kaggle. The third dataset focused on brain tumors. The experimental assessment demonstrated the superiority of our proposed model, achieving unprecedented accuracy rates of 98.50%, 98.83%, and 97.12% for the datasets mentioned earlier, respectively.
1. Introduction
Around the world, more than 286 million people suffer from brain disease, according to the World Health Organization [1]. There are 246 million mentally ill people and 39 million people who are in critical condition, according to [2]. The brain, being one of the largest and most intricate parts of the body, plays an important role in several functions, such as generating ideas, problem-solving, reasoning, making decisions, imagination, and memory [1].
Alzheimer’s disease (AD), which affects millions of people, is the most prevalent type of dementia. As people get older, their anxiety about getting Alzheimer’s increases. Alzheimer’s disease slowly kills brain cells, leaving patients unable to recognize family members, recall memorization, or remember familiar faces. As a result, they become disoriented and lose the ability to recognize their surroundings. In advanced stages, they also lose the ability to eat, cough, and breathe. The cost of providing health and social care for the 50 million people affected by dementia globally is equal to the 18th largest economy in the world [2]. Additionally, by 2050, it is anticipated that there will be 152 million new cases of AD and other dementias annually, or one case every three seconds. The symptoms of AD and vascular dementia (VD) overlap, such as memory impairment, language and communication difficulties, and behavioral and psychological symptoms, making the diagnosis of AD challenging [3,4]. Through the monitoring of its progression, early and accurate AD diagnosis is crucial for patient care, treatment, and prevention.
A brain tumor is another severe condition extremely dangerous for the brain. Since the brain’s veins and nerves are already compromised, tumors frequently develop there. Depending on the tumor stage, this can cause partial or total blindness [5]. Family history, ethnicity, and severe myopia are additional contributing factors [6]. It is made to prevent nerve vessels from enlarging and is also brought on by poor blood flow. This disease is typically detected after progressing to a critical stage, as mentioned in [7], and is typically painless before that point. As a result, today’s most advanced societies have an ever-growing need for quick and automated discovery for early diagnosis techniques.
In many scientific fields, images are crucial. Medical imaging has also advanced into a powerful tool for understanding brain activity. Magnetic resonance imaging (MRI), a type of brain imaging that allows for the representation of the structure and functionality of the brain, has been used in the healthcare diagnosis of brain conditions. Medical professionals assess the symptoms and signs of AD and brain tumors [8]. Doctors may request additional laboratory examinations, brain imaging exams, or memory tests for patients. By excluding other conditions that cause comparable symptoms, these tests can assist doctors in making diagnoses. Using MRI, it is possible to identify brain abnormalities linked to mild cognitive impairment (MCI) and to foretell which MCI patients will go on to develop AD and brain tumors. The MRI images will be examined for anomalies, such as a decrement in the size of different brain regions that primarily influence memorization [9].
As a result of technological advancements and the expansion of data gathered by brain-imaging techniques, Deep Neural Networks (DNN) are becoming increasingly crucial for extracting accurate and highly relevant information and making accurate predictions of AD and brain tumors from brain-imaging data.
Deep Neural Networks (DNN) have proven they can use a hierarchical model, millions of parameters, and learn from large databases to solve classification problems. CNNs are a sub-type of DNN comprising several convolutional, pooling, and fully connected layers. They have been successfully used for pattern recognition, classification, and image or video processing. CNN has attracted attention in recent years for outperforming competitors in several computer vision-related applications, including natural language processing and medicine [10,11].
Different CNN architectures (such as ResNet-50 [12] and DarkNet-19 [13]) can produce different classification results due to the many parameters that comprise them. Finding the optimal hyper-parameter values requires a complex search procedure, typically based on trial and error, a series of tests, or manual adjustment. It has been demonstrated that certain hyper-parameter selection algorithms can match or exceed the performance of human experts [14]. However, they still need to be widely used due to their high computational complexity. Various state-of-the-art techniques are available, from the basic grid and random searches [15] to sophisticated methods that balance exploring and exploiting the solution space [16]. Model-based approaches [17] and Bayesian optimization using Gaussian processes (GP) [14,16] are included in the latter category. While evolutionary algorithms have been proven effective in solving a wide variety of difficult optimization problems [18], they have yet to be used to optimize CNN’s hyper-parameters in all applications.
Based on the effective performance of DNN and CNN methods in various image classification tasks [8,10], the study goal is to help design a more efficient system for making a highly accurate prediction for AD and brain tumor diseases using a highly efficient optimization algorithm known as Particle Swarm Optimization (PSO). Our main contributions can be recapped as follows:
- We develop a hybrid framework that employs the PSO algorithm to determine the best hyper-parameters’ configuration for CNN architectures to improve prediction accuracy for brain diseases and decrease the loss function value.
- We utilize PSO as a wrapper around the training process to retrieve hyper-parameters (such as the number of convolution filters, the size of the filters used in the convolutional layer, the size of the pool in the max pooling layer, and the size of the strides used in the max pooling layer).
- We evaluate our model on three distinct modern brain disease datasets, namely the Alzheimer’s disease dataset [19,20], and the brain tumor dataset [21].
- We contrast our PSO-optimized CNN model with three distinct CNN models: the ResNet, the InceptionNet, and the VGG models. Finally, we benchmarked our proposed model against state-of-the-art models employing different optimization algorithms.
The remainder of this paper is structured as follows: Section 2 provides related studies of AD and brain tumor diagnosis and classification. The proposed CNN-PSO model is built and evaluated in Section 3, which also presents the methodology. Section 4 presents the experimental and evaluation results; Section 5 concludes the paper and discusses future works.
2. Related Work
Various classification strategies have been proposed for AD and brain tumors as part of the proposed diagnosis and detection systems. This section reviews recent studies using conventional ML and DL methods for AD and brain tumor detection and diagnosis. Traditional machine-learning techniques [22] were employed in some of the earlier studies on the diagnosis of Alzheimer’s disease and brain tumors. They focused on developing models that analyze the anatomy or systemic brain images obtained through MRIs and the functioning of the brain in order to find any flaws or disorders. They heavily relied on manually made features and feature representations for voxel, region, or patch-based methods and saw segmentation issues as classification issues. Many expert-segmented images were required, which added to the time required to train the classification models.
The summarized studies from the review are shown in Table 1 below, which also distinguishes them based on (1) dataset type (brain tumors or AD), (2) proposed methodology, since some of the studies are based on CNN architecture only, on the other hand, other studies used optimization algorithms in order to optimize the classification results; also, many studies used the segmentation approach for the classification of the MRI images, (3) the limitation of the proposed study and (4) performance evaluation results. Table 2 shows the usage of the PSO algorithm for each study.
Related to Alzheimer’s brain disease, the authors in the paper [23] suggested an inherent structure-based multiview learning (ISML) method for classifying AD/MCI. The suggested approach is composed of three stages: (1) multi-view extraction of features using multiple templates and using gray matter (GM) tissues as tissue-segmented brain images for feature extraction; (2) subclass clustering-based feature selection through using voxel selection that improves the power of features; and (3) using SVM-based ensemble classification. They used the MRI baseline dataset from the ADNI database to assess the effectiveness of the suggested method. According to the experiment’s findings, the proposed ISML method achieves an accuracy of 93.83% when comparing AD and NC.
The authors of the paper [9] use two different 3D CNN approaches for classification—3D-VGGNet and 3D-ResNet—along with Softmax nonlinearity. They employ the 3D structural MRI brain scans from the ADNI dataset. According to the outcome, ResNet and Voxnet both achieve an accuracy of 79% and 80% for AD/CN classification, respectively. Additionally, their algorithms are easier to implement and do not require manual extraction. Recent research led the authors of [24] to suggest a straightforward CNN for AD pre-detection. Two MRI scans provided by ADNI are used in their study’s two experiments. As the most popular detection technique, they use the SVM classifier. They made this choice under the presumption that an effective AD detection method could be successfully applied to an AD pre-detection method. The first experiment shows 84.41% accuracy for the SVM classifier. The proposed CNN model was used in the second experiment. With various datasets and image segmentation techniques, they tested the utility of the CNN model using the six evaluation steps. Extended ROI without edge detection was the most accurate image segmentation technique, with a 96% accuracy rate.
The authors of [25] proposed a new classification method that distinguishes patients with AD from HC based on MRI data. Utilizing AlexNet, sequential feature selection (SFS), and feature selection based on principal component analysis (PCA). In addition to that, the CNN architecture is used to extract the feature. The findings demonstrate that the AD/CN classification accuracy reaches 90%. The study [26] additionally proposed a model for the early diagnosis and classification of AD and MCI from elderly patients with no cognitive impairments in addition to the prediction and diagnosis of early and late MCI patients. The ADNI database provides the dataset. For each scan, they used FreeSurfer analysis to extract 68 features of the cortical thickness and used those features to build the model. The scans were then used to test various machine learning methods, such as linear SVM, non-linear SVM (RBF kernel), naive Bayesian, K-nearest neighborhood, random forest, and decision trees. The non-linear SVM classifier with radial basis function showed a 75% accuracy rate for classifying tasks.
In other research studies, CNN architectures are optimized using the PSO algorithm, yielding positive outcomes in the accuracy of various applications. In [27], the authors focused on the PSO algorithm for improving the behavior of the Patch Image Differential Clustering (PIDC) algorithm to segment the subjects’ brains and examine the stages of Alzheimer’s disease. Compared to fuzzy C-Means and K-Means clustering algorithms, the PSO-based PIDC algorithm provides better segmentation of various brain subjects, demonstrating that 92% of segmentation accuracy was achieved with the PSO and the PIDC algorithms. While in paper [28], the PSO algorithm is used with the decision tree method, the PSO algorithm is used for the feature selection process, and according to the experiment’s findings, the PSO-based random forest algorithm achieved a 93.56% accuracy rate to detect Alzheimer’s disease.
Additionally, the authors in [29] classified Alzheimer’s disease using three different types of algorithms: the Extreme Learning Machine (ELM) for classification, with a PSO to optimize its performance; a GA algorithm for feature selection; and a Voxel-Based Morphometry (VBM) approach for feature extraction from the MRI images. This study has demonstrated that using all three techniques together yields better classification outcomes. This method can help distinguish between very mild cases of AD and normal cases with a testing accuracy of 87.23%, which shows how effective it is at observing the onset of AD.
For brain tumor diseases, the CNN architecture was used by the authors of the paper [30] in their investigation. They have primarily focused on creating a CNN model for classifying brain tumors in T1-weighted contrast-enhanced MRI images. The proposed process has two key phases: pre-process the images using various image processing techniques and then use CNN to classify them. Three different types of brain tumors are included in the dataset of 3064 images used in the study (glioma, meningioma, pituitary). They achieved a testing accuracy of 94.39% using the CNN model. Additionally, the authors of the paper [31] used a support vector machine and a genetic algorithm to segment and categorize brain MRI images. The results of classifying the brain MRI images into normal and abnormal cases were about 91% accurate.

Table 1.
Summary of reviewed related works.
Table 1.
Summary of reviewed related works.
| Reference | Dataset Type | Proposed Model | Study Limitation | Evaluation Results |
|---|---|---|---|---|
| [18] | AD Dataset | 3D CNN (VoxCNN, ResNet), Softmax | Small dataset size, model complexity, lack of interpretability and external validation | AD vs. NC Accuracy: 79% VoxCNN Accuracy: 80% ResNet AUC: 88% VoxCNN AUC: 87% ResNet |
| [19] | AD Dataset | CNN, SVM | Lack of implementation, training, and parameter details | AD vs. NC Accuracy: 96% |
| [20] | AD Dataset | CNN (AlexNet), SVM | Insufficient discussion on feature selection and extraction from MRI data | AD vs. NC Accuracy: 90% Specificity: 91% Sensitivity: 87% |
| [21] | AD Dataset | FreeSurfer, SVM, Naive Bayesian, Random Forest, Decision Tree | Limitations in choice of evaluation metrics | AD vs. NC Accuracy: 75% Specificity: 77% Sensitivity: 75% F-score: 72% AUC: 76% |
| [22] | AD Dataset | PSO-based PIDC algorithm, Softmax | Lack of extensive details and evaluation of the hybrid algorithm for brain image segmentation | AD vs. NC Accuracy: 92% |
| [23] | AD Dataset | PSO with Decision Tree Methods | Insufficient analysis or discussion of feature selection process | AD vs. NC Accuracy: 93.56% |
| [24] | AD Dataset | GA algorithm, ELM, PSO | Lack of thorough comparison with other classifiers or methods | AD vs. NC Accuracy: 87.23% |
| [25] | Brain Tumor Dataset | CNN, Softmax | Insufficient details or analysis of CNN architecture for brain tumor classification | Normal vs. Not Normal Accuracy: 94.39% |
| [26] | Brain Tumor Dataset | GA algorithm, SVM | Lack of extensive details or analysis of optimization technique for brain tumor detection | Normal vs. Not Normal Accuracy: 91% |
| [27] | Brain Tumor Dataset | CNN, ELM, SVM | Insufficient details or analysis of ensemble classifier for brain tumor segmentation and classification | Normal vs. Not Normal Accuracy: 91.17% |
| [29] | Brain Tumor Dataset | CNN (VGG19), Softmax | Lack of details or analysis of deep CNN architecture and hyper-parameters for brain tumor classification | Normal vs. Not Normal Accuracy: 90.67% |
| [31] | Brain Tumor Dataset | CNN with DWT, SVM | Lack of details or analysis of PSO-based segmentation technique for brain MRI images and comparison with other methods | Normal vs. Not Normal Accuracy: 85% |
| [32] | Brain Tumor Dataset | CNN with PSO, Softmax | Lack of details or analysis of modified PSO algorithm for brain tumor detection and limitations of the modification | Normal vs. Not Normal Accuracy: 92% |

Table 2.
Usage of PSO algorithm.
Table 2.
Usage of PSO algorithm.
| Reference | Usage of PSO |
|---|---|
| [18] | Not used PSO |
| [19] | Not Used PSO |
| [20] | Not Used PSO |
| [21] | Not Used PSO |
| [22] | PSO was used for optimizing the model performance by selecting the optimal parameters and weight |
| [23] | PSO was used for the feature selection process |
| [24] | PSO was used for optimizing the model performance by selecting the optimal parameters and weight |
| [25] | Not used PSO |
| [26] | Not used PSO |
| [27] | Not used PSO |
| [29] | Not used PSO |
| [31] | PSO was used for the feature selection process |
| [32] | PSO was used for the feature selection process |
Using ensemble methods, the segmentation and classification of brain tumors were carried out in a different study by the author of the paper [32]. In ensemble methods, neural networks, Extreme Learning Machines (ELM), and support vector machine classifiers are all combined. The suggested system has several phases: pre-processing, segmentation, feature extraction, and classification. Pre-processing operations are first performed on the input MRI image using the median filtering algorithm. Next, segmentation is performed using the FCM clustering algorithm. The third stage involves extracting features using the Gray Level Co-occurrence Matrix (GLCM). The automatic stage of a brain tumor is established using ensemble classification. Tumor and non-tumor images are distinguished using the ensemble classifier. As a result of the experiments, the method was discovered to be more reliable, efficient, and precise. An accuracy of 91.17% was obtained using the suggested method.
Furthermore, in the paper [33], the authors employed machine learning methods to recognize tumors in MRI images for the proposed work. The proposed model uses a CNN model to segment MRI images automatically. Segmentation and classification are performed with the same method. The proposed model includes several key phases: data collection, pre-processing, average filtering, segmentation, feature extraction, and classification. On the UCI dataset, this model had an overall accuracy of 91.00%. Another study [34] proposed a detailed augmentation-based model that divides the stages of a brain tumor into four categories. In this method, images are segmented using the CNN model and then submitted to the CNN model (VGG19) for feature extraction and classification after extensive data augmentation. On the Radiopaedia dataset [35], the suggested method achieved 90.67% accuracy.
Several studies used the CNN with PSO to achieve efficient results in terms of accuracy to detect brain tumor diseases; the authors of the paper [36] propose a model to categorize tumorous and non-tumorous brains, PSO extracts thirteen different features using Discrete Wavelet Transform (DWT)-based features and segments the precise tumor location from the images; these features were developed for the classification of tumorous and non-tumorous brains from MR images using an SVM classifier with two different kernel functions, a dataset of 50 brain MR images is used to validate the proposed model and it delivers results with an accuracy of 85%. In addition, the paper [37] used CNN with PSO to classify the tumorous and non-tumorous brain MRI images; the feature optimization process enhances the classifier’s feature selection process with an accuracy of 92%.
3. Proposed Methodology
3.1. MRI Datasets
In this paper, we focused on the binary class classification for brain diseases (Alzheimer’s disease and brain tumor disease). We utilized three well-known benchmark sets—the ADNI dataset [20], the AD dataset [19], and the brain tumor dataset [21]. The ADNI dataset [20] contains 6410 images, two classes (normal/not normal), and the image size is 180 × 180 pixels. Related to the [19] dataset, it contains 6400 images, two classes (normal/not normal), and the image size is 180 × 180 pixels. The brain tumor dataset [21] contains a total of 7023 images; it contains two classes (tumor/no tumor), and the image size is 180 × 180 pixels—Figure 1 lists samples of images from these datasets.
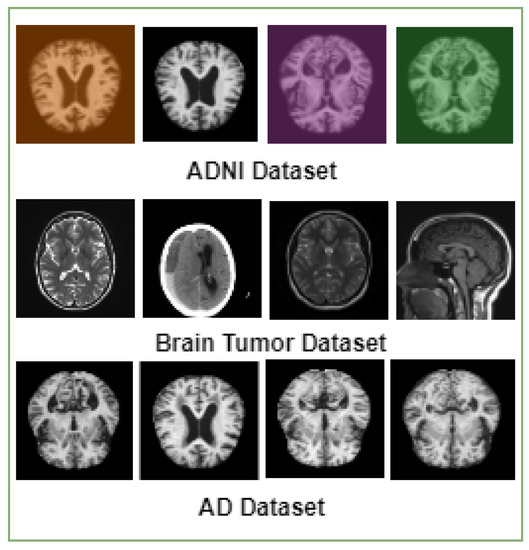
Figure 1.
MRI datasets.
3.2. Data Pre-Processing
Data pre-processing involves cleaning and preparing data to be utilized in a machine-learning model, thereby enhancing the accuracy and efficiency of the model. In the case of MRI datasets containing brain images, it is observed that the images differ in terms of their width, height, and overall size. To ensure consistency for training purposes, all the images are resized to a standard dimension of 180 × 180 pixels. Additionally, the input photos are converted to grayscale, which aids in reducing complexity. Figure 1 shows some samples of MRI datasets.
3.3. Proposed Detection Framework
3.3.1. Convolutional Neural Network (CNN)
CNN architecture is one of the most popular types of ANN and is mainly used for image-based pattern recognition problems. Through a series of deep and hidden layers, it is possible to identify objects by recognizing distinctive patterns in the input data. The initial layers are responsible for detecting the lines and curves, and as you add additional layers, it becomes possible to recognize complicated structures such as faces. These networks are made specifically to work with image processing. Its architecture was created to mimic how the brain’s visual cortex acts when processing and identifying images [36]. The primary goal of using convolution layers is to find and learn characteristic patterns such as curves, lines, color tones, and so on, which aid in object identification and classification. The five layers that comprise the fundamental CNN architecture, as shown in Figure 2, are the input layer, convolution layer, non-linearity or activation function layer (ReLu), pooling layer, and finally, the classification layer.
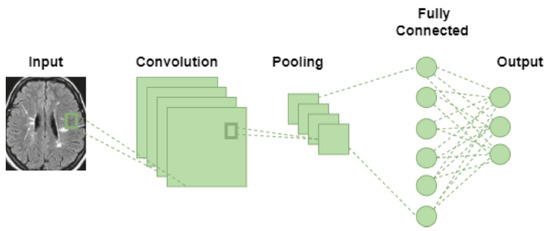
Figure 2.
CNN architecture.
CNNs are frequently used in applications where artificial vision techniques are required. Even though the results are extremely encouraging, they come at a high computational cost; for this reason, it is critical to use strategies that boost performance. Optimization of the CNN parameters is presented in this study in order to improve the recognition rate and reduce computational costs. In Figure 3, we can see a few parameters for each CNN layer that require optimization.
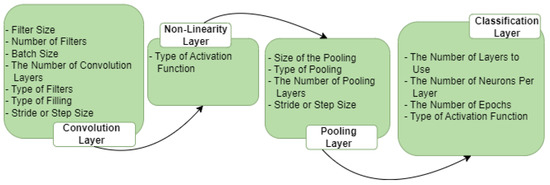
Figure 3.
CNN layers and the parameters for each layer.
3.3.2. Particle Swarm Optimization (PSO)
Particle Swarm Optimization is a meta-heuristic search algorithm built on the swarm’s intelligence and modeled after how birds search for food; each bird is represented by particles that “move” in a complex search environment and “change” based on your own and your neighbors’ experiences. The article, which can be viewed as “an individual element in a flock”, represents one possible solution. Using a fitness function and the particle’s velocities, PSO analyzes local and global data to determine the best solution.
The selection of PSO over other optimization algorithms was justified based on its effectiveness, particularly in optimizing parameters in high-dimensional search spaces. PSO balances exploration and exploitation, converges quickly, and requires fewer parameter settings. Its simplicity of implementation and previous successful applications in similar domains further supported its choice.
The PSO’s procedure is described in Algorithm 1. The equations defining this algorithm allow for updating the position, as shown in Equation (1), and updating the velocity, as shown in Equation (2).
Pi(t) in Equation (1) represents the location of particle i in the search space at iteration t. Velocity, xi(t), can alter the particle’s position.
The particle is denoted by i in Equation (2), and the velocity is represented by x. Indicated by parameters and , the cognitive and social factors are defined, respectively. The best particle position (pbesti), as well as the best global position (gbest), are determined by and y, respectively. The random values in the range [0, 1] are represented by and , which represent inertia weight.
where .
| Algorithm 1: Particle Swarm Optimization (PSO) Algorithm | |||||||
| Require: Objective function | |||||||
| Require: Hyperparameters n, Fitness function F | |||||||
| Ensure: Optimal solution | |||||||
 | |||||||
To compute particle fitness with a maximization task, an objective function f is implemented under the assumption that the swarm consists of n particles. Equations (3) and (4), respectively, are used at iteration t to update the personal and global best values.
3.3.3. Optimal Selection of Hyper-Parameters via PSO Algorithm
This section describes our method for using the PSO algorithm to optimize the parameters of CNN architectures. The first goal is to decide which parameters are most important for obtaining good CNN performance and then to use the PSO algorithm to find these ideal parameters. After analyzing a CNN’s performance in an experimental study where the parameters were manually changed, the parameters to be optimized were chosen. Because different CNN parameter values, as already mentioned, produce a variety of potential findings for the same task, the objective is to identify the best architectures. The following variables were picked for optimization in this study:
- The number of filters in convolutional layers.
- The size of filters in convolutional layers.
- The size of the pool in the max pooling layer.
- The size of the strides used in the max pooling layer.
Algorithm 1 illustrates the PSO algorithm and its role in our methodology in detail; let denote an objective function based on the provided algorithm; n represents the hyper-parameters, and F represents the fitness function, which measures the accuracy of detection of the trained CNN model. The objective of the fitness function in our study is to find a solution for which for all , where is the set of all hyper-parameters. In PSO, evolution occurs with a swarm of particles representing the values of the hyper-parameters. Each particle in the swarm has a position in the search space defined by , and a velocity defined by which influences particle movement. Let denote the global position in the swarm, and represent the local position of the particle. The proposed PSO algorithm is independent of the optimized CNN and can easily adapt to any new CNN architecture.
Our implemented PSO algorithm contains two main processes; the first is known as “Swarm Initialization”, and the second is called “Swarm Evaluation”.
- 1.
- Initialization of the SwarmIn the swarm, each particle’s initial position in the n-dimensional space is randomly selected from a uniform distribution U(, ), where and represent the lower and upper limits. The particle’s position is then designated as its best-known position, denoted by . If the fitness value exceeds the fitness value of the swarm’s best global position, , is stored as the new best position in the swarm, referred to as . The particle’s velocity is randomly determined from a uniform distribution, considering the constraints of the hyper-parameter limits. Following the initialization, the swarm, consisting of s particles represented as tuples for , undergoes evolutionary processes.
- 2.
- Evaluation of the SwarmIn each generation of a swarm (referred to as gen, where represents the maximum number of generations), the velocity values of all particles are updated using the following equation:Here, and are randomly drawn from a uniform distribution to add a stochastic element to the velocity updates, enhancing search space exploration. The inertia weight scales the velocity, while and are acceleration coefficients that determine the influence of the best particle position () and the best swarm position () on the velocity changes. Subsequently, the particle’s position is updated accordingly.Following this, the best position for each particle and the best swarm position are modified. These updates are only applied if there has been a change. The evolutionary process continues until one of the following termination conditions is met:
- (a)
- The best position in the swarm () has been displaced by an amount smaller than a specified minimum step size denoted as .
- (b)
- The fitness value of the best particle has improved by an amount less than a predefined threshold denoted by .
- (c)
- The maximum number of swarm generations, , has been reached.
The first termination condition is designed to prevent high-quality oscillation between two neighboring solutions. The second condition is satisfied when the swarm optimization converges to a well-fitted particle unlikely to improve further. Finally, the best position in the swarm () is returned as the output.The efficiency of PSO is influenced by the number of hyper-parameters involved, and this can be denoted aswhere s and are constants, the time complexity primarily stems from the evaluation of , which scales linearly with the parameter n.Figure 4 illustrates the whole architecture of our methodology used in this study. The CNN initially uses the PSO algorithm for parameter optimization. The PSO is initialized in this process by the execution parameters, and this generates the particles. Each solution represents a completed CNN training period because each particle is a possible solution, and its position has a parameter that needs to be used in the proposed CNN architecture. Our CNN architecture is designed with a concise yet flexible structure. It comprises a block comprising convolutional and max pooling layers, followed by a Softmax activation function for classification. Table 3 and Table 4 list the convolutional and maximum pooling layer parameters and the permitted ranges for each.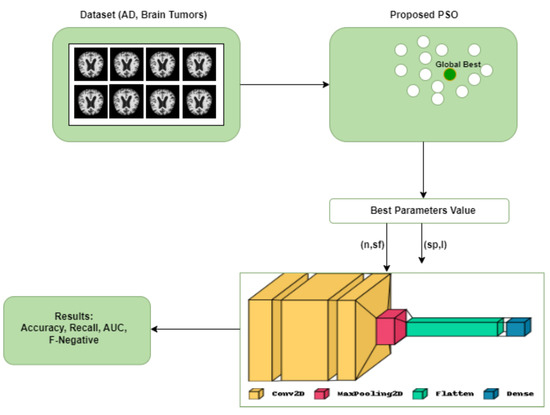 Figure 4. Proposed CNN-PSO architecture.
Figure 4. Proposed CNN-PSO architecture. Table 3. Parameters of the layers in CNN-PSO proposed model.
Table 3. Parameters of the layers in CNN-PSO proposed model. Table 4. Parameters of CNN and PSO.
Table 4. Parameters of CNN and PSO.
In the following are the detailed steps for optimizing the CNN using the PSO algorithm, which is also represented as a flowchart in Figure 5.
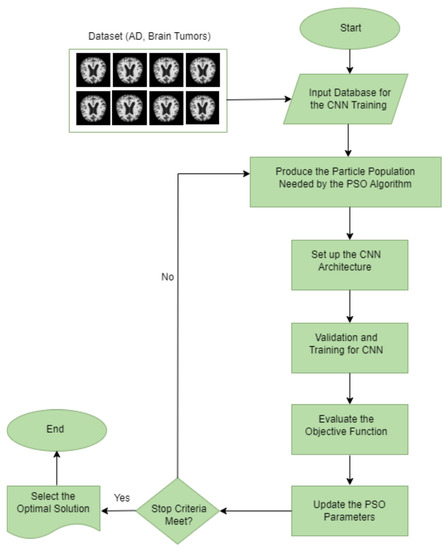
Figure 5.
Flowchart of the proposed CNN-PSO architecture.
- 1.
- Input database for the CNN training: this step chooses the database that will be processed and classified for CNN. It is important to note that each database’s components must maintain a consistent structure or set of attributes with the same pixel size and file format.
- 2.
- Produce the particle population needed by the PSO algorithm: the PSO parameters were set to include the experiment’s number of iterations, particle numbers, inertial weight, cognitive constant (C1), and social constant (C2). Table 4 lists the PSO parameters used in the experiment.
- 3.
- Set up the CNN architecture: create the CNN architecture using the PSO parameter (the number of filters and the size of the filters in the convolution layers, the size of the pool in the max pooling layer, and the size of the strides in the max pooling layer), along with the additional parameters listed in Table 4.
- 4.
- Validation and training for CNN: after reading and processing the input databases and collecting the images for training, validation, and testing, the CNN generates a recognition rate in this step. The objective function’s return value includes these values for the PSO.
- 5.
- Determine the objective function: the PSO algorithm evaluates the objective function defined in Equation (1) to select the best parameters.
- 6.
- Update the PSO parameters: each particle adjusts its velocity and location at each iteration based on its best position (Pbest) in the search space and the best position for the entire swarm (Gbest).
- 7.
- Repeat the process: the number of iterations is the stopping criterion in our study, which involves evaluating all the particles until the stopping criteria are satisfied.
- 8.
- Select the optimal solution: the particle Gbest represents the best solution in this process for the CNN model.
4. Experiments and Results
Our proposed model was implemented using Python programming and the TensorFlow deep learning library. TensorFlow provided the necessary tools and capabilities for building and training our deep neural network. We utilized a T4 GPU hardware configuration to optimize computational performance, facilitating faster training and inference processes. The combination of Python, TensorFlow, and the T4 GPU allowed us to effectively develop and evaluate our hybrid model.
The experimental findings of the proposed study are presented in this section, emphasizing the assessment of the suggested transfer learning model. Multiple performance metrics, such as accuracy, area under the curve (AUC), recall, and precision, have been used to thoroughly evaluate the model’s performance. These metrics are crucial in the medical field, where effective patient care and treatment planning depend on accurate and trustworthy diagnostic tools. While AUC quantifies the model’s capacity to distinguish between positive and negative cases, accuracy measures the model’s overall predictive accuracy. Due to the significance of making effective diagnoses and disease identifications, attaining high accuracy and AUC values is essential.
Additionally, our proposed model’s performance is evaluated in comparison to that of other transfer learning models, including Inception v3, ResNet50, and VGG16. We can learn more about our strategy’s effectiveness and comparative performance by benchmarking it against these models. Additionally, we contrast our findings with the comparative studies mentioned in the related works section. This comparative analysis allows us to assess the improvements and contributions of our proposed model compared to the most state-of-the-art methodologies currently in use, providing us with a thorough understanding of its benefits and drawbacks. The performance matrices that we used to evaluate our proposed method are presented in the below equations:
where: True Positive (TP) represents the number of correctly predicted positive classes in binary classification, where the actual class is positive; True Negative (TN) represents the number of correctly predicted negative classes in binary classification, where the actual class is negative, False Positives (FP) represents the number of incorrectly predicted positive classes in binary classification, where the actual class is negative, and False Negatives (FN) represents the number of incorrectly predicted negative classes in binary classification, where the actual class is positive.
4.1. Optimization Results Obtained by the PSO-CNN Method
Our previous section discussed our proposed method, which aims to create a hybrid model that utilizes the PSO algorithm. The objective is to find the optimal parameter configuration (as listed in Table 3) for CNN architectures. This configuration will enhance the accuracy of brain disease prediction and minimize the loss of function value. In our method, we employ the parameter values mentioned in Table 4. Additionally, we set the number of epochs to 15 and the batch size to 32.
The PSO-CNN method was employed to achieve optimized results in three different datasets: ADNI [20], AD [19], and brain tumor [21] as listed in Table 5, Table 6 and Table 7. In the ADNI dataset, the PSO-CNN model demonstrated promising performance in Alzheimer’s disease prediction. The best accuracy of 98.50% was achieved with the hyper-parameter values [] = [12, 8, 4, 3]. Here, ‘n’ refers to the number of filters, ‘sf’ denotes the size of filters, ‘sp’ represents the size of the max pooling layer, and ‘l’ indicates the step size. Several other configurations, such as [8, 7, 4, 3] and [9, 8, 2, 4], also yielded high accuracies above 97%. However, certain configurations, e.g., [1, 5, 2, 3] and [1, 5, 2, 2], resulted in significantly lower accuracies of 84.20% and 50%, respectively. Moving on to the AD dataset, the PSO-CNN method showcased excellent performance in disease prediction. The best accuracy achieved was 98.83% with hyper-parameter values [] = [15, 7, 2, 4]. Configurations such as [16, 2, 4, 4] and [16, 5, 4, 4] also yielded accuracies above 97%. Conversely, the [1, 5, 2, 2] configuration resulted in a lower accuracy of 85.40%. Lastly, in the tumor dataset, the PSO-CNN method achieved notable results in tumor detection. The best accuracy obtained was 97.12% with the hyper-parameter values [] = [12, 5, 3, 2]. Configurations such as [8, 5, 3, 4] and [12, 7, 4, 2] also yielded accuracies above 96%. However, the [1, 5, 2, 2] and [5, 5, 2, 2] configurations resulted in lower accuracies of 82.40% and 60.53%, respectively. These results demonstrate the potential of the PSO-CNN method in optimizing hyper-parameters [] and achieving high accuracies across diverse datasets.

Table 5.
Proposed CNN hyper-parameters by PSO for the ADNI dataset.

Table 6.
Proposed CNN hyper-parameters by PSO for the AD dataset.

Table 7.
Proposed CNN hyper-parameters by PSO for the brain tumor dataset.
After applying the highest hyper-parameters obtained through the PSO-CNN method for each dataset, we evaluated the CNN architecture. The results, as presented in Table 8, showcase the performance of the proposed model in terms of accuracy, precision, recall, and AUC. In the ADNI dataset, the proposed model achieved an impressive accuracy of 98.50%, as shown in Figure 6a, indicating its ability to classify Alzheimer’s disease cases accurately. The hyper-parameter values [] used in this dataset were [12, 8, 4, 3]. The precision and recall values were equally remarkable, with 97.53% precision and 98.60% recall. Additionally, the AUC value of 99.83% further signifies the model’s effectiveness in distinguishing between different classes, as shown in Figure 6b. Moving to the AD dataset, the proposed model showcased outstanding performance, attaining an accuracy of 98.83%, as shown in Figure 7a. The hyper-parameter values [] used in this dataset were [15, 7, 2, 4]. This highlights its capability to predict the presence of the disease accurately. The precision and recall values of 98.15% and 99.22%, respectively, indicate the model’s ability to achieve a high proportion of true positive predictions while minimizing false negatives. Moreover, the AUC value of 99.88% demonstrates the model’s excellent discriminatory power, as shown in Figure 7b. In the brain tumor dataset, the proposed model exhibited strong performance, achieving an accuracy of 97.12% as shown in Figure 8a. The hyper-parameter values [] used in this dataset were [12, 5, 3, 2]. The precision value of 92.66% indicates the model’s ability to accurately identify positive cases, while the recall value of 99.02% showcases its effectiveness in capturing a high proportion of true positives. Furthermore, the AUC value of 99.24% confirms the model’s robustness in distinguishing between tumor and non-tumor cases, as shown in Figure 8b. These results illustrate the effectiveness of the proposed model in accurately detecting the datasets, emphasizing its potential as a reliable tool for disease prediction and diagnosis.

Table 8.
Performance metrics on different datasets.
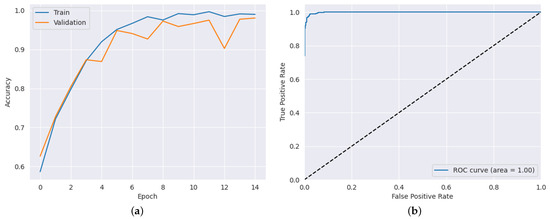
Figure 6.
Results for ADNI dataset: (a) training and validation accuracy results (b) AUC result.
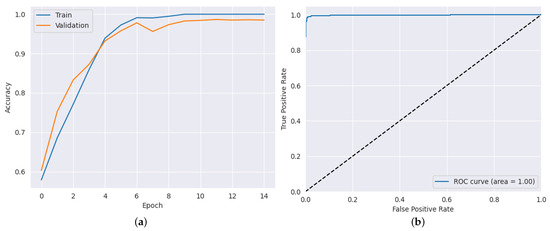
Figure 7.
Results for AD dataset: (a) training and validation accuracy results (b) AUC result.
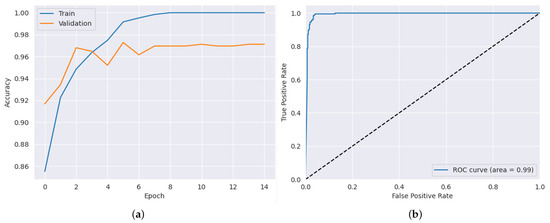
Figure 8.
Results for tumor dataset: (a) training and validation accuracy results (b) AUC result.
4.2. Comparison with Existing Transfer Learning Model
Table 9 comprehensively compares different transfer learning models on multiple datasets, providing insights into their accuracy, precision, recall, and AUC performance. Among the evaluated models, VGG16 demonstrates a satisfactory accuracy of 82% on the ADNI dataset. However, its precision and recall scores fall below the desired thresholds, indicating potential limitations in accurately identifying Alzheimer’s disease cases. Inception V3 exhibits intermediate results across all datasets, lacking the desired level of accuracy and precision. ResNet50, while showing improvements over VGG16 and Inception V3, fails to achieve optimal performance, particularly in terms of AUC.

Table 9.
Comparison with existing transfer learning models.
In contrast, the proposed model consistently outperforms other transfer learning models across all datasets, underscoring its significance and potential impact. On the ADNI dataset, the proposed model achieves an outstanding accuracy of 98.50%, accompanied by remarkable precision and recall scores. These exceptional results signify the model’s ability to effectively classify Alzheimer’s disease cases, positioning it as a promising tool for early detection and diagnosis. Additionally, on the AD dataset, the proposed model maintains its superiority with a remarkable accuracy of 98.83% and well-balanced precision and recall scores. These findings demonstrate its robustness in accurately identifying cases of Alzheimer’s disease in diverse datasets, thereby enhancing diagnostic accuracy. Notably, the proposed model also showcases remarkable efficacy on the brain tumor dataset, achieving an accuracy of 97.12%. This outstanding performance underscores its potential to assist medical professionals in brain tumor detection and classification. The high precision and recall scores further emphasize the model’s reliability and effectiveness in distinguishing between tumor and non-tumor samples. In addition, the proposed model achieved low False Negative Rates (FNR) of 1.72%, 1.56%, and 1.98% on the ADNI, AD, and brain tumor datasets, respectively. These low FNR values indicate that the proposed model correctly identified positive instances related to brain diseases, with only a small proportion of missed cases.
4.3. Comparison with Existing Transfer Learning Model
Compared with related works for Alzheimer’s brain disease (listed in Table 1 and Table 2), the proposed model is a highly effective approach for AD vs. NC detection. The proposed model achieves exceptional performance on the ADNI dataset by leveraging PSO to select the best hyper-parameters. With an accuracy of 98.50%, a precision of 97.53%, a recall of 98.60%, and an impressive AUC of 99.83%, the proposed model outperforms the referenced studies in several key aspects. Notably, the accuracy and precision of the proposed model on the AD dataset [19] are equally remarkable, reaching 98.83% and 98.15%, respectively. Comparing these results with the VoxCNN and ResNet models presented in [9], which achieved accuracies of 79% and 80%, and AUCs of 88% and 87%, respectively, it becomes evident that the proposed model demonstrates superior performance. Similarly, the proposed model surpasses the accuracy reported in [24] (96%) and [25] (90%) on the ADNI dataset.
Furthermore, in terms of specificity, sensitivity, and F-score, the proposed model showcases competitive performance compared to the results presented in [26]. Notably, the utilization of PSO for optimizing model performance or feature selection, as explored in [27,28,29], also demonstrates the effectiveness of such an approach. The achieved accuracy, precision, recall, and AUC by the proposed model highlight its potential as a high-performance CNN architecture for AD vs. NC detection when leveraging PSO for hyper-parameter selection.
While compared with related works for brain tumor disease (listed in Table 1 and Table 2), various methodologies were employed to classify brain tumors using diverse techniques. Notably, the authors of [30] achieved an accuracy of 94.39% for normal vs. not normal classification on the brain tumor dataset without utilizing the PSO algorithm. Similarly, the authors of [31,32,34] also obtained accuracies of 91%, 91.17%, and 90.67%, respectively, for the same classification task, without incorporating PSO. In contrast, the authors of [36,37] utilized PSO for feature selection and achieved accuracies of 85% and 92%, respectively, for normal vs. not normal classification on the brain tumor dataset. These works demonstrated the potential of PSO in enhancing classification accuracy.
The proposed model presented in this study advanced the state-of-the-art by utilizing PSO for feature selection and optimal hyper-parameters in constructing a high-performance CNN architecture. The results of the proposed model are remarkable, exhibiting an outstanding accuracy of 97.12% for AD vs. NC detection, accompanied by precision, recall, and AUC values of 92.66%, 99.02%, and 99.24%, respectively. The superior performance of the proposed model, surpassing the related works, can be attributed to the comprehensive utilization of PSO for both feature selection and hyper-parameter optimization. By leveraging PSO in these crucial aspects, the proposed model effectively distinguishes between AD and NC brain tumor classes, demonstrating the potential of PSO in significantly improving the detection accuracy of brain tumor diseases.
While this model combines CNN and PSO, we achieved computational efficiency through an optimized implementation. The PSO algorithm was responsible for selecting the best parameters, and it took approximately 8 min to complete this optimization process. The CNN component, responsible for training and validation accuracy, exhibited efficient performance, completing the process in approximately 3 min. The efficient execution times of the PSO and CNN components contribute to the overall computational efficiency of our proposed model. By effectively utilizing PSO for parameter selection and optimizing the CNN training process, our model demonstrates a balance between accuracy and computational efficiency, making it well-suited for practical applications.
However, it is important to acknowledge the limitations of our model in accurately classifying certain images. One of the key challenges we encountered was misclassifying images due to their low resolution and unclear characteristics. These factors significantly impact the model’s ability to extract meaningful features and patterns for accurate classification. The lack of clarity and fine details in low-resolution images pose difficulties for the model in capturing essential discriminative information. As a result, the model may struggle to classify such images, leading to misidentifications. Although efforts were made to optimize the model’s performance, including fine-tuning the architecture and adjusting parameters, our current approach could not completely overcome the inherent limitations posed by low resolution and unclear image quality. Addressing this limitation requires further research and potential improvements in pre-processing techniques or considering alternative approaches specifically tailored for handling low-resolution or unclear images. As an example, Figure 9a illustrates the incorrect image classification of Alzheimer’s disease, while Figure 9b illustrates the correct image classification of Alzheimer’s disease.
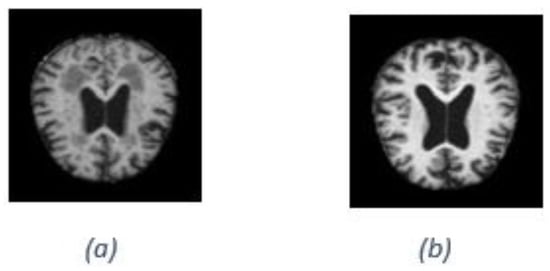
Figure 9.
Alzheimer’s disease classification: (a) incorrect image classification (b) correct image classification.
5. Conclusions and Future Work
This proposed model focused on the CNNs for detecting MRI images, specifically targeting the identification of Alzheimer’s disease and brain tumors. The performance of CNNs heavily depends on selecting various parameters, which has traditionally been a challenging task requiring trial-and-error or expert judgment. To address this challenge, we proposed a hybrid methodology incorporating the PSO algorithm to determine the optimal configuration of parameters for CNN architectures. Using the PSO algorithm, we aimed to enhance the accuracy and the Area Under Curve (AUC) results of disease prediction and reduce the loss function value.
The proposed model was evaluated using three benchmark datasets: the ADNI dataset, an international dataset obtained from Kaggle, and a dataset specifically designed for brain tumors. The experimental results demonstrated the effectiveness of our approach, achieving accuracy rates of 98.50%, 98.83%, and 97.12% for the respective datasets.
Future research could explore the proposed methodology’s scalability and generalizability to larger, more diverse datasets. Additionally, investigating the interpretability of the CNN models and integrating other optimization algorithms could further enhance the accuracy and robustness of disease detection.
Author Contributions
Conceptualization, R.I. and R.G.; Data curation, R.I.; Formal analysis, Q.A.A.-H.; Funding acquisition, Q.A.A.-H.; Investigation, R.I. and R.G.; Methodology, R.I.; Resources, R.I. and R.G.; Software, R.I.; Supervision, R.G. and Q.A.A.-H.; Validation, Q.A.A.-H.; Visualization, R.G.; Writing—riginal draft, R.I., R.G. and Q.A.A.-H.; Writing—review & editing, R.I., R.G. and Q.A.A.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data associated with this research can be received online from the Kaggle repository via: https://www.kaggle.com/datasets/tourist55/alzheimers-dataset-4-class-of-images (accessed on 22 March 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anton, A.; Fallon, M.; Cots, F.; Sebastian, M.A.; Morilla-Grasa, A.; Mojal, S.; Castells, X. Cost and detection rate of glaucoma screening with imaging devices in a primary care center. Clin. Ophthalmol. 2017, 16, 337–346. [Google Scholar] [CrossRef] [PubMed]
- Alzheimer’s Disease International. World Alzheimer Report 2018. The State of the Art of Dementia Research: New Frontiers; Alzheimer’s Disease International (ADI): London, UK, 2018; pp. 14–20. [Google Scholar]
- Huang, J.; van Zijl, P.C.; Han, X.; Dong, C.M.; Cheng, G.W.; Tse, K.H.; Knutsson, L.; Chen, L.; Lai, J.H.; Wu, E.X.; et al. Altered d-glucose in brain parenchyma and cerebrospinal fluid of early Alzheimer’s disease detected by dynamic glucose-enhanced MRI. Sci. Adv. 2020, 6, eaba3884. [Google Scholar] [CrossRef] [PubMed]
- Castellazzi, G.; Cuzzoni, M.G.; Cotta Ramusino, M.; Martinelli, D.; Denaro, F.; Ricciardi, A.; Vitali, P.; Anzalone, N.; Bernini, S.; Palesi, F.; et al. A machine learning approach for the differential diagnosis of alzheimer and vascular dementia fed by MRI selected features. Front. Neuroinform. 2020, 14, 25. [Google Scholar] [CrossRef] [PubMed]
- Zaw, H.T.; Maneerat, N.; Win, K.Y. Brain tumor detection based on Naïve Bayes Classification. In Proceedings of the 2019 5th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Luang Prabang, Laos, 2–5 July 2019; pp. 1–4. [Google Scholar]
- Ghnemat, R.; Khalil, A.; Al-Haija, Q.A. Ischemic stroke lesion segmentation using mutation model and generative adversarial network. Electronics 2023, 12, 590. [Google Scholar] [CrossRef]
- Salam, A.A.; Khalil, T.; Akram, M.U.; Jameel, A.; Basit, I. Automated detection of glaucoma using structural and non structural features. Springerplus 2016, 5, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Yadav, A.S.; Kumar, S.; Karetla, G.R.; Cotrina-Aliaga, J.C.; Arias-Gonzáles, J.L.; Kumar, V.; Srivastava, S.; Gupta, R.; Ibrahim, S.; Paul, R.; et al. A feature extraction using probabilistic neural network and BTFSC-net model with deep learning for brain tumor classification. J. Imaging 2022, 9, 10. [Google Scholar] [CrossRef] [PubMed]
- Korolev, S.; Safiullin, A.; Belyaev, M.; Dodonova, Y. Residual and plain convolutional neural networks for 3D brain MRI classification. In Proceedings of the 2017 IEEE 14th international symposium on biomedical imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017; pp. 835–838. [Google Scholar]
- Hemanth, D.J.; Deperlioglu, O.; Kose, U. An enhanced diabetic retinopathy detection and classification approach using deep convolutional neural network. Neural Comput. Appl. 2020, 32, 707–721. [Google Scholar] [CrossRef]
- Wang, W.; Gang, J. Application of convolutional neural network in natural language processing. In Proceedings of the 2018 International Conference on Information Systems and Computer Aided Education (ICISCAE), Changchun, China, 6–8 July 2018; pp. 64–70. [Google Scholar]
- Al-Haija, Q.A.; Adebanjo, A. Breast Cancer Diagnosis in Histopathological Images Using ResNet-50 Convolutional Neural Network. In Proceedings of the 2020 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS 2020), Vancouver, BC, Canada, 9–12 September 2020. [Google Scholar]
- Al-Haija, Q.A.; Smadi, M.; Al-Bataineh, O.M. Identifying Phasic dopamine releases using DarkNet-19 Convolutional Neural Network. In Proceedings of the 2021 IEEE International IOT, Electronics and Mechatronics Conference (IEMTRONICS 2021), Toronto, ON, Canada, 21–24 April 2021; p. 590. [Google Scholar]
- Liang, S.D. Optimization for deep convolutional neural networks: How slim can it go? IEEE Trans. Emerg. Top. Comput. Intell. 2018, 4, 171–179. [Google Scholar] [CrossRef]
- Ma, B.; Li, X.; Xia, Y.; Zhang, Y. Autonomous deep learning: A genetic DCNN designer for image classification. Neurocomputing 2020, 379, 152–161. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Proceedings of the Learning and Intelligent Optimization: 5th International Conference, LION 5, Rome, Italy, 17–21 January 2011; Selected Papers 5. Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar]
- Poma, Y.; Melin, P.; González, C.I.; Martínez, G.E. Optimization of convolutional neural networks using the fuzzy gravitational search algorithm. J. Autom. Mob. Robot. Intell. Syst. 2020, 14, 109–120. [Google Scholar] [CrossRef]
- Anima890. Alzheimer’s Disease Classification Dataset. Kaggle. 2019. Available online via: https://www.kaggle.com/datasets/tourist55/alzheimers-dataset-4-class-of-images (accessed on 22 March 2023).
- Alzheimer’s Disease Neuroimaging Initiative. ADNI (Alzheimer’s Disease Neuroimaging Initiative). Available online: https://adni.loni.usc.edu/ (accessed on 11 May 2023).
- Nickparvar, M. Brain Tumor MRI Dataset. Available online: https://www.kaggle.com/datasets/masoudnickparvar/brain-tumor-mri-dataset (accessed on 11 May 2021).
- Al-Haija, Q.A.; Smadi, M.; Al-Bataineh, O.M. Early Stage Diabetes Risk Prediction via Machine Learning. In Proceedings of the 13th International Conference on Soft Computing and Pattern Recognition (SoCPaR 2021); Springer: Cham, Switzerland, 2022; Volume 417. [Google Scholar]
- Liu, M.; Zhang, D.; Adeli, E.; Shen, D. Inherent structure-based multiview learning with multitemplate feature representation for Alzheimer’s disease diagnosis. IEEE Trans. Biomed. Eng. 2015, 63, 1473–1482. [Google Scholar] [CrossRef] [PubMed]
- Gunawardena, K.; Rajapakse, R.; Kodikara, N. Applying convolutional neural networks for pre-detection of alzheimer’s disease from structural MRI data. In Proceedings of the 2017 24th International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Auckland, New Zealand, 21–23 November 2017; pp. 1–7. [Google Scholar]
- Lin, L.; Zhang, B.; Wu, S. Hybrid CNN-SVM for Alzheimer’s Disease Classification from Structural MRI and the Alzheimer’s Disease Neuroimaging Initiative (ADNI). Age (Years) 2018, 72, 199–203. [Google Scholar]
- Rallabandi, V.S.; Tulpule, K.; Gattu, M.; Alzheimer’s Disease Neuroimaging Initiative. Automatic classification of cognitively normal, mild cognitive impairment and Alzheimer’s disease using structural MRI analysis. Inform. Med. Unlocked 2020, 18, 100305. [Google Scholar] [CrossRef]
- Arunprasath, T.; Rajasekaran, M.P.; Vishnuvarathanan, G. MR Brain image segmentation for the volumetric measurement of tissues to differentiate Alzheimer’s disease using hybrid algorithm. In Proceedings of the 2019 IEEE International Conference on Clean Energy and Energy Efficient Electronics Circuit for Sustainable Development (INCCES), Krishnankoil, India, 18–20 December 2019; pp. 1–4. [Google Scholar]
- Saputra, R.; Agustina, C.; Puspitasari, D.; Ramanda, R.; Pribadi, D.; Indriani, K. Detecting Alzheimer’s disease by the decision tree methods based on particle swarm optimization. J. Phys. Conf. Ser. 2020, 1641, 012025. [Google Scholar] [CrossRef]
- Saraswathi, S.; Mahanand, B.; Kloczkowski, A.; Suresh, S.; Sundararajan, N. Detection of onset of Alzheimer’s disease from MRI images using a GA-ELM-PSO classifier. In Proceedings of the 2013 Fourth International Workshop on Computational Intelligence in Medical Imaging (CIMI), Singapore, 15–19 April 2013; pp. 42–48. [Google Scholar]
- Das, S.; Aranya, O.R.R.; Labiba, N.N. Brain tumor classification using convolutional neural network. In Proceedings of the 2019 1st International Conference of the Advances in Science, Engineering and Robotics Technology (ICASERT), Dhaka, Bangladesh, 3–5 May 2019; pp. 1–5. [Google Scholar]
- Narayana, T.L.; Reddy, T.S. An efficient optimization technique to detect brain tumor from MRI images. In Proceedings of the 2018 International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 13–14 December 2018; pp. 168–171. [Google Scholar]
- Kumar, P.; VijayKumar, B. Brain tumor MRI segmentation and classification using ensemble classifier. Int. J. Recent Technol. Eng. (IJRTE) 2019, 8, 244–252. [Google Scholar]
- Hemanth, G.; Janardhan, M.; Sujihelen, L. Design and implementing brain tumor detection using machine learning approach. In Proceedings of the 2019 3rd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 23–25 April 2019; pp. 1289–1294. [Google Scholar]
- Sajjad, M.; Khan, S.; Muhammad, K.; Wu, W.; Ullah, A.; Baik, S.W. Multi-grade brain tumor classification using deep CNN with extensive data augmentation. J. Comput. Sci. 2019, 30, 174–182. [Google Scholar] [CrossRef]
- Modiya, P.; Vahora, S. Brain Tumor Detection Using Transfer Learning with Dimensionality Reduction Method. Int. J. Intell. Syst. Appl. Eng. 2022, 10, 201–206. [Google Scholar]
- Dixit, A.; Nanda, A. Brain MR image classification via PSO based segmentation. In Proceedings of the 2019 Twelfth International Conference on Contemporary Computing (IC3), Noida, India, 8–19 August 2019; pp. 1–5. [Google Scholar]
- Srinivasalu, P.; Palaniappan, A. Brain Tumor Detection by Modified Particle Swarm Optimization Algorithm and Multi-Support Vector Machine Classifier. Int. J. Intell. Eng. Syst. 2022, 15, 91–100. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).