Abstract
Artificial intelligence (AI) plays a critical role in the operation of robot vacuum cleaners, enabling them to intelligently navigate to clean and avoid indoor obstacles. Due to limited computational resources, manufacturers must balance performance and cost. This necessitates the development of lightweight AI models that can achieve high performance. Traditional uniform weight quantization assigns the same number of levels to all weights, regardless of their distribution or importance. Consequently, this lack of adaptability may lead to sub-optimal quantization results, as the quantization levels do not align with the statistical properties of the weights. To address this challenge, in this work, we propose a new technique called low bitwidth strong non-uniform quantization, which largely reduces the memory footprint of AI models while maintaining high accuracy. Our proposed non-uniform quantization method, as opposed to traditional uniform quantization, aims to align with the actual weight distribution of well-trained neural network models. The proposed quantization scheme builds upon the observation of weight distribution characteristics in AI models and aims to leverage this knowledge to enhance the efficiency of neural network implementations. Additionally, we adjust the input image size to reduce the computational and memory demands of AI models. The goal is to identify an appropriate image size and its corresponding AI models that can be used in resource-constrained robot vacuum cleaners while still achieving acceptable accuracy on the object classification task. Experimental results indicate that when compared to the state-of-the-art AI models in the literature, the proposed AI model achieves a 2-fold decrease in memory usage from 15.51 MB down to 7.68 MB while maintaining the same accuracy of around 93%. In addition, the proposed non-uniform quantization model reduces memory usage by 20 times (from 15.51 MB down to 0.78 MB) with a slight accuracy drop of 3.11% (the classification accuracy is still above 90%). Thus, our proposed high-performance and lightweight AI model strikes an excellent balance between model complexity, classification accuracy, and computational resources for robot vacuum cleaners.
1. Introduction
Currently, artificial intelligence (AI) has been adopted in robot vacuum cleaners to improve their performance and efficiency in smart building systems. For example, AI algorithms can create room maps and plan the most efficient cleaning path to navigate and avoid obstacles. Another exciting feature is object recognition and classification. AI algorithms can recognize different indoor objects, such as toys, furniture, or charging cables, and adjust the cleaning path accordingly. The use of AI techniques helps to ensure that robot vacuum cleaners clean all room areas and avoid becoming stuck or damaging anything. To date, several AI models have been proposed for indoor object classification to identify cleanable litter and non-cleanable hazardous obstacles. However, these studies mainly focus on the high accuracy in object classification, while ignoring the fact that robot vacuum cleaners require lightweight AI models due to their limited computational and memory resources. As an example of edge computing devices, robot vacuum cleaners typically have limited hardware resources (CPU, memory and power) compared to other computing devices such as desktop computers or servers. Rather than relying on the cloud-based computing resource, robot vacuum cleaners involve processing data and running AI models on the device itself [1,2]. This means that they cannot handle large and complex AI models that require high computational power, making lightweight models a better fit. Additionally, robot vacuum cleaners need to process data in real-time to recognize objects in video streams from built-in cameras. Lightweight AI models are often faster and more efficient than larger models, making them better suited for real-time object classification applications. In addition, robot vacuum cleaners are designed for mass production, which means they need to be cost-effective. Therefore, lightweight AI models help to reduce the cost of robot vacuum cleaners by using less powerful and low-cost hardware components, thereby, overcoming the limitations of computational resources and implementation costs.
Generally, there are several potential techniques to reduce the complexity of AI models, including weight quantization [3,4,5,6,7], network pruning [8,9,10,11,12], transfer learning [13,14], the input image resizing [15,16], well-designed model architecture [17], and so on. In deep AI models, weights are typically represented as 32-bit floating-point numbers, which require a large amount of memory. Weight quantization allows us to represent weights using fewer bits, reducing the memory requirements. For example, converting a 32-bit floating-point weight to an 8-bit integer weight reduces the memory size by a factor of 4. The researchers have presented post-training weight quantization, which involves quantizing the weights of a pre-trained model after it has been trained [2,18], so there is no need for retraining, making it convenient to use. In contrast, the researchers [3,6,7,19] present quantization-aware training, which involves quantizing the weights of AI models during training, taking into account the quantization constraints during the optimization process. Training-aware quantization can result in more accurate quantization and reduced accuracy loss, since it allows the model to adapt and learn to perform effectively with quantized weights and activations. During quantization-aware training, additional techniques can be applied to improve the performance of the quantized model. For example, techniques like precision scaling, where different layers are assigned different bit precisions, can be employed to optimize the model’s accuracy and efficiency further. Furthermore, post-training quantization often requires an additional calibration step to determine optimal quantization parameters for each layer. This calibration process can be time-consuming. In contrast, quantization-aware training avoids the need for post-training calibration by incorporating the quantization process directly into the training phase. Both post-training quantization and quantization-aware training typically use linear quantization, while the weight distribution of well-trained neural network models is often non-linear. Figure 1 plots the weight distribution curves of two typical deep neural networks (VGG-19 and ResNet-50), respectively. It is observed that these weight distributions are centered around zero. This means that most weights have positive and negative values, with a mean close to zero. In addition, the weight distribution in deep neural networks is often assumed to follow a normal or Gaussian distribution. This assumption is supported by the central limit theorem, which states that the sum of many independent and identically distributed random variables tends to follow a Gaussian distribution. Therefore, as the number of layers and weights increases in a deep neural network, the weight distribution tends to approach a Gaussian distribution. Traditional uniform quantization is insensitive to weight distribution characteristics because they treat all weights equally, without considering the specific distribution characteristics of weight values. Therefore, these traditional uniform quantization methods that do not match the actual weight distribution will inevitably limit the performance of the model.
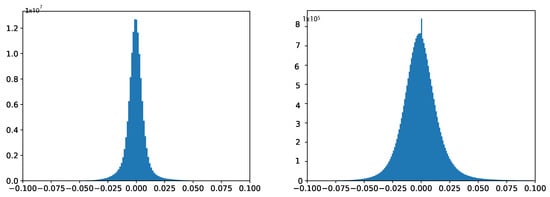
Figure 1.
Weight distribution plots of well-trained VGG-16 and ResNet50 models, respectively.
Network pruning reduces the size of AI models by removing unnecessary weights, neurons, or connections. Since weights that are close to zero are usually considered to be redundant or unnecessary, removing them can result in slight performance degradation and a significant reduction in the size of AI models. However, pruning cannot reduce computational cost unless customized hardware accelerators are used. This is because network pruning often leads to irregular sparsity patterns where certain connections or weights are removed while others are preserved. This irregular sparsity poses challenges for hardware architectures, such as CPUs or micro-controllers, which are designed for dense matrix operations. These architectures may not efficiently utilize the sparsity in the pruned network and still perform computations on the unused connections, resulting in limited computational savings. Since customized hardware accelerators are not affordable in cost-effective robot vacuum cleaners, network pruning is not a suitable approach for reducing memory requirements in this context.
Transfer learning is another popular technique in deep learning for object classification tasks, where a pre-trained AI model is used as a starting point for a new classification task. The pre-trained model has already been trained on a large dataset, typically using millions of images, and has learned to recognize a wide range of features that can be useful for many other tasks. Transfer learning consists of four steps: choosing a pre-trained model, freezing the pre-trained layers, replacing the classification layers, and fine-tuning the model. Despite the benefits of transfer learning, it involves a very high training cost. Robot vacuums often have limited computational resources and memory compared to larger computing systems used in training deep neural networks. This can restrict the complexity and size of the transferred model that can be deployed on the robot vacuum cleaner. The limited hardware capabilities may hinder the performance and scalability of the transferred model, affecting its ability to handle complex object recognition tasks.
Because the training image size affects the size of AI models, input image resizing has significant impacts on the performance of AI models [14,15]. Larger training images generally contain more details and information about the objects or scenes they represent. This additional information can help the model learn more discriminative features and improve its ability to distinguish between different classes. Consequently, using larger training images can potentially lead to better model performance. However, if the training images are too large, the AI model may not fit into the memory of robot vacuum cleaners, which can slow down the training or inference process due to high memory usage or computational cost per training iteration. On the other hand, if the input images are too small, the AI model may not be able to capture the important visual features of the image, which can result in lower accuracy and generalization performance. Therefore, the architecture and size of AI models should be appropriately chosen to be compatible with the input image size. It has been reported that the performance of well-designed model architecture [17] can rival that of much larger models. However, the effectiveness of such architectures heavily relies on the experience of designers. In many cases, the availability of experienced model design experts is limited, especially when dealing with diverse applications. It is important to strike a balance between training image size, computational resources, and the specific requirements of the task at hand.
In this work, we investigate and develop a lightweight AI model with low bitwidth non-uniform quantization technique. The proposed design needs very little memory usage and computational resources for easy deployment on resource-constrained robot vacuum cleaners. Since the weight distribution of well-trained AI models (for example, Figure 1) has been observed to exhibit a resemblance to a power-of-N function [20], therefore, we propose to adopt a power-of-N quantization scheme. In this proposed scheme, weight values are discretized into a set of predefined levels that are distributed according to the power-of-N pattern. This proposed scheme ensures that the weight levels are distributed in a way that aligns with the underlying power-of-N trend, capturing the statistical characteristics of the weight distribution.
Experiments are first carried out using the same training image size (256 × 256 × 3) as that of the existing design [4]. Compared with our recent design [4] whose memory usage is 15.51 MB and accuracy result is 93.39%, our experimental results indicate that the high-performance uniform quantization model could achieve half the memory footprint (from 15.51 MB down to 7.76 MB) with a negligible accuracy drop of 0.05%. By ensuring a classification accuracy of over 90%, the minimum memory requirement for our model is determined to be 1.04 MB. This signifies a substantial reduction in memory, specifically a 15-fold decrease from the initial 15.51 MB down to 1.04 MB. Experimental results also show that when compared with the state-of-the-art AI models in the literature, the proposed non-uniform quantized AI model achieves a 1.6-fold decrease in memory usage from 15.51 MB down to 9.69 MB while maintaining the same accuracy of around 93.39%. In addition, the proposed strong non-uniform quantization AI model may minimize memory usage by 20 times (from 15.51 MB down to 0.78 MB) with an accuracy drop of 3.11% (the classification accuracy is still above 90%). These above results demonstrate that the proposed strong non-uniform weight quantization approach is advantageous in high-performance and low-memory applications. Next, experiments are also conducted using smaller training image sizes (128 × 128 × 3) and (64 × 64 × 3) to evaluate their impact on memory usage and object classification accuracy. Through the utilization of our proposed strong non-uniform quantization and downscaled input image size of (128 × 128 × 3), we have discovered that SqueezeNet can attain an accuracy level of 90.28% while utilizing only 0.78 MB of memory. Therefore, our proposed AI models may fit better into the available memory on robot vacuum cleaners, without worrying about performance degradation or even crashes. Note that existing studies in the literature only consider the parameter size of their AI models when calculating memory usage, ignoring the memory used for the forward and backward passes. The forward and backward passes in AI models require a significant amount of memory because they involve a large number of matrix operations. In the forward pass, the input data undergo multiplication with the weight matrices and subsequently pass through activation functions. The intermediate results of these operations are stored in memory to be used in the backward pass. The output of the forward pass is also stored in memory for later use. In the backward pass, the gradient of loss function concerning each weight is computed by carrying out a series of matrix operations in reverse order. The intermediate results of these operations are also stored in memory to be used in the weight updates. Therefore, the memory usage for forward and backward passes often exceed the parameter size itself. In our study, we adopt a practical approach to present the memory footprint by incorporating various factors such as input image size, parameter size, and the memory needed for both forward and backward passes. This enables a comprehensive understanding of the memory requirements involved in the process.
The rest of this paper is organized as follows. Section 2 introduces related work on several state-of-the-art deep AI models, and traditional uniform weight quantization technique. Section 3 describes the concepts of proposed low bitwidth strong non-uniform weight quantization and input image size adjustment. Section 4 describes the dataset preparation, experimental setup, and various experimental results, and comprehensive comparison with the state-of-the-art works in the literature. Section 5 concludes the paper and discusses future work.
2. Related Work
2.1. State-of-the-Art AI Models
In this subsection, let us review the state-of-the-art AI models of object classification for robot vacuum cleaners in the literature. Several recent works are plotted in Figure 2 to show their results in memory footprints and classification accuracy.
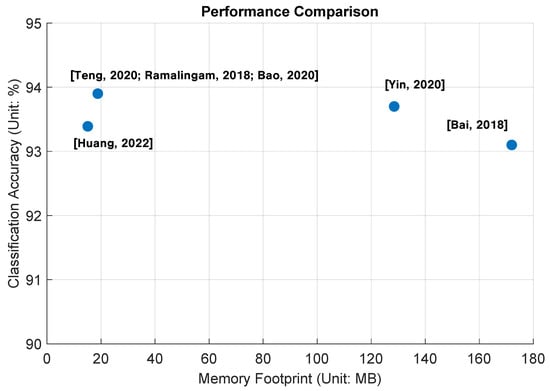
Figure 2.
Performance comparison of test classification accuracy vs. memory footprint among existing state-of-the-art works [4,21,22,23,24,25] in the literature.
In [21], the researchers use the ResNet-34 model for garbage classification on grass. ResNet-34 is a convolutional neural network (CNN) architecture that was first introduced in 2016. ResNet-34 has 34 layers, including a convolutional layer, a pooling layer, and multiple residual blocks. Each residual block contains multiple convolutional layers and a shortcut connection that allow the network to bypass some layers and retain information from earlier layers. The use of residual connections is intended to address the problem of vanishing gradients in deep neural networks, allowing for the successful training of very deep CNNs. As shown in Figure 2, this ResNet-34 model occupies 172 MB of memory and achieves a classification accuracy of 93.1%.
In [22], the researchers use a 16-layer CNN model to classify food trash into either solid or liquid categories. This model consists of nine convolutional layers and other types of layers such as pooling and averaging layers. In typical CNN architecture, convolutional layers are designed to learn local features from the input data by applying a set of learned filters across the input image. On the other hand, fully connected layers take the output of convolutional layers and apply a set of learned weights to make predictions for each class. Because fully connected layers have to connect each neuron from the previous layer to each neuron in this current layer, fully connected layers have more parameters than convolutional layers. Therefore, fully connected layers are not used in [22] to minimize the size of AI models. Consequently, the reported memory footprint is 128.5 MB and the object classification accuracy is 93.7%.
In [23,24,25], the researchers propose to use the MobileNet-V2 model [26,27] for indoor garbage classification, since MobileNet is a convolutional neural network architecture designed for mobile and embedded applications. MobileNet-V2 uses depthwise separable convolutions to significantly reduce the number of parameters and computations required compared to standard convolutions. MobileNet-V2 also uses linear bottleneck layers, which are a combination of 1 × 1 and 3 × 3 convolutional layers that are used to increase the non-linearity of the network while minimizing the computational cost. Due to the above features, the memory footprint is 18.8 MB while maintaining a high classification accuracy of 93.9%.
In [4], the researchers propose to use the SqueezeNet model [17] for indoor garbage classification. SqueezeNet is a neural network architecture designed to be very small in size while maintaining high accuracy on image classification tasks. SqueezeNet achieves its small size by using a combination of techniques, including: using 1 × 1 convolutions to reduce the number of input channels to a layer, using “fire” modules to extract features, and using global average pooling in the final layer. With the proposed 8-bit integer uniform weight quantization technique, the total memory footprint is 15.51 MB and the classification accuracy is 93.39%. This total memory includes 0.75 MB for input image size, 14.53 MB for forward/backward pass size, and 0.23 MB for parameter size.
From Figure 2, we can see that even though the use of 8-bit uniform weight quantization helps to reduce the memory size, existing works need at least 15.51 MB of memory to run AI models for indoor trash classification. It is worth investigating advanced weight quantization techniques to further shrink the memory size, even down to 1 MB, which is the memory capacity of micro-controllers such as the STM32F7 series [28].
2.2. Traditional Uniform Weight Quantization
Weight quantization aims to obtain low-precision networks with high performance. In uniform weight quantization, all weights of AI models are quantized to the same precision, resulting in a fixed-size memory footprint. The first step involves identifying the range of weights across all network layers and determining the appropriate quantization bitwidth. The next step is to quantize weights. The weight values are mapped to discrete levels within the weight range based on the number of bits allocated. The mapping process divides the weight range into equal intervals corresponding to the available discrete levels. Finally, the quantized weights are stored in memory. During inference, the quantized weights are used instead of the original full-precision weights. For example, given a weight w, which requires b bits of precision. We first determine a scaling factor s that is the power of 2, such that s is the largest value that can be represented by n bits.
Then, we quantize w to the nearest value that can be represented by n bits and is a multiple of s. The quantized value of w (denoted as q) is expressed as
The quantization step size determines the level of granularity with which the original range is represented by the quantized values. The quantization step is expressed as
Uniform quantization treats all weights equally and hence fails to leverage the information provided by the weight distribution, potentially compromising the efficiency and accuracy of the quantized model. As the quantization bit decreases, the quantization loss increases, resulting in a decrease in the overall accuracy of AI models. Binary quantization is an extreme case, where weight values can be +1 or −1. However, using fewer bits can result in a smaller model size and faster inference times, making it a trade-off between model size and classification accuracy. The researchers in [4] have verified the feasibility of 8-bit uniform weight quantization. In this work, we will investigate the classification accuracy when the uniform quantization bitwidth is down to 2.
3. Proposed AI Models with Non-Uniform Weight Quantization and Downsized Input
To deal with the memory limitation challenge, we propose to use non-uniform weight quantization and downsized input images. Figure 3a illustrates the conventional process of training an AI model (forward pass for one network layer) in [21,22,23,24,25]. In this process, the input undergoes a linear operation with floating-point weight, followed by the addition of bias to the resulting output. Linear operation forms the basis of many fundamental computations in neural networks, such as matrix multiplications in fully connected layers or convolutions in convolutional layers. It helps in transforming the input data into a higher-dimensional space, enabling the network to learn complex patterns and make predictions. Next, information is subjected to batch normalization to normalize the values, and then it is passed through an activation function (for example, ReLU) to obtain the final output. Due to the utilization of floating-point weights, there is a significant demand for a large memory footprint (for example, 172 MB in [21], 128.5 MB in [22], 18.8 MB in [23,24,25]). Figure 3b illustrates the model training process in [4], where weights undergo 8-bit uniform quantization. 8-bit quantization reduces the precision of weights to only 8 bits, resulting in a limited range of possible values. This reduction in precision helps in reducing memory requirements and computational complexity, but it may introduce some loss of accuracy compared to using floating-point weights. In order to further minimize the memory size, we propose to perform low-bitwidth non-uniform quantization, as depicted in Figure 3c. The weights of a neural network are quantized to a reduced number of bits, typically much less than 8 bits, while using a non-uniform quantization scheme. This is particularly beneficial for deployment on resource-constrained devices or in scenarios where memory efficiency is critical.
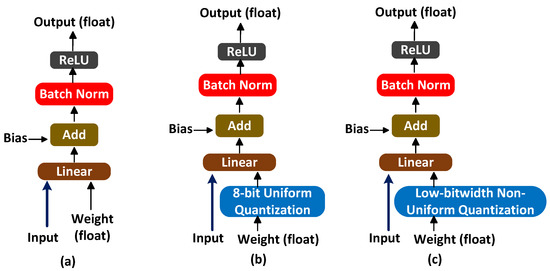
Figure 3.
(a) Traditional AI model training process (forward pass for one network layer) without weight quantization [21,22,23,24,25], (b) AI model training process (forward pass for one network layer) with 8-bit uniform quantization [4], and (c) AI model training process (forward pass for one network layer) with proposed low-bitwidth non-uniform quantization.
3.1. Low-Bitwidth Strong Non-Uniform Weight Quantization
Compared to uniform weight quantization where the step sizes between quantization levels are constant, the quantization step size of non-uniform quantization varies and depends on the value being quantized. Non-uniform quantization allows for a better representation of data, especially in cases where the weight distribution is skewed. Please note that the effectiveness of the power-of-N quantization scheme may vary depending on the specific AI model, dataset, and application domain. Experiments are necessary to determine the optimal values of N and evaluate the impact on model accuracy, memory footprint, and computational efficiency. The choice of N plays a crucial role in determining the non-linearity and uniformity of the quantization levels. A larger N implies that the levels are spaced farther apart, resulting in a more significant distinction between adjacent quantization values. In other words, the probability of weight values falling into each quantization level is not evenly distributed. The introduction of nonlinearity and non-uniformity through a larger N value allows the power-of-N quantization scheme to better adapt to the specific distribution of weights in AI models. It can capture the fine-grained variations in weight values while allocating quantization levels in a way that reflects the underlying statistical properties of the well-trained model. However, it is essential to strike a balance when selecting the value of N. If N is chosen to be excessively large, it may result in an overly fine-grained quantization scheme. Therefore, careful consideration and experimentation are necessary to determine the optimal value of N based on the specific model, dataset, and weight bitwidth.
Table 1 shows how the number of weight elements vary with quantization bitwidth. In this work, the relationship between the bitwidth b and the number of weight elements e for weight quantization can be expressed as:

Table 1.
Bitwidth versus the number of weight elements for weight quantization.
This equation shows that the number of weight elements e grows exponentially with increasing bitwidth b. For example, if b = 4, then the number of weight elements would be 15. If b = 5, then the number of weight elements would be 31. Therefore, reducing the bitwidth can significantly reduce the number of weight elements, which can lead to a smaller model size and faster inference on resource-constrained devices. However, reducing the bi-width too much (for example, b = 2 or 3) may result in a loss of accuracy or failed convergence. This is because very low-bit width neural networks have limited representation capacity. As a result, the quantized weights may struggle to capture the full richness of the original model with high precision.
As shown in Table 2, we adopt five different non-uniform quantization options: power-of-2 [29,30], power-of-3, power-of-4, power-of-5, and power-of-6. The idea of power-of-2 quantization is based on the fact that many processors or circuits can perform operations on binary numbers faster than on other number bases. By quantizing weights to power-of-2 values, the computations can be performed using simple shift and add operations, rather than using more complex multiplication and division operations. This leads to faster execution times and reduced memory requirements, which are critical for resource-constrained environments such as mobile and embedded systems. In [29], power-of-2 quantization has demonstrated great advantages on 8-bit AI models in terms of power and hardware resources. According to [31], in well-trained deep AI models, the weight values often follow a skewed distribution, with many values heavily clustering around zero and a few large values representing important weights. In other words, the majority of weights are concentrated around zero, while a small fraction of weights have much larger magnitudes. Being inspired by [29] and the skewed weight distribution histograms, we think stronger non-uniform weight quantization (for example, power-of-4) is considered better than the existing power-of-2 quantization for low bitwidth (such as 4–5 bits), because it allows for a more efficient use of the available bits by allocating more bits to important weight values around zero and fewer bits to less important ones. Stronger non-uniform quantization can take advantage of this heavily skewed weight distribution to achieve higher accuracy with fewer bits.

Table 2.
List of non-uniform weight values.
Within the weight range of [−1, 1] across all layers, symmetric weight quantization is applied where the range of weights is divided symmetrically around zero. This means that both the positive and negative values are represented with the same number of elements. For example, in a 3-bit symmetric weight quantization, the range of weights would be divided into 6 intervals, with 3 intervals for positive values and 3 intervals for negative values. This symmetrical approach is preferred because it enables the use of signed arithmetic and leads to efficient hardware implementation and faster inference time.
3.2. Input Image Size Adjustment
The complexity of an AI model varies with the input image size. Typically, as the input image size increases, the number of parameters in the model also increases to handle the increased information. This is because larger images contain more fine-grained details that require a more complex model to capture and process. On the other hand, reducing the input image size can simplify the model by reducing the number of parameters and computations required, but it may also lead to a loss of information and reduced accuracy. It is important to balance the input image size with the model complexity to achieve optimal performance.
Downsizing input images for neural networks has both positive and negative impacts on their performance and computational efficiency. On the positive side, downsizing input images reduces the computational burden on the network, which makes training and inference faster and requires less memory. This is especially important when working with resource-limited devices. On the negative side, downsizing input images can lead to a loss of information and details, which can negatively impact the accuracy of the network. This is especially true for tasks that require high precision, such as object detection or image segmentation, where small details can be crucial. Additionally, if the downsizing factor is too large, the network may lose the ability to recognize certain objects or features, which can severely limit its usefulness.
Overall, the impact of downsizing input images on neural network performance depends on the specific task and the extent of the downsizing. It is important to carefully consider the trade-offs between computational efficiency and accuracy when deciding on an appropriate image size for a given neural network. In this work, the original input image size is 256 × 256 × 3, we downsize it to be 128 × 128 × 3, and 64 × 64 × 3, respectively. Table 3 displays the number of trainable parameters and multiplier–adder operations for each model, respectively. It is apparent that decreasing the input image size significantly reduces the computational complexity of AI models. Table 4 lists their breakdown of memory usage results when 8-bit quantization is employed. As we reduce the size of input images, we observe a significant decrease in the required memory usage. In the next section, we will run experiments to the corresponding object classification results.

Table 3.
Number of trainable parameters, and number of multiplier–adder operation usage for different input image sizes.

Table 4.
Memory usage for different input image sizes when 8-bit quantization is employed.
4. Experimental Discussion
4.1. Dataset Preparation and Experimental Setup
A large-scale and high-quality dataset with balanced classes and good annotation has been created in our recent work [4]. The number of samples for the training set, validation set, and testing set are 14,000, 3000, and 3000, respectively. This dataset is used for this study to make a fair comparison with existing works in the literature. Table 5 provides instances of indoor litters that can be cleaned and obstacles that cannot be cleaned. In general, any objects larger than 2 cm will be avoided by robot vacuums. Figure 4 shows several images in the dataset for pet feces, soybean, sunflower seed shell and rock.

Table 5.
Examples of indoor cleanable litters and non-cleanable obstacles in our dataset [4].

Figure 4.
Several sample images for pet feces, soybean, sunflower seed shell, and rock.
Python and TensorFlow are utilized for programming and coding the architectures of AI models in this work. We specify quantized weight elements by using custom quantization tables. For example, within the weight range of [−1, 1], the custom weight table for 3-bit power-of-4 quantization includes . Low-bitwidth quantization-aware training is carried out. The network is trained using a combination of full-precision and low-bitwidth quantized weights. The full-precision weights are used to update the weights and biases of the network, while the low-bitwidth quantized operations are used to simulate the effects of quantization during inference. In order to reduce the effects of randomness and ensure the robustness of the AI model, the training process uses different seeds to generate average results. In other words, we train the same model architecture multiple times with different random initializations of the model parameters. To expedite the training and evaluation process, experiments are conducted on a GPU machine.
In our experiment setup, the SqueezeNet models are trained using the SGD optimizer with a momentum of 0.875. We employ a learning rate configured as an exponential decay function, gradually reducing the learning rate from an initial value. Specifically, we set the initial learning rate and the decay rate to 0.1 and 0.0001, respectively. The CosineAnnealingLR scheduler is used to adjust the learning rate during the training process based on a cosine annealing schedule. The training process is conducted over 100 epochs, which has been empirically determined to ensure satisfactory convergence. To accommodate computational resource limitations, we utilize a mini-batch size of 32 for SqueezeNet during training. In order to obtain statistically reliable results, we perform multiple runs to measure the inference performance of baseline architectures. Different seeds are used to initialize network weights with different random values. This prevents weights from becoming stuck in local minima during training.
4.2. Results of Low-Bitwidth Uniform Quantization
Figure 5 plots the results of using low-bitwidth uniform quantization for the input image size of 256 × 256 × 3. The classification accuracy of using floating-point weights is reported to be 93.54%. It is evident the SqueezeNet model achieves good convergence and attains an accuracy of approximately 93%, when the bitwidth is 4 or higher. If the bitwidth is 2, the SqueezeNet model fails to converge, which is because the precision loss in weight and gradient updates makes gradients become too small or too large during backpropagation. Therefore, big discrepancy between the gradients and actual weights makes it difficult for gradient descent algorithms to converge effectively. Figure 6 plots the required memory for each uniform weight quantization solution. We can see that the 4-bit uniform weight quantization needs 7.76 MB to realize an accuracy of 93.34%. Compared with the existing work [4], there is a slight accuracy drop of 0.05% with a memory reduction of 7.75 MB.
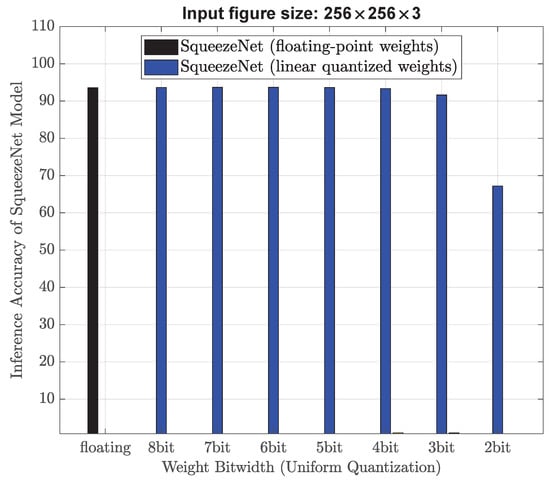
Figure 5.
Classification performance when uniform quantization is performed to SqueezeNet model for input figure size of 256 × 256 × 3.
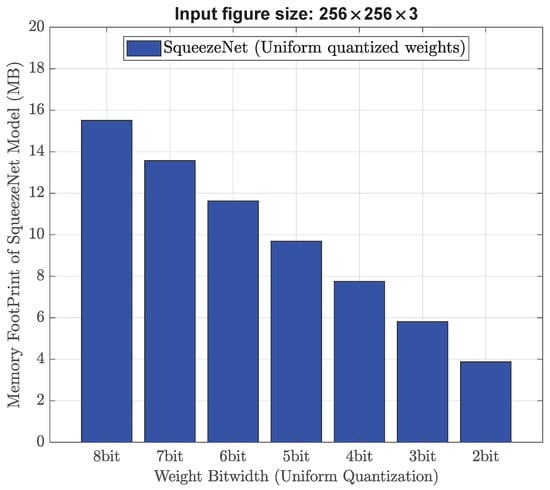
Figure 6.
Memory footprint when uniform quantization is performed to SqueezeNet model.
In addition, we evaluate the performance and memory usage of AI models when the input images were downsized from 256 × 256 × 3 to 128 × 128 × 3, and even further to 64 × 64 × 3. Figure 7 and Figure 8 plot the inference accuracy when using 128 × 128 × 3 and 64 × 64 × 3 as input image size, respectively. Table 6 illustrates that SqueezeNet models face convergence challenges when the bitwidth is set to 5. Therefore, these results indicate that a minimum bitwidth of 6 is required for uniform quantization, thereby limiting the further reduction in memory usage. With a memory budge of 1 MB, 6-bit uniform quantization is unable to attain a classification accuracy of at least 90%, which may be achievable by using strong non-uniform quantization.
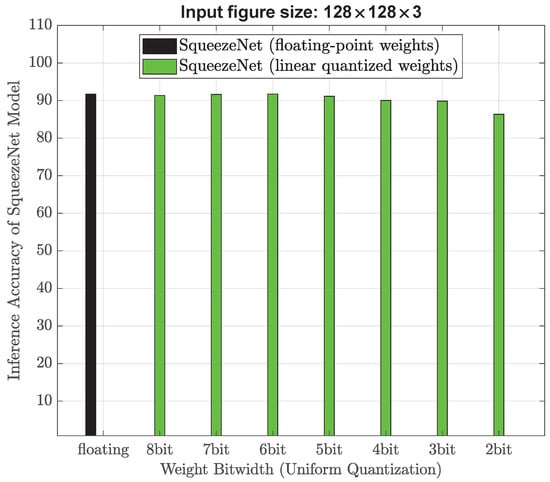
Figure 7.
Classification performance when uniform quantization is performed to SqueezeNet model for input figu size of 128 × 128 × 3.
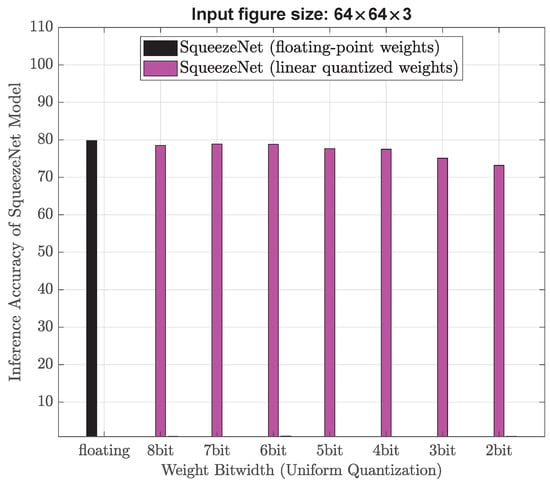
Figure 8.
Classification performance when uniform quantization is performed to SqueezeNet model for input figure size of 64 × 64 × 3.

Table 6.
Accuracy and memory usage for three different input sizes and uniform quantization.
4.3. Results of Low-Bitwidth Strong Non-Uniform Quantization
Figure 9 plots the inference accuracy results of using low-bitwidth strong non-uniform quantization for the input image size of 256 × 256 × 3. As the bitwidth decreases from 5, it becomes increasingly difficult for uniform or power-of-2 quantization to converge. When bitwidth is down to 2, the uniform or power-of-2 quantization scheme fails to converge. On the other hand, other forms of strong non-uniform quantization (for example, power-of-4, -5, or -6) are easy to converge and still exhibit promising classification accuracy. As shown in Figure 9, it is feasible to achieve an accuracy of 91.03% at a bitwidth of 2 when using a strong non-uniform quantization, specifically power-of-6. Please note that for power-of-6 quantization with a bitwidth of 2, there are only five weight elements available: −1, −0.17, 0, 0.17, and 1.
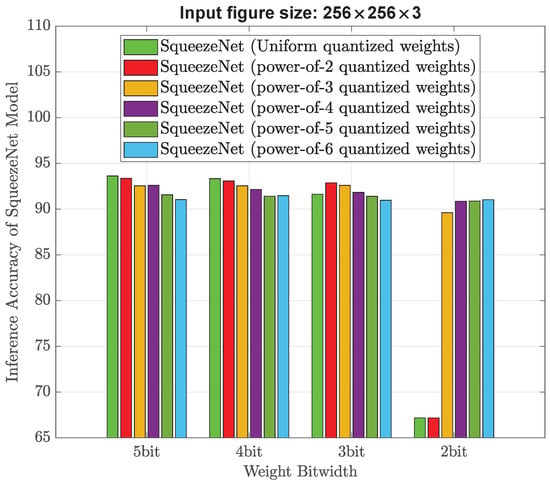
Figure 9.
Classification performance when non-uniform quantization is performed to SqueezeNet model and the input image size is 256 × 256 × 3.
Figure 10 and Figure 11 show the inference accuracy of trained SqueezeNet model using an input image size of 128 × 128 × 3 and 64 × 128 × 3, respectively. Regarding the training image size of 128 × 128 × 3, as depicted in Figure 10, the accuracy gradually drops with a decrease in the weight bitwidth. If the bitwidth is equal to or greater than 3, the power-of-2 quantization leads to an accuracy exceeding 90%. If the bitwidth is 2, the best quantization scheme is power-of-3, which results in an accuracy of 87.92%. These findings indicate that reducing the size of training images slightly diminishes the accuracy of the network. As illstrated in Figure 11, when the training image size is further reduced, even with strong non-uniform quantization schemes, the resultant inference accuracy falls below 80%. The observed phenomenon can likely be attributed to the loss of fine-grained details in downsized images, which subsequently hampers the network ability to capture and represent the learned features effectively.
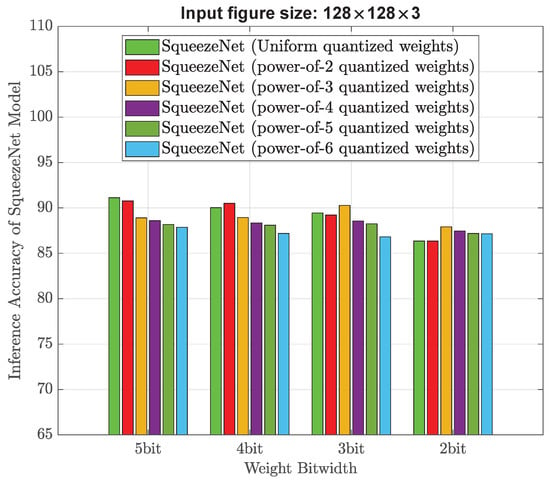
Figure 10.
Classification performance when non-uniform quantization is performed to SqueezeNet model and the input image size is 128 × 128 × 3.
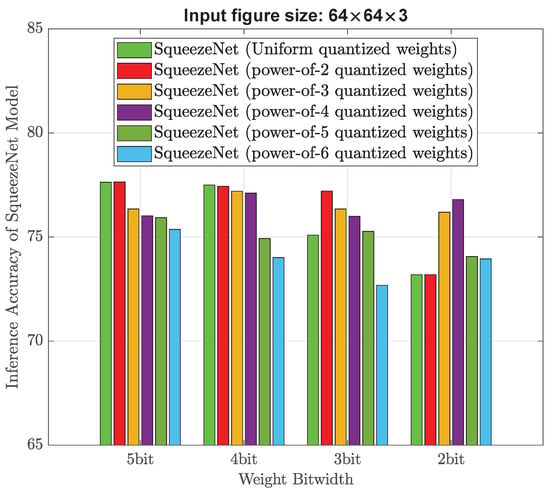
Figure 11.
Classification performance when non-uniform quantization is performed to SqueezeNet model and the input image size is 64 × 64 × 3.
Table 7 summarizes the best classification accuracy for each input image size, when low bitwidth non-uniform weight quantization is applied. When the input image size is 128 × 128 × 3, if 3-bit power-of-4 quantization is chosen, the resulting classification accuracy is 90.28%. However, if the input image is further downsized to 64 × 64 × 3, the resulting accuracy is significantly lower than 80%, even though the memory usage is much smaller. Therefore, we consider the combination of an image size of 128 × 128 × 3 and 3-bit power-of-3 quantization to be a better design choice.

Table 7.
Accuracy and memory usage for three different input sizes and non-uniform quantization.
The simulation results of validation accuracy are plotted in Figure 12 and Figure 13 for the input training image size of 128 × 128 × 3. Figure 12 corresponds to floating-point weights (no quantization), while Figure 13 represents 4-bit power-of-3 quantization. After the training is complete, the weight distributions for both cases are plotted in Figure 14 and Figure 15. We can see that these floating-point weights exhibit a distribution resembling a normal or Gaussian distribution centered around zero. On the other hand, these quantized weights are only confined to a specific set of values, namely , 0, 0.037, 0.111, 0.333, and 1.
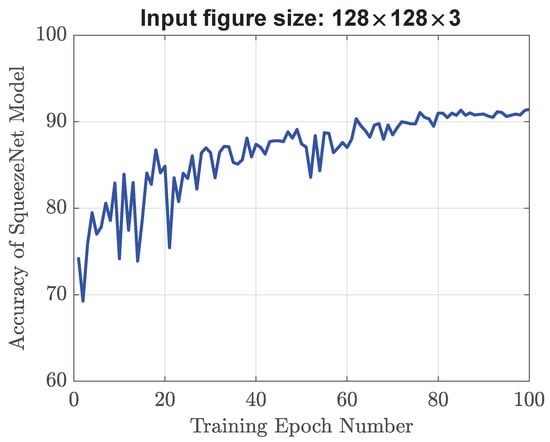
Figure 12.
Validation accuracy of the SqueezeNet model with the input image size of 128 × 128 × 3 and floating-point weights (no quantization).
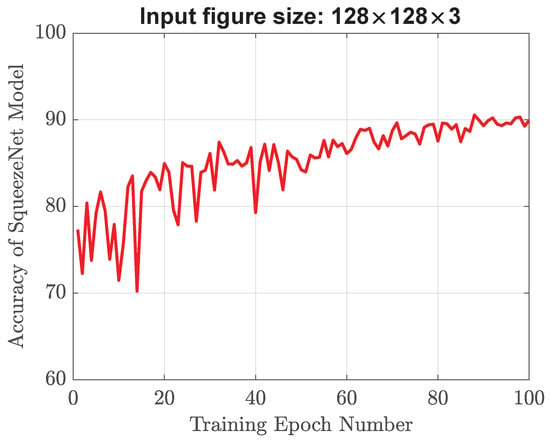
Figure 13.
Validation accuracy of the SqueezeNet model with the input image size of 128 × 128 × 3 and 4-bit power-of-3 quantization. The weight elements include: , 0, 0.037, 0.111, 0.333, and 1.
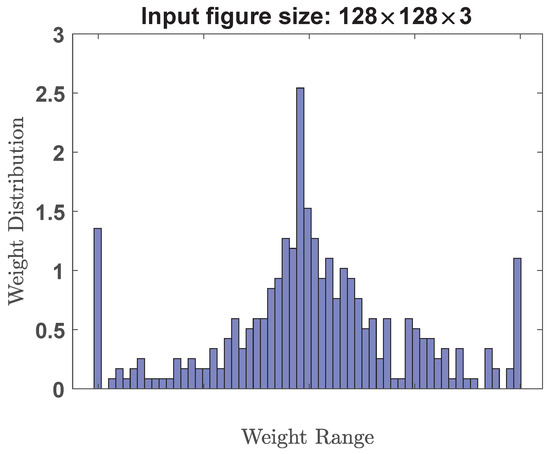
Figure 14.
Weight distribution plots of SqueezeNet with the training image size of 128 × 128 × 3 and floating-point weights (no quantization).
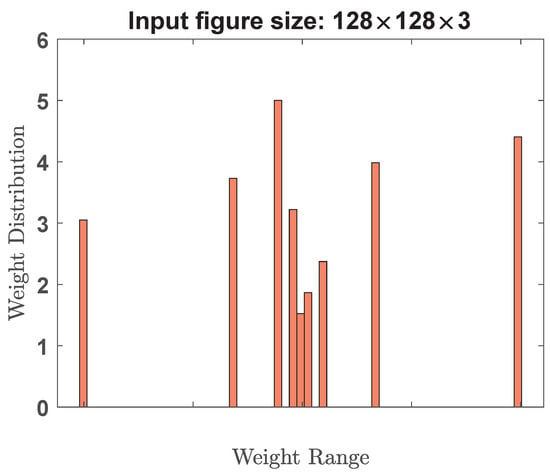
Figure 15.
Weight distribution plots of SqueezeNet with the training image size of 128 × 128 × 3 and 4-bit power-of-3 quantization. The weight elements include: , 0, 0.037, 0.111, 0.333, and 1.
4.4. Comprehensive Results Comparison
The accuracy of this work and other state-of-the-art methods in the literature is plotted against memory usage in Figure 16, where the results of both the uniform and strong non-uniform quantization are plotted for comparative analysis. Compared to the recent work [4], if 4-bit uniform quantization is applied across all layers, it leads to memory reduction by a factor of 2, albeit with a 0.05% decrease in accuracy. Furthermore, 4-bit non-uniform (power-of-2) quantization achieves a memory reduction by a factor of 2, albeit with a 0.22% decrease in accuracy. When selecting an appropriate training image size and employing lower bitwidth quantization, non-uniform quantization outperforms uniform quantization. Figure 16 shows the experimental results of using 3-, 4-, and 5-bit quantization with the training image size of 128 × 128 × 3. The accuracy of 5-bit uniform or non-uniform quantization approaches is nearly 91%. However, as we decrease the bitwidth to 4 or 3, non-uniform quantization surpasses uniform quantization in terms of performance. From example, compared to the recent work [4], the memory footprint is reduced by a factor of 20, 3-bit uniform and non-uniform quantization leads to 3.95% and 3.11% reduction in accuracy, respectively. In this scenario, the memory requirement of is approximately 0.78 MB, and the resultant accuracy of non-uniform quantization remains above 90%. This work enables constraints-aware software and hardware co-design for AI systems.
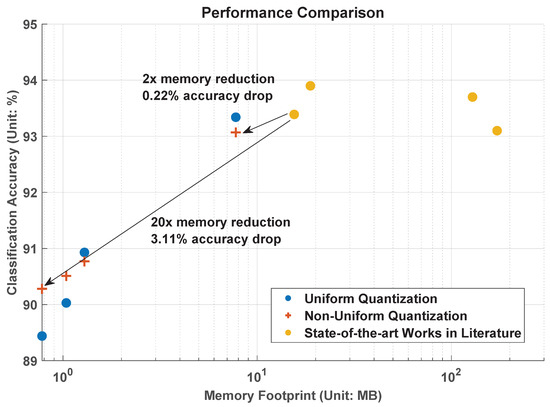
Figure 16.
Performance comparison of test classification accuracy vs. memory footprint between this work and existing state-of-the-art works in the literature.
5. Conclusions and Future Works
One of the key challenges in robot vacuum cleaners is to develop lightweight AI models that enable the robot vacuum to effectively navigate and clean environments while using limited computational resources and memory. Lightweight AI models are easier to deploy and update in resource-limited devices, as they require less storage space and bandwidth. In this work, we propose low-bitwidth strong non-uniform quantization and use input image downsizing techniques to address the above challenge. The proposed strong non-uniform weight quantization provides the flexibility to allocate bits based on the weight distribution. It enables data-driven bit allocation schemes that adaptively assign more bits to important weights and fewer bits to less important ones. This adaptability helps to maximize the classification accuracy while maintaining a low bitwidth. Experimental results show that the proposed AI model can achieve comparable classification accuracy around 93%, while also reducing the memory footprint by a factor of 2. By adjusting the training image size and using low bitwidth non-uniform quantization, it is feasible to build an AI model that fits with a memory budget of 0.78 MB (that is a 20-fold memory reduction) and retains classification accuracy above 90%. Therefore, our proposed AI models may fit better into the available memory on robot vacuum cleaners, without worrying about performance degradation or even crashes.
One area of future work is to investigate the impact of different quantization schemes on AI model performance. While strong non-uniform quantization has shown promising results, there may be other quantization schemes that could achieve even better performance or memory reduction. There may exist an optimal quantization technique for each individual network layer of AI models. It is interesting to explore how non-uniform quantization could be combined with other techniques, such as network pruning or knowledge distillation, to create even more efficient and accurate AI models.
Right now, we provide simulation results using PyTorch Platform on GPU machines for fast evaluation and assessment. The PyTorch Platform reports the memory usage information and object classification accuracy. This is a typical way for machine learning researchers to evaluate new quantization methods. Our proposed model can be applied to the real world (i.e., integration the trained AI model within a robotic vacuum cleaner) with the technical support of robotic vacuum manufacturers. Since it is a time-consuming process to negotiate and interact with interested robotic vacuum manufacturers, we have not implemented it in robotic vacuum cleaners now. We will continue to make efforts to apply our developed AI model to the real world.
Author Contributions
Conceptualization, methodology, formal analysis, investigation, writing, visualization, Q.H.; Software and validation, Z.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Singh, R.; Gill, S. Edge AI: A survey. Internet Things Cyber-Phys. Syst. 2023, 3, 71–92. [Google Scholar]
- Jayaram, R.; Dandge, R. Optimizing Cleaning Efficiency of Robotic Vacuum Cleaner. TATA ELXSI Report. Available online: https://www.tataelxsi.com/ (accessed on 13 February 2022).
- Huang, Q.; Hsieh, C.; Hsieh, J.; Liu, C. Memory-Efficient AI Algorithm for Infant Sleeping Death Syndrome Detection in Smart Buildings. AI 2021, 2, 705–719. [Google Scholar] [CrossRef]
- Huang, Q. Weight-Quantized SqueezeNet for Resource-Constrained Robot Vacuums for Indoor Obstacle Classification. AI 2022, 3, 180–193. [Google Scholar] [CrossRef]
- Jacob, B.; Kligys, S.; Chen, B.; Zhu, M.; Tang, M.; Howard, A.; Kalenichenko, D. Quantization and Training of Neural Networks for Efficient Integer-arithmetic-only Inference. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2704–2713. [Google Scholar]
- Esser, S.K.; McKinstry, J.L.; Bablani, D.; Appuswamy, R.; Modha, D.S. Learned Step Size Quantization. arXiv 2019, arXiv:1902.08153. [Google Scholar]
- Nagel, M.; Fournarakis, M.; Amjad, R.A.; Bondarenko, Y.; Van Baalen, M.; Blankevoort, T. A White Paper on Neural Network Quantization. arXiv 2021, arXiv:2106.08295. [Google Scholar]
- Tang, Z.; Luo, L.; Xie, B.; Zhu, Y.; Zhao, R.; Bi, L.; Lu, C. Automatic Sparse Connectivity Learning for Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2022. [Google Scholar] [CrossRef]
- Kaplan, C.; Bulbul, A. Goal Driven Network Pruning for Object Recognition. Pattern Recognit. 2021, 110, 107468. [Google Scholar] [CrossRef]
- Han, S.; Mao, H.; Dally, W.J. Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- Frankle, J.; Carbin, M. The lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. arXiv 2018, arXiv:1803.03635. [Google Scholar]
- Zhu, M.; Gupta, S. To Prune, or not to Prune: Exploring the Efficacy of Pruning for Model Compression. arXiv 2017, arXiv:1710.01878. [Google Scholar]
- Zheng, J.; Lu, C.; Hao, C.; Chen, D.; Guo, D. Improving the Generalization Ability of Deep Neural Networks for Cross-Domain Visual Recognition. IEEE Trans. Cogn. Dev. Syst. 2020, 13, 607–620. [Google Scholar] [CrossRef]
- Bu, X.; Peng, J.; Yan, J.; Tan, T.; Zhang, Z. Gaia: A Transfer Learning System of Object Detection that Fits Your Needs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 274–283. [Google Scholar]
- Rukundo, O. Effects of Image Size on Deep Learning. Electronics 2023, 12, 985. [Google Scholar] [CrossRef]
- Talebi, H.; Milanfar, P. Learning to Resize Images for Computer Vision Tasks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 20–25 June 2021; pp. 497–506. [Google Scholar]
- Iandola, F.; Han, S.; Moskewicz, M.; Ashraf, K.; Dally, W.; Keutzer, K. SqueezeNet: AlexNet-Level Accuracy with 50× Fewer Parameters and <0.5 MB Model Size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Nagel, M.; Baalen, M.V.; Blankevoort, T.; Welling, M. Data-free Quantization Through Weight Equalization and Bias Correction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1325–1334. [Google Scholar]
- Krishnamoorthi, R. Quantizing Deep Convolutional Networks for Efficient Inference: A Whitepaper. arXiv 2018, arXiv:1806.08342. [Google Scholar]
- Li, Y.; Dong, X.; Wang, W. Additive Powers-of-two Quantization: An Efficient Non-uniform Discretization for Neural Networks. arXiv 2019, arXiv:1909.13144. [Google Scholar]
- Bai, J.; Lian, S.; Liu, Z.; Wang, K.; Liu, D. Deep Learning Based Robot for Automatically Picking up Garbage on the Grass. IEEE Trans. Consum. Electron. 2018, 64, 382–389. [Google Scholar] [CrossRef]
- Yin, J.; Apuroop, K.G.S.; Tamilselvam, Y.K.; Mohan, R.E.; Ramalingam, B.; Le, A.V. Table Cleaning Task by Human Support Robot Using Deep Learning Technique. Sensors 2020, 20, 1698. [Google Scholar] [CrossRef]
- Teng, T.; Veerajagadheswar, P.; Ramalingam, B.; Yin, J.; Mohan, R.; Gomez, F. Vision Based Wall Following Framework: A Case Study with HSR Robot for Cleaning Application. Sensors 2020, 20, 3298. [Google Scholar]
- Ramalingam, B.; Lakshmanan, A.K.; Ilyas, M.; Le, A.V.; Elara, M.R. Cascaded Machine-Learning Technique for Debris Classification in Floor-Cleaning Robot Application. Appl. Sci. 2018, 8, 2649. [Google Scholar] [CrossRef]
- Bao, L.; Lv, C. Ecovacs Robotics: The AI Robotic Vacuum Cleaner Powered by TensorFlow. 2020. Available online: https://blog.tensorflow.org/2020/01/ecovacs-robotics-ai-robotic-vacuum.html (accessed on 13 February 2022).
- Howard, A.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L. MobileNetV2: Inverted Residuals and Linear bottlenecks. In Proceedings of the IEEE Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- STM32F7 Series. Available online: www.st.com/en/microcontrollers-microprocessors/stm32f7-series.html (accessed on 1 July 2023).
- Przewlocka-Rus, D.; Sarwar, S.S.; Sumbul, H.E.; Li, Y.; Salvo, B.D. Power-of-two Quantization for Low Bitwidth and Hardware Compliant Neural Networks. arXiv 2022, arXiv:2203.05025. [Google Scholar]
- Kulkarni, U.; Hosamani, A.S.; Masur, A.S.; Keutzer, K. A Survey on Quantization Methods for Optimization of Deep Neural Networks. In Proceedings of the 2022 International Conference on Automation, Computing and Renewable Systems (ICACRS), Pudukkottai, India, 13–15 December 2022; pp. 827–834. [Google Scholar]
- Lee, E.; Hwang, Y. Layer-wise Network Compression Using Gaussian Mixture Model. Electronics 2021, 10, 72. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).