Abstract
Perhaps one of the best-known machine learning models is the artificial neural network, where a number of parameters must be adjusted to learn a wide range of practical problems from areas such as physics, chemistry, medicine, etc. Such problems can be reduced to pattern recognition problems and then modeled from artificial neural networks, whether these problems are classification problems or regression problems. To achieve the goal of neural networks, they must be trained by appropriately adjusting their parameters using some global optimization methods. In this work, the application of a recent global minimization technique is suggested for the adjustment of neural network parameters. In this technique, an approximation of the objective function to be minimized is created using artificial neural networks and then sampling is performed from the approximation function and not the original one. Therefore, in the present work, learning of the parameters of artificial neural networks is performed using other neural networks. The new training method was tested on a series of well-known problems, a comparative study was conducted against other neural network parameter tuning techniques, and the results were more than promising. From what was seen after performing the experiments and comparing the proposed technique with others that have been used for classification datasets as well as regression datasets, there was a significant difference in the performance of the proposed technique, starting with 30% for classification datasets and reaching 50% for regression problems. However, the proposed technique, because it presupposes the use of global optimization techniques involving artificial neural networks, may require significantly higher execution time than other techniques.
1. Introduction
Artificial neural networks (ANNs) are parametric models [1,2,3] in machine learning, and they are widely used in pattern recognition problems. A series of practical problems from the fields of physics [4,5,6], chemistry [7,8,9], economics [10,11,12], medicine [13,14], etc., can be transformed to pattern recognition problems and then solved using artificial neural networks. Furthermore, neural networks have been used with success to solve differential equations [15,16,17], solar radiation prediction [18,19], spam detection [20,21,22], etc. Moreover, variations of artificial neural networks have been employed to solve agricultural problems [23,24], facial expression recognition [25], prediction of the speed of wind [26], the gas consumption problem [27], intrusion detection [28], hydrological systems [29], etc. Furthermore, Swales and Yoon discussed the application of artificial neural networks to investment analysis in their work [30].
A neural network can be denoted as a function where the vector stands for the input vector and the vector is the set of the parameters of the neural network that should be estimated. The input vector is usually called pattern in the relevant literature and the vector is usually called the weight vector. Artificial neural network training methods adjust the vector of weights in order to minimize the following quantity:
In the previous equation, what will be called training error, the set is the input training dataset for the neural network with M patterns. The value is the expected output for the pattern . Equation (1) can be minimized with respect to the weight vector using any local or global optimization method such as the back-propagation method [31,32], the hill climbing method [33], the RPROP method [34,35,36], quasi Newton methods [37,38], simulated annealing [39,40], genetic algorithms [41,42], particle swarm optimization [43,44], differential optimization methods [45,46], evolutionary computation [47], the whale optimization algorithm [48], etc. Furthermore, Cui et al. suggested the usage of a new stochastic optimization algorithm that simulates the plant growing process for neural network training. Furthermore, recently, the bird mating optimizer [49] was suggested as a training method for artificial neural networks [50], and hybrid methods have been developed by various researchers to optimize the weight vector, such as the work of Yaghini et al. [51] that combined particle swarm optimization with a back-propagation algorithm to minimize the error function. Moreover, Chen et al. [52] used a hybrid technique that combines particle swarm optimization and cuckoo search [53] to optimize the weight vector of neural networks.
In addition, many researchers have addressed the issue of the initial values for the weights of neural networks, such as the incorporation of decision trees [54], an initialization method using Cauchy’s inequality [55], incorporation of discriminant learning [56], methods based on genetic algorithms [57], etc. A paper discussing all the aspects of weight initialization strategies was written by Narkhede et al. [58].
Moreover, various groups of researchers are dealing with the issue of constructing the structure of artificial neural networks, such as the incorporation of genetic algorithms [41], the usage of the grammatical evolution method [59] for the construction of neural networks [60], a construction and pruning approach to optimize the structure of ANNs [61], usage of cellular automata [62], etc. Furthermore, because the training of artificial neural networks with optimization methods requires a significantly longer computing time, parallel techniques have been developed that take advantage of modern parallel computing units [63,64,65].
Another area of research in the field of artificial neural networks that attracts a multitude of researchers is the problem of overfitting that occurs in many cases. In this problem, although the artificial neural network has achieved a satisfactory level of training, this is not reflected in unknown patterns that were not present during training. This set of patterns will be called the test set in the following. Commonly used methods that tackle the overfitting problem are weight sharing [66,67], methods that reduce the number of parameters (weight pruning) [68,69,70], the method of dropout [71,72], weight decaying methods [73,74], the Sarprop method [75], positive correlation methods [76], etc.
In this paper, the use of a recent global minimization technique [77] called NeuralMinimizer, is proposed to find the optimal set for the weights of artificial neural networks. This innovative global minimization technique constructs an approximation of the objective function to be minimized using a limited number of its samples. These limited samples form the training set of an artificial neural network that can be trained with any optimization method. Subsequently, the sampling for the continuation of the global optimization method is not performed by the objective function but by the previously trained artificial neural network. The samples obtained by artificial neural networks before being fed into the global minimization method are classified and those with the smallest functional value will finally be input into the global minimization method. From the experimental results, it was shown that this global minimization method requires a limited number of samples from the objective function to find the global minimum and is also more efficient than other techniques for discovery of the global minimum. Therefore, this paper proposes using artificial neural networks to train other artificial neural networks. This new procedure will be tested on a series of known problems in order to evaluate its effectiveness.
2. The Proposed Method
In this section, some basic principles for artificial neural networks are presented and then a new training method that incorporates a modified version of the NeuralMinimizer global optimization technique is outlined.
2.1. Preliminaries
Let us consider an artificial neural network with only one hidden layer in which the sigmoid function is used as an activation function. The output value for every node in this layer is calculated as:
where the value is the weight vector, and denotes the bias for the node The sigmoid function is defined as:
and it is graphically illustrated in Figure 1.
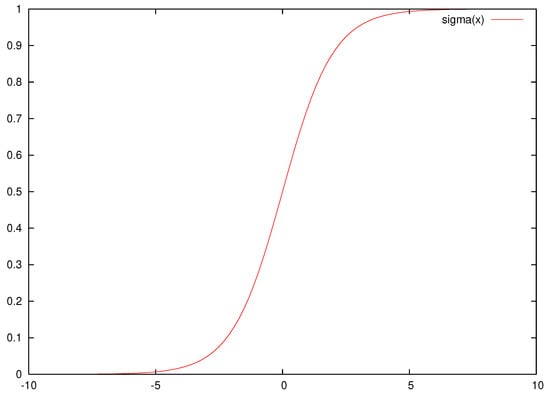
Figure 1.
The sigmoid function .
When the neural network has H processing nodes, the output can be formulated as:
where stands for the output weight for node i. Hence, by using one vector for all the parameters (weights and biases) the neural network can be written in the following form:
where d is the dimension of vector . From Equation (5) we can conclude that number of elements in the weight vector is:
2.2. The Modified NeuralMinimizer Method
In its original version, the NeuralMinimizer method employed RBF neural networks [78] to build a model of the objective function. Even though radial basis function (RBF) networks have been used with success in a variety of problems [79,80,81,82], it is not possible to apply them to the training of the parameters of an artificial neural network due to the large dimension of the problem, as shown in Equation (6). Hence, in the current work, the RBF network has been replaced by an artificial neural network that implements Equation (5). The training of the artificial neural network was performed using a local minimization technique that is not particularly demanding in calculations and storage space, such as limited memory BFGS (L-BFGS) [83]. Obviously, any other technique that is not extremely memory intensive could be used in its place. Such a technique could be the Adam method [84], the SGD method [85,86], or even a simple global minimization method such as a genetic algorithm with a limited number of chromosomes. The L-BFGS method is a variation of the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method [87] using a limited amount of computer memory. This local minimization method has found wide application in difficult and memory-intensive optimization problems such as image reconstruction [88], inverse eigenvalue problems [89], seismic waveform tomography [90], etc. Because of the application of this technique to large-dimensional problems, a number of modifications have been proposed that make use of modern parallel computing systems [91,92,93]. A numerical study on the limited memory BFGS methods is provided in the work of Morales [94]. In the original publication on the NeuralMinimizer optimization method, an RBF neural network was used to generate the approximation function of the objective function. However, this would not always be possible in cases where the objective function to be minimized is the error of an artificial neural network, because an artificial neural network usually has a large number of parameters, and this would require an extremely large storage space for training the global minimization method’s RBF neural network. Of course, in some cases with small artificial neural networks, an RBF neural network could be used as the training model in the global optimization method NeuralMinimizer. However, when an artificial neural network is used to approach large and complex problems (something extremely common) then a relatively under powered RBF neural network should be used. In those cases, the RBF network will not be able to be an efficient approximation of the artificial neural network, which is, of course, the original aim of the NeuralMinimizer method.
In the following, the main steps of the modified NeuralMinimizer method for the training of neural networks are listed. In these steps, the neural network used by the NeuralMinimizer method will be called .
- Initialization step.
- (a)
- SetH the number of weights of the neural network. In the current method the same number of weights was used for both and artificial neural networks.
- (b)
- Set as the samples that will be initially drawn from . At this stage, the training error for the artificial neural network will be used as an objective function to minimize
- (c)
- Set as the number of points that will be utilized as local minimization method starters in every iteration.
- (d)
- Set as the number of samples that will be drawn from the network in each iteration.
- (e)
- Set as the maximum number of iterations allowed.
- (f)
- Set Iter = 0, the current iteration number.
- (g)
- Set as the global minimum discovered by the method. Initially
- Creation Step.
- (a)
- Set , the used training set for the neural network.
- (b)
- For do
- Draw a new sample from .
- Calculate using Equation 1
- (c)
- EndFor
- (d)
- Train the neural network on set T using the L-BFGS method.
- Sampling Step
- (a)
- Set
- (b)
- For do
- Produce randomly a sample from neural network
- Set
- (c)
- EndFor
- (d)
- Sort in ascending with respect to the values
- Optimization Step.
- (a)
- For do
- Get the next item from .
- Train the neural network on the training set of the objective problem using the L-BFGS method and obtain the corresponding training error .
- Update
- Train the network again on the modified set T. In this step, the original training set used by is updated to include the new discovered local minimum. This operation is used in order to construct a more accurate approximation of the real objective function.
- If then
- If the termination rule proposed in [95], then apply the produced network on the test set of the objective problem, report the test error and terminate.
- (b)
- EndFor
- Set iter=iter+1
- Goto to Sampling step.
A flowchart of the proposed method is graphically outlined in Figure 2.
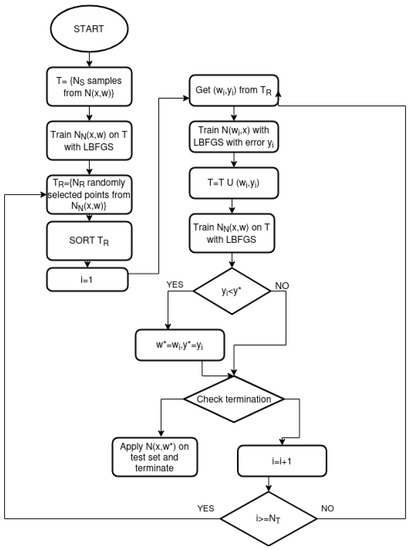
Figure 2.
The flowchart of the proposed method.
3. Experiments
The effectiveness of the proposed artificial neural network training technique was evaluated using a series of data sets from the relevant literature. These datasets have been studied by various researchers in the relevant literature and cover a wide range of research areas from physics to economics. These datasets are freely available from the following websites:
- The UCI repository, https://archive.ics.uci.edu/ (accessed on 12 July 2023) [96]
- The Keel repository, https://sci2s.ugr.es/keel/datasets.php (accessed on 17 June 2023) [97].
- The Statlib URL ftp://lib.stat.cmu.edu/datasets/index.html (accessed on 17 June 2023). This repository is used mainly for the regression datasets.
3.1. Experimental Datasets
The following classification datasets from the relevant literature were used in the experiments:
- Appendicitis, a dataset used for medical purposes; it was found in [98,99].
- Australian dataset [100], an economic dataset, related to bank transactions.
- Balance dataset [101], which is related to psychological experiments.
- Cleveland dataset, a medical dataset found in the following research papers [102,103].
- Bands dataset, related to printing problems [104].
- Dermatology dataset [105], a dataset related to dermatology problems.
- Hayes-Roth dataset [106].
- Heart dataset [107], a medical dataset used to detect heart diseases.
- HouseVotes dataset [108], related to the Congressional voting records of USA.
- Ionosphere dataset, related to measurements from the ionosphere an thoroughly studied in a series of research papers [109,110].
- Liverdisorder dataset [111,112], a medical dataset.
- Lymography dataset [113].
- Mammographic dataset [114], a medical dataset related to breast cancer diagnosis.
- Page Blocks dataset [115].
- Parkinsons dataset [116,117], a medical dataset applied to the Parkinson’s decease.
- Pima dataset [118], a medical dataset.
- Popfailures dataset [119], a dataset related to meteorological data.
- Regions2 dataset, a medical dataset for liver biopsy images [120].
- Saheart dataset [121], a medical dataset related to heart diseases.
- Segment dataset [122], a dataset related to image segmentation.
- Wdbc dataset [123], a dataset related to breast tumors.
- Wine dataset, a dataset related to chemical analysis of wines [124,125].
- Eeg datasets [126,127], an EEG dataset, and the following cases were used in the experiments:
- (a)
- Z_F_S,
- (b)
- ZO_NF_S
- (c)
- ZONF_S.
- Zoo dataset [128], suggested for the detection of the proper classes of animals.
A table showing the number of classes for every classification dataset is shown in Table 1.

Table 1.
Description for every classification dataset.
The following regression datasets were used:
- Abalone dataset [129], proposed to predict the age of abalones.
- Airfoil dataset, a dataset provided by NASA [130], created from a series of aerodynamic and acoustic tests.
- Baseball dataset, a dataset using baseball games.
- BK dataset [131], used to predict the points scored in a basketball game.
- BL dataset, used in machine problems.
- Concrete dataset [132], a dataset proposed to calculate the compressive strength of concrete.
- Dee dataset, used to detect the electricity energy prices.
- Diabetes dataset, a medical dataset.
- Housing dataset [133].
- FA dataset, used to fit body fat to other measurements.
- MB dataset [131].
- Mortgage dataset. The goal is to predict the 30-year conventional mortgage rate.
- PY dataset, (pyrimidines problem) [134].
- Quake dataset, used to approximate the strength of a earthquake given its the depth of its focal point, its latitude and its longitude.
- Treasure dataset, which contains economic data information from the USA, where the goal is to predict the 1-month CD Rate.
- Wankara dataset, a weather dataset.
3.2. Experimental Setup
The proposed method was tested on the regression and classification problems mentioned previously, and it was compared against the results of several other well-known optimization methods in the relevant literature. For greater reliability of the experimental results, the 10-fold validation technique was employed for every classification or regression dataset. Every experiment was executed 30 times, with different initialization for the random generator each time. Furthermore, the srand48() random generator of the C-programming language was utilized. The used code was implemented in ANSI C++ using the freely available OPTIMUS optimization library available from https://github.com/itsoulos/OPTIMUS/(accessed on 18 July 2023). For the case of the classification datasets, the average classification error was measured for every method. For regression datasets, the average mean squared error was measured in the test set. The number of hidden nodes for the neural networks was set to for every method. All the experiments were performed using an AMD Ryzen 5950X with 128 GB of RAM. The running operating system was Debian Linux. The methods used in the experimental results are the following:
- A genetic algorithm with 200 chromosomes was used to train a neural network with H hidden nodes. This method was denoted as GENETIC in the tables holding the experimental results.
- A radial basis function (RBF) network [78] with H hidden nodes.
- The Adam optimization method [84]. Here, the method was used to minimize the train error of a neural network with H hidden nodes.
- The resilient back-propagation (RPROP) optimization method [34,35,36] was also employed to train a neural network with H hidden nodes.
- The NEAT method (NeuroEvolution of Augmenting Topologies ) [135].
The values used for every parameter are listed in Table 2 and they are similar to the values used in the original publication of the NeuralMinimizer method.

Table 2.
Experimental settings.
3.3. Experimental Results
The experimental results for the classification datasets are shown in Table 3 and those of the regression datasets are shown in Table 4. The column PROPOSED represents the usage of the proposed method to train a neural network with H hidden nodes. Furthermore, the Figure 3 shows a scatter plot and the Wilcoxon signed-rank test for the classification datasets. In the same direction, Figure 4 shows the scatter plot for the regression datasets.

Table 3.
Experimental results for the classification datasets. The numbers in cells denote average classification error of 30 independent runs.

Table 4.
Average regression error for the regression datasets.
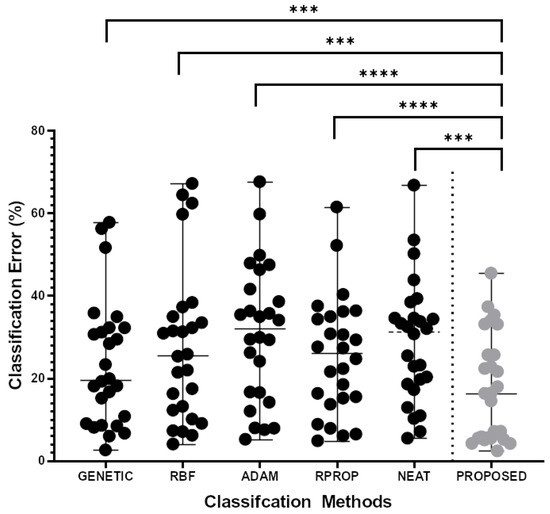
Figure 3.
Scatter plot representation and the two-sample paired (Wilcoxon) signed-rank test results of the comparison for each of the five (5) clas-sification methods (GENETIC, RBF, ADAM, RPROP, NEAT) with the PROPOSED method regarding the classification error in twenty-six (26) different public available classification datasets. The stars only intend to flag significance levels for three of the most used groups. A p-value of less than 0.001 is flagged with three stars (***). A p-value of less than 0.0001 is flagged with four stars (****).
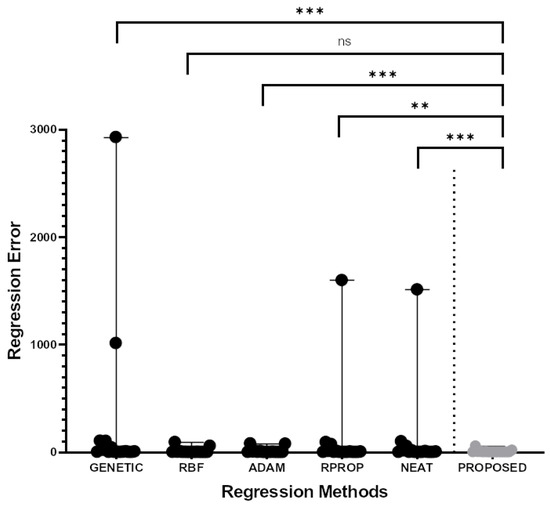
Figure 4.
Scatter plot representation and the two-sample paired (Wilcoxon) signed-rank test of the comparison for each of the five (5) regression methods (GENETIC, RBF, ADAM, RPROP, NEAT) with the PROPOSED method regarding the regression error in sixteen (16) different publicly available classification datasets. The stars only intend to flag significance levels for three of the most used groups. A p-value of less than 0.01 is flagged with two stars (**). A p-value of less than 0.001 is flagged with three stars (***). The notation “ns” denotes “not significant”.
The experimental results and their graphical representation demonstrate the superiority of the proposed technique over the others in terms of the average error, as measured in the test set. For example, in the case of datasets used for classification, the proposed method outperforms the remaining techniques in 19 out of 26 datasets (73% percent). Furthermore, in several cases, the percentage reduction in error exceeds 50%. For the classification problems, the immediate most effective training method after the proposed one is the genetic algorithm and, on average, the proposed technique achieves lower classification error than the genetic algorithm error by 24%. Moreover, in regression problems, the next most effective method after the proposed one is the RBF neural network with small differences from the ADAM optimizer. However, in the case of regression problems, the improvement in average error using the proposed technique exceeds 49%. Of course, the proposed technique is quite time-consuming, because it requires the continuous training of an artificial neural network.
4. Conclusions
In this work, the application of a recent global minimization method for the training of artificial neural networks was proposed. The application of this method was used in artificial neural networks both for classification problems and for regression problems. This new global minimization method constructs an approximation of the objective function using neural networks. This construction is performed with a limited number of samples from the objective function. However, each time a local minimization takes place, this approximation is readjusted. Subsequently, the sampling for the minimization is performed from the approximate function and not from the objective one, even taking samples from the approximation with the smallest function value in order to speed up the discovery of the global minimum. In this particular case, the artificial neural network of the global minimization method is used to train the artificial neural network. However, due to the large time and storage requirements of artificial neural networks, the RBF network of the original NeuralMinimizer method was replaced with an artificial neural network that was trained using the local minimization method L-BFGS. The new artificial neural network training technique is tested on a wide collection of classification and regression problems from the relevant literature and is shown to significantly improve the learning error over other established artificial neural network training techniques. This improvement is 25% on average for the case of classification problems and rises significantly to 50% for regression problems. The proposed method outperforms the other methods and models in the majority of cases. For example, in the classification datasets, the proposed method outperforms the genetic algorithm in 22 datasets, the RBF model in 21 datasets, the ADAM optimizer in 23 cases, the RPROP optimizer in 22 cases and finally, the NEAT method in 25 datasets.
Nevertheless, the proposed procedure can be extremely slow, especially as the size of the artificial neural network increases. The size of the artificial neural network directly depends on the dimension of the input dataset. Future improvements to the methodology may include the use of parallel programming techniques, such as parallel implementations of the L-BFGS optimization method, in order to accelerate the training of artificial neural networks by taking advantage of modern computing structures. Furthermore, in the present phase, as a minimization method in step 4 of the proposed training method, a local minimization method is used. Future extensions could explore the possibility of also using global minimization techniques in this step, although care should be taken to make use of parallel computing techniques to avoid long execution times.
Author Contributions
I.G.T. and A.T. conceived of the idea and the methodology and I.G.T. implemented the corresponding software. I.G.T. conducted the experiments, employing objective functions as test cases, and provided the comparative experiments. A.T. performed the necessary statistical tests. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research has been co-financed by the European Regional Development Fund of the European Union and Greek national funds through the Operational Program Competitiveness, Entrepreneurship and Innovation, under the call Research–Create–Innovate, project name “Create a system of recommendations and augmented reality applications in a hotel” (project code: T1EDK-03745).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Baldi, P.; Cranmer, K.; Faucett, T.; Sadowski, P.; Whiteson, D. Parameterized neural networks for high-energy physics. Eur. Phys. J. C 2016, 76, 235. [Google Scholar] [CrossRef]
- Valdas, J.J.; Bonham-Carter, G. Time dependent neural network models for detecting changes of state in complex processes: Applications in earth sciences and astronomy. Neural Netw. 2006, 19, 196–207. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef]
- Shen, L.; Wu, J.; Yang, W. Multiscale Quantum Mechanics/Molecular Mechanics Simulations with Neural Networks. J. Chem. Theory Comput. 2016, 12, 4934–4946. [Google Scholar] [CrossRef]
- Manzhos, S.; Dawes, R.; Carrington, T. Neural network-based approaches for building high dimensional and quantum dynamics-friendly potential energy surfaces. Int. J. Quantum Chem. 2015, 115, 1012–1020. [Google Scholar] [CrossRef]
- Wei, J.N.; Duvenaud, D.; Aspuru-Guzik, A. Neural Networks for the Prediction of Organic Chemistry Reactions. ACS Cent. Sci. 2016, 2, 725–732. [Google Scholar] [CrossRef]
- Falat, L.; Pancikova, L. Quantitative Modelling in Economics with Advanced Artificial Neural Networks. Procedia Econ. Financ. 2015, 34, 194–201. [Google Scholar] [CrossRef]
- Namazi, M.; Shokrolahi, A.; Maharluie, M.S. Detecting and ranking cash flow risk factors via artificial neural networks technique. J. Bus. Res. 2016, 69, 1801–1806. [Google Scholar] [CrossRef]
- Tkacz, G. Neural network forecasting of Canadian GDP growth. Int. J. Forecast. 2001, 17, 57–69. [Google Scholar] [CrossRef]
- Baskin, I.I.; Winkler, D.; Tetko, I.V. A renaissance of neural networks in drug discovery. Expert Opin. Drug Discov. 2016, 11, 785–795. [Google Scholar] [CrossRef] [PubMed]
- Bartzatt, R. Prediction of Novel Anti-Ebola Virus Compounds Utilizing Artificial Neural Network (ANN). World J. Pharm. Res. 2018, 7, 16. [Google Scholar]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Effati, S.; Pakdaman, M. Artificial neural network approach for solving fuzzy differential equations. Inf. Sci. 2010, 180, 1434–1457. [Google Scholar] [CrossRef]
- Rostami, F.; Jafarian, A. A new artificial neural network structure for solving high-order linear fractional differential equations. Int. J. Comput. Math. 2018, 95, 528–539. [Google Scholar] [CrossRef]
- Yadav, A.K.; Chandel, S.S. Solar radiation prediction using Artificial Neural Network techniques: A review. Renew. Sustain. Energy Rev. 2014, 33, 772–781. [Google Scholar] [CrossRef]
- Qazi, A.; Fayaz, H.; Wadi, A.; Raj, R.G.; Rahim, N.A.; Khan, W.A. The artificial neural network for solar radiation prediction and designing solar systems: A systematic literature review. J. Clean. Prod. 2015, 104, 1–12. [Google Scholar] [CrossRef]
- Wu, C.H. Behavior-based spam detection using a hybrid method of rule-based techniques and neural networks. Expert Syst. Appl. 2009, 36, 4321–4330. [Google Scholar] [CrossRef]
- Ren, Y.; Ji, D. Neural networks for deceptive opinion spam detection: An empirical study. Inf. Sci. 2017, 385–386, 213–224. [Google Scholar] [CrossRef]
- Madisetty, S.; Desarkar, M.S. A Neural Network-Based Ensemble Approach for Spam Detection in Twitter. IEEE Trans. Comput. Soc. Syst. 2018, 5, 973–984. [Google Scholar] [CrossRef]
- Topuz, A. Predicting moisture content of agricultural products using artificial neural networks. Adv. Eng. 2010, 41, 464–470. [Google Scholar] [CrossRef]
- Escamilla-García, A.; Soto-Zarazúa, G.M.; Toledano-Ayala, M.; Rivas-Araiza, E.; Gastélum-Barrios, A. Applications of Artificial Neural Networks in Greenhouse Technology and Overview for Smart Agriculture Development. Appl. Sci. 2020, 10, 3835. [Google Scholar] [CrossRef]
- Boughrara, H.; Chtourou, M.; Ben Amar, C.; Chen, L. Facial expression recognition based on a mlp neural network using constructive training algorithm. Multimed. Tools Appl. 2016, 75, 709–731. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F.; Zhang, L. Comparison of four Adaboost algorithm based artificial neural networks in wind speed predictions. Energy Convers. Manag. 2015, 92, 67–81. [Google Scholar] [CrossRef]
- Szoplik, J. Forecasting of natural gas consumption with artificial neural networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
- Bahram, H.; Navimipour, N.J. Intrusion detection for cloud computing using neural networks and artificial bee colony optimization algorithm. ICT Express 2019, 5, 56–59. [Google Scholar]
- Chen, Y.S.; Chang, F.J. Evolutionary artificial neural networks for hydrological systems forecasting. J. Hydrol. 2009, 367, 125–137. [Google Scholar] [CrossRef]
- Swales, G.S.; Yoon, Y. Applying Artificial Neural Networks to Investment Analysis. Financ. Anal. J. 1992, 48, 78–80. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Chen, T.; Zhong, S. Privacy-Preserving Backpropagation Neural Network Learning. IEEE Trans. Neural Netw. 2009, 20, 1554–1564. [Google Scholar] [CrossRef] [PubMed]
- Chalup, S.; Maire, F. A study on hill climbing algorithms for neural network training. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: Toulouse, France, 1999; Volume 3, pp. 2014–2021. [Google Scholar]
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; IEEE: Toulouse, France, 1993; pp. 586–591. [Google Scholar]
- Pajchrowski, T.; Zawirski, K.; Nowopolski, K. Neural Speed Controller Trained Online by Means of Modified RPROP Algorithm. IEEE Trans. Ind. Informatics 2015, 11, 560–568. [Google Scholar] [CrossRef]
- Hermanto, R.P.S.; Nugroho, A. Waiting-Time Estimation in Bank Customer Queues using RPROP Neural Networks. Procedia Comput. Sci. 2018, 135, 35–42. [Google Scholar] [CrossRef]
- Robitaille, B.; Marcos, B.; Veillette, M.; Payre, G. Modified quasi-Newton methods for training neural networks. Comput. Chem. Eng. 1996, 20, 1133–1140. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, J.; Sang, R.; Li, J.; Zhang, T.; Zhang, Q. Fast Neural Network Training on FPGA Using Quasi-Newton Optimization Method. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 1575–1579. [Google Scholar] [CrossRef]
- Yamazaki, A.; de Souto, M.C.P.; Ludermir, T.B. Optimization of neural network weights and architectures for odor recognition using simulated annealing. In Proceedings of the 2002 International Joint Conference on Neural Networks, IJCNN’02, Honolulu, HI, USA, 12–17 May 2002; IEEE: Toulouse, France, 2002; Volume 1, pp. 547–552. [Google Scholar]
- Da, Y.; Xiurun, G. An improved PSO-based ANN with simulated annealing technique. Neurocomputing 2005, 63, 527–533. [Google Scholar] [CrossRef]
- Leung, F.H.F.; Lam, H.K.; Ling, S.H.; Tam, P.K.S. Tuning of the structure and parameters of a neural network using an improved genetic algorithm. IEEE Trans. Neural Netw. 2003, 14, 79–88. [Google Scholar] [CrossRef]
- Yao, X. Evolving artificial neural networks. Proc. IEEE 1999, 87, 1423–1447. [Google Scholar]
- Zhang, C.; Shao, H.; Li, Y. Particle swarm optimisation for evolving artificial neural network. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Nashville, TN, USA, 8–11 October 2000; IEEE: Toulouse, France, 2000; pp. 2487–2490. [Google Scholar]
- Yu, J.; Wang, S.; Xi, L. Evolving artificial neural networks using an improved PSO and DPSO. Neurocomputing 2008, 71, 1054–1060. [Google Scholar] [CrossRef]
- Ilonen, J.; Kamarainen, J.K.; Lampinen, J. Differential Evolution Training Algorithm for Feed-Forward Neural Networks. Neural Process. Lett. 2003, 17, 93–105. [Google Scholar] [CrossRef]
- Slowik, A.; Bialko, M. Training of artificial neural networks using differential evolution algorithm. In Proceedings of the 2008 Conference on Human System Interactions, Krakow, Poland, 25–27 May 2008; IEEE: Toulouse, France, 2008; pp. 60–65. [Google Scholar]
- Rocha, M.; Cortez, P.; Neves, J. Evolution of neural networks for classification and regression. Neurocomputing 2007, 70, 2809–2816. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Artificial neural network training using a new efficient optimization algorithm. Appl. Soft Comput. 2013, 13, 1206–1213. [Google Scholar] [CrossRef]
- Cui, Z.; Yang, C.; Sanyal, S. Training artificial neural networks using APPM. Int. J. Wirel. And Mobile Comput. 2012, 5, 168–174. [Google Scholar] [CrossRef]
- Yaghini, M.; Khoshraftar, M.M.; Fallahi, M. A hybrid algorithm for artificial neural network training. Eng. Appl. Artif. Intell. 2013, 26, 293–301. [Google Scholar] [CrossRef]
- Chen, J.F.; Do, Q.H.; Hsieh, H.N. Training Artificial Neural Networks by a Hybrid PSO-CS Algorithm. Algorithms 2015, 8, 292–308. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Engineering Optimisation by Cuckoo Search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Ivanova, I.; Kubat, M. Initialization of neural networks by means of decision trees. Knowl.-Based Syst. 1995, 8, 333–344. [Google Scholar] [CrossRef]
- Yam, J.Y.F.; Chow, T.W.S. A weight initialization method for improving training speed in feedforward neural network. Neurocomputing 2000, 30, 219–232. [Google Scholar] [CrossRef]
- Chumachenko, K.; Iosifidis, A.; Gabbouj, M. Feedforward neural networks initialization based on discriminant learning. Neural Netw. 2022, 146, 220–229. [Google Scholar] [CrossRef]
- Itano, F.; de Sousa, M.A.d.A.; Del-Moral-Hernandez, E. Extending MLP ANN hyper-parameters Optimization by using Genetic Algorithm. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; IEEE: Toulouse, France, 2018; pp. 1–8. [Google Scholar]
- Narkhede, M.V.; Bartakke, P.P.; Sutaone, M.S. A review on weight initialization strategies for neural networks. Artif. Intell. Rev. 2022, 55, 291–322. [Google Scholar] [CrossRef]
- O’Neill, M.; Ryan, C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001, 5, 349–358. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Gavrilis, D.; Glavas, E. Neural network construction and training using grammatical evolution. Neurocomputing 2008, 72, 269–277. [Google Scholar] [CrossRef]
- Han, H.G.; Qiao, J.F. A structure optimisation algorithm for feedforward neural network construction. Neurocomputing 2013, 99, 347–357. [Google Scholar] [CrossRef]
- Kim, K.J.; Cho, S.B. Evolved neural networks based on cellular automata for sensory-motor controller. Neurocomputing 2006, 69, 2193–2207. [Google Scholar] [CrossRef]
- Martínez-Zarzuela, M.; Díaz Pernas, F.J.; Díez Higuera, J.F.; Rodríguez, M.A. Fuzzy ART Neural Network Parallel Computing on the GPU. In Computational and Ambient Intelligence. IWANN 2007; Lecture Notes in Computer Science; Sandoval, F., Prieto, A., Cabestany, J., Graña, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4507. [Google Scholar]
- Sierra-Canto, X.; Madera-Ramirez, F.; Uc-Cetina, V. Parallel Training of a Back-Propagation Neural Network Using CUDA. In Proceedings of the 2010 Ninth International Conference on Machine Learning and Applications, Washington, DC, USA, 12–14 December 2010; IEEE: Toulouse, France, 2010; pp. 307–312. [Google Scholar]
- Huqqani, A.A.; Schikuta, E.; Chen, S.Y.P. Multicore and GPU Parallelization of Neural Networks for Face Recognition. Procedia Comput. Sci. 2013, 18, 349–358. [Google Scholar] [CrossRef]
- Nowlan, S.J.; Hinton, G.E. Simplifying neural networks by soft weight sharing. Neural Comput. 1992, 4, 473–493. [Google Scholar] [CrossRef]
- Kim, J.K.; Lee, M.Y.; Kim, J.Y.; Kim, B.J.; Lee, J.H. An efficient pruning and weight sharing method for neural network. In Proceedings of the 2016 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), Seoul, Republic of Korea, 26–28 October 2016; IEEE: Toulouse, France, 2016; pp. 1–2. [Google Scholar]
- Hanson, S.J.; Pratt, L.Y. Comparing biases for minimal network construction with back propagation. In Advances in Neural Information Processing Systems; Touretzky, D.S., Ed.; Morgan Kaufmann: San Mateo, CA, USA, 1989; Volume 1, pp. 177–185. [Google Scholar]
- Mozer, M.C.; Smolensky, P. Skeletonization: A technique for trimming the fat from a network via relevance assesment. In Advances in Neural Processing Systems; Touretzky, D.S., Ed.; Morgan Kaufmann: San Mateo, CA, USA, 1989; Volume 1, pp. 107–115. [Google Scholar]
- Augasta, M.; Kathirvalavakumar, T. Pruning algorithms of neural networks—a comparative study. Cent. Eur. Comput. Sci. 2003, 3, 105–115. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Iosifidis, A.; Tefas, A.; Pitas, I. DropELM: Fast neural network regularization with Dropout and DropConnect. Neurocomputing 2015, 162, 57–66. [Google Scholar] [CrossRef]
- Gupta, A.; Lam, S.M. Weight decay backpropagation for noisy data. Neural Netw. 1998, 11, 1127–1138. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, M.; Ludermir, T.B. Particle Swarm Optimization of Feed-Forward Neural Networks with Weight Decay. In Proceedings of the 2006 Sixth International Conference on Hybrid Intelligent Systems (HIS’06), Rio de Janeiro, Brazil, 13–15 December 2006; IEEE: Toulouse, France, 2006; p. 5. [Google Scholar]
- Treadgold, N.K.; Gedeon, T.D. Simulated annealing and weight decay in adaptive learning: The SARPROP algorithm. IEEE Trans. Neural Netw. 1998, 9, 662–668. [Google Scholar] [CrossRef] [PubMed]
- Shahjahan, M.D.; Kazuyuki, M. Neural network training algorithm with possitive correlation. IEEE Trans. Inf. Syst. 2005, 88, 2399–2409. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Tzallas, A.; Karvounis, E.; Tsalikakis, D. NeuralMinimizer: A Novel Method for Global Optimization. Information 2023, 14, 66. [Google Scholar] [CrossRef]
- Park, J.; Sandberg, I.W. Universal Approximation Using Radial-Basis-Function Networks. Neural Comput. 1991, 3, 246–257. [Google Scholar] [CrossRef] [PubMed]
- Mai-Duy, N.; Tran-Cong, T. Numerical solution of differential equations using multiquadric radial basis function networks. Neural Netw. 2001, 14, 185–199. [Google Scholar] [CrossRef]
- Mai-Duy, N. Solving high order ordinary differential equations with radial basis function networks. Int. J. Numer. Meth. Engng. 2005, 62, 824–852. [Google Scholar] [CrossRef]
- Laoudias, C.; Kemppi, P.; Panayiotou, C.G. Localization Using Radial Basis Function Networks and Signal Strength Fingerprints in WLAN. In Proceedings of the GLOBECOM 2009—2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; IEEE: Toulouse, France, 2009; pp. 1–6. [Google Scholar]
- Azarbad, M.; Hakimi, S.; Ebrahimzadeh, A. Automatic recognition of digital communication signal. Int. J. Energy Inf. Commun. 2012, 3, 21–33. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the Limited Memory Method for Large Scale Optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. ADAM: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Wang, L.; Yang, Y.; Min, R.; Chakradhar, S. Accelerating deep neural network training with inconsistent stochastic gradient descent. Neural Netw. 2017, 93, 219–229. [Google Scholar] [CrossRef]
- Sharma, A. Guided Stochastic Gradient Descent Algorithm for inconsistent datasets. Appl. Soft Comput. 2018, 73, 1068–1080. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef]
- Wang, H.; Gemmeke, H.; Hopp, T.; Hesser, J. Accelerating image reconstruction in ultrasound transmission tomography using L-BFGS algorithm. In Medical Imaging 2019: Ultrasonic Imaging and Tomography; 109550B (2019); SPIE Medical Imaging: San Diego, CA, USA, 2019. [Google Scholar] [CrossRef]
- Dalvand, Z.; Hajarian, M. Solving generalized inverse eigenvalue problems via L-BFGS-B method. Inverse Probl. Sci. Eng. 2020, 28, 1719–1746. [Google Scholar] [CrossRef]
- Rao, Y.; Wang, Y. Seismic waveform tomography with shot-encoding using a restarted L-BFGS algorithm. Sci. Rep. 2017, 7, 8494. [Google Scholar] [CrossRef] [PubMed]
- Fei, Y.; Rong, G.; Wang, B.; Wang, W. Parallel L-BFGS-B algorithm on GPU. Comput. Graph. 2014, 40, 1–9. [Google Scholar] [CrossRef]
- D’Amore, L.; Laccetti, G.; Romano, D.; Scotti, G.; Murli, A. Towards a parallel component in a GPU—CUDA environment: A case study with the L-BFGS Harwell routine. Int. J. Comput. Math. 2015, 92, 59–76. [Google Scholar] [CrossRef]
- Najafabadi, M.M.; Khoshgoftaar, T.M.; Villanustre, F.; Holt, J. Large-scale distributed L-BFGS. J. Big Data 2017, 4, 22. [Google Scholar] [CrossRef]
- Morales, J.L. A numerical study of limited memory BFGS methods. Appl. Math. Lett. 2002, 15, 481–487. [Google Scholar] [CrossRef]
- Tsoulos, I.G. Modifications of real code genetic algorithm for global optimization. Appl. Math. Comput. 2008, 203, 598–607. [Google Scholar] [CrossRef]
- Kelly, M.; Longjohn, R.; Nottingham, K. The UCI Machine Learning Repository. 2023. Available online: https://archive.ics.uci.edu (accessed on 18 July 2023).
- Alcalá-Fdez, J.; Fernandez, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J.-Mult.-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Weiss, S.M.; Kulikowski, C.A. Computer Systems That Learn: Classification and Prediction Methods from Statistics, Neural Nets, Machine Learning, and Expert Systems; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1991. [Google Scholar]
- Wang, M.; Zhang, Y.Y.; Min, F. Active learning through multi-standard optimization. IEEE Access 2019, 7, 56772–56784. [Google Scholar] [CrossRef]
- Quinlan, J.R. Simplifying Decision Trees. Int.-Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Shultz, T.; Mareschal, D.; Schmidt, W. Modeling Cognitive Development on Balance Scale Phenomena. Mach. Learn. 1994, 16, 59–88. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Jiang, Y. NeC4.5: Neural ensemble based C4.5. IEEE Trans. Knowl. Data Eng. 2004, 16, 770–773. [Google Scholar] [CrossRef]
- Setiono, R.; Leow, W.K. FERNN: An Algorithm for Fast Extraction of Rules from Neural Networks. Appl. Intell. 2000, 12, 15–25. [Google Scholar] [CrossRef]
- Evans, B.; Fisher, D. Overcoming process delays with decision tree induction. IEEE Expert 1994, 9, 60–66. [Google Scholar] [CrossRef]
- Demiroz, G.; Govenir, H.A.; Ilter, N. Learning Differential Diagnosis of Eryhemato-Squamous Diseases using Voting Feature Intervals. Artif. Intell. Med. 1998, 13, 147–165. [Google Scholar]
- Hayes-Roth, B.; Hayes-Roth, B.F. Concept learning and the recognition and classification of exemplars. J. Verbal Learn. Verbal Behav. 1977, 16, 321–338. [Google Scholar] [CrossRef]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- French, R.M.; Chater, N. Using noise to compute error surfaces in connectionist networks: A novel means of reducing catastrophic forgetting. Neural Comput. 2002, 14, 1755–1769. [Google Scholar] [CrossRef]
- Dy, J.G.; Brodley, C.E. Feature Selection for Unsupervised Learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Perantonis, S.J.; Virvilis, V. Input Feature Extraction for Multilayered Perceptrons Using Supervised Principal Component Analysis. Neural Process. Lett. 1999, 10, 243–252. [Google Scholar] [CrossRef]
- Garcke, J.; Griebel, M. Classification with sparse grids using simplicial basis functions. Intell. Data Anal. 2002, 6, 483–502. [Google Scholar] [CrossRef]
- Mcdermott, J.; Forsyth, R.S. Diagnosing a disorder in a classification benchmark. Pattern Recognit. Lett. 2016, 73, 41–43. [Google Scholar] [CrossRef]
- Cestnik, G.; Konenenko, I.; Bratko, I. Assistant-86: A Knowledge-Elicitation Tool for Sophisticated Users. In Progress in Machine Learning; Bratko, I., Lavrac, N., Eds.; Sigma Press: Wilmslow, UK, 1987; pp. 31–45. [Google Scholar]
- Elter, M.; Schulz-Wendtland, R.; Wittenberg, T. The prediction of breast cancer biopsy outcomes using two CAD approaches that both emphasize an intelligible decision process. Med. Phys. 2007, 34, 4164–4172. [Google Scholar] [CrossRef] [PubMed]
- Malerba, F.E.F.D.; Semeraro, G. Multistrategy Learning for Document Recognition. Appl. Artif. Intell. 1994, 8, 33–84. [Google Scholar]
- Little, M.; Mcsharry, P.; Roberts, S.; Costello, D.; Moroz, I. Exploiting Nonlinear Recurrence and Fractal Scaling Properties for Voice Disorder Detection. BioMed. Eng. OnLine 2007, 6, 23. [Google Scholar] [CrossRef]
- Little, M.A.; McSharry, P.E.; Hunter, E.J.; Spielman, J.; Ramig, L.O. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. IEEE Trans. Biomed. Eng. 2009, 56, 1015–1022. [Google Scholar] [CrossRef]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In Proceedings of the Symposium on Computer Applications and Medical Care; IEEE Computer Society Press: Piscataway, NJ, USA; American Medical Informatics Association: Bethesda, MD, USA, 1988; pp. 261–265. [Google Scholar]
- Lucas, D.D.; Klein, R.; Tannahill, J.; Ivanova, D.; Brandon, S.; Domyancic, D.; Zhang, Y. Failure analysis of parameter-induced simulation crashes in climate models. Geosci. Model Dev. 2013, 6, 1157–1171. [Google Scholar] [CrossRef]
- Giannakeas, N.; Tsipouras, M.G.; Tzallas, A.T.; Kyriakidi, K.; Tsianou, Z.E.; Manousou, P.; Hall, A.; Karvounis, E.C.; Tsianos, V.; Tsianos, E. A clustering based method for collagen proportional area extraction in liver biopsy images. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; IEEE: Toulouse, France, 2015; pp. 3097–3100. [Google Scholar]
- Hastie, T.; Tibshirani, R. Non-parametric logistic and proportional odds regression. JRSS-C (Appl. Stat.) 1987, 36, 260–276. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H.; Scheuermann, P.; Tan, K.L. Fast hierarchical clustering and its validation. Data Knowl. Eng. 2003, 44, 109–138. [Google Scholar] [CrossRef]
- Wolberg, W.H.; Mangasarian, O.L. Multisurface method of pattern separation for medical diagnosis applied to breast cytology. Proc. Natl. Acad. Sci. USA 1990, 87, 9193–9196. [Google Scholar] [CrossRef] [PubMed]
- Raymer, M.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man. Cybern. 2003, 33, 802–813. [Google Scholar] [CrossRef]
- Zhong, P.; Fukushima, M. Regularized nonsmooth Newton method for multi-class support vector machines. Optim. Methods Softw. 2007, 22, 225–236. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. 2001, 64, 061907. [Google Scholar] [CrossRef]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Automatic Seizure Detection Based on Time-Frequency Analysis and Artificial Neural Networks. Comput. Intell. Neurosci. 2007, 2007, 80510. [Google Scholar] [CrossRef]
- Koivisto, M.; Sood, K. Exact Bayesian Structure Discovery in Bayesian Networks. J. Mach. Learn. Res. 2004, 5, 549–573. [Google Scholar]
- Nash, W.J.; Sellers, T.L.; Talbot, S.R.; Cawthor, A.J.; Ford, W.B. The Population Biology of Abalone (haliotis species). In Blacklip Abalone (H. rubra) from the North Coast and Islands of Bass Strait; Tasmania, I., Ed.; Technical Report; Sea Fisheries Division: Tasmania, Australia, 1994; ISSN 1034-3288. [Google Scholar]
- Brooks, T.F.; Pope, D.S.; Marcolini, A.M. Airfoil Self-Noise and Prediction; Technical report; NASA: Washington, DC, USA, 1989. [Google Scholar]
- Simonoff, J.S. Smooting Methods in Statistics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Yeh, I.C. Modeling of strength of high performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Harrison, D.; Rubinfeld, D.L. Hedonic prices and the demand for clean ai. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- King, R.D.; Muggleton, S.; Lewis, R.; Sternberg, M.J.E. Drug design by machine learning: The use of inductive logic programming to model the structure-activity relationships of trimethoprim analogues binding to dihydrofolate reductase. Proc. Natl. Acad. Sci. USA 1992, 89, 11322–11326. [Google Scholar] [CrossRef]
- Stanley, K.O.; Miikkulainen, R. Evolving Neural Networks through Augmenting Topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).