Abstract
Protein–protein interactions (PPIs) are involved in an extensive variety of biological procedures, including cell-to-cell interactions, and metabolic and developmental control. PPIs are becoming one of the most important aims of system biology. PPIs act as a fundamental part in predicting the protein function of the target protein and the drug ability of molecules. An abundance of work has been performed to develop methods to computationally predict PPIs as this supplements laboratory trials and offers a cost-effective way of predicting the most likely set of interactions at the entire proteome scale. This article presents an innovative feature representation method (CAA-PPI) to extract features from protein sequences using two different encoding strategies followed by an ensemble learning method. The random forest methodwas used as a classifier for PPI prediction. CAA-PPI considers the role of the trigram and bond of a given amino acid with its nearby ones. The proposed PPI model achieved more than a 98% prediction accuracy with one encoding scheme and more than a 95% prediction accuracy with another encoding scheme for the two diverse PPI datasets, i.e., H. pylori and Yeast. Further, investigations were performed to compare the CAA-PPI approach with existing sequence-based methods and revealed the proficiency of the proposed method with both encoding strategies. To further assess the practical prediction competence, a blind test was implemented on five other species’ datasets independent of the training set, and the obtained results ascertained the productivity of CAA-PPI with both encoding schemes.
1. Introduction
The word protein comes from the Greek word “protos”, meaning the first element [1]; undoubtedly, proteins are fundamental to life. Proteins are complexes made from 20 types of amino acids, which are linked through bonds called -peptide bonds. Proteins on their own cannot perform any function; they accomplish their roles by interacting with other molecules, such as DNA, RNA, or other proteins, which catalyse different biological functions at the system or cellular level. PPIs can create a novel binding site for small effector molecules according to various research. PPIs are a consequence of hydrophobic and electrostatic interactions and hydrogen bonds, all contributing to the binding interaction. The significance of hydrophobic forces has been proven [2]. There are some important properties of PPIs that are noteworthy. First, the changes in the kinematic properties of enzymes due to PPIs might cause delicate fluctuations in substrate binding or allosteric effects. Secondly, PPIs can form a new binding site for small effector molecules. Next, they can deactivate or suppress a protein. Interacting with different binding partners, PPIs can alter the precision of proteins with respect to their substrates. PPIs come in various types and can be categorized based on their stability, affinity and composition of the consequential complex [3], and being transient or permanent, non-obligate or obligate interactions, respectively. Similarly, they can be characterized based on their homo- or hetero-oligomeric complexes regarding the similarity of the protein pair involved in the interaction. The interactions are obligate if the PPI complexes are unsteady in vivo, whereas the resultant complexes of non-obligate interactions can occur autonomously. Non-obligate interactions are either transient or permanent. Transient interactions occur provisionally in vivo, though in permanent interactions, the complexes remain intact after the interaction. PPIs imply various effects such as the following [4]:
- –
- permitting substrate channelling;
- –
- the formation of a novel binding site;
- –
- deactivating or destroying a protein;
- –
- the alteration of the specificity of a protein;
- –
- forcing a different role in an upstream or a downstream event.
All the above has great influence on many biochemical events; consequently, the exploration of PPIs allows scholars to uncover the functions and structures of tissues, identify syndromes, and find drug targets for gene therapy. In the past few years, numerous experimental methods have been employed to detect PPIs, resulting in high-productivity methods such as immunoprecipitation, the yeast two-hybrid system, affinity purification–mass spectrometry (AP-MS), and protein microarrays. On the other hand, biological experiments are rather expensive and laborious. Furthermore, the FN and FP rates of these methods are both very high [5]. Thus, developing reliable computational models for PPI prediction has great practical significance.
As per Galileo’s concept of the book of nature, nature is written in the language of mathematics; therefore, the possible interactions of proteins can be mapped using different mathematical approaches by using their properties and associated data as the input for different computational models.Up to now, multiple research models have been introduced to predict PPIs, which are categorized into [6] gene data-, network topology-, structural profile-, and ML-based methods, as shown in Figure 1. Genetic linkage, genetic fusion, polygenetic profile, and in silico two-hybrid systems for PPI prediction are used in the genetic approach. Proteins’ three-dimensional information is used in the structural approach, whereas in the network-topology-based approach, a confidence score matrix is generated for prediction purposes. ML-based methods train the prediction models on the diverse features of the interacting proteins, and pre-trained models then predict the interaction of the proteins.
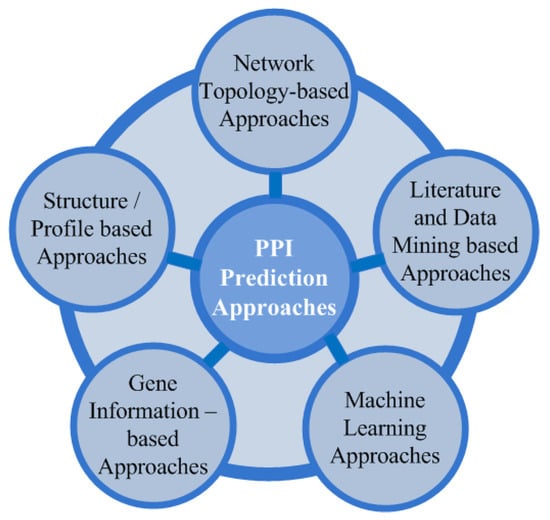
Figure 1.
Computational approaches to predicting PPIs.
In the proposed approach, an ML-based model named connecting amino acid feature-based PPI (CAA-PPI) is introduced to predict PPIs. A major contribution of the given model is the novel feature-generation method using the hypothesis of the association of different amino acids with a residue in a given trigram. CAA-PPI employs PCA to eliminate irrelevant and redundant features from the dataset. In addition, the CAA-based feature extraction approach is implemented with two different encoding schemes named ES1 and ES2, trailed by an RF classifier to train the model. The performance of CAA-PPI with the RF classifier model is verified on two different PPI datasets that are Yeast and H. pylori. The average accuracies of 98.25 and 98.25% were achieved with 98.69% for one encoding scheme, and 95.49% with another encoding scheme. Moreover, the comparison results of CAA-PPI with competitive approaches proved it as the more accurate approach. The proposed model was also tested on a random dataset (five species dataset) termed as an independent dataset due to its independence from the training dataset. The overall outcomes of the proposed method proved that this approach was more efficient in the PPI prediction with both encoding strategies.
The structure of this research article is as follows: Firstly, the importance and challenges of PPI and the need for PPI prediction are discussed. Next, previously published studies concerning PPI are deliberated including research related to the encoding strategy and feature extraction approach. In the next section, the details of the additional materials used to carry out the experimental work are presented. A detailed description of the proposed approach, including systematic workflow and pseudo code, is then given with an example to further explain the CAA-PPI approach. Next, the performance of CAA-PPI with ES1 and ES2 on two diverse datasets is presented with seven standard measures followed by their respective Bonferroni post hoc analysis comparisons with state-of-the-art models. In the end, the research is concluded with possible prospective applications in CAA-PPI.
2. Literature Review
The knowledge to build a PPI prediction model using sequences is primarily dependent on three factors:
- –
- selection of an appropriate manner to cover the possible essential information concerning PPI;
- –
- develop a strategy for protein sequence feature extraction;
- –
- apply a favourable classification algorithm.
This article mainly concentrates on the first two factors and therefore this section concisely considers their study as collated in Table 1. Several investigations have been performed to try and develop an encoding scheme to fully capture biological sequence information [7,8]. Shen [9] suggested seven classes of amino acids centred on their dipole and side-chain volumes to extract the features of the protein pairs. Another research work used three different encoding strategies based on the chemical properties, polarity, and structure of amino acids with three newly created feature sets [10]. In 2017, Zhou encoded a multi-scale protein sequence using seven properties, covering the qualitative and quantitative explanation of amino acids. These encodings were then used to represent each protein sequence in terms of five different protein descriptors, i.e., AC, composition, frequency, transformation, and distribution [11]. In 2020, researchers used two counterpart amino acid encoding schemes, compared using CNN, RNN, and a hybrid CNN–RNN architecture, applied to two challenging problems [12]. In 2020, a broad review was reported by Jing about various encoding methods for amino acids followed by a systematic analysis of encoding methods, comparing the performances of 16 different representative encoding methods classified into five categories [13].

Table 1.
Brief overview of previously reported feature extraction methods for PPI prediction.
Numerous computational methods have been proposed by several publishers to extract sequence features, mostly dealing with the evolutionary information of proteins, physiochemical information, or structure information. One of the popular feature extraction methods published by Chou [23] reflects the amino acids’ composition and progressions of the amino acid locus information. Ref. [14] deliberated the residues’ interaction in both continuous and discontinuous regions, extracting more information on PPIs present in the protein sequence and proposed LD and a KNN model.
A notable work by Guo accounted for the discontinuous amino acid fragments of protein sequence by using an AC-based method [15]. The process considered physicochemical properties, and a descriptor ‘signature product’ was developed to determine PPIs [16]. The research work by [17] proposed a new hierarchical model by first extracting the information that causes protein sequence interaction using CT, AC, MAC, and LD and then using PCA and finally employing an E-ELM classifier to predict PPIs. Another great research work by [18] considered the interfaces between serially remote but spatially near amino acid residues. Again in 2015, ref. [19] suggested another innovative feature representation approach, postulating that the interaction between protein pairs could be possible in unceasing amino acid fragments of different segment lengths. A notable work was proposed by [20] using image processing methods for feature extraction using a physicochemical PR matrix and then employed LPQ to mine complex and essential coefficients from obtained features. The RoF classifier was used to predict favourable PPIs, showing an efficient performance when compared with existing approaches. The authors of [21] improved the prediction precision using an AAC matrix to obtain an SMR matrix followed by SVD and HOG algorithms that generate a feature vector. Another brilliant work published by [22] used both local and global features in a PSSM-based local encoding approach to create a novel multi-feature fusion matrix (CPSSM). Subsequently, they employed local average group (LAG) and bigram probability (BP) to extracted key features from the obtained matrix. In the current research article, an innovative feature representation method CAA-PPI is projected to extract key information present in protein sequence which takes into consideration the association of different amino acids with a residue in a given trigram. These novel features were extracted using two different encoding schemes for representing amino acids. Then, RF was used as a classifier to prove the efficacy of the approach for predicting interaction between protein pairs. The proposed PPI model achieved prediction accuracies of 98.25% and 98.25% with one encoding scheme; 98.69% and 95.49% with another encoding scheme respectively when applied on two diverse PPI datasets including Yeast and H. Pylori. Further investigations were made to compare the proposed approach with existing sequence-based methods and revealed outstanding results which proved the proficiency of the proposed method. Further, to evaluate the practical prediction competence, a blind test was implemented on five other species’ datasets which are autonomous to the training set, and obtained results ascertained the productivity of CAA-PPI.
3. Materials and Methods
3.1. Dataset
The data was collected from DIP [24] and PIR to validate the CAA-PPI approach. Evaluation was performed on Yeast and H. pylori, all having different numbers of interacting protein pairs. For S. cerevisiae, which is a Yeast protein, their PPI datasets were taken from DIP with reference from An’s work [22] in PPI prediction. Replication of the protein pair was performed by scrutiny of a dataset with similarity less than 40%. In total 5594 datasets of interacting pairs were obtained. For effective testing of model performance, the datsets needs to include non-interacting pairs to train the model. Consequently, 5594 datasets of non-interacting or negative pairs are selected consisting of diverse subcellular localizations. Finally, atotal of 11,188 protein pairs from the Yeast dataset needed to be evaluated. H. pylori was the next PPI dataset considered, comprising 2916 pairs of proteins containing 1458 interacting or non-interacting pairs [16]. Besides these, the PPI dataset of the following five species M. musculus, H. pylori, C. elegans, E. coli, H. sapien were also used to test the performance of CAA-PPI, comprising 313, 1420, 4013, 6954, and 1412 interacting pairs, respectively [25].
3.2. Cross Validation
A cross-validation system is a typical procedure for circumventing any cross-sectional prejudices as well as corroborating the reliability of the model [26]. In this article, a five-fold cross-validation technique was performed to assess the classifier’s performance. In the X-fold cross-validation technique (X is any valid number), the complete dataset is randomly fragmented into X equal fragments as folds; out of X folds, X − 1 are used for training and the remaining one is used as a test set in each fold of the cross-validation. Similarly, this practice recurs X times to achieve X distinct models. Lastly, the outcomes of X distinct trials are averaged to contribute to an inclusive assessment.
3.3. Performance Evaluation
With the purpose of quantitatively appraising the efficacy and constancy of a classifier, a number of broadly performed statistical measures were considered in this work, namely accuracy (A), sensitivity/recall (Se), specificity (Sp), positive predictive value/precision (Pr), NPV, F-score (Fs) and Mathew’s correlation coefficient MCC. These measures are expressed as follows:
Here, TP is the measure of true PPI pairs correctly predicted as interacting pairs. TN defines the quantity of true non-interacting pairs correctly predicted. FP is the amount of true non-interacting pairs that are incorrectly predicted as interacting ones. FN states the number of incorrectly predicted true interacting pairs as non-interacting pairs. Though A is a simple assessment measure, it may lead to a very biased evaluation in the case of a discrepant dataset. Pr confirms the total number of predicted pairs that are allied in the PPIs. As Pr and Se contradict each other, Fs is evaluated as the weighted harmonic mean of Pr and Se to inclusively reveal the prediction performance of PPIs [27]. The higher the value of Fs, so too is Pr and Se. The MCC is a different objective index imitating the whole method performance that considers under- and over-predictions [28].
3.4. Principal Component Analysis (PCA)
PCA [29] is an unsupervised linear dimensionality reduction method, used for the projection of a data space into a smaller dimensional space by using orthogonal transformation. It is a widely used method for eliminating redundant and noisy data, and extracting relevant features. The objective of PCA is to condense a big feature set into a smaller one without losing suitable information from the original set. The process of reduction using PCA is given below in six basic steps:
- •
- The entire dataset is transformed into matrix of dimension i × j and the class label is ignored.
- •
- The mean vector of the matrix is calculated.
- •
- The covariance of entire magnitude is calculated.
- •
- The eigenvalues and analogous eigenvectors are computed.
- •
- The eigenvectors are arranged by declining eigenvalues and any p eigenvector with the highest eigenvalue in a matrix of dimension j × p is selected.
- •
- The resultant j × p matrix is used to convert the sample space to a new subspace.
3.5. Random Forest Classifier
RF is a booming classifier in the area of machine learning. It is a procedure of ensemble classification that appoints a set of DTs to diminish the resultant variance of distinct trees to develop a constancy and accuracy of the classification. RFcarefully takes advantage of two influential ML techniques:
- •
- for each tree, the election of training samples;
- •
- the random feature selection to fragment the dataset.
The selection of training samples is implemented by using a bootstrap sample from the original data (termed bagging). The outcomes of bagging lead to two dismember bags, one holding the around 63.2% of the training data and the other holding the remaining samples, termed out-of-bag (OOB) samples. Usually, in-bag samples are used to build the RF classifier and OOB samples are used for prediction assessment. The next powerful ML technique selects a features’ subgroup at every single node in the respective classification tree, i.e., RF randomly hand-picked a fixed amount of features at every tree node and one with a consistent decrease in the Gini index [30] is selected for the split when emerging from the tree.
Naturally, a forest is made up of trees and more trees mean a more robust forest. In the same way, the RF algorithm generates DTs on data samples and acquires the prediction from each to choose the best result through voting. This ensemble scheme is superior to a solitary DT as this condenses the overfitting by averaging the outcome.
The RF algorithm can be understood with the help of the following steps:
- •
- Firstly, random samples are selected from the assumed dataset.
- •
- Then, a DT is generated by the algorithm for every sample and the prediction outcome from each DT is achieved.
- •
- Then, for every predicted outcome, voting is implemented.
- •
- In the end, the final prediction result is most voted prediction result.
4. The Workings of CAA-PPI
The proposed approach is based on the fact that interaction possibility-related information exists in the sequence of protein pairs. This information can be generated by deriving different features from the sequence by applying a varied feature extraction approach. The number of generated features cannot vary when the length of the protein sequence is changed; hence, the feature is generated with respect to the amino acids.
CAA-PPI can generate these features using a ratio combining the presences of in the protein sequence and the number of central amino acids present in the same trigram. Here, a trigram (3-mer) represents a set of three consecutive symbols in the protein sequence. Since a protein sequence contains 20 amino acids, a trigram contains 203 tri-peptide combinations; therefore, a total of 8000 feature values are needed to be generated for each combination of tri-peptides of a protein. Hence, a protein pair has about 16,000 values in its feature set. It will therefore be challenging to work with huge feature sets.
Encoding reduces the number of a protein’s features by aggregating 20 amino acids into seven classes, reducing the number of features from 203 to 73. Encoding enhances the speed of the proposed model, but still has the performance issues analysed by taking multiple encoding schemes and selecting the best one. The proposed work evaluates results based on the encoding scheme proposed in [9] (ES1) and [31] (ES2). Both encoding schemes aggregate 20 amino acids into seven classes; nonetheless, the combination approaches are dissimilar, as shown in Figure 2 and Figure 3. In ES1, amino acids are categorized based on chemical properties such as dipole scale and volume scale; whereas ES2 is based on the structure of side chains, which influence the deciding properties of the amino acid.
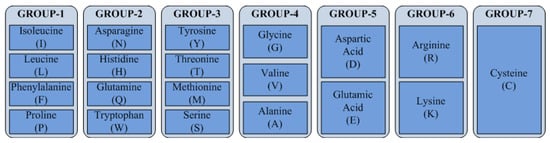
Figure 2.
Classification of amino acids based on ES1.
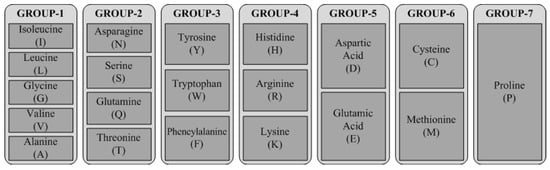
Figure 3.
Classification of amino acids based on ES2.
Encoding the protein sequence is the first step of CAA-PPI, which converts amino acids into specific symbols (‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’). Now, in the case of a trigram, there are 73 combinations in total for which a feature value is to be generated. For example, if the sequence is ‘AWGVWEGIAVGWAWG’.
Then for combination ‘AWG’, the feature value will be:
• Number of ‘AWG’ in a given sequence/Number of W in a given sequence = 2/4 = 0.5
For instance, the input dataset has positive (interacting) and negative (non-interacting) protein pairs, so labelling is performed with 1 and −1, respectively. Now, PCA will apply to the resultant feature for the feature selection process, followed by a five-fold cross-validation process of the dataset, as shown in Figure 4. The five-fold process divides the dataset into five equal parts from which one part is used as the test dataset and the remaining are used as a training dataset; hence, it represents 1–4 partitions of data. The selected training dataset is used to train the model using the RF classification method. The trained model predicts the class of the test dataset, supporting in calculating the performance measures A, Pr, Se, MCC, Fs, Sp, and NPV.
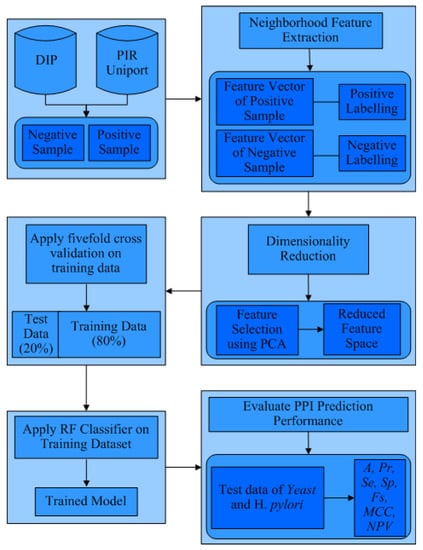
Figure 4.
Flowchart of the CAA-PPI approach.
The proposed feature generation algorithm is depicted in Algorithms 1–3, representing CAA-PPI. The main procedure of the model takes the protein sequence (seq), encoding pattern style (encoding_pattern), and number of elements in combination (p_gram) as arguments. The first step is encoding, performed by the function encoding_PPI using a sequence of proteins and an encoding pattern, such as an input argument, and generates an encoded protein sequence either according to ES1 or ES2 depending on the value of the encoding pattern. The next step of the procedure generates features of CAA-PPI performed by the function Generate_Feature_CAA by counting trigrams and central amino acids in a given sequence, and generating all features for all combinations of a given sequence and return value CAA_featureset. The PCA function is applied to filter out the correlated data from feature sets that return CAA_filtered_featureset, which is further labelled by the Add_label function after testing as to whether the protein pairs are interacting or not.
| Algorithm 1: Initialization of CAA_PPI. |
| Algorithm 2: Encoding a given protein sequence. |
| Algorithm 3: Generate feature CAA. |
5. Results and Discussion
5.1. Performance of the PPI Prediction
This section discussion the performance of the neighbourhood-based feature representation approach to predict PPIs via two diverse PPI datasets with the two encoding strategies discussed in previous sections. The outcomes are then compared with numerous existing approaches suggested in previously published work. Subsequently, a blind test was implemented on five other species datasets (M. musculus, H. sapiens, C. elegans, H. pylori and E. coli) autonomous to the training set to prove the productivity of CAA-PPI.
5.1.1. Performance of CAA-PPI Model Using ES1 and ES2 on the Yeast Dataset
CAA representation of the protein sequence with RF predictor was tested using five-fold cross-validation with the Yeast dataset, as shown in Table 2 using ES1 and ES2. It is noteworthy that from Table 2 a great prediction accuracy of 98.25% was attained for the CAA-PPI approach with ES1. The values of the other six standard measures were also assessed for the proposed model to thoroughly evaluate its prediction capability, achieving a decent performance with both encoding schemes; however, the ES1 performed comparatively better than ES2.

Table 2.
Five-fold cross-validation result of CAA-PPI using ES1 and ES2 on the Yeast dataset.
Furthermore, the prediction model using the CAA-PPI with ES1 and ES2 was compared against methodologies proposed by various publishers [15,18,20,22,25]. The Bonferroni post-hoc analysis is presented in Table 3. These approaches, discussed in previous sections, distinctly use LCPSSMMF, PSSMMF, LCPSSMAB, LCPSSMBG, AC + CT + LD + MAC, MCD, PR-LPQ, LD, ACC, and AC to encode amino acid sequences and predict PPIs using SVM, RF, RoF, E-ELM classifiers. It is notable from Table 3 that CAA-PPI, using ES1 and ES2, ouperformed all competitive methods, i.e., it generally had a significant difference in prediction accuracy than the state-of-art PPI predictors for the Yeast dataset, depicted by Figure 5. The notations in Figure 5 are the same as those mentioned in Table 3.

Table 3.
Bonferroni post-hoc analysis of CAA-PPI using ES2 and ES2 compared with existing approaches for overall prediction accuracy for the yeast dataset.
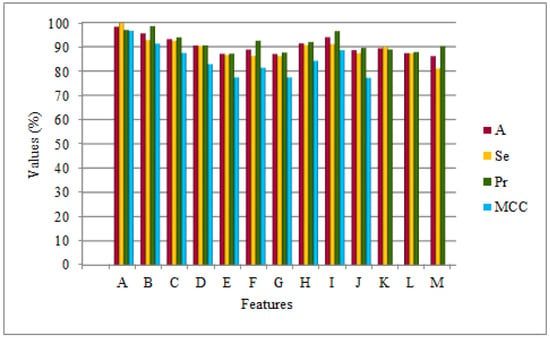
Figure 5.
Comparison of CAA-PPI applied to the Yeast dataset using ES1 and ES2 with existing approaches.
5.1.2. Performance of the CAA-PPI Model Using ES1 and ES2 on the H. pylori Dataset
Further, to evaluate the efficacy of the proposed method, the CAA-PPI model with ES1 and ES2 was tested on the H. pylori dataset using five-fold cross-validation, as shown in Table 4. From Table 4, it can be seen that the average accuracy of the proposed model is 98.25% with ES1 and 98.69% with ES2. Moreover, the performance of CAA-PPI was comprehensively computed with other evaluation metrics, including Se, Sp, Pr, NPV, Fs, MCC, as shown in Table 4. Likewise, the performance of CAA-PPI with both ES1 and ES2 was compared with the approaches from previous literature and the Bonferroni post-hoc analysis are presented in Table 5. These comparative approaches independently used HOG + SVD [21], AC + CT + LD + MAC [17], MCD [18], DCT + SMR [32]), LD [25], phylogenetic bootstrap [33], HKNN [34], ensemble of HKNN [35], signature products [16], and boosting [36] to express amino acid sequence and use a favourable classifier to predict PPIs. From Table 5, it is worth noting that CAA-PPI is more effective than the other competitive methods with both ES1 and ES2, i.e., it generally has a significant difference from the state-of-the-art PPI predictors for the H. pylori dataset, as presented in Figure 6. The notations in Figure 5 are the same as those mentioned in Table 5.

Table 4.
Five-fold cross-validation results of CAA-PPI using ES1 and ES2 on the H. pylori dataset.

Table 5.
Bonferroni post-hoc analysis results of CAA-PPI using ES1 and ES2 compared with existing approaches for overall prediction accuracy for the H. pylori dataset.
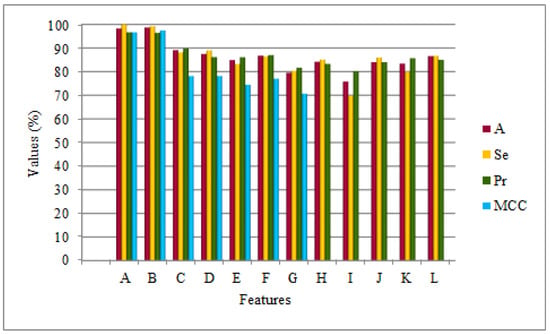
Figure 6.
Comparison of CAA-PPI applied to the H. pylori dataset using ES1 and ES2 with existing approaches.
5.1.3. Outcomes on Five Species Datasets
To assess the hands-on prediction aptitude, initially, CAA-PPI was trained with PPIs of the Yeast dataset using ES1 and ES2 separately, and used five independent species’ datasets to test, comprising 6954 interacting pairs of E. coli, 4013 interacting pairs of C. elegans, 1420 interacting pairs of H. pylori, 1412 interacting pairs of H. sapiens and of 313 interacting pairs of M. musculus. The postulation behind this procedure was that orthologue proteins have alike functional natures and so is their interacting nature [37]. Henceforth, in this section, the above stated and experimentally demonstrated interaction of any one species with the Yeast dataset (with 11,188 samples in this case) was employed to predict the interactions of other ones. Then, a blind test was employed with five other species’ datasets, autonomous to the training set, using the same proposed approach. The resultant performances are shown in Table 6. The outstanding results of the proposed method using both ES1 and ES2 ascertains the significant proficiency (p < 0.05) of the CAA-PPI compared to the published works from Table 8.

Table 6.
Performance of PPI prediction on five species’ datasets taking the Yeast dataset as training (in terms of accuracy).
5.1.4. Implementation and Comparison with a Similar Approach
A similar approach was followed by [9], the only difference in the input feature of the proposed study from previous studies is that the former CT was the triad frequency in a sequence while in the proposed study this frequency was weighted by the frequency of central amino acids in a triad. Therefore, to prove the benefit of the weighted features, Table 7 shows the comparison of the CAA-PPI approach with Shen’s approach. For this implementation, the H. sapien dataset was applied to the proposed approach, same as Shen’s, and the table shows the average results of the five-fold cross-validation.

Table 7.
Implementation and comparison with a similar approach.
5.1.5. Performance Analysis of the Proposed Approach with Varied p_gram Value
With the aim to investigate the performance of the proposed approach to its hyper-parameters, CAA-PPI was ran with the p_gram value set to 2. Table 8 and Table 9 show the comparison results of the average five-fold cross-validation using ES1 and ES2 on the Yeast and H. pylori datasets with different p_gram values, respectively. It can be clearly observed that the outcomes are not satisfactory with 2_gram compared to 3_gram.

Table 8.
Performance analysis of proposed approach using ES1 and ES2 on the Yeast dataset with different p_gram values.

Table 9.
Performance analysis of proposed approach using ES1 and ES2 on the H. pylori dataset with different p_gram values.
6. Conclusions and Future Scope
With the growing number of PPI calculation methods, the codification of numerous amino acid feature vectors is also evolving. Even though considerable advancement has been achieved, further operational approaches are required to deal with different areas. This research presents an ML-based model (CAA-PPI) to predict PPI using two distinct encoding strategies. A major contribution of the given model is the novel feature generation method using the association of different amino acids with a residue in a given trigram. The CAA-based feature extraction approach is implemented with different encoding schemes followed by an RF classifier to train the model. The proposed CAA-PPI with RF classifier model’s performance was verified with two diverse PPI datasets, Yeast and H. pylori, and attained favourable outcomes with both encoding schemes. Additionally, it is worth noting that both encoding strategies were equally effective with the CAA-PPI approach to better predict new PPIs.
It is said that there is always room for improvement or change, the only challenge is to discover the same. The next step should be to discover more interacting protein pairs and generate a new set of features using the proposed approach. Moreover, CAA-PPI can be assessed using other encoding strategies and applying them to other organisms. Likewise, a new encoding scheme can be developed with the systematic categorization of amino acids. The proposed approach can also be extended to investigate the interaction of proteins with other molecules.
Author Contributions
B.M.: Software, writing—original draft preparation, investigation. G.S.: Conceptualization, methodology. S.L.: Validation, formal analysis, data curation, writing—review and editing, supervision. R.K.: Planning and direction, and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to express their deepest gratitude to the editors and referees for their invaluable suggestions which led to the betterment of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Ethics Statement
This article used already available data in the research community.
Abbreviations
| AAC | Amino Acid Contact | AC | Auto Covariance |
| ACC | Auto Cross Covariance | CAA-PPI | Connecting Amino Acids Feature-Based |
| CT | Conjoint Triad | PPI Approach | |
| DCT | Discrete Cosine Transform | DIP | Database of Interacting Proteins |
| DT | Decision Tree | E-ELM | Ensemble Extreme Learning Machine |
| ES | Encoding Strategy | FN | False Negatives |
| FP | False Positives | HKNN | K-Local Hyperplane Distance Nearest |
| HOG | Histogram of Oriented Gradient | Neighbour | |
| KNN | K-Nearest Neighbour | LCPSSMAB | Local Coding PSSM Average Bigram |
| LCPSSMBG | Local Coding PSSM Bigram Group | LCPSSMMF | Multi-Features Fusion based on Local Coding |
| LDA | Latent Dirichlet Allocation | PSSM Matrix | |
| LD | Local Descriptors | LPQ | Local Phase Quantization |
| LR | Logistic Regression | MAC | Moran Autocorrelation |
| MCD | Multi-Scale Continuous and | ML | Machine Learning |
| Discontinuous | MLD | Multi-Scale Local Descriptor | |
| MCC | Matthew’s Correlation Coefficient | NPV | Negative Predictive Value |
| PC | Principal Components | PCA | Principal Component Analysis |
| PCVM | Probabilistic Classification Vector Machine | PIR | Protein Information Resource |
| PR | Property Response | PSSM | Position-Specific Scoring Matrix |
| PSSMMF | Multi-features Fusion Based on Original | RF | Random Forest |
| Protein Sequence PSSM matrix | RNN | Recurrent Neural Networks | |
| RoF | Rotation Forest | SVD | Singular Value Decomposition |
| SD | Standard Deviation | ||
| SMR | Substitution Matrix Representation | SVM | Support Vector Machine |
| TN | True Negatives | TP | True Positives |
References
- Reeds, P.J. Dispensable and indispensable amino acids for humans. J. Nutr. 2000, 130, 1835S–1840S. [Google Scholar] [CrossRef] [PubMed]
- Maleki, M.; Vasudev, G.; Rueda, L. The role of electrostatic energy in prediction of obligate protein-protein interactions. Proteome Sci. 2013, 11, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Keskin, O.; Tuncbag, N.; Gursoy, A. Predicting protein–protein interactions from the molecular to the proteome level. Chem. Rev. 2016, 116, 4884–4909. [Google Scholar] [CrossRef] [PubMed]
- Golemis, E.; Adams, P.D. Protein-Protein Interactions: A Molecular Cloning Manual; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, Long Island, NY, USA, 2002. [Google Scholar]
- Prieto, D.A.; Johann, D.J., Jr.; Wei, B.R.; Ye, X.; Chan, K.C.; Nissley, D.V.; Simpson, R.M.; Citrin, D.E.; Mackall, C.L.; Linehan, W.M.; et al. Mass spectrometry in cancer biomarker research: A case for immunodepletion of abundant blood-derived proteins from clinical tissue specimens. Biomark. Med. 2014, 8, 269–286. [Google Scholar] [CrossRef] [PubMed]
- Rai, S.; Bhatnagar, S. Computational Methods for Prediction of Protein-Protein Interactions: PPI Prediction Methods. In Materials Science and Engineering: Concepts, Methodologies, Tools, and Applications; IGI Global: Hershey, PA, USA, 2017; pp. 309–340. [Google Scholar]
- Wang, J.; Zhang, L.; Jia, L.; Ren, Y.; Yu, G. Protein-protein interactions prediction using a novel local conjoint triad descriptor of amino acid sequences. Int. J. Mol. Sci. 2017, 18, 2373. [Google Scholar] [CrossRef] [PubMed]
- Sahni, G.; Mewara, B.; Lalwani, S.; Kumar, R. CF-PPI: Centroid based new feature extraction approach for Protein-Protein Interaction Prediction. J. Exp. Theor. Artif. Intell. 2022, 1–21. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, J.; Luo, X.; Zhu, W.; Yu, K.; Chen, K.; Li, Y.; Jiang, H. Predicting protein–protein interactions based only on sequences information. Proc. Natl. Acad. Sci. USA 2007, 104, 4337–4341. [Google Scholar] [CrossRef]
- Al-Daoud, E. Improving Protein-Protein Interaction Prediction by Using Encoding Strategies and Random Indices. Interaction 2011, 1, 2. [Google Scholar]
- Zhou, C.; Yu, H.; Ding, Y.; Guo, F.; Gong, X.J. Multi-scale encoding of amino acid sequences for predicting protein interactions using gradient boosting decision tree. PLoS ONE 2017, 12, e0181426. [Google Scholar] [CrossRef]
- ElAbd, H.; Bromberg, Y.; Hoarfrost, A.; Lenz, T.; Franke, A.; Wendorff, M. Amino acid encoding for deep learning applications. BMC Bioinform. 2020, 21, 1–14. [Google Scholar] [CrossRef]
- Le, N.; Nguyen, B. Prediction of FMN Binding Sites in Electron Transport Chains based on 2-D CNN and PSSM Profiles. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 18, 2189–2197. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Xia, J.F.; Gui, J. Prediction of protein–protein interactions from protein sequence using local descriptors. Protein Pept. Lett. 2010, 17, 1085–1090. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Yu, L.; Wen, Z.; Li, M. Using support vector machine combined with auto covariance to predict protein–protein interactions from protein sequences. Nucleic Acids Res. 2008, 36, 3025–3030. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.; Roe, D.; Faulon, J.L. Predicting protein–protein interactions using signature products. Bioinformatics 2005, 21, 218–226. [Google Scholar] [CrossRef]
- You, Z.H.; Lei, Y.K.; Zhu, L.; Xia, J.; Wang, B. Prediction of protein–protein interactions from amino acid sequences with ensemble extreme learning machines and principal component analysis. In Proceedings of the BMC Bioinformatics, Nanning, China, 28–31 July 2013; Springer: Berlin/Heidelberg, Germany, 2013; Volume 14, pp. 1–11. [Google Scholar]
- You, Z.H.; Zhu, L.; Zheng, C.H.; Yu, H.J.; Deng, S.P.; Ji, Z. Prediction of protein–protein interactions from amino acid sequences using a novel multi-scale continuous and discontinuous feature set. BMC Bioinform. 2014, 15, S9. [Google Scholar] [CrossRef]
- You, Z.H.; Chan, K.C.; Hu, P. Predicting protein–protein interactions from primary protein sequences using a novel multi-scale local feature representation scheme and the random forest. PLoS ONE 2015, 10, e0125811. [Google Scholar] [CrossRef]
- Wong, L.; You, Z.H.; Li, S.; Huang, Y.A.; Liu, G. Detection of protein–protein interactions from amino acid sequences using a rotation forest model with a novel PR-LPQ descriptor. In Proceedings of the International Conference on Intelligent Computing, Fuzhou, China, 20–23 August 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 713–720. [Google Scholar]
- Ding, Y.; Tang, J.; Guo, F. Identification of protein–protein interactions via a novel matrix-based sequence representation model with amino acid contact information. Int. J. Mol. Sci. 2016, 17, 1623. [Google Scholar] [CrossRef]
- An, J.Y.; Zhou, Y.; Zhao, Y.J.; Yan, Z.J. An efficient feature extraction technique based on local coding PSSM and multifeatures fusion for predicting protein–protein interactions. Evol. Bioinform. 2019, 15, 1176934319879920. [Google Scholar] [CrossRef]
- Chou, K.-C. Pseudo Amino Acid Composition and its Applications in Bioinformatics. Proteom. Syst. Biol. Curr. Proteom. 2009, 6, 262–274. [Google Scholar] [CrossRef]
- Xenarios, I.; Fernandez, E.; Salwinski, L.; Duan, X.J.; Thompson, M.J.; Marcotte, E.M.; Eisenberg, D. DIP: The database of interacting proteins: 2001 update. Nucleic Acids Res. 2001, 29, 239–241. [Google Scholar] [CrossRef]
- Zhou, Y.Z.; Gao, Y.; Zheng, Y.Y. Prediction of protein–protein interactions using local description of amino acid sequence. In Advances in Computer Science and Education Applications; Springer: Berlin/Heidelberg, Germany, 2011; pp. 254–262. [Google Scholar]
- Stone, M. Cross-validation and multinomial prediction. Biometrika 1974, 61, 509–515. [Google Scholar] [CrossRef]
- Hripcsak, G.; Rothschild, A.S. Agreement, the f-measure, and reliability in information retrieval. J. Am. Med. Inform. Assoc. 2005, 12, 296–298. [Google Scholar] [CrossRef]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta (BBA)-Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Bruni, V.; Cardinali, M.L.; Vitulano, D. A short review on minimum description length: An application to dimension reduction in PCA. Entropy 2022, 24, 269. [Google Scholar] [CrossRef]
- Qi, Y. Random forest for bioinformatics. In Ensemble Machine Learning: Methods and Applications; Springer: Boston, MA, USA, 2012; pp. 307–323. [Google Scholar]
- Talwar, G. Textbook of Biochemistry, Biotechnology, Allied and Molecular Medicine; PHI Learning Pvt. Ltd.: New Delhi, India, 2015. [Google Scholar]
- Huang, Y.A.; You, Z.H.; Gao, X.; Wong, L.; Wang, L. Using weighted sparse representation model combined with discrete cosine transformation to predict protein-protein interactions from protein sequence. BioMed Res. Int. 2015, 2015, 902198. [Google Scholar] [CrossRef]
- Bock, J.R.; Gough, D.A. Whole-proteome interaction mining. Bioinformatics 2003, 19, 125–134. [Google Scholar] [CrossRef]
- Nanni, L. Hyperplanes for predicting protein–protein interactions. Neurocomputing 2005, 69, 257–263. [Google Scholar] [CrossRef]
- Nanni, L.; Lumini, A. An ensemble of K-local hyperplanes for predicting protein–protein interactions. Bioinformatics 2006, 22, 1207–1210. [Google Scholar] [CrossRef]
- Liu, B.; Yi, J.; Aishwarya, S.; Lan, X.; Ma, Y.; Huang, T.H.; Leone, G.; Jin, V.X. QChIPat: A quantitative method to identify distinct binding patterns for two biological ChIP-seq samples in different experimental conditions. BMC Genom. 2013, 14, 1–11. [Google Scholar] [CrossRef]
- Shi, M.G.; Xia, J.F.; Li, X.L.; Huang, D.S. Predicting protein–protein interactions from sequence using correlation coefficient and high-quality interaction dataset. Amino Acids 2010, 38, 891–899. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).