A General Hybrid Modeling Framework for Systems Biology Applications: Combining Mechanistic Knowledge with Deep Neural Networks under the SBML Standard
Abstract
1. Introduction
2. Methods
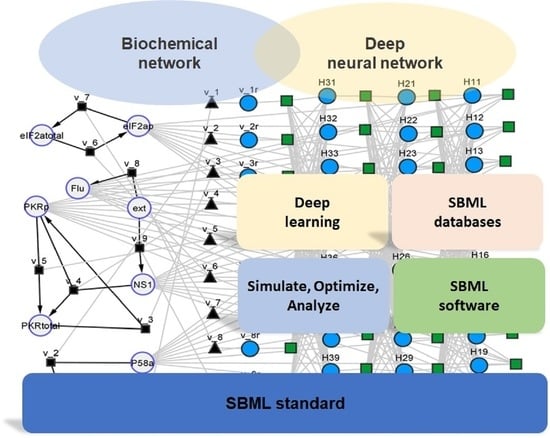
2.1. General SBML Hybrid Model
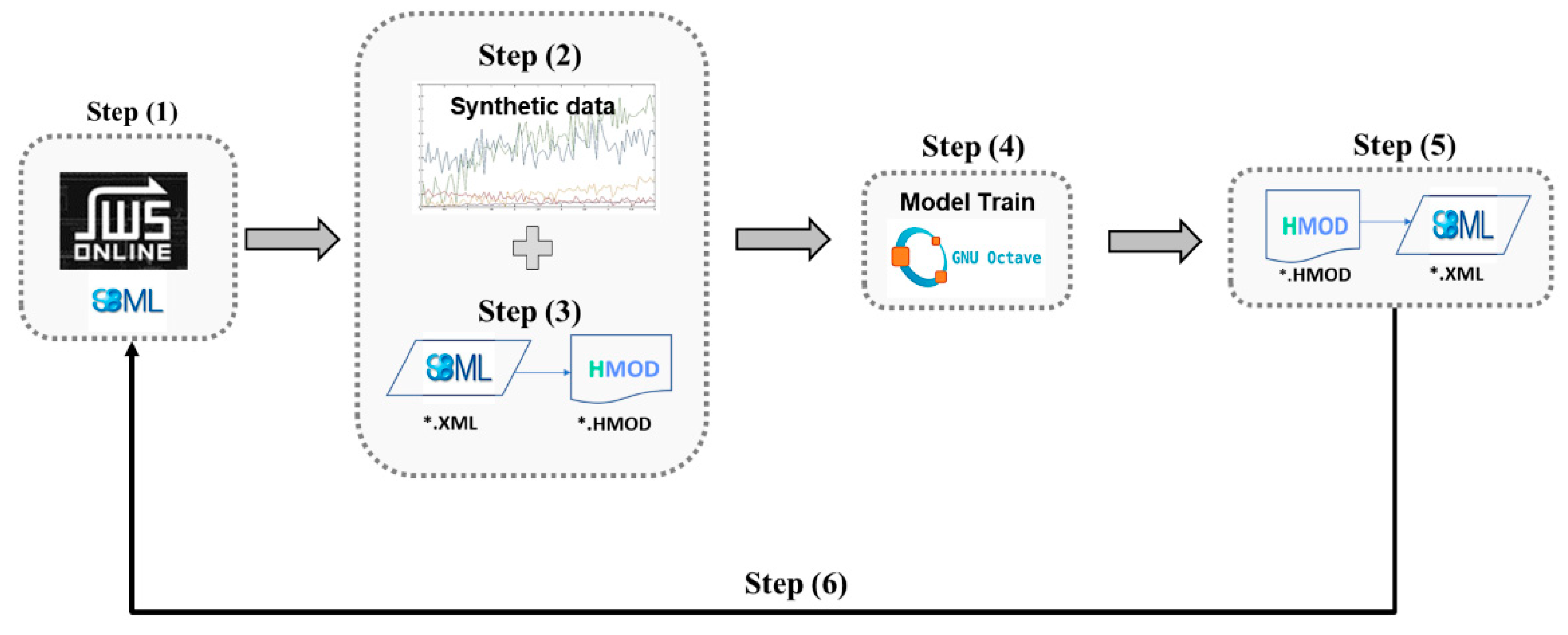
2.2. Interfacing with SBML Databases and SBML Modeling Tools
2.3. Case Studies
3. Results and Discussion
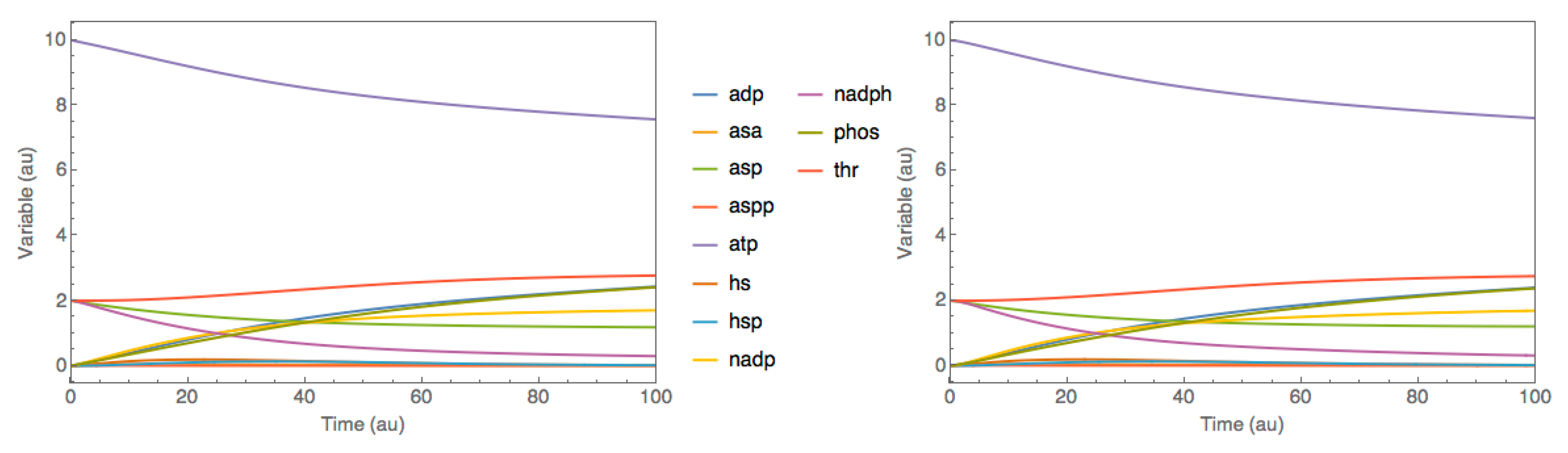
3.1. Case Study 1: Threonine Synthesis Pathway in E. coli
3.2. Case Study 2: P58IPK Signal Transduction Pathway
3.3. Case Study 3: Yeast Glycolytic Oscillations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- von Stosch, M.; Oliveira, R.; Peres, J.; de Azevedo, S.F. Hybrid semi-parametric modeling in process systems engineering: Past, present and future. Comput. Chem. Eng. 2014, 60, 86–101. [Google Scholar] [CrossRef]
- Psichogios, D.C.; Ungar, L.H. A Hybrid Neural Network-1st Principles Approach to Process Modeling. Aiche J. 1992, 38, 1499–1511. [Google Scholar] [CrossRef]
- Thompson, M.L.; Kramer, M.A. Modeling Chemical Processes Using Prior Knowledge and Neural Networks. Aiche J. 1994, 40, 1328–1340. [Google Scholar] [CrossRef]
- Schubert, J.; Simutis, R.; Dors, M.; Havlik, I.; Lubbert, A. Hybrid Modeling of Yeast Production Processes—Combination of a-Priori Knowledge on Different Levels of Sophistication. Chem. Eng. Technol. 1994, 17, 10–20. [Google Scholar] [CrossRef]
- Teixeira, A.P.; Clemente, J.J.; Cunha, A.E.; Carrondo, M.J.T.; Oliveira, R. Bioprocess iterative batch-to-batch optimization based on hybrid parametric/nonparametric models. Biotechnol. Prog. 2006, 22, 247–258. [Google Scholar] [CrossRef] [PubMed]
- Teixeira, A.P.; Alves, C.; Alves, P.M.; Carrondo, M.J.; Oliveira, R. Hybrid elementary flux analysis/nonparametric modeling: Application for bioprocess control. BMC Bioinform. 2007, 8, 30. [Google Scholar] [CrossRef] [PubMed]
- von Stosch, M.; Oliveira, R.; Peres, J.; de Azevedo, S.F. A novel identification method for hybrid (N)PLS dynamical systems with application to bioprocesses. Expert Syst. Appl. 2011, 38, 10862–10874. [Google Scholar] [CrossRef]
- Pinto, J.; de Azevedo, C.R.; Oliveira, R.; von Stosch, M. A bootstrap-aggregated hybrid semi-parametric modeling framework for bioprocess development. Bioprocess Biosyst. Eng. 2019, 42, 1853–1865. [Google Scholar] [CrossRef]
- Rajulapati, L.; Chinta, S.; Shyamala, B.; Rengaswamy, R. Integration of machine learning and first principles models. Aiche J. 2022, 68, e17715. [Google Scholar] [CrossRef]
- Glassey, J.; von Stosch, M. Hybrid Modeling in Process Industries, 1st ed.; Taylor&Francis, Ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Agharafeie, R.; Oliveira, R.; Ramos, J.; Mendes, J. Application of Hybrid Neural Models to Bioprocesses: A Systematic Literature Review. Authorea 2023. [Google Scholar] [CrossRef]
- Le, N.Q.K.; Do, D.T.; Hung, T.N.K.; Lam, L.H.T.; Huynh, T.T.; Nguyen, N.T.K. A Computational Framework Based on Ensemble Deep Neural Networks for Essential Genes Identification. Int. J. Mol. Sci. 2020, 21, 9070. [Google Scholar] [CrossRef] [PubMed]
- Le, N.Q.K. Potential of deep representative learning features to interpret the sequence information in proteomics. Proteomics 2022, 22, e2100232. [Google Scholar] [CrossRef]
- Greener, J.G.; Kandathil, S.M.; Moffat, L.; Jones, D.T. A guide to machine learning for biologists. Nat. Rev. Mol. Cell Biol. 2022, 23, 40–55. [Google Scholar] [CrossRef]
- Cuperlovic-Culf, M.; Nguyen-Tran, T.; Bennett, S.A.L. Machine Learning and Hybrid Methods for Metabolic Pathway Modeling. Methods Mol. Biol. 2023, 2553, 417–439. [Google Scholar] [CrossRef] [PubMed]
- Antonakoudis, A.; Barbosa, R.; Kotidis, P.; Kontoravdi, C. The era of big data: Genome-scale modelling meets machine learning. Comput. Struct Biotec. 2020, 18, 3287–3300. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kim, G.B.; Lee, S.Y. Machine learning applications in genome-scale metabolic modeling. Curr. Opin. Syst. Biol. 2021, 25, 42–49. [Google Scholar] [CrossRef]
- Carinhas, N.; Bernal, V.; Teixeira, A.P.; Carrondo, M.J.T.; Alves, P.M.; Oliveira, R. Hybrid metabolic flux analysis: Combining stoichiometric and statistical constraints to model the formation of complex recombinant products. BMC Syst. Biol. 2011, 5, 34. [Google Scholar] [CrossRef] [PubMed]
- Isidro, I.A.; Portela, R.M.; Clemente, J.J.; Cunha, A.E.; Oliveira, R. Hybrid metabolic flux analysis and recombinant protein prediction in Pichia pastoris X-33 cultures expressing a singlechain antibody fragment. Bioprocess Biosyst. Eng. 2016, 39, 1351–1363. [Google Scholar] [CrossRef]
- Ferreira, A.R.; Dias, J.M.L.; von Stosch, M.; Clemente, J.; Cunha, A.E.; Oliveira, R. Fast development of Pichia pastoris GS115 Mut(+) cultures employing batch-to-batch control and hybrid semi-parametric modeling. Bioprocess Biosyst. Eng. 2014, 37, 629–639. [Google Scholar] [CrossRef]
- Teixeira, A.P.; Dias, J.M.L.; Carinhas, N.; Sousa, M.; Clemente, J.J.; Cunha, A.E.; von Stosch, M.; Alves, P.M.; Carrondo, M.J.T.; Oliveira, R. Cell functional enviromics: Unravelling the function of environmental factors. BMC Syst. Biol. 2011, 5, 92. [Google Scholar] [CrossRef]
- von Stosch, M.; Peres, J.; de Azevedo, S.F.; Oliveira, R. Modelling biochemical networks with intrinsic time delays: A hybrid semi-parametric approach. BMC Syst. Biol. 2010, 4, 131. [Google Scholar] [CrossRef]
- Folch-Fortuny, A.; Marques, R.; Isidro, I.A.; Oliveira, R.; Ferrer, A. Principal elementary mode analysis (PEMA). Mol. Biosyst. 2016, 12, 737–746. [Google Scholar] [CrossRef] [PubMed]
- von Stosch, M.; Hamelink, J.M.; Oliveira, R. Hybrid modeling as a QbD/PAT tool in process development: An industrial E-coli case study. Bioprocess Biosyst. Eng. 2016, 39, 773–784. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Jayaraman, A.; Kwon, J.S. Development of a hybrid model for a partially known intracellular signaling pathway through correction term estimation and neural network modeling. PLoS Comput. Biol. 2020, 16, e1008472. [Google Scholar] [CrossRef] [PubMed]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Baskonus, H.M.; Yao, S.W.; Ilhan, E. A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells. Results Phys. 2021, 25, 104235. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Shoaib, M.; Gupta, M.; Sanchez, Y.G. A Stochastic Intelligent Computing with Neuro-Evolution Heuristics for Nonlinear SITR System of Novel COVID-19 Dynamics. Symmetry 2020, 12, 1628. [Google Scholar] [CrossRef]
- Yang, J.H.; Wright, S.N.; Hamblin, M.; McCloskey, D.; Alcantar, M.A.; Schrubbers, L.; Lopatkin, A.J.; Satish, S.; Nili, A.; Palsson, B.O.; et al. A White-Box Machine Learning Approach for Revealing Antibiotic Mechanisms of Action. Cell 2019, 177, 1649–1661.e9. [Google Scholar] [CrossRef]
- Lewis, J.E.; Kemp, M.L. Integration of machine learning and genome-scale metabolic modeling identifies multi-omics biomarkers for radiation resistance. Nat. Commun. 2021, 12, 2700. [Google Scholar] [CrossRef]
- Vijayakumar, S.; Rahman, P.K.S.M.; Angione, C. A Hybrid Flux Balance Analysis and Machine Learning Pipeline Elucidates Metabolic Adaptation in Cyanobacteria. Iscience 2020, 23, 101818. [Google Scholar] [CrossRef]
- Ramos, J.R.C.; Oliveira, G.P.; Dumas, P.; Oliveira, R. Genome-scale modeling of Chinese hamster ovary cells by hybrid semi-parametric flux balance analysis. Bioprocess Biosyst. Eng. 2022, 45, 1889–1904. [Google Scholar] [CrossRef]
- Le Novere, N.; Bornstein, B.; Broicher, A.; Courtot, M.; Donizelli, M.; Dharuri, H.; Li, L.; Sauro, H.; Schilstra, M.; Shapiro, B.; et al. BioModels Database: A free, centralized database of curated, published, quantitative kinetic models of biochemical and cellular systems. Nucleic Acids Res. 2006, 34, D689–D691. [Google Scholar] [CrossRef] [PubMed]
- Olivier, B.G.; Snoep, J.L. Web-based kinetic modelling using JWS Online. Bioinformatics 2004, 20, 2143–2144. [Google Scholar] [CrossRef] [PubMed]
- Mochao, H.; Barahona, P.; Costa, R.S. KiMoSys 2.0: An upgraded database for submitting, storing and accessing experimental data for kinetic modeling. Database J. Biol. Databases Curation 2020, 2020, baaa093. [Google Scholar] [CrossRef] [PubMed]
- Hucka, M.; Fineey, A.; Sauro, H.M.; Bolouri, H.; Doyle, J.C.; Kitano, H.; Arkin, A.P.; Bornstein, B.J.; Bray, D.; Cornish-Bowden, A.; et al. The systems biology markup language (SBML): A medium for representation and exchange of biochemical network models. Bioinformatics 2003, 19, 524–531. [Google Scholar] [CrossRef] [PubMed]
- Pinto, J.; Costa, R.S.; Alexandre, L.; Ramos, J.; Oliveira, R. SBML2HYB: A Python interface for SBML compatible hybrid modelling. Bioinformatics 2023, 39, btad044. [Google Scholar] [CrossRef] [PubMed]
- Pinto, J.; Mestre, M.; Ramos, J.; Costa, R.S.; Striedner, G.; Oliveira, R. A general deep hybrid model for bioreactor systems: Combining first principles with deep neural networks. Comput. Chem. Eng. 2022, 165, 107952. [Google Scholar] [CrossRef]
- Chassagnole, C.; Fell, D.A.; Rais, B.; Kudla, B.; Mazat, J.P. Control of the threonine-synthesis pathway in Escherichia coli: A theoretical and experimental approach. Biochem. J. 2001, 356, 433–444. [Google Scholar] [CrossRef] [PubMed]
- Goodman, A.G.; Tanner, B.C.W.; Chang, S.T.; Esteban, M.; Katze, M.G. Virus infection rapidly activates the P58(IPK) pathway, delaying peak kinase activation to enhance viral replication. Virology 2011, 417, 27–36. [Google Scholar] [CrossRef] [PubMed]
- Dano, S.; Madsen, M.F.; Schmidt, H.; Cedersund, G. Reduction of a biochemical model with preservation of its basic dynamic properties. Febs J. 2006, 273, 4862–4877. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arxiv 2014, arXiv:1412.6980. [Google Scholar]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI—A COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [PubMed]
- Konig, M.; Drager, A.; Holzhutter, H.G. CySBML: A Cytoscape plugin for SBML. Bioinformatics 2012, 28, 2402–2403. [Google Scholar] [CrossRef] [PubMed]
- Li, B.B.; Morris, J.; Martin, E.B. Model selection for partial least squares regression. Chemom. Intell. Lab. 2002, 64, 79–89. [Google Scholar] [CrossRef]
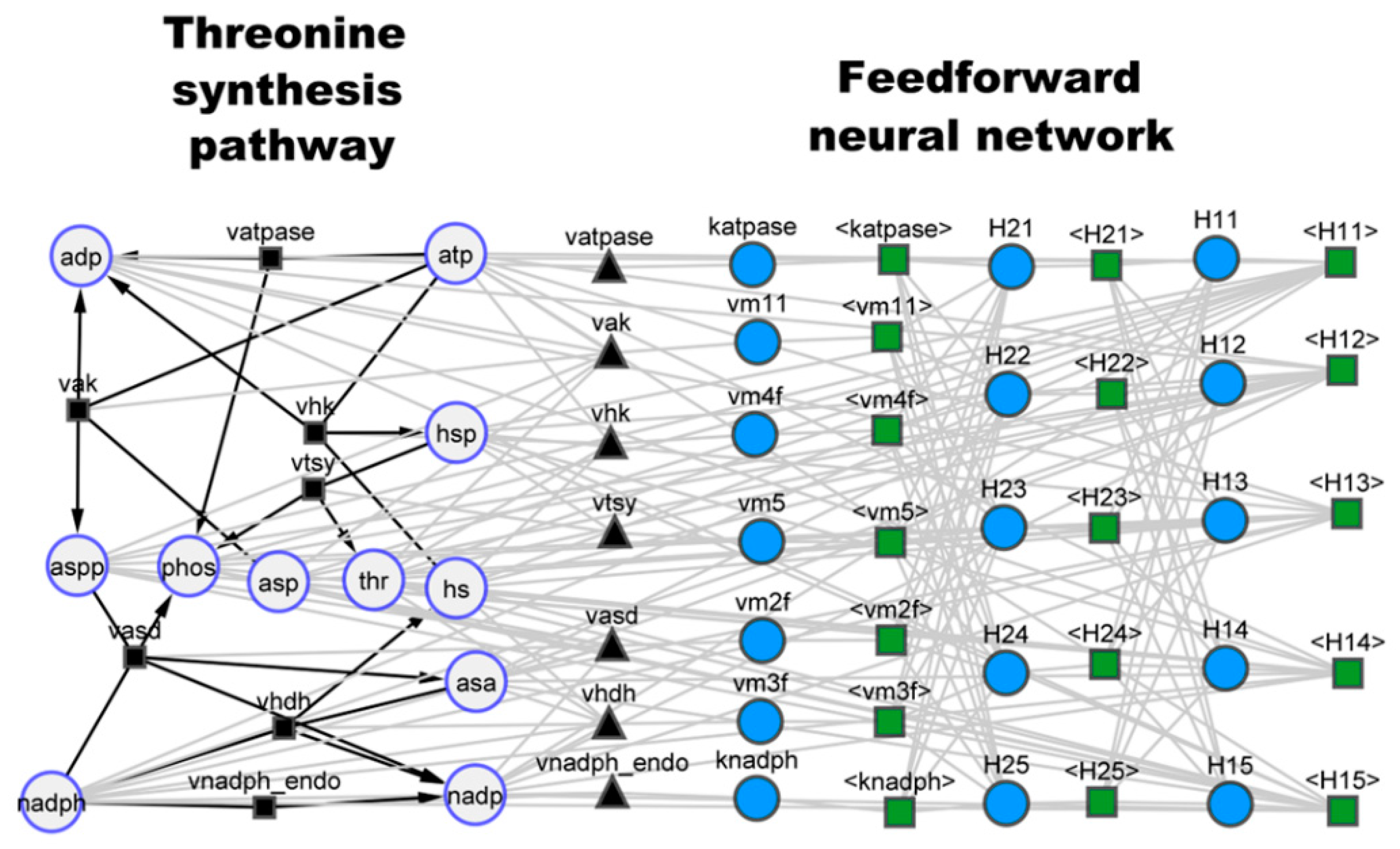




| Case Study | Number of Species | Number of Reactions | Number of Parameters | JWS Online ID | Reference |
|---|---|---|---|---|---|
| E. coli threonine synthesis pathway | 11 | 7 | 47 | chassagnole1 | [38] |
| P58IPK signal transduction pathway | 9 (4 fixed) | 9 | 10 | goodman | [39] |
| Yeast glycolytic oscillations | 7 (1 fixed) | 11 | 31 | dano1 | [40] |
| Hybrid Model | WMSE Train | WMSE Test | WMSE Test (Noise Free) | AICc | CPU Time (h:m:s) | Number of Weights |
|---|---|---|---|---|---|---|
| 11 × 5 × 5 × 7 | 1.03 | 0.99 | 0.07 | 838 | 00:31:00 | 132 |
| 11 × 10 × 10 × 7 | 1.07 | 1.00 | 0.08 | 2510 | 00:29:00 | 307 |
| 11 × 15 × 15 × 7 | 1.04 | 0.99 | 0.08 | 2102 | 00:35:00 | 532 |
| 11 × 20 × 20 × 7 | 1.03 | 0.98 | 0.07 | 2400 | 00:33:00 | 807 |
| 11 × 5 × 5 × 5 × 7 | 1.03 | 0.99 | 0.07 | 918 | 00:32:00 | 162 |
| 11 × 10 × 10 × 10 × 7 | 1.05 | 0.98 | 0.07 | 1890 | 00:40:00 | 417 |
| 11 × 15 × 15 × 15 × 7 | 1.04 | 1.01 | 0.08 | 2659 | 00:36:00 | 772 |
| 11 × 20 × 20 × 20 × 7 | 1.04 | 1.00 | 0.07 | 3684 | 00:35:00 | 1227 |
| Hybrid Model | WMSE Train | WMSE Test | WMSE Test (Noise Free) | AICc | CPU Time (h:m:s) | Number of Weights |
|---|---|---|---|---|---|---|
| 5 × 5 × 5 × 9 | 1.60 | 1.51 | 0.54 | 1916 | 00:12:10 | 114 |
| 5 × 10 × 10 × 9 | 1.59 | 1.48 | 0.53 | 2181 | 00:11:54 | 269 |
| 5 × 15 × 15 × 9 | 1.61 | 1.50 | 0.56 | 2810 | 00:15:15 | 474 |
| 5 × 20 × 20 × 9 | 1.58 | 1.49 | 0.51 | 3480 | 00:20:48 | 729 |
| 5 × 5 × 5 × 5 × 9 | 1.45 | 1.50 | 0.48 | 1890 | 00:13:15 | 144 |
| 5 × 10 × 10 × 10 × 9 | 1.23 | 1.28 | 0.12 | 1430 | 00:16:10 | 379 |
| 5 × 15 × 15 × 15 × 9 | 1.35 | 1.36 | 0.31 | 2140 | 00:19:30 | 714 |
| 5 × 20 × 20 × 20 × 9 | 1.34 | 1.40 | 0.36 | 4150 | 00:27:12 | 1149 |
| Hybrid Model | WMSE Train | WMSE Test | WMSE Test (Noise Free) | AICc | CPU Time (h:m:s) | Number of Weights |
|---|---|---|---|---|---|---|
| 7 × 5 × 5 × 11 | 20.12 | 21.05 | 20.14 | 5730 | 01:05:00 | 136 |
| 7 × 10 × 10 × 11 | 1.87 | 1.99 | 1.67 | 3818 | 01:20:00 | 311 |
| 7 × 15 × 15 × 11 | 1.74 | 1.78 | 1.56 | 4120 | 01:15:00 | 536 |
| 7 × 20 × 20 × 11 | 1.16 | 1.43 | 0.98 | 2740 | 01:24:00 | 811 |
| 7 × 5 × 5 × 5 × 11 | 5.33 | 5.84 | 5.14 | 3930 | 01:33:00 | 166 |
| 7 × 10 × 10 × 10 × 11 | 0.93 | 0.94 | 0.11 | −41 | 01:31:00 | 421 |
| 7 × 15 × 15 × 15 × 11 | 0.98 | 0.97 | 0.21 | 784 | 01:20:00 | 776 |
| 7 × 20 × 20 × 20 × 11 | 0.97 | 0.97 | 0.17 | 2213 | 01:40:00 | 1231 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinto, J.; Ramos, J.R.C.; Costa, R.S.; Oliveira, R. A General Hybrid Modeling Framework for Systems Biology Applications: Combining Mechanistic Knowledge with Deep Neural Networks under the SBML Standard. AI 2023, 4, 303-318. https://doi.org/10.3390/ai4010014
Pinto J, Ramos JRC, Costa RS, Oliveira R. A General Hybrid Modeling Framework for Systems Biology Applications: Combining Mechanistic Knowledge with Deep Neural Networks under the SBML Standard. AI. 2023; 4(1):303-318. https://doi.org/10.3390/ai4010014
Chicago/Turabian StylePinto, José, João R. C. Ramos, Rafael S. Costa, and Rui Oliveira. 2023. "A General Hybrid Modeling Framework for Systems Biology Applications: Combining Mechanistic Knowledge with Deep Neural Networks under the SBML Standard" AI 4, no. 1: 303-318. https://doi.org/10.3390/ai4010014
APA StylePinto, J., Ramos, J. R. C., Costa, R. S., & Oliveira, R. (2023). A General Hybrid Modeling Framework for Systems Biology Applications: Combining Mechanistic Knowledge with Deep Neural Networks under the SBML Standard. AI, 4(1), 303-318. https://doi.org/10.3390/ai4010014